Как по координатам найти вектор: Как найти координаты вектора? Ответ на webmath.ru

Нахождение координат вектора через координаты точек. Как найти вектор по двум точкам

Отложим от начала координат единичные векторы, то есть векторы, длины которых равны единице. Направление вектора i→ должно совпадать с осью Ox, а направление вектора j→ с осью Oy.

Определение 1

Векторы i→ и j→ называют координатными векторами.

Координатные векторы неколлинеарны. Поэтому любой вектор p→ можно разложить по векторам p→=xi→+yj→. Коэффициенты x и y определяются единственным образом. Коэффициенты разложения вектора p→ по координатным векторам называются координатами вектора p→ в данной системе координат.

Координаты вектора записываются в фигурных скобках p→x; y. На рисунке вектор OA→ имеет координаты 2; 1, а вектор b→ имеет координаты 3;-2. Нулевой вектор представляется в виде 0→0; 0.

Если векторы a→ и b→ равны, то и y1=y2. Запишем это так: a→=x1i→+y1j→=b→=x2i→+y2j→, значит x1=x2, y1=y2 .

Таким образом, координаты равных векторов соответственно равны.

Если точка координат не совпадает с его началом системы координат, тогда рассмотрим задачу. Пусть в декартовой системе координат на Oxy заданы координаты точек начала и конца AB→: Axa, ya, Bxb, yb. Найти координаты заданного вектора.

Изобразим координатную ось.

Из формулы сложения векторов имеем OA→+AB→=OB→, где O – начало координат. Отсюда следует, что AB→=OB→-OA→.

OA→ и OB→ – это радиус-векторы заданных точек А и В, значит координаты точек имеют значения OA→=xa, ya, OB→=xb, yb.

По правилу операций над векторами найдем AB→=OB→-OA→=xb-xa, yb-ya.

Нахождение в трехмерном пространстве проходит по такому же принципу, только для трех точек.

Для нахождения координат вектора, необходимо найти разность его точек конца и начала.

Пример 1

Найти координаты OA→ и AB→ при значении координат точек A(2,-3), B(-4,-1).

Решение

Для начала определяется радиус-вектор точки A. OA→=(2,-3).

Чтобы найти AB→, нужно вычесть значение координат точек начала из координат точек конца.

Получаем: AB→=(-4-2,-1-(-3))=(-6, 2).

Ответ: OA→=(2,-3), AB→=(-6,-2).

Пример 2

Задано трехмерное пространство с точкой A=(3, 5, 7), AB→=(2, 0,-2). Найти координаты конца AB→.

Решение

Подставляем координаты точки A: AB→=(xb-3, yb-5, zb-7).

По условию известно, что AB→=(2, 0,-2).

Известно, что равенство векторов справедливо тогда, когда координаты равны соответственно. Составим систему уравнений: xb-3=2yb-5=0zb-7=-2

Отсюда следует, что координаты точки B AB→равны: xb=5yb=5zb=5 

Ответ:  B(5, 5, 5).

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Координаты вектора / Метод координат / Справочник по геометрии 7-9 класс

1. Главная
2. Справочники
3. Справочник по геометрии 7-9 класс
4. Метод координат
5. Координаты вектора

Прямоугольная система координат (декаротова система координат) — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Для задания прямоугольной системы координат нужно провести две взаимно перпендикулярные прямые, на каждой из них выбрать направление (оно обозначается стрелкой) и выбрать единицу измерения отрезков.

На рисунке выше оси и перпендикулярны. При выбранной единице измерения отрезков длина каждого отрезка выражается положительным числом. В дальнейшем под длиной отрезка мы будем понимать это число. Так,

единичный вектор — это вектор, длина которого равна 1.

Отложим от начала координат О единичные векторы и так, чтобы их направления совпадали с направлениями осей и соответственно.

Векторы и называют координатными векторами.

Координатные векторы не коллинеарны, поэтому любой вектор можно разложить по координатным векторам, т.е. представить в виде , причем коэффициенты разложения и определяются единственным образом. Коэффициенты разложения вектора по координатным векторам называются координатами вектора

в данной системе координат.

Координаты вектора записывают в фигурных скобках после обозначения вектора: .

На рисунке выше .

Нулевой вектор можно представить в виде , следовательно, его координаты равны нулю: .

Если векторы и равны, то и . Значит, координаты равных векторов соответственно равны.

Правила, позволяющие по координатам векторов находить координаты их суммы, разности и произведения вектора на число:

10. Каждая координата суммы двух и более векторов равна сумме соответствующих координат этих векторов.

Доказательство

Дано: , , .

Доказать: .

Доказательство:

По условию и , тогда и .

Сложим последние два равенства и применим свойства сложения векторов и умножения вектора на число, получим: , следовательно, координаты вектора равны , т.е. .

Что и требовалось доказать.

20. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.

Доказательство

Дано: , , .

Доказать: .

Доказательство:

По условию и , тогда (1)  и .  (2) 

Вычтем из равенства (1) равенство (2) и применим свойства сложения векторов и умножения вектора на число, получим: , следовательно, координаты вектора равны , т.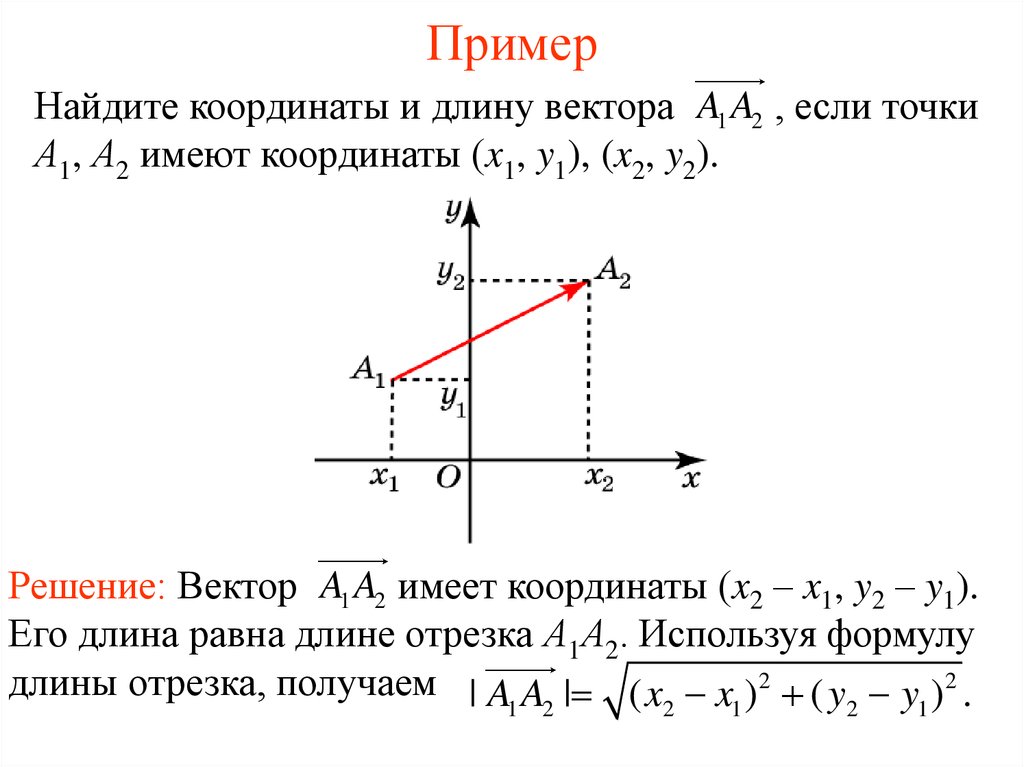 е. . Что и требовалось доказать.

30. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.

Доказательство

Дано: , — число, .

Доказать: .

Доказательство:

По условию , значит, .

Умножим последнее равенство на число и используя свойства умножения вектора на число, получим: , следовательно, координаты вектора равны , т.е. . Что и требовалось доказать.

Данные правила позволяют определить координаты любого вектора, представленного в виде алгебраической суммы данных векторов с известными координатами.

Пример

Найти координаты вектора , если известно, что .

Решение:

По правилу 3⁰ вектор будет иметь координаты , т.е. , вектор координаты , т. е. .

Так как , то координаты вектора можно найти по правилу 1⁰

: , т.е. .

Ответ: .

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Разложение вектора по двум неколлинеарным векторам

Связь между координатами вектора его начала и конца

Простейшие задачи в координатах

Уравнение линии на плоскости

Уравнение окружности

Уравнение прямой

Взаимное расположение двух окружностей

Метод координат

Правило встречается в следующих упражнениях:

7 класс

Задание 922, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 931, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 934, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 951, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 953, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 956, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 957, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 5, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 17, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1006, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

---

математика — Как найти относительный угол от одного вектора координат GPS к другому?

Задать вопрос

спросил

2 года 10 месяцев назад

Изменено 2 года, 10 месяцев назад

Просмотрено 343 раза

Я извлек набор из трех координат и хочу найти относительные углы между их двумя векторами.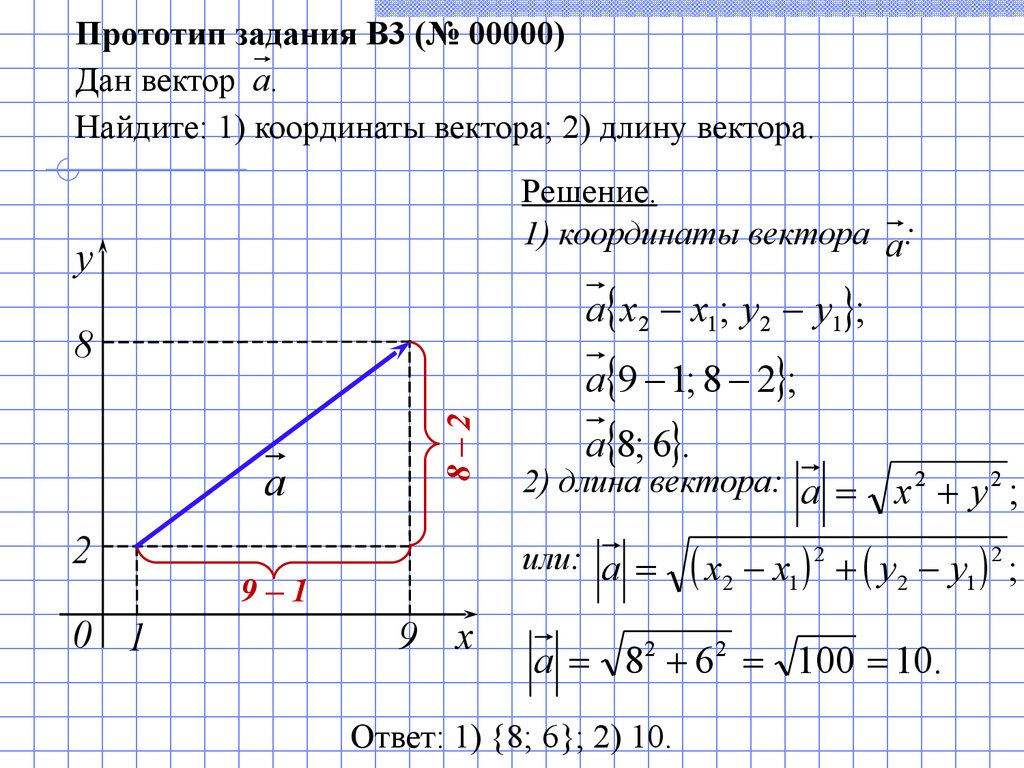

• P1: 57.3112, 25.24871
• С1: 57.31105, 25.24875
• Т1: 57.31086, 25.24803

Например: V1 = C1 - P1 , V2 = T1 - C1 , а затем получить угол от V1 до V2 .

Но я боюсь, что декартовы функции здесь не помогут, потому что в реальном приложении координаты могут охватывать разные широты и долготы.

Я искал в Google, но функции, которые я видел, меня не убеждают. Я также попробовал некоторые из них в своем приложении, но возвращенные углы не дали ожидаемых результатов.

Для этих трех точек, выведя визуально, я ожидаю, что угол будет где-то в районе 120-140 градусов.

У меня ограниченные познания в географических вычислениях, и я не в курсе.

Как рассчитать угол?

• математика
• угол
• гео

Используя формулы с этой страницы, рассчитайте пеленги (азимуты) от средней точки к первой и к третьей.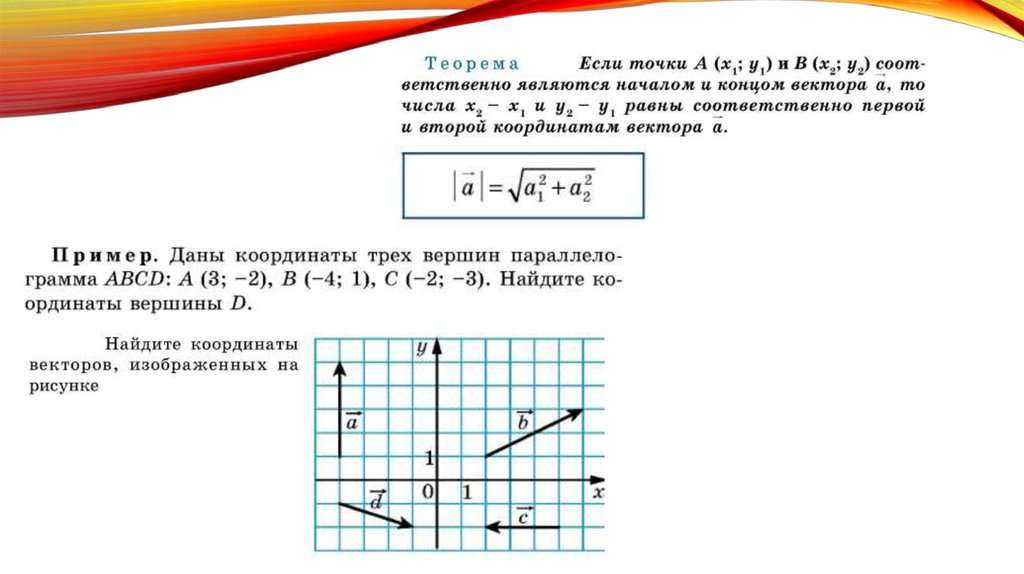

 θ = atan2( sin Δλ ⋅ cos φ2 , cos φ1 ⋅ sin φ2 − sin φ1 ⋅ cos φ2 ⋅ cos Δλ )
где φ1,λ1 — начальная точка, φ2,λ2 — конечная точка (Δλ — разница долготы)
 

Подчеркну, что для «угла поворота» пеленги должны рассчитываться от точки поворота — потому что для дуг А-В пеленги будут различаться начальной и конечной точками (за исключением особых случаев, таких как меридианы или параллельные дуги). На следующей картинке направление v отличается от направления u (кратчайший путь на сфере — так называемая «дуга большого круга»)

Имея два пеленга, можно получить их разность, чтобы узнать нужный угол (не не забудьте обработать переход через 360 градусов)

---

Есть еще метод из сферической тригонометрии — теорема сферического косинуса (здесь часть перестановки), но он требует найти длины дуг для всех сторон треугольника (можно найти по первой ссылке — но больше вычислений)

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Прямоугольная система координат

Последующее обсуждение ограничено векторами в двумерной координатной плоскости, хотя концепции могут быть расширены и на более высокие измерения.

Если вектор сдвинут так, что его начальная точка находится в начале прямоугольной координатной плоскости, говорят, что он находится в стандартной позиции . Если вектор равен вектору и имеет начальную точку в начале координат, говорят, что он является стандартным вектором для . Другие названия стандартного вектора включают радиус-вектор и вектор положения (рис. 1).

Рисунок 1 
              Векторы, нарисованные на плоскости.

Вектор — это стандартный вектор для всех векторов на плоскости с тем же направлением и величиной, что и . Чтобы найти стандартный вектор для геометрического вектора в координатной плоскости, необходимо найти только координаты точки P , потому что точка 0 находится в начале координат. Если координаты точки A равны ( x _a , y _a ) and the coordinates of point B are ( x _b , y _b ), then the coordinates of point P are ( x _b − x _a , y _ab − y _a ).

Пример 1: Если конечные точки вектора имеют координаты A (−2, −7) и B (3, 2), то каковы координаты точки P , которая является стандартным вектором и = (см. рис. 2)?

Рисунок 2 
              Чертеж для примера 1.

Если координаты точки P равны ( x , y ),

Алгебраический вектор представляет собой упорядоченную пару действительных чисел. Алгебраический вектор, соответствующий стандартному геометрическому вектору, обозначается как ⟨ a, b ⟩, если конечная точка P имеет координаты (a, b) . Числа a и b называются компонентами вектора ⟨ a, b ⟩ (см. рисунок 3 ).

         

Рисунок 3 
              Компоненты вектора.

Если a, b, c и d — все действительные числа такие, что a = c и b = d , то вектор v 13 ⩽ a , вектора u = ⟨ c, d ⟩ считаются равными. То есть алгебраические векторы с равными соответствующими компонентами равны. Если обе компоненты вектора равны нулю, говорят, что вектор является нулевой вектор . Величина вектора v = ⟨a, b⟩ равна .

Пример 2: Какова величина вектора u = ⟨3, −5⟩?

Сложение векторов определяется как сложение соответствующих компонентов векторов, то есть если v = ⟨ a, b ⟩ и u = ⟨c, d ⟩ , то v + 2 = 2 ⟨а + в, б + d⟩ (рис. 4 ).

Рисунок 4 
              Добавление вектора.

Скалярное умножение определяется как умножение каждого компонента на константу, то есть, если v = ⟨a, b⟩ и q является константой, то q v = q ⟨a, q⟨ б⟩ = ⟨qa, qb⟩ .

Пример 3: Если v = ⟨8, −2⟩ и w = ⟨3, 7⟩, то найти 5 v −2 w .

Единичный вектор — это вектор, величина которого равна 1. Единичный вектор v с тем же направлением, что и ненулевой вектор u , можно найти следующим образом:

Пример 4 : Найдите единичный вектор v с тем же направлением, что и вектор u , учитывая, что u = ⟨7, − 1⟩.

Два специальных единичных вектора, i = ⟨1, 0⟩ и j = ⟨0, 1⟩, можно использовать для выражения любого вектора v = ⟨a, b⟩ .

Пример 5: Запишите u = ⟨5, 3⟩ с точки зрения единичных векторов i и j (рис. 5).

Рисунок 5 
             Чертеж для примера 5.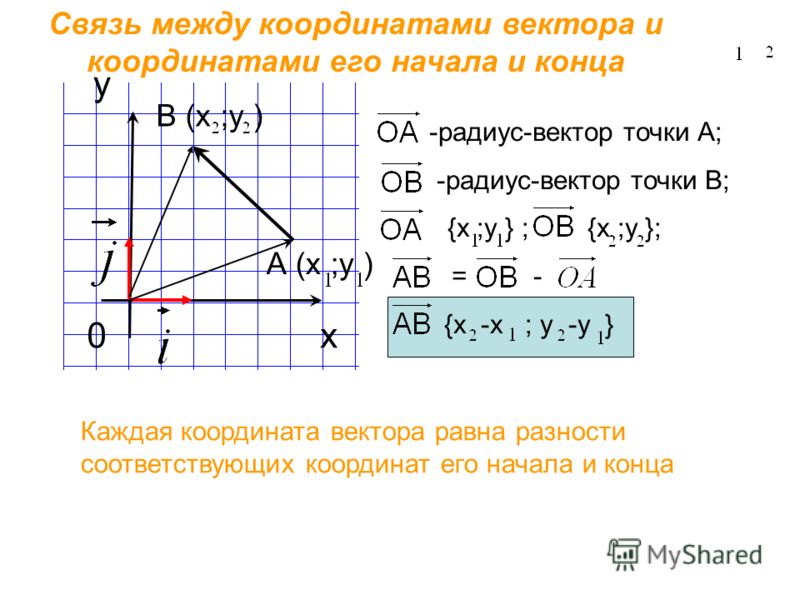

Векторы обладают алгебраическими свойствами, аналогичными свойствам действительных чисел (таблица 1).

Пример 6: Найдите 4 u + 5 v , если u = 7 i − 3 j и v = −2 1 2 i

+

Учитывая два вектора, U = ⟨A, B⟩ = A I + B J и V = ⟨C, D⟩ = C

111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111,

2 11111111111111111. d j , скалярное произведение , записанное как u · v , является скалярной величиной u ˙ v = ac + bd . Если u, v и w — векторы, а q — действительное число, то скалярные произведения обладают следующими свойствами:

Последнее свойство, u ˙ v = | и | | против | cos α можно использовать для нахождения угла между двумя ненулевыми векторами u и v . Если два вектора перпендикулярны друг другу и образуют 90 °, они называются ортогональными . Поскольку cos 90° = 0, скалярное произведение любых двух ортогональных векторов равно 0,

.

Пример 7: Учитывая, что u = ⟨ 5 , −3⟩ и v = ⟨6, 10⟩, покажите, что u и v ортогональны, показав, что 1u06 скалярное произведение и v равно нулю.

Пример 8: Чему равен угол между u = ⟨5, −2⟩ и v = ⟨6, 11⟩?

Говорят, что объект находится в состоянии статического равновесия , если сумма всех векторов сил, действующих на объект, равна нулю.

Пример 9: Канатоходец весом 150 фунтов стоит ближе к одному концу веревки, чем к другому. Веревка меньшей длины отклоняется от горизонтали на 5°. Более длинная веревка отклоняется на 3°. Чему равно натяжение каждой части веревки?

Нарисуйте диаграмму силы со всеми тремя векторами силы в стандартном положении (рис.

No related posts.