Как найти длину окружности если её радиус равен 36 см
Статьи › Находится › Длина окружности как находится
Длина окружности находтся по формуле L = 2 * пи * r. Где число пи = 3,14 (округленное до сотых), r — радиус окружности. Тогда вместо радуса подставим данные значения и найдем длину каждой окружности. Если r = 36 сантиметров, то L = 2 * пи * 36 = 2 * 3,14 * 36 = 6,28 * 36 = 226,08 сантиметров.
- Как узнать длину окружности если есть радиус
- Как можно вычислить длину окружности
- Как найти диаметр окружности по радиусу
- Как найти длину окружности если радиус равен 3 5 см
- Чему равна длина окружности радиус которой равен 5 см
- Чему равна длина окружности радиус которой равен 4 см
- Как узнать длину окружности по его диаметру
- Как найти длину окружности радиус которой равен 12 см
- Чему равна длина окружности круга
- Как найти диаметр окружности 5 класс
- Чему равна длина окружности диаметр которой равен 8 см
- Как найти диаметр не зная радиус
- Как найти длину окружности если радиус равен 3 см
- Чему равна длина окружности радиус которой равен 7 см
- Как вычислить длину окружности радиус которой равен 7 5 см
- Как найти длину дуги если известен радиус
- Как найти длину окружности если её радиус равен 4 5 см
- Как вычислить длину окружности радиуса R
- Чему равна длина окружности если ее диаметр равен 50 см
- Как найти площадь окружности по радиусу
- Как высчитать длину окружности калькулятор
- Как найти диаметр окружности если радиус 9 см
- Как найти диаметр окружности с радиусом 3 см
- Чему равен диаметр круга
- Какой диаметр у окружности 12 см
- Чему равен радиус окружности если ее диаметр равен 16 см
- Чему равна длина окружности если ее радиус равен 1 54 м
Как узнать длину окружности если есть радиус
Формула для вычисления длины окружности через радиус: C = 2πr, где C — длина окружности, r — радиус окружности. То есть длина окружности равна удвоенному произведению радиуса на пи (π примерно равно 3,14).
То есть длина окружности равна удвоенному произведению радиуса на пи (π примерно равно 3,14).
Как можно вычислить длину окружности
Мы имеем формулу для вычисления длины окружности, если известен диаметр: C = π ⋅ d. Если вспомним, что d = 2 r, то формула длины окружности будет выглядеть так: C = 2 π ⋅ r.
Как найти диаметр окружности по радиусу
Общая формула.
Исходя из основных определений нам известно, что значение диаметра равно двум радиусам: D = 2 × R, где D — диаметр, R — радиус.
Как найти длину окружности если радиус равен 3 5 см
Формула: L=2×пи(3,14)×R. L (или D, везде по разному) — это длина окружности, R — это радиус. L(D) =2×пи(3,14)×R= 2 ×пи(3,14) × 3,5 =21,98 сантиметров.
Чему равна длина окружности радиус которой равен 5 см
Итак, длина окружности с заданным радиусом R = 5 см равна 31,4 см.
Чему равна длина окружности радиус которой равен 4 см
L = 25,12 см. Ответ: Длинна окружности с радиусом 4 см, составит 25,12 см.
Как узнать длину окружности по его диаметру
Просто умножьте диаметр на число пи.1. Как найти длину окружности через диаметр:
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- d —диаметр окружности.
Как найти длину окружности радиус которой равен 12 см
1. Длина окружности радиусом 12 cм. равна: 2 * 3,1 * 12 = 74,4 сантиметра.
Чему равна длина окружности круга
Длина окружности обозначается через \(C\), диаметр и радиус \(D = 2R\), значит, C = π ⋅ D, или C = 2 π ⋅ R. Так как длина всей окружности равна C = 2 π ⋅ R, то длина дуги в \(1°\) равна 2 π R 360 ° = π R 180 °.
Как найти диаметр окружности 5 класс
Длина диаметра равна длине двух радиусов \(D = 2R\). Точки на окружности делят окружность на части, которые называются дугами, а точки — концами этих дуг.
Чему равна длина окружности диаметр которой равен 8 см
R = D ÷ 2, где R — радиус окружности, D — диаметр. R = 8 ÷ 2 = 4 см.
R = 8 ÷ 2 = 4 см.
Как найти диаметр не зная радиус
Если вам известна длина окружности, то, для того чтобы вычислить диаметр, следует разделить ее на π(пи).
Как найти длину окружности если радиус равен 3 см
С=2π*3=6π — длина окружности. Значит правильный ответ В.
Чему равна длина окружности радиус которой равен 7 см
Для нахождения длины окружности есть своя формула: C = 2пR, где R — это радиус данной окружности, число п = 3,14. Подставим в формулу известные значения и вычислим: C = 2 * 3,14 * 7 = 43,96 (см).
Как вычислить длину окружности радиус которой равен 7 5 см
При радиусе 7,5 см длина окружности составит: С = 2 * 3,14 * 7,5 = 47,1 (см).
Как найти длину дуги если известен радиус
Длина дуги в n градусов находится по формуле p=πrn/180, где p — длина дуги, r -радиус окружности, n — величина угла соответствующей дуги.
Как найти длину окружности если её радиус равен 4 5 см
Вычислим длину окружности, зная, что её радиус равен 4,5 см: P = 2 * 3,14 * 4,5 = 28,26 см. Ответ: длина заданной окружности равна 28,26 см.
Ответ: длина заданной окружности равна 28,26 см.
Как вычислить длину окружности радиуса R
Таким образом, для длины окружности C радиуса R можем записать следующую формулу: C = 2πR. Теорема. Отношение длин двух окружностей равно отношению их радиусов.
Чему равна длина окружности если ее диаметр равен 50 см
L = 2 * 3,14 * 50 = 314 см.
Как найти площадь окружности по радиусу
Площадь круга через радиус
S = π × r2, где r — это радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.
Как высчитать длину окружности калькулятор
P=2πr, где P — длина окружности; π — константа, которая всегда равна 3,14; r — радиус окружности, длину которой необходимо найти.
Как найти диаметр окружности если радиус 9 см
Давайте найдем диаметр окружности, если известно, что центр окружности находится в начале системы координат (0) и в положительном направлении она пересекает ось OX в точке 9, то есть радиус окружности равен 9 см. Для вычисления диаметра применим формулу: D = 2R = 2 * 9 см = 18 см диаметр окружности.
Для вычисления диаметра применим формулу: D = 2R = 2 * 9 см = 18 см диаметр окружности.
Как найти диаметр окружности с радиусом 3 см
D = 2 * r = r + 3см; 2 * r — r = 3см; r = 3см. Теперь найдём диаметр окружности. d = 2 * r = 2 * 3см = 6см. Задача решена.
Чему равен диаметр круга
Греч. διάμετρος — поперечник) — отрезок, соединяющий две точки на окружности и проходящий через центр окружности, а также длина этого отрезка. Диаметр равен двум радиусам.
Какой диаметр у окружности 12 см
L = П * d, где П — постоянное число, равное 3.14; d — диаметр окружности. 2) Найдем длину окружности, диаметр которой равен 12см: l = 3.14 * 12 = 37.68см.
Чему равен радиус окружности если ее диаметр равен 16 см
Известно, что радиус окружности равен половине ее диаметра (D): R = D / 2. Узнаем радиус окружности, если ее диаметр равен 16 см: R = 16 / 2 = 8 см.
Чему равна длина окружности если ее радиус равен 1 54 м
Ответ: 9,68 м.
Длина окружности и ее площадь .
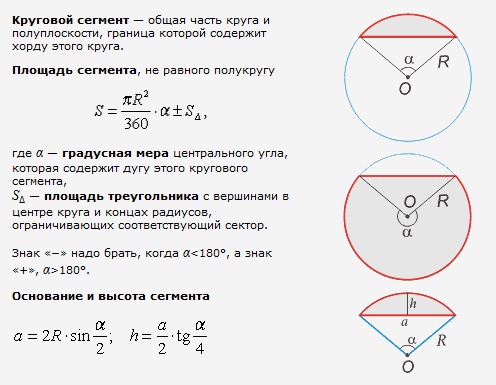 Магия математики [Как найти x и зачем это нужно]
Магия математики [Как найти x и зачем это нужно]Диаметр окружности – это величина D, обозначающая расстояние между двумя максимально удаленными друг от друга точками окружности и определяющаяся как его удвоенный радиус. То есть
Периметр окружности (то есть расстояние, пройденное по кругу от некой точки до нее же) называется ее, окружности, длиной (или периферией) и обозначается буквой C. На рисунке хорошо видно, что C длиннее, чем 2D, потому что идти по полукругу от точки P к точке Q придется явно дольше, чем напрямик по D, равно как и обратный путь от точки Q к точке P по другому полукругу займет больше времени. Следовательно, C > 2D. А раз уж мы заметили это, почему бы нам не заметить, что C даже немного длиннее, чем 3
На самом деле для того, чтобы сопоставить длину окружности с ее диаметром, нам нужно «распрямить» круг, измерить получившуюся линию, а потом разделить результат на диаметр. И вы с удивлением обнаружите, что, независимо от того, измеряете вы монетку, дно стакана, тарелку или гимнастический круг, у вас всегда получится
И вы с удивлением обнаружите, что, независимо от того, измеряете вы монетку, дно стакана, тарелку или гимнастический круг, у вас всегда получится
C/D ? 3,14
Число ? определяется как постоянная величина, представляющая собой соотношение длины круга к его диаметру. То есть
? = C/D
И ? остается неизменным для абсолютно любой окружности! Если хотите, можете преобразовать эту формулу для подсчета длины окружности: зная диаметр D или радиус r той или иной окружности, вы можете просто посчитать
C = ?D
или
C = 2?r
Цифровое выражение ? начинается с
? = 3,14159…
Чуть позже мы узнаем, что идет дальше, после 9, а заодно обсудим некоторые свойства этого числа.
Отступление
Определить длину окружности «на глазок» не так-то легко. Испытайте себя – возьмите высокий стакан и постарайтесь прикинуть, что больше: его высота или длина окружности? Уверен, большинство проголосует за высоту… и почти наверняка вы окажетесь неправы: чаще всего больше будет именно длина окружности. Не верите? Проверить достаточно легко: просто измерьте большим и указательным пальцами диаметр стакана и трижды отложите этот отрезок вдоль его стенки.
Теперь можно смело отвечать на первый из двух вопросов, заданных в начале главы. Если мы представим экватор в виде идеального круга с длиной окружности, равной 40 075 км, его радиус составит
Но значение радиуса не так уж для нас и важно – куда важнее знать, насколько увеличится этот радиус, если к длине окружности прибавится три метра – совсем ненамного, примерно на 3/2? ? 0,5 метра. Следовательно, под веревкой окажется достаточно места, чтобы проползти, но недостаточно, чтобы пройти в полный рост (если, конечно, вы не танцор лимбо[21]).
Но самым удивительным здесь будет не столько сам ответ, сколько тот факт, что полученные нами 0,5 м ни капельки не зависят от изначальной длины окружности – вы придете к тому же результату независимо от того, обвязываете ли вы веревкой Землю, Юпитер, Плутон или теннисный мячик. Например, радиус круга с длиной окружности, равной 15 м, составит 15/(2?) ? 2,38. Прибавив 3 метра, получим новый радиус 18/(2?) ? ? 2,86, который будет больше старого примерно на 0,5 метра.
Отступление
А вот еще один очень важный факт из геометрии окружностей.
Теорема: Предположим, что точки X и Y лежат на окружности строго друг напротив друга. Тогда при любом положении третьей точки P ?XPY = 90°.
На рисунке, например, хорошо видно, что углы ?XAY, ?XBY и ?XCY являются прямыми.
Доказательство: Проведем линию радиуса из точки O к точке P. Положим ?XPO = x, а ?YPO = y. Наша цель – показать, что
Положим ?XPO = x, а ?YPO = y. Наша цель – показать, что
Так как отрезки OX и OP суть радиусы окружности, их длина равна r, следовательно, треугольник XPO будет равнобедренным. Согласно теореме о равнобедренных треугольниках, ?OXP = ?XPO = x. По той же логике отрезок OY является радиусом, а ?OYP = ?YPO = y. Поскольку сумма углов треугольника XYP должна быть равна 180°, получаем 2x + 2y = 180°, а значит, x + y = 90°, что и требовалось доказать.?
Теорема эта является частным случаем другой, самой любимой моей во всей геометрии теоремы о центральном угле, которой посвящено следующее «Отступление».
Отступление
Ответ на второй вопрос нашей мини-викторины может дать теорема о центральном угле. Возьмем две случайные точки X и Y, расположенные на окружности.
Например, если ?XOY = 100°, тогда при любом положении P на большей дуге, проходящей от X к Y, ?XPY = 50°, а при любом положении Q на меньшей дуге, проходящей от X к Y, ?XQY = 130°.
Зная длину окружности, мы можем вывести очень важную формулу – формулу вычисления ее площади.
Теорема: Площадь круга с радиусом r
Вы наверняка помните эту формулу со школы. Что ж, тем больше удовольствия вы получите, узнав, наконец, из чего она вытекает. Конечно, правильнее всего было бы использовать метод вычислений, но пока вполне можно удовлетвориться и другим, не менее эффективным, доказательством.
Конечно, правильнее всего было бы использовать метод вычислений, но пока вполне можно удовлетвориться и другим, не менее эффективным, доказательством.
Доказательство 1: Представьте себе круг как совокупность концентрически расходящихся колец, как это показано на рисунке. Сделайте в нем прорезь от верхнего края к центру, а затем «разогните» кольца, чтобы они сложились в фигуру, напоминающую треугольник. Чему будет равна площадь этой фигуры?
Надеюсь, вы не забыли, что площадь треугольника с основанием b и высотой h составляет Основание получившейся у нас фигуры равно 2?r (длине окружности), а его высота – r (расстоянию от центра окружности до его нижнего края). Так как наш «очищенный» круг становится тем более треугольным, чем больше мы добавляем к нему колец, его площадь составляет
что и требовалось доказать.?
Теорема эта настолько прекрасна, что просто невозможно устоять и не доказать ее еще раз. Только если в предыдущем случае мы чистили луковицу, теперь будем разрезать пиццу.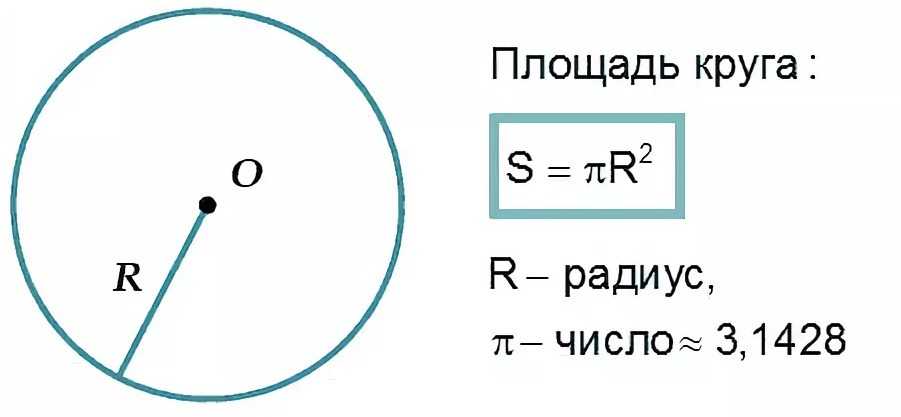
Доказательство 2: Разделите круг на четное количество равных секторов-«кусочков». Возьмите «кусочек» из верхней половинки и положите рядом с «кусочком» из нижней половинки, как показано на рисунках (в наших примерах мы разрезали «пиццу» сначала на 8, а потом – на 16 частей). Разложите так весь круг. С увеличением количества секторов форма каждого из них будет все больше и больше напоминать треугольник с высотой r. Чередование нижних секторов (назовем их «сталагмитами») с верхними («сталактитами») дает нам фигуру, по форме очень близкую к прямоугольнику, с шириной, равной
прямоугольной с увеличением количества этих секторов, площадь окружности составит
bh = (?r)(r) = ?r?
как мы и предполагали. ?
?
А еще можно взять окружность и представить ее на плоскости в виде графика.
Для круга с радиусом r и центральной точкой, расположенной в координатах (0, 0) работает формула
x? + y? = r?
что хорошо видно по графику чуть ниже. Чтобы в этом разобраться, возьмем некую лежащую на окружности точку с координатами (x, y). Опустим из нее до оси x перпендикулярную этой оси линию – получится прямоугольный треугольник с катетами x и y и гипотенузой r. Тогда, согласно теореме Пифагора, x? + y? = r?.
Круг с r = 1 называется единичным. Если мы «растянем» такой круг по горизонтали с коэффициентом a и по вертикали с коэффициентом b, получится эллипс (или овал) вроде этого:
Подобная фигура имеет формулу
и площадь ?ab, что вполне логично, потому что площадь изначального единичного круга равняется ?, после чего мы растянули ее на ab. Обратите внимание, что при a = b = r мы получим круг (а не эллипс) с радиусом r – ?ab же, таким образом, превратится в ?r?.
Обратите внимание, что при a = b = r мы получим круг (а не эллипс) с радиусом r – ?ab же, таким образом, превратится в ?r?.
Существует несколько забавных фактов, связанных с эллипсами, которыми я хотел бы с вами поделиться. Например, вы можете нарисовать овал с помощью двух канцелярских кнопок, лески и карандаша.
Возьмите кнопки, воткните их в лист бумаги или картона и накиньте на них колечко из лески или прочной нитки (но до предела не натягивайте). Поставьте карандаш кончиком в центр получившейся конструкции и оттяните один из концов лески так, чтобы получился треугольник. А теперь постепенно передвигайте карандаш по бумаге вокруг кнопок, не ослабляя леску. Диаграмма, получившаяся в результате, будет иметь эллиптическую форму.
Местоположения кнопок называются фокусами эллипса, и они, конечно же, тоже волшебные. Если вместо кнопки в точку одного фокуса положить бильярдный шар и ударить по нему так, чтобы он покатился в случайном направлении, то после всего лишь одного касания о периметр он обязательно пройдет через точку второго фокуса.
Кстати, космические тела, вроде планет и комет, путешествуют вокруг солнца именно по эллиптической орбите. Естественно, я не смог удержаться:
И даже у затмения
Овальное строение!
Отступление
А вот вам еще один очень интересный факт – не существует такой формулы, которая позволила бы просчитать длину эллипса. Зато есть некое приближенное представление, придуманное математическим гением по имени Сриниваса Рамануджан[22] и позволяющее оценить эту длину хотя бы примерно:
?(3a + 3b – ?((3a + b)(3b + a)))
Обратите внимание, что при a = b = r выражение упрощается до (6r – ?(16r?)) = 2?r – длины окружности.
Число ? появляется и в трехмерных фигурах. Возьмем для примера консервную банку, которая для любого математика является цилиндром. Так вот, объем цилиндра (то есть его внутреннее пространство) с радиусом r и высотой h составит
Vцилиндра = ?r?h
Объяснить эту формулу можно, представив цилиндр как совокупность окружностей, расположенных одна на другой так, чтобы образовалась стопка высотой h (представьте себе стопку подносов в ресторане и поймете, что я имею в виду).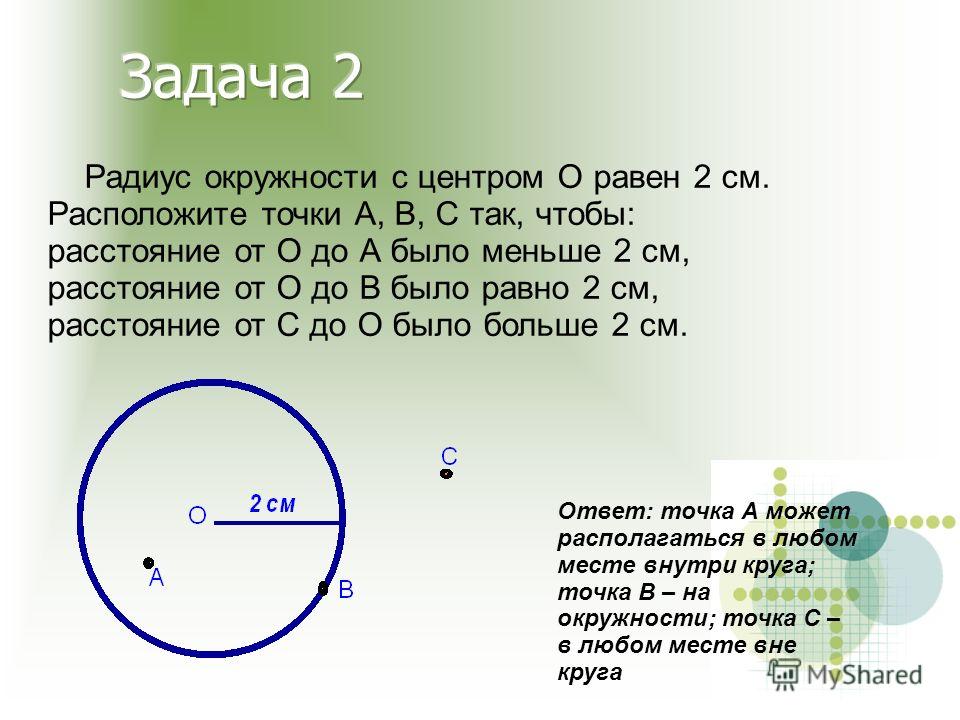
А чему будет равна площадь поверхности цилиндра? Иными словами, сколько краски нам понадобится, чтобы покрасить все его внешние стороны, включая «крышку» и «донышко»? Держать ответ в памяти нет никакой необходимости – его можно получить в любой момент, условно разделив цилиндр на три части. Площади «крышки» и «донышка» будут равны ?r?. Значит, их общий вклад в площадь поверхности цилиндра составит 2?r?. Чтобы узнать площадь третьей части, разрежем оставшийся «тубус» вдоль от верха до низа и разогнем его. У нас получится прямоугольник с шириной h и длиной 2?r (которая берется из длины прилегающей окружности). Его площадь будет равна 2?rh, что позволяет нам «собрать» формулу общей площади цилиндра:
Aцилиндра = 2?r? + 2?rh
Сфера есть трехмерный объект, в котором все наружные точки равноудалены от центра. Чему будет равен объем сферы с радиусом r? Начнем с того, что такого размера объект войдет в цилиндр, имеющий радиус r и высоту 2r, следовательно, его объем будет меньше ?r?(2r) = 2?r?. По случайному стечению обстоятельств (надежно подкрепленному скрупулезными вычислениями) сфера займет ровно две трети этого пространства. Другими словами,
Чему будет равен объем сферы с радиусом r? Начнем с того, что такого размера объект войдет в цилиндр, имеющий радиус r и высоту 2r, следовательно, его объем будет меньше ?r?(2r) = 2?r?. По случайному стечению обстоятельств (надежно подкрепленному скрупулезными вычислениями) сфера займет ровно две трети этого пространства. Другими словами,
Формула для нахождения площади поверхности сферы выглядит еще проще, хотя путь к ней куда более тернист:
Aсферы = 4?r?
Давайте завершим раздел примерами, где у ? появляется вкус мороженого и пиццы. Представьте себе рожок мороженого (также известный как конусовидный стаканчик) с высотой h и радиусом верхней окружности r. Длину образующей конуса – линии, проведенной от его кончика к любой точке верхней окружности – обозначим буквой s (самый простой способ ее вычислить – теорема Пифагора, потому что h? + r? = s?).
Конус этот легко уместится в цилиндр радиусом r и высотой h, поэтому неудивительно, что его объем будет меньше ?r?h. Зато удивительно (и при этом очевидно без всяких вычислений) то, что меньше он будет ровно в 3 раза. Другими словами,
И хотя вычисления здесь и в самом деле совершенно не нужны, отказать себе в удовольствии, которое дарит нам эта красота и простота, совершенно невозможно: площадь поверхности конуса равна
Aконуса = ?rs
Ну, и наконец, пицца, имеющая радиус z и толщину a, как видно на рисунке. Каков будет ее объем?
Это лакомство – не что иное, как необычной формы цилиндр (радиус z, высота a), объем которого равен
V = ?z?a
Немного переделаем эту формулу – уверен, у вас слюнки потекут:
V = pi z z a
| 1 | Найти том | сфера (5) | | |
| 2 | Найти площадь | круг (5) | | |
| 3 | Найдите площадь поверхности | сфера (5) | | |
| 4 | Найти площадь | круг (7) | | |
| 5 | Найти площадь | круг (2) | | |
| 6 | Найти площадь | круг (4) | | |
| 7 | Найти площадь | круг (6) | | |
| 8 | Найти том | сфера (4) | | |
| 9 | Найти площадь | круг (3) | | |
| 10 9(1/2) | ||||
| 11 | Найти простую факторизацию | 741 | ||
| 12 | Найти том | сфера (3) | | |
| 13 | Оценить | 3 квадратный корень из 8*3 квадратный корень из 10 | ||
| 14 | Найти площадь | круг (10) | | |
| 15 | Найти площадь | круг (8) | | |
| 16 | Найдите площадь поверхности | сфера (6) | | |
| 17 | Найти простую факторизацию | 1162 | ||
| 18 | Найти площадь | круг (1) | | |
| 19 | Найдите окружность | круг (5) | | |
| 20 | Найти том | сфера (2) | | |
| 21 | Найти том | сфера (6) | | |
| 22 | Найдите площадь поверхности | сфера (4) | | |
| 23 | Найти том | сфера (7) | | |
| 24 | Оценить | квадратный корень из -121 | ||
| 25 | Найти простую факторизацию | 513 | ||
| 26 | Оценка | квадратный корень из 3/16* квадратный корень из 3/9 | ||
| 27 | Найти том | коробка (2)(2)(2) | | |
| 28 | Найдите окружность | круг (6) | | |
| 29 | Найдите окружность | круг (3) | | |
| 30 | Найдите площадь поверхности | сфера (2) | | |
| 31 | Оценить | 2 1/2÷22000000 | ||
| 32 | Найдите Том | коробка (5)(5)(5) | | |
| 33 | Найти том | коробка (10)(10)(10) | | |
| 34 | Найдите окружность | круг (4) | | |
| 35 | Преобразование в проценты | 1,7 | ||
| 36 | Оценить | (5/6)÷(4/1) | ||
| 37 | Оценить | 3/5+3/5 | ||
| 38 | Оценить | ф(-2) | 92 | |
| 40 | Найти площадь | круг (12) | | |
| 41 | Найти том | коробка (3)(3)(3) | | |
| 42 | Найти том | коробка (4)(4)(4) | 92-4*-1+2||
| 45 | Найти простую факторизацию | 228 | ||
| 46 | Оценить | 0+0 | ||
| 47 | Найти площадь | круг (9) | | |
| 48 | Найдите окружность | круг (8) | | |
| 49 | Найдите окружность | круг (7) | | |
| 50 | Найти том | сфера (10) | | |
| 51 | Найдите площадь поверхности | сфера (10) | | |
| 52 | Найдите площадь поверхности | сфера (7) | | |
| 53 | Определить, является простым или составным | 5 | ||
| 60 | Преобразование в упрощенную дробь | 2 1/4 | ||
| 61 | Найдите площадь поверхности | сфера (12) | | |
| 62 | Найти том | сфера (1) | | |
| 63 | Найдите окружность | круг (2) | | |
| 64 | Найти том | коробка (12)(12)(12) | | |
| 65 | Добавить | 2+2= | ||
| 66 | Найдите площадь поверхности | коробка (3)(3)(3) | | |
| 67 | Оценить | корень пятой степени из 6* корень шестой из 7 | ||
| 68 | Оценить | 7/40+17/50 | ||
| 69 | Найти простую факторизацию | 1617 | ||
| 70 | Оценить | 27-(квадратный корень из 89)/32 | ||
| 71 | Оценить | 9÷4 | ||
| 72 | Оценка 92 | |||
| 74 | Оценить | 1-(1-15/16) | ||
| 75 | Преобразование в упрощенную дробь | 8 | ||
| 76 | Оценка | 656-521 | 9-2 | |
| 79 | Оценить | 4-(6)/-5 | ||
| 80 | Оценить | 3-3*6+2 | ||
| 81 | Найдите площадь поверхности | коробка (5)(5)(5) | | |
| 82 | Найдите площадь поверхности | сфера (8) | | |
| 83 | Найти площадь | круг (14) | | |
| 84 | Преобразование в десятичное число | 5 ноября | ||
| 85 9-2 | ||||
| 88 | Оценить | 1/2*3*9 | ||
| 89 | Оценить | 4/4-17/-4 | ||
| 90 | Оценить | 11. 02+17.19 02+17.19 | ||
| 91 | Оценить | 3/5+3/10 | ||
| 92 | Оценить | 4/5*3/8 | ||
| 93 | Оценить | 6/(2(2+1)) | ||
| 94 | Упростить | квадратный корень из 144 | ||
| 95 | Преобразование в упрощенную дробь | 725% | ||
| 96 | Преобразование в упрощенную дробь | 6 1/4 | ||
| 97 | Оценить | 7/10-2/5 | ||
| 98 | Оценить | 6÷3 | ||
| 99 | Оценить | 5+4 | ||
| 100 | Оценить | квадратный корень из 12- квадратный корень из 192 |
какова длина окружности радиусом 3 см?
Вот ответ на вопросы типа: как найти периметр круга радиусом 3 см?
Калькулятор окружности
| ||||||||||||
Длина окружности с радиусом 3 равна 18,85 (*) | ||||||||||||
| ||||||||||||
| ||||||||||||
Используйте приведенный выше калькулятор длины окружности, чтобы найти периметр окружности по ее радиусу или другим параметрам.
Формула для вычисления длины окружности
Вот три способа нахождения длины окружности или периметра круга:
Формула длины окружности через радиус
C = 2·π·r
Формула длины окружности через диаметр
C = π·d
Формула длины окружности через площадь
C = √4·π·A
Вопросы, на которые может ответить этот калькулятор:
- Как найти периметр круга с радиусом 3 см?
- Круг имеет диаметр 6 см.



