Как понять четная или нечетная функция: Чётные и нечётные функции — урок. Алгебра, 9 класс.

ГДЗ Четная или нечетная функция? Алимов Алгебра 10-11 класс Упр 704 параграф 39 – Рамблер/класс

ГДЗ Четная или нечетная функция? Алимов Алгебра 10-11 класс Упр 704 параграф 39 – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Прив! Подсказывайте!
Требуется определить, является ли данная функция чётной или нечётной:

5) у = 3cos х;
6) у = х | sin х | sin3 х
 

ответы

Из интереса порылась в решебнике. ..вот что нашла:

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

ЕГЭ

9 класс

11 класс

Химия

похожие вопросы 5

Алгебра. 9 класс. Алимов Ш. А. Параграф 9. Упражнение №116. Провсти доказательство

Даровчики. Помощь нужна с алгеброй…никак решить не могу(((
Доказать, что —
(Подробнее…)

ГДЗАлгебраАлимов Ш.А.Школа9 класс

Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308

 Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее…)

ГДЗ11 классКолмогоров А.Н.Алгебра

Почему сейчас школьники такие агрессивные ?

Читали новость про 10 классника который растрелял ? как вы к этому относитесь 

Новости10 классБезопасность

ГДЗ Тема 21 Физика 7-9 класс А. В.Перышкин Задание №475 В обоих случаях поплавок плавает. В какую жидкость он погружается глубже?

Привет. Выручайте с ответом по физике…
Поплавок со свинцовым грузилом внизу опускают
сначала в воду, потом в масло. В обоих (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.

Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

Как проверить функцию на четность. Как определять четные и нечетные функции

Которые в той или иной степени были вам знакомы. Там же было замечено, что запас свойств функций будет постепенно пополняться. О двух новых свойствах и пойдет речь в настоящем параграфе.

Определение 1.

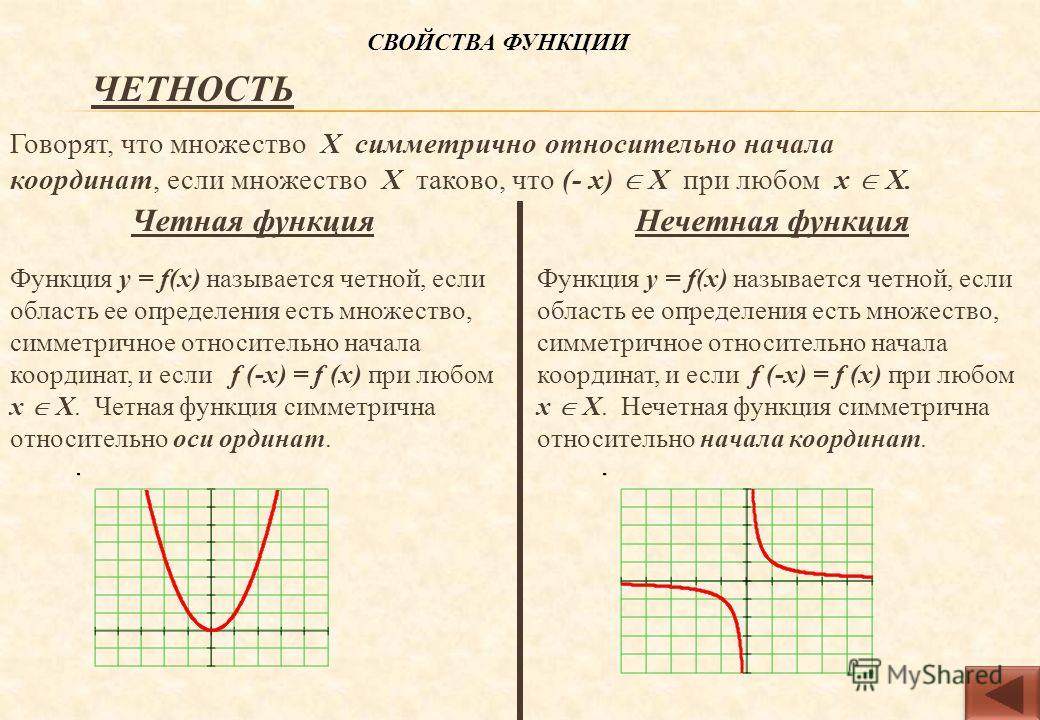
Функцию у = f(x), х є Х, называют четной, если для любого значения х из множества X выполняется равенство f (-х) = f (х).

Определение 2.

Функцию у = f(x), х є X, называют нечетной, если для любого значения х из множества X выполняется равенство f (-х) = -f (х).

Доказать, что у = х 4 — четная функция.

Решение. Имеем: f(х) = х 4 , f(-х) = (-х) 4 . Но (-х) 4 = х 4 . Значит, для любого х выполняется равенство f(-х) = f(х), т.е. функция является четной.

Аналогично можно доказать, что функции у — х 2 ,у = х 6 ,у — х 8 являются четными.

Доказать, что у = х 3 ~ нечетная функция.

Решение. Имеем: f(х) = х 3 , f(-х) = (-х) 3 . Но (-х) 3 = -х 3 . Значит, для любого х выполняется равенство f (-х) = -f (х), т.е. функция является нечетной.

Аналогично можно доказать, что функции у = х, у = х 5 , у = х 7 являются нечетными.

Мы с вами не раз уже убеждались в том, что новые термины в математике чаще всего имеют «земное» происхождение, т.е. их можно каким-то образом объяснить. Так обстоит дело и с четными, и с нечетными функциями. Смотрите: у — х 3 , у = х 5 , у = х 7 — нечетные функции, тогда как у = х 2 , у = х 4 , у = х 6 — четные функции. И вообще для любой функции вида у = х» (ниже мы специально займемся изучением этих функций), где n — натуральное число , можно сделать вывод: если n — нечетное число, то функция у = х» — нечетная; если же n — четное число, то функция у = хn — четная.

Существуют и функции, не являющиеся ни четными, ни нечетными. Такова, например, функция у = 2х + 3. В самом деле, f(1) = 5, а f (-1) = 1. Как видите, здесь Значит, не может выполняться ни тождество f(-х) = f (х), ни тождество f(-х) = -f(х).

Итак, функция может быть четной, нечетной, а также ни той ни другой.

Изучение вопроса о том, является ли заданная функция четной или нечетной, обычно называют исследованием функции на четность.

В определениях 1 и 2 речь идет о значениях функции в точках х и -х. Тем самым предполагается, что функция определена и в точке х, и в точке -х. Это значит, что точка -х принадлежит области определения функции одновременно с точкой х. Если числовое множество X вместе с каждым своим элементом х содержит и противоположный элемент -х, то X называют симметричным множеством.

2\,1 \end{cases} \quad\Leftrightarrow\quad \begin{cases} x=0\\ \mathrm{tg}\,(\cos x)=\mathrm{tg}\,1 \end{cases}\quad\Leftrightarrow\quad x=0\] Следовательно, значение \(a=-\mathrm{tg}\,1\) нам подходит.

Ответ:

\(a\in \{-\mathrm{tg}\,1;0\}\)

Задание 2 #3923

Уровень задания: Равен ЕГЭ

Найдите все значения параметра \(a\) , при каждом из которых график функции \

симметричен относительно начала координат.

Если график функции симметричен относительно начала координат, то такая функция является нечетной, то есть выполнено \(f(-x)=-f(x)\) для любого \(x\) из области определения функции. Таким образом, требуется найти те значения параметра, при которых выполнено \(f(-x)=-f(x).\)

\[\begin{aligned} &3\mathrm{tg}\,\left(-\dfrac{ax}5\right)+2\sin \dfrac{8\pi a+3x}4= -\left(3\mathrm{tg}\,\left(\dfrac{ax}5\right)+2\sin \dfrac{8\pi a-3x}4\right)\quad \Rightarrow\quad -3\mathrm{tg}\,\dfrac{ax}5+2\sin \dfrac{8\pi a+3x}4= -\left(3\mathrm{tg}\,\left(\dfrac{ax}5\right)+2\sin \dfrac{8\pi a-3x}4\right) \quad \Rightarrow\\ \Rightarrow\quad &\sin \dfrac{8\pi a+3x}4+\sin \dfrac{8\pi a-3x}4=0 \quad \Rightarrow \quad2\sin \dfrac12\left(\dfrac{8\pi a+3x}4+\dfrac{8\pi a-3x}4\right)\cdot \cos \dfrac12 \left(\dfrac{8\pi a+3x}4-\dfrac{8\pi a-3x}4\right)=0 \quad \Rightarrow\quad \sin (2\pi a)\cdot \cos \frac34 x=0 \end{aligned}\]

Последнее уравнение должно быть выполнено для всех \(x\) из области определения \(f(x)\) , следовательно, \(\sin(2\pi a)=0 \Rightarrow a=\dfrac n2, n\in\mathbb{Z}\) . 2\) .

1) Пусть \(a>0\) . Тогда график функции \(f(x)\) будет выглядеть следующим образом:

Тогда для того, чтобы уравнение имело 4 решения, нужно, чтобы график \(g(x)=|a+2|\cdot \sqrtx\) проходил через точку \(A\) :

Следовательно, \[\dfrac{64}9a=|a+2|\cdot \sqrt8 \quad\Leftrightarrow\quad \left[\begin{gathered}\begin{aligned} &9(a+2)=32a\\ &9(a+2)=-32a \end{aligned} \end{gathered}\right. \quad\Leftrightarrow\quad \left[\begin{gathered}\begin{aligned} &a=\dfrac{18}{23}\\ &a=-\dfrac{18}{41} \end{aligned} \end{gathered}\right.\] Так как \(a>0\) , то подходит \(a=\dfrac{18}{23}\) .

2) Пусть \(a

Нужно, чтобы график \(g(x)\) прошел через точку \(B\) : \[\dfrac{64}9a=|a+2|\cdot \sqrt{-8} \quad\Leftrightarrow\quad \left[\begin{gathered}\begin{aligned} &a=\dfrac{18}{23}\\ &a=-\dfrac{18}{41} \end{aligned} \end{gathered}\right.\] Так как \(a

3) Случай, когда \(a=0\) , не подходит, так как тогда \(f(x)=0\) при всех \(x\) , \(g(x)=2\sqrtx\) и уравнение будет иметь только 1 корень. {\log_{\sqrt2} t_1}\) , то первое уравнение совокупности перепишется в виде \ Как мы уже говорили, любое кубическое уравнение имеет не более трех решений, следовательно, каждое уравнение из совокупности будет иметь не более трех решений. А значит и вся совокупность будет иметь не более шести решений.

Значит, чтобы исходное уравнение имело шесть решений, квадратное уравнение \((*)\) должно иметь два различных решения, а каждое полученное кубическое уравнение (из совокупности) должно иметь три различных решения (причем ни одно решение одного уравнения не должно совпадать с каким-либо решением второго!)
Очевидно, что если квадратное уравнение \((*)\) будет иметь одно решение, то мы никак не получим шесть решений у исходного уравнения.

Таким образом, план решения становится ясен. Давайте по пунктам выпишем условия, которые должны выполняться.

1) Чтобы уравнение \((*)\) имело два различных решения, его дискриминант должен быть положительным: \

2) Также нужно, чтобы оба корня были положительными (так как \(t>0\) ). 2+2}\cdot \ln 2\cdot 2x\) . Ноль производной: \(x=0\) . При \(x0\) , при \(x>0\) : \(g» Функция \(f(x)\) при \(x>0\) является возрастающей, а при \(x Действительно, при \(x>0\) первый модуль раскроется положительно (\(|x|=x\) ), следовательно, вне зависимости от того, как раскроется второй модуль, \(f(x)\) будет равно \(kx+A\) , где \(A\) – выражение от \(a\) , а \(k\) равно либо \(13-10=3\) , либо \(13+10=23\) . При \(x Найдем значение \(f\) в точке минимума: \

Для того, чтобы уравнение имело хотя бы одно решение, нужно, чтобы графики функций \(f\) и \(g\) имели хотя бы одну точку пересечения. Следовательно, нужно: \ Решая данную совокупность систем, получим ответ: \\]

Ответ:

\(a\in \{-2\}\cup\)

Для этого воспользуйтесь миллиметровкой или графическим калькулятором. Выберите несколько любых числовых значений независимой переменной x {\displaystyle x} и подставьте их в функцию, чтобы вычислить значения зависимой переменной y {\displaystyle y} .

{2}+1} мы получили следующие координаты точек:

• (1,3) и (-1,3)
• (2,9) и (-2,9)

Обратите внимание, что при x=1 и x=-1 зависимая переменная у=3, а при x=2 и x=-2 зависимая переменная у=9. Таким образом, функция четная. На самом деле, чтобы точно выяснить вид функции, нужно рассмотреть более двух точек, но описанный способ является хорошим приближением.

Проверьте, симметричен ли график функции относительно начала координат. Начало координат – это точка с координатами (0,0). Симметрия относительно начала координат означает, что положительному значению y {\displaystyle y} (при положительном значении x {\displaystyle x} ) соответствует отрицательное значение y {\displaystyle y} (при отрицательном значении x {\displaystyle x} ), и наоборот. Нечетные функции обладают симметрией относительно начала координат.

• Если в функцию подставить несколько положительных и соответствующих отрицательных значений x {\displaystyle x} , значения y {\displaystyle y} будут различаться по знаку. {2}} . Будучи записанной в такой форме, функция кажется четной, потому что присутствует четный показатель степени. Но этот пример доказывает, что вид функции нельзя быстро определить, если независимая переменная заключена в скобки. В этом случае нужно раскрыть скобки и проанализировать полученные показатели степени.

Четные и нечетные полиномы

Цели обучения

• Понимать свойства четных и нечетных функций.

• Алгебраически докажите, является ли полиномиальная функция четной, нечетной или ни той, ни другой.

Краткий план урока

Первый опыт:

Симметрия представляет интерес даже для самых ранних цивилизаций с важными приложениями в области науки и природы, искусства, музыки, литературы, архитектуры и конечно, математика. Сегодня мы погрузимся в значение четных и нечетных функций, замечая закономерности на графиках, делая предположения и формируя обобщения. Студентов просят заметить особенности на графике и соединить их с упорядоченными парами в таблице. Затем их просят разработать собственный метод алгебраической проверки, является ли данная функция четной или нечетной. Соединение нескольких представлений — ключевой аспект этого урока! Последний вопрос предназначен для развлечения, и на него можно ответить разными способами. Попросите учащихся объяснить, почему лицо Энн Хэтэуэй четное или нечетное. Предложите учащимся использовать доказательства из упорядоченных пар на фотографии. Поскольку ни одно лицо не является идеально симметричным, учащиеся могут по-разному судить о том, является ли ее лицо «ровным» или нет, основываясь на строгом математическом определении.

​

Контрольные вопросы:

• Все ли квадратичные уравнения имеют симметрию по оси Y?

• Сколько точек вам потребуется, чтобы убедиться, что функция обладает симметрией по оси Y (если вы не видели ее график)?

• Может ли граф проходить через (-4, 8) и (4,-8) и не иметь симметрии начала координат?

• Как вы думаете, как мы называем функцию с симметрией по оси X?

Формализация Позже:

Этот урок предоставляет прекрасную возможность связать идеи из геометрии о преобразованиях. В большинстве курсов по геометрии рассматриваются упорядоченные парные правила для различных преобразований, таких как (x, y) → (-x, y) для отражения по оси y. Попросите учащихся подумать, почему симметрия начала координат совпадает с симметрией вращения на 180°, что связано с правилом упорядоченной пары (x, y) → (-x, -y). Еще одна связь заключается в том, что исходная симметрия представляет собой функцию, которая отражается по оси Y И оси X (опять же, привязка к правилам упорядоченных пар).

​

Студентам интересно задать вопрос, почему нет слова для функции с симметрией по оси x. Учащиеся должны прийти к выводу, что такой «функции» не существует, поскольку отношение с симметрией оси X по определению не является функцией.

​

Некоторые неверные представления о четных и нечетных функциях появляются, когда учащиеся делают вывод, что все функции с четной степенью четные, а все функции с нечетной степенью нечетные. Мы анализируем некоторые из этих утверждений в вопросах «Проверьте свое понимание».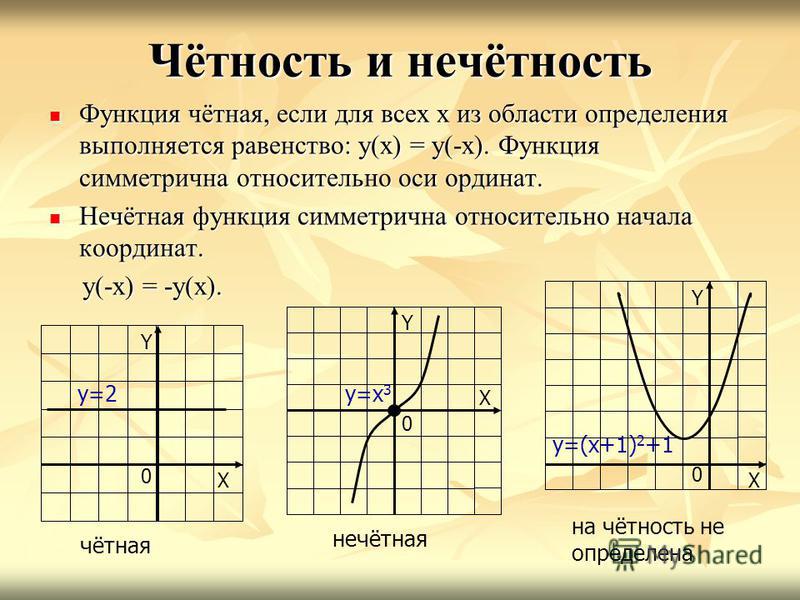

​

Решите, будете ли вы требовать от учащихся алгебраического доказательства того, почему функция является четной и нечетной, или просто предоставите доказательства того, что функция является четной или нечетной. Последнее можно сделать с некоторыми упорядоченными парными примерами, но первое требует алгебраической обработки выражений при вычислении функций в точке -x.

​

python — Понимание рекурсивных нечетных/четных функций

спросил 6 лет, 6 месяцев назад

Изменено 6 лет, 6 месяцев назад

Просмотрено 814 раз

В настоящее время я изучаю Python на http://www.sololearn.com/Play/Python, и мне трудно понять, почему этот код работает.

 по определению is_even(x):
    если х == 0:
        вернуть Истина
    еще:
        вернуть is_odd (x-1)
определение is_odd(x):
    вернуть не is_even(x)
печать (есть_нечетное (1))
 

Я понимаю, как работает рекурсия для чисел Фибоначчи и факториала, но не могу понять этого.

• Python
• Python-3.x
• рекурсия

2

is_even' s базовый случай разрешается в True . Поскольку is_odd(x) возвращает , а не is_even(x) , значение True будет частью выражения, возвращаемого is_odd . Вопрос в том, сколько раз это Истинное значение должно быть инвертировано . Отслеживая вызовы, вы можете видеть, что они будут инвертированы четное количество раз и, следовательно, «сохранят» свою истинность, когда x нечетно [например: x=3 ==> (не (не (не () не Истинно)))) == Истинно ] и нечетное число раз, а значит «теряет» свою истинность, когда х четно [например: х=2 ==> (не (не (неправда))) == Ложь ]. Вероятно, есть какой-то логический термин, обозначающий это общее свойство многократного отрицания.

1

Он основан на индуктивном определении четности:

• Ноль равен
• Если какое-то число «n» четное, то «n+1» не четное
• Если какое-то число «n» нечетное, то «n+1» четное

«нечетное» явно не «четное».

Код берет это определение и проверяет его в обратном направлении, используя рекурсию.

• Если у меня ноль, то даже
• Если у меня есть какое-то другое число «n», то оно четное, если «n-1» не четное, то есть если «n-1» нечетное.

Эта рекурсивная функция — плохой способ обучения рекурсии, вы должны применять рекурсию только тогда, когда это полезно. Фактически, протестируйте эти функции с отрицательными числами, и вы получите RuntimeError: максимальная глубина рекурсии превысила ошибки.

Для проверки чисел четности лучше использовать оператор % или и и оператор, т.е.:

 def is_even(x):
    возврат (х и 1) == 0
определение is_odd(x):
    возврат (х и 1) == 1
 

Тем не менее, я думаю, что ответы @Elazar и @DAXaholic должны дать вам некоторое представление об этой ошибочной рекурсивной функции и понять ее.