Как понять четная или нечетная функция по графику: Чётные и нечётные функции — урок. Алгебра, 9 класс.

Содержание

Четная функция и нечетная функция: определение, свойства, графики, примеры

Содержание:

Что такое четная функция
Что такое нечетная функция
Как понять, четная или нечетная функция
Свойства четных и нечетных функций
Графики, примеры

Содержание

Что такое четная функция
Что такое нечетная функция
Как понять, четная или нечетная функция
Свойства четных и нечетных функций
Графики, примеры

Что такое четная функция

Функция f(х) является четной в том случае, когда для каких-либо значений, принимаемых за х и составляющих область, где определяется рассматриваемая функция, справедливо данное соотношение:

$f(-х)=f(х)$

На координатной плоскости четная функция расположена симметрично по отношению к оси ординат. 3+х)=-f(х).\)

Как понять, четная или нечетная функция

Разновидности функций определяют правила нахождения переменных, которые входят в состав уравнений и с помощью которых рассматриваемые функции записаны, а также позволяют идентифицировать положение графика. Заметим, что это значит наличие зависимости принадлежности к тому или иному типу от симметрии. Предусмотрена пара методов определения четности или нечетности анализируемых функций. В первом случае задачу допустимо решать, прибегая к алгебраическим вычислениям. Второй способ заключается в изучении графика в рамках координатной плоскости. Кроме всего прочего, такая информация позволяет спрогнозировать, как будут вести себя на схеме определенные совокупности функций, записанные с помощью тех или иных формул.

Разберем анализ четности функции с точки зрения алгебры. Здесь важно понимание термина противоположных значений переменных. Запись такого значения подразумевает использование знака минуса. Когда изначально переменная записана со знаком минуса, ее противоположным значением является та же переменная, но с положительным знаком.

{2}+1=2(4)+1=8+1=9\), координаты точки (-2,9).

Источник: ru.wikihow.com

Расположение графика функции:

В том случае, когда функция графически представляет собой симметрию по отношению к оси ОУ, можно с уверенностью говорить о четности данной функции.
Если на некой плоскости с обозначенным началом координат, осями ОХ и ОУ, наблюдается такая ситуация, при которой график симметричен по отношению к точке с координатами (0;0), то следует сформулировать вывод о нечетности рассматриваемой функции.
При отсутствии какого-либо симметричного расположения функция имеет общий вид.

Источник: ru.wikihow.com Источник: ru.wikihow.com

Существует еще две закономерности:

при четном степенном показателе переменной функция является четной;
при нечетном степенном показателе переменной функция определена, как нечетная.

Свойства четных и нечетных функций

Перечислим важные свойства, характерные для четных и нечетных функций:

При действиях $\div$ или $\times$ (произведение) пары функций, характеризующиеся аналогичной четностью, получается четная функция.
При действиях $\div$ или $\times$ пары функций, характеризующиеся не одинаковой четностью, получается нечетная функция.
При действиях + или — функций, определяющиеся, как четные, получается в итоге четная функция.
При + или — функций, определяющиеся, как нечетные, получается в итоге нечетная функция.
При условии четности функции f(х) соотношение $f(х)=c \ (c\in \mathbb{R})$ обладает одним решением при нулевом значении переменной х.
При условии четности или нечетности функции f(х) соотношение f(x)=0 обладает решением в виде х= b, тогда вторым решением является х= — b.

Разберем еще одно важное понятие такое, как периодическая функция f(x) на X при каком-то числе Т, отличном от нуля, когда справедливым является следующее соотношение:

$f(x)=f(x+T)$

Здесь $x+T\in X$.

Минимальное Т при справедливом соотношении, записанном выше, представляет собой ключевой (главный) период функции. 2\,1 \end{cases} \quad\Leftrightarrow\quad \begin{cases} x=0\\ \mathrm{tg}\,(\cos x)=\mathrm{tg}\,1 \end{cases}\quad\Leftrightarrow\quad x=0\)

В результате вычислений, имеем, что:

$a=-\mathrm{tg}\,1$

По итогам расчетов можно записать ответ.

Ответ: $a\in \{-\mathrm{tg}\,1;0\}.$

Задача 2

Имеется некая функция, которая описана следующим соотношением:

$f(x)=3\mathrm{tg}\,\dfrac{ax}5 +2\sin \dfrac{8\pi a-3x}4$

Нужно вычислить такие значения переменной а, при которых график рассматриваемой функции расположен симметрично по отношению к точке с координатами (0;0).

Решение

Проанализируем исходные данные в примере. Заметим, что выполнение условия задачи возможно лишь в том случае, когда функция определена, как нечетная. Сформулируем этот вывод в математической форме, то есть:

$f(-x)=-f(x)$

Исходя из вышесказанного, преобразуем начальное выражения из условия примера и запишем следующее справедливое равенство:

$\begin{aligned} &3\mathrm{tg}\,\left(-\dfrac{ax}5\right)+2\sin \dfrac{8\pi a+3x}4= -\left(3\mathrm{tg}\,\left(\dfrac{ax}5\right)+2\sin \dfrac{8\pi a-3x}4\right)\quad \Rightarrow\quad -3\mathrm{tg}\,\dfrac{ax}5+2\sin \dfrac{8\pi a+3x}4= -\left(3\mathrm{tg}\,\left(\dfrac{ax}5\right)+2\sin \dfrac{8\pi a-3x}4\right) \quad \Rightarrow\\[3ex] \Rightarrow\quad &\sin \dfrac{8\pi a+3x}4+\sin \dfrac{8\pi a-3x}4=0 \quad \Rightarrow \quad2\sin \dfrac12\left(\dfrac{8\pi a+3x}4+\dfrac{8\pi a-3x}4\right)\cdot \cos \dfrac12 \left(\dfrac{8\pi a+3x}4-\dfrac{8\pi a-3x}4\right)=0 \quad \Rightarrow\quad \sin (2\pi a)\cdot \cos \frac34 x=0 \end{aligned}$

Рассмотрим, чему соответствует область определения последнего соотношения. 2+4a+4\leqslant 0 \end{cases} \end{aligned} \end{gathered}\right.\)

После выполнения всех необходимых вычислений и преобразований получим, что а с учетом условий, указанных в задании, соответствует следующим значениям:

$a\in \{-2\}\cup[22-4\sqrt{30};22+4\sqrt{30}]$

Ответ: $a\in \{-2\}\cup[22-4\sqrt{30};22+4\sqrt{30}]$.

Задача 5

Требуется рассчитать значения, которые принимает а, при условии наличия у следующего уравнения корней:

$\cos x+\dfrac32 \cos \dfrac{2x}3+3\cos \dfrac x3=a$

Решение

Рассмотрим исходные данные. Руководствуясь свойствами функций и стандартным алгоритмом решения подобных примеров, в первую очередь запишем и проанализирует такую функцию:

$f(x)=\cos x+\frac32 \cos \frac{2x}3+3\cos \frac x3$

Далее попробуем вычислить основной период, который с учетом вводных характеристик в данном случае составит:

$у \cos x$ соответствует $2\pi$

$у \cos \frac{2x}3$ соответствует $\dfrac{2\pi}{\frac23}=3\pi$

$у \cos\frac x3$ соответствует $\dfrac{2\pi}{\frac13}=6\pi$

В результате главный период соответствует $6\pi$, что следует из определения этого понятия. Вспомним правила нахождения функций. Запишем условия для наличия у функции корней:

$\mathrm{min}\,f(x)\leqslant a\leqslant \mathrm{max}\,f(x)$

Рассмотрим в качестве примера интервал $[0;6\pi]$. Выполним соответствующие преобразования и математические вычисления:

$f'(x)=\sin x+\sin \dfrac{2x}3+\sin \dfrac x3=0\quad \Rightarrow \quad \left(\sin x+\sin \dfrac{x}3\right)+\sin \dfrac{2x}3=0 \quad \Rightarrow \Rightarrow \quad 2\sin \dfrac{2x}3\cos \dfrac x3+\sin \dfrac{2x}3=0 \quad \Rightarrow \quad \sin \dfrac{2x}3\left(2\cos \dfrac x3+1\right)=0\quad \Rightarrow \Rightarrow \quad \left[ \begin{gathered} \begin{aligned} &\dfrac{2x}3=\pi n, n\in\mathbb{Z}\\[3pt] & \dfrac x3=\pm \dfrac{2\pi}3+2\pi k, k\in\mathbb{Z} \end{aligned} \end{gathered} \right. \quad \Rightarrow \quad \left[ \begin{gathered} \begin{aligned} &x=\dfrac32\pi n, n\in\mathbb{Z}\\[3pt] &x=\pm 2\pi+6\pi k, k\in\mathbb{Z} \end{aligned} \end{gathered} \right. $

Рассмотрим некоторый отрезок $[0;6\pi]$. Заметим, что здесь расположены следующие точки:

$0;\ \frac{3\pi}2;\ 2\pi;\ 3\pi;\ 4\pi; \ \frac{9\pi}2;\ 6\pi.$

На следующем этапе потребуется определить, какими знаками обладают полученные интервалы. Используя стандартный алгоритм расстановки плюсов и минусов, допустимо обозначить знаки производной таким образом:

Источник: Источник: shkolkovo.net

Проанализируем полученные промежутки. Исходя из интервала $[0;6\pi]$, функция обладает самым маленькими значениями в какой-то из точек:

$\frac{3\pi}2;\ 3\pi;\ \frac{9\pi}2$

Поступим таким же оборазом, чтобы найти максимумы. Аналогично предыдущим расчетам, максимальными значениями станут следующие:

$0;\ 2\pi;\ 4\pi; \ 6\pi.$

В результате поэтапного разбора интервалов и вычислений можно записать такую систему:

$\begin{aligned} &f(0)=f(6\pi)=\dfrac{11}2\\[4pt] &f\left(\dfrac{3\pi}2\right)=f\left(\dfrac{9\pi}2\right)=-\dfrac32\\[4pt] &f(2\pi)=f(4\pi)=-\dfrac54\\[4pt] &f(3\pi)=-\dfrac52 \end{aligned} $

Изобразим полученные условия на схеме:

Источник: Источник: shkolkovo.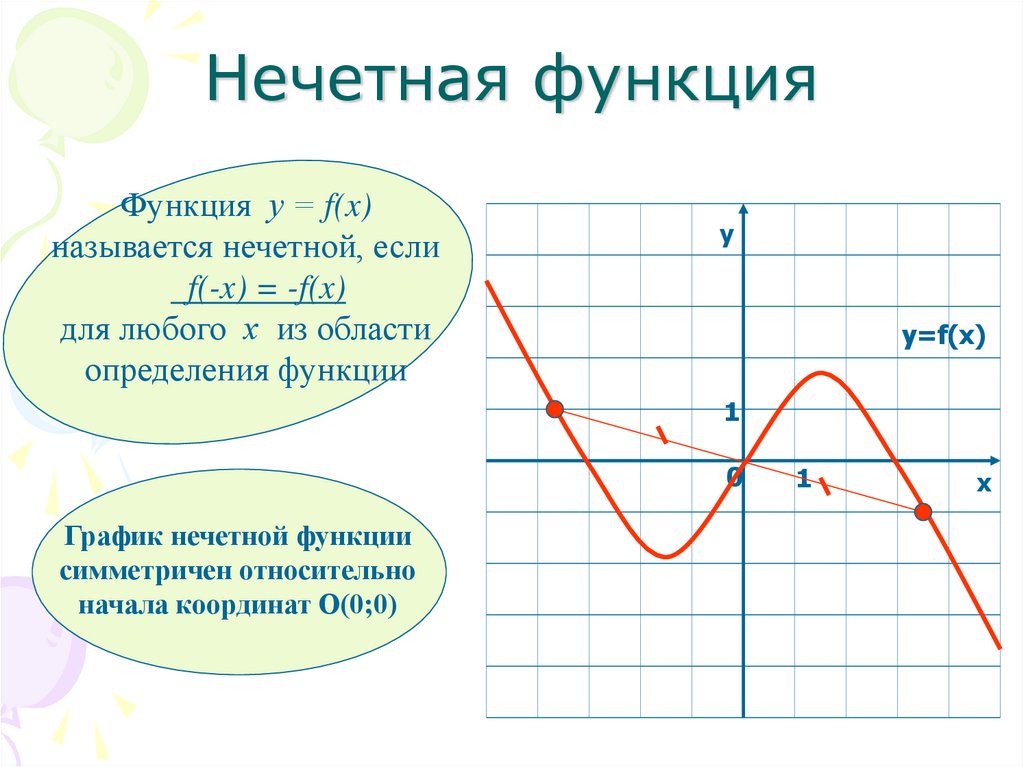

net

После выполнения всех необходимых расчетов и с учетом логичных выводов целесообразно записать следующие равенства:

$\mathrm{min}\,f(x)=-\dfrac52, \ \mathrm{max}\,f(x)=\dfrac{11}2.$

Таким образом, достаточно просто определить значения, которым соответствует а, согласно условиям задачи:

$a\in\left[-\dfrac52;\dfrac{11}2\right]$

Ответ: $a\in \left[-\dfrac52;\dfrac{11}2\right].$

Краткий курс высшей математики

Шнейдер В. Е. и др. Краткий курс высшей математики. Учеб. пособие для втузов. М., «Высш. школа», 1972. 640 с.

Данное учебное пособие предназначено для студентов вечерних факультетов втузов и заводов-втузов. Оно в основном охватывает весь материал, предусмотренный обязательной программой. Достаточное количество решенных примеров и задач способствует лучшему усвоению теоретического материала.

ПРЕДИСЛОВИЕ
ГЛАВА I. МЕТОД КООРДИНАТ. ПОНЯТИЕ ФУНКЦИИ
§ 1. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. КООРДИНАТЫ ТОЧКИ НА ПРЯМОЙ
2. Геометрическое изображение действительных чисел. Координаты точки на прямой
3. Абсолютная величина действительного числа
4. Расстояние между двумя точками на прямой
§ 2. КООРДИНАТЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
2. Расстояние между двумя точками на плоскости
3. Деление отрезка в данном отношении
4. Координаты точки в пространстве
5. Расстояние между двумя точками в пространстве
§ 3. УГОЛ МЕЖДУ ДВУМЯ ОСЯМИ. ПОЛЯРНЫЕ КООРДИНАТЫ
2. Полярные координаты
3. Зависимость между декартовыми и полярными координатами
§ 4. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ
2. Понятие функции
3. График функции
4. Способы задания функций
5. Основные элементарные функции и их графики
6.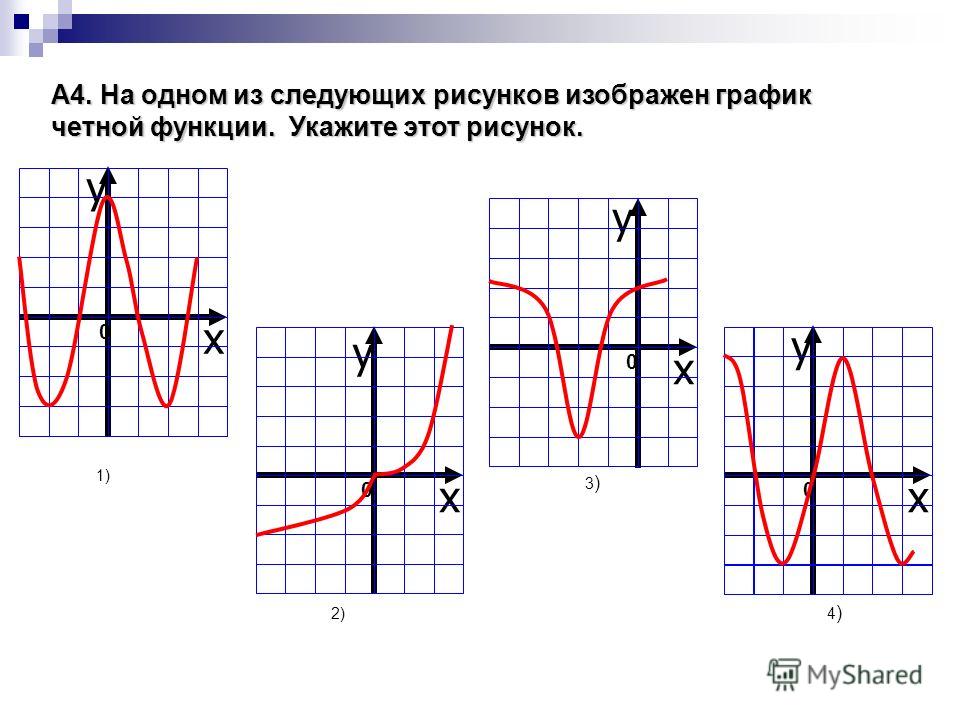

Сложные функции. Элементарные функции
7. Целые и дробно-рациональные функции
8. Функции четные и нечетные. Периодические функции
§ 5. УРАВНЕНИЕ ЛИНИИ
2. Нахождение уравнения линии по ее геометрическим свойствам
§ 6 ПРЕОБРАЗОВАНИЕ КООРДИНАТ
2. Поворот осей координат
ГЛАВА II. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
§ 1. ПРЯМАЯ
2. Уравнение прямой с угловым коэффициентом
3. Уравнение прямой, параллельной оси ординат
4. Общее уравнение прямой и его частные случаи
5. Точка пересечения прямых. Построение прямой по ее уравнению
6. Вычисление угла между двумя прямыми. Условия параллельности и перпендикулярности двух прямых
7. Уравнение прямой, проходящей через данную точку в заданном направлении
8. Пучок прямых
9. Уравнение прямой, проходящей через две данные точки
10. Расстояние от точки до прямой
§ 2. КРИВЫЕ ВТОРОГО ПОРЯДКА
2. Окружность
3. Эллипс
4. Гипербола
5. Парабола
6. Окружность, эллипс, гипербола и парабола как конические сечения
7.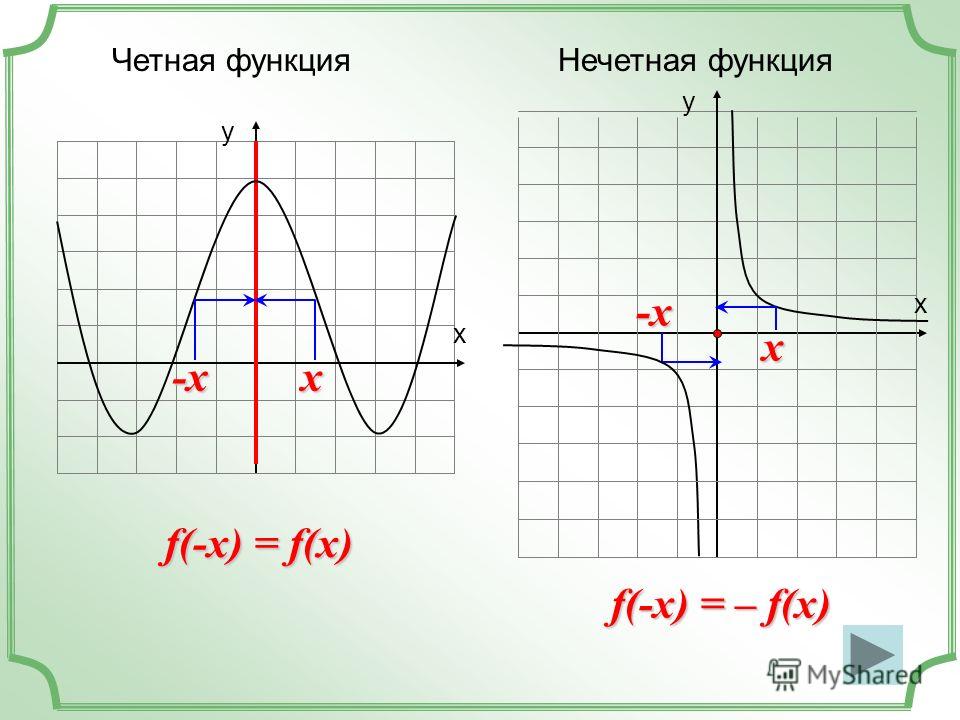

Упрощение уравнения кривой второго порядка. График квадратного трехчлена
8. Уравнение равносторонней гиперболы, асимптоты которой приняты за оси координат
9. График дробно-линейной функции
10. Преобразование уравнения кривой второго порядка, не содержащего члена с произведением координат
ГЛАВА III. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ И ВЕКТОРНОЙ АЛГЕБРЫ
§ 1. ЭЛЕМЕНТЫ ТЕОРИИ ОПРЕДЕЛИТЕЛЕЙ
2. Определитель третьего порядка
3. Понятие об определителях высших порядков
§ 2. СИСТЕМЫ УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ
2. Однородная система двух уравнений первой степени с тремя неизвестными
3. Система трех уравнений первой степени с тремя неизвестными
4. Однородная система трех уравнений первой степени с тремя неизвестными
§ 3. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
2. Линейные операции над векторами
4. Проекция вектора на ось и составляются вектора по оси
5. Разложение вектора на составляющие по осям координат
6. Направляющие косинусы вектора
7. Условие коллинеарности двух векторов
8.

Скалярное произведение
9. Выражение скалярного произведения через проекции перемножаемых векторов
10. Косинус угла между двумя векторами
11. Векторное произведение
12. Выражение векторного произведения через проекции перемножаемых векторов
13. Смешанное произведение трех векторов
14. Геометрический смысл смешанного произведения
15. Условие компланарности трех векторов
§ 4. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ
2. Равенство матриц. Действия над матрицами
3. Обратная матрица
4. Матричная запись и матричное решение системы уравнений первой степени
§ 5. ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ
2. Преобразование координат
3. Приведение квадратичной формы к каноническому виду
4. Упрощение общего уравнения кривой второго порядка
ГЛАВА IV. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
§ 1. ПЛОСКОСТЬ
2. Нормальный вектор плоскости. Уравнение плоскости, проходящей через данную точку
3. Общее уравнение плоскости и его частные случаи
4. Построение плоскости по ее уравнению
5.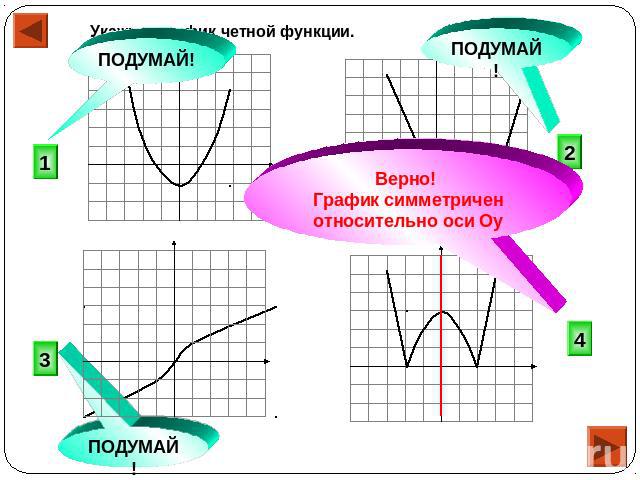

Угол между плоскостями. Условия параллельности и перпендикулярности двух плоскостей
6. Точка пересечения трех плоскостей
§ 2. ПРЯМАЯ В ПРОСТРАНСТВЕ
2. Общие уравнения прямой
3. Векторное уравнение прямой. Параметрические уравнения прямой
4. Канонические уравнения прямой
5. Уравнения прямой, проходящей через две точки
6. Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых
§ 3. Прямая и плоскость в пространстве
2. Точка пересечения прямой с плоскостью
3. Расстояние от точки до плоскости
4. Пучок плоскостей
§ 4. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
2. Цилиндрические поверхности
3. Конические поверхности
4. Поверхность вращения
6. Гиперболоиды
7. Параболоиды
ГЛАВА V. ТЕОРИЯ ПРЕДЕЛОВ
§ 1. ПРЕДЕЛ ФУНКЦИИ
2. Предел функции при х -> -оо
3. Предел функции при х->х0
4. Бесконечно малые функции. Ограниченные функции
5. Бесконечно большие функции и их связь с бесконечно малыми функциями
6.

Основные теоремы о пределах
7. Предел функции при x -> 0
8. Последовательность. Число e
9. Натуральные логарифмы
10. Сравнение бесконечно малых функций
§ 2. НЕПРЕРЫВНЫЕ ФУНКЦИИ
2. Операции над непрерывными функциями. Непрерывность элементарных функций
3. Свойства функций, непрерывных на сегменте
4. Понятие об обратной функции
5. Обратные тригонометрические функции
6. Показательная и логарифмическая функции
7. Понятие о гиперболических функциях
ГЛАВА VI. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
1. Приращение аргумента и приращение функции
2. Определение непрерывности функции с помощью понятии приращения аргумента и приращения функции
3. Задачи, приводящие к понятию производной
4. Определение производной и ее механический смысл
5. Дифференцируемость функции
6. Геометрический смысл производной
7. Производные некоторых основных элементарных функций
8. Основные правила дифференцирования
9. Производная обратной функции
10.

Производные обратных тригонометрических функций
11. Производная сложной функции
§ 12. Производные гиперболических функций
13. Производная степенной функции с любым показателем
14. Сводная таблица формул дифференцирования
15. Неявные функции и их дифференцирование
16. Уравнения касательной а нормали к кривой
17. Графическое дифференцирование
§ 2. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ
1. Нахождение производных высших порядков
2. Механический смысл второй производной
§ 3. ДИФФЕРЕНЦИАЛ ФУНКЦИИ
2. Производная как отношение дифференциалов
3. Дифференциал суммы, произведения и частного функций
4. Дифференциал сложной функции. Инвариантность формы дифференциала
5. Применение дифференциала к приближенным вычислениям
6. Дифференциалы высших порядков
§ 4. ФУНКЦИИ, ЗАДАННЫЕ ПАРАМЕТРИЧЕСКИ, И ИХ ДИФФЕРЕНЦИРОВАНИЕ
2. Дифференцирование функций, заданных параметрически
§ 5. ВЕКТОРНАЯ ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
2. Векторная функция скалярного аргумента и ее производная
3.

Уравнения касательной прямой и нормальной плоскости к пространственной кривой
4. Механический смысл первой и второй производных векторной функции скалярного аргумента
§ 6. НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
2. Теорема Ролля
3. Теорема Лагранжа
4. Правило Лопиталя
§ 7. ПРИЛОЖЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ПОСТРОЕНИЮ ГРАФИКОВ
2. Максимум и минимум функции
3. Достаточный признак существования экстремума, основанный на знаке второй производной
4. Отыскание наибольшего и наименьшего значений функции
5. Применение теории максимума и минимума к решению задач
6. Выпуклость и вогнутость графика функции. Точки перегиба
7. Асимптоты графика функции
8. Общая схема исследования функции и построение ее графика
§ 8. ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ
2. Уточнение найденных значений корней методом хорд и касательных
§ 9. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА ЛАГРАНЖА
ГЛАВА VII. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА
2.

Геометрический смысл неопределенного интеграла
3. Таблица основных интегралов
4. Основные свойства неопределенного интеграла
§ 2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
2. Интегрирование методом замены переменной
3. Интегрирование по частям
§ 3. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
2. Рациональные дроби. Выделение правильной рациональной дроби
3. Интегрирование простейших рациональных дробей
4. Разложение правильной рациональной дроби на простейшие дроби
5. Метод неопределенных коэффициентов
6. Интегрирование рациональных дробей
§ 4. Интегрирование тригонометрических функций
2. Рациональные функции двух переменных
3. Интегралы вида
§ 5. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ
2. Интеграл вида
3. Интегралы видов
4. Интегралы вида
§ 6. ОБЩИЕ ЗАМЕЧАНИЯ О МЕТОДАХ ИНТЕГРИРОВАНИЯ. ИНТЕГРАЛЫ, НЕ БЕРУЩИЕСЯ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
2. Понятие об интегралах, не берущихся в элементарных функциях
ГЛАВА VIII. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1.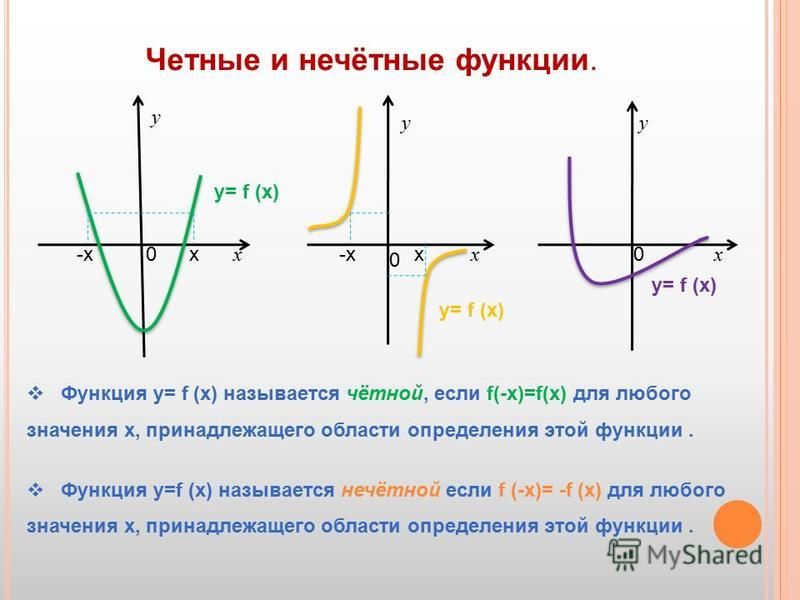

ЗАДАЧИ, ПРИВОДЯЩИЕ К ОПРЕДЕЛЕННОМУ ИНТЕГРАЛУ
2. Задача о работе переменной силы
§ 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
2. Свойства определенного интеграла
3. Производная интеграла по переменной верхней границе
4. Формула Ньютона—Лейбница
5. Замена переменной в определенном интеграле
6. Интегрирование по частям в определенном интеграле
§ 3. ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
2. Вычисление площади в полярных координатах
3. Вычисление объема тела по известным поперечным сечениям
4. Объем тела вращения
5. Длина дуги кривой
6. Дифференциал дуги
7. Площадь поверхности вращения
8. Общие замечания о решении задач методом интегральных сумм
§ 4. КРИВИЗНА ПЛОСКОЙ КРИВОЙ
2. Вычисление кривизны
3. Радиус кривизны. Круг кривизны. Центр кривизны
4. Эволюта и эвольвента
§ 5. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
2. Интегралы от разрывных функций
3. Признаки сходимости несобственных интегралов
§ 6. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
2.

Метод трапеций
3. Метод параболических трапеций (метод Симпсона)
ГЛАВА IX. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
§ 1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
2. График функции двух переменных
3. Функции трех и большего числа переменных
§ 2. Предел функции нескольких переменных. Непрерывность функции. Точки разрыва
2. Непрерывность функции нескольких переменных
3. Понятие области
4. Точки разрыва
5. Свойства функций, непрерывных в ограниченной замкнутой области
§ 3. ЧАСТНЫЕ ПРОИЗВОДНЫЕ
2. Геометрический смысл частных производных функции двух переменных
3. Частные производные высших порядков
§ 4. ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
2. Полный дифференциал функции
3. Приложение полного дифференциала к приближенным вычислениям
§ 5. Дифференцирование сложных и неявных функций
2. Инвариантность формы полного дифференциала
3. Дифференцирование неявных функций
§ 6. СКАЛЯРНОЕ ПОЛЕ
2. Производная по направлению
3.

Градиент
4. Касательная плоскость а нормаль к поверхности
5. Геометрический смысл полного дифференциала функции двух переменных
§ 7. ЭКСТРЕМУМ ФУНКЦИЙ ДВУХ ПЕРЕМЕННЫХ
2. Наибольшее и наименьшее значения функции двух переменных
ГЛАВА X. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
§ 1. ДВОЙНОЙ ИНТЕГРАЛ
2. Двойной интеграл. Теорема существования
3. Свойства двойного интеграла
4. Вычисление двойного интеграла в декартовых координатах
5. Вычисление двойного интеграла в полярных координатах
6. Приложения двойного интеграла
§ 2. ТРОЙНОЙ ИНТЕГРАЛ
2. Тройной интеграл и его свойства
3. Вычисление тройного интеграла в декартовых координатах
4. Вычисление тройного интеграла в цилиндрических координатах
5. Приложения тройного интеграла
§ 3. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ
2. Задача о работе. Криволинейный интеграл
3. Вычисление криволинейного интеграла
4. Формула Остроградского — Грина
5. Независимость криволинейного интеграла от пути интегрирования
6.

Отыскание первообразной по полному дифференциалу
7. Криволинейный интеграл по длине дуги
ГЛАВА XI. РЯДЫ
§ 1. ЧИСЛОВЫЕ РЯДЫ
2. Геометрическая прогрессия
3. Простейшие свойства числовых рядов
4. Необходимый признак сходимости ряда
5. Достаточные признаки сходимости знакоположительных рядов
6. Знакопеременные ряды
7. Остаток ряда и его оценка
§ 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
2. Правильно сходящиеся функциональные ряды и их свойства
§ 3. СТЕПЕННЫЕ РЯДЫ
2. Свойства степенных рядов
3. Ряды по степеням разности х-а
4. Разложение функций в степенные ряды. Ряд Тейлора
5. Разложение некоторых элементарных функций в ряды Тейлора и Маклорена
§ 4. ПРИЛОЖЕНИЕ РЯДОВ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ
2. Приближенное вычисление интегралов
§ 5. ПОНЯТИЕ О ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ. СТЕПЕННЫЕ РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ
2. Числовые ряды с комплексными членами
3. Степенные ряды в комплексной области
§ 6. РЯДЫ ФУРЬЕ
2. Ряд Фурье
3.

Сходимость ряда Фурье
4. Ряды Фурье для четных и нечетных функций
5. Разложение в ряд Фурье функций с периодом 2l
ГЛАВА XII. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
§ 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
2. Дифференциальные уравнения первого порядка
3. Уравнения с разделяющимися переменными
4. Однородные уравнения
5. Линейные уравнения
6. Уравнение в полных дифференциалах
7. Особые решения
8. Приближенное решение дифференциальных уравнений первого порядка методом Эйлера
§ 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
2. Простейшие уравнения второго порядка, допускающие понижение порядка
3. Понятие о дифференциальных уравнениях высших порядков
§ 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
2. Линейные однородные дифференциальные уравнения второго порядка
3. Линейные неоднородные дифференциальные уравнения второго порядка
4. Метод вариации произвольных постоянных
§ 4. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
2.

Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
3. Приложение линейных дифференциальных уравнений второго порядка к изучению механических и электрических колебаний
§ 5. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ
2. Линейные дифференциальные уравнения n-го порядка с постоянными коэффициентами
§ 6. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ РЯДОВ
§ 7. ПОНЯТИЕ О СИСТЕМАХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
2. Системы линейных дифференциальных уравнений с постоянными коэффициентами
ПРИЛОЖЕНИЕ 1. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА
ПРИЛОЖЕНИЕ 2. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

Предварительное исчисление алгебры

— четные и нечетные функции, может ли кто-нибудь помочь мне понять это?

Этот ответ касается свойств симметрии некоторых графиков и понятий четных и нечетных функций. Во-первых, свойство графика функции иметь симметрию (либо зеркальное отражение, либо вращение/начало отражения) встречается редко. Большинство функций не имеют ни того, ни другого.

Четная функция. С геометрической точки зрения график четной функции обладает зеркальной симметрией относительно оси $y$, т. е. $(x, y)$ находится на графике тогда и только тогда, когда $(-x, y)$ находится на графике. Но это означает, что $f(-x) = y = f(x)$, что является алгебраическим условием, которое вы упомянули внизу.

График $f$, с которым вы работаете, представляет собой параболу (поскольку это квадратичная полиномиальная функция), и вы, вероятно, знаете, что параболы имеют отражательную симметрию, но в этом случае осью симметрии является вертикальная линия $x = 5$ (среднее значение корней). Как мы можем понять, это означает, что $f(5-x) = f(5+x)$ для всех $x$, но у этой симметрии нет имени вроде даже . Вы даже можете убедиться в этом, заполнив квадрат $x$. (Попробуйте сами, прежде чем раскрывать спойлер. 92 — 16, $$

и в этой форме легко видеть, что $f(X) = f(-X)$ для всех $X$, он имеет симметрию относительно вертикальной линии $X = 0$.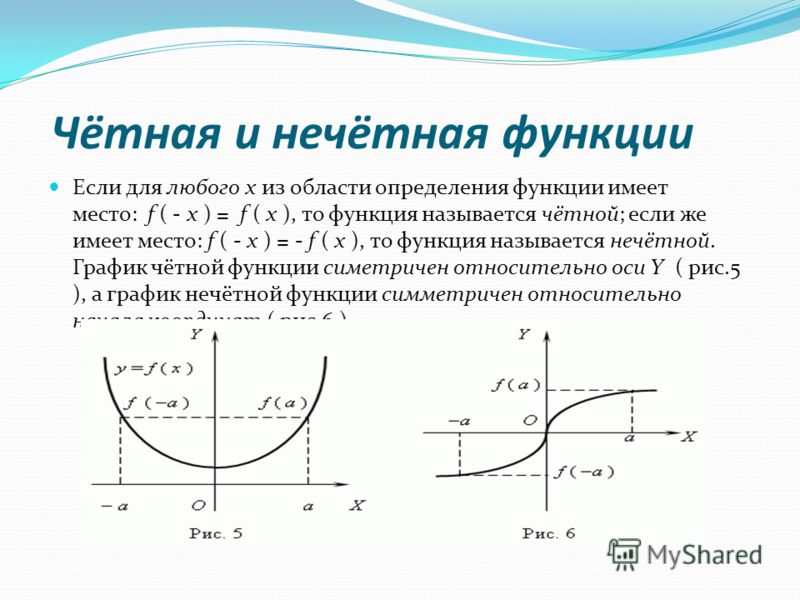 Переводя это обратно в исходную горизонтальную координату $x$, мы видим, что $f(5-x) = f(5+x)$ и что вертикальная линия $x = 5$ является осью симметрии параболы.

Вероятно, вы можете понять, что ваша функция $g$ на самом деле четна. (Оказывается, что для многочленов функций быть четными означает иметь только ненулевые члены четной степени, а многочлен четвертой степени $g$ имеет члены степеней $4$, $2$ и $0$.) Это общее наблюдение о многочленах также демонстрирует, почему $f$ равно 9\circ$ вращение.

Четные и нечетные функции – Блог для учителей математики

Понятия четных и нечетных функций обычно вводятся на курсах алгебры высшей школы, алгебры колледжа, тригонометрии или предварительного исчисления. Студенты, изучающие тригонометрию, узнают, как применять концепции четных и нечетных функций для упрощения тригонометрических выражений. Студенты, изучающие математику, узнают, как применять понятия четных и нечетных функций для упрощения вычисления определенного интеграла.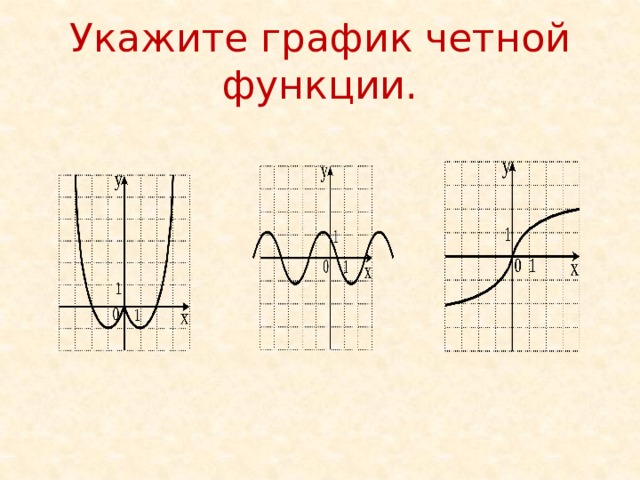 Когда учащиеся понимают и могут распознавать четные и нечетные функции, они обычно удивляются, как часто эти функции появляются в прикладных задачах.

В этом посте обсуждаются четные и нечетные функции как с алгебраической, так и с геометрической точки зрения. Читателям предлагается загрузить мой бесплатный раздаточный материал Четные и нечетные функции , который является удобным справочником, который учителя могут дать ученикам.

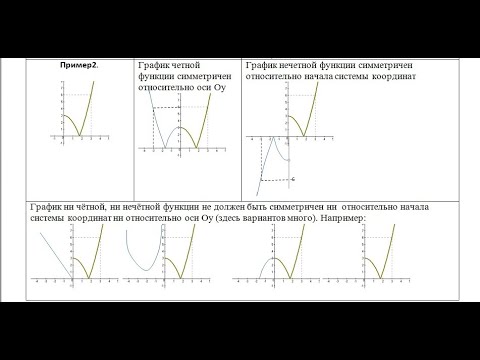
Начну обсуждение с описания даже функций . Текстовое поле ниже дает описание четной функции с нескольких точек зрения. График А иллюстрирует, что мы имеем в виду, когда говорим, что график имеет симметрию относительно оси Y.

Текстовое поле ниже дает описание нечетной функции с нескольких точек зрения. График B иллюстрирует, что мы имеем в виду, когда говорим, что граф обладает симметрией относительно начала координат.

Текстовое поле ниже содержит некоторые основные наблюдения о четных и нечетных функциях. Мой бесплатный раздаточный материал Четные и нечетные функции дает более подробный список важных свойств этих функций.

Текстовое поле ниже показывает разложение функции y = Cos(x) в бесконечный ряд Тейлора. График C показывает график y = Cos(x) и график первых пяти членов разложения Cos(x) в ряд Тейлора. Обратите внимание, что разложение Cos(x) в ряд Тейлора представляет собой сумму и разность четных функций!

Текстовое поле ниже показывает разложение функции y = Sin(x) в бесконечный ряд Тейлора. График D показывает график y = Sin(x) и график первых пяти членов разложения Sin(x) в ряд Тейлора. Обратите внимание, что разложение Sin(x) в ряд Тейлора представляет собой сумму и разность нечетных функций!

Я закончу этот пост, показав вам, как создать четную или нечетную функцию из любой функции y = f(x), которая не обязательно является четной или нечетной. Текстовое поле ниже показывает, как и почему это можно сделать. На графике E показаны результаты создания четной функции и нечетной функции из функции y = f(x) = 0,25(x – 4) ² – 3Sin(x – 4) – 5. Этот результат объясняет, почему гиперболические функции ch(x) и sh(x) — четная и нечетная функции соответственно.

Дополнительные полезные инструменты из ресурса для учителей математики

• Графики в этом посте были созданы с помощью моего программного обеспечения Basic Trig Functions. Я думаю, что вы найдете его очень полезным для преподавания математических понятий в классе и разработки пользовательских учебных материалов. Проверьте это на mathteachersresource.com/trigonometry.

• В дополнение к раздаточному материалу по четным и нечетным функциям , указанному в этом сообщении, Ресурс для учителей математики предлагает широкий выбор бесплатных раздаточных материалов, уроков и упражнений по математике, доступных на странице mathteachersresource.com/instructional-content.