Системы исчисления [АйТи бубен]
Системы исчисления: двоичная, восьмеричная, десятичная, шестнадцатеричная.
Двоичная система счисления Материал из Википедии
Представление числовых данных в памяти ЭВМ
Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления числа записываются с помощью двух символов (1 и 0). Компьютер может различить только нулевое и единичное состояние бита, и работает компьютер в системе исчисления с основанием 2 или в двоичной системе.
Бит получил свое название от английского Binary digit (двоичная цифра).
Сочетанием двоичных цифр (битов) можно представить любое значение. Значение двоичного числа определяется относительной позицией каждого бита и наличием единичных битов. Ниже показано восьмибитовое число, содержащее все единичные биты:
значения: 128 64 32 16 8 4 2 1 биты: 1 1 1 1 1 1 1 1
Самая правая цифра имеет весовое значение 1, следующая цифра влево — 2, следующая — 4 и т.
(1+2+4+8+16+32+64+128=255)
Преобразование чисел
Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2:
512 256 128 64 32 16 8 4 2 1
Начиная с цифры 1 все цифры умножаются на два.
Допустим, нам нужно перевести число 17 в двоичное. Согласно таблице степеней оснований (см. выше) 17=16+1. Значит на место значимых цифр 16 и 1 ставим 1 — остальные нули. Получаем 17=10001
512 256 128 64 32 16 8 4 2 1 0 0 0 0 0 1 0 0 0 1
Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой :
19 /2 = 9 с остатком 1 9 /2 = 4 c остатком 1 4 /2 = 2 с остатком 0 2 /2 = 1 с остатком 0 1 /2 = 0 с остатком 1
Итак, мы делим каждое частное на 2 и записываем остаток в начало двоичной записи. Продолжаем делить на 2 частные от деления до тех пор, пока частное не станет равным 0.
В обратную сторону нужно десятичные сложить, основываясь на таблице степеней основания 2.
Арифметические действия в двоичном формате
Компьютер выполняет арифметические действия только в двоичном формате. Поэтому, необходимо знать правила сложения в двоичной системе исчисления. Напомним их:
0 + 0 = 0 1 + 0 = 1 1 + 1 = 10
Давайте рассмотрим использование этих правил на конкретном примере.
Пример: сложить числа 65 и 42, представленные в двоичной системе исчисления.
В десятичной системе исчисления все осуществляется достаточно просто: 65+42=107. Для сложения этих чисел в двоичной системе исчисления нужно сначала перевести их в эту систему, например, как показано на рисунке:
Таким образом, получаем: 65 в 10-ой системе = 01000001 в 2-ой системе. Обратите внимание на то, что ведущий ноль в двоичном представлении числа добавлен для дополнения двоичного представления до восьми бит.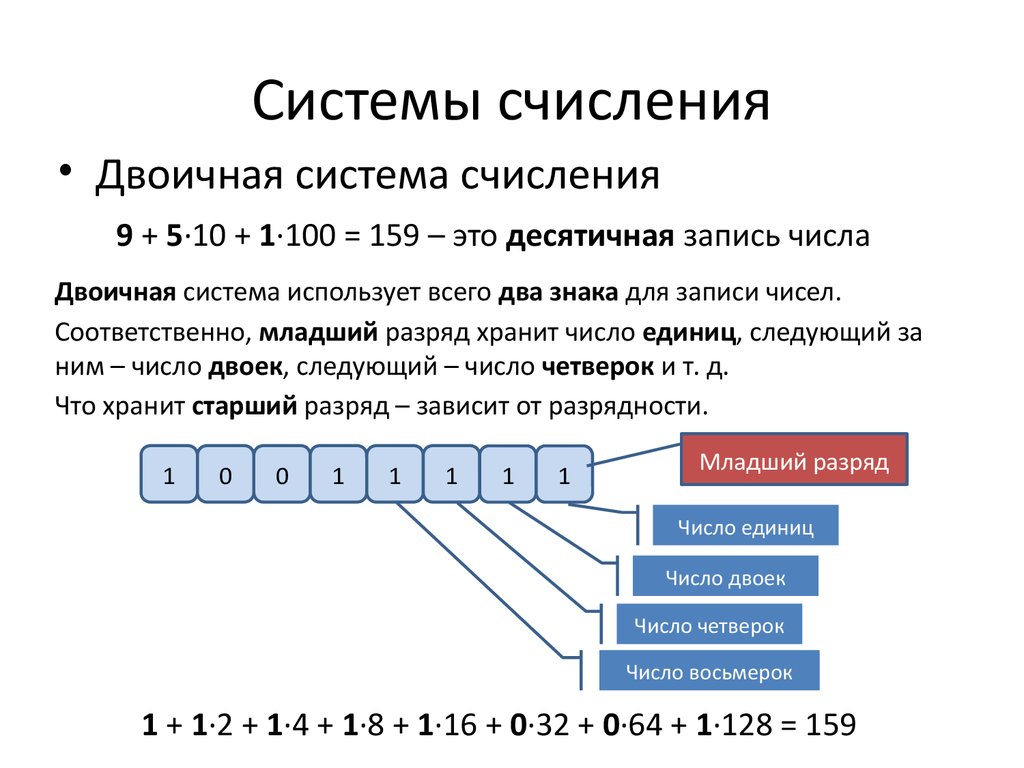
01000001 + 00101010 -------- 01101011
Можете перепроверить и убедиться, что 01101011 в 2=107 в 10:
0*27+1*26+1*25+0*24+1*23+0*22+1*21+1*20 = 64+32+8+2+1 = 107
Вычитание
Для выполнения операции вычитания последнее заменяется сложением, а в качестве второго слагаемого берется противоположное число. Например, пусть надо выполнить вычитание: 65 — 42. Заменим его сложением: 65 + (-42).
Двоичные числа имеют положительные значения, что обозначается нулевым значением самого левого, старшего разряда. Отрицательные двоичные числа содержат единичный бит в старшем разряде.
27 /16 = 1 с остатком 11 11 /16 = 0 c остатком 1
И того получим 1B.
Остаток от деления на 16 всегда меньше 16. Это относится ко всем системам счисления.
Рассмотрим несколько простых примеров шестнадцатеричной арифметики.
Следует помнить, что после шестнадцатеричного числа F следует шестнадцатеричное 10, что равно десятичному числу 16:
6+4=A 5+8=D F+1=10 F+F=1E 10+10=20 FF+1=100
Как объяснять двоичную систему счисления / Хабр
Кто-то только входит в IT-мир, кто-то объясняет информатику своему чаду.
Довольно быстро вы обнаружите, что не так-то просто объяснить, как работает двоичный счёт.
Это вам очевидно, что после 11 идёт 100, а новичку это ещё долго может быть непонятно.
Так вот, чтобы увеличить скорость понимания, мы решили сделать дидактический материал.
Проблема
Важно отметить, что даже распиаренный курс Гарвардского университета по компьютерным наукам «CS50» не помогает.
Парень из американского университета просто заявляет, что «нуль — это нуль», «один — это один», а потом идёт 10, а потом 11. Понятно? Думаю, нет. Вот спросите кого-то, кто не программист, а каким будет следующее число — высока вероятность, что он не сможет ответить.
То же самое касается школьных методов перевода: во-первых, методы эти академически сухи, во-вторых, не интуитивны — например, не очевидно, почему после каскадного деления на 2 нужно ставить биты задом наперёд.
А если непонятно, то и не интересно. А если нет интереса, то и запоминается с трудом.
Мы это всё учли, и решили сделать интересное и постепенное объяснение.
Что мы предлагаем
Сначала нужно объяснить, как вообще работает обычная десятичная система счисления — и про конечный «алфавит» цифр, и про идею переноса разряда. Так развивается понимание принципа «системы счисления».
Только потом можно переходить к идее двоичной системы — и вот обучаемый уже медленно, но довольно уверенно говорит «1, 10, 11, 100».
Далее, мы решили попробовать совсем не школьный метод — объяснение двоичного счёта на пальцах: это когда загнутый палец это 0, а разогнутый это 1.
Я проверял это на подростках: показываешь им: «это 1, это 2, это 3 — теперь покажите мне 4». И весь класс сосредоточенно, медленно показывает средние пальцы. Отличницы в эсхатологическом восторге, задние парты тыкают друг другу в лицо и кричат «на тебе четвёрку!».
Провокативно? Да. Запоминается? 100%.
Теперь, когда тема стала «своей», можно переходить к теме перевода чисел из одной системы счисления в другую — начать лучше с классического школьного сухого перевода (если честно, то больше чтобы постращать).
А уже потом с помощью анимации объяснить идею перевода прямо на пальцах, и потом опять же на пальцах пересчитать число 132 в средние пальцы уже на обеих руках.
На десерт показываем, где двоичная и 16-ричная системы применяется в реальной жизни.
Двоичная система — это например QR-коды вокруг нас.
А 16-ричная система это в основном коды цветов в CSS и хеши разных стилей, от MD5 до UUID.
Итак, вот весь пакет видео-уроков (они бесплатные, в Ютубе):
- Двоичная система счисления
- Перевод из 2 в 10 систему счисления
- Перевод из 10 в 2 систему счисления
- Применение двоичной системы счисления в реальной жизни
- Шестнадцатеричная система счисления
- Применение шестнадцатеричной системы счисления в жизни
- Применение восьмиричной системы счисления — права доступа к файлу
Надеемся, этот материал будет вам полезен в нелёгком деле обучения программированию.
Что такое двоичный код и как он используется в вычислениях?
К
- Рахул Авати
Двоичный описывает схему нумерации, в которой есть только два возможных значения для каждой цифры — 0 или 1 — и является основой для всего двоичного кода, используемого в вычислительных системах. Эти системы используют этот код для понимания операционных инструкций и пользовательского ввода, а также для представления пользователю соответствующих выходных данных.
Термин двоичный также относится к любой системе цифрового кодирования/декодирования, в которой есть ровно два возможных состояния. В памяти, хранении, обработке и передаче цифровых данных значения 0 и 1 иногда называют low и high соответственно. В транзисторах 1 означает поток электричества, а 0 означает отсутствие потока электричества.
Двоичная система счисления была усовершенствована в 17 веке Готфридом Лейбницем. В математике и вычислительных системах двоичная цифра или бит — это наименьшая единица данных. Каждый бит имеет единственное значение либо 1, либо 0, что означает, что он не может принимать никакое другое значение.
Компьютеры могут представлять числа с помощью двоичного кода в виде цифровых единиц и нулей внутри центрального процессора (ЦП) и ОЗУ. Эти цифровые числа являются электрическими сигналами, которые либо включены, либо выключены внутри ЦП или ОЗУ.
Двоичный и десятичный Поскольку двоичная система использует только две цифры или бита и представляет числа с использованием различных комбинаций единиц и нулей, она известна как система с основанием 2 .
Напротив, десятичная система счисления представляет собой систему с основанием 10 , где каждое возможное место в числе может быть одним из 10 цифр (0-9). В многозначном числе крайняя правая цифра стоит на первом месте, цифра рядом с ней слева — на 10-м месте, цифра левее — на 100-м месте и так далее.
Пример
В четырехзначном числе 1980 вот места, занимаемые каждой цифрой.
| 1 | 9 | 8 | 0 |
1000 место | 100 место | 10 место | 1 место |
Двоичная система счисления является основой всех вычислительных систем и операций.
- просмотр веб-сайтов;
- создавать и обновлять документы;
- играть в игры;
- просмотра потокового видео и других видов графической информации; программное обеспечение доступа
- ; и
- выполнять расчеты и анализ данных.
Двоичная схема цифровых единиц и нулей предлагает простой и элегантный способ работы компьютеров. Он также предлагает эффективный способ управления логическими схемами и определения истинного (1) и ложного (0) состояний электрического сигнала.
Как работают двоичные числа Двоичная система является основным языком вычислительных систем. Внутри этих систем двоичное число состоит из последовательности восьми битов. Эта серия известна как байт .
В двоичной схеме положение каждой цифры определяет ее десятичное значение. Таким образом, зная положение каждого бита, двоичное число можно преобразовать в десятичное число.
В десятичных числах каждое дополнительное место умножается на 10 при движении справа налево (первое место, 10-е место, 100-е место и т. д.). Но в двоичных числах каждое дополнительное место при движении справа налево умножается на два. Два приведенных ниже примера поясняют эту идею.
Пример 1
Вот как вычисляются десятичные значения для 8-битного (байтового) двоичного числа 01101000.
В этом номере первая цифра крайняя справа, а восьмая цифра крайняя левая. Цифры со второй (0) по седьмую (1) читаются справа налево.
Битовая позиция | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Бит | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
Двоично-десятичный расчет (экспонента) | 2 0 | 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 | 2 7 |
Десятичное значение (x2) | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 |
По мере увеличения позиции бита с единицы до восьми предыдущее десятичное значение умножается на два.
Вот почему первый бит имеет значение 1, второй бит имеет значение 2, третий бит имеет значение 4 и так далее.
Окончательное значение десятичного числа вычисляется путем сложения отдельных значений из приведенной выше таблицы. Однако следует добавлять только те значения, в которых бит равен 1. Эти значения представляют положение «включено». Нули представляют положение «выключено», поэтому они не учитываются при вычислении десятичного значения.
Итак, для двоичного числа 01101000 десятичное значение вычисляется следующим образом:
8 + 32 + 64 = 104
Пример 2
Вот как вычисляются десятичные значения для двоичного числа 11111111.
Битовая позиция | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Бит | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Двоично-десятичный расчет (экспонента) | 2 0 | 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 | 2 7 |
Десятичное значение | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 |
В этом двоичном числе каждый бит имеет значение 1, поэтому складываются все отдельных значений.
Итак, для этого числа , десятичное значение следующее:
1 + 2 + 4 + 8 + 16+ 32 + 64 +128 = 255
Представление десятичных чисел в двоичном форматеКак упоминалось ранее, двоичная система счисления работает только с 1 и 0. Однако положение только этих двух цифр может представлять гораздо больше чисел. Примеры в предыдущем разделе показывают, как любое десятичное число от 0 до 255 может быть представлено с помощью двоичных чисел. Числа больше 255 также можно представить, добавив больше битов к 8-битному двоичному числу.
Вот десятичные числа от нуля до 20 и их двоичные эквиваленты.
| Десятичное число | Двоичный номер | Десятичное число | Двоичный номер |
0 | 0 | 11 | 1011 |
1 | 1 | 12 | 1100 |
2 | 10 | 13 | 1101 |
3 | 11 | 14 | 1110 |
4 | 100 | 15 | 1111 |
5 | 101 | 16 | 10000 |
6 | 110 | 17 | 10001 |
7 | 111 | 18 | 10010 |
8 | 1000 | 19 | 10011 |
9 | 1001 | 20 | 10100 |
10 | 1010 | — | — |
Преобразование двоичных чисел в текстовые символыДвоичные числа можно преобразовать в текстовые символы, используя коды американского стандарта для обмена информацией (ASCII) для хранения информации в ОЗУ или ЦП компьютера. Приложения с поддержкой ASCII, такие как текстовые процессоры, могут считывать текстовую информацию из ОЗУ или ЦП. Они также могут хранить текстовую информацию, которая затем может быть извлечена пользователем позднее. Коды ASCII хранятся в таблице ASCII, состоящей из 128 текстовых или специальных символов. Каждый символ имеет соответствующее десятичное значение.
символов ASCII включают символы a-z, A-Z, 0-9 и набор знаков препинания. В первом примере предыдущего раздела двоичное число равно 01101000 (десятичное число 104). В ASCII это число будет h в нижнем регистре. Чтобы образовать слова, нужно добавить больше букв к h . В двоичном выражении это означает добавление дополнительных двоичных чисел к двоичному числу для ч .
Пример
Двоичный код строчной буквы ASCII i равно 01101001. Итак, чтобы создать слово hi , двоичное число для i добавляется к двоичному числу для h . Это дает следующее двоичное число:
.01101000 + 01101001 = 0110100001101001
В десятичном выражении десятичные числа для h и i равны 104 и 105 соответственно.
Другими распространенными примерами преобразования двоичных чисел в текстовый код ASCII являются следующие.
| Двоичный номер | Десятичное число | Код ASCII |
110000 | 48 | 0 |
1000001 | 65 | А (верхний регистр) |
1111111 | 127 | Клавиша DEL |
11011 | 27 | Клавиша ESC |
См.
также: Символы ASCII ; киби, меби, гиби, теби, пеби и эксби ; кодирование и декодирование ; старший бит или байт ; и Расширенный двоично-десятичный код обмена .
Последнее обновление: май 2022 г.
Продолжить чтение о бинарнике- Объяснение двоичных и шестнадцатеричных чисел для разработчиков
- Новые функции Java 7: двоичная запись и литеральная инициализация переменных
- Введение в бинарное сравнение для этичных хакеров
- ТБ и ГБ: терабайт больше гигабайта?
- Преобразование двоичного кода в десятичный
распознавание голоса
Распознавание голоса или говорящего — это способность машины или программы принимать и интерпретировать диктовку или понимать и выполнять голосовые команды.
Сеть
- система управления сетью
Система управления сетью, или NMS, представляет собой приложение или набор приложений, которые позволяют сетевым инженерам управлять сетевыми .
.. - хост (в вычислениях)
Хост — это компьютер или другое устройство, которое взаимодействует с другими хостами в сети.
- Сеть как услуга (NaaS)
Сеть как услуга, или NaaS, представляет собой бизнес-модель для предоставления корпоративных услуг глобальной сети практически на основе подписки.
..Безопасность
- API веб-аутентификации
API веб-аутентификации (WebAuthn API) — это программный интерфейс приложения (API) для управления учетными данными, который позволяет …
- Общая система оценки уязвимостей (CVSS)
Общая система оценки уязвимостей (CVSS) — это общедоступная система оценки серьезности уязвимостей безопасности в …
- Вредоносное ПО Dridex
Dridex — это форма вредоносного ПО, нацеленное на банковскую информацию жертв с основной целью кражи учетных данных онлайн-аккаунта .
..
..ИТ-директор
- программа аудита (план аудита)
Программа аудита, также называемая планом аудита, представляет собой план действий, в котором документируются процедуры, которым аудитор будет следовать для проверки …
- децентрализация блокчейна
Децентрализация — это распределение функций, контроля и информации вместо того, чтобы быть централизованным в едином учреждении.
- аутсорсинг
Аутсорсинг — это деловая практика, при которой компания нанимает третью сторону для выполнения задач, управления операциями или предоставления услуг…
HRSoftware
- командное сотрудничество
Совместная работа в команде — это подход к общению и управлению проектами, который делает упор на командную работу, новаторское мышление и равенство ..
. - самообслуживание сотрудников (ESS)
Самообслуживание сотрудников (ESS) — это широко используемая технология управления персоналом, которая позволяет сотрудникам выполнять множество связанных с работой …
- платформа обучения (LXP)
Платформа обучения (LXP) — это управляемая искусственным интеллектом платформа взаимного обучения, предоставляемая с использованием программного обеспечения как услуги (…
.Служба поддержки клиентов
- сегментация рынка
Сегментация рынка — это маркетинговая стратегия, в которой используются четко определенные критерии для разделения общей адресной доли рынка бренда …
- воронка продаж
Воронка продаж — это визуальное представление потенциальных клиентов и того, где они находятся в процессе покупки.
- анализ потребительской корзины
Анализ потребительской корзины — это метод интеллектуального анализа данных, используемый розничными торговцами для увеличения продаж за счет лучшего понимания покупательских покупок.
..
..Как работает двоичная система?
МАТЕМАТИКА — Числа
Задумывались ли вы когда-нибудь…
- Как работает двоичная система?
- Как называется двоичная цифра?
- Какие числа использует двоичная система?
Теги:
Просмотреть все теги
- Математика,
- Компьютер,
- Электронный,
- цифровой,
- Устройство,
- Технология, Код
- ,
- Программное обеспечение,
- Двоичная система,
- Основание-10,
- Номер, Система
- ,
- База-2,
- цифра,
- Бит,
- Место,
- Значение,
- Электричество,
- Переключатель,
- Цепь,
- Письмо,
- Символ,
- Математика,
- Компьютер,
- Электронный,
- цифровой,
- Устройство,
- Технология, Код
- ,
- Программное обеспечение,
- Двоичная система,
- База-10,
- Номер,
- Система,
- База-2,
- цифра,
- Бит,
- Место,
- Значение,
- Электричество,
- Переключатель,
- Цепь,
- Письмо,
- Символ
Сегодняшнее чудо дня было вдохновлено Нихилом.
Нихил Уондерс , “ Как двоичная последовательность преобразуется в символ? «Спасибо, что ДУМАЕТЕ вместе с нами, Нихил!
Как часто вы пользуетесь компьютером? Если вы подумаете обо всех гаджетах, которые вы используете каждый день, вы, вероятно, поймете, что используете больше компьютеров, чем думаете. Помимо ноутбуков или настольных компьютеров, которые вы используете в школе или дома, вы также можете использовать калькуляторы, смартфоны, планшеты, музыкальные плееры, электронные ридеры, цифровые видеомагнитофоны, видеоигры и всевозможные другие устройства.
В современном мире, наполненном технологиями, трудно не пользоваться компьютерами. На самом деле, мы держим пари, что многие из наших чудесных друзей однажды будут работать на работах, которые требуют от вас постоянного использования компьютеров. Некоторые из вас могут даже собирать компьютеры или писать код для создания программного обеспечения, видеоигр и приложений для смартфонов!
Когда вы изучаете основы компьютерного программирования, вы рано узнаете, что в основном все, что входит (ввод) или выходит из (выход) компьютера, состоит из последовательности нулей и единиц.
В этом суть цифровых данных, и они основаны на двоичной системе.
Когда вы изучаете математику в школе, вы используете систему счисления с основанием 10. Это означает, что ваша система счисления состоит из 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Когда вы прибавляете единицу к девяти, вы перемещаете 1 на одно деление влево в десятки. расставьте и поставьте 0 вместо единиц: 10.
Двоичная система, с другой стороны, является системой счисления с основанием 2. Это означает, что он использует только два числа: 0 и 1. Когда вы прибавляете единицу к единице, вы перемещаете единицу на единицу влево на разряд двоек и ставите 0 на разряд единиц: 10. Итак, в системе с основанием 10 системе 10 равно десяти. В системе с основанием 2 10 равняется двум.
В системе с основанием 10, с которой вы знакомы, разрядные значения начинаются с единиц и увеличиваются до десятков, сотен и тысяч по мере продвижения влево. Это потому, что система основана на степенях числа 10.
Аналогично, в системе с основанием 2 разряды начинаются с единиц и переходят к двойкам, четверкам и восьмерам по мере продвижения влево.
Это потому, что система с основанием 2 основана на степени двойки. Каждая двоичная цифра известна как бит.
Не волнуйтесь, если двоичная система сейчас кажется запутанной. Это довольно легко подобрать, если вы поработаете с ним некоторое время. Сначала это кажется запутанным, потому что все числа состоят только из 0 и 1. Знакомая система с основанием 10 так же проста, как 1-2-3, а двоичная система с основанием 2 так же проста, как 1-10-11.
Вам может быть интересно, почему компьютеры используют двоичную систему. Компьютеры и другие электронные системы работают быстрее и эффективнее, используя двоичную систему, потому что использование в системе только двух чисел легко воспроизвести с помощью системы включения/выключения.
Электричество либо включено, либо выключено, поэтому устройства могут использовать переключатель включения/выключения в электрических цепях для простой обработки двоичной информации. Например, off может равняться 0, а on может равняться 1.
Каждая буква, цифра и символ на клавиатуре представлены восьмибитным двоичным числом.
Например, для вашего компьютера буква А на самом деле 01000001!
Чтобы помочь вам лучше понять двоичную систему и ее связь с десятичной системой, с которой вы знакомы, вот как десятичные числа 1–10 выглядят в двоичной системе:
1 = 1
2 = 10
3 = 11
4 = 100
5 = 101
6 = 110
7 = 111
8 = 1000
9 = 1001
10 = 1010
Common Core, Научные стандарты следующего поколения и Национальный совет по социальным исследованиям.»> Стандарты: CCRA.L.3, CCRA.L.6, CCRA.R.1, CCRA.R.2, CCRA.R.4, CCRA.R.10, CCRA.SL.1
Интересно, что дальше?
Мы не хотим на вас давить, но надеемся, что завтра вы присоединитесь к нам в Вандерополисе!
Попробуйте
Готовы ли вы узнать больше о силе нулей и единиц? Попросите друга или члена семьи помочь вам изучить следующие виды деятельности:
- Чувствуете себя хитрым? Вы можете узнать больше о двоичных числах и о том, как компьютеры используют их как часть своего кода, с помощью этого веселого задания «Ожерелье двоичного кода».
