Как понять дроби: Как объяснить дроби

Для начала объясните ребенку понятия “часть” и “целое”. Вот шоколадка, целая, вкусная. Она состоит из долек, кусочков, частей. Предположим, их 10. Малыш отломал кусочек — и вот у него в руках 1 кусочек из 10. Отломал еще для мамы кусочек — получилось уже два кусочка из 10. Регулярно повторяйте подобные эксперименты с пиццей, мандаринами или стаканом молока. Теория должна хорошенько закрепиться и усвоиться. Отрабатывать полученные знания на практике можно также на нашем сайте — в блоке “Обучение” есть много интересных заданий по математике, с помощью которых ребенок может потренироваться в изучении частей и целого.

Далее можно приступать к объяснению понятия “доли”. Пусть ребенок разделит апельсин или шоколадку на равные части, чтобы всем хватило и никто не обиделся. Эти части называются доли. Доли — это то, из чего состоит целый предмет. В шоколадке, состоящей из 10 равных кусочков, 10 долей. Если яблоко разрезать пополам, будет две доли, каждая из которых представляет собой половину целого яблока.

Когда ребенок достаточно успешно разберется в том, что такое часть, целое и доли, можно вводить понятие “дробь” и начинать дробить вместе с ним все, что попадется под руку: те же шоколадки или яблоки. Смысл самого процесса остается прежним. Дроби придумали для того, чтобы обозначать количество долей, взятых из целого и оставшихся в целом. Показатель под чертой (знаменатель) обозначает количество долей в целом предмете, а число над чертой (числитель) — количество долей, которые мы хотим взять. То есть если у нас была шоколадка из 5 равных кусочков, а мы взяли 1, то дробь, выражающая это наше действие, выглядит как 1/5, а произносится как “одна пятая” (слово доля здесь опускается, но подразумевается).

Целый предмет тоже можно выразить через дробь. Для демонстрации этого отлично подойдет упаковка конфет. Коробочка целая, если в ней 10 конфет, каждая конфетка на своем месте. 10 конфет — 10 частей, и целая упаковка — 10 штук. Получается, что 10/10 — это целая упаковка конфет, 1 упаковка.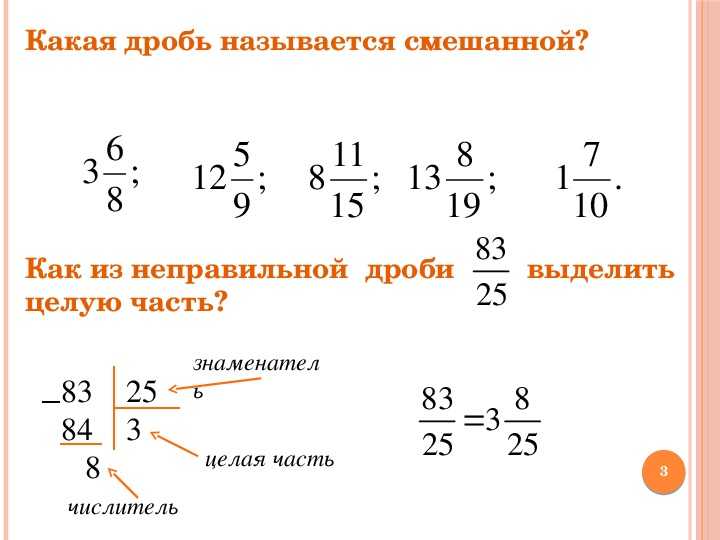 При изображении целого числа с помощью дроби числитель и знаменатель — всегда одно и то же число, обозначающее все доли, составляющие целый предмет.

Таким образом, если ребенок уже умеет писать и готов учиться записывать дроби, постарайтесь постоянно напоминать ему последовательность, задавая наводящие вопросы. Сколько всего частей в целом предмете? Пишем под чертой. А сколько частей мы взяли из этого целого предмета? Пишем над чертой. Это довольно просто, если разобраться.

Автор: педагог-психолог Антонина Валевич

Понравилось? Поделитесь с друзьями:

Онлайн-занятия на сайте «Разумейкин»:

• развивают внимание, память, мышление, речь — а именно это является основой для успешного обучения в школе;

• помогают изучить буквы и цифры, научиться читать, считать, решать примеры и задачи, познакомиться с основами окружающего мира;

• обеспечивают качественную подготовку ребёнка к школе;

• позволяют ученикам начальных классов освоить и закрепить наиболее важные и сложные темы школьной программы;

• расширяют кругозор детей и в доступной форме знакомят их с основами различных наук (биологии, географии, физики, химии).

Дроби — как объяснить ребенку действия с дробями

Тема дробей — одна из самых непростых для школьников. Понять их неподготовленному ребенку, а тем более выполнять с ними операции, может быть достаточно сложно. Но даже самая трудная задача может стать простой и понятной, если правильно к ней подойти. Для детей нужно использовать фантазию, наглядность и элементы игры. А также – сохранять спокойствие и терпеливо объяснять, даже если это потребуется сделать много раз.

Как объяснить суть дробей ребенку?

Слово «дробь» будто говорит само за себя — оно означает дробление, деление. В школьной программе к изучению дробей приступают только в 5 классе, освоив все действия с целыми числами. Но знакомство с ними целесообразно начинать заранее, еще в старшем дошкольном возрасте. Это формирует пространственные представления у детей и тренирует логическое мышление.

Для начала нужно объяснить ребенку понятие долей. Это очень легко сделать на наглядных повседневных примерах. Самый простой и доступный — еда. Например, пирог — целый. Разделить его можно на несколько одинаковых частей. Один кусочек такого пирога и будет называться одной долей из всех возможных. Поделив пирог на четыре части, один кусочек называют одной четвертой частью.

Таким образом делить можно все, что угодно: яблоки, апельсины, плитки шоколада, конфеты в коробке и т. д. Еще один прекрасный наглядный материал для изучения дробей — кубики конструктора Lego. С их помощью можно поделить целое на равные части очень легко. Дети быстро запоминают форму кубиков, и им не требуется постоянно пересчитывать количество выступающих элементов на них.

Если ребенок увидит практическое применение дробей и востребованность их в реальной жизни, ему будет проще понять их и осознать важность получения математических знаний и навыков.

Что нужно знать о дробях?

1. Дробь — число нецелое, оно обозначает количество долей целого.

2. Дробь меньше целого.

3. Чем на большее число долей поделено целое, тем эти доли меньше и наоборот — чем долей меньше, тем они, соответственно, больше.

Для обозначения долей в математике используют понятие обыкновенная дробь. С ее помощью можно записать абсолютно любое необходимое количество долей.

Обыкновенная дробь представляет собой две части, именуемые числителем и знаменателем. Записываются они разделенными горизонтальной чертой либо наклонной вправо линией. Знаменатель пишется внизу либо справа от дробной черты, он показывает общее количество частей от целого, на которое оно было поделено. А числитель пишется вверху или слева от дробной черты и показывает, сколько долей целого сейчас взяли.

Вернемся к нашему пирогу. Очевидно, что разделить его реально на сколько угодно равных частей. В зависимости от того, на сколько частей его разделили, меняется и знаменатель дроби. У пирога, разделенного одной прямой линией на две части, знаменатель будет равен 2, у разделенного на три части — 3 и т. д. Числитель же, в свою очередь, показывает, сколько частей сейчас взято. Если взяли только одну часть из двух, то получится дробь 1/2, только две из трех — 2/3 и т.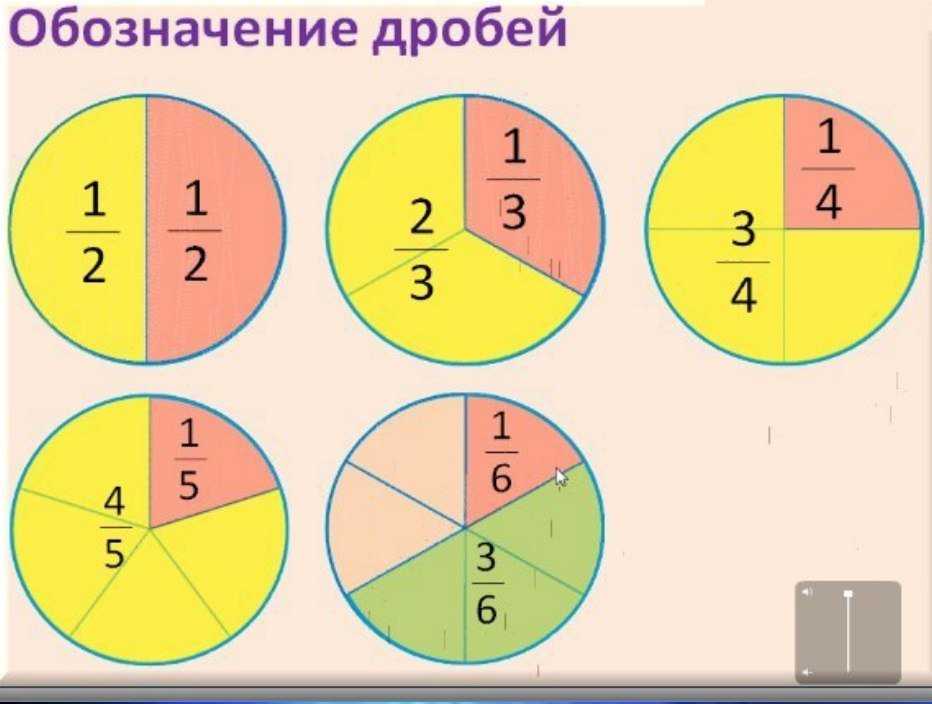 д.

Что такое смешанные дроби?

В математике выделяют дроби правильные и неправильные. Правильные — те, у которых числитель меньше знаменателя. Например:

У таких дробей можно отделить целую часть и оставшуюся после этого дробную. То есть будет видно, сколько взято целых пирогов и плюс определенное количество его частей. Нужно хорошо представить себе описанное, или даже проверить на практике, а не просто заучивать формулы. Тогда сокращение дробей будет выполняться ребенком осмысленно и безошибочно.

Для того чтобы трансформировать неправильную дробь в смешанное число, следует сперва числитель поделить на знаменатель. В результате почти всегда получим целое число и какой-то остаток. Целое число и нужно записать, как целую часть.

Неправильными называют и дроби с одинаковым числом над и под дробной чертой: 6/6, 12/12 и т. д. Очевидно, что превратить их можно в 1. Наглядно это взято столько кусочков пирога, на сколько он и был поделен, т. е. целый пирог.

Примеры:

• 14/5 = (5*2+4) / 5 = 2 4/5
• 21/6 = (6*3+ 3) / 6 = 3 3/6

Задание:

Выделите целую часть из неправильных дробей:

• 15/4,
• 22/12,
• 30/7.

Можно провести противоположную процедуру — превратить смешанное число в неправильную дробь. Эта операция часто применяется в математических вычислениях, поэтому будет полезным узнать о ней. Для этого нужно сперва умножить целую часть и знаменатель. Затем получившееся число прибавить к числителю, а знаменатель оставить прежним.

Примеры:

• 3 1/8 = (3*8+1) / 8 = 25/8
• 7 4/9 = (7*9+4) / 9 = 67/9

Задание:

1. Преобразовать в смешанное число неправильную дробь:

• 27/4,
• 18/5,
• 45/7.

2. Выполнить обратную первой задачу — смешанное число превратить в неправильную дробь:

• 3 4/5;
• 12 7/11.

Десятичные дроби

Дроби, в знаменателях которых есть числа, кратные десяти — 10, 100, 1000 и т. д. — в математике можно обозначать следующим образом. Сначала пишется целая часть, а потом числитель из дробной части, отделенный запятой.

Например, 5 4/10 попробуем записать в виде десятичной дроби. Пишем целую часть (5), ставим запятую и далее пишем числитель дробной части (4). Получаем: 5,4. Читается эта дробь так: «пять целых и четыре десятых». Число, представленное в таком виде, именуется десятичной дробью.

Существуют также десятичные дроби без целой части. Например: 7/100. Как быть в таком случае? Чтобы записать подобную дробь, пишут ноль, ставят запятую и далее записывают числитель дроби — 0,07. Такая дробь читается как «ноль целых, семь сотых».

Десятичные дроби очень удобны, они используются в точных вычислениях. Десятичная система исчисления  применяется человечеством с самых древних времен. Она интуитивна понятна и проста.

Задание:

Преобразовать следующие дроби в десятичные:

• 8/10,
• 4/100,
• 7/1000.

Сокращение дробей

Сокращение дробей выполняют для того, чтобы их упростить. Если числитель и знаменатель дроби таковы, что делятся на одно и то же число (имеют общий делитель), то можно просто разделить их на это число, упростив тем самым дробь. Эта математическая операция называется сокращением дробей. Чтобы разобраться с этим, рассмотрим пару таких примеров.

Пример 1. Сократить дробь 8/12

Решение будет следующим. Наибольшее число, на которое делятся и 8, и 12, — это 4. Поэтому, чтобы сократить дробь, просто поделим ее числитель и знаменатель на 4:

8/12 = 8:4 / 12:4 = 2/3

Пример 2.

Решение. Наибольшее число, на которое делятся и 10, и 25, — это 5. Потому, чтобы сократить дробь, поделим ее числитель и знаменатель на 5:

10/25 = 10:5 / 25:5 = 2/5

Несократимой называется дробь, у которой числитель и знаменатель имеют только один общий делитель — единицу.

Задание:

Сократите следующие дроби:

• 6/18,
• 20/40;
• 7/21.

Сложение дробей

Сначала разберем сложение дробей с одинаковыми знаменателями. В этом случае операция предельно простая. Складываются числители дробей, а знаменатель остается прежним.

Примеры:

• 1/7 + 2/7 = 3/7
• 3/8 + 5/8 = 8/8 = 1

Задание:

Выполни сложение дробей с одинаковыми знаменателями:

Но все усложняется, если нужно сложить дроби с разными знаменателями. В этом случае необходимо привести дроби к наименьшему общему знаменателю. Чтобы это сделать, необходимо найти наименьшее общее кратное. Это такое число, которое делится на оба эти числа без остатка. Например: 3/7 + 2/6. Наименьшее общее кратное для чисел 7 и 6 будет 42.

Далее ищем дополнительные множители для каждой из дробей. Для этого найденное на предыдущем этапе наименьшее общее кратное делим по очереди на знаменатель каждой из дробей:

• 42 / 7 = 6 — это будет дополнительный множитель для 3/7;
• 42 / 6 = 7 — это, соответственно, дополнительный множитель для 2/6.

Обе части каждой из наших дробей, и числитель и знаменатель, умножаем на свой, определенный выше, множитель:

• 3*6 / 7*6 = 18/42;
• 2*7 / 6*7 = 14/42.

Складываем полученные дроби аналогичным образом, как уже разобранные выше дроби с одинаковыми знаменателями:

• 18/42 + 14/42 = 32/42

Если это возможно, то дробь сокращают. Если дробь получилась неправильная, то следует целую часть из нее выделить.

Задание:

Выполни сложение дробей с разными знаменателями:

Вычитание дробей

Эта операция проводится аналогично сложению.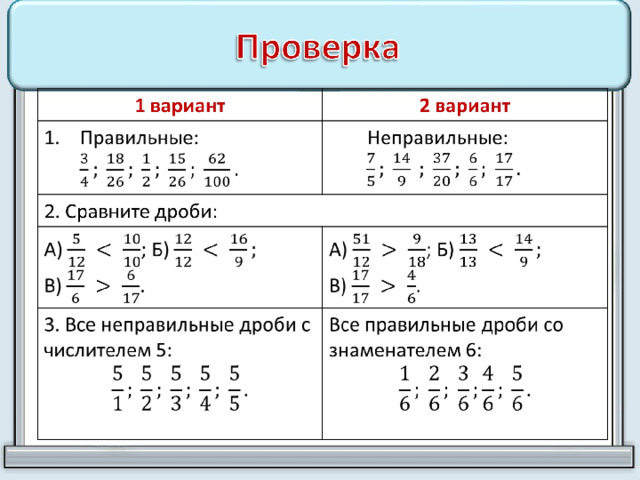 Чтобы вычесть две дроби с одинаковыми знаменателями, нужно найти разность их числителей, а знаменатель оставить тем же.

Пример:

7/9 — 2/9 = (7-2) / 9 = 5/9

Задание:

Выполни вычитание дробей с одинаковыми знаменателями:

Для дробей с разными знаменателями также придется найти наименьшее общее кратное и дополнительные множители. Затем, по аналогии со сложением, произвести вычитание.

Пример:

6/7 — 8/10 = (6*10-8*7) / 70 = (60-56) / 70 = 4/70

Задание:

Выполни вычитание дробей с разными знаменателями:

Умножение дробей

Существует два варианта умножения дробей. Рассмотрим каждый из них в деталях.

Умножение обыкновенных дробей

В этом случае числители обеих дробей перемножаются — это будет новый числитель. Знаменатели обеих дробей также перемножаются — это будет новый знаменатель.

Пример:

2/5 * 3/4 = (2*3) / (5*4) = 6/20 = 3/10

Если это возможно, то следует сократить дроби перед перемножением. Это облегчит дальнейшие действия.

Пример:

24/35 * 25/36 = (24*25) / (35*36) = (2*5) / (7*3) = 10/21

Умножение смешанных дробей

Чтобы это сделать, необходимо превратить дроби в неправильные и далее действовать по алгоритму, приведенному в первом пункте.

Пример:

4 2/7 * 5 3/5 = 30/7 * 28/5 = (30*28) / (7*5) = (6*4) / (1*1) = 24/1 = 24

Задание:

Выполните умножение дробей:

• 5/7 * 6/8;
• 6/11 * 2/3;
• 2 3/7 * 4 5/9;
• 4 6/7 * 7 9/10.

Деление дробей

Освоив умножение, с делением также можно справиться легко. Правило деления дробей заключается в следующем: при делении одной дроби на другую нужно первую перемножить на обратную (перевернутую) вторую дробь. Или, иными словами, числитель первой умножить на знаменатель второй (это будет новый числитель), а знаменатель первой умножить на числитель второй (это будет новый  знаменатель).

Пример:

4/7 : 2/5 = 4/7 * 5/2 = 20/14 = 10/7 = 1 3/7

Бывают ситуации, когда дробь нужно разделить на целое число. В этом случае следует представить дробь как неправильную. Числителем у нее будет это целое число, а знаменателем просто единица. Далее действовать нужно по уже знакомому правилу деления дробей из предыдущего случая.

Пример:

5/9 : 2 = 5/9 : 2/1 = (5*1) / (9*2) = 5/18

Задание:

Выполните деление дробей:

• 6/11 : 3;
• 7/15 : 2;
• 9/12 : 4.

Сравнение дробей

Если сравниваются дроби с одинаковыми знаменателями, то очевидно, что большей будет та, числитель у которой больше.

Пример:

1/5 < 4/5, так как знаменатели одинаковы, а в числителе 1 меньше 5.

Если сравниваются дроби с одинаковыми числителями, то большей будет та, знаменатель у которой меньше.

Пример:

1/2 > 1/8, так как числители одинаковы, а в знаменателе 8 больше 2.

Дроби же с разными знаменателями так просто не сравнишь. Нужно сперва определить их общий знаменатель и привести к нему обе дроби. Правила этой операции были приведены выше. Получим дроби, сравнить которые можно очень легко.

Пример:

Сравниваем дроби 2/5 и 1/10. Для этого приводим их к общему знаменателю — 10. Получаем 4/10 и 1/10. Теперь сравниваем дроби, уже имеющие одинаковые знаменатели: 4/10 > 1/10.

Есть один секрет, который нужно запомнить. Если одна из сравниваемых дробей неправильная, то она всегда больше правильной. Если подумать и вспомнить свойства дробей, то все становится понятно.  Ведь неправильная дробь всегда будет больше единицы, тогда как правильная, наоборот, всегда будет меньше.

Задание:

Определите, какие дроби изображены на рисунке, и сравните их:

Итак, мы рассмотрели дроби, правила всех действий с ними. Надеемся, что наши объяснения и рекомендации будут очень полезны. Начинайте знакомить детей с дробями еще до школы. Хорошо усвоив эти понятия, ребенок без труда справится затем и с записью дробей, и с действиями с ними.

Математика и логика для детей 7-13 лет

Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате

узнать подробнее

Читайте также:

• Таблица умножения для детей
• Как объяснить ребенку состав числа?

Способ облегчить понимание дробей учащимися старших классов

Факты умножения. Я никогда не понимал, почему за все те годы, что я преподавал математику, мы все еще называем строки и столбцы пропущенных чисел фактами умножения. На мой взгляд, разве они не являются фактами деления? 5 х 6 равно 30, что я довольно легко могу найти на моей таблице умножения, но 30 разделить на 5 имеет только один ответ, 6. Все, что мне нужно сделать, это найти 30 на таблице, найти 5 слева, и я найдем 6 выше. Вуаля. Я могу использовать ту же самую диаграмму, что и диаграмму фактов деления, чтобы найти ответ, если я думаю об этом таким образом.

Я также обнаружил другие способы использования этой диаграммы, которые могут помочь новым учителям упростить понимание учащимися более сложных математических понятий.

Один из моих любимых способов использовать это с дробями. В течение года мы с учениками «развиваем» таблицу умножения в таблицу дробей. Я хотел бы поставить себе в заслугу все способы, которыми я научился пользоваться этой развитой диаграммой, но я не могу. Год за годом дети придумывают самые невероятные способы его использования для любой части работы с дробями, о которой только можно подумать. Вот некоторые из них, которые были успешными в моем классе.

1. Используйте таблицу дробей для поиска эквивалентов

Равнозначные дроби часто находятся путем умножения или деления на одно и то же число как числителя, так и знаменателя. Например, 4/8 можно разделить на 2, чтобы найти 2/4. Или 4/8 можно умножить на 2, чтобы получить 8/16. Обе эти дроби равны 1/2. Хорошо, если новые учителя также обязательно помогут учащимся построить модели этих эквивалентов.

Таблица умножения также может дать вам эквивалентные дроби, просто выровняв числитель и знаменатель в одном столбце. Попробуйте. Найдите 4 и 8 на диаграмме, где 4 и 8 находятся в одном столбце. Двигайтесь вправо и найдите эквивалентные дроби или влево и найдите эквивалентные дроби. Правильный выбор означает, что дробь имеет больше частей, но они меньше. Движение влево означает, что дробь имеет меньше частей, но части больше. Работает для любой дроби. Для 6/24 идите вправо на один столбец и получите 7/28 или на два столбца и получите 8/32. Вернитесь на один столбец назад и получите 5/20. Продолжайте, и все эти дроби равны 1/4.

Предоставлено Томасом Кортни

2. Используйте таблицу дробей для упрощения дробей

Мои студенты и я часто пользуемся таблицей, чтобы наши ответы были в самой простой форме. Скажите, что ваш ответ 32/40. Как правило, мы можем обнаружить наибольший общий делитель, или GCF, и «разделить». Это дает нам 32, деленное на GCF 8, что равно 4, и 40, деленное на 8, что равно 5. Следовательно, 32/40 равно 4/5 в простейшей форме. Но не все видят это так просто, и даже создание моделей может занять много времени. Просто найдите 32 и 40 на графике, когда они находятся в одном столбце. Затем двигайтесь влево, пока не дойдете до первого столбца, что дает вам 4/5.

Обратите внимание: если дроби, которые вы хотите упростить, находятся не в соседних строках, вы можете получить более простые дроби, которые не будут полностью упрощены. Например, используя тот же метод, 36/48 приведет вас влево к 6/8, что не полностью упрощено. Если вы затем возьмете 6/8 в столбце, где они оказались в соседней строке, вы получите упрощенную дробь 3/4, сдвигая влево.

3. Используйте таблицу дробей для сравнения дробей

У каждого есть система для сравнения дробей. В моем классе мы строим числовые ряды, делаем модели и особенно находим общие знаменатели. Но опять же, таблица дробей здесь, чтобы помочь. Возьмем 1/4 и 1/5. Мы знаем, что 1/4 больше, чем 1/5. Может быть, мы видим модель в наших умах. Возможно, мы знаем, что 4 — это меньше штук, и поэтому 1 из 4 — это большая доля, чем 1 из 5.

Предоставлено Томасом Кортни

Может быть, мы преобразуем каждую дробь так, чтобы в знаменателе было 20, и мы обнаружим, что 5/20 больше, чем 4/20. Мы можем использовать таблицу дробей в качестве резервной копии. Просто найдите 1 и 4 в самом левом столбце, а также найдите 1 и 5. Переместите 1/4 и 1/5 на графике, пока не дойдете до того же знаменателя, 20. Вы заметите, что 1/5 стопов сначала на 4/20, а 1/4 продолжается, пока не достигнет 5/20. Это работает и с другими фракциями. Например, 2/5 и 2/3: 2/5 останавливается на 6/15, а 2/3 продолжается до 10/15. Следовательно, 2/3 или 10/15 больше, чем 2/5 или 6/15.

4. Используйте таблицу дробей для сложения и вычитания дробей

Если учащийся прибавляет 1/3 к 1/4 и получает 2/7, мы знаем, что это неправильный ответ, потому что 1/3 и 1/4 равны двум. фракции разного размера. Чтобы решить эту проблему, мы обычно находим общий знаменатель, чтобы складывать куски одинакового размера. Хорошая новость заключается в том, что наша таблица дробей — это готовый способ найти наименьшее общее кратное, или НОК.

Предоставлено Томасом Кортни

Учащиеся могут проследить пропущенные числа как в строке 3, так и в строке 4, пока не получат 12 в качестве НОК для обоих чисел. Затем они могут правильно подсчитать количество перемещений или столбцов, которые они переместили, чтобы попасть туда. Это говорит им, на что умножать как для числителя, так и для знаменателя. В этом случае было перемещено четыре столбца, чтобы 3 стало 12, поэтому 1/3 умножается сверху и снизу на 4 и получается 4/12. Между тем, мы переместили три столбца, чтобы получить 1/4 к общему знаменателю 12. Таким образом, 1/4 умножается сверху и снизу на 3, чтобы получить 3/12.

Конечно, ученики могут просто написать числа, кратные 3 и 4. Большинство учебников по математике даже предлагают это делать. Но не все студенты способны на это или имеют время. В моем классе было много учеников с особыми потребностями, и они с большим успехом используют диаграмму дробей. Наличие другого ресурса для закрепления этих концепций очень полезно для студентов.

Я обнаружил, что важно думать о диаграмме как о ресурсе, а не как об уловке. Часто это еще один инструмент для проверки их работы, и моим детям это нравится, потому что мы все пытаемся доказать свою работу. В моем классе учащиеся по-прежнему много работают с моделями и оценивают, но мы также узнаем, как наша таблица умножения может проверить нашу работу с дробями.

Вместо того, чтобы скрывать от учащихся закономерности, существующие в таблице, почему бы не позволить им использовать ее, пока они находят закономерности в эквивалентности дробей, упрощают и сравнивают дроби, а также складывают или вычитают дроби? Эти расчеты, как известно, сложны для детей, но использование таблицы дробей дает им еще один способ определить разумность и предсказуемость ответов.

Как учить дроби для взрослых

Обновлено 24 апреля 2017 г.

Автор: вторник Фуллер

Дроби используются в математике для представления различных математических данных. Дробь 3/4 представляет отношение (три из четырех кусков пиццы были с пепперони), измерение (три четверти дюйма) и задачу деления (три разделить на четыре). В элементарной математике у некоторых учеников возникают проблемы с пониманием сложности дробей и их процессов. Взрослые, однако, столкнулись с различными методами обучения и опытом и разработали больше способов понимания дробей. Эти новые навыки дают возможность взрослому освежить в памяти дроби и изучить новые математические концепции и приложения.

Определение частей дроби

Посмотрите на дробь 3/4. Диагональная косая черта, обычно называемая косой чертой, представляет собой солидус и разделяет два числа.

Найдите числитель. Числитель равен 3 и представляет части целого, например. трое из четырех щенков были черными. Он также представляет собой дивиденд в задаче о делении, например. три разделить на четыре.

Найдите знаменатель. Знаменатель равен четырем и представляет целую часть, например. весь помет щенков. Он также представляет делитель, число, выполняющее деление.

Определение типов дробей

Посмотрите на следующий список дробей: 1/2, 6/5, 1 1/5 и 17/1.

Выберите дробь, представляющую правильную дробь. У правильной дроби числитель меньше знаменателя. В данном случае 1/2 — правильная дробь.

Выберите неправильную дробь, т. е. дробь, у которой числитель больше знаменателя. Дроби, написанные таким образом, не являются неправильными, а вместо этого представляют собой сокращенные способы записи смешанных чисел. Дробь 6/5 неправильная дробь.

Найдите дробь, являющуюся смешанным числом. Смешанное число содержит как целую цифру, так и дробь. 1 1/5 — смешанное число. Если смешанное число записать в виде неправильной дроби, то оно будет 6/5.

Посмотрите на дробь 17/1. Это представляет термин «невидимый знаменатель». Под всеми целыми числами находится невидимый знаменатель 1. (Если вы разделите число на 1, вы получите то же число. )

Сложение и вычитание дробей

Добавить 3/7 + 2/7. Знаменатели одинаковы, поэтому сначала добавьте числители: 3 + 2 = 5. Оставьте знаменатель прежним. Ответ 5/7.

Вычесть 9/10 – 8/10. Опять же, знаменатели одинаковы, поэтому вычтите числители и оставьте знаменатель прежним: 9 – 8 = 1. Напишите 1 над знаменателем для решения, 1/10.

Добавить 2/5 + 4/7. Знаменатели теперь другие. Чтобы вычесть эти две дроби, они должны представлять одно и то же целое, т. е. из квадратов нельзя брать круги. Вместо этого преобразуйте дроби так, чтобы они были эквивалентны и имели один и тот же знаменатель или целые.

Найдите наименьшее общее кратное (НОК) между 5 и 7, т.е. одно и то же число и 5, и 7 делятся нацело. Самый простой способ — умножить 5 на 7, чтобы получить произведение 35.

Умножьте числитель 2 на тот же коэффициент, который используется для определения НОК, например. 2 х 7 = 14. Эквивалент первой дроби равен 14/35.

Умножьте числитель 4 на тот же коэффициент LCM, который использовался для преобразования 7 в 35, например. 4 х 5 = 20. Эквивалент второй дроби равен 20/35. Теперь, когда оба знаменателя одинаковы, складываем как обычно: 14/35 + 20/35 = 34/35.

Вычесть 6/8 – 9/10. Найдите НОК, чтобы составить эквивалентные дроби с одинаковым знаменателем. В этом случае и 8, и 10 идут в 40 поровну.

Умножьте числители на множители, используемые для получения одинаковых знаменателей: 6 x 5 = 30 и 9 x 4 = 36. Перепишите дроби в их эквивалентных формах: 30/40 – 36/40.

Вычесть числители 30 – 36 = -6. Дробь -6/40 приводится к более простой форме. Разделите числитель и знаменатель на 2, чтобы получить дробь в наименьшей форме, -3/20. (При написании вертикально не имеет значения, падает ли отрицательный знак на числитель или знаменатель, или если он написан перед всей дробью.)

Умножение и деление дробей

Умножение дроби 3/4 x 1/2. Для этого умножьте оба числителя, а затем оба знаменателя. Ответ 3/8.

Разделить 4/9 ÷ 2/3. Для этого сначала переверните вторую дробь, называемую обратной, и умножьте две дроби.

Перепишите задачу, чтобы отразить обратную величину второй дроби и изменение операции: 4/9 x 3/2.

Умножьте как обычно: 4 x 3 = 12 и 9 x 2 = 18. Ответ: 12/18. Оба числа делятся на 6 для дроби в простейшей форме: 2/3.

Сравнение дробей

Сравните дроби 6/11 и 3/12. Чтобы сравнить дроби, используйте процесс, называемый перекрестным умножением, чтобы увидеть, какая дробь больше.

Умножьте 12 x 6, чтобы получить 72. Напишите 72 над первой дробью.

Умножьте 11 x 3, чтобы получить 33. Напишите 33 над второй дробью. Сравнивая два числа над дробями, становится ясно, что 6/11 больше, чем 3/12.

Преобразование дробей

Преобразование 8/9до десятичной. Разделите числитель на знаменатель: 8 ÷ 9 = 0,8 повторения.

No related posts.