Как посчитать на инженерном калькуляторе логарифм: Как считать логарифм с калькулятором 🚩 как считать на инженерном калькуляторе 🚩 Математика

Как посчитать lg на калькуляторе

Десятичный логарифм

Логарифм, взятый по основанию 10 , носит название — десятичный логарифм.

Десятичные логарифмы принято обозначать так: lg N.

Десятичный логарифм единицы равен нулю.

Десятичный логарифм чисел 10 , 100 , 1000 равен соответвенно 1 , 2 , 3 , и т.д. т.е. имеют столько положительных единиц сколько нулей стоит после единицы.

Десятичный логарифм чисел 0.1 , 0.01 , 0.001 равен соответвенно -1 , -2 , -3 , и т.д. т.е. имеют столько отрицательных единиц сколько нулей стоит перед единицей, считая и ноль целых.

Как вычислить lg

Десятичные логарифмы применяются при решении уравнений, содержащих неизвестные показатели степеней. Из названия этого типа логарифмов вытекает, что основанием его является число десять. Десятичный логарифм определяет, в какую степень надо возвести десятку, чтобы получить указанный в нем аргумент. Вычисление такого рода логарифмов при наличии компьютера не представляет сложности.

Воспользуйтесь, например, поисковой системой Google для вычисления десятичного логарифма. Этот поисковик имеет встроенный калькулятор, который очень прост в использовании, не требует разбираться в его интерфейсе и запускать какие-либо дополнительные программы. Все что от вас требуется — перейти на сайт Google и ввести соответствующий запрос в единственное поле на этой странице. Например, для вычисления десятичного логарифма для числа 900 введите в поле поискового запроса lg 900 и сразу (даже без нажатия кнопки) получите ответ 2.95424251.

Используйте калькулятор, если нет доступа к поисковой системе. Это может быть и программный калькулятор из стандартного набора ОС Windows. Самый простой способ запустить его — нажать сочетание клавиш WIN +R, ввести команду calc и щелкнуть кнопку «OK». Другой способ — раскрыть меню на кнопке «Пуск» и выбрать в нем пункт «Все программы». Затем надо открыть раздел «Стандартные» и перейти в подраздел «Служебные», чтобы щелкнуть там ссылку «Калькулятор». При использовании ОС Windows 7 можно нажать клавишу WIN и ввести в поле поиска «Калькулятор», а затем щелкнуть соответствующую ссылку в результатах поиска.

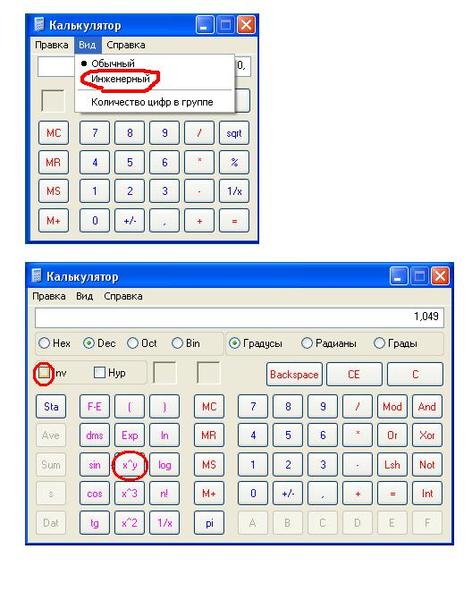
Переключите интерфейс калькулятора в расширенный режим, так как в открываемом по умолчанию базовом варианте нужная вам операция не предусмотрена. Для этого раскройте в меню программы раздел «Вид» и выберите пункт «научный» либо «инженерный» — в зависимости от того, которая версия операционной системы установлена в вашем компьютере.

Введите число, десятичный логарифм для которого нужно рассчитать, а затем щелкните кнопку с надписью log — в этом калькуляторе функция вычисления десятичного логарифма обозначена именно так, а не lg. Программа посчитает и отобразит результат.

Математический калькулятор

Математический калькулятор вычисляет значение заданного математического выражения. В выражении можно использовать операции сложения, умножения, вычитания, деления возведения в степень, константу pi, различные математические функции: sqrt — квадратный корень, exp — e в указанной степени, lb — логарифм по основанию 2, lg — логарифм по основанию 10, ln — натуральный логарифм (по основанию e), sin — синус, cos — косинус, tg — тангенс, ctg — котангенс, sec — секанс, cosec — косеканс, arcsin — арксинус, arccos — арккосинус, arctg — арктангенс, arcctg — арккотангенс, arcsec — арксеканс, arccosec — арккосеканс, versin — версинус, vercos — коверсинус, haversin — гаверсинус, exsec — экссеканс, excsc — экскосеканс, sh — гиперболический синус, ch — гиперболический косинус, th — гиперболический тангенс, cth — гиперболический котангенс, sech — гиперболический секанс, csch — гиперболический косеканс, root3 — кубический корень, rootN — корень указанной степени, logN — логарифм с заданным основанием.

Калькулятор был создан в ответ на многочисленные запросы наших пользователей, которые желают воспользоваться нашим сервисом чтобы посчитать результат какого-либо математического выражения, например, что-нибудь сложить, вычесть, поделить возвести в степень, извлечь корень и т. п. Вводите последовательность математических выражений в поле математическое выражение и получайте результат.

Все тригонометрические функции принимают аргументы в радианах, а не в градусах. Обратные тригонометрические функции, также возвращают угол в радианах. Для преобразования градусов в радианы — умножайте градусы на pi/180, например, sin 30 градусов надо записывать как sin(30*pi/180).

Калькулятор десятичных логарифмов

Для обозначения десятичного логарифма существует несколько способов:

• lg
• log10
• log ₁₀

Так же возможно написание прописными буквами.

Что такое десятичный логарифм

Десятичный логарифм очень прост для понимания.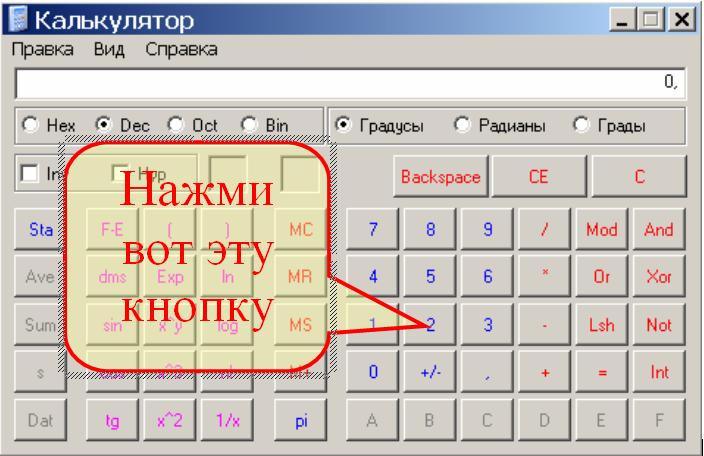 К примеру, десятичный логарифм числа 100 равен 2. А числа 100 000 — 5. Таким образом,

Здесь y — число, логарифм которого мы ищем, а x — это искомый логарифм.

То есть десятичный логарифм — это степень, в которую нужно возвести число 10 для получения исходного числа, логарифм которого мы ищем. Как мы видим, для чисел кратных 10 десятичный логарифм находится просто. Для чисел, не кратных 10 логарифм будет дробным. К примерку, десятичный логарифм числа 7 равен 0.84509804001426. И тут наш калькулятор поможет с расчетом.

Как использовать калькулятор Windows 10

Встроенный калькулятор Windows прошел долгий путь с момента его появления в Windows 1.0 в 1985 году. Он включает в себя различные режимы, вычисление даты и некоторые удобные функции ежедневных преобразований.

Переключение между режимами калькулятора

Как вы увидите ниже, калькулятор делает намного больше, чем простое сложение, вычитание, умножение и деление. Вы можете выбрать один из четырех режимов, в зависимости от ваших потребностей.

Чтобы переключиться между режимами, нажмите кнопку меню в верхнем левом углу, а затем выберите режим из следующих параметров.

Вот на что способны эти режимы.

Стандартный режим

Стандартный режим полезен для основных математических операций, таких как сложение, вычитание, умножение и деление, а также поиска квадратных корней, вычисления процентов и работы с простыми функциями. Вероятно, это режим, в котором большинство людей будет чувствовать себя комфортно.

Инженерный режим

Инженерный режим калькулятора представляет собой расширенный в стандартный режим, предоставляя вам дополнительные функции, которые вы найдёте в типичном научном калькуляторе. В дополнение к операторам стандартного режима он содержит функции типа log, mod, exp, тригонометрические градусы и SIN, COS и TAN.

Режим программиста

Этот режим предназначен для программистов. Он добавляет возможность переключения между различными системами счисления – двоичная, десятичная, шестнадцатеричная и восьмеричная. Он также добавляет новые операции для работы с логическими затворами: Or, And, Xor, Not и битами – Lsh, Rsh, RoR и RoL.

Кроме того, режим Программист позволяет переключаться между байтами (8 бит), Word (16 бит), DWord (32 бита) и QWord (64 бита) и имеет возможность переключения на бинарный бит.

Режим расчета даты

Режим расчета даты – удобный инструмент, который позволяет рассчитать разницу между двумя конкретными датами. Это идеально подходит для выяснения таких вещей, сколько дней осталось до следующего отпуска.

Все, что вам нужно сделать, это выбрать дату начала и окончания, а калькулятор будет определять месяцы, недели и дни между ними.

Преобразование измерений в калькуляторе

Вы нашли рецепт, но он требует использования жидких унций, или совершаете покупки в интернете, а все цены в евро?

Нажмите кнопку меню калькулятора и выберите тип преобразования из списка в разделе «Преобразователь».

Нажмите первое измерение – это будет вход – и выберите единицу измерения из предоставленного списка.

Нажмите второе измерение – это будет выход – и выберите там единицу измерения.

Теперь введите своё значение, и калькулятор преобразует его для вас. Он также показывает несколько других связанных преобразований внизу.

Сохранение значений в памяти

Если вы часто используете определенные числа и не хотите вводить их в свой калькулятор каждый раз, хранить их в памяти калькулятора. Это супер полезная функция, доступная в режимах стандарт, инженерный и программист. Вы будете управлять функциями памяти с помощью кнопок MS, MR, M+, M- и MC.

Вот как они работают:

• MS: сохранить новое значение в памяти.
• MR: вставить значение из памяти.
• M+: добавляет значение из поля ввода к самому последнему сохраненному значению.
• M-: вычитает значение на входе из последнего сохраненного значения.
• MC: очищает все значения из памяти.
• M: отображает все значения, сохраненные в памяти.

Использование кнопок MR, M+ и M- работает также, как и на физическом калькуляторе. Однако, в калькуляторе Windows у вас также есть доступ к любым другим значениям, которые вы сохранили в памяти во время текущего сеанса. Чтобы увидеть их, нажмите кнопку M со стрелкой вниз справа. Затем вы можете щелкнуть любое значение, чтобы вставить его.

Если вы предпочитаете, чтобы ваша очередь памяти всегда открывалась, измените размер калькулятора по горизонтали, и тогда она должна открыться.

История вычислений калькулятора

Если вам нужно взглянуть на все вычисления, выполненные в текущем сеансе, они хранятся в удобной истории калькулятора. Калькулятор сохраняет историю даже при переключении режимов, но она удаляется, когда вы закрываете приложение.

Доступ к истории калькулятора

Существует два способа доступа к истории внутри приложения. Первый – щелкнуть кнопку истории, расположенную в верхнем правом углу. Это показывает список последних вычислений. Щелчок по чему-либо в истории загрузит его обратно в поле ввода калькулятора.

Если вы хотите сохранить историю открытой, измените размер окна калькулятора по горизонтали, и оно должно появиться, когда окно достаточно велико.

Удаление истории калькулятора

Вы можете удалить отдельные записи из своей истории или удалить всю историю сразу.

Чтобы удалить отдельную запись, щелкните её правой кнопкой мыши и выберите команду «Удалить». Чтобы удалить всю историю, щелкните значок маленькой корзины в правом нижнем углу панели.

Горячие клавиши Калькулятора

В приложении Calculator доступны сочетания клавиш, позволяющие выполнять некоторые вычисления намного легче и быстрее. Полный список этих сочетаний можно найти на странице «Горячие клавиши Microsoft Windows», но вот несколько наиболее полезных:

• Alt + (1-4): Удерживайте нажатой клавишу Alt и нажмите любое число от одного до четырех, чтобы переключиться в разные режимы калькулятора.
• Del: очистить текущий вход (это работает как ключ CE на калькуляторе)
• Esc: очистить все входные данные (это работает как клавиша C на калькуляторе)
• Ctrl + H: включение и отключение истории.

Наверное, это больше, чем вы когда-либо хотели знать о калькуляторе Windows. Тем не менее, это недооцененный инструмент, который содержит множество полезных функций.

Log Calculator — Z SCORE TABLE

Log Calculator

Log калькулятор — это мощный онлайн-инструмент, с помощью которого можно быстро и легко вычислить логарифмические значения. Благодаря удобному интерфейсу этот калькулятор является отличным ресурсом для всех, кому необходимо работать с логарифмами, включая студентов, исследователей и специалистов в различных областях. Калькулятор может решать как обычные, так и натуральные логарифмические функции, что делает его универсальным инструментом для широкого круга приложений. Просто введите основание и аргумент, и калькулятор выдаст вам логарифмическое значение. Он также может предоставить объяснения логарифмических вычислений, что делает его отличным ресурсом для образовательных целей. Изучаете ли вы математику, инженерное дело или любую другую область, требующую логарифмических вычислений, калькулятор логарифмов — это полезный и надежный способ получить нужные вам ответы. Это быстро, просто и бесплатно, так что попробуйте прямо сейчас и упростите свои логарифмические вычисления.

Log Calculator

Укажите любые два значения для расчета log

_b x = y

9 0018

Значение (x):
Основание (b):
Значение (г):

91 Советы по расчету с помощью Micros…

Включите JavaScript

91 Советы по расчету в Microsoft Excel Навыки расчета в кратчайшие сроки с помощью этих коротких и простых учебных пособий

Инструкции по использованию калькулятора логарифмов

Это простой калькулятор для расчета логарифмов. Чтобы использовать калькулятор, выполните следующие действия:
​

1. Введите значение x в поле ввода «Значение (x)». Это значение, для которого вы хотите вычислить логарифм.
2. Введите основание логарифма в поле ввода «Основание (b)». По умолчанию в качестве базы установлено значение «е», что представляет собой натуральный логарифм. Вы можете изменить базу на любое другое значение, введя его в поле ввода.
3. Введите значение y в поле ввода «Значение (y)». Это результат логарифмирования.
4. Нажмите на кнопку «Рассчитать», чтобы получить ответ. Результат отобразится в поле «Результат» внизу.

Обратите внимание, что калькулятор может вычислить любые два из трех значений (x, b и y) и вычислит третье значение. Итак, если вы введете значение x и y, калькулятор рассчитает базу. Точно так же, если вы введете основание и значение y, калькулятор рассчитает значение x.

​

Логарифмы: важнейшая математическая функция

​Логарифмы — это математическое понятие, которое играет жизненно важную роль в различных областях науки, включая науку, инженерию, финансы и другие.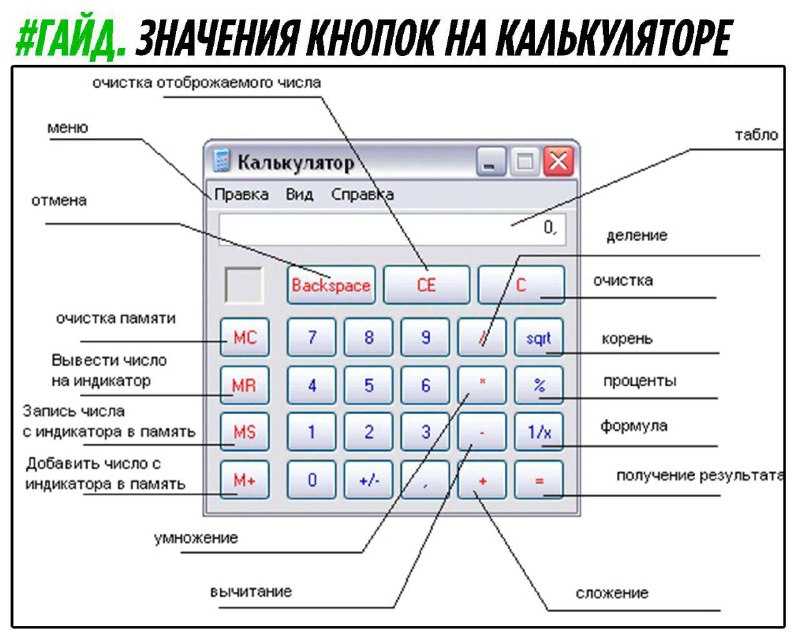 Они являются важным инструментом, который помогает нам решать сложные уравнения и упрощать математические задачи. В этой статье мы обсудим, что такое логарифмы, их свойства и значение в различных областях.

Что такое логарифмы? 93 равно 1000.

Свойства логарифмов

Логарифмы обладают несколькими свойствами, которые необходимы при решении математических уравнений. Вот некоторые из этих свойств:
 
Свойство продукта: logb (xy) = logb (x) + logb (y)
Это свойство указывает, что логарифм произведения двух чисел равен сумме логарифмов каждого числа.
 
Свойство частного логарифмов гласит, что логарифм частного двух чисел по общему основанию «b» равен разности между логарифмами отдельных чисел с одинаковым основанием «b». Математически это можно выразить как logb(x/y) = logb(x) — logb(y). 9у) = у logb(x).

Применение логарифмов

Логарифмы имеют множество применений в реальных сценариях и широко используются в различных областях исследований. Некоторые из областей, где используются логарифмы, включают:
 
В финансы логарифмы используются для расчета сложных процентных ставок. Например, если вы вкладываете 1000 долларов на сберегательный счет с годовой процентной ставкой 5%, начисляемой ежемесячно, сумму денег, которую вы будете иметь через 10 лет, можно рассчитать по формуле: 9-5)
pH = 5
 
В физике логарифмы используются для измерения интенсивности землетрясений по шкале Рихтера. Магнитуда землетрясения измеряется по шкале Рихтера, которая представляет собой логарифмическую шкалу, которая оценивает амплитуду сейсмических волн, вызванных землетрясением. Например, землетрясение магнитудой 7 баллов по шкале Рихтера в 10 раз мощнее землетрясения магнитудой 6 баллов.0004, логарифмы используются для измерения уровня сигнала электрических цепей и интенсивности звука. Например, шкала в децибелах (дБ), используемая для измерения интенсивности звука, представляет собой логарифмическую шкалу, которая связывает интенсивность звука с эталонной интенсивностью. Формула для уровня децибел:
 
дБ = 10 log(I/I0)
 
В этом контексте «I» представляет интенсивность звука, а «I0» — эталонную интенсивность. Звук, который в 10 раз интенсивнее эталонного звука, имеет уровень децибел 10 дБ.
 
В информатика логарифмы используются в таких алгоритмах, как алгоритмы двоичного поиска и сортировки. Например, при бинарном поиске алгоритм многократно делит отсортированный массив на две половины, пока не найдет нужный элемент. Количество раз деления массива пропорционально логарифму размера массива. Это делает бинарный поиск очень эффективным алгоритмом для поиска в больших массивах.
 
В статистика , логарифмы используются для преобразования данных, которые искажены или имеют широкий диапазон значений. Например, если данные подчиняются степенному закону распределения, логарифмирование данных может преобразовать их в нормальное распределение. Это упрощает анализ и сравнение данных с использованием статистических методов.
 
В биология логарифмы используются для измерения интенсивности света с использованием шкалы поглощения. Поглощение раствора определяется как отрицательный логарифм пропускания света через раствор. Это позволяет ученым измерять концентрацию вещества в растворе, сравнивая его абсорбцию со стандартной кривой.
 
Это всего лишь несколько примеров использования логарифмов в различных областях. Логарифмы — это мощный математический инструмент, который позволяет нам преобразовывать мультипликативные отношения в аддитивные и сжимать большие диапазоны значений в меньшие. Они необходимы во многих областях науки, техники и математики и используются в повседневной жизни, даже если мы этого не осознаем.

Решение уравнений с помощью логарифмов

Логарифмы можно использовать для упрощения сложных уравнений путем преобразования задач на умножение и деление в более простые задачи на сложение и вычитание. x = 8. Логарифмируя обе части уравнения по основанию 2, мы получаем: 9x = 8 равно x = 3.
 
Подводя итог, можно сказать, что логарифмы — это важная математическая функция, имеющая многочисленные применения в различных областях науки. Они помогают нам решать сложные уравнения и упрощать математические задачи, делая изучение математики более эффективным и результативным. Понимая свойства логарифмов, мы можем использовать их для решения сложных уравнений и получения информации о различных сценариях реального мира. Применения логарифмов огромны, и они являются важным инструментом, который помогает нам понимать и анализировать мир вокруг нас.

Посетите нас на z-table.com, чтобы получить больше математических и статистических калькуляторов.

Умственное вычисление функций научного калькулятора

На этой странице показано, как грубо вычислять функции, распространенные в научных калькуляторах — экспоненты и логарифмы, тригонометрические функции, корни — и одну функцию, которая, как мне кажется, должна быть более распространенной на научном калькуляторе: гамма-функция [1].

В целом приближения на этой странице хороши до пары значащих цифр. Более подробная информация приводится для каждого приближения.

Логарифмы

В этом разделе показано, как мысленно вычислять логарифмы по основанию 10, e и 2. x ≤ 3.

В более общем случае логарифмическая база b может быть сведена к случаю 1/√ b ≤ x ≤ √ b.

Основание 10

Для 0,3 ≤ x ≤ 3.

log ₁₀ х ≈ ( х -1)/( х +1).

Это приближение имеет максимальную ошибку около 0,03 и очень точную для x около 1. ≤ √ е,

log _e x ≈ 2 ( x – 1)/( x + 1).

Это приближение имеет максимальную ошибку около 0,03 и очень точно для x около 1.

Подробнее здесь.

Основание 2

Для 1/√2 ≤ x ≤ √2.

логарифм ₂ х ≈ 3( х – 1)/( х + 1).

Это приближение имеет максимальную ошибку около 0,015 и очень точно для x около 1.

Подробнее здесь.

Все вместе

Между прочим,

лог ₂ x ≈ лог _e x + журнал ₁₀ x .

Подробнее здесь.

Экспоненты

В этом разделе показано, как вычислить в уме 10 ^x и e ^x .

Нам нужно учитывать только x между -0,5 и 0,5, потому что мы можем свести общий случай к этому случаю.

Base 10

Для x между -0,5 и 0,5,

10 ^x ≈ (1+ x )/(1- x ).

Максимальная относительная ошибка составляет около 0,08. Простая вариация может уменьшить это значение до 0,03. Подробнее здесь.

Base

e

Для x между -0,5 и 0,5,

e ^x ≈ (2 + 9 0184 x )/(2 – x ).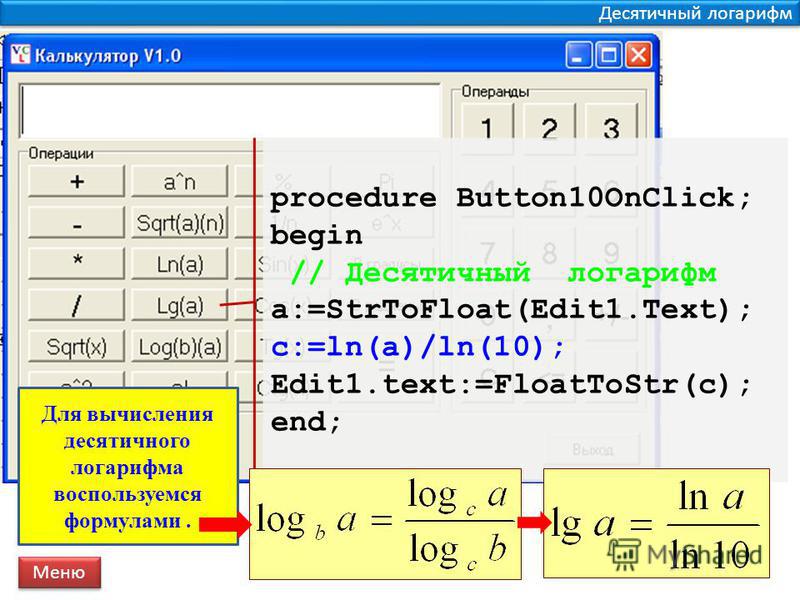

Это приближение имеет максимальную относительную погрешность около 0,01. Подробнее здесь.

Основание 2

Часто, когда вычислительная мощность равна 2, показатель степени является целым числом, и вам нужен точный целочисленный результат, а не приближение. Поэтому стоит запомнить цифры 2 ⁿ для n целое число до 10.

Тем не менее, если вам нужно вычислить 2 ^x для реальных x , между -0,5 и 0,5, приближение

2 ^x ≈ (3+ x )/(3- x )

хорошо с точностью до 0,015.

Корни

В этом разделе дается несколько методов мысленного вычисления корней. Обратите внимание, что вы также можете вычислять корни, используя логарифмы и экспоненты с помощью описанных выше приемов.

Квадратные корни

Чтобы вычислить квадратный корень из числа x , возьмите корень g и вычислите среднее значение g и x / g . Вы можете получить столько точности, сколько захотите, повторив этот процесс достаточное количество раз.

Подробнее здесь.

Корни более высокого порядка

Существует способ вычисления корней более высокого порядка, связанный с описанными выше методами вычисления логарифмических и экспоненциальных величин.

См. этот пост для деталей.

Триггерные функции

Для малых углов (в радианах) триггерные функции проще всего вычислить из одночленного ряда Тейлора. Все следующие приближения имеют точность в пределах 1%.

• sin x ≈ x для | х | < 0,244.
• cos x ≈ 1 – x ²/2 для | х | < 0,662.
• загар x ≈ x для | х | < 0,173.
• угл x ≈ x для | х | < 0,242.
• arccos x ≈ π/2 – x для | х | < 0,4.
• арктан x ≈ x для | х | < 0,173.

Вы можете использовать тригонометрические тождества, чтобы свести задачу вычисления любой тригонометрической функции для любого угла к задаче вычисления тригонометрической функции для углов от 0 до π/4 радиан = 45°.

Для углов в градусах с x между 0 и 45 справедливы следующие приближения:

Синусоидальная аппроксимация с точностью до 0,02 и косинусная аппроксимация с точностью до 0,005. Ошибка тангенсной аппроксимации может достигать 0,1, но более точным является отношение синусоидальной и косинусной аппроксимаций. Смотрите этот пост для ссылок и деталей.

Следующая аппроксимация для косинуса верна с точностью до 0,001 для x от 0 до 40. 000

См. этот пост для ссылок и подробностей.

Гамма-функция

Задачу вычисления гамма-функции для любого вещественного аргумента можно свести к задаче вычисления гамма-функции на интервале длины 1.

Для 2 ≤ x ≤ 3,

Γ( х ) ≈ 2/(4 – х ).