Котангенс онлайн калькулятор
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Данный калькулятор вычислит синус, косинус, тангенс, котангенс, секанс, косеканс угла как в градусной, так и в радианной мере.
Введите число
синус (sin)косинус (cos)тангенс (tg)котангенс (ctg)секанс (sec)косеканс (cosec)градусырадианы
Что такое котангенс угла
Пусть задан прямоугольный треугольник ABC с острым углом α, тогда котангенсом угла α будет отношение прилежащего катета к противолежащему ctg α = AB/BC.
Котангенс угла можно определить как отношение косинуса угла к синусу данного угла
ctg = cos α / sin α
Так же для определения котангенса угла можно воспользоваться окружностью, построенной в декартовой системе координат, радиуса R и центром в начале координат O.
На окружности отметим точку P с координатами (1;0), теперь повернем луч OP на некоторый угол α. Направление против часовой стрелки считается положительным, по часовой стрелки – отрицательным.
Котангенсом угла α будет отношение абсциссы точки XP к ординате точки YP.
ctg α = XP/YP.
Для вычисления котангенса угла, можно также воспользоваться осью котангенсов. Определим окружность радиуса R как единичную с центром в начале координат O.
Параллельно оси x, на расстоянии равном радиусу окружности расположим прямую y=1. На окружности отметим точку P с координатами (1;0), теперь повернем луч OP на некоторый угол α и продолжим луч OP до
пересечения с прямой y=1.
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Таблица котангенсов, найти котангенс угла
Тригонометрические функции – это соотношение катетов и гипотенузы угла в прямоугольном треугольнике. Это очень важно. Длина сторон может изменяться, но соотношение останется прежним. На этом основании были созданы таблицы Брадиса, в котором указаны синус, косинус, тангенс и котангенс угла.
Это очень важно. Длина сторон может изменяться, но соотношение останется прежним. На этом основании были созданы таблицы Брадиса, в котором указаны синус, косинус, тангенс и котангенс угла.
Котангенс – это соотношение катетов угла прямоугольного треугольника. Записывается следующим образом: ctg (А) = АС/ВС, где АС – ближний к углу катет, ВС – противолежащий катет.
Все данные есть в таблице котангенсов угла. Зная угол и одну из сторон, можно получить остальные данные. Производить расчеты можно на сайте посредством онлайн-калькулятора. Утверждение: знаю угол – знаю его тригонометрические функции, верно во все времена.
|
|
|
|
|
|
|
|
|
|
Select rating12345
Рейтинг: 4. 3 (Голосов 3)
3 (Голосов 3)
Сообщить об ошибке
Смотрите также
Таблица котангенсов углов, вычислить котангенс угла
Угол
Тригонометрия является разделом математики, в которой рассматривается зависимость между сторонами треугольника и углами. Как известно, в прямоугольном треугольнике один угол обязательно прямой, остальные острые. Стороны, прилежащие к углу в 90 градусов, являются катетами треугольника, а сторона, расположенная против прямого угла, — его гипотенуза. Соотношения двух сторон прямоугольного треугольника представляют собой тригонометрические функции. Котангенс острого угла является одной из таких тригонометрических функций. Котангенсом угла является отношение величины прилежащего катета к величине противолежащего катета.
ctg (А) = в / а
где в — катет, прилежащий углу А;
а — противолежащий катет.
Если известен острый угол прямоугольника, можно найти котангенс угла, воспользовавшись таблицей тригонометрических функций.
Это следует помнить! Если известен угол, вы легко найдете его тригонометрические функции по таблице Брадиса.
Если известны катеты треугольника, можно определить котангенс угла и угол.
Если известен угол и одна из сторон треугольника, можно определить котангенс угла и остальные стороны треугольника.
Получить быстрое и правильное решение вам поможет онлайн калькулятор.
Рассчитать котангенс угла
ctg (°) =
Таблица котангенсов углов от 0° до 180°
|
|
|
Таблица котангенсов углов от 180° до 360°
|
|
|
cos online
cos onlineВы искали cos online? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и cos вычислить, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «cos online».
Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «cos online».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как cos online,cos вычислить,cos калькулятор,cos калькулятор онлайн,cos онлайн,cos онлайн калькулятор,ctg калькулятор,ctg онлайн калькулятор,online cos,online sin,sin cos tg ctg калькулятор,sin cos калькулятор,sin online,sin калькулятор,sin калькулятор онлайн,sin онлайн калькулятор,tg online,tg калькулятор,tg калькулятор онлайн,tg онлайн калькулятор,вычисление косинуса,вычисление косинуса онлайн,вычисление косинусов и синусов,вычисление косинусов и синусов онлайн,вычисление синуса онлайн,вычисление синусов и косинусов,вычисление синусов и косинусов онлайн,вычисление тангенса онлайн,вычисление тригонометрических функций онлайн,вычислите cos,вычислите sin,вычислить cos,вычислить sin,вычислить tg,вычислить косинус,вычислить косинус онлайн,вычислить косинус угла,вычислить косинус угла онлайн,вычислить онлайн синус,вычислить онлайн синус угла,вычислить синус,вычислить синус онлайн,вычислить синус угла онлайн,вычислить угол по косинусу онлайн,зная косинус найти угол онлайн,как косинус перевести в градусы,как перевести в градусы косинус,как перевести градусы в косинус,как перевести градусы в синус,как перевести косинус в градусы,как перевести синус в градусы,как синус в градусы перевести,как синус перевести в градусы,калькулятор cos,калькулятор cos sin,калькулятор ctg,калькулятор ctg онлайн,калькулятор sin,калькулятор sin cos,калькулятор sin cos tg ctg,калькулятор sin cos tg ctg онлайн,калькулятор sin онлайн,калькулятор tg,калькулятор tg ctg sin cos,калькулятор tg онлайн,калькулятор для косинусов и синусов,калькулятор для синусов и косинусов,калькулятор косинус,калькулятор косинус синус,калькулятор косинус синус онлайн,калькулятор косинуса,калькулятор косинуса и синуса,калькулятор косинусов,калькулятор косинусов и синусов,калькулятор косинусов и синусов онлайн,калькулятор косинусов и синусов онлайн с минутами,калькулятор косинусов и синусов с минутами онлайн,калькулятор косинусов онлайн,калькулятор косинусов с минутами,калькулятор котангенс,калькулятор котангенсов,калькулятор онлайн cos,калькулятор онлайн ctg,калькулятор онлайн sin,калькулятор онлайн sin cos tg ctg,калькулятор онлайн tg,калькулятор онлайн косинус в градусах,калькулятор онлайн косинус синус,калькулятор онлайн косинус угла,калькулятор онлайн косинусов,калькулятор онлайн косинусы синусы,калькулятор онлайн с синусами и косинусами,калькулятор онлайн синус косинус,калькулятор онлайн синусов,калькулятор онлайн синусы косинусы,калькулятор онлайн тангенс в градусах,калькулятор с косинусами и синусами,калькулятор с косинусами и синусами онлайн,калькулятор с котангенсом,калькулятор с синусами,калькулятор с синусами и косинусами,калькулятор с синусами и косинусами онлайн,калькулятор с тангенсом,калькулятор синус,калькулятор синус косинус,калькулятор синус косинус онлайн,калькулятор синус угла,калькулятор синуса,калькулятор синуса и косинуса,калькулятор синусов,калькулятор синусов и косинусов,калькулятор синусов и косинусов онлайн,калькулятор синусов и косинусов онлайн с градусами,калькулятор синусов и косинусов онлайн с минутами,калькулятор синусов косинусов тангенсов котангенсов,калькулятор синусов онлайн,калькулятор синусы косинусы онлайн,калькулятор тангенса,калькулятор тангенсов онлайн,кос онлайн,косинус в градусах онлайн,косинус в градусы,косинус в радианах,косинус в радианах онлайн,косинус вычислить,косинус вычислить онлайн,косинус и синус онлайн,косинус калькулятор,косинус калькулятор онлайн,косинус калькулятор онлайн в градусах,косинус онлайн,косинус онлайн в градусах,косинус онлайн в радианах,косинус онлайн калькулятор,косинус онлайн калькулятор в градусах,косинус онлайн калькулятор в градусах и минутах,косинус перевести в синус,косинус перевести в тангенс,косинус посчитать,косинус посчитать онлайн,косинус синус калькулятор,косинус синус онлайн калькулятор,косинус угла вычислить онлайн,косинус угла калькулятор онлайн,косинус угла онлайн,косинус угла онлайн калькулятор,косинус угла посчитать онлайн,косинусы и синусы онлайн,косинусы онлайн,котангенс калькулятор,найти косинус онлайн,найти синус онлайн,найти синус угла онлайн,найти тангенс угла онлайн,найти угол зная косинус онлайн,найти угол онлайн по косинусу,найти угол онлайн через косинус,найти угол по косинусу онлайн,найти угол по косинусу онлайн калькулятор,найти угол по синусу онлайн,найти угол по тангенсу калькулятор онлайн,найти угол по тангенсу онлайн,найти угол по тангенсу онлайн калькулятор,найти угол через косинус онлайн,онлайн cos,онлайн вычисление синуса,онлайн вычисление синусов и косинусов,онлайн вычисление тригонометрических функций,онлайн калькулятор cos,онлайн калькулятор ctg,онлайн калькулятор sin,онлайн калькулятор sin cos tg ctg,онлайн калькулятор tg,онлайн калькулятор косинус,онлайн калькулятор косинус синус,онлайн калькулятор косинусов,онлайн калькулятор косинусов и синусов,онлайн калькулятор косинусов и синусов с минутами,онлайн калькулятор косинусы синусы,онлайн калькулятор с синусами и косинусами,онлайн калькулятор синус,онлайн калькулятор синус косинус,онлайн калькулятор синусов,онлайн калькулятор синусов и косинусов,онлайн калькулятор синусов и косинусов с градусами,онлайн калькулятор синусов и косинусов с минутами,онлайн калькулятор тангенс,онлайн калькулятор тангенсов,онлайн калькулятор тригонометрические функции,онлайн косинус в градусах,онлайн косинус и синус,онлайн косинус угла,онлайн косинусы,онлайн косинусы и синусы,онлайн перевод тангенса в градусы,онлайн расчет косинуса,онлайн синус и косинус,онлайн синусы и косинусы,онлайн тангенс калькулятор,перевести в градусы косинус,перевести тангенс в косинус,перевод косинуса в градусы,перевод косинуса в синус,перевод косинуса в тангенс,перевод синуса в градусы,перевод тангенса в градусы онлайн,по синусу угол онлайн,посчитать косинус,посчитать косинус онлайн,посчитать косинус угла онлайн,посчитать онлайн косинус,посчитать онлайн косинус угла,посчитать синус,посчитать синус онлайн,рассчитать синус,расчет косинуса онлайн,расчет онлайн косинуса,расчет тангенса онлайн,расчет тангенса угла онлайн,синус в радианах онлайн,синус вычислить онлайн,синус и косинус онлайн,синус калькулятор,синус калькулятор онлайн,синус калькулятор онлайн в градусах,синус калькулятор угла,синус косинус калькулятор,синус косинус онлайн калькулятор,синус онлайн,синус онлайн в радианах,синус онлайн калькулятор,синус онлайн калькулятор в градусах,синус посчитать,синус посчитать онлайн,синус рассчитать,синус угла вычислить онлайн,синус угла калькулятор,синус угла калькулятор онлайн,синус угла онлайн,синус угла онлайн калькулятор,синусы и косинусы онлайн,синусы косинусы калькулятор онлайн,синусы косинусы онлайн калькулятор,синусы онлайн,тангенс вычислить онлайн,тангенс калькулятор онлайн,тангенс онлайн калькулятор,тангенс онлайн калькулятор в градусах,тангенс посчитать онлайн,тангенс угла найти онлайн,тригонометрический калькулятор онлайн,тригонометрический онлайн калькулятор,угол по косинусу онлайн,угол по синусу онлайн. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и cos online. Просто введите задачу в окошко и нажмите
«решить» здесь (например, cos калькулятор).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и cos online. Просто введите задачу в окошко и нажмите
«решить» здесь (например, cos калькулятор).
Решить задачу cos online вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Котангенс угла онлайн. Таблица котангенсов. Формула котангенса угла.
Котангенс угла через градусы, минуты и секунды
+−
Котангенс угла через десятичную запись угла
Определение котангенса
Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.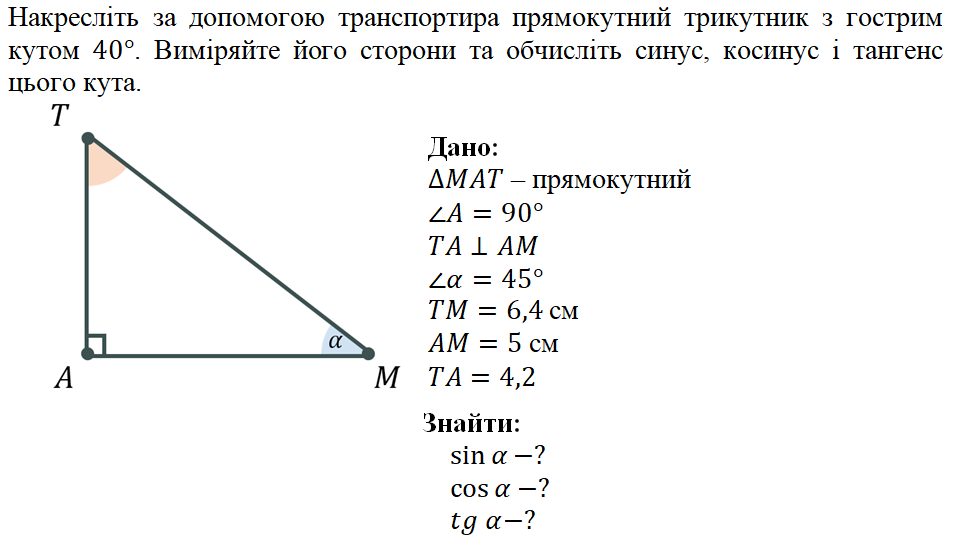
tg(α) = cos(α)/sin(α)
сtg(α) = 1/tg(α)
Таблица котангенсов в радианах
ctg(0°) = ∞ctg(π/12) = ctg(15°) = 3.732050808ctg(π/6) = ctg(30°) = 1.732050808ctg(π/4) = ctg(45°) = 1ctg(π/3) = ctg(60°) = 0.577350269ctg(5π/12) = ctg(75°) = 0.2679491924ctg(π/2) = ctg(90°) = 0ctg(7π/12) = ctg(105°) = -0.2679491924ctg(2π/3) = ctg(120°) = -0.577350269ctg(3π/4) = ctg(135°) = -1ctg(5π/6) = ctg(150°) = -1.732050808ctg(11π/12) = ctg(165°) = -3.732050808ctg(π) = ctg(180°) = ∞ctg(13π/12) = ctg(195°) = 3.732050808ctg(7π/6) = ctg(210°) = 1.732050808ctg(5π/4) = ctg(225°) = 1ctg(4π/3) = ctg(240°) = 0.577350269ctg(17π/12) = ctg(255°) = 0.2679491924ctg(3π/2) = ctg(270°) = 0ctg(19π/12) = ctg(285°) = -0.2679491924ctg(5π/3) = ctg(300°) = -0.577350269ctg(7π/4) = ctg(315°) = -1ctg(11π/6) = ctg(330°) = -1.732050808ctg(23π/12) = ctg(345°) = -3.732050808
Таблица Брадиса котангенсы
| ctg(0) = ∞ | ctg(120) = -0.577350269 | ctg(240) = 0.577350269 |
ctg(1) = 57. 28996162 28996162 | ctg(121) = -0.6008606192 | ctg(241) = 0.5543090515 |
| ctg(2) = 28.63625328 | ctg(122) = -0.6248693519 | ctg(242) = 0.5317094318 |
| ctg(3) = 19.08113669 | ctg(123) = -0.6494075931 | ctg(243) = 0.5095254494 |
| ctg(4) = 14.30066626 | ctg(124) = -0.6745085166 | ctg(244) = 0.4877325885 |
| ctg(5) = 11.4300523 | ctg(125) = -0.7002075381 | ctg(245) = 0.466307658 |
| ctg(6) = 9.514364451 | ctg(126) = -0.7265425283 | ctg(246) = 0.4452286853 |
| ctg(7) = 8.144346428 | ctg(127) = -0.7535540499 | ctg(247) = 0.4244748162 |
| ctg(8) = 7.115369723 | ctg(128) = -0.7812856266 | ctg(248) = 0.4040262259 |
| ctg(9) = 6.313751516 | ctg(129) = -0.8097840329 | ctg(249) = 0.383864035 |
| ctg(10) = 5.67128182 | ctg(130) = -0.8390996309 | ctg(250) = 0.3639702343 |
ctg(11) = 5. 144554017 144554017 | ctg(131) = -0.869286738 | ctg(251) = 0.3443276133 |
| ctg(12) = 4.704630109 | ctg(132) = -0.9004040442 | ctg(252) = 0.3249196963 |
| ctg(13) = 4.331475875 | ctg(133) = -0.9325150862 | ctg(253) = 0.3057306815 |
| ctg(14) = 4.010780934 | ctg(134) = -0.9656887746 | ctg(254) = 0.2867453857 |
| ctg(15) = 3.732050808 | ctg(135) = -1 | ctg(255) = 0.2679491924 |
| ctg(16) = 3.487414443 | ctg(136) = -1.035530314 | ctg(256) = 0.2493280028 |
| ctg(17) = 3.270852618 | ctg(137) = -1.07236871 | ctg(257) = 0.2308681911 |
| ctg(18) = 3.077683537 | ctg(138) = -1.110612515 | ctg(258) = 0.2125565617 |
| ctg(19) = 2.904210878 | ctg(139) = -1.150368407 | ctg(259) = 0.1943803091 |
| ctg(20) = 2.747477419 | ctg(140) = -1.191753593 | ctg(260) = 0.1763269807 |
ctg(21) = 2. 605089065 605089065 | ctg(141) = -1.234897157 | ctg(261) = 0.1583844403 |
| ctg(22) = 2.475086854 | ctg(142) = -1.279941632 | ctg(262) = 0.1405408347 |
| ctg(23) = 2.355852366 | ctg(143) = -1.327044822 | ctg(263) = 0.1227845609 |
| ctg(24) = 2.246036774 | ctg(144) = -1.37638192 | ctg(264) = 0.1051042353 |
| ctg(25) = 2.14450692 | ctg(145) = -1.428148007 | ctg(265) = 0.08748866355 |
| ctg(26) = 2.050303841 | ctg(146) = -1.482560969 | ctg(266) = 0.06992681193 |
| ctg(27) = 1.962610505 | ctg(147) = -1.539864964 | ctg(267) = 0.05240777928 |
| ctg(28) = 1.880726465 | ctg(148) = -1.600334529 | ctg(268) = 0.0349207695 |
| ctg(29) = 1.804047755 | ctg(149) = -1.664279482 | ctg(269) = 0.01745506493 |
| ctg(30) = 1.732050808 | ctg(150) = -1.732050808 | ctg(270) = 0 |
ctg(31) = 1. 664279482 664279482 | ctg(151) = -1.804047755 | ctg(271) = -0.01745506493 |
| ctg(32) = 1.600334529 | ctg(152) = -1.880726465 | ctg(272) = -0.0349207695 |
| ctg(33) = 1.539864964 | ctg(153) = -1.962610505 | ctg(273) = -0.05240777928 |
| ctg(34) = 1.482560969 | ctg(154) = -2.050303841 | ctg(274) = -0.06992681193 |
| ctg(35) = 1.428148007 | ctg(155) = -2.14450692 | ctg(275) = -0.08748866355 |
| ctg(36) = 1.37638192 | ctg(156) = -2.246036774 | ctg(276) = -0.1051042353 |
| ctg(37) = 1.327044822 | ctg(157) = -2.355852366 | ctg(277) = -0.1227845609 |
| ctg(38) = 1.279941632 | ctg(158) = -2.475086854 | ctg(278) = -0.1405408347 |
| ctg(39) = 1.234897157 | ctg(159) = -2.605089065 | ctg(279) = -0.1583844403 |
| ctg(40) = 1.191753593 | ctg(160) = -2.747477419 | ctg(280) = -0. 1763269807 1763269807 |
| ctg(41) = 1.150368407 | ctg(161) = -2.904210878 | ctg(281) = -0.1943803091 |
| ctg(42) = 1.110612515 | ctg(162) = -3.077683537 | ctg(282) = -0.2125565617 |
| ctg(43) = 1.07236871 | ctg(163) = -3.270852618 | ctg(283) = -0.2308681911 |
| ctg(44) = 1.035530314 | ctg(164) = -3.487414443 | ctg(284) = -0.2493280028 |
| ctg(45) = 1 | ctg(165) = -3.732050808 | ctg(285) = -0.2679491924 |
| ctg(46) = 0.9656887746 | ctg(166) = -4.010780934 | ctg(286) = -0.2867453857 |
| ctg(47) = 0.9325150862 | ctg(167) = -4.331475875 | ctg(287) = -0.3057306815 |
| ctg(48) = 0.9004040442 | ctg(168) = -4.704630109 | ctg(288) = -0.3249196963 |
| ctg(49) = 0.869286738 | ctg(169) = -5.144554017 | ctg(289) = -0.3443276133 |
| ctg(50) = 0.8390996309 | ctg(170) = -5. 67128182 67128182 | ctg(290) = -0.3639702343 |
| ctg(51) = 0.8097840329 | ctg(171) = -6.313751516 | ctg(291) = -0.383864035 |
| ctg(52) = 0.7812856266 | ctg(172) = -7.115369723 | ctg(292) = -0.4040262259 |
| ctg(53) = 0.7535540499 | ctg(173) = -8.144346428 | ctg(293) = -0.4244748162 |
| ctg(54) = 0.7265425283 | ctg(174) = -9.514364451 | ctg(294) = -0.4452286853 |
| ctg(55) = 0.7002075381 | ctg(175) = -11.4300523 | ctg(295) = -0.466307658 |
| ctg(56) = 0.6745085166 | ctg(176) = -14.30066626 | ctg(296) = -0.4877325885 |
| ctg(57) = 0.6494075931 | ctg(177) = -19.08113669 | ctg(297) = -0.5095254494 |
| ctg(58) = 0.6248693519 | ctg(178) = -28.63625328 | ctg(298) = -0.5317094318 |
| ctg(59) = 0.6008606192 | ctg(179) = -57.28996162 | ctg(299) = -0.5543090515 |
ctg(60) = 0. 577350269 577350269 | ctg(180) = ∞ | ctg(300) = -0.577350269 |
| ctg(61) = 0.5543090515 | ctg(181) = 57.28996162 | ctg(301) = -0.6008606192 |
| ctg(62) = 0.5317094318 | ctg(182) = 28.63625328 | ctg(302) = -0.6248693519 |
| ctg(63) = 0.5095254494 | ctg(183) = 19.08113669 | ctg(303) = -0.6494075931 |
| ctg(64) = 0.4877325885 | ctg(184) = 14.30066626 | ctg(304) = -0.6745085166 |
| ctg(65) = 0.466307658 | ctg(185) = 11.4300523 | ctg(305) = -0.7002075381 |
| ctg(66) = 0.4452286853 | ctg(186) = 9.514364451 | ctg(306) = -0.7265425283 |
| ctg(67) = 0.4244748162 | ctg(187) = 8.144346428 | ctg(307) = -0.7535540499 |
| ctg(68) = 0.4040262259 | ctg(188) = 7.115369723 | ctg(308) = -0.7812856266 |
| ctg(69) = 0.383864035 | ctg(189) = 6.313751516 | ctg(309) = -0.8097840329 |
ctg(70) = 0. 3639702343 3639702343 | ctg(190) = 5.67128182 | ctg(310) = -0.8390996309 |
| ctg(71) = 0.3443276133 | ctg(191) = 5.144554017 | ctg(311) = -0.869286738 |
| ctg(72) = 0.3249196963 | ctg(192) = 4.704630109 | ctg(312) = -0.9004040442 |
| ctg(73) = 0.3057306815 | ctg(193) = 4.331475875 | ctg(313) = -0.9325150862 |
| ctg(74) = 0.2867453857 | ctg(194) = 4.010780934 | ctg(314) = -0.9656887746 |
| ctg(75) = 0.2679491924 | ctg(195) = 3.732050808 | ctg(315) = -1 |
| ctg(76) = 0.2493280028 | ctg(196) = 3.487414443 | ctg(316) = -1.035530314 |
| ctg(77) = 0.2308681911 | ctg(197) = 3.270852618 | ctg(317) = -1.07236871 |
| ctg(78) = 0.2125565617 | ctg(198) = 3.077683537 | ctg(318) = -1.110612515 |
| ctg(79) = 0.1943803091 | ctg(199) = 2.904210878 | ctg(319) = -1.150368407 |
ctg(80) = 0. 1763269807 1763269807 | ctg(200) = 2.747477419 | ctg(320) = -1.191753593 |
| ctg(81) = 0.1583844403 | ctg(201) = 2.605089065 | ctg(321) = -1.234897157 |
| ctg(82) = 0.1405408347 | ctg(202) = 2.475086854 | ctg(322) = -1.279941632 |
| ctg(83) = 0.1227845609 | ctg(203) = 2.355852366 | ctg(323) = -1.327044822 |
| ctg(84) = 0.1051042353 | ctg(204) = 2.246036774 | ctg(324) = -1.37638192 |
| ctg(85) = 0.08748866355 | ctg(205) = 2.14450692 | ctg(325) = -1.428148007 |
| ctg(86) = 0.06992681193 | ctg(206) = 2.050303841 | ctg(326) = -1.482560969 |
| ctg(87) = 0.05240777928 | ctg(207) = 1.962610505 | ctg(327) = -1.539864964 |
| ctg(88) = 0.0349207695 | ctg(208) = 1.880726465 | ctg(328) = -1.600334529 |
| ctg(89) = 0.01745506493 | ctg(209) = 1.804047755 | ctg(329) = -1.664279482 |
| ctg(90) = 0 | ctg(210) = 1. 732050808 732050808 | ctg(330) = -1.732050808 |
| ctg(91) = -0.01745506493 | ctg(211) = 1.664279482 | ctg(331) = -1.804047755 |
| ctg(92) = -0.0349207695 | ctg(212) = 1.600334529 | ctg(332) = -1.880726465 |
| ctg(93) = -0.05240777928 | ctg(213) = 1.539864964 | ctg(333) = -1.962610505 |
| ctg(94) = -0.06992681193 | ctg(214) = 1.482560969 | ctg(334) = -2.050303841 |
| ctg(95) = -0.08748866355 | ctg(215) = 1.428148007 | ctg(335) = -2.14450692 |
| ctg(96) = -0.1051042353 | ctg(216) = 1.37638192 | ctg(336) = -2.246036774 |
| ctg(97) = -0.1227845609 | ctg(217) = 1.327044822 | ctg(337) = -2.355852366 |
| ctg(98) = -0.1405408347 | ctg(218) = 1.279941632 | ctg(338) = -2.475086854 |
| ctg(99) = -0.1583844403 | ctg(219) = 1.234897157 | ctg(339) = -2.605089065 |
ctg(100) = -0. 1763269807 1763269807 | ctg(220) = 1.191753593 | ctg(340) = -2.747477419 |
| ctg(101) = -0.1943803091 | ctg(221) = 1.150368407 | ctg(341) = -2.904210878 |
| ctg(102) = -0.2125565617 | ctg(222) = 1.110612515 | ctg(342) = -3.077683537 |
| ctg(103) = -0.2308681911 | ctg(223) = 1.07236871 | ctg(343) = -3.270852618 |
| ctg(104) = -0.2493280028 | ctg(224) = 1.035530314 | ctg(344) = -3.487414443 |
| ctg(105) = -0.2679491924 | ctg(225) = 1 | ctg(345) = -3.732050808 |
| ctg(106) = -0.2867453857 | ctg(226) = 0.9656887746 | ctg(346) = -4.010780934 |
| ctg(107) = -0.3057306815 | ctg(227) = 0.9325150862 | ctg(347) = -4.331475875 |
| ctg(108) = -0.3249196963 | ctg(228) = 0.9004040442 | ctg(348) = -4.704630109 |
| ctg(109) = -0.3443276133 | ctg(229) = 0.869286738 | ctg(349) = -5. 144554017 144554017 |
| ctg(110) = -0.3639702343 | ctg(230) = 0.8390996309 | ctg(350) = -5.67128182 |
| ctg(111) = -0.383864035 | ctg(231) = 0.8097840329 | ctg(351) = -6.313751516 |
| ctg(112) = -0.4040262259 | ctg(232) = 0.7812856266 | ctg(352) = -7.115369723 |
| ctg(113) = -0.4244748162 | ctg(233) = 0.7535540499 | ctg(353) = -8.144346428 |
| ctg(114) = -0.4452286853 | ctg(234) = 0.7265425283 | ctg(354) = -9.514364451 |
| ctg(115) = -0.466307658 | ctg(235) = 0.7002075381 | ctg(355) = -11.4300523 |
| ctg(116) = -0.4877325885 | ctg(236) = 0.6745085166 | ctg(356) = -14.30066626 |
| ctg(117) = -0.5095254494 | ctg(237) = 0.6494075931 | ctg(357) = -19.08113669 |
| ctg(118) = -0.5317094318 | ctg(238) = 0.6248693519 | ctg(358) = -28.63625328 |
| ctg(119) = -0.5543090515 | ctg(239) = 0. 6008606192 6008606192 | ctg(359) = -57.28996162 |
Котангенс 118 градусов
Котангенс 279 градусов
Котангенс 322 градусов
Котангенс 236 градусов
Котангенс 200 градусов
Расчет тангенса. Синус, косинус, тангенс и котангенс в тригонометрии: определения, примеры
Где были рассмотрены задачи на решение прямоугольного треугольника, я пообещал изложить приём запоминания определений синуса и косинуса. Используя его, вы всегда быстро вспомните – какой катет относится к гипотенузе (прилежащий или противолежащий). Решил в «долгий ящик не откладывать», необходимый материал ниже, прошу ознакомиться 😉
Дело в том, что я не раз наблюдал, как учащиеся 10-11 классов с трудом вспоминают данные определения. Они прекрасно помнят, что катет относится к гипотенузе, а вот какой из них — забывают и путают. Цена ошибки, как вы знаете на экзамене – это потерянный бал.
Информация, которую я представлю непосредственно к математике не имеет никакого отношения. Она связана с образным мышлением, и с приёмами словесно-логической связи. Именно так, я сам, раз и на всегда запомнил
данные определения. Если вы их всё же забудете, то при помощи представленных приёмов всегда легко вспомните.
Она связана с образным мышлением, и с приёмами словесно-логической связи. Именно так, я сам, раз и на всегда запомнил
данные определения. Если вы их всё же забудете, то при помощи представленных приёмов всегда легко вспомните.
Напомню определения синуса и косинуса в прямоугольном треугольнике:
Косинус острого угла в прямоугольном треугольнике — это отношение прилежащего катета к гипотенузе:
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Итак, какие ассоциации у вас вызывает слово косинус?
Наверное, у каждого свои 😉 Запоминайте связку:
Таким образом, у вас сразу в памяти возникнет выражение –
«… отношение ПРИЛЕЖАЩЕГО катета к гипотенузе ».
Проблема с определением косинуса решена.
Если нужно вспомнить определение синуса в прямоугольном треугольнике, то вспомнив определение косинуса, вы без труда установите, что синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе. Ведь катетов всего два, если прилежащий катет «занят» косинусом, то синусу остаётся только противолежащий.
Ведь катетов всего два, если прилежащий катет «занят» косинусом, то синусу остаётся только противолежащий.
Как быть с тангенсом и котангенсом? Путаница та же. Учащиеся знают, что это отношение катетов, но проблема вспомнить какой к которому относится – то ли противолежащий к прилежащему, то ли наоборот.
Определения:
Тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему:
Котангенс острого угла в прямоугольном треугольнике — это отношение прилежащего катета к противолежащему:
Как запомнить? Есть два способа. Один так же использует словесно-логическую связь, другой – математический.
СПОСОБ МАТЕМАТИЧЕСКИЙ
Есть такое определение – тангенсом острого угла называется отношение синуса угла к его косинусу:
*Запомнив формулу, вы всегда сможете определить, что тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему.
Аналогично. Котангенсом острого угла называется отношение косинуса угла к его синусу:
Итак! Запомнив указанные формулы вы всегда сможете определить, что:
— тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему
— котангенс острого угла в прямоугольном треугольнике — это отношение прилежащего катета к противолежащему.
СПОСОБ СЛОВЕСНО-ЛОГИЧЕСКИЙ
О тангенсе. Запомните связку:
То есть если потребуется вспомнить определение тангенса, при помощи данной логической связи, вы без труда вспомните, что это
«… отношение противолежащего катета к прилежащему»
Если речь зайдёт о котангенсе, то вспомнив определение тангенса вы без труда озвучите определение котангенса –
«… отношение прилежащего катета к противолежащему»
Есть интересный приём по запоминанию тангенса и котангенса на сайте » Математический тандем » , посмотрите.
СПОСОБ УНИВЕРСАЛЬНЫЙ
Можно просто зазубрить. Но как показывает практика, благодаря словесно-логическим связкам человек запоминает информацию надолго, и не только математическую.
Но как показывает практика, благодаря словесно-логическим связкам человек запоминает информацию надолго, и не только математическую.
Надеюсь, материал был вам полезен.
С уважением, Александр Крутицких
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Тангенс — тригонометрическая функция, численно равная соотношению длин противолежащего и прилежащего катета. Тангенс широко используется во многих современных приложениях.
История вопроса
Тригонометрия берет свое начало в , когда ученые изучали свойства сторон прямоугольного треугольника. Именно тогда была сформулирована теорема, постулирующая соотношение катетов и гипотенузы, доказанная только через полторы тысячи лет самосским математиком Пифагором. Изначально использовался только синус, который рассчитывался как половина хорды окружности, описанной вокруг .
Тангенс появился гораздо позднее, когда перед учеными возникла задача определения длины тени, отбрасываемой объектами, стоящими перпендикулярно к поверхности земли. Тангенс был введен арабским математиком Абу-ль-Вафой в десятом веке. Восточный ученый составил специальные таблицы для определения тангенсов и котангенсов, однако это открытие так и не попало на европейский континент.
Тангенс был введен арабским математиком Абу-ль-Вафой в десятом веке. Восточный ученый составил специальные таблицы для определения тангенсов и котангенсов, однако это открытие так и не попало на европейский континент.
В Европе тангенсы были вновь открыты только в XIV веке: немецкий математик Иоганн Мюллер Региомонтан использовал функцию в астрономических расчетах. Термин «тангенс» произошел от латинского слова tanger, что означает «касание» и был введен в обиход в конце XVI века. Данный термин использовался для описания линии тангенсов, то есть касательной к единичной окружности. Региомонтан доказал теорему тангенсов, а также составил специальные таблицы значений функции, которые подошли как для плоской, так и для сферической геометрии.
Определение тангенса
Геометрически тангенс определяется как соотношение противолежавшего катета к прилежащему. Функция всегда рассчитывается для угла и не зависит от длин сторон. Пусть у нас есть треугольник со сторонами A, B и C, где C — гипотенуза. Тангенс угла AC будет рассчитываться как соотношение противолежащего катета B к прилежащему A или tgAC = B/A. Для угла BC тангенс рассчитывается как дробь, в числителе которой длина противолежащего углу катета A к прилежащему B, что математически записывается как tgBC = A/B. Угол AB образуется при двумя катетами, поэтому его невозможно посчитать. Катеты — стороны, образующие прямой угол, поэтому для угла в 90 градусов тангенс не существует.
Тангенс угла AC будет рассчитываться как соотношение противолежащего катета B к прилежащему A или tgAC = B/A. Для угла BC тангенс рассчитывается как дробь, в числителе которой длина противолежащего углу катета A к прилежащему B, что математически записывается как tgBC = A/B. Угол AB образуется при двумя катетами, поэтому его невозможно посчитать. Катеты — стороны, образующие прямой угол, поэтому для угла в 90 градусов тангенс не существует.
Помимо геометрического определения, тангенс легко выразить через другие тригонометрические функции. Так, для угла A тангенс можно выразить при помощи отношения синуса и косинуса:
tgA = sinA / cosA.
Наша программа позволяет определить численное значение тангенса для любого значения угла. Для этого достаточно выбрать в меню соответствующую функцию и ввести в ячейку «Угол» величину угла в градусах или радианах. Если необходимо найти угол по известному значению тригонометрической функции, используйте функцию арктангенса. Для этого введите значение тангенса в соответствующую ячейку, после чего калькулятор вернет вам величину угла.
Рассмотрим пару примеров
Вычисление угла
Пусть в школьной задаче задан прямоугольный треугольник со сторонами A = 5 см, B = 12 см, C = 13 см. Требуется найти величины всех углов. Итак, очевидно, что угол AB, то есть угол, образуемый двумя катетами — прямой. Это известно из самого определения катетов. Теперь мы можем найти тангенс угла BC, который численно будет равен дроби, в числителе которой противолежащий катет A, а в знаменателе — прилежащий B. Следовательно, tgBC = A/B = 5/12 = 0,416. Зная тангенс, мы легко можем вычислить соответствующий угол при помощи онлайн-калькулятора. Для это выберем в меню функцию тангенса и введем значение 0,416 в ячейку tgα. Программа мгновенно отобразит величину угла, равную 22,58 градуса. Вычислить последний угол не составит труда, так согласно постулату о сумме углов треугольника, угол AC = 180 − 90 − 22,58 = 67,42 градуса.
Вычисление тангенса
В школьных задачах чаще всего используются стандартные углы, поэтому школьникам важно знать значения основных тригонометрических функций для этих углов буквально наизусть. Давайте при помощи калькулятора определим значения тангенсов для наиболее распространенных в задачах углов:
Давайте при помощи калькулятора определим значения тангенсов для наиболее распространенных в задачах углов:
- tg30 = 0,577;
- tg45 = 1;
- tg60 = 1,732;
- tg90 — не рассчитывается;
- tg120 = -1,732;
- tg150 = -0,577;
- tg180 = 0.
Выше мы выяснили, почему тангенс не рассчитывается для значений 90 градусов. Еще одно интересное значение — угол в 45 градусов. Почему тангенс равен 1? Ответ очевиден, ведь если в прямоугольном треугольнике один угол равен 45 градусам, то и второй имеет такую же величину. Следовательно, треугольник равнобедренный, его катеты имеют одинаковую длину, а их соотношение в любом случае будет равно 1.
Заключение
Тригонометрия — сложная наука, которая не находит практически никакого применения в повседневной жизни. Однако без тригонометрии не было бы современных технологий, поэтому специалистам прикладных наук без нее никуда. Используйте наши онлайн-калькуляторы для расчета значений тригонометрических функций.
Тангенс — это одна из тригонометрических функций . Изначально тригонометрические функции выражают зависимости элементов прямоугольных треугольников — сторон и углов. В прямоугольном треугольнике катеты — это стороны, образующие прямой угол, гипотенуза — третья сторона. Тогда тангенс угла — это отношение противолежащего катета к прилежащему. Таким образом, это безразмерная величина, т.е. она не измеряется в градусах или метрах, это просто число. Обозначается как tg . Для решения многих геометрических и математически задач требуется вычислить тангенс угла. Найти его можно разными способами.
Необходимо:
— калькулятор;
— MS Excel;
— базовые знания в области математики, геометрии и тригонометрии.
Инструкция:
- Данную величину можно определить как отношения синуса угла к косинусу этого же угла. Если они известны, то нужную характеристику можно вычислить по формуле tg(a)=sin(a)/cos(a) .

- Значение можно вычислить с помощью инженерного калькулятора. Для этого наберите число и нажмите клавишу tg . Значение тангенса может быть сколь угодно большим или малым, но для значений углов, кратных 90 градусам, эта характеристика не существует.
- Значение tg можно определить по графику функции Y=tg(x) . Для этого надо на оси X найти значение угла, для которого ищется данная характеристика, провести из этой точки перпендикуляр к оси абсцисс (ось ОX ) до пересечения с графиком, затем из точки пересечения провести перпендикуляр к оси ординат (ось OY ). Значение Y в этой точке и будет искомым значением тангенса.
- Как найти тангенс угла, если под рукой нет калькулятора? Можно посчитать его в программе Excel . Введите в любой ячейке =tan(радианы(а)) , где а — число, от которого ищется значение характеристики, нажмите Enter . В ячейке появится значение данной величины.
- Также тригонометрические функции иногда определяют через ряды .
 5+… Сумму этого бесконечно ряда можно посчитать, пользуясь свойствами пределов .
5+… Сумму этого бесконечно ряда можно посчитать, пользуясь свойствами пределов .
Тангенс угла – это число, которое определяется соотношением противолежащего и прилежащего к этому углу катетов в треугольнике. Зная только это соотношение дозволено узнать величину угла, скажем, воспользовавшись тригонометрической функцией, обратной тангенсу – арктангенсом.
Инструкция
1. Если у вас есть под рукой таблицы Брадиса в бумажном либо электронном виде, то определение угла сведется к поиску значения в таблице тангенсов. Ему будет сопоставлена величина угла – то есть то, что и требуется обнаружить.
2. Если таблиц нет, то придется вычислять значение арктангенса. Дозволено применять для этого, скажем, типовой калькулятор из состава ОС Windows. Раскройте основное меню, щелкнув кнопку «Пуск» либо нажав клавишу WIN, перейдите в раздел «Все программы», после этого в подраздел «Типовые» и выберите пункт «Калькулятор». Это же дозволено сделать через диалог запуска программ – нажмите сочетание клавиш WIN + R либо выберите в основном меню строку «Исполнить», наберите команду calc и нажмите клавишу Enter либо щелкните кнопку «OK» .
3. Переключите калькулятор в режим, тот, что разрешает вычислять тригонометрические функции. Для этого раскройте в его меню раздел «Вид» и выберите пункт «Инженерный» либо «Ученый» (в зависимости от версии применяемой операционной системы).
4. Введите знаменитое значение тангенса. Это дозволено сделать как с клавиатуры, так и щелкая надобные кнопки интерфейса калькулятора.
5. Удостоверитесь, что в поле «Градусы» стоит отметка, дабы получить итог вычисления именно в градусах, а не в радианах либо градах.
6. Поставьте отметку в чекбоксе с надписью Inv – этим вы инвертируете значения вычисляемых функций, обозначенные на кнопках калькулятора.
7. Щелкните кнопку с надписью tg (тангенс) и калькулятор вычислит значение функции обратной тангенсу – арктангенс. Оно и будет являться желанным углом.
8. Все это же дозволено проделать и с применением онлайн-калькуляторов тригонометрических функций. Обнаружить такие сервисы в интернете довольно легко с подмогой поисковых систем. Да и некоторые из поисковиков (скажем, Google) сами имеют встроенные калькуляторы.
Да и некоторые из поисковиков (скажем, Google) сами имеют встроенные калькуляторы.
Сайты имеют настоль трудную систему, что порой бывает сложно обнаружить его главное меню . Почаще каждого такой пункт бывает расположен в «шапке» сайта для стремительного перехода к нему. В некоторых случаях переход осуществляется посредством открытия основной страницы, тут все зависит от типа сайта.
Вам понадобится
- – браузер;
- – подключение к интернету.
Инструкция
1. Зайдите на основную страницу сайта и обнаружьте на ней ссылку на меню . Также оно может располагаться прямо на ней. Изредка главное меню может быть спрятано в выпадающем списке, для его просмотра вам нужно будет щелкнуть по ссылке для его раскрытия. Изредка оно имеет вид обыкновенного проводника Windows, и для перехода по его пунктам либо для просмотра оглавления вам нужно будет щелкнуть по плюсику рядом с наименованием директории.
2. Если вы находитесь на определенной странице сайта и не можете обнаружить ссылку для перехода к основной странице, наблюдательно посмотрите на его оглавление и обнаружьте ссылку в виде логотипа либо обыкновенного текстового наименования источника. Также вы можете перейти к основной странице при помощи ввода основного адреса сайта в соответствующую строку вашего обозревателя.
3. Обратите внимание, многие сайты могут содержать несколько меню , скажем, меню настройки профиля пользователя, где указывается его персональная информация и данные для входа, и меню сайта для перехода по его содержимому. В первом случае это может быть ссылка на управление профилем либо редактирование личных данных, параметры учетной записи и так дальше. Во втором – обыкновенное меню , которое упорядочивает содержимое, обеспечивающее переход по разделам согласно их назначению.
4. Если вам нужно обнаружить карту сайта, просмотрите основную страницу на присутствие ссылки на нее. Многие из них легко не содержат карты сайта, от того что ими дюже редко пользуются. Для перехода к основному меню сайта также обращайте внимание на основные его функции, ссылки на которые сохраняются при переходе по страницам. Находясь в определенной ветке какого-нибудь форума, вы можете перейти по ссылкам вверху либо низу блока с темами, обыкновенно там прописывается дерево папок подфорума, в котором вы находитесь.
Многие из них легко не содержат карты сайта, от того что ими дюже редко пользуются. Для перехода к основному меню сайта также обращайте внимание на основные его функции, ссылки на которые сохраняются при переходе по страницам. Находясь в определенной ветке какого-нибудь форума, вы можете перейти по ссылкам вверху либо низу блока с темами, обыкновенно там прописывается дерево папок подфорума, в котором вы находитесь.
Полезный совет
Пользуйтесь меню на основной странице.
Тангенс угла, как и другие тригонометрические функции, выражает связанность между сторонами и углами прямоугольного треугольника. Использование тригонометрических функций дозволяет заменить в расчетах величины в градусном измерении на линейные параметры.
Инструкция
1. При наличии транспортира данный угол треугольника дозволено измерить и по таблице Брадиса обнаружить значение тангенса. Если нет вероятности определить градусную величину угла, определите его тангенс с поддержкой замеров линейных величин фигуры. Для этого сделайте вспомогательные построения: из произвольной точки на одной из сторон угла опустите перпендикуляр на иную сторону. Измерьте расстояние между концами перпендикуляра на сторонах угла, запишите итог измерения в числитель дроби. Сейчас измерьте расстояние от вершины заданного угла до вершины прямого угла, т. е. до точки на стороне угла, в которую был опущен перпендикуляр. Полученное число запишите в знаменатель дроби. Составленная по итогам измерений дробь равна тангенсу угла.
Для этого сделайте вспомогательные построения: из произвольной точки на одной из сторон угла опустите перпендикуляр на иную сторону. Измерьте расстояние между концами перпендикуляра на сторонах угла, запишите итог измерения в числитель дроби. Сейчас измерьте расстояние от вершины заданного угла до вершины прямого угла, т. е. до точки на стороне угла, в которую был опущен перпендикуляр. Полученное число запишите в знаменатель дроби. Составленная по итогам измерений дробь равна тангенсу угла.
2. Тангенс угла дозволено определить расчетным путем как отношение противолежащего ему катета к прилежащему. Также дозволено вычислить тангенс через прямые тригонометрические функции рассматриваемого угла — синус и косинус. Тангенс угла равен отношению синуса этого угла к его косинусу. В различие от постоянных функций синуса и косинуса, тангенс имеет обрыв и не определен при величине угла 90 градусов. При нулевом значении угла его тангенс равен нулю. Из соотношений прямоугольного треугольника видимо, что угол 45 градусов имеет тангенс, равный единице, от того что катеты такого прямоугольного треугольника равны.
3. При значениях угла от 0 до 90 градусов его тангенс имеет позитивное значение, от того что синус и косинус в этом промежутке позитивны. Пределы метаморфозы тангенса на этом участке – от нуля до беспредельно крупных значений при углах, близких к прямому. При негативных значениях угла его тангенс также меняет знак. График функции Y=tg(x) на промежутке -90°
Прямая y=f(x) будет касательной к изображенному на рисунке графику в точке х0 в том случае, если она проходит через точку с координатами (х0; f(x0)) и обладает угловым коэффициентом f»(x0). Найти такой коэффициент, зная особенности касательной, несложно.
Вам понадобится
- — математический справочник;
- — простой карандаш;
- — тетрадь;
- — транспортир;
- — циркуль;
- — ручка.
Инструкция
Если значения f‘(x0) не существует, то либо касательной нет, либо она проходит вертикально. Ввиду этого, наличие производной функции в точке х0 обусловлено существованием невертикальной касательной, соприкасающейся с графиком функции в точке (х0, f(х0)). В этом случае угловой коэффициент касательной равен будет f»(х0). Таким образом, становится ясен геометрический смысл производной – расчет углового коэффициента касательной.
В этом случае угловой коэффициент касательной равен будет f»(х0). Таким образом, становится ясен геометрический смысл производной – расчет углового коэффициента касательной.
Изобразите на дополнительные касательные, которые бы соприкасались с графиком функции в точках x1, х2 и х3, а также отметьте углы, образуемые этими касательными с осью абсцисс (такой угол отсчитывают в положительном направлении от оси до касательной прямой). К примеру, угол, то есть, α1, будет острым, второй (α2) – тупой, а третий (α3) равен нулю, поскольку касательная прямая параллельна оси ОХ. В таком случае тангенс тупого угла – отрицательное , тангенс острого угла – положительное, а при tg0 результат равен нулю.
Обратите внимание
Правильно определите угол, образуемый касательной. Для этого используйте транспортир.
Полезный совет
Две наклонные прямые будут параллельными в том случае, если их угловые коэффициенты равны между собой; перпендикулярными, если произведение угловых коэффициентов этих касательных равно -1.
Источники:
- Касательная к графику функции
Косинус, как и синус, относят к «прямым» тригонометрическим функциям. Тангенс (вместе с котангенсом) причисляют к другой паре, называемой «производными». Существует несколько определений этих функций, которые делают возможным нахождение тангенса заданного по известному значению косинуса от этой же величины.
Инструкция
Вычтите частное от единицы на возведенное в значение косинуса заданного угла, а из результата извлеките квадратный корень — это и будет значение тангенса от угла, выраженное его косинус: tg(α)=√(1-1/(cos(α))²). При этом обратите внимание на то, что в формуле косинус стоит в знаменателе дроби. Невозможность деления на ноль исключает использование этого выражения для углов, равных 90°, а также отличающихся от этой величины на числа, кратные 180° (270°, 450°, -90° и т.д.).
Существует и альтернативный способ вычисления тангенса по известному значению косинуса. Его можно применять, если не установлено ограничение на использование других . Для реализации этого способа сначала определите величину угла по известному значению косинуса — это можно сделать с помощью функции арккосинус. Затем просто рассчитайте тангенс для угла полученной величины. В общем виде этот алгоритм можно записать так: tg(α)=tg(arccos(cos(α))).
Для реализации этого способа сначала определите величину угла по известному значению косинуса — это можно сделать с помощью функции арккосинус. Затем просто рассчитайте тангенс для угла полученной величины. В общем виде этот алгоритм можно записать так: tg(α)=tg(arccos(cos(α))).
Есть и еще экзотический вариант с использованием определения косинуса и тангенса через острые углы прямоугольного треугольника. Косинусу в таком определении соответствует отношение длины прилежащего к рассматриваемому углу катета к длине гипотенузы. Зная значение косинуса можно подобрать соответствующие ему длины этих двух сторон. Например, если cos(α)=0,5, то прилежащий можно принять равным 10см, а гипотенузу — 20см. Конкретные числа здесь значения не имеют — одинаковое и правильное вы получите с любыми значениями, имеющими же . Затем по теореме Пифагора определите длину недостающей стороны — противолежащего катета. Она будет равна квадратному корню из разницы между длинами возведенных в квадрат гипотенузы и известного катета: √(20²-10²)=√300. Тангенсу по определению соответствует отношение длин противолежащего и прилежащего катетов (√300/10) — рассчитайте его и получите значение тангенса, найденное с использованием классического определения косинуса.
Тангенсу по определению соответствует отношение длин противолежащего и прилежащего катетов (√300/10) — рассчитайте его и получите значение тангенса, найденное с использованием классического определения косинуса.
Источники:
- косинус через тангенс формула
Одна из тригонометрических функций, чаще всего обозначаемая буквами tg, хотя встречаются и обозначения tan. Проще всего представить тангенс как отношение синуса угла к его косинусу. Это нечетная периодическая и не непрерывная функция, каждый цикл которой равен числу Пи, а точка разрыва соответствует отметке в половину этого числа.
Калькулятор котангенса – пример с шагами
Калькулятор котангенса(cot(x)) позволит вам вычислить котангенс угла, который не равен 90 градусам. Это важно в математике как одна из наиболее сложных тригонометрических функций. С помощью этой статьи и нашего калькулятора вы разберетесь с этой ненормальной функцией. У нас также есть пошаговое решение на нашем калькуляторе и несколько примеров здесь.
Что такое кроватка(х)?
Котангенс cot(x) равен косинусу x, деленному на синус x. В отличие от синуса и косинуса, которые мы вычисляем из прямоугольного треугольника, мы вычисляем котангенс либо из тангенса, либо из косинуса и синуса.
Важно отметить, что котангенс не является обратной функцией косинуса или тангенса. Скорее, у котангенса есть обратная функция, записанная как arccot (x) (или обратная для котангенса). Область арккотангенса для x равна [отрицательная бесконечность, x, положительная бесконечность]. Следовательно, мы можем заключить, что для области оси Y 0 < y < pi.
Как было сказано ранее, котангенс x равен косинусу, деленному на синус. Если мы посмотрим под правильным углом, мы сможем лучше понять такой вопрос. Например, на следующем рисунке у нас есть прямоугольный треугольник. Во-первых, мы бы вычислили косинус, во-вторых, синус. Наконец, мы получили бы кроватку(х) после деления этих двух значений.
Рисунок 1. Прямоугольный треугольникФормула котангенса
Формула котангенса требует, чтобы мы знали тангенс как синуса, так и косинуса. Например, котангенс равен обратному значению тангенса. В то же время, если мы подставим значение отклонения, синус х, деленный на косинус х, мы получим Формулу для кроватки(х). Давайте сосредоточимся на прямоугольном треугольнике с рисунка 1. Мы знаем, что значение синуса — это отношение противолежащего катета и гипотенузы. Далее вычисляем косинус. Косинус из предыдущего рисунка эквивалентен балансу прилежащего катета и гипотенузы.
Например, котангенс равен обратному значению тангенса. В то же время, если мы подставим значение отклонения, синус х, деленный на косинус х, мы получим Формулу для кроватки(х). Давайте сосредоточимся на прямоугольном треугольнике с рисунка 1. Мы знаем, что значение синуса — это отношение противолежащего катета и гипотенузы. Далее вычисляем косинус. Косинус из предыдущего рисунка эквивалентен балансу прилежащего катета и гипотенузы.
Теперь мы можем определить котангенс, используя первый вариант. Если мы подставим значения синуса и косинуса, то получим Формулу.
Котангенс(х) = \frac{1}{Тангенс(х)} Другой способ вычисления котангенса – рассмотрение общего значения тангенса. Мы делим синус и косинус на косинус (x), чтобы получить следующую формулу. Над дробной чертой у нас есть косинус (x) / косинус (x), равный единице. Ниже дробной линии у нас есть синус (х) / косинус (х).
Если мы вставим значение тангенса. Мы получаем формулу для котангенса, используя тангенс x.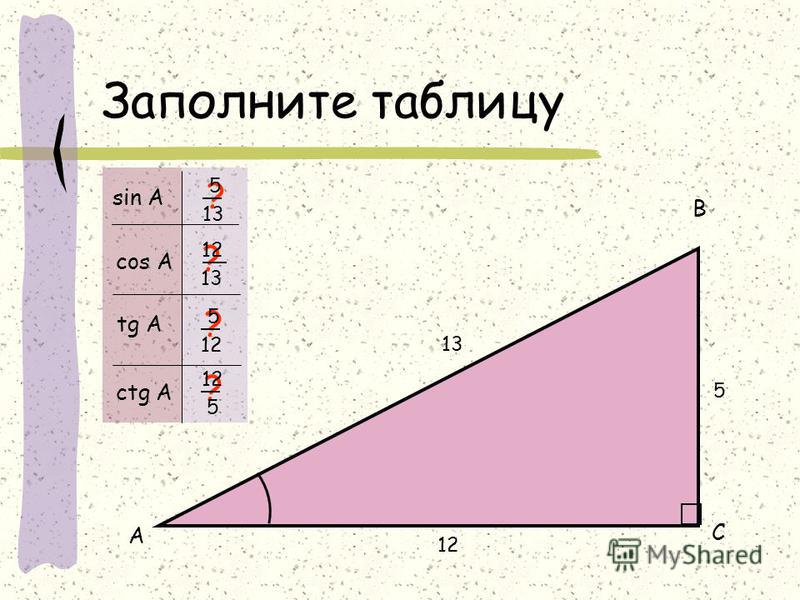
График котангенса
В отличие от синуса или косинуса, котангенс имеет разные домены. Например, областью для кроватки(х) является [отрицательный инфинитив, положительная бесконечность] на оси у. Область определения оси x равна [0, pi]. Во-первых, давайте посмотрим на график кроватки (x).
Рисунок 2: График котангенсаНапример, мы можем заключить, что период котангенса равен пи, где пи — константа, равная 3,14. Как мы уже говорили, у котангенса нет амплитуды. Область значений y варьируется от отрицательной бесконечности до положительной бесконечности. Это означает, что граф продолжается вечно до бесконечности. Другой важный факт выводится, когда мы смотрим на рисунок для графиков тангенса и котангенса. Например, у нас есть диаграммы тангенса и котангенса на следующем рисунке.
Рисунок 3: Графики котангенса и тангенса Мы можем заметить, что графики для наших двух функций смотрят в разные стороны. Однако мы также можем отметить пересечение двух функций. Они пересекаются для значений отрицательного и положительного. Обе эти функции имеют один и тот же домен на оси Y. Однако ассортимент разный. Котангенс имеет диапазон от 0 до pi. Тангенс имеет диапазон от -pi/2 до pi/2.
Обе эти функции имеют один и тот же домен на оси Y. Однако ассортимент разный. Котангенс имеет диапазон от 0 до pi. Тангенс имеет диапазон от -pi/2 до pi/2.
Единичная окружность котангенса
Мы уже говорили о единичных окружностях в наших калькуляторах синуса, косинуса и подобных им тригонометрических функций. Однако единичная окружность для котангенса и тангенса не совпадает. Например, единичный круг для косинуса использует определенные точки на круге, чтобы определить значение наиболее распространенных углов. Так что, наоборот, мы не можем использовать ту же единичную окружность для тангенса и котангенса, которую мы используем для косинуса и синуса. Для этого примера рассмотрим два единичных круга. Первый единичный круг — это косинусы и синусы. Другой — это единичная окружность котангенса.
Рисунок 4: Единичная окружность для котангенса Как видите, наша единичная окружность имеет линию, параллельную оси x, и является касательной к нашей единичной окружности. Названия тангенс и котангенс получили свои названия от этого падежа. Они оба касаются единичной окружности. Разница заключается в том, как они касаются единичной окружности в точке pi/2 и 0. Кроме того, касательная касается единичной окружности в точке 0 (или 2pi).
Названия тангенс и котангенс получили свои названия от этого падежа. Они оба касаются единичной окружности. Разница заключается в том, как они касаются единичной окружности в точке pi/2 и 0. Кроме того, касательная касается единичной окружности в точке 0 (или 2pi).
У нас есть тангенс и котангенс единичной окружности на следующем рисунке.
Обратите внимание, что котангенс касается единичной окружности в точке pi/2. Как мы используем единичный круг? Если мы даем определенный угол. Например, угол x = pi/4. Теперь вернемся к нашему единичному кругу. На ней, для угла пи/4, на касательной имеем значение единицы.
Рисунок 5: Котангенс и тангенсКак вычислить котангенс заданного угла?
При вычислении котангенса угла у нас есть много инструментов, которые мы можем использовать. Первый вариант — использовать единичный круг. Затем, если мы получим задачу по вычислению котангенса угла, мы можем использовать последнюю цифру для вычисления наиболее распространенных значений котангенса.
Задача: вычислить котангенс и тангенс x = pi/3. Глядя на единичную окружность, мы видим, что для угла pi/3 значение котангенса равно корню из 3 из 3. Используя нашу единичную касательную окружность, мы можем определить значение тангенса для угла x = pi/3. . Tan(pi/3) = корень из 3 ·
Использование формулы тангенса — еще один способ вычисления котангенса заданного угла. Сначала напишем процедуру.
Котангенс(х) = \frac{1}{Касательная(х)} Теперь мы можем решить задачу несколькими способами. Например, если у нас есть только стороны треугольника, мы могли бы использовать синусы и косинусы для вычисления котангенса. Мы также можем использовать касательные. Мы знаем, что котангенс есть величина, обратная тангенсу. Так что Формула будет.
Котангенс(х) = \frac{косинус(х)}{синус(х)} 92} Гипотенуза = 36см. Далее вычисляем синус и косинус этого угла. Мы можем использовать формулу синуса и косинуса. Если вы не знаете, как рассчитать синус и косинус, воспользуйтесь другими нашими калькуляторами для получения дополнительных пояснений. После вычисления синуса (33,7 градуса) и косинуса (33,5 градуса) мы можем определить значение кроватки (х). Мы используем Формулу.
После вычисления синуса (33,7 градуса) и косинуса (33,5 градуса) мы можем определить значение кроватки (х). Мы используем Формулу.
Котангенс = \frac{косинус(x)}{синус(x)} Получаем, что кроватка(х) примерно равна 44,7 градусам (кроватка 45 градусов равна единице). Еще одним полезным калькулятором является калькулятор преобразования углов, который можно использовать при преобразовании градусов в радианы.
Применение функции котангенса
Котангенс и тригонометрия используются во многих предметах. Некоторые из тем, где тригонометрия имеет решающее значение, включают авиацию, криминологию, морскую биологию, навигацию, расчет высоты зданий и т. д.
В авиации и навигации тригонометрия вычисляет пройденное расстояние, расстояние до цели и многие другие важные факты. Сегодня тригонометрические функции наиболее широко используются в архитектуре (для расчета высоты зданий). Обычно это калькуляторы, так как работать вручную может быть утомительно. Другое использование этих функций в видеоиграх. Например, в популярной игре «Супер Марио» используется 2D-пространство, в котором персонаж перемещается по осям X и Y. Используя приведенные выше формулы, вы можете рассчитать расстояние прыжка Марио. Наконец, в криминологии мы используем тригонометрические функции, чтобы примерно определить, где, например, стоял стрелок.
Например, в популярной игре «Супер Марио» используется 2D-пространство, в котором персонаж перемещается по осям X и Y. Используя приведенные выше формулы, вы можете рассчитать расстояние прыжка Марио. Наконец, в криминологии мы используем тригонометрические функции, чтобы примерно определить, где, например, стоял стрелок.
Связанные тригонометрические функции
Когда дело доходит до связанных тригонометрических функций, наиболее примечательной является тангенс. Это связано с тем, что тангенс представляет собой ожидаемое значение котангенса. Однако важно отметить, что такие процессы, как синус или косинус, также связаны между собой. Чтобы показать эту связь между двумя функциями, мы должны сначала рассмотреть, чему равен тангенс. Тангенс(х) = синус(х)/косинус(х). Тогда, если мы подставим эту формулу в первую упомянутую формулу, мы можем получить значение котангенса по его синусам и косинусам. Котангенс(х) = косинус(х)/синус(х).
Пример: использование калькулятора котангенса
Чтобы использовать наш калькулятор котангенса «Calcon», сначала загрузите наше приложение из магазина Google Play или Apple App Store. Далее в строке поиска введите «Калькулятор котангенса». Как только приложение найдет подходящий калькулятор, вы им воспользуетесь. Сначала введите значение угла, для которого вы хотите найти котангенс. После нажатия «Рассчитать» отобразятся результаты и пошаговое руководство по расчету вручную.
Далее в строке поиска введите «Калькулятор котангенса». Как только приложение найдет подходящий калькулятор, вы им воспользуетесь. Сначала введите значение угла, для которого вы хотите найти котангенс. После нажатия «Рассчитать» отобразятся результаты и пошаговое руководство по расчету вручную.
Калькулятор котангенса – нахождение котангенса в градусах или радианах
Онлайн-калькулятор котангенса находит значение котангенса по значению заданного угла. Кроме того, этот калькулятор детской кроватки отображает конечный результат в градусах, радианах, м радианах или пи радианах в соответствии с вашими требованиями. Он функционирует, чтобы автоматически следовать стандартному уравнению детской кроватки.
Что ж, продолжайте читать, чтобы найти ответ о том, как найти котангенс (cot) и некоторую важную информацию о кроватке (x).
Что такое детская кроватка в математике? В тригонометрии кроватку можно определить как обратную сторону касательной. Однако в случае прямоугольного треугольника, когда мы делим длину смежной стороны на длину стороны, противоположной углу, тогда полученное свойство известно как котангенс и сокращенно кроватка.
Однако в случае прямоугольного треугольника, когда мы делим длину смежной стороны на длину стороны, противоположной углу, тогда полученное свойство известно как котангенс и сокращенно кроватка.
Котангенс является обратной величиной тангенса:
Cot(x) = 1 / tan(x) = tan(x)-1. Или b/a
Однако котангенс можно представить в терминах синуса(х) и косинуса(х).
Cot(x) = cos(x)/sin(x)
Пример:
Вычислить котангенс угла α в прямоугольном треугольнике, если длина прилежащей стороны равна 20, а противолежащая сторона равна до 4.
- Просто подставьте указанные значения в приведенную выше формулу: cot(α) = 20 / 4 = 5
Помимо этого, вы также можете использовать калькулятор котангенса для получения безошибочных результатов.
Однако используйте онлайн-калькулятор тангенса, чтобы вычислить значения тангенса для заданного угла в градусах, радианах, м радианах или пи (π) радианах.
В прямоугольном треугольнике СОТ угла можно определить, взяв отношение прилежащего угла к противоположному углу. Однако формула COT для расчета угла:
Однако формула COT для расчета угла:
Cot (α) = смежный b / напротив a
Вместо этого калькулятор кроватки может быть хорошим выбором для нахождения котангенса угла за долю секунды.
Таблица котангенсовВ следующей таблице показаны значения котангенсов обычных углов в радианах и градусах. Впрочем, все эти значения можно рассчитать и с помощью раскладного калькулятора.
| Градусы | Радиан | Y=котангенс(X) |
| 180 ̊ | Π | Вне диапазона |
| 150 ̊ | 5π/6 | -1.732051 |
| 135 ̊ | 3π/4 | -1 |
| 120 ̊ | 2π/3 | -0,57735 |
| 90 ̊ | №/2 | 0 |
| 60 ̊ | №/3 | 0,57735 |
| 45 ̊ | №/4 | 1 |
| 30 ̊ | №/6 | 1. 732051 732051 |
| 0 ̊ | 0 | 0 |
Кроме того, бесплатный онлайн-калькулятор арктангенса позволяет найти функцию арктангенса или арктангенс (x) в радианах, градусах и других единицах измерения.
График для котангенса:В виде графика функция котангенса для другого угла выглядит как серия повторяющихся кривых. Кроме того, при построении графика важно помнить, что котангенс угла никогда не будет равен:
- Ноль (0)
- кратно π радиан
- 180°
Вы можете вычислить котангенс в этом калькуляторе в два простых шага:
Ввод:- Введите угол в заданном пространстве.
- Теперь выберите в раскрывающемся меню градусы, радианы, М-радиан или пи-радиан.
- Нажмите кнопку «Рассчитать».
После того, как вы введете угол и единицу измерения, калькулятор раскладушки покажет:
- Значение COT будет отображаться в градусах, радианах, M-радианах и пи-радианах в зависимости от поля ввода.

- Повторите расчет, чтобы выполнить другой расчет.
На единичном круге мы можем вычислить его для угла, используя координаты x и y этой конкретной связанной точки на единичном круге:
- кроватка*t=cos*t sin*t=x.y
- т = х . г
Однако, калькулятор котангенса является отличной поддержкой для расчета значений котангенса для угла в мгновение ока. Кроме того, если заданы значения тангенса, калькулятор cot-1 найдет его, поскольку кроватка также является обратной величиной тангенса.
Что такое 3 взаимных тождества?По понятию взаимных тождеств статистики определяют три взаимных соотношения:
- Косеканс
- Секанс
- Котангенс
Котангенс можно применять так же, как синус, косинус и тангенс. Вы можете использовать его на основе концепции прямоугольного треугольника. Его также можно использовать на основе единичного круга, и в этом случае угол результатов будет отображаться в радианах.
Вы можете использовать его на основе концепции прямоугольного треугольника. Его также можно использовать на основе единичного круга, и в этом случае угол результатов будет отображаться в радианах.
Несколько советов по решению детской тригонометрии :
- Начните вычисления с более сложной стороны.
- Всегда предпочитаю выражать все в виде синуса и косинуса.
- Применение тождеств Пифагора для преобразования между sin²x и cos²x.
- Всегда знайте, когда подходящее время, чтобы применить формулу двойного угла и формулу сложения
Калькулятор котангенса поможет вам узнать о функции cottrig и ее соответствующих элементах. Пожалуй, раскладушка — одна из сложных тригонометрических функций, когда речь идет о ручных вычислениях. Тем не менее, вы все равно можете научиться находить котангенс с помощью этого бесплатного онлайн-калькулятора.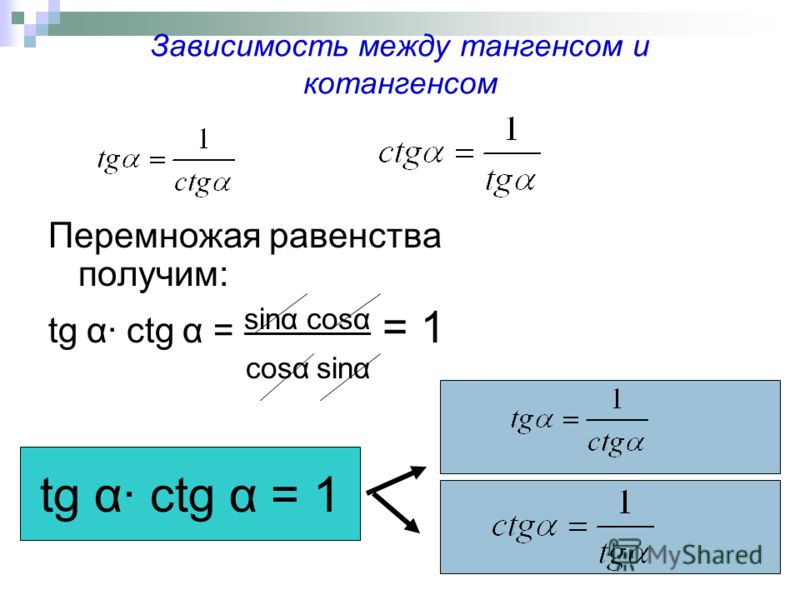 К счастью, это лучший вариант для студентов и профессионалов, чтобы узнать об определении детской кроватки, расчетах уравнения детской кроватки, а также о связанных терминах.
К счастью, это лучший вариант для студентов и профессионалов, чтобы узнать об определении детской кроватки, расчетах уравнения детской кроватки, а также о связанных терминах.
Из источника Википедии: радианы и градусы, определения единичного круга, алгебраические значения.
Из источника KhanAcademy: Взаимные тригонометрические соотношения, Нахождение обратных тригонометрических соотношений, Котангенс (котангенс).
Из источника Purple Math: тригонометрические функции и их графики, кофункции, график котангенса.
Калькулятор — cotan(tan(a)) — Solumaths
Котан, расчет онлайн
Резюме:
Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
котанг онлайн
Описание:
Тригонометрическая функция котангенс отмеченный котанг ,
это калькулятор котангенса , он позволяет онлайн вычислять котангенс угла, можно использовать разные угловые единицы: градусы, грады
или радианы, которые являются угловыми единицами по умолчанию.
Котангенс является обратным тангенсу: `cotan(x)=1/tan(x)` .
- Расчет котангенса
- Первообразная котангенса
Вычисление котангенса угла в радианах
Для расчета котангенса котангенса угла в радианах необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого действия вы можете начать свои расчеты.
Чтобы вычислить котангенс `pi/6`, введите cotan(`pi/6`), после вычисления, результат возвращается.
Вычисление котангенса угла в градусах
Чтобы рассчитать онлайн котангенс угла в градусах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого действия вы можете начать свои расчеты.
Итак, чтобы вычислить котангенс числа 60, необходимо ввести котанг (60), после вычисления возвращается результат.
Чтобы вычислить котангенс котангенс числа 60, введите cotan(60), после вычисления, результат возвращается.
Вычисление котангенса угла в градианах
Чтобы вычислить котангенс угла в градусах, вы должны сначала выбрать нужную единицу, нажав на кнопку параметров расчетного модуля. После этого действия вы можете начать свои расчеты.
92`.Первообразная котангенса равна `ln(sin(x))`.
Синтаксис:
cotan(x), где x — число.
Примеры:
cotan(`1/2`), возвращает 1.83048772171
Производный котангенс :
Чтобы дифференцировать котангенс функции онлайн, можно использовать калькулятор производной, который позволяет вычислить производную функции котангенса 92`
Первообразная котангенса :
Калькулятор первообразной позволяет вычислить первообразную функции котангенса.
Первообразная cotan(x) является первообразной(`»»cotan»»(x)`)=`ln(sin(x))`
Предельный котангенс :
пределы функции котангенса.предел cotan(x) is limit(`»»cotan»»(x)`)
Графический котангенс :
Графический калькулятор может отображать функцию котангенса в заданном интервале.
Свойство котангенса функции:
Функция котангенса является нечетной функцией.
Расчет онлайн с котангенсом
См. также
Список связанных калькуляторов:
- Арккосинус : arccos.
 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. - Арксинус: арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
- Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
- Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
- Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
- Косеканс: косеканс Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Котангенс : котанг. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
- Тригонометрическое расширение: expand_trigo.
 Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения. - Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
- Упрощение калькулятора: упрощение. Калькулятор, который может упростить алгебраическое выражение онлайн.
- Секанс: сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Синус: синус. Тригонометрическая функция sin для вычисления греха угла в радианах, градусов или градианов.
- Касательная: рыжевато-коричневая. Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.
Напоминания о курсах, калькуляторы, упражнения и игры: Тригонометрические функции, Вещественные функции0001
Санкет Дханетия
В этом руководстве мы покажем вам все, что вам нужно знать о том, как вычислить котангенс на калькуляторе, так что продолжайте читать!
Ниже вы можете найти 5 различных методов расчета котангенса на калькуляторе,
- Метод 1 – Как найти секанс, косеканс и котангенс на калькуляторе
- Метод 2 – Как вычислить котангенс с помощью калькулятора
- Метод 3 – Как Сделать Csc, Sec и кроватку на Casio Fx-300Es
- Метод 4 – Как поместить Csc Sec Cot в калькулятор
- Метод 5 – Алгебра 2 – Как вычислить арккотангенс с помощью графического калькулятора
Метод 1 – Как найти секанс косеканс и котангенс на калькуляторе вы делаете г-н.
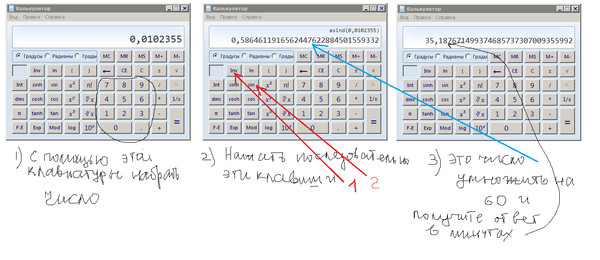 Сегодня Оз Ли собирался поговорить о том, как найти пропорции взаимности. На калькуляторе хорошо, что такое обратное отношение, ну, обратное отношение, как правило, это то, о чем здесь думали. Или в тригонометрии у нас есть секанс, косеканс и котангенс, и они связаны с обратными функциями нашего.
Сегодня Оз Ли собирался поговорить о том, как найти пропорции взаимности. На калькуляторе хорошо, что такое обратное отношение, ну, обратное отношение, как правило, это то, о чем здесь думали. Или в тригонометрии у нас есть секанс, косеканс и котангенс, и они связаны с обратными функциями нашего.Типичные коэффициенты триггера k синус косинус тангенс поэтому самый простой способ позволяет сказать, что наша проблема здесь, они хотят, чтобы мы. Найдите секанс хорошо секанс 83 0,25 градусов как мы найдем это хорошо я знаю, что. Функция секанса такая же, как 1 по косинусу, хорошо, поэтому она обратна моей функции косинуса, хорошо. Здесь проще всего найти функцию косинуса, а затем сначала взять обратную. Давайте перейдем к нашему калькулятору, я хочу, чтобы вы нажали режим, хорошо, спуститесь сюда и убедитесь, что степень.
Подсвечивается, что очень важно, хорошо, если это не подсвечивается, значит, вы будете работать в радианах. Нет. Хорошо, хорошо, поэтому мы работали в градусах здесь, когда вы нажимаете второй удар, чтобы выйти, и это возвращает нас к этому. Наш обычный экран хорошо напоминает нам здесь, что задача говорит о секансе восьмидесяти трех и двух пяти. Градусы — это самый простой способ, я хочу, чтобы вы сказали один, и вы не видите его на моем калькуляторе, вот и все. Хорошо, половина ряда выгоревших битых пикселей здесь, так что собирались сказать, что один разделен.
Наш обычный экран хорошо напоминает нам здесь, что задача говорит о секансе восьмидесяти трех и двух пяти. Градусы — это самый простой способ, я хочу, чтобы вы сказали один, и вы не видите его на моем калькуляторе, вот и все. Хорошо, половина ряда выгоревших битых пикселей здесь, так что собирались сказать, что один разделен.
По косинусу этого числа пытались придумать ладно восемьдесят три запятая два пять нажали энтер и. Там, дамы и господа, наш секанс в порядке, поэтому мы сказали, что единица делится на косинус этого числа и. Это всплывает из нашего ответа другим способом, которым вы можете это сделать, если вы скажете косинус 80 3,25. Введите хорошо, затем я хочу, чтобы вы сказали 1/2 этой кнопки здесь, хорошо, этой кнопки здесь. Я собираюсь использовать это значение здесь, поскольку оно означает ответ, поэтому 1 делится на мой ответ, нажмите Enter.
И вы заметите, что это те же самые восемь целых пять ноль семь восемь целых пять ноль семь, это сработает. То же самое и для синуса, и для тангенса, и для косеканса, и для котангенса, как вы это называете, это работает, ребята, хорошего дня. Посетите мой канал, чтобы получить дополнительную помощь по математике.
Посетите мой канал, чтобы получить дополнительную помощь по математике.
Метод 2 – Как вычислить котангенс с помощью калькулятора
Ребята, если вы посмотрите на свой калькулятор, вы заметите, что в калькуляторе нет ключа котангенса, я сказал, что знаю. У некоторых из вас, ребята, нет вычислений перед вами, но нет правильного ключа котангенса, но. Нам нужно понять, что котангенс и тангенс обратны друг другу, поэтому все, что нам просто нужно сделать. Что касается ввода этого в наш калькулятор, введите единицу, деленную на тангенс числа пи, деленного на восемь.
Хорошо, так что просто помните, что котангенс, косеканс и секанс не в вашем калькуляторе в порядке или, по крайней мере, в этом калькуляторе, я не знаю о тригонометрии, их там тоже нет, поэтому вам нужно сделать 1. Разделить на тогда и другое Важно, что мой угол больше не в градусах, а в радианах. Итак, вы должны убедиться, что вам удобно менять режим, возвращаясь к радианам. И тогда я просто делаю 1, деленное на тангенс числа пи, деленное на 8, и когда я это делаю, i.
Набери примерно 2,4 1/4, так что в домашней работе это основное.
Метод 3 – Как сделать Csc, Sec и Cot на Casio Fx-300Es
Привет, я собираюсь научить вас, как сделать косеканс, секанс и котангенс на Casio fx 308s сначала вы. Хотите убедиться, что ваш калькулятор в радианах, и вы делаете это, сначала проверяя, есть ли r. Тут же вы знаете, что это в радианах, если нет, если там написано d, то вы хотите щелкнуть. Режим Shift и 4 для сияния, а затем, если вы хотите вернуться к градусам, просто сделайте Shift.
Режим и вернитесь к градусам, поэтому, если вы посмотрите, хотите ли вы сначала сделать косеканс, вы хотите. Щелкните знак, затем угол, поэтому давайте посмотрим, когда число пи превышает 4, нажмите Enter, а затем вы хотите. Нажмите на этот x, чтобы сначала ввести отрицательный знак, и это косеканс числа пи более 4, то же самое касается секанса. И котангенс, если вы хотите секанс пи больше 4, сначала вы хотите сделать косинус пи больше 4. Введите и отрицательный x отрицательный 1 показатель степени и введите и то же самое для котангенса на этот раз, скажем, вы хотите.
Чтобы узнать, какой котангенс 5 пи на 6 равен марне 1/2 тангенса 5 5 пи на 6, нажмите Enter. Затем вы хотите щелкнуть ввод и накрыть, и у вас будет 5 пи больше 6, но это то, что мы сделали. Да отрицательный квадратный корень из 3.
Способ 4 – Как ввести Csc Sec Cot в калькулятор
Примечание. Этот раздел скоро будет обновлен.
Метод 5 – Алгебра 2 – Как вычислить арккотангенс с помощью графического калькулятора
Здесь нас попросили использовать наш графический калькулятор для вычисления арккотангенса, как для вычисления арккотангенса. Из пяти наш калькулятор не имеет явной функции для обратного котангенса, если мы помним котангенс, обратный пяти. Если мы хотим назвать это тета, это означает, что котангенс теты равен пяти котангенса теты. Мы можем записать как единицу над касательной к тета, чтобы получить единицу над касательной к тета, равной пяти.
Вы решаете это для касательной теты, и вы получаете касательную тету, равную одной пятой, которую действительно пытались найти. Из того, чему равна тета, мы получаем, что тета равна тангенсу, обратному одной пятой, и мы можем идти. К нашему калькулятору, нашему главному экрану здесь, вы хотели бы нажать режим, чтобы дважды проверить, в каком режиме были. Были в радианном режиме, так что хорошо нажмите «Очистить», чтобы вернуться на главный экран, нажмите вторую и касательную, чтобы получить. Обратный тангенс, затем введите одну пятую, закройте скобки и нажмите Enter, и вы увидите, что обратная котангенс пяти равна.
Из того, чему равна тета, мы получаем, что тета равна тангенсу, обратному одной пятой, и мы можем идти. К нашему калькулятору, нашему главному экрану здесь, вы хотели бы нажать режим, чтобы дважды проверить, в каком режиме были. Были в радианном режиме, так что хорошо нажмите «Очистить», чтобы вернуться на главный экран, нажмите вторую и касательную, чтобы получить. Обратный тангенс, затем введите одну пятую, закройте скобки и нажмите Enter, и вы увидите, что обратная котангенс пяти равна.
Примерно ноль целых девять десятых девять семь радиан.
Заключение. Как рассчитать котангенс на калькуляторе (csc)(sec) на моем калькуляторе?, найти sec и cot с помощью калькулятора, ⭐️⭐️ легко найти значение тригонометрических соотношений – casio – fx991es, как построить график котангенса на ti 84, учебник по калькулятору 13: тригонометрия на научном калькуляторе , как пользоваться тригонометрическими функциями на casio fx-991 научный калькулятор, как использовать тригонометрические функции на калькуляторе ti-84, как использовать тригонометрические функции на калькуляторе ti-36x pro, как использовать тригонометрические функции на калькуляторе ti-30x iis, научиться строить график котангенса, как использование тригонометрических функций на калькуляторе ba ii plus, построение графиков тригонометрических функций, фазовый сдвиг, период, преобразования, тангенс, косеканс, косинус, как использовать тригонометрические функции на калькуляторе Sharp el-501x, построение графика tan и cot.
Спасибо, что посетили Softwarediscover.com и прочитали эту статью! Если вы нашли эту статью полезной, поделитесь ею с друзьями и помогите распространить знания.
Категории Практические руководстваформул, примеры и многое другое о COTG(x)
Вы хотите рассчитать котангенс онлайн ? С нашим калькулятором вы можете сделать это для любого угла, как в градусах, так и в радианах. После нажатия кнопки расчета вы получите значение котг.
Если вы тоже хотите больше узнать об этой обратной тригонометрической функции, в статье мы научим вас всему, что нужно знать о ней.
Секции изделий
- Cotangent formula
- Table of cotangent values
- Cotangent of 0
- Features
- Derivative of the cotangent
- Integral of the cotangent
- How to calculate the cotangent in Excel
- Cotangent as a function of other trigonometric ratios
- Calculate котангенс в калькуляторе
Формула котангенса
Что такое котангенс угла? Это тригонометрическая функция, которая рассчитывается путем деления соседнего катета на противоположный катет. Он также определяется как обратная касательной.
Он также определяется как обратная касательной.
На основании вышеизложенного у нас осталась следующая формула для расчета котангенса:
Таблица значений котангенса
Ниже вы найдете таблицу с обычными значениями, которые котангенс принимает для типичных углов всех квадрантов:
| Марки | Радианы | Котангенс |
|---|---|---|
| 0º | 0 | ±∞ |
| 30º | π/6 | 1,7320 |
| 45º | π/4 | 1 |
| 60º | π/3 | 0,5773 |
| 90º | π/2 | 0 |
| 135º | 3π/4 | -1 |
| 180º | π | ±∞ |
| 225º | 5π/4 | 1 |
| 270° | 3π/2 | 0 |
| 315º | 7π/4 | -1 |
Если мы проанализируем результаты таблицы выше, мы увидим, что значение котангенса будет :
- Отрицательное значение , если угол находится во 2-м или 4-м квадранте
- Положительный , если угол находится в первом или третьем квадранте
То, что мы только что рассказали, можно увидеть на следующем графике:
Котангенс числа 0
Чему равен котангенс числа 0? Если вы попытаетесь решить этот ответ с помощью калькулятора, то увидите, что в результате получите ошибку. Почему? Давай посмотрим
Почему? Давай посмотрим
Ранее мы говорили, что котангенс является обратной величиной тангенса, поэтому:
тангенс 0º = 0
Теперь вычисляем стоимость кота:
cog = 1 / tan 0º = 1 / 0 = ±∞
Помните, что что-то между нулем равно бесконечности, но калькулятор рассматривает это как неопределенность и поэтому возвращает ошибку. в расчете.
Почему котангенс 0 равен бесконечности ? Чтобы увидеть это более наглядно, давайте посмотрим на график функции котангенса:
Если мы посмотрим на значение 0 по оси X, мы увидим, что функция не определена, а в зависимости от того, подходим ли мы слева или справа, ее значение стремится к -∞ или +∞. соответственно. Можно сказать, что есть асимптота.
Это также происходит для значений, кратных nπ, где n — целое число.
Особенности
Основная характеристика котангенса состоит в том, что его область определения состоит из всех действительных чисел (ℝ), кроме тех углов, которые кратны nπ , так как, как мы видели в предыдущем разделе, при этих значениях функция не определена и стремится к бесконечности.
Его диапазон составляет ℝ.
Производная котангенса
Производная котангенса равна -1 минус котангенс квадрата x. Мы можем выразить это математически следующим образом:
f(x) = cotgx → f'(x) = -csc 2 x = -1 — cotg 2 x
Интеграл от котангенса
Если мы хотим вычислить интеграл котангенса, то мы будем использовать эту формулу:
Как вычислить котангенс в Excel
В Excel мы также можем легко вычислить котангенс с помощью специальная функция, встроенная в программу электронных таблиц Microsoft. Для проверки откройте новую таблицу и введите в пустой ячейке следующую функцию:
Если угол в градусах:
=COT((РАДИАНЫ(угол)))
Если угол в радианах:
=COT(угол)
Sólo tienes que cambiar la palabra «ángulo» de la fórmula por la cantidad de grados o radianes que quieras. Por ejemplo, si queremos рассчитаем котангенс числа 90 , формулу запишем так:
Por ejemplo, si queremos рассчитаем котангенс числа 90 , формулу запишем так:
=COT((РАДИАНЫ(90))))
Котангенс как функция других тригонометрических отношений
Поскольку все тригонометрические функции связаны друг с другом, можно выразить котангенс как функцию любой из них. Ниже у вас есть все формулы:
В зависимости от синуса::
В зависимости от косинуса:
В зависимости от тангенса: эта формула является самой простой формулой из всех, так как, как мы видели в начале поста, по определению, по определение котангенс равен обратному тангенсу .
В зависимости от секанса:
В зависимости от косеканса:
Все формулы с обозначением (1) в правой части означают, что в зависимости от четверти, к которой принадлежит угол, результат будет быть положительным или отрицательным.
Вычислить котангенс в калькуляторе
Если вы хотите вычислить котангенс угла с помощью калькулятора .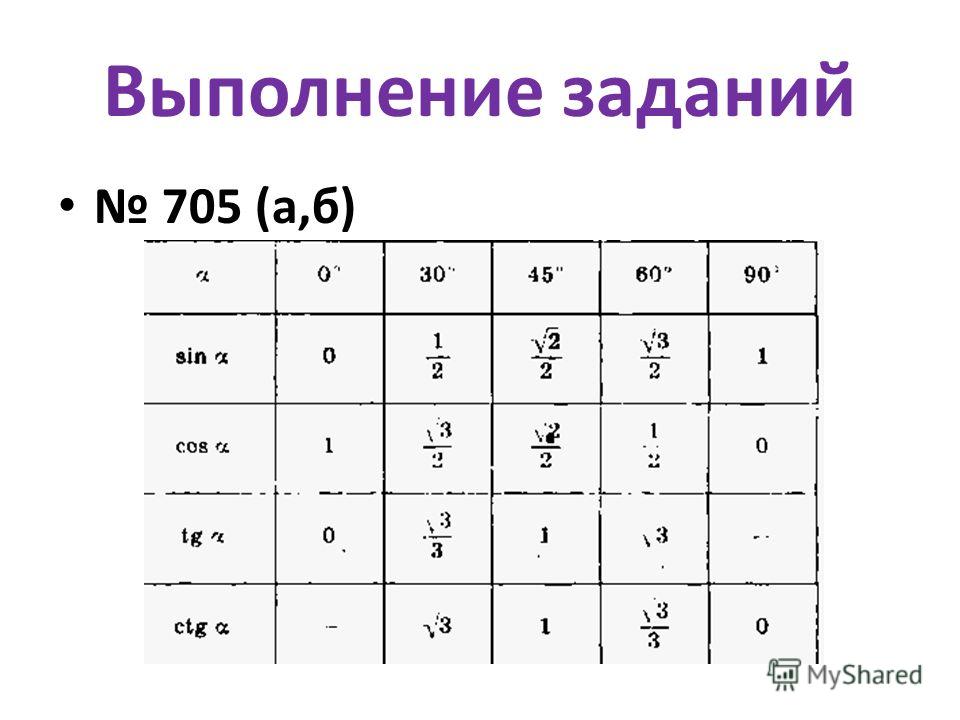 Если у вас нет научного или программируемого калькулятора, вы не найдете ни одной кнопки для выполнения этой операции. Однако есть метод, разделенный на несколько шагов, который позволит нам это сделать.
Если у вас нет научного или программируемого калькулятора, вы не найдете ни одной кнопки для выполнения этой операции. Однако есть метод, разделенный на несколько шагов, который позволит нам это сделать.
Как мы видели в начале этого поста, котангенс равен обратному тангенсу . Поэтому разобьем расчет операции на следующие шаги:
- Вычислить тангенс угла
- Вычислите результат, обратный результату, полученному на предыдущем шаге.
Например, посмотрим, чему равен котангенс числа 30 с помощью калькулятора. Для этого первое, что мы сделаем, это вычислим тангенс угла, нажав следующие клавиши:
TAN > 30 > = =
Получив результат на экране, мы должны найти ключ с символом x -1 и нажмите кнопку равенства (=), чтобы решить операцию, таким образом получив обратное значение, которое является значением cog.
Если мы выполнили шаги правильно, на дисплее калькулятора должен появиться результат, равный 1,73. Если вы получили что-то другое, проверьте шаги и настройте ли вы калькулятор для работы в градусах, а не в радианах.
Если вы получили что-то другое, проверьте шаги и настройте ли вы калькулятор для работы в градусах, а не в радианах.
Если у вас есть какие-либо вопросы или проблемы, связанные с котангенсом , оставьте нам комментарий, и мы поможем вам решить ваши вопросы.
Nacho
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En Esta веб-те Ayudo hacer cálculos у преобразования sencillas дие кон-эль-Пасо-де-лос-Años се-нос-ха olvidado Cómo себе Hace. Si tienes dudas, déjame un commentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, напишите мне сообщение.
Sin, cos, tan, cot, sec, cosec тригонометрический калькулятор _ онлайн-инструмент для расчета, онлайн-вычисления, онлайн-калькулятор, калькулятор онлайн-расчет
Категория: Тригонометрический
Помогите изменить
Входное значение:
Если входное значение радиан
Синус (грех)
Косинус (Cos)
Тангенс (Тан)
Котангенс(Кот)
секанс (сек)
Косеканс (Косек)
Дуговой синус (ASin)
Арккосинус (ACos)
Арктангенс(ATan)
Дугкотангенс(ACot)
Секущая дуги (ASec)
Косеканс дуги (ACosec)
Если введенное значение градус
Синус (грех)
Косинус (Cos)
Тангенс (Тан)
Котангенс(Кот)
секанс (сек)
Косеканс(Косек)
Дуговой синус (ASin)
Арккосинус (ACos)
Арктангенс(ATan)
Дугкотангенс(ACot)
Секущая дуги (ASec)
Косеканс дуги (ACosec)
Описание приложения
Синусоидальная функция :
Каждому вещественному числу x соответствует уникальный угол (равный
этому вещественному числу в радианной системе), и этот угол соответствует
к однозначно определенному значению синуса sin x.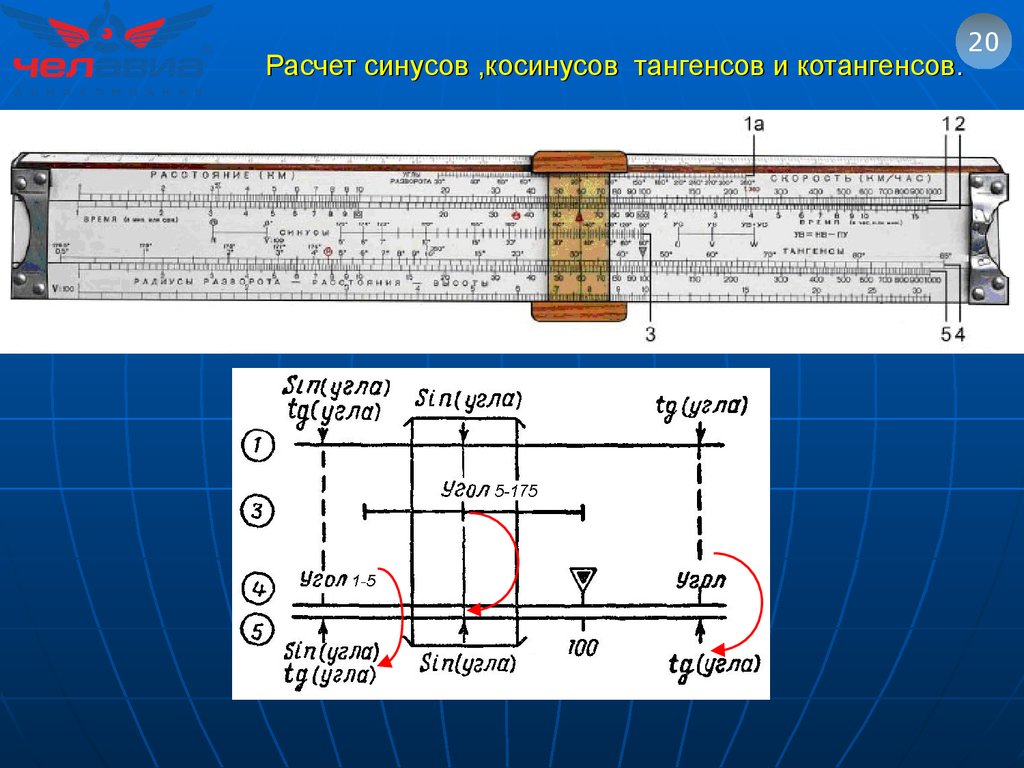 Таким образом, для любого реального
числа x, существует однозначно определенное значение sin x и ему соответствует
к функции, установленной в соответствии с этим соответствующим законом,
выражается как f(x)=sin x, называемая синусоидальной функцией.
Таким образом, для любого реального
числа x, существует однозначно определенное значение sin x и ему соответствует
к функции, установленной в соответствии с этим соответствующим законом,
выражается как f(x)=sin x, называемая синусоидальной функцией.
Теорема синуса: в треугольнике отношение каждого сторона к его диагональному синусу равна, то есть a/sin A=b/sin B=c/sin C. 92).
Функция косинуса :
Косинус = длина крюка/длина хорды
Поместите струну Пифагора в круг. Аккорд – это линия две точки на окружности. Самая большая хорда — это диаметр. Если нить прямоугольного треугольника положить на диаметр, то нить — это длинная струна, то есть синус, а крючок — это короткая струна, то есть оставшаяся хорда, косинус.
Говоря современным языком, синус — это отношение противоположной стороны к гипотенуза прямоугольного треугольника. 9(1/2).
cos =x/r
Косинус имеет максимальное значение 1 и минимальное значение -1.
Касательная функция
Касательная функция прямоугольный треугольник, отношение противоположного
сторона к соседней стороне называется касательной. В прямоугольном
система координат.
В прямоугольном
система координат.
Tan берет угол и возвращает отношение двух правых сторон прямоугольного треугольника. Это отношение представляет собой отношение длины противоположная сторона угла равна длине прилежащей стороны в прямоугольный треугольник.
Следовательно, до 1990-х годов функция тангенса выражалась в через TG θ, а после 1990-х годов выражается через Tan θ.
Функция котангенса :
Cot + angle используется для cot+angle, например: cot30° равно cot30°, Котангенс угла a выражается как cotA.
Если абсцисса любой точки конечного края угла делится по отличной от нуля ординате точки вершина угла совпадает с началом плоской прямоугольной системы координат, а начало угла совпадает с положительной осью x.
Котангенс и тангенс обратны друг другу.
В прямоугольном треугольнике отношение смежных прямых углов и относительных прямых углов острого угла называется котангенсом острый угол.
Секущая функция :
Пусть △ABC, ∠C = 90° (средняя школа — тригонометрическая функция с
острый угол) AC=b,BC=a,AB=c,∪[1,+∞)) функция секущей: sec∠A=c/b(скос/прилегающая кромка),y=secx.

 1443
1443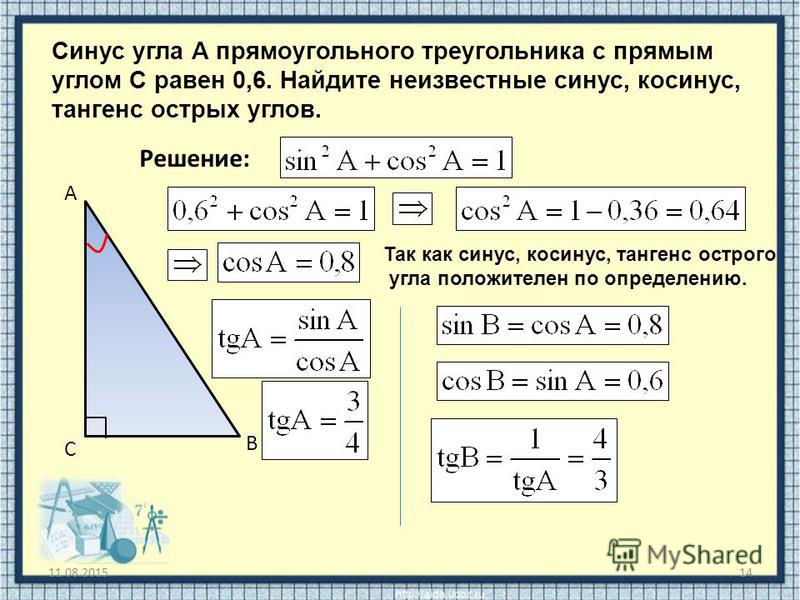 6003
6003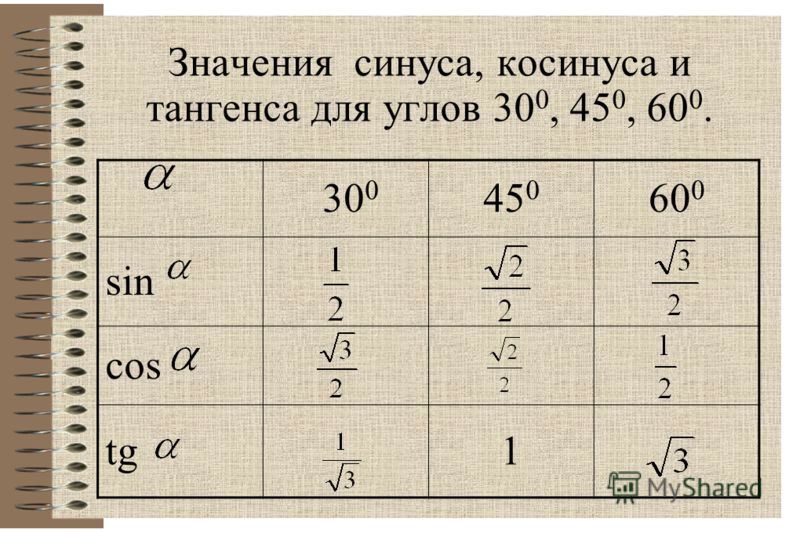 6745
6745 1763
1763 2679
2679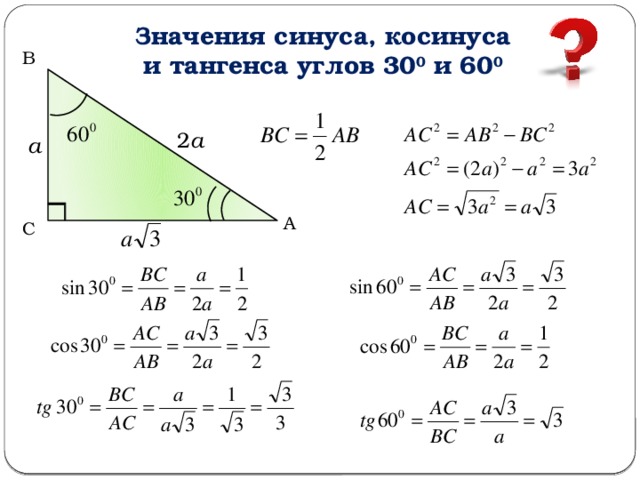 7813
7813 804
804 4301
4301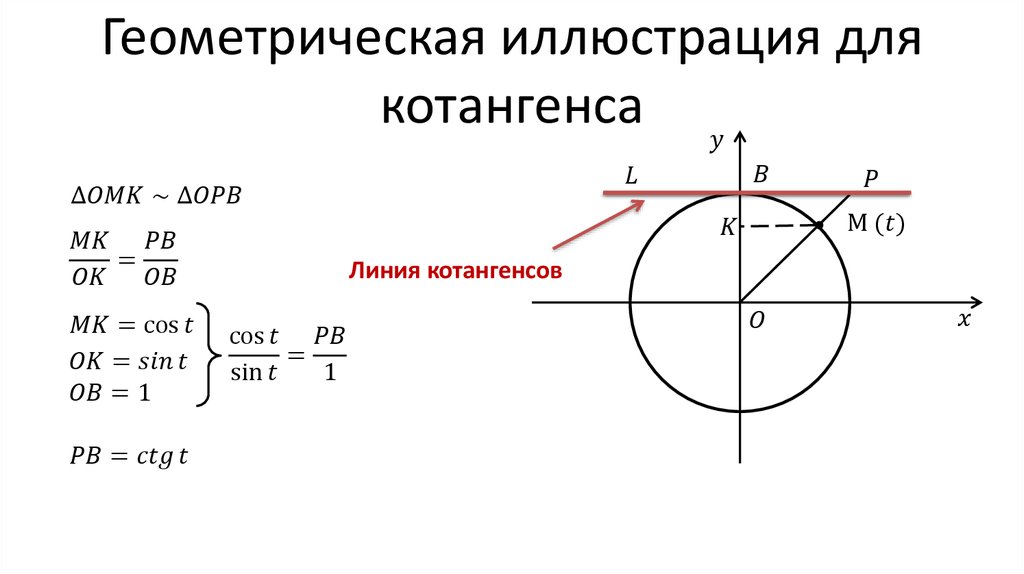 2709
2709 1918
1918 4877
4877 0524
0524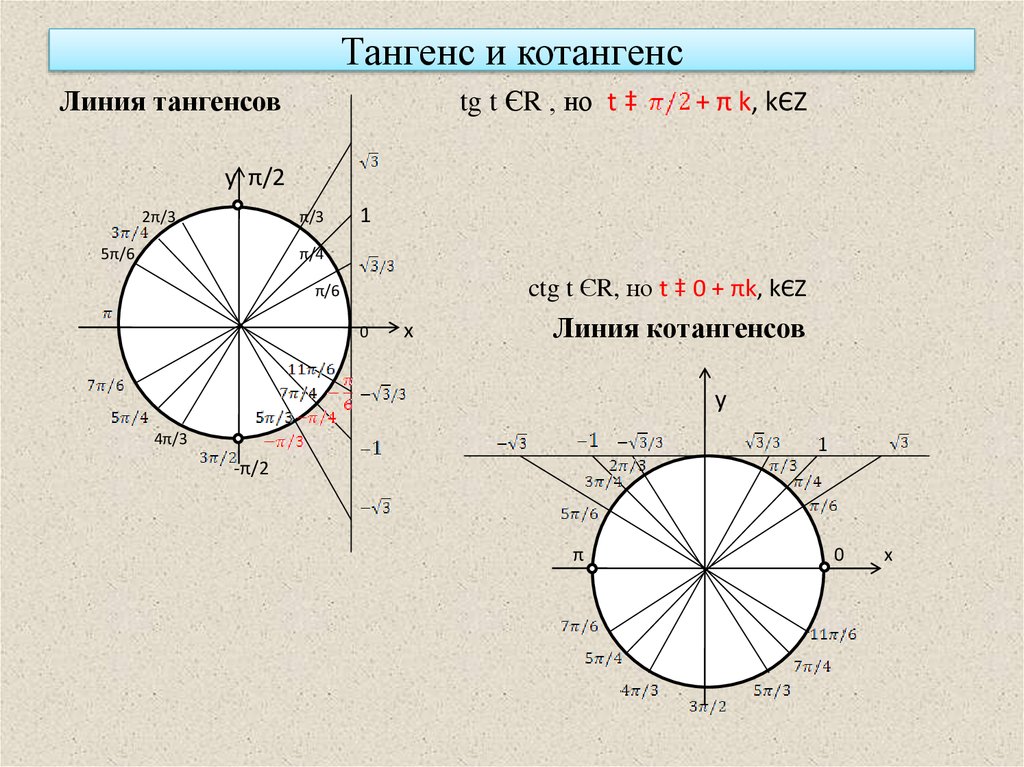 364
364 9657
9657 3559
3559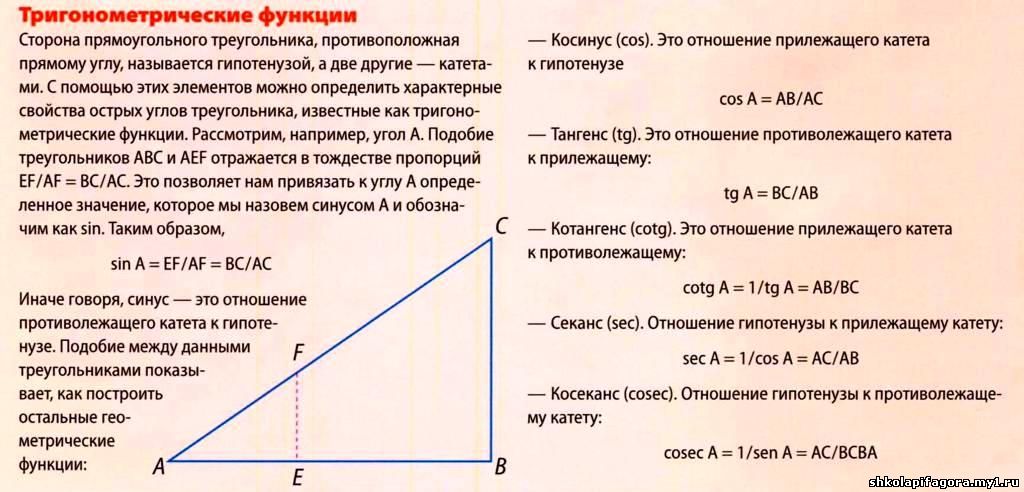 7046
7046 4281
4281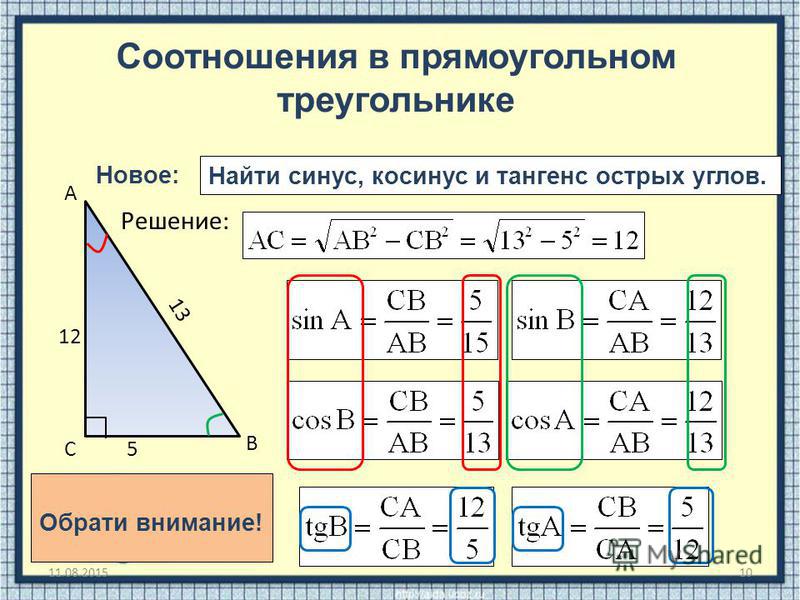 6249
6249 1763
1763 2309
2309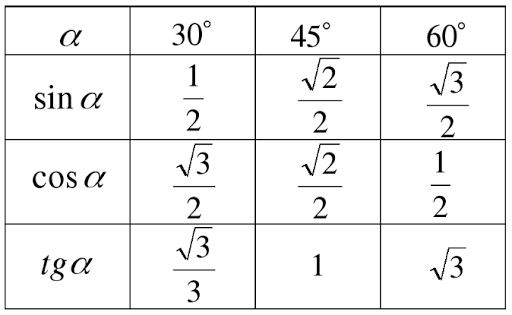 6745
6745 4826
4826 7046
7046 1154
1154 6643
6643 7265
7265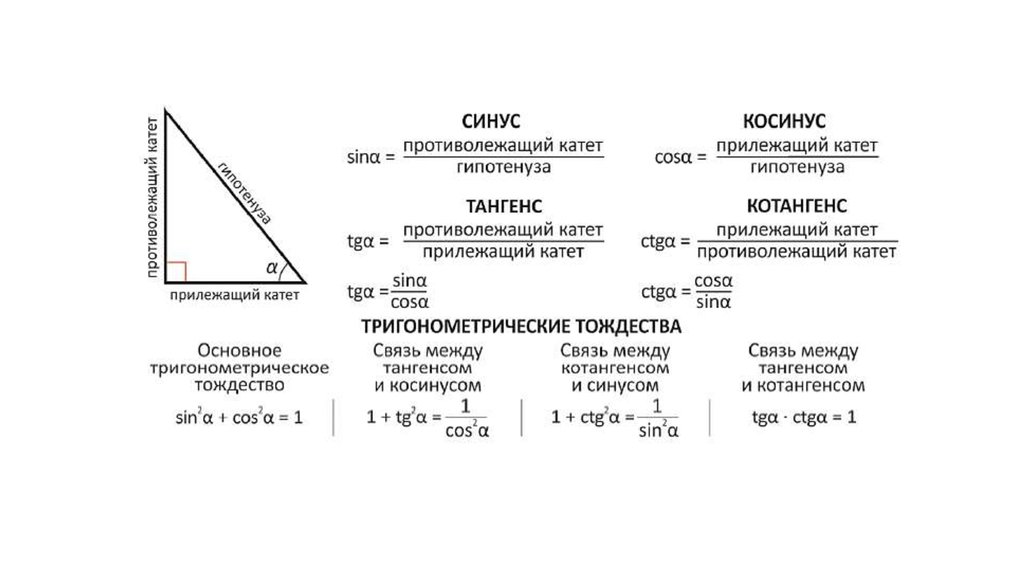 2493
2493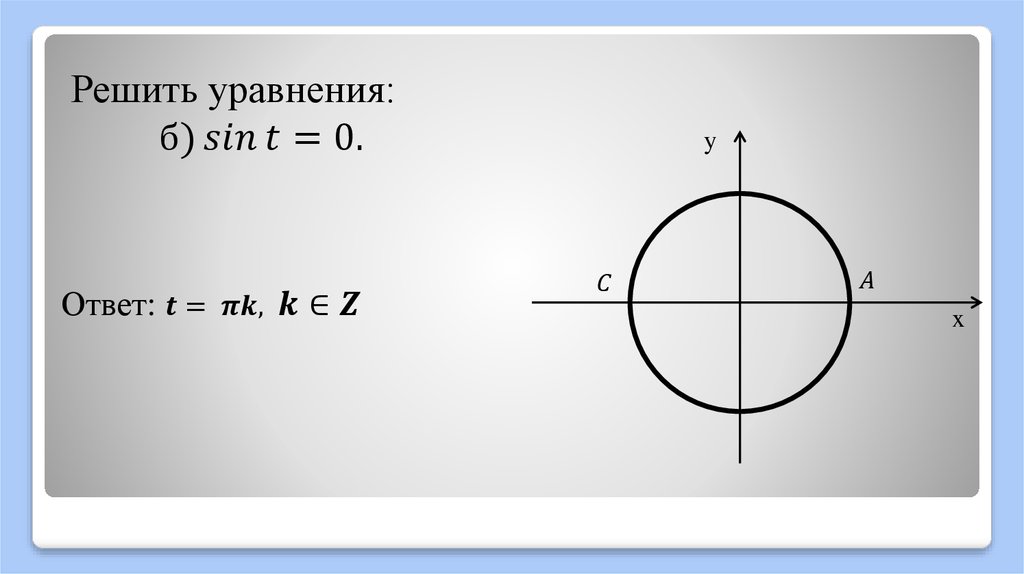 1584
1584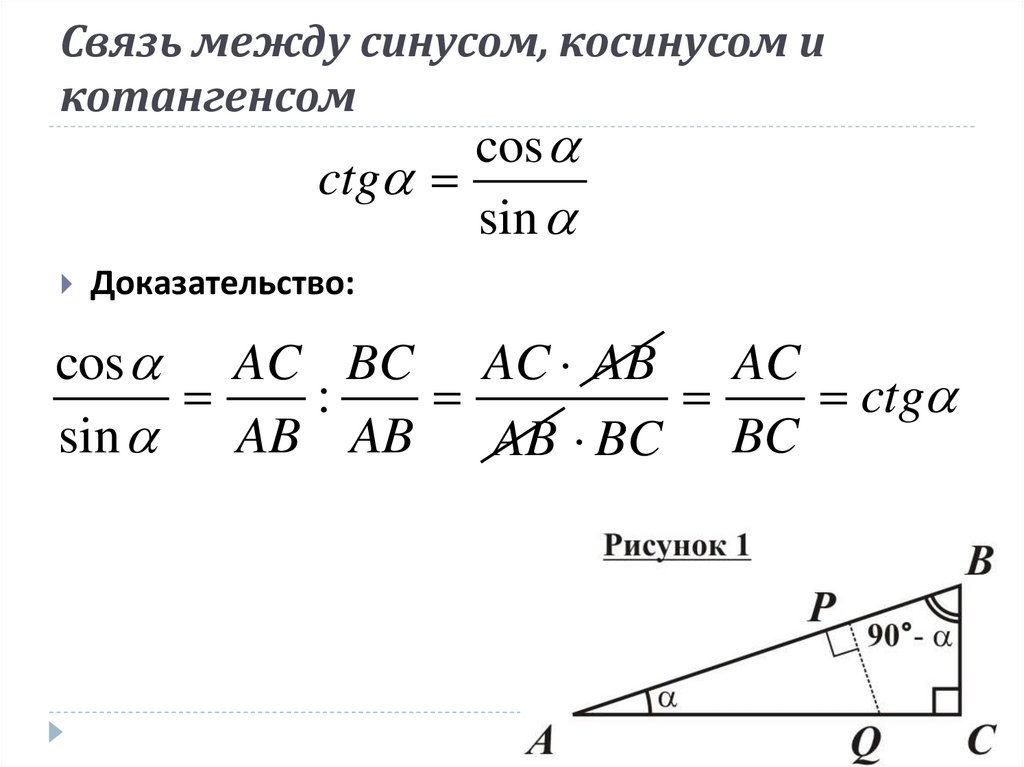 6009
6009 327
327 7321
7321
 5+… Сумму этого бесконечно ряда можно посчитать, пользуясь свойствами пределов .
5+… Сумму этого бесконечно ряда можно посчитать, пользуясь свойствами пределов .
 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения.