Построение графиков функций на Python. Pygame / Хабр
Привет, Хабр! Я хотел бы рассказать, как написать программу для построения графиков функций. Программу будем писать на Python с использованием библиотеки PyGame.
P.S. Программа простая и предназначена больше для учебных целей, чем для повседневного использования(хотя и с этим алгоритм может справится).
Основной алгоритм
Основной алгоритм заключается в вычислении функции на интервале: [-10,10]. Так как целых значений немного, то будем увеличивать параметр с малым шагом, к примеру 0.0001.
Функция имеет вид y = f(x). Формат ввода, соответственно, string(так как пользователь вводить функцию с использованием символов).
Получается следующий алгоритм:
Пишем код
Для начала следует импортировать библиотеки. Это библиотека PyGame, с её помощью будем рисовать. И библиотека math, она добавляет больше математических функций(sin, cos, sqrt и т.д.).
from math import * import pygame
Теперь напишем несколько системных строк, которые создадут нам окно, в котором будет находится система координат.
pygame.init() # запустить pygame
screen = pygame.display.set_mode((500,500)) # создать окно 500x500
pygame.display.set_caption("func_graph") # название окна
all_sprites=pygame.sprite.Group() # группа спрайтов
clock = pygame.time.Clock()
running = True
fps=60Создадим класс, который будет рисовать координатные оси(ординат и абсцисс).
class Line(pygame.sprite.Sprite):
def __init__(self,pos,x,y):
pygame.sprite.Sprite.__init__(self)
if pos=="x": # ось абсцисс
self.image=pygame.Surface((3,400)) # линия 3x400
self.image.fill((0,0,0)) # закрасить черным цветом
self.rect = self.image.get_rect()
self.rect.centerx = x # центр по x
self.rect.centery = y # центр по y
elif pos=="y": # ось ординат
self.image=pygame.Surface((400,3)) # линия 3x400
self.image.fill((0,0,0)) # закрасить черным цветом
self.rect = self.image.get_rect()
self.rect.
centerx = x # центр по x
self.rect.centery = y # центр по yТеперь класс для точки, так как точек будет очень много, то график будет казаться сплошным.
class Dot(pygame.sprite.Sprite):
def __init__(self,x,y):
pygame.sprite.Sprite.__init__(self)
self.image=pygame.surface.Surface((5,5)) # точка 5x5
self.image.fill((0,0,0)) # закрасить черным цветом
self.rect=self.image.get_rect()
self.rect.centerx=x # центр по x
self.rect.centery=y # центр по y Теперь приступим к основному алгоритму. Функцию считает модуль eval, а с ним нужно быть очень аккуратным в плане ввода(т.е. «x» желательно брать в скобки, чтобы модуль учитывал знак минус, степень — это два знака умножить(**), и т.д.). Конечно, можно сделать так, чтобы ввод пользователя преобразовывался в нормальный вид, это аналогично части с заменой «x» на значение(строка 6), но и тут есть свои проблемы.
def Calc(func):
i=-10 # начальное значение аргумента
while i<=10: # пока аргумент меньше 10
mass="" # темп-строка
for j in func: # для каждого символа в строке func(наша функция)
if j == "x": # если символ = x, то добавляем i в темп-строку
mass+=str(i)
else: # если нет, то добавить исходный символ
mass+=j
i+=0. 0001 # увеличить аргумент на 0.0001
try:
res1=eval(mass) # посчитать функцию и получить результат
except:
res1=10000 # если функцию нельзя посчитать, то результат число вне координат(знаю, костыль)
dot=Dot(250+i*10,250-res1*10) # dot - точка с координатой(0+x,0+y), так как это дисплей, то вектор "y" направлен вниз
all_sprites.add(dot) # добавить точку в группу спрайтов
0001 # увеличить аргумент на 0.0001
try:
res1=eval(mass) # посчитать функцию и получить результат
except:
res1=10000 # если функцию нельзя посчитать, то результат число вне координат(знаю, костыль)
dot=Dot(250+i*10,250-res1*10) # dot - точка с координатой(0+x,0+y), так как это дисплей, то вектор "y" направлен вниз
all_sprites.add(dot) # добавить точку в группу спрайтовТеперь заключительная часть кода.
func = str(input("y = ")) # ввод данных
calc = Calc(func) # вызвать функцию Calc от func
line = Line("y",250,250) # добавить ось ординат
all_sprites.add(line)
line1 = Line("x",250,250) # добавить ось абсцисс
all_sprites.add(line1)
while running: # основной цикл
clock.tick(fps)
for event in pygame.event.get():
if event.type == pygame.QUIT: # если закрыл окно - завершить программу
running = False
screen.fill((255,255,255)) # залить поле белым цветом
all_sprites.draw(screen) # нарисовать все спрайты(т. е. наши точки)
pygame.display.flip()
pygame.quit()
е. наши точки)
pygame.display.flip()
pygame.quit()Вот такой получился код:
from math import *
import pygame
pygame.init()
screen = pygame.display.set_mode((500,500))
pygame.display.set_caption("func_graph")
all_sprites=pygame.sprite.Group()
clock = pygame.time.Clock()
running = True
fps=60
class Line(pygame.sprite.Sprite):
def __init__(self,pos,x,y):
pygame.sprite.Sprite.__init__(self)
if pos=="x":
self.image=pygame.Surface((3,400))
self.image.fill((0,0,0))
self.rect = self.image.get_rect()
self.rect.centerx = x
self.rect.centery = y
elif pos=="y":
self.image=pygame.Surface((400,3))
self.image.fill((0,0,0))
self.rect = self.image.get_rect()
self.rect.centerx = x
self.rect.centery = y
class Dot(pygame.sprite.Sprite):
def __init__(self,x,y):
pygame.sprite.Sprite.__init__(self)
self.image=pygame.
surface.Surface((5,5))
self.image.fill((0,0,0))
self.rect=self.image.get_rect()
self.rect.centerx=x
self.rect.centery=y
def Calc(func):
i=-10
while i<=10:
mass=""
for j in func:
if j == "x":
mass+=str(i)
else:
mass+=j
i+=0.0001
try:
res1=eval(mass)
except:
res1=10000
dot=Dot(250+i*10,250-res1*10)
all_sprites.add(dot)
func = str(input("y = "))
calc = Calc(func)
line = Line("y",250,250)
all_sprites.add(line)
line1 = Line("x",250,250)
all_sprites.add(line1)
while running:
clock.tick(fps)
for event in pygame.event.get():
if event.type == pygame.QUIT:
running = False
screen.fill((255,255,255))
all_sprites.draw(screen)
pygame.display.flip()
pygame.quit() Итоги
В заключение можно сказать, что получилась простая программа, которая справляется со своими функциями, Ба-Дум-Тсс. Конечно, здесь есть свои проблемы(в основном — модуль eval), но главная задача статьи — понять, как компьютер строит графики.
Конечно, здесь есть свои проблемы(в основном — модуль eval), но главная задача статьи — понять, как компьютер строит графики.
P.S. Код ещё можно доработать. К примеру, я доработал программу до discord бота. Если будет интересно, то я могу написать об этом. Так как я заметил, что на Хабре есть только ознакомительные статьи про ботов.
Общие свойства функций и построение графиков
Используй поиск, чтобы найти научные материалы и собрать список литературы
База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны
Содержание статьи
1. График функции и его построение
2. Четность и нечетность функции
3. Возрастание и убывание функции
4. Выпуклость и вогнутость функции
5. Пример исследования и построения функции
График функции и его построение
Определение 1
Графиком функции $f(x)$ будет называться множество точек координатной плоскости, которые имеют вид $(x,\ f\left(x\right))$.
Схема для построения графиков функций:
- Найти $D(f)$ и $E(f)$.
- Исследовать на свойство четности и нечетности, а также на свойство периодичности.
- Найти пересечение с координатными осями и промежутки, на которых $f\left(x\right) >0$ и $f\left(x\right)
- Найти промежутки где функция возрастает и убывает, найти экстремумы.
- Найти интервалы выпуклости $и$ вогнутости функции.
- Вычислить пределы на границах $D(f)$.
- Найти дополнительные точках при необходимости.
- Изобразить график.
Четность и нечетность функции
Определение 2
Функцию $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть четной, если для всех точек из множества $X$ будет выполняться
\[f\left(x\right)=f(-x)\]
График этих функции будет подчиняться закону осевой симметрии по отношению к оси ординат (рис. 1).
Рисунок 1.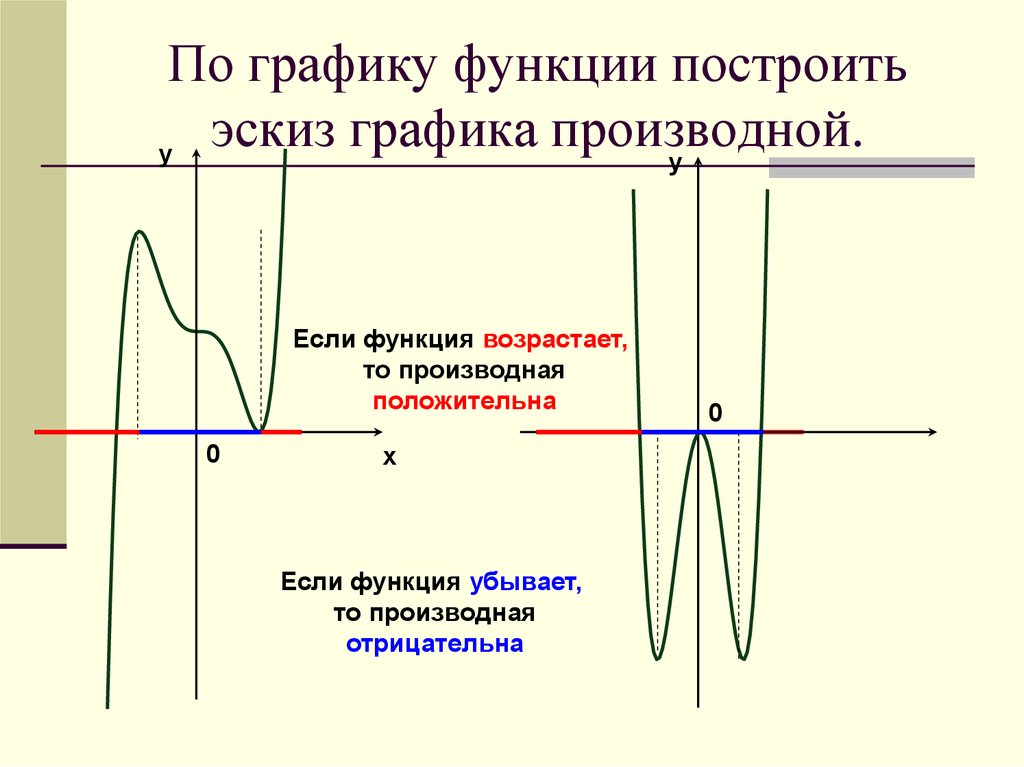
Определение 3
Функцию $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть нечетной, если для всех точек из множества $X$ будет выполняться
\[f\left(-x\right)=-f(x)\]
График этих функции будет подчиняться закону центральной симметрии по отношению к началу координат (рис. 2).
Рисунок 2.
Для исследования функции в её аналитической записи заменяют переменную $x$ на переменную $-x$, производят, при необходимости элементарные преобразования, и проверяют условия определений 2 и 3.
Возрастание и убывание функции
Определение 4
Функция $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть возрастающей, если подставив любые две точки получим, что$»$ будет верно $f(x’)
Определение 5
Функция $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть убывающей, если подставив любые две точки получим, что будет верно $f\left(x’\right) >f(x»)$.
Чаще всего функции исследуют на возрастание и убывание с помощью средств математического анализа, а именно производной.
Приведем схему для такого исследования.
- Найти $D(f)$;
- Найти $f'(x)$;
- точки, когда $f’\left(x\right)=0$;
- точки, когда $f'(x)$ не будет существовать;
- Отметить на координатной прямой $D(f)$ и все найденные выше точки;
- знак $f'(x)$ на всех получившихся промежутках;
- Сделать вывод: там, где $f’\left(x\right)0$ функция будет возрастать.
Выпуклость и вогнутость функции
Определение 6
Функция $y=f(x)$, которая имеет своей областью определения множество $X$ будет называться выпуклой, если подставив любые две точки получим, что неравенство
\[f\left(\frac{x’+x»}{2}\right)\le \frac{f(x’)+f(x»)}{2}\]
верно.
Определение 7
Функция $y=f(x)$, которая имеет своей областью определения множество $X$ будет называться вогнутой, если подставив любые две точки получим, что неравенство
\[f\left(\frac{x’+x»}{2}\right)\ge \frac{f(x’)+f(x»)}{2}\]
верно.
Схема исследования:
Найти
- $D(f)$;
- $f»(x)$;
- точки, когда $f»\left(x\right)=0$;
- точки, когда $f»(x)$ не будет существовать;
- знак $f»(x)$ на каждом из найденных промежутков;
- если $f»\left(x\right)0$ то вогнутой.
Пример исследования и построения функции
Пример 1
Исследовать данную функцию и построить график:
\[f\left(x\right)=sinx-cosx\]
$D\left(f\right)=R$
\[\ E\left(f\right)=\left(-\infty ,0\right)\cup (0,+\infty ).\]- \[f\left(-x\right)=-cosx-sinx\]
- \[sinx-cosx=0\] \[x=\frac{\pi }{4}+\pi n,n\in Z\]
Пересечение с осью $Ox$: $\left(\frac{\pi }{4}+\pi n,0\right)$
Пересечение с осью $Oy$: $\left(0,-1\right)$
На интервале $x\in \left(\frac{\pi }{4}+2\pi n,\frac{5\pi }{4}+2\pi n\right)$ функция будет принимать положительные значения, на интервале $x\in \left(-\frac{3\pi }{4}+2\pi n,\frac{\pi }{4}+2\pi n\right)$ функция будет принимать отрицательные значения.
 {»}=cosx-sinx\] \[-sinx+cosx=0\] \[x=\frac{\pi }{4}+\pi n,n\in Z\]
{»}=cosx-sinx\] \[-sinx+cosx=0\] \[x=\frac{\pi }{4}+\pi n,n\in Z\]На интервале $\left(\frac{\pi }{4}+2\pi n,\frac{5\pi }{4}+2\pi n\right)$ функция вогнута, на интервале $\left(-\frac{3\pi }{4}+2\pi n,\frac{\pi }{4}+2\pi n\right)$ функция выпукла.
Рисунок 3.
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 13.07.2022
Выполнение любых типов работ по математике
Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами
Подбор готовых материалов по теме
Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы
1.
 3;
3;введите ранжированную переменную x:=-10, -9.9 .. 10;
в панели математических знаков щелкните на кнопке с изображением графика — на экране появится палитра графиков;
в палитре графиков щелкните на кнопке с изображением двумерного графика — на экране появится шаблон графика с уже введенной по оси Y функцией;
введите в место ввода у оси x имя независимого аргумента — x;
щелкните вне пределов графика левой кнопкой мыши — график будет построен;
введите в область графика курсор мыши и дважды щелкните левой клавишей мыши. В появившейся панели форматирования графика задайте его параметры (тип осей, цвет линии и ее тип) так, чтобы получить график, представленный на рис. 1.8.
Р ис. 1.8. График функции одной переменной и
панель его форматирования
Заметьте, что вы можете «ухватиться»
курсором мыши за рамку выделенного
графика и перенести его в любое удобное
место в окне документа.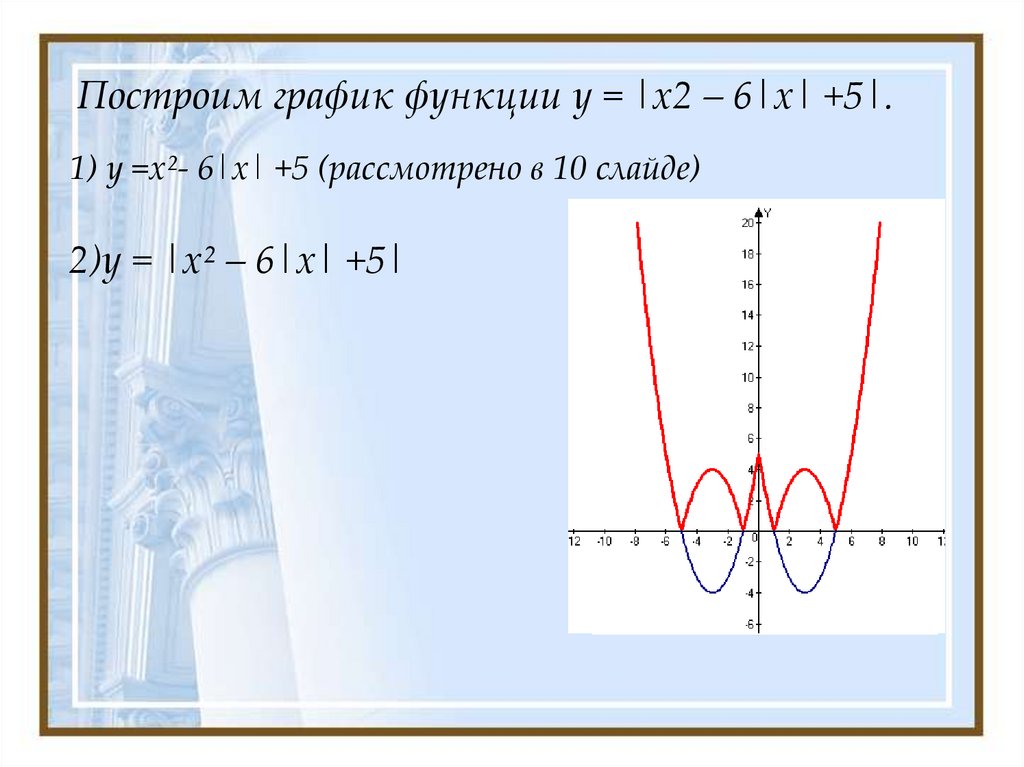 Вы можете также
растягивать график по вертикали,
горизонтали и диагонали, «цепляясь»
курсором мыши за соответствующие темные
прямоугольники на линиях выделения
графика.
Вы можете также
растягивать график по вертикали,
горизонтали и диагонали, «цепляясь»
курсором мыши за соответствующие темные
прямоугольники на линиях выделения
графика.
Обратите внимание: когда график находится в рамке, на нем в характерных черных уголках появляются числа, идентифицирующие масштаб графика по оси Y и по оси X. По умолчанию по оси X график строится на отрезке изменения аргумента x от –10 до +10. Масштаб по оси Y Mathcad устанавливает по умолчанию автоматически. Изменив эти числа, можно задать свой масштаб графика.
П ример 1.7. Построить на одном рисунке графики двух функций: sin(x)2, sin(x)/x и cos(x). Для этого их надо просто перечислить после первой функции в месте ввода возле оси Y, отделяя выражения для функций запятыми. Полученный график представлен на рис. 1.9.
Рис. 1.9. Двумерный график с тремя кривыми
Обратите внимание на то, что Mathcad
автоматически отображает каждую кривую
своим стилем и своим цветом.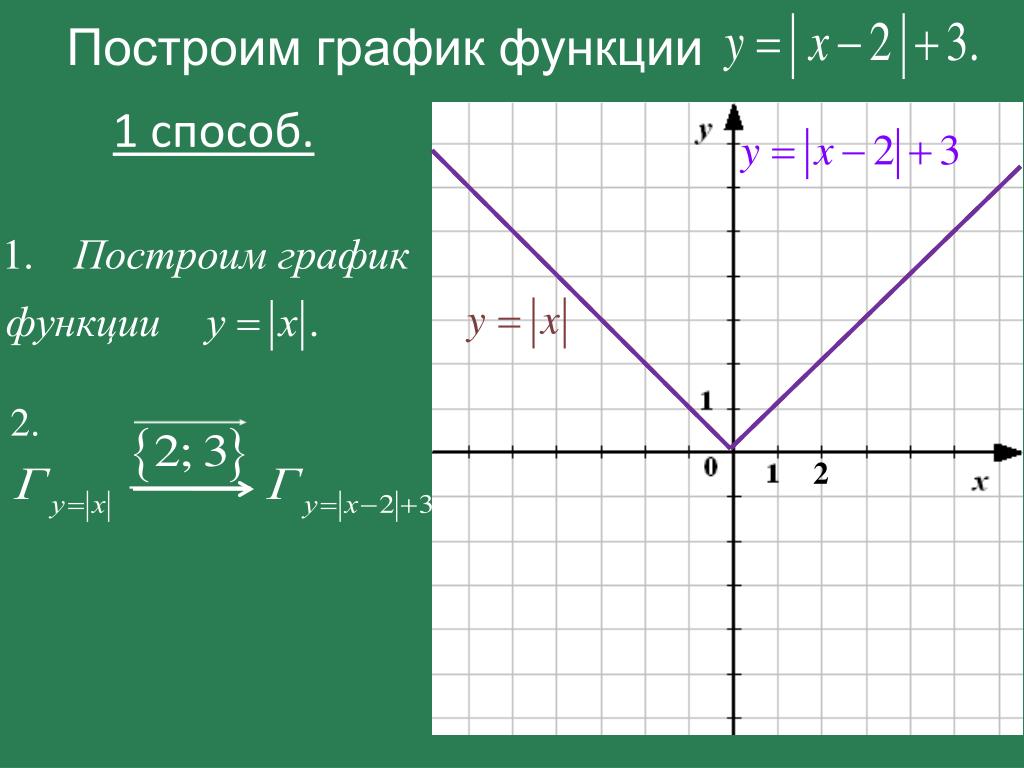 И делает
это весьма недурно — редко кто из
пользователей вмешивается в решение
системы. Но форматированием графиков
их вид можно менять, например, для
изменения стиля и цвета линий, нанесения
на график масштабной сетки, изменения
фона, нанесения у координатных осей
надписей и так далее.
И делает
это весьма недурно — редко кто из
пользователей вмешивается в решение
системы. Но форматированием графиков
их вид можно менять, например, для
изменения стиля и цвета линий, нанесения
на график масштабной сетки, изменения
фона, нанесения у координатных осей
надписей и так далее.
Построение графиков поверхностей (их называют также трехмерными или 3D-графиками) – сложная задача. Связано это с тем, что такие графики даже в простейшем случае требуют создания матрицы точек (аппликат) зависимости z(x,y), то есть функции двух переменных. Создание такой матрицы – нетривиальная задача, что приводило не только к усложнению построений, но и к потере их наглядности.
Однако в новейших версиях Mathcad 2000/2001/2001i/11 эта трудность блестяще преодолена. Теперь трехмерный график построить даже проще, чем двумерный (см. пример ниже).
Пример 1.8. Построить график
параболической поверхности (x2 + y2).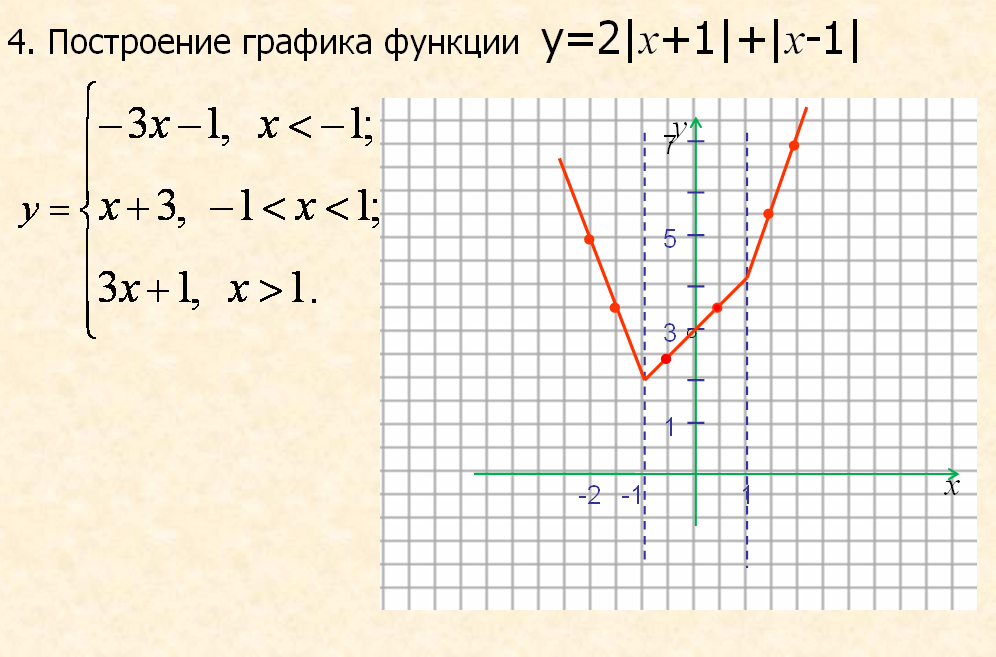 Для этого надо выполнить представленные
ниже действия.
Для этого надо выполнить представленные
ниже действия.
Определите функцию z(x,y) двух переменных x и y. В качестве примера рассмотрим график функции суммы квадратов(x2 + y2). Тогда определение функции будет выглядеть следующим образом:
z(x,y) := x2 + y2.
Используя палитру графики, введите шаблон трехмерного графика.
На единственное место ввода под шаблоном введите имя функции — z.
Выведите указатель мыши за пределы графика и щелкните левой кнопкой мыши — будет построен график в виде «проволочного каркаса».
Растяните (или сожмите) график и поместите его в нужное место экрана (рис. 1.10).
Поместив в окно графика курсор мыши и нажав и удерживая левую клавишу мыши, попробуйте вращать график перемещением мыши.
 Тем
самым вы можете менять углы обзора
графика и даже заставить график вращаться
в заданном направлении автоматически.
Тем
самым вы можете менять углы обзора
графика и даже заставить график вращаться
в заданном направлении автоматически.
Р ис. 1.10. График поверхности в виде «проволочного каркаса»
Обратите внимание на то, что в этом примере мы впервые задали функцию пользователя как функцию двух переменных x и y. Наша функция пользователя имеет простое имя z и список параметров (x, y), т. е. переменных x и y, от которых зависят значения z. С помощью функций пользователя мы можем пополнять набор функций, встроенных в систему.
График в виде «проволочного каркаса» не слишком эстетичен, хотя иногда и полезен, поскольку сквозь каркас видны обычно невидимые детали. Для изменения вида графиков трехмерных поверхностей используется их форматирование. Окно форматирования имеет множество возможностей, включая изменение типа графиков.
Пример
1. 9. Отформатировать представленный
в предыдущем примере график с тем, что
бы он представлял поверхность в виде
контурных линий (рис. 1.11). Такие линии
образуются при пересечении поверхности
рядом параллельных плоскостей,
расположенных на одинаковом расстоянии
друг от друга.
9. Отформатировать представленный
в предыдущем примере график с тем, что
бы он представлял поверхность в виде
контурных линий (рис. 1.11). Такие линии
образуются при пересечении поверхности
рядом параллельных плоскостей,
расположенных на одинаковом расстоянии
друг от друга.
Рис. 1.11. Контурный график поверхности с функциональной окраской и оцифровкой контурных линий
Новые версии Mathcad дают возможность построения на одном графике ряда поверхностей. Это делается предельно просто: определите ряд функций двух переменных, описывающих поверхности, и введите через запятую имена этих функций в месте ввода шаблона трехмерного графика.
Пример 1.10. Построить две объемные параболы, пересекающиеся в пространстве, и отформатировать их для придания наглядности рисунку. Зададим уравнения парабол функциями пользователя:
z1(x,y) := x2 + y2 — 20 z2(x,y) := -(x2 + y2) + 20
Укажем
их имена в шаблоне поверхности и,
используя окно форматирования, выберем
построение поверхностей с функциональной
окраской. Заметим, что каждая поверхность
может форматироваться отдельно.
Полученный рисунок представлен на рис.
1.12.
Заметим, что каждая поверхность
может форматироваться отдельно.
Полученный рисунок представлен на рис.
1.12.
Р ис. 1.12. Построение двух пересекающихся в пространстве объемных парабол (вращая график мышью, можно рассмотреть его с разных сторон), а в окне форматирования графика выбрать разные схемы освещения
Окно форматирования трехмерной графики позволяет строить графики в нескольких системах координат, например, в сферической и цилиндрической системах координат. Сферическая система координат применяется в картографии, например, при построении карт на шаре — глобусе. Вид трехмерных графиков очень сильно зависит от того, в каких координатах строится график.
Для более детального знакомства с обширными возможностями визуализации геометрических понятий и результатов математических вычислений рекомендуется ознакомиться с литературой [5, 7] и примерами из справки по системе Mathcad.
Построение графиков функций | Образовательная социальная сеть
ГБОУ лицей 1575
Автор работы: Бодров Филипп Александрович учащийся 9«В» класса ГБОУ лицея № 1575
Руководитель: Мардашева Татьяна Павловна, учитель математики ГБОУ лицея № 1575
г. Москва
Москва
2016 г.
Аннотация
Тема: «Построение графиков функций вида»
Автор: Бодров Филипп учащийся 9 «В» класса ГБОУ лицея 1575
Научный руководитель: Мардашева Татьяна Павловна, учитель математики ГБОУ лицея 1575
Актуальность: На данный момент у многих возникает сложность в построении графиков типа , т.к. приходится долгое время просчитывать точки. Мы предлагаем инновационный способ построения подобных графиков
Проблема: Можно ли построить графики некоторых функций нетрадиционными методами?
Предмет исследования: Графики функций и методы их построения.
Гипотеза: Существует упрощённый способ построения графиков функций
Цель: Найти новый подход к построению графиков функций вида
и поделиться своей находкой с другими людьми, увлекающимися математикой.
Методы исследования: поиск‚ анализ‚ синтез
План выполнения работы:
1 этап
- Изучение теории. Познакомиться с понятием функции, свойствами функций и способами построения графиков функций.

- Проанализировать способы построения графиков различных функций
- Ознакомиться с основными способами построения графиков
- Рассмотреть возможные варианты построения графиков
2 этап
Собранный материал представить в виде исследования.
Краткое описание работы: В работе описан новый способ построения графиков функций
Основные выводы и результаты: Проделав данную работу, мы нашли и усовершенствовали новый способ построения графиков типа . Этот способ можно использовать при условии, что функция достаточно сложная и найти точки подсчётом будет трудно. К концу работы мы упростили этот способ и теперь попытаемся внедрить его в жизнь.
Содержание
- Введение
- Идея метода
- Примеры построения
- Заключение
Введение
При решении неравенств и уравнений иногда приходится использовать функционально – графический метод. После решения нескольких таких уравнений, я понял, что умения строить графики различных функций и знание их свойств является важным условием решения нестандартных уравнений и неравенства.
Исследование посвящено проблеме совершенствования умений и навыков построения графиков сложных функций. Актуальность этой проблемы определяется тем, что нестандартные уравнения и неравенства часто решаются функционально – графическим методом. В заданиях ЕГЭ (и в части В, и в части С) имеются задания, при решении которых используется функционально – графический метод, свойства функций. Многие задачи с параметрами невозможно решить другим методом.
В пособиях для поступающих много заданий на построение графиков функций.
На уроках математики мы много времени уделяем теме «Построение графиков функций», меня заинтересовала эта тема и я решил изучить различные методы построения графиков функций .
Построение графиков элементарных функций не составляет труда, в школьном курсе математики они достаточно хорошо описаны. Я предположил: если знаем свойства элементарных функций и умеем строить их графики, то сможем построить и графики сложных функций.
Идея метода построения графиков функций вида
График функции
График этой функции, как нетрудно догадаться из общих соображений, представляет собой красивую кривую, ординаты которой монотонно убывают от максимального значения, равного единице в точке х=0, нуля при удалении от начала системы координат.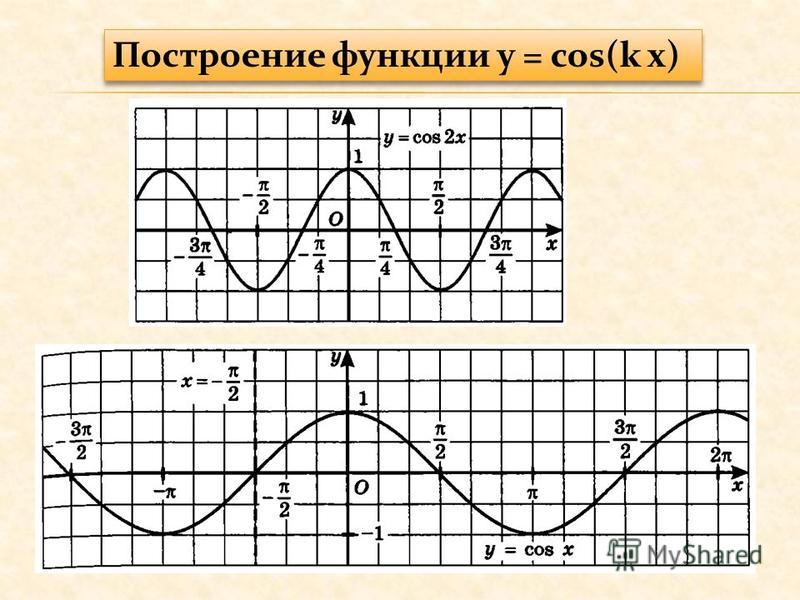 Эта кривая получила название : «локон Марии Аньезе» в честь французского математика XVIII века. Если на этой же координатной плоскости построить ещё график функции у=х2+1, то в глаза бросается «подобие» кривых графиков функций у=х2+1 и
Эта кривая получила название : «локон Марии Аньезе» в честь французского математика XVIII века. Если на этой же координатной плоскости построить ещё график функции у=х2+1, то в глаза бросается «подобие» кривых графиков функций у=х2+1 и
Это «подобие» выражается в «отраженном» характере графика функции , если его рассматривать относительно «оригинала» — графика функции у=х2+1. Закон этого «отражения» в математической записи имеет вид: , т.е. числовое значение ординаты функции-оригинала заменяется на обратное число, например: 2→1/2, 5→1/5 и т.д. Поэтому ясно, что ординаты точек первоначального графика функции у=х2+1, которые удовлетворяли условию: у≥1, при переходе к графику функции теперь будут удовлетворять обратному условию: 0
Заметим, что это преобразование «отражения» носит взаимно обратный характер: график функции у=х2+1 можно рассматривать как «отражение» графика функции . Причем, если точки исходного графика функции y=f(x) имеют ординаты как большие единицы, так и меньшие, то они при преобразовании «отражения» совершат переходы в соответствующие области координатной плоскости.
Рассмотрим небольшое видоизменение начального примера :
На верхнем рисунке стрелочками показаны переходы точек графика функции-оригинала у=х2+0,25 в точки «отраженного» графика функции . Например, точка минимума графика функции у=х2+0,25 с ординатой у=0,25 переходит в точку максимума графика функции с ординатой у=4.
Выясним природу несимметричного характера рассматриваемого преобразования-«отражения». Нетрудно заметить, что при настоящем симметричном отражении парабола должна принимать уже отрицательные значения для нижележащих точек, но при числовом обратном преобразовании по закону знак не должен измениться! Поэтому при «отражении» параболе приходится прижимать свои ветви к оси абсцисс сверху.
Ясно, что те же самые рассуждения можно применить и в случае, если графики функций принимают отрицательные значения, которые при «отражении» будут также оставаться в своей нижней части координатной плоскости, только роль «зеркала» будет играть прямая у = -1.
Рассмотрим более общий случай, когда заданная функция может принимать как положительные, так и отрицательные значения. Например, функция имеет в качестве своего «оригинала» функцию у=х2-1, график которой представляет собой параболу, минимум которой лежит на оси ординат в точке у=-1, а ветви направлены вверх.
Например, функция имеет в качестве своего «оригинала» функцию у=х2-1, график которой представляет собой параболу, минимум которой лежит на оси ординат в точке у=-1, а ветви направлены вверх.
Обобщение метода построения графиков функций на случай
Так как оси 0х и 0у равноправны, то можно рассмотреть подобные преобразования-«отражения» графиков функций уже относительно вертикальных прямых х=-1 и х=1, которые связаны с переходом . Рассмотрим пример функции , имеющей свой «образ-оригинал» , имеющий форму графика перевернутой параболы с вершиной в точке у=4 на оси ординат:
На графике стрелками показаны взаимные отражения точек из областей слева от х=-1 и справа от х=1 в узкие полосы –1, когда «отражаемые» части графика не могли пересекать ось абсцисс).
Мы рассмотрели обобщенные приемы преобразования графиков функций при переходе от зависимости y=f(x) к функциям вида и на примере квадратичных выражений. Эти обобщенные приемы не зависят от конкретных зависимостей y=f(x), главное, чтобы был известен вид графика функции y=f(x).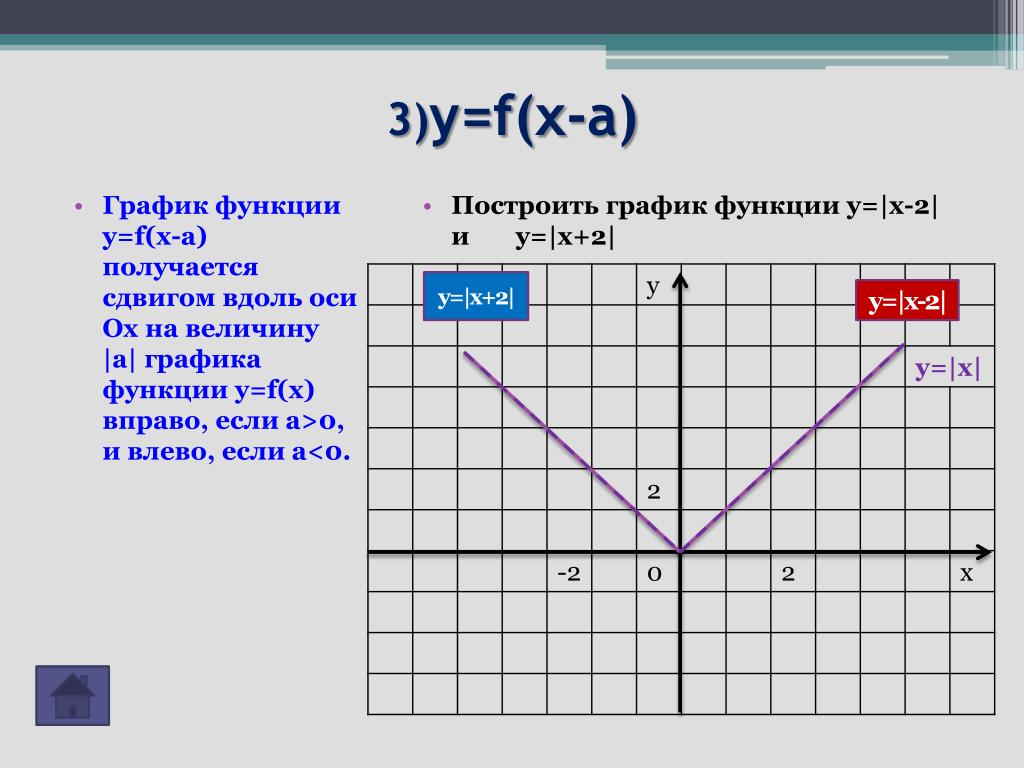 В качестве общего модельного примера рассмотрим ещё элементарный случай у=х, когда из графика прямой можно получить график гиперболы при этом можно использовать приемы «отражения» как от пары прямых у=1 и у= -1, так и от другой пары х=1 и х= -1.
В качестве общего модельного примера рассмотрим ещё элементарный случай у=х, когда из графика прямой можно получить график гиперболы при этом можно использовать приемы «отражения» как от пары прямых у=1 и у= -1, так и от другой пары х=1 и х= -1.
Рассмотрим более сложный случай, когда функция y=f(x) задана изначально графиком, а её математическое выражение неизвестно:
Даже не зная математики можно увидеть на последних рисунках «подобие» двух графиков. Особенно бросается в глаза соответствие точек минимума и максимума графиков основной и «отраженной» функций!
Заключение.
Я провел работу по построению графиков функции вида и сделал следующие выводы:
1.Графики функций можно построить без использования производных, особенно этот метод особенно подходит, если f(x) элементарные функции.
2.Для построения графиков нужно знать свойства функции, уметь читать графики полученных функции, исследовать поведение графиков в бесконечности.
3. Построение графиков, как и всевозможные другие способы геометрической интерпретации, является весьма эффективным средством для решения алгебраических задач, в том числе и задач с параметрами. Поэтому научиться строить графики функции, в том числе и более сложных, для решения задач просто необходимо. При выполнении этой работы, я выяснил, что есть класс уравнений и неравенств, при решении которых требуется умения и навыки построения графиков функций и умения их читать. (Многие уравнения неравенства с параметрами решаются функционально — графическим методом).
Итак, в результате графических и компьютерных экспериментов, я убедился, что графики сложных функций можно строить не только с помощью производных, но и путём исследования функций, преобразованиями элементарных функций.
При выполнении этой работы:
— повторил и углубил знания свойств и методов построения графиков элементарных функций;
— приобрел опыт построения графиков таких функций, как:
. Научился работать с дополнительной литературой и материалами, производить отбор научных сведений; приобрел опыт выполнения графических работ на компьютере;
Научился работать с дополнительной литературой и материалами, производить отбор научных сведений; приобрел опыт выполнения графических работ на компьютере;
— узнал, что тема « Методы построения графиков функций», очень объемная и интересная, рассмотреть все методы сразу невозможно, т.е. можно дальше продолжать работу по данной теме.
По моему мнению, умение проводить такие преобразования (построения) графиков функций позволяет ученикам:
1) научиться читать графики различных функций и использовать их при решении уравнений и неравенств;
2) освоить свойства функций;
3) лучше различать графики различных функций.
На мой взгляд, использование этого способа на практике целесообразно, т.к. это поможет успешно и эффективно подготовится к выпускным и вступительным экзаменам.
При построении графиков функций я использовал программы для построения графиков функций.
Литература.
- В.Дьяконов.Maple 6: учебный курс.- СПб.
 :Питер,2001.
:Питер,2001. - В.К.Егерев, Б.А.Радунский, Д.А.Тальский. Методика построения графиков функций.- М. : «Высшая школа», 1970 .
- В.П.Моденов. Задачи с параметрами. Координатно-параметрический метод: учебное пособие. – М.: Издательство «Экзамен», 2006.
- А.Г. Мордкович. Алгебра. 7,8,9 классы. Учебник для общеобразовательных учреждений.- М. : «Мнемозина»,2010.
- Е.М.Родионов, С.Л. Синякова. Математика. Пособие для поступающих в вузы. –М.: «Ориентир»,2003.
Построение графиков функции
Оглавление:
Построение графиков функции. Изучение отдельных функций с помощью аналитического оборудования разработанного нашей компанией и построение его графиков должно осуществляться в следующем порядке: 1.Определяет область существования функции, область непрерывности и точки разрыва. 2.Найдите асимптоту. 3.In проект, создайте график функции. 4. Вычислите 1-ю производную и, при необходимости, вычислите 2-ю производную (производная более высокого порядка часто может быть опущена). 1s и является contiguous. As вы уже знаете (см.§ 14.4), имеют асимптоты y = x-4 и x—1、 Также f (x) x-4; следовательно, f (x) x-4 x-1 (график функции находится выше асимптоты) и/(x) для x-x-1, 4 (график ниже асимптоты).
1s и является contiguous. As вы уже знаете (см.§ 14.4), имеют асимптоты y = x-4 и x—1、 Также f (x) x-4; следовательно, f (x) x-4 x-1 (график функции находится выше асимптоты) и/(x) для x-x-1, 4 (график ниже асимптоты).
График функции f(x) пересекает ось Ox в точке x2-3x-2 = 0, то есть в точке xx2 =(3±y17)/ 2, или в точке X1 = 3.5, x2 = 0.5.Ось Oy пересекает график в точке y =-2.Это позволяет построить график функции I (x) в виде, показанном на рисунке. 56. Целью дальнейших исследований является нахождение экстремумов точек перегиба и интервалов, выпуклости верхнего и нижнего графика функции. Для этого мы находим y ’ и y». Х2 + 2х-1 г (х + 1) 2 ’ Из этого x—1 | / A2?Вы можете видеть, что для −2.4 и для x—1 + + Y 2«0.4, y’ = 0.At точка x = −1, производные y ’ и y «не существуют. Отредактируйте таблицу изменения знака 1-й и 2-й производных, включая в нее ключевые моменты, в зависимости от изменения аргументов. Из этой таблицы видно, что функция/(x) имеет строгий минимум в терминах x = −1 + Y ^ 2 и строгий максимум в терминах x = −1-Y2.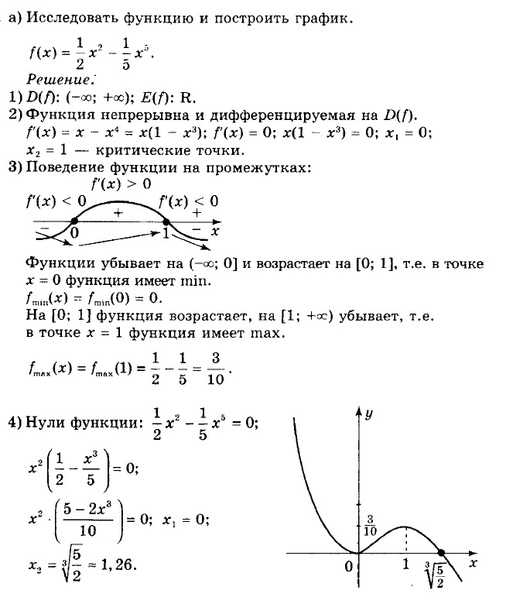 для Х-1, то функция является строго выпуклой вверх, и для Х-1, то функция является строго выпуклой вниз. при x =-1 функция прерывиста, поэтому точки перегиба нет. Общее поведение функции было следующим found.
для Х-1, то функция является строго выпуклой вверх, и для Х-1, то функция является строго выпуклой вниз. при x =-1 функция прерывиста, поэтому точки перегиба нет. Общее поведение функции было следующим found.
- To чтобы точнее построить график, нужно найти на графике много точек, как описано выше. В дальнейшем для краткости используйте таблицы, похожие на таблицы. 1, вызовите таблицу поведения функции и немедленно отметьте эти экстремумы, точки перегиба, выпуклые точки интервала. Пример 2.Построить функцию) (x)=(x + 1) 3y / r! Область этой функции представляет собой множество всех действительных чисел, причем вертикальных асимптот не существует, так как они непрерывны в каждой точке. От того, что В результате не существует наклонных асимптот. Чтобы построить диаграмму、 1) F (x) исчезает в точках x (-1) и x = 0. 2) x-1 as/ 0, x * 0; 3) / x b-1I при 0 4) ФМ Ф (Х)= + ОО и FM [(х) со. Обзор графиков функций, которые можно построить на основе этих утверждений, показан на рисунке.
 x3.Его внешний вид показан на схеме. 53.As (см. рисунок 57). Разработанное устройство позволяет строить графики локально параметрических заданных функций. x = x (1), y = y (()здесь пара функций x = x ({), y = y {1) равна y = y (x) или x = x( y).Граф параметрической определяемой функции подразумевает объединение графа всех функций в виде формулы x = x (1), Y = Y ({), Y = Cx) и x =§(y).
x3.Его внешний вид показан на схеме. 53.As (см. рисунок 57). Разработанное устройство позволяет строить графики локально параметрических заданных функций. x = x (1), y = y (()здесь пара функций x = x ({), y = y {1) равна y = y (x) или x = x( y).Граф параметрической определяемой функции подразумевает объединение графа всех функций в виде формулы x = x (1), Y = Y ({), Y = Cx) и x =§(y).Вы можете видеть, что мы использовали исследование производных, чтобы значительно уточнить тип графика. Людмила Фирмаль
- Давайте сделаем предварительное замечание. Чтобы найти асимптоты, параллельные оси Oy, необходимо найти значение*, имеющее конечный предел Если такое начальное значение существует、 х = а(14.14) Уравнение асимптоты должно быть найдено. Аналогично, если мы найдем асимптоту, параллельную оси Ox, мы уменьшим ее до значения определения конечного предела fm y (1) b или fm y (() = b, и fm x (()) 10, где fm () присутствует. Соответственно, Fm x (() равно+ che или-oo.
 Если окажется, что такое значение 10 существует、 г = Б(14.15) Уравнение асимптоты должно быть найдено. Наконец, чтобы найти асимптоту.
Если окажется, что такое значение 10 существует、 г = Б(14.15) Уравнение асимптоты должно быть найдено. Наконец, чтобы найти асимптоту.
Смотрите также:
Предмет математический анализ
Функция — Проектирование зданий
Мы используем файлы cookie, чтобы обеспечить вам максимальное удобство на нашем веб-сайте. Вы можете узнать о наших файлах cookie и о том, как отключить файлы cookie, в нашей Политике конфиденциальности. Если вы продолжите использовать этот веб-сайт без отключения файлов cookie, мы будем считать, что вы довольны их получением. Закрывать.
Редактировать эту статью
Последняя редакция 24 мая 2021 г.
См. вся история
По отношению к искусственной среде термин «9Функция 0013 ’ относится к назначению здания или сооружения. Это также может относиться к правильной работе, процессу или производительности чего-либо и тому, как это работает, например, установка, инструменты, лифт, строительные услуги.

В архитектуре функционализм (или «форма следует за функцией») — это принцип, согласно которому здания проектируются не в соответствии с прошлыми прецедентами или стилистическими тенденциями (эстетика), а основная цель здания должна определять его форму.
Здания имеют широкий спектр различных выполняет функции , например, дом предназначен для проживания, офис служит местом работы для ведения бизнеса, торговый центр предназначен для доступа потребителей к торговым точкам, школа предназначена для учащихся и учителей для получения образования и скоро.
Здания могут иметь ряд различных функций (например, фабрика может включать в себя офисы, ресторан, сборочные линии и т. д.), а некоторые функции могут конфликтовать друг с другом, например, доступ и безопасность, виды против конфиденциальности и так далее.
Изделия, материалы, компоненты и системы могут быть оценены с точки зрения их функциональности, то есть пригодности и возможностей, с которыми они служат конкретной цели или практичности, для которой они были предназначены.

См. также: Основная функция.
- Эстетика и архитектура.
- Строительная система.
- От краха до могилы.
- Строительные работы.
- Контекст.
- Соответствие назначению.
- Форма следует за функцией.
- Оценка жизненного цикла.
- Основная функция.
- Доля
- Добавить комментарий
- Отправьте нам отзыв
Создать статью
Поделиться
- Подписаться
- Твиттер
- Ютуб
Избранные статьи и новости
Строительство комплексной ветроэнергетики
Хотя многие пытались, немногим это удалось.
Принадлежность
Что такое и как это относится к зданиям ?
Серия CIAT Film
Создание домов с целостным дизайном.

Внедоговорное возмещение
Скидка 10% на новую книгу для наших пользователей.
Всемирный день электромобиля 2022 и новые исследования
От имени Партнерства по электротехническим навыкам.
APM Women in Project Management Conference
Свежий взгляд на проблемы современной работы.
Награды CIOB 2022
Признание достижений руководителей строительства.
Утилизация строительного мусора
Перспектива компаний по обращению с отходами.
Оксинитрид алюминия, ALON®, также известный как «Прозрачный алюминий!»
Впервые показан в фильме «Звёздный путь 4: Путешествие домой».
Награды Ассоциации специалистов по вводу в эксплуатацию 2022 г.
При поддержке BSRIA Instrument Solutions.
Ответ CIOB Ирландии на бюджет на 2023 год
Ожидается, что в этом году экономика Ирландии вырастет на 10%.

Грант на руководство по страхованию древесины, присужденный ПБАМ
Справочник по массовому страхованию лесоматериалов для отрасли.
Правительственный обзор политики чистого нуля в текущем контексте
Минимальные потребительские расходы, экономический рост и энергетическая безопасность.
Объявлен новый стул APM
Милла Мазилу, главный менеджер по управлению программами в NR.
Ведущий ученик получает награду ECA Edmundson Award 2022
Вероника Дженнингс признана ведущим учеником.
Последний отчет Школы устойчивого развития цепочки поставок
Отчет о справедливости, включении и уважении (FIR) за 2022 год.
История последней деревни на побережье Гамбии
История, деревня, экокурорт и фонд.
Планируя отпуск, помните, что 27 числа…
«Переосмысление туризма» — ставить людей и планету на первое место.

Министры жилищного строительства по БД
Четвертый в этом году министр жилищного строительства вступает в новую должность.
Объявление мини-бюджета Государственного плана роста
Снижение налогов, замораживание и облегчение, а также новые инвестиционные зоны.
Схемы оплаты счетов за электроэнергию
Гарантия цен на энергию, схемы поддержки счетов и льгот.
APM отвечает на объявление мини-бюджета канцлера
«Приверженность текущим инвестициям в проекты, которые необходимы… для ускорения экономического роста и достижения нулевого результата»
CIOB реагирует на объявление мини-бюджета канцлера
«Учитесь на ошибках () гранта Green Homes … Реализация национальной (энергетической) стратегии модернизации»
Флюгеры
От грифонов и драконов до англо-саксонских загадок.
Работающие девушки
Греческая улица, 59: дом Театрального женского клуба.
 Обзор книги.
Обзор книги.Коротко о конкурсе на БД
От проектирования до тендеров.
Бесплатное знакомство с членством в IHBC.
Сессия назначена на 13:00 в четверг, 13 октября.
Смотрите больше новостей.
Функции здания — общее ядро: старшая школа
Все общее ядро: старшая школа — ресурсы функций
6 диагностических тестов 82 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 5 6 7 8 9 10 11 Следующая →
Common Core: High School — Помощь по функциям » Building Functions
Салли хочет купить новый компьютер на следующий год. Компьютер, на который она положила глаз, стоит . Салли работает выгульщиком собак и получает почасовую оплату. Если Салли работает восемь часов в неделю, сколько недель работы ей потребуется, чтобы заработать достаточно денег, чтобы купить новый компьютер?
Возможные ответы:
Салли нужно будет работать недель.

Салли нужно будет работать недель.
Салли нужно будет работать недель.
Салли нужно будет работать недель.
Салли нужно будет работать недель.
Правильный ответ:
Салли нужно будет работать недель.
Пояснение:
Этот вопрос проверяет способность распознавать функции в повседневных ситуациях и строить математическую модель, показывающую взаимосвязь между двумя величинами. Такой вопрос требует изучения поведения между величинами, будь то явное выражение, рекурсивный процесс или многошаговое вычисление. Это также требует использования алгебраических операций для решения поставленного вопроса, а затем построения функции, моделирующей взаимосвязь.
В соответствии с Общими базовыми стандартами написание функции, описывающей взаимосвязь, относится к Кластеру А построения функции, моделирующей взаимосвязь между концепциями двух величин (CCSS.
 Math.content.HSF.BF.A). Вопросы в этом кластере в значительной степени зависят от построения понимания между реальными жизненными ситуациями, рассматриваемыми с математической точки зрения.
Math.content.HSF.BF.A). Вопросы в этом кластере в значительной степени зависят от построения понимания между реальными жизненными ситуациями, рассматриваемыми с математической точки зрения.Зная стандарт и концепцию, к которой он относится, теперь мы можем выполнить пошаговый процесс решения рассматриваемой проблемы.
Шаг 1: Определите, к чему относится вопрос.
Шаг 2: Определите, что дано/известно из вопроса.
Шаг 3: Используя алгебраические методы, создайте функцию для описания отношений.
Шаг 4: Ответьте на вопрос.
Действия, перечисленные выше для этой конкретной проблемы, выполняются следующим образом.
Шаг 1: Определите, к чему относится вопрос.
Сколько недель Салли нужно будет работать, чтобы заработать достаточно денег, чтобы купить новый компьютер?
Шаг 2: Определите, что дано/известно из вопроса.
Компьютер стоит
Салли зарабатывает
Салли работает
Шаг 3: Используя алгебраические методы, создайте функцию для описания отношений.

Шаг 4: Ответьте на вопрос.
Из этой модели подставьте известные значения и решите количество проработанных недель, чтобы ответить на вопрос.
Используя алгебраические операции, разделите обе стороны на 64, чтобы вычислить количество недель, в течение которых Салли должна работать.
Сообщить об ошибке
Джейн хочет купить новый рюкзак на следующий год. Рюкзак, на который она положила глаз, стоит . Джейн работает мойщиком автомобилей и получает почасовую оплату. Если Джейн работает по несколько часов в неделю, сколько недель работы ей понадобится, чтобы заработать достаточно денег, чтобы купить новый рюкзак?
Возможные ответы:
Джейн нужно будет работать несколько недель, чтобы купить новый рюкзак.
Джейн потребуется несколько недель, чтобы купить новый рюкзак.
Джейн потребуется несколько недель, чтобы купить новый рюкзак.
Джейн потребуется несколько недель, чтобы купить новый рюкзак.

Джейн потребуется несколько недель, чтобы купить новый рюкзак.
Правильный ответ:
Джейн нужно будет работать несколько недель, чтобы купить новый рюкзак.
Пояснение:
Этот вопрос проверяет способность распознавать функции в повседневных ситуациях и строить математическую модель, показывающую взаимосвязь между двумя величинами. Такой вопрос требует изучения поведения между величинами, будь то явное выражение, рекурсивный процесс или многошаговое вычисление. Это также требует использования алгебраических операций для решения поставленного вопроса, а затем построения функции, моделирующей взаимосвязь.
В соответствии с Общими базовыми стандартами написание функции, описывающей взаимосвязь, относится к Кластеру А построения функции, моделирующей взаимосвязь между концепциями двух величин (CCSS.MATH.CONTENT.HSF.BF.A). Вопросы в этом кластере в значительной степени зависят от построения понимания между реальными жизненными ситуациями, рассматриваемыми с математической точки зрения.

Зная стандарт и концепцию, к которой он относится, теперь мы можем выполнить пошаговый процесс решения рассматриваемой проблемы.
Шаг 1: Определите, к чему относится вопрос.
Шаг 2: Определите, что дано/известно из вопроса.
Шаг 3: Используя алгебраические методы, создайте функцию для описания отношений.
Шаг 4: Ответьте на вопрос.
Действия, перечисленные выше для этой конкретной проблемы, выполняются следующим образом.
Шаг 1: Определите, к чему относится вопрос.
Сколько недель Джейн придется работать, чтобы заработать достаточно денег, чтобы купить новый рюкзак?
Шаг 2: Определите, что дано/известно из вопроса.
Рюкзак стоит
Джейн зарабатывает
Джейн работает
Шаг 3: Используя алгебраические методы, создайте функцию для описания отношений.
Шаг 4: Ответьте на вопрос.
Из этой модели подставьте известные значения и решите количество проработанных недель, чтобы ответить на вопрос.

Используя алгебраические операции, разделите обе стороны на 12, чтобы вычислить количество недель, в течение которых Джейн нужно будет работать.
Сообщить об ошибке
Дженни хочет купить новый велосипед на следующий год. Велосипед, на который она положила глаз, стоит . Дженни косит газоны и получает деньги за каждую лужайку. Сколько газонов нужно скосить Дженни, чтобы заработать достаточно денег, чтобы купить новый велосипед?
Возможные ответы:
Дженни нужно косить газоны.
Дженни нужно косить газоны.
Дженни нужно косить газоны.
Дженни нужно косить газоны.
Дженни нужно косить газоны.
Правильный ответ:
Дженни нужно косить газоны.
Пояснение:
Этот вопрос проверяет способность распознавать функции в повседневных ситуациях и строить математическую модель, показывающую взаимосвязь между двумя величинами.
 Такой вопрос требует изучения поведения между величинами, будь то явное выражение, рекурсивный процесс или многошаговое вычисление. Это также требует использования алгебраических операций для решения поставленного вопроса, а затем построения функции, моделирующей взаимосвязь.
Такой вопрос требует изучения поведения между величинами, будь то явное выражение, рекурсивный процесс или многошаговое вычисление. Это также требует использования алгебраических операций для решения поставленного вопроса, а затем построения функции, моделирующей взаимосвязь.В соответствии с Общими базовыми стандартами написание функции, описывающей взаимосвязь, относится к Кластеру А построения функции, моделирующей взаимосвязь между концепциями двух величин (CCSS.MATH.CONTENT.HSF.BF.A). Вопросы в этом кластере в значительной степени зависят от построения понимания между реальными жизненными ситуациями, рассматриваемыми с математической точки зрения.
Зная стандарт и концепцию, к которой он относится, теперь мы можем выполнить пошаговый процесс решения рассматриваемой проблемы.
Шаг 1: Определите, к чему относится вопрос.
Шаг 2: Определите, что дано/известно из вопроса.
Шаг 3: Используя алгебраические методы, создайте функцию для описания отношений.

Шаг 4: Ответьте на вопрос.
Действия, перечисленные выше для этой конкретной проблемы, выполняются следующим образом.
Шаг 1: Определите, к чему относится вопрос.
Сколько газонов придется обработать Дженни, чтобы заработать достаточно денег на новый велосипед?
Шаг 2: Определите, что дано/известно из вопроса.
Велосипед стоит
Дженни зарабатывает
Шаг 3: Используя алгебраические методы, создайте функцию для описания отношений.
Шаг 4: Ответьте на вопрос.
Из этой модели подставьте известные значения и решите количество проработанных недель, чтобы ответить на вопрос.
Используя алгебраические операции, разделите на 5 с обеих сторон, чтобы вычислить количество газонов, которое Дженни потребуется для работы.
Сообщить об ошибке
Дженни хочет накопить денег на поездку с классом. Если Дженни косит газоны и получает деньги за каждую лужайку. Сколько газонов нужно скосить Дженни, чтобы спасти .

Возможные ответы:
Дженни нужно косить газоны.
Дженни нужно косить газоны.
Дженни нужно косить газоны.
Дженни нужно косить газоны.
Дженни нужно косить газоны.
Правильный ответ:
Дженни нужно косить газоны.
Пояснение:
Этот вопрос проверяет способность распознавать функции в повседневных ситуациях и строить математическую модель, показывающую взаимосвязь между двумя величинами. Такой вопрос требует изучения поведения между величинами, будь то явное выражение, рекурсивный процесс или многошаговое вычисление. Это также требует использования алгебраических операций для решения поставленного вопроса, а затем построения функции, моделирующей взаимосвязь.
В соответствии с Общими базовыми стандартами написание функции, описывающей взаимосвязь, относится к Кластеру А построения функции, моделирующей взаимосвязь между концепциями двух величин (CCSS.
 MATH.CONTENT.HSF.BF.A). Вопросы в этом кластере в значительной степени зависят от построения понимания между реальными жизненными ситуациями, рассматриваемыми с математической точки зрения.
MATH.CONTENT.HSF.BF.A). Вопросы в этом кластере в значительной степени зависят от построения понимания между реальными жизненными ситуациями, рассматриваемыми с математической точки зрения.Зная стандарт и концепцию, к которой он относится, теперь мы можем выполнить пошаговый процесс решения рассматриваемой проблемы.
Шаг 1: Определите, к чему относится вопрос.
Шаг 2: Определите, что дано/известно из вопроса.
Шаг 3: Используя алгебраические методы, создайте функцию для описания отношений.
Шаг 4: Ответьте на вопрос.
Действия, перечисленные выше для этой конкретной проблемы, выполняются следующим образом.
Шаг 1: Определите, к чему относится вопрос.
Сколько газонов нужно Дженни, чтобы заработать?
Шаг 2: Определите, что дано/известно из вопроса.
Общая сумма сэкономленных денег
Дженни зарабатывает
Шаг 3: Используя алгебраические методы, создайте функцию для описания отношений.
Шаг 4: Ответьте на вопрос.

Из этой модели подставьте известные значения и решите количество проработанных недель, чтобы ответить на вопрос.
Используя алгебраические операции, разделите на 5 с обеих сторон, чтобы вычислить количество газонов, которое Дженни потребуется для работы.
Сообщить об ошибке
Джейн хочет купить новый рюкзак на следующий год. Рюкзак, на который она положила глаз, стоит . Джейн работает мойщиком автомобилей и получает почасовую оплату. Если Джейн работает по несколько часов в неделю, сколько недель работы ей понадобится, чтобы заработать достаточно денег, чтобы купить новый рюкзак?
Возможные ответы:
Джейн придется работать семь недель, чтобы купить новый рюкзак.
Джейн придется отработать пять недель, чтобы купить новый рюкзак.
Джейн придется работать шесть недель, чтобы купить новый рюкзак.
Джейн придется работать три недели, чтобы купить новый рюкзак.

Джейн придется работать четыре недели, чтобы купить новый рюкзак.
Правильный ответ:
Джейн придется работать шесть недель, чтобы купить новый рюкзак.
Пояснение:
Этот вопрос проверяет способность распознавать функции в повседневных ситуациях и строить математическую модель, показывающую взаимосвязь между двумя величинами. Такой вопрос требует изучения поведения между величинами, будь то явное выражение, рекурсивный процесс или многошаговое вычисление. Это также требует использования алгебраических операций для решения поставленного вопроса, а затем построения функции, моделирующей взаимосвязь.
В соответствии с Общими базовыми стандартами написание функции, описывающей взаимосвязь, относится к Кластеру А построения функции, моделирующей взаимосвязь между концепциями двух величин (CCSS.MATH.CONTENT.HSF.BF.A). Вопросы в этом кластере в значительной степени зависят от построения понимания между реальными жизненными ситуациями, рассматриваемыми с математической точки зрения.

Зная стандарт и концепцию, к которой он относится, теперь мы можем выполнить пошаговый процесс решения рассматриваемой проблемы.
Шаг 1: Определите, к чему относится вопрос.
Шаг 2: Определите, что дано/известно из вопроса.
Шаг 3: Используя алгебраические методы, создайте функцию для описания отношений.
Шаг 4: Ответьте на вопрос.
Действия, перечисленные выше для этой конкретной проблемы, выполняются следующим образом.
Шаг 1: Определите, к чему относится вопрос.
Сколько недель Джейн придется работать, чтобы заработать достаточно денег, чтобы купить новый рюкзак?
Шаг 2: Определите, что дано/известно из вопроса.
Рюкзак стоит
Джейн зарабатывает
Джейн работает
Шаг 3: Используя алгебраические методы, создайте функцию для описания отношений.
Шаг 4: Ответьте на вопрос.
Из этой модели подставьте известные значения и решите количество проработанных недель, чтобы ответить на вопрос.

Используя алгебраические операции, разделите на с обеих сторон, чтобы рассчитать количество недель, в течение которых Джейн нужно будет работать.
Сообщить об ошибке
Салли хочет купить новый компьютер на следующий год. Компьютер, на который она положила глаз, стоит . Салли работает выгульщиком собак и получает почасовую оплату. Если Салли работает восемь часов в неделю, сколько недель работы ей потребуется, чтобы заработать достаточно денег, чтобы купить новый компьютер?
Возможные ответы:
Салли нужно отработать девять недель, чтобы купить новый компьютер.
Салли нужно отработать шесть недель, чтобы купить новый компьютер.
Салли нужно отработать семь недель, чтобы купить новый компьютер.
Салли нужно отработать пять недель, чтобы купить новый компьютер.
Салли нужно отработать четыре недели, чтобы купить новый компьютер.
Правильный ответ:
Салли нужно отработать семь недель, чтобы купить новый компьютер.

Пояснение:
Этот вопрос проверяет способность распознавать функции в повседневных ситуациях и строить математическую модель, показывающую взаимосвязь между двумя величинами. Такой вопрос требует изучения поведения между величинами, будь то явное выражение, рекурсивный процесс или многошаговое вычисление. Это также требует использования алгебраических операций для решения поставленного вопроса, а затем построения функции, моделирующей взаимосвязь.
В соответствии с Общими базовыми стандартами написание функции, описывающей взаимосвязь, относится к Кластеру А построения функции, моделирующей взаимосвязь между концепциями двух величин (CCSS.Math.content.HSF.BF.A). Вопросы в этом кластере в значительной степени зависят от построения понимания между реальными жизненными ситуациями, рассматриваемыми с математической точки зрения.
Зная стандарт и концепцию, к которой он относится, теперь мы можем выполнить пошаговый процесс решения рассматриваемой проблемы.

Шаг 1: Определите, к чему относится вопрос.
Шаг 2: Определите, что дано/известно из вопроса.
Шаг 3: Используя алгебраические методы, создайте функцию для описания отношений.
Шаг 4: Ответьте на вопрос.
Действия, перечисленные выше для этой конкретной проблемы, выполняются следующим образом.
Шаг 1: Определите, к чему относится вопрос.
Сколько недель Салли нужно будет работать, чтобы заработать достаточно денег, чтобы купить новый компьютер?
Шаг 2: Определите, что дано/известно из вопроса.
Компьютер стоит
Салли зарабатывает
Салли работает
Шаг 3: Используя алгебраические методы, создайте функцию для описания отношений.
Шаг 4: Ответьте на вопрос.
Из этой модели подставьте известные значения и решите количество проработанных недель, чтобы ответить на вопрос.
Используя алгебраические операции, разделите на с обеих сторон, чтобы рассчитать количество недель, в течение которых Салли должна работать.

Сообщить об ошибке
Боб хочет накопить достаточно денег, чтобы купить маме новое дорогое ожерелье. Если Боб зарабатывает час, сколько часов ему нужно будет работать?
Возможные ответы:
Бобу нужно будет отработать часов.
Бобу нужно будет отработать часов.
Бобу нужно будет отработать часов.
Бобу нужно будет отработать часов.
Бобу нужно будет отработать часов.
Правильный ответ:
Бобу нужно будет отработать несколько часов.
Пояснение:
Этот вопрос проверяет способность распознавать функции в повседневных ситуациях и строить математическую модель, показывающую взаимосвязь между двумя величинами. Такой вопрос требует изучения поведения между величинами, будь то явное выражение, рекурсивный процесс или многошаговое вычисление.
 Это также требует использования алгебраических операций для решения поставленного вопроса, а затем построения функции, моделирующей взаимосвязь.
Это также требует использования алгебраических операций для решения поставленного вопроса, а затем построения функции, моделирующей взаимосвязь.В соответствии с Общими базовыми стандартами написание функции, описывающей взаимосвязь, относится к Кластеру А построения функции, моделирующей взаимосвязь между концепциями двух величин (CCSS.MATH.CONTENT.HSF.BF.A). Вопросы в этом кластере в значительной степени зависят от построения понимания между реальными жизненными ситуациями, рассматриваемыми с математической точки зрения.
Зная стандарт и концепцию, к которой он относится, теперь мы можем выполнить пошаговый процесс решения рассматриваемой проблемы.
Шаг 1: Определите, к чему относится вопрос.
Шаг 2: Определите, что дано/известно из вопроса.
Шаг 3: Используя алгебраические методы, создайте функцию для описания отношений.
Шаг 4: Ответьте на вопрос.
Действия, перечисленные выше для этой конкретной проблемы, выполняются следующим образом.

Шаг 1: Определите, к чему относится вопрос.
Сколько часов Боб должен работать, чтобы заработать?
Шаг 2: Определите, что дано/известно из вопроса.
Цена ожерелья .
Боб зарабатывает
Шаг 3: Используя алгебраические методы, создайте функцию для описания отношений.
Шаг 4: Ответьте на вопрос.
Из этой модели подставьте известные значения и решите количество проработанных недель, чтобы ответить на вопрос.
Используя алгебраические операции, разделите обе стороны на 2, чтобы вычислить количество часов, в течение которых Боб должен будет работать.
Сообщить об ошибке
Боб хочет сохранить . Если Боб зарабатывает час, сколько часов ему нужно будет работать, чтобы достичь своей цели по сбережениям?
Возможные ответы:
Бобу нужно будет работать часов, чтобы достичь своей цели сбережений.
Бобу нужно будет работать часов, чтобы достичь своей цели сбережений.

Бобу нужно будет работать часов, чтобы достичь своей цели сбережений.
Бобу нужно будет работать часов, чтобы достичь своей цели сбережений.
Бобу нужно будет работать часов, чтобы достичь своей цели сбережений.
Правильный ответ:
Бобу нужно будет работать часов, чтобы достичь своей цели сбережений.
Пояснение:
Этот вопрос проверяет способность распознавать функции в повседневных ситуациях и строить математическую модель, показывающую взаимосвязь между двумя величинами. Такой вопрос требует изучения поведения между величинами, будь то явное выражение, рекурсивный процесс или многошаговое вычисление. Это также требует использования алгебраических операций для решения поставленного вопроса, а затем построения функции, моделирующей взаимосвязь.
В соответствии с Общими базовыми стандартами написание функции, описывающей взаимосвязь, относится к Кластеру А построения функции, моделирующей взаимосвязь между концепциями двух величин (CCSS.
 MATH.CONTENT.HSF.BF.A). Вопросы в этом кластере в значительной степени зависят от построения понимания между реальными жизненными ситуациями, рассматриваемыми с математической точки зрения.
MATH.CONTENT.HSF.BF.A). Вопросы в этом кластере в значительной степени зависят от построения понимания между реальными жизненными ситуациями, рассматриваемыми с математической точки зрения.Зная стандарт и концепцию, к которой он относится, теперь мы можем выполнить пошаговый процесс решения рассматриваемой проблемы.
Шаг 1: Определите, к чему относится вопрос.
Шаг 2: Определите, что дано/известно из вопроса.
Шаг 3: Используя алгебраические методы, создайте функцию для описания отношений.
Шаг 4: Ответьте на вопрос.
Действия, перечисленные выше для этой конкретной проблемы, выполняются следующим образом.
Шаг 1: Определите, к чему относится вопрос.
Сколько часов Боб должен работать, чтобы заработать?
Шаг 2: Определите, что дано/известно из вопроса.
Общая цель экономии – .
Боб зарабатывает
Шаг 3: Используя алгебраические методы, создайте функцию для описания отношений.
Шаг 4: Ответьте на вопрос.

Из этой модели подставьте известные значения и решите количество проработанных недель, чтобы ответить на вопрос.
Используя алгебраические операции, разделите на с обеих сторон, чтобы рассчитать количество часов, которые Боб должен будет отработать.
Сообщить об ошибке
Боб хочет накопить достаточно денег, чтобы купить маме новое ожерелье по цене . Если Боб зарабатывает час, сколько часов ему нужно будет работать?
Возможные ответы:
Бобу нужно будет работать шесть часов.
Бобу нужно будет работать восемь часов.
Бобу нужно будет работать девять часов.
Бобу нужно будет работать десять часов.
Бобу нужно будет работать пять часов.
Правильный ответ:
Бобу нужно будет работать девять часов.
Пояснение:
Этот вопрос проверяет способность распознавать функции в повседневных ситуациях и строить математическую модель, показывающую взаимосвязь между двумя величинами.
 Такой вопрос требует изучения поведения между величинами, будь то явное выражение, рекурсивный процесс или многошаговое вычисление. Это также требует использования алгебраических операций для решения поставленного вопроса, а затем построения функции, моделирующей взаимосвязь.
Такой вопрос требует изучения поведения между величинами, будь то явное выражение, рекурсивный процесс или многошаговое вычисление. Это также требует использования алгебраических операций для решения поставленного вопроса, а затем построения функции, моделирующей взаимосвязь.В соответствии с Общими базовыми стандартами написание функции, описывающей взаимосвязь, относится к Кластеру А построения функции, моделирующей взаимосвязь между концепциями двух величин (CCSS.MATH.CONTENT.HSF.BF.A). Вопросы в этом кластере в значительной степени зависят от построения понимания между реальными жизненными ситуациями, рассматриваемыми с математической точки зрения.
Зная стандарт и концепцию, к которой он относится, теперь мы можем выполнить пошаговый процесс решения рассматриваемой проблемы.
Шаг 1: Определите, к чему относится вопрос.
Шаг 2: Определите, что дано/известно из вопроса.
Шаг 3: Используя алгебраические методы, создайте функцию для описания отношений.

Шаг 4: Ответьте на вопрос.
Действия, перечисленные выше для этой конкретной проблемы, выполняются следующим образом.
Шаг 1: Определите, к чему относится вопрос.
Сколько часов Боб должен работать, чтобы заработать?
Шаг 2: Определите, что дано/известно из вопроса.
Цена ожерелья .
Боб зарабатывает
Шаг 3: Используя алгебраические методы, создайте функцию для описания отношений.
Шаг 4: Ответьте на вопрос.
Из этой модели подставьте известные значения и решите количество проработанных недель, чтобы ответить на вопрос.
Используя алгебраические операции, разделите на с обеих сторон, чтобы рассчитать количество часов, которые Боб должен будет отработать.
Сообщить об ошибке
Боб хочет накопить достаточно денег, чтобы купить маме новое ожерелье по цене . Если Боб зарабатывает час, сколько часов ему нужно будет работать?
Возможные ответы:
Бобу нужно будет работать два часа.

Бобу нужно будет работать четыре часа.
Бобу нужно будет работать три часа.
Бобу нужно будет работать восемь часов.
Бобу нужно будет работать пять часов.
Правильный ответ:
Бобу нужно будет работать четыре часа.
Пояснение:
Этот вопрос проверяет способность распознавать функции в повседневных ситуациях и строить математическую модель, показывающую взаимосвязь между двумя величинами. Такой вопрос требует изучения поведения между величинами, будь то явное выражение, рекурсивный процесс или многошаговое вычисление. Это также требует использования алгебраических операций для решения поставленного вопроса, а затем построения функции, моделирующей взаимосвязь.
В соответствии с Общими базовыми стандартами написание функции, описывающей взаимосвязь, относится к Кластеру А построения функции, моделирующей взаимосвязь между концепциями двух величин (CCSS.
 MATH.CONTENT.HSF.BF.A). Вопросы в этом кластере в значительной степени зависят от построения понимания между реальными жизненными ситуациями, рассматриваемыми с математической точки зрения.
MATH.CONTENT.HSF.BF.A). Вопросы в этом кластере в значительной степени зависят от построения понимания между реальными жизненными ситуациями, рассматриваемыми с математической точки зрения.Зная стандарт и концепцию, к которой он относится, теперь мы можем выполнить пошаговый процесс решения рассматриваемой проблемы.
Шаг 1: Определите, к чему относится вопрос.
Шаг 2: Определите, что дано/известно из вопроса.
Шаг 3: Используя алгебраические методы, создайте функцию для описания отношений.
Шаг 4: Ответьте на вопрос.
Действия, перечисленные выше для этой конкретной проблемы, выполняются следующим образом.
Шаг 1: Определите, к чему относится вопрос.
Сколько часов Боб должен работать, чтобы заработать?
Шаг 2: Определите, что дано/известно из вопроса.
Цена ожерелья .
Боб зарабатывает
Шаг 3: Используя алгебраические методы, создайте функцию для описания отношений.
Шаг 4: Ответьте на вопрос.

Из этой модели подставьте известные значения и решите количество проработанных недель, чтобы ответить на вопрос.
Используя алгебраические операции, разделите на с обеих сторон, чтобы рассчитать количество часов, которые Боб должен будет отработать.
Сообщить об ошибке
← Предыдущий 1 2 3 4 5 6 7 8 9 10 11 Следующий →
Уведомление об авторских правах
All Common Core: High School — Ресурсы функций
6 Диагностические тесты 82 практических теста Вопрос дня Карточки Learn by Concept
Средняя школа: Функции | СС
- Давайте сделаем предварительное замечание. Чтобы найти асимптоты, параллельные оси Oy, необходимо найти значение*, имеющее конечный предел Если такое начальное значение существует、 х = а(14.14) Уравнение асимптоты должно быть найдено. Аналогично, если мы найдем асимптоту, параллельную оси Ox, мы уменьшим ее до значения определения конечного предела fm y (1) b или fm y (() = b, и fm x (()) 10, где fm () присутствует. Соответственно, Fm x (() равно+ che или-oo.
Как написать уравнение для перевода функции абсолютного значения?
Хотите написать уравнение для перевода графика уравнения абсолютного значения? Этот учебник проведет вас через этот процесс шаг за шагом! Возьмите уравнение абсолютного значения и выполните вертикальное и горизонтальное смещение, чтобы создать новое уравнение.
 Смотрите все это в этом уроке.
Смотрите все это в этом уроке.Как построить график функции абсолютного значения?
Построение графика уравнения абсолютного значения может быть сложным, если вы не знаете, как анализировать уравнение, чтобы найти и использовать наклон и переводы. Следуйте инструкциям, поскольку этот учебник покажет вам, как определить необходимые части уравнения и использовать их для построения графика уравнения абсолютного значения.
Что делает константа ‘k’ в y = |x|+k?
Когда вы изучаете перевод уравнений с абсолютными значениями, ОБЯЗАТЕЛЬНО изучите вертикальные переводы! Ознакомьтесь с этим учебным пособием и узнайте, что нужно для вертикального перевода уравнения абсолютного значения.
Что делает константа ‘h’ в y = |x-h|?
Когда вы изучаете преобразование уравнений с абсолютными значениями, ОБЯЗАТЕЛЬНО изучите горизонтальные преобразования! Ознакомьтесь с этим учебным пособием и узнайте, что нужно для перевода уравнения абсолютного значения по горизонтали.

Что такое функция абсолютного значения?
Функция абсолютного значения — это просто функция, которая содержит абсолютные значения. Этот учебник дает отличное введение в эту очень полезную функцию!
Как построить график экспоненциальной функции с помощью таблицы?
График экспоненциальной функции? Нет пота! Создайте таблицу значений, чтобы получить упорядоченные пары. Затем нанесите эти упорядоченные пары на координатную плоскость и соедините точки, чтобы построить график! Следуйте этому руководству, поскольку оно показывает вам все шаги.
Как определить экспоненциальное поведение по шаблону в данных?
Посмотрите, как вы определяете экспоненциальное поведение по шаблону в ваших данных. Вы также увидите, как определить, представляет ли этот паттерн экспоненциальный рост или экспоненциальный спад. Проверьте это!
Как решить задачу с экспоненциальным ростом?
Если что-то увеличивается с постоянной скоростью, вы можете получить экспоненциальный рост.
 В этом уроке вы узнаете, как превратить текстовую задачу в функцию экспоненциального роста. Затем решите функцию и получите ответ!
В этом уроке вы узнаете, как превратить текстовую задачу в функцию экспоненциального роста. Затем решите функцию и получите ответ!Как решить задачу с экспоненциальным затуханием?
Если что-то падает в цене с постоянной скоростью, вы можете столкнуться с экспоненциальным спадом. В этом уроке вы узнаете, как превратить текстовую задачу в функцию экспоненциального затухания. Затем решите функцию и получите ответ!
Как написать правило для геометрической последовательности?
Пытаетесь найти значение определенного члена в геометрической прогрессии? Используйте формулу нахождения n-го члена геометрической прогрессии, чтобы записать правило. Затем используйте это правило, чтобы найти значение каждого термина, который вы хотите! Этот учебник проведет вас через это шаг за шагом.
Как решить текстовую задачу с помощью экспоненциальной функции?
Словесные задачи позволяют увидеть математику в реальном мире! В этом учебном пособии показано, как создать таблицу и идентифицировать закономерность в словесной задаче.
 Затем вы можете увидеть, как создать экспоненциальную функцию из данных и решить функцию, чтобы получить ответ!
Затем вы можете увидеть, как создать экспоненциальную функцию из данных и решить функцию, чтобы получить ответ!Что делает значение ‘a’ в экспоненциальной функции f(x)= a (bx)?
Умножение экспоненциальной функции на константу изменяет график функции. Посмотрите обучающее видео, чтобы узнать, как это сделать!
Что такое экспоненциальная функция?
Ищете уравнение с переменной в показателе степени? У вас есть экспоненциальная функция! Узнайте об экспоненциальных функциях в этом руководстве.
Что такое экспоненциальный рост?
Экспоненциальные функции часто включают скорость увеличения или уменьшения чего-либо. Когда это скорость увеличения, у вас есть экспоненциальная функция роста! Проверьте эти виды экспоненциальных функций в этом уроке!
Что такое экспоненциальный спад?
Экспоненциальные функции часто включают скорость увеличения или уменьшения чего-либо.
 Когда это скорость убывания, у вас есть экспоненциальная функция затухания! Проверьте эти виды экспоненциальных функций в этом уроке!
Когда это скорость убывания, у вас есть экспоненциальная функция затухания! Проверьте эти виды экспоненциальных функций в этом уроке!Что такое явная формула для n-го члена геометрической последовательности?
Пытаетесь найти значение определенного члена в геометрической прогрессии? Не хотите просматривать условия один за другим, чтобы найти то, что вам нужно? Используйте формулу, чтобы найти n-й член в геометрической прогрессии! Этот урок покажет вам, как найти эту формулу!
Как построить график рациональной функции с помощью таблицы?
Построение графика рациональной функции может быть увлекательным занятием, особенно если вы сначала составите таблицу значений! В этом уроке вы увидите, как составить таблицу упорядоченных пар, которую можно использовать для построения графика рациональной функции. Взглянем!
Что такое функция?
Функциональные правила похожи на инструкции о том, как преобразовать входные значения в соответствующие выходные значения.
 В этом руководстве показано, как написать правило функции для заданного отношения. Проверьте это!
В этом руководстве показано, как написать правило функции для заданного отношения. Проверьте это!Как определяется функция?
Вы не сможете пройти алгебру, не изучив функции. В этом руководстве показано определение функции и приведен пример функции. Взглянем!
Что такое линейная функция?
Как написать уравнение прямой в форме пересечения наклона, если у вас есть две точки?
Пытаетесь написать уравнение в форме пересечения наклона? Есть две точки на вашей линии? Вам нужно будет найти свой наклон и y-перехват. Посмотрите этот урок и узнайте, что нужно сделать, чтобы написать уравнение в форме пересечения наклона!
Как найти общую разность в арифметической последовательности?
Пытаетесь найти общую разницу в арифметической прогрессии? Вам нужно выяснить, какое число нужно добавить к каждому члену, чтобы получить следующий член в последовательности.
 Это проще, чем вы думаете! Посмотрите этот урок и узнайте, как найти общую разность в арифметической прогрессии.
Это проще, чем вы думаете! Посмотрите этот урок и узнайте, как найти общую разность в арифметической прогрессии.Как найти следующие члены арифметической последовательности?
Чтобы найти следующие несколько членов арифметической последовательности, вам сначала нужно найти общую разность, постоянную величину изменения между числами в арифметической последовательности. Как только вы узнаете общую разницу, вы можете использовать ее, чтобы найти следующие термины! Этот учебник проведет вас через этот процесс, поэтому обязательно ознакомьтесь с ним!
Как найти N-й член арифметической последовательности?
Есть арифметическая последовательность? Пытаетесь найти более поздний термин в этой последовательности? Не хотите продолжать добавлять общее различие к каждому термину, пока не доберетесь до нужного? Тогда вместо этого используйте уравнение для n-го члена арифметической прогрессии! Этот урок покажет вам, как!
Как написать уравнение прямого изменения с заданной точкой?
Хотите попрактиковаться с прямой вариацией? Посмотрите этот урок и получите эту практику! В этом руководстве показано, как взять заданную информацию и превратить ее в уравнение прямой вариации.
 Затем посмотрите, как использовать это уравнение, чтобы найти значение одной из переменных.
Затем посмотрите, как использовать это уравнение, чтобы найти значение одной из переменных.Как написать уравнение прямого изменения из таблицы?
Хотите попрактиковаться с прямой вариацией? Посмотрите этот урок и получите эту практику! В этом учебном пособии показано, как взять таблицу значений и описать отношение с помощью уравнения прямой вариации.
Как нарисовать вертикальную линию?
Чтобы изобразить вертикальную линию, проходящую через заданную точку, сначала начертите эту точку. Затем нарисуйте прямую линию вверх и вниз, проходящую через точку, и все готово! Чтобы увидеть этот процесс в действии, посмотрите этот урок!
Как нарисовать горизонтальную линию?
Чтобы изобразить горизонтальную линию, проходящую через заданную точку, сначала начертите эту точку. Затем нарисуйте прямую линию слева и справа, которая проходит через точку, и все готово! Чтобы увидеть этот процесс в действии, посмотрите этот урок!
Как использовать точки пересечения X и Y для построения графика в стандартной форме?
Чтобы найти точку пересечения по оси x заданного линейного уравнения, просто удалите «y» и найдите «x».
 Чтобы найти точку пересечения с осью y, удалите «x» и найдите «y». В этом уроке вы увидите, как найти точки пересечения по осям x и y для заданного линейного уравнения. Проверьте это!
Чтобы найти точку пересечения с осью y, удалите «x» и найдите «y». В этом уроке вы увидите, как найти точки пересечения по осям x и y для заданного линейного уравнения. Проверьте это!Как нарисовать линию, если известны наклон и точка пересечения?
Пытаетесь построить линию с заданным наклоном и точкой пересечения с осью Y? Думаете, вам нужно сначала найти уравнение? Подумайте еще раз! В этом руководстве вы увидите, как использовать заданный наклон и точку пересечения по оси Y для построения графика линии.
Как написать уравнение прямой в форме точка-наклон, если у вас есть наклон и одна точка?
Пытаетесь написать уравнение в форме точка-наклон? Нашли точку на линии и наклоне? Правильно подставьте эти значения в форму точки-наклона линии, и вы получите ответ! Посмотрите этот урок, чтобы узнать все подробности!
Как написать уравнение прямой в форме точка-наклон, если у вас есть две точки?
Пытаетесь написать уравнение в форме точка-наклон? Есть две точки, но нет наклона? Вам нужно будет использовать эти точки, чтобы сначала найти уклон.
 Посмотрите этот урок и узнайте, что нужно сделать, чтобы написать уравнение в форме точка-наклон!
Посмотрите этот урок и узнайте, что нужно сделать, чтобы написать уравнение в форме точка-наклон!Как написать уравнение прямой в форме точка-наклон и в стандартной форме, если у вас есть две точки?
Попрактикуйтесь в формуле «точка-наклон» и стандартной форме уравнения! В этом руководстве показано, как использовать две заданные точки для написания уравнения в обеих формах. Взглянем!
Как написать уравнение прямой в форме пересечения наклона, если у вас есть наклон и пересечение Y?
Хотите написать уравнение в форме пересечения наклона? У вас уже есть наклон и точка пересечения по оси Y? Идеальный! Просто правильно подставьте эти значения в уравнение, и все готово! Узнайте, как в этом уроке.
Что такое X-Intercept?
Когда у вас есть линейное уравнение, точка пересечения с осью x является точкой пересечения графика линии с осью x.
 В этом руководстве вы узнаете о x-intercept. Проверьте это!
В этом руководстве вы узнаете о x-intercept. Проверьте это!Что такое арифметическая последовательность?
Видите закономерность в последовательности? Это может быть арифметическая прогрессия! Узнайте об арифметических последовательностях, посмотрев этот урок.
В чем общая разница?
Знаете ли вы, что константа, которую вы добавляете к термину в арифметической последовательности, чтобы получить следующий термин, имеет имя? Это называется общая разница! Это руководство — отличный способ узнать больше об общей разнице арифметической прогрессии.
Откуда берется формула члена арифметической последовательности?
Пытаетесь найти значение определенного термина в арифметической последовательности? Не хотите просматривать условия один за другим, чтобы найти то, что вам нужно? Используйте формулу, чтобы найти n-й член в арифметической прогрессии! Этот урок покажет вам, как найти эту формулу!
Что такое Y-перехват?
Когда у вас есть линейное уравнение, точка пересечения с осью y является точкой, в которой график линии пересекает ось y.
 В этом уроке вы узнаете об y-перехвате. Проверьте это!
В этом уроке вы узнаете об y-перехвате. Проверьте это!Как найти нули квадратичной функции на графике?
Нули квадратного уравнения – это точки пересечения графика квадратного уравнения с осью x. В этом уроке вы увидите, как использовать график квадратного уравнения, чтобы найти нули уравнения. Взглянем!
Как решить квадратное уравнение с помощью факторинга?
Одним из многих способов решения квадратного уравнения является его разложение на множители. В этом уроке вы увидите, как факторизовать квадратное уравнение, используя метод факторинга «догадка и проверка». Затем используйте свойство нулевого произведения, чтобы найти решение!
Как решить квадратное уравнение, составив квадрат?
Одним из многих способов решения квадратного уравнения является завершение квадрата. В этом методе вы хотите превратить одну часть уравнения в идеальный квадратный трехчлен.
 В этом учебном пособии вы пошагово пошагово решаете квадратное уравнение, заполняя квадрат. Проверьте это!
В этом учебном пособии вы пошагово пошагово решаете квадратное уравнение, заполняя квадрат. Проверьте это!Как построить график квадратичной функции?
Когда вы пытаетесь построить график квадратного уравнения, очень полезно составить таблицу значений. Прежде чем составить таблицу, сначала найдите вершину квадратного уравнения. Таким образом, вы можете выбрать значения с любой стороны, чтобы увидеть, что делает график по обе стороны от вершины. Посмотрите этот урок, чтобы узнать, как построить график квадратного уравнения!
Как определить, будет ли вершина максимальной или минимальной?
Вершина квадратного уравнения является либо максимумом, либо минимумом функции. Но как узнать, будет ли это максимум или минимум? Посмотрите этот урок и найдите ответ на этот вопрос!
Как определить, представляет ли график линейную, экспоненциальную или квадратичную функцию?
Графики бывают самых разных форм и размеров.
 В алгебре чаще всего встречаются три основных типа графиков: линейный, квадратичный и экспоненциальный. Ознакомьтесь с этим руководством и узнайте, как определить, представляет ли график линейную, квадратичную или экспоненциальную функцию!
В алгебре чаще всего встречаются три основных типа графиков: линейный, квадратичный и экспоненциальный. Ознакомьтесь с этим руководством и узнайте, как определить, представляет ли график линейную, квадратичную или экспоненциальную функцию!Что такое вершина квадратичной функции?
Каждое квадратное уравнение имеет либо максимум, либо минимум, а вы знали, что эта точка имеет особое имя? В квадратном уравнении эта точка называется вершиной! Взгляните на вершину квадратного уравнения, просмотрев этот урок.
Каков максимум квадратичной функции?
Когда вы имеете дело с квадратичными функциями, очень вероятно, что вы встретите максимум и минимум. В этом уроке рассматривается максимум квадратичной функции. Проверьте это!
Что такое минимум квадратичной функции?
Когда вы имеете дело с квадратичными функциями, очень вероятно, что вы встретите максимум и минимум.
 В этом уроке рассматривается минимум квадратичной функции. Проверьте это!
В этом уроке рассматривается минимум квадратичной функции. Проверьте это!Что такое квадратичная функция?
Вы не можете пройти алгебру, не видя квадратичных функций. Графики квадратичных функций представляют собой параболы; они имеют тенденцию выглядеть как улыбка или хмурый взгляд. В этом уроке вы познакомитесь с квадратичными функциями, посмотрите на их графики и увидите несколько примеров квадратичных функций!
Как построить график функции квадратного корня с помощью таблицы?
Составление таблицы значений является полезным способом построения графика функции квадратного корня. Просто не забудьте выбрать значения x, для которых определена функция! Посмотрите обучающее видео, чтобы узнать больше.
Что делает константа ‘k’ в функции f(x)=[квадратный корень из](x)+k?
Когда вы изучаете преобразование квадратного корня, ОБЯЗАТЕЛЬНО изучите вертикальное преобразование! Ознакомьтесь с этим руководством и узнайте, что нужно для перевода функции квадратного корня по вертикали.

Как перевести функцию квадратного корня по горизонтали?
Когда вы изучаете преобразование функций квадратного корня, ОБЯЗАТЕЛЬНО изучите горизонтальные преобразования! Ознакомьтесь с этим руководством и узнайте, что нужно для перевода функции квадратного корня по горизонтали.
Как сделать примерный график из текстовой задачи?
Иногда проблема со словом описывает ситуацию, которую можно было бы лучше понять, если бы она была представлена в виде графика. В этом уроке приводится пример одной такой текстовой задачи. Проверьте это!
Как вы используете формулу прямого изменения?
Если две величины прямо пропорциональны, можете поспорить, что для решения вам потребуется использовать формулу прямой вариации! В этом руководстве вы увидите, как использовать формулу прямой вариации, чтобы найти константу вариации, а затем найти ответ.
Как использовать график линейного уравнения для решения текстовой задачи?
Словесные задачи — отличный способ увидеть математику в реальном мире! В этом уроке вы узнаете, как определить, сколько времени потребуется, чтобы популяция кроликов вымерла.
 Вы также увидите, как настроить таблицу и график, чтобы помочь найти ответ!
Вы также увидите, как настроить таблицу и график, чтобы помочь найти ответ!Как решить задачу Word с помощью функции?
Словесные задачи — отличный способ увидеть математику в действии! Эта проблема со словами связана с расчетом прибыли через определенное количество лет. Посмотрите, как использовать функцию от слова задача для решения!
Как построить график линейного уравнения, составив таблицу?
График функции? Было бы очень полезно, если бы у вас была таблица значений, соответствующих вашему уравнению. Вы можете нанести эти значения на координатную плоскость и соединить точку, чтобы построить график. Все это смотрите в этом уроке!
Как найти f(x), если у вас есть значение x?
Чтобы решить функцию для заданного значения, подставьте это значение в функцию и упростите. Убедитесь в этом сами, посмотрев этот урок!
Что такое домен?
Знаете ли вы, что отношение имеет домен? Домен отношения — это набор первых координат из упорядоченных пар.
 Этот учебник определяет домен отношения!
Этот учебник определяет домен отношения!Что такое диапазон отношений?
Знаете ли вы, что отношение имеет диапазон? Диапазон отношения — это набор вторых координат из упорядоченных пар. Этот учебник определяет диапазон отношения!
Что такое функция?
Вы не сможете пройти алгебру, не изучив функции. Этот урок покажет вам отличный подход к размышлению о функциях! Изучите определение функции и посмотрите, как могут быть представлены функции. Взглянем!
Что такое обозначение функций?
Каждый раз видел «f(x)» в своей математике? Это обозначение функций! Это способ указать, что уравнение является функцией. Узнайте об обозначении функций, посмотрев это руководство.
Как построить график кусочной функции?
Если вы хотите построить график кусочно-линейной функции, постройте график каждой функции на определенном интервале отдельно.
 Соберите все это вместе, и вы получите свой график! В этом руководстве показан весь процесс построения графика кусочно-линейной функции.
Соберите все это вместе, и вы получите свой график! В этом руководстве показан весь процесс построения графика кусочно-линейной функции.Как перевести функцию?
Подумайте о том, чтобы положить монетку на стол. Все, что вы делаете, это перемещаете пенни в новое место на столе. Это в основном все, что происходит, когда вы переводите функцию! Когда вы переводите функцию, вы просто перемещаете ее в новое место на координатной плоскости!
Как построить график перевода функции?
Практика — отличный способ лучше понять, как переводить функцию! Этот учебник проведет вас через этапы построения графика функции, которая была переведена вверх и вправо.
Как отразить функцию?
Когда вы смотрите в зеркало, вы видите свое отражение. Отражения в математике включают переворачивание чего-то над линией, называемой линией отражения. В этом руководстве показано, как отразить функцию в выбранной строке!
Как найти f(x), если значение x содержит другие переменные?
Когда вы оцениваете функцию, вам обычно дается число для подстановки переменной, но что, если подставляемое выражение содержит другие переменные? Посмотрите, как вставить выражение с переменными в функцию! Этот урок покажет вам!
Как изобразить отражение функции?
Если вы замените такую функцию, как f(x), на f(-x), она перевернет функцию по оси Y! Следуйте этому руководству, чтобы узнать, как взять функцию и отразить ее по оси Y.

Что такое родительская функция кубической функции?
График линейной функции представляет собой линию. График квадратичной функции представляет собой параболу. Как выглядит график кубической функции? Этот учебник знакомит вас с базовой (родительской) функцией для кубических функций!
Как решить квадратное уравнение со сложными решениями, заполнив квадрат?
Вы можете решить квадратное уравнение, составив квадрат! В этом руководстве показаны шаги, необходимые для решения квадратного уравнения с использованием этого метода.
Как преобразовать квадратичную форму из стандартной формы в вершинную, заполнив квадрат?
Вершинная форма квадратного уравнения может помочь вам быстро определить вершину этого квадратного уравнения. Следуйте этому руководству, чтобы узнать, как использовать метод завершения квадрата, чтобы изменить квадратное уравнение из стандартной формы в вершинную форму!
Как преобразовать квадрат из стандартной формы в форму вершины, дополнив квадрат, если a≠1?
Вы можете преобразовать квадратное уравнение из стандартной формы в вершинную, заполнив квадрат! Этот учебник шаг за шагом проведет вас через процесс.

Как построить квадратное уравнение в форме перехвата?
Построить квадратное уравнение в виде отрезка очень просто! Вся необходимая информация содержится в уравнении. Вам просто нужно выбрать его и использовать его. Следуйте этому руководству, чтобы узнать, как взять форму пересечения уравнения и использовать ее для нахождения точек пересечения по оси x, вершины и оси симметрии.
Как построить график полиномиальной функции, составив таблицу?
Как построить график сложной полиномиальной функции? Конечно, сделав стол! В этом руководстве вы увидите, как создается таблица и используется для построения графика полиномиальной функции более высокого порядка.
Как перевести полиномиальную функцию по вертикали?
Перевод функций может быть интересным, если вы знаете, что делать. Этот учебник поможет вам попрактиковаться в переводе функции и написании новой функции и графика!
Как найти сумму двух функций?
Добавлять функции проще, чем вы думаете! Следуйте этому руководству, чтобы узнать, как сложить две функции вместе.

Что такое функциональные операции?
Как вычислить логарифм?
Если вы хотите решить логарифм, вы можете переписать его в экспоненциальной форме и решить таким образом! Следуйте этому руководству, чтобы попрактиковаться в решении логарифма, сначала преобразовав его в экспоненциальную форму.
Как преобразовать логарифмическую форму в экспоненциальную?
Преобразование логарифма в экспоненциальной форме может упростить решение. В этом уроке вы увидите, как взять логарифм и переписать его в экспоненциальной форме!
Как преобразовать экспоненциальную форму в логарифмическую?
Хорошо иметь задачу в экспоненциальной форме, но можно ли преобразовать ее в логарифмическую? Этот урок покажет вам этот процесс шаг за шагом!
Как упростить логарифмы, используя свойство произведения?
Если вы складываете логарифмы с одинаковым основанием, вы можете использовать свойство продукта логарифмов, чтобы упростить эту работу! Следуйте инструкциям в этом руководстве, чтобы увидеть, как свойство продукта логарифмов используется для сложения логарифмов с одинаковым основанием.

Как преобразовать экспоненциальную форму в натуральную логарифмическую форму?
Преобразование экспоненциальной формы в натуральную логарифмическую проще, чем вы думаете! Следуйте этому руководству, чтобы узнать, как выполнить это преобразование.
Как преобразовать натуральный логарифм в показательную форму?
Преобразование натурального логарифма в экспоненциальную форму может упростить решение. В этом руководстве показано, как взять натуральный логарифм и преобразовать его в экспоненциальную форму!
Что делает константа ‘k’ с графиком f(x)=log(x)+k?
Перевод логарифмической функции по вертикали может быть увлекательным занятием, особенно если вы знаете, как это делается! В этом руководстве показано, что нужно для сдвига логарифмической функции вверх и вниз!
Как построить график экспоненциальной функции естественного основания?
Хотите построить график экспоненциальной функции с естественным основанием? Составьте таблицу баллов! Затем нанесите точки, соедините их, и у вас есть график! Следуйте этому руководству, чтобы увидеть весь процесс шаг за шагом.

Как решить логарифмическое уравнение возведением в степень?
Уравнения с логарифмами не должны пугать. Просто избавьтесь от логарифма, возведя в степень, и решите, как любое другое уравнение! В этом руководстве показаны все шаги.
Что такое логарифм?
Логарифмы могут быть сложными, но они станут намного проще, если вы поймете, как они связаны с показателями степени. Следуйте вместе с учебником, чтобы узнать об этих отношениях.
Что такое натуральный логарифм?
Натуральный логарифм — это логарифм, имеющий особое основание. В этом уроке вы познакомитесь с натуральными логарифмами!
Что такое е?
В математике «е» — это не просто буква, это иррациональное число! В этом руководстве показано, как математики используют букву «е» для обозначения определенного значения, и как наличие основания «е» называется естественным основанием.

Что такое экспоненциальная функция естественного основания?
Экспоненциальная функция с естественным основанием на самом деле является функцией, которая короче своего имени! Этот учебник знакомит вас с этой специальной функцией и показывает, как она выглядит.
Что такое угол в стандартном положении?
Понимание того, как образуются углы в координатной плоскости, — большой шаг к пониманию тригонометрии. В этом уроке показано, как можно построить угол в координатной плоскости!
Как выглядит график функции синуса?
Как выглядит график функции косинуса?
Вы можете использовать единичный круг, чтобы построить график функции косинуса! В этом уроке вы узнаете, как сделать именно это!
Как выглядит график касательной функции?
Если вы хотите построить график функции тангенса, вы можете использовать единичный круг для построения точек.
 В этом уроке показано, как использовать единичный круг для построения графика касательной!
В этом уроке показано, как использовать единичный круг для построения графика касательной!Что такое периодическая функция?
Периодические функции имеют некоторые особенности! В этом уроке вы познакомитесь с этими функциями и узнаете, что должен иметь график, чтобы называться периодической функцией.
Как горизонтально перевести тригонометрический график?
Перевод графика синуса или косинуса по горизонтали может быть забавным, но вам нужно понять, как это работает. Следуйте этому руководству, чтобы узнать, как сместить графики синуса и косинуса по горизонтали!
Как использовать формулу сложных процентов?
Если у вас уже есть банковский счет или вы планируете открыть его в будущем, вам обязательно нужно ознакомиться с этим руководством! Следите за тем, как в этом уроке рассматривается проблема слов, связанная со сложными процентами.

Что такое формула сложных процентов?
Такие вещи, как банковские счета, кредиты, инвестиции и ипотечные кредиты, являются частью жизни, и почти всегда речь идет о процентах. Иногда вам нужно иметь дело со сложными процентами, поэтому было бы неплохо знать его формулу! В этом уроке вы увидите формулу сложных процентов. Взглянем!
Как найти скорость изменения между двумя точками на графике?
Скорость изменения — это скорость, которая описывает, как одна величина изменяется по отношению к другой величине. В этом руководстве потренируйтесь находить скорость изменения с помощью графика. Проверьте это!
Как найти скорость изменения между двумя точками в таблице?
Скорость изменения — это скорость, которая описывает, как одна величина изменяется по отношению к другой величине. В этом учебном пособии показано, как использовать информацию, приведенную в таблице, для определения скорости изменения значений в таблице.
 Взглянем!
Взглянем!Как написать уравнение прямой в форме пересечения наклона, если у вас есть график?
Работаете с графиком линии? Пытаетесь найти уравнение для этого графика? Просто выберите две точки на линии и используйте их, чтобы найти уравнение. В этом учебном пособии показано, как взять две точки на графике линии и использовать их, чтобы найти форму пересечения наклона линии!
Как написать уравнение прямой в форме пересечения наклона, если у вас есть таблица?
Глядя на таблицу значений, которая представляет собой линейное уравнение? Хотите найти это уравнение? Тогда посмотрите этот урок! Вы увидите, как использовать значения из таблицы, чтобы найти форму пересечения наклона линии, описанной в таблице.
Как использовать форму точка-наклон для записи уравнения из таблицы?
Глядя на таблицу значений, которая представляет собой линейное уравнение? Хотите найти это уравнение? Тогда посмотрите этот урок! Вы увидите, как использовать значения из таблицы и форму точки-наклона линии, чтобы найти форму наклона-пересечения линии, описанной в таблице.

Что такое скорость изменения?
Пытаетесь описать, как что-то меняется по отношению к чему-то другому? Используйте скорость изменения! В этом уроке вы узнаете о скорости изменения и увидите разницу между положительной и отрицательной скоростью изменения!
- Перейдите к рабочему процессу Step Functions, который вы хотите преобразовать, и выберите Действия , Копировать в новый.
- Выберите Визуальное оформление рабочего процесса .
- Выберите Express , затем выберите Next .
- Следующие два шага позволят вам внести изменения в схему вашего рабочего процесса. Выберите Next дважды.
- Назовите рабочий процесс, назначьте разрешения, конфигурации ведения журналов и трассировки, затем выберите Создать конечный автомат .

15 Примеры миметической архитектуры под влиянием функций здания — RTF
Помните детский мультсериал «Освальд», который мы смотрели в детстве? История синего осьминога и его друзей? Какими завораживающими были здания в его «Большом городе»! Будь то палатка, ракета или мяч, эти странные строения всегда привлекали наше внимание в детстве. Все это были прекрасные примеры миметической архитектуры. Миметическая или новаторская архитектура — это стиль, в котором форма здания или возвышение повторяют или символизируют цель или функцию здания. Во многих случаях это могут быть объекты, продукты, связанные с компанией, существа и т. д. Это началось как придорожная архитектура в 19 веке.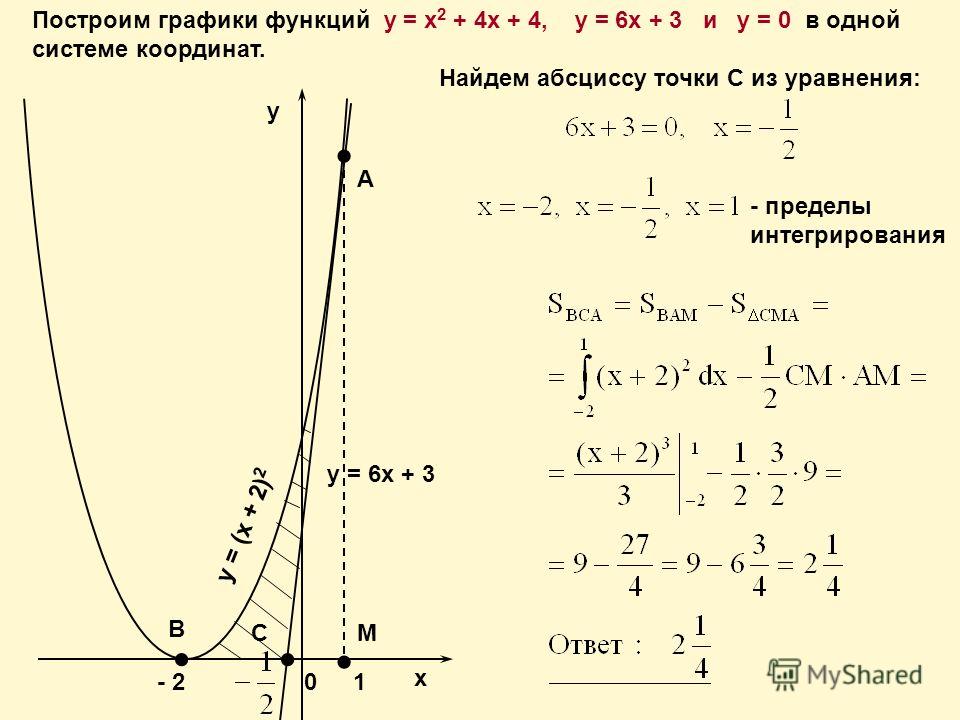 30-х годов, и сейчас мы можем увидеть множество своеобразных, но привлекательных сооружений, которые стали национальными достопримечательностями.
30-х годов, и сейчас мы можем увидеть множество своеобразных, но привлекательных сооружений, которые стали национальными достопримечательностями.
Ниже приведены некоторые примеры новаторской архитектуры, на которые повлияли их функции.
1. Dubai Frame, Zabeel Park, ДубайДизайн – Фернандо Донис
Построенное в 2018 году, это сооружение является одним из многих архитектурных чудес Дубая. Построенная как удивительная мозаика из стекла, стали, алюминия и железобетона, Рамка Дубая представляет собой пустоту размером 150 на 105 метров, предназначенную для обрамления прошлого, настоящего и будущего города. Он расположен в таком месте, где с одной стороны кадра посетители могут увидеть характерные достопримечательности Дубая, а с другой — старые части города. В нем есть кафе, стеклянные дорожки, смотровые галереи и несколько лифтов, из которых открывается панорамный вид на фантастический горизонт города.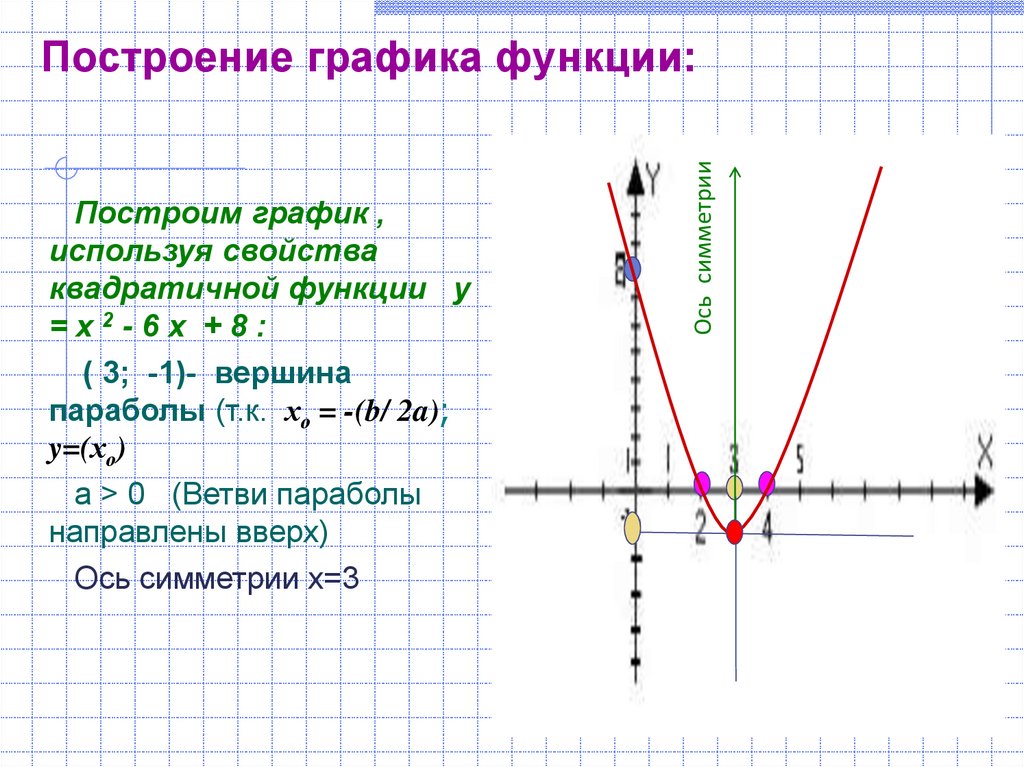
Дизайн — Фрэнк Гери
Как следует из названия, это Здание было построено в 1996 году как дань уважения знаменитым танцорам Фреду Астеру и Джинджер Роджерс. Каменная башня представляет Фреда, а стеклянная башня волнистой формы представляет его партнершу Джинджер. Это здание в стиле деконструктивизма выделяется изогнутыми колоннами, волнообразными молдингами и эстетическими характерами. Сейчас это отель с 21 роскошным номером, кафе и рестораном на верхнем этаже, названным в честь этих танцоров.
Отель Dancing House – Изогнутые колонны ©WikiArquitectura Отель Dancing House – Вдохновение ©archidialog.com Отель Dancing House – Вид на здание ©prague.com 3. Piano House, Shannan, ChinaДизайн – Hefei University of Technology
На этом здании, выполненном в масштабе 50:1, изображено пианино и прислоненная к нему скрипка. Фортепиано поддерживается тремя огромными бетонными колоннами и вмещает два больших концертных зала. Он построен из черных стеклянных панелей, переплетенных с чередующимися прозрачными и белыми стеклянными полосами, которые символизируют клавиши фортепиано. Скрипка — это вход в концертные залы, построенный из прозрачных стеклянных панелей. В нем размещаются эскалаторы и лестницы. Терраса на крыше защищена навесом в форме открытой крышки пианино.
Фортепиано поддерживается тремя огромными бетонными колоннами и вмещает два больших концертных зала. Он построен из черных стеклянных панелей, переплетенных с чередующимися прозрачными и белыми стеклянными полосами, которые символизируют клавиши фортепиано. Скрипка — это вход в концертные залы, построенный из прозрачных стеклянных панелей. В нем размещаются эскалаторы и лестницы. Терраса на крыше защищена навесом в форме открытой крышки пианино.
Дизайн – Moshe Safdie
Расположен на На набережной Марина-Бэй находится самое дорогое казино в мире, комплексный отель примерно на 2500 номеров, конференц-центр, художественный и выставочный центр, музей, большой театр, несколько ресторанов, принадлежащих знаменитым шеф-поварам, два грандиозных хрустальных павильона и The Shoppes, огромный торговый центр в Marina Bay Sands. Все это объединено в три башни, напоминающие три колоды карт. На вершине этих башен находится небесный парк, парк площадью 3 акра с бассейнами, беговыми дорожками и садами в форме огромной вытянутой лодки.
Все это объединено в три башни, напоминающие три колоды карт. На вершине этих башен находится небесный парк, парк площадью 3 акра с бассейнами, беговыми дорожками и садами в форме огромной вытянутой лодки.
Дизайн – Фариборз Сахба
Храм Лотоса — это зал поклонения, следующий вере бахаи, которая верит в создание пространства для людей всех религий, где они могут собираться и поклоняться. Его форма происходит от лотоса, потому что это священный цветок, который символизирует чистоту и божественность как в индуизме, так и в буддизме. Есть три слоя 9лепестков каждый, внутренний и центральный слой изогнуты внутрь, образуя центральный купол, тогда как самый внешний слой изогнут снаружи, образуя навесы над девятью входами в зал. Он облицован белым мрамором, а под конструкцией устроены бассейны, создающие впечатление лотоса, парящего над водой.
Разработано Dimensional Innovations
Публичная библиотека Канзас-Сити, построенная в 2004 году, представляет собой интересный образец архитектуры. Его гараж хорошо известен своим инновационным фасадом, который выглядит как гигантская книжная полка. Фасад демонстрирует корешки 22 книг размером 25 на 9 футов, выбранных жителями Канзас-Сити, что иллюстрирует разнообразие тем для чтения, доступных в библиотеке.
Публичная библиотека Канзас-Сити – Фрагмент книг ©CollabCubed 7. Большая корзина, Ньюарк, Огайо Это здание было построено как штаб-квартира компании Longaberger, американского производителя корзин из кленового дерева ручной работы. Форма — копия самого продаваемого продукта компании — корзины Medium Market. Это семиэтажное здание, построенное в 1997 году, имеет центральный атриум и стеклянный потолок для естественного освещения. Две ручки наверху сделаны из стали и имеют внутри нагревательные элементы, предотвращающие замерзание льда и тем самым защищающие стеклянный потолок.
Две ручки наверху сделаны из стали и имеют внутри нагревательные элементы, предотвращающие замерзание льда и тем самым защищающие стеклянный потолок.
Дизайн – UAD и Charlie Smith Design
Выставка произведений искусства и мастерство изготовления сумок, это пятиэтажное здание по форме напоминает массивную сумку. Он также известен как «Здание BagStage Building». В структуру входят музейное кафе и сувенирный магазин, флагманский магазин Simone, еще один мультибрендовый магазин, в котором представлены все современные бренды со всего мира, современная галерея, демонстрирующая историю сумок 20-го и 21-го веков, историческая галерея, в которой выставлены архивы с 16 по 20 век. 19го века и многочисленные мастерские.
Музей сумок Simone – Интерьер кафе ©Pinterest Музей сумок Simone – Интерьер галереи ©AfarSimone Музей сумок – вид ©Pinterest 9. Fish Building, Хайдарабад, Индия
Fish Building, Хайдарабад, Индия Эта структура, широко известная как Fish Building, была спроектирована как региональный офис Национального совета по развитию рыболовства. Он был построен в 2012 году по мотивам монументальной скульптуры Фрэнка Гери «Рыба» в Барселоне. Здание облицовано панелями из нержавеющей стали и окнами с сине-фиолетовыми тонированными стеклами. Плавник действует как навес над входной лестницей.
Fish Building – Inspiration – Fish Sculpture by Gehry ©PinterestFish Building – View ©unsusalspaces.com 10. Обувной дом Haines, ПенсильванияДизайн – Фред Дж. Ремпп
Этот дом принадлежал успешному продавцу обуви Махлону Хейнсу. (он же Shoe Wizard) и идентичен одному из его рабочих ботинок. Он был построен в 1948 году на деревянном каркасе с лепниной и витражами. Гостиная расположена ближе к носку, тогда как пятка содержит кухню, а в щиколотке две спальни.
Обувной дом Haines – Интерьер кухни ©Atlas Obscura Обувной дом Haines – Интерьер гостиной ©LancasterOnline Обувной дом Haines – вид ©Designing Buildings WikiHaines Shoe House – Фрагмент окна ©Atlas Obscura 11. Torre Telefonica, Сантьяго, Чили
Torre Telefonica, Сантьяго, Чили Designed by – Mario Paredes & Arquitectos Asociados
Этот 34-этажный небоскреб, построенный в 1996 году, был построен для Movistar Telecom. Он напоминает сотовые телефоны коробчатого типа, которые были доступны в 99-м.0 с. Это коммерческая структура, а также вертолетная площадка на 35-м этаже. Все здание облицовано стеклянными и алюминиевыми панелями с железобетонным каркасом.
Torre Telefonica – Вдохновение – Ретро мобильные телефоны 90-х годов ©Parade.comTorre Telefonica – Tower ©Pinterest 12. Дом LEGO, Биллунд, ДанияДизайн – Bjarke Ingels Groups
Дом LEGO был построен как выставка и мастерство центр разработки различных форм и сцен, созданных из крошечных блоков LEGO. Здание, построенное в 2017 году, напоминает 21 гигантский блок LEGO, поставленных друг на друга, с фасадом, покрытым белой глазурованной керамической плиткой, каждый из которых выглядит как классические кирпичи LEGO 2×4. Каждый блок имеет цветовую кодировку, чтобы создать различные уголки развития навыков для детей. Наверху находится галерея шедевров с восемью круглыми световыми люками, похожими на блоки.
Наверху находится галерея шедевров с восемью круглыми световыми люками, похожими на блоки.
Дизайн – С.Н. Murthy
Это здание было спроектировано как дань уважения скрипичному маэстро индийской карнатической музыки Тирумакудалу Чоудиа. Это зрительный зал и культурный центр, построенный в форме семиструнной скрипки. В этом здании исследуются компоненты, выходящие за рамки внешней формы скрипки, а также сложные детали струн, клавиш, моста и смычка.
Мемориальный зал Чоудия — вид с воздуха © New Indian Express Мемориальный зал Чоудия — фрагмент ключей © Google Images Мемориальный зал Чоудия — интерьер зрительного зала © Twitter 14. Музей чайной культуры, Мейтан, Китай Музей чая Мейтан — это уникальное сооружение, копирующее гигантский глиняный чайник. Сопровождает его еще одно здание, примыкающее к нему в форме чаши. Мейтан хорошо известен своим чаем, поэтому здание в этом городе имеет такую причудливую форму. Издалека он выглядит как скульптура в центре города, но по мере приближения окна выдают его истинное предназначение.
Мейтан хорошо известен своим чаем, поэтому здание в этом городе имеет такую причудливую форму. Издалека он выглядит как скульптура в центре города, но по мере приближения окна выдают его истинное предназначение.
Дизайн – Карл Шванцер и Ателье Брюкнер
Башни штаб-квартиры BMW были построены в 1993 году. форма четырех цилиндров в двигателе автомобиля. Автомобильный музей BMW рядом с ним представляет собой головку блока цилиндров, которая была добавлена к кампусу в 2008 году. Музей имеет однородный фасад, облицованный алюминиевыми панелями, а башни имеют сочетание алюминия и стеклянных панелей.
Штаб-квартира BMW – вид с воздуха ©Pinterest Штаб-квартира BMW – музей ©Wheelchair TravelСоздание экономичных рабочих процессов AWS Step Functions
Строители создают рабочие процессы AWS Step Functions для организации нескольких сервисов в критически важных для бизнеса приложениях с минимальным кодом. Клиенты ищут передовой опыт и рекомендации по созданию экономичных рабочих процессов с помощью Step Functions.
Клиенты ищут передовой опыт и рекомендации по созданию экономичных рабочих процессов с помощью Step Functions.
В этом сообщении блога объясняется разница между рабочими процессами Standard и Express. Он показывает стоимость выполнения той же рабочей нагрузки, что и экспресс- или стандартные рабочие процессы. Затем в нем рассказывается, как перейти от Standard к Express, как объединить типы рабочих процессов для оптимизации затрат и как разделить один рабочий процесс на модули и вложить его в другой.
Пошаговые функции Express Workflows
Express Workflows управляют сервисами AWS с более высокой пропускной способностью — до 100 000 переходов между состояниями в секунду. Он также обеспечивает более низкую стоимость в размере 1 доллара США за миллион вызовов по сравнению с 25 долларами США за миллион для стандартных рабочих процессов.
Экспресс-рабочие процессы могут выполняться не более 5 минут и не поддерживают шаблон интеграции . waitForTaskToken или .sync . Большинство рабочих процессов Step Functions, которые не используют эти шаблоны интеграции и завершаются в пределах 5-минутной продолжительности, получают оптимизацию затрат и пропускной способности за счет преобразования типа рабочего процесса из Standard в Express.
waitForTaskToken или .sync . Большинство рабочих процессов Step Functions, которые не используют эти шаблоны интеграции и завершаются в пределах 5-минутной продолжительности, получают оптимизацию затрат и пропускной способности за счет преобразования типа рабочего процесса из Standard в Express.
Рассмотрим следующий пример, наивную реализацию рабочего процесса электронной торговли:
При запуске отправляет сообщение в очередь Amazon SQS. Функция AWS Lambda обрабатывает и утверждает это асинхронно (не показано). После обработки функция Lambda сохраняет состояние в таблице Amazon DynamoDB. Рабочий процесс опрашивает таблицу, чтобы проверить, завершено ли действие. Затем он переходит к обработке платежа, где шаблон повторяется. Наконец, рабочий процесс последовательно запускает серию задач обновления перед завершением.
Я запускаю этот рабочий процесс 1000 раз как стандартный рабочий процесс. Затем я конвертирую это в экспресс-рабочий процесс и запускаю еще 1000 раз. Я создаю панель мониторинга Amazon CloudWatch для отображения среднего времени выполнения. Рабочий процесс Express работает в среднем на 0,5 секунды быстрее, чем стандартный рабочий процесс, а также показывает снижение затрат:
Я создаю панель мониторинга Amazon CloudWatch для отображения среднего времени выполнения. Рабочий процесс Express работает в среднем на 0,5 секунды быстрее, чем стандартный рабочий процесс, а также показывает снижение затрат:
Время выполнения рабочего процесса
Запуск стандартного рабочего процесса 1000 раз стоит приблизительно 0,42 доллара США. Сюда не входят 4000 переходов между состояниями, включенных в ежемесячный уровень бесплатного пользования AWS, и используемые дополнительные сервисы. В отличие от этого, запуск Express Workflow 1000 раз стоит 0,01 доллара США. Как это рассчитывается?
Стандартная формула расчета стоимости рабочего процесса :
Плата за стандартные рабочие процессы взимается в зависимости от количества переходов состояний, необходимых для выполнения рабочей нагрузки. Функции шага подсчитывают переход состояния каждый раз, когда выполняется шаг вашего рабочего процесса. Плата взимается за общее количество переходов между состояниями всех ваших конечных автоматов, включая повторные попытки. Стоимость составляет 0,025 доллара США за 1000 переходов между состояниями.
Стоимость составляет 0,025 доллара США за 1000 переходов между состояниями.
Удачный путь в рабочем процессе состоит из 17 переходов (включая начало и конец).
Общая стоимость = (количество переходов на выполнение x количество выполнений) x 0,000025 USD
Общая стоимость = (17 X 1000) X 0,000025 = 0,42 USD *
*За исключением 4000 переходов между состояниями, включенных в уровень бесплатного пользования AWS каждый месяц.
Формула расчета стоимости Express Workflow :
Плата за рабочие процессы Express Workflow взимается в зависимости от количества запросов и их продолжительности. Продолжительность рассчитывается с момента начала выполнения вашего рабочего процесса до его завершения или иного завершения, округленного до ближайших 100 мс, и объема памяти, используемого при выполнении вашего рабочего процесса, оплачиваемого блоками по 64 МБ.
Общая стоимость = (Стоимость выполнения + Стоимость продолжительности) x Количество запросов
Стоимость продолжительности = (Средняя заявленная продолжительность мс / 100) * цена за 100 мс
Стоимость выполнения t = 0,000001 USD за запрос
Общая стоимость = (0,00000 долл. США + 0,0000117746) x 1000 = 0,01 долл. США
Стоимость продолжительности = (11300 мс /100) * $ 0,0000001042 = 0,0000117746
9 rekeption $ 4.0013 $ $ $ $ $ .0014
Эта стоимость меняется в зависимости от количества используемых ГБ-часов и объема памяти. Использование памяти для этого конечного автомата составляет менее 64 МБ.
Подробную информацию см. на странице цен на Step Functions.
Преобразование стандартного рабочего процесса в ускоренный рабочий процесс
Учитывая экономическую выгоду, показанную в предыдущем разделе, преобразование существующих стандартных рабочих процессов в экспресс-рабочие процессы часто является хорошей идеей. Однако, прежде чем делать это, следует сделать некоторые выводы. Рабочий процесс должен завершиться менее чем за 5 минут и не использовать .WaitForTaskToken или .sync шаблоны интеграции. Экспресс-рабочие процессы отправляют историю журналов в журналы CloudWatch за дополнительную плату.
Однако, прежде чем делать это, следует сделать некоторые выводы. Рабочий процесс должен завершиться менее чем за 5 минут и не использовать .WaitForTaskToken или .sync шаблоны интеграции. Экспресс-рабочие процессы отправляют историю журналов в журналы CloudWatch за дополнительную плату.
Дополнительным соображением является идемпотентность, а также требования выполнения ровно один раз против хотя бы одного выполнения. Если для рабочей нагрузки требуется модель гарантированного однократного выполнения, предпочтительным является стандартный рабочий процесс. Здесь задачи и состояния никогда не запускаются более одного раза, если вы не указали поведение повторных попыток на языке состояний Amazon (ASL). Благодаря этому они подходят для организации неидемпотентных действий, таких как запуск кластера Amazon EMR или обработка платежей. Экспресс-процессы используют хотя бы один раз модель , где существует вероятность того, что выполнение может быть запущено более одного раза. Это делает их идеальными для организации идемпотентных действий. Идемпотентность относится к операции, которая дает один и тот же результат (для данного входа) независимо от того, сколько раз она применяется.
Это делает их идеальными для организации идемпотентных действий. Идемпотентность относится к операции, которая дает один и тот же результат (для данного входа) независимо от того, сколько раз она применяется.
Чтобы преобразовать стандартный рабочий процесс в экспресс-рабочий процесс непосредственно из консоли Step Functions:
При преобразовании стандартного рабочего процесса, определенного на языке шаблонов, таком как AWS CDK или AWS SAM, необходимо изменить как значение Type , так и имя Resource . В следующем примере показано, как это сделать в AWS SAM:
. StateMachine в DDBStandard:
Тип: AWS::Serverless::StateMachine
Характеристики:
Тип: СТАНДАРТ
становится:
StateMachine в DDBExpress:
Тип: AWS::Serverless::StateMachine
Характеристики:
Тип: ЭКСПРЕСС
Это не перезаписывает существующий рабочий процесс, а создает новый рабочий процесс с новым именем и типом.
Вместе лучше
Для некоторых рабочих нагрузок может потребоваться сочетание длительных рабочих процессов и рабочих процессов с высокой частотой событий. Используя рабочие процессы Step Functions, вы можете создавать более крупные и сложные рабочие процессы из более мелких и простых рабочих процессов.
Например, на начальном этапе предыдущего рабочего процесса может потребоваться пауза для взаимодействия с человеком, которая занимает более 5 минут, после чего следует выполнение ряда идемпотентных действий. Эти типы рабочих нагрузок идеально подходят для одновременного использования как стандартных, так и экспресс-типов рабочих процессов. Этого можно достичь, вложив «дочерний» экспресс-процесс в «родительский» стандартный рабочий процесс. Предыдущий пример рабочего процесса был реорганизован как вложенный рабочий процесс родитель-потомок.
Разверните это вложенное решение рабочего процесса из коллекции бессерверных рабочих процессов.
Вложение рабочих процессов
Родительский стандартный рабочий процесс
Детский экспресс-процесс
Вложенные показатели рабочего процесса
Этот новый смешанный рабочий процесс имеет ряд преимуществ. Сначала шаблон опроса заменяется на .WaitForTaskToken . Это приостанавливает рабочий процесс до тех пор, пока не будет получен ответ, указывающий на успех или неудачу. В этом случае ответ отправляется лямбда-функцией (не показана). Эта пауза может длиться до 1 года, и время ожидания не оплачивается.
Это приостанавливает рабочий процесс до тех пор, пока не будет получен ответ, указывающий на успех или неудачу. В этом случае ответ отправляется лямбда-функцией (не показана). Эта пауза может длиться до 1 года, и время ожидания не оплачивается.
Это не только упрощает рабочий процесс, но и уменьшает количество переходов между состояниями. Затем идемпотентные шаги перемещаются в экспресс-процесс, что снижает количество переходов между состояниями из стандартного рабочего процесса и дает преимущества за счет высокой пропускной способности, обеспечиваемой экспресс-процессами. Дочерний рабочий процесс вызывается с помощью вызова API StartExecution StepFunctions из родительского рабочего процесса.
Эта новая комбинация рабочих процессов выполняется 1000 раз, общая стоимость составляет 20 центов. Дополнительная плата за запуск вложенного рабочего процесса не взимается: он рассматривается как еще один переход состояния. Сам вложенный рабочий процесс оплачивается так же, как и все рабочие процессы Step Functions.
Вот как рассчитывается стоимость:
Родительский стандартный рабочий процесс:
Общая стоимость = (количество переходов на выполнение x количество выполнений) x 0,000025 USD
Общая стоимость = (8*1000) *0,000025 = 0,20 USD
Детский экспресс-процесс :
Общая стоимость = (Стоимость выполнения + Стоимость продолжительности) x Нет запросов
Стоимость продолжительности = (Средняя выставленная продолжительность мс / 100) * цена за 100 мс
Стоимость выполнения = 0,000001 USD за запрос
Общая стоимость = (0,00000 долл. США + 0,0000013546) x 1000 = $ 0,0002 Общая стоимость вложенного рабочего процесса = (стоимость родительского стандартного рабочего процесса) + (стоимость дочернего рабочего процесса Express) В этом сообщении блога объясняется разница между рабочими процессами Standard и Express. Он описывает ровно один раз, и , по крайней мере, одну модель исполнения , и как это связано с идемпотентностью. В нем сравнивается стоимость выполнения той же рабочей нагрузки, что и в экспресс- и стандартном рабочих процессах, показано, как перейти от одного к другому, и какие соображения необходимо принять перед этим. Наконец, объясняется, как комбинировать типы рабочих процессов для оптимизации затрат. Вложение конечных автоматов между типами позволяет командам работать над отдельными рабочими процессами, превращая их в модульные строительные блоки многократного использования. Посетите коллекцию бессерверных рабочих процессов, чтобы просмотреть множество развертываемых рабочих процессов, помогающих создавать бессерверные приложения. Вы можете запускать код JavaScript с помощью Node.js в AWS Lambda. Lambda предоставляет среды выполнения для Node.js, которые запускают ваш код для обработки событий. Ваш код работает
в среде, включающей AWS SDK для JavaScript, с учетными данными из роли AWS Identity and Access Management (IAM), которой вы управляете. Lambda поддерживает следующие среды выполнения Node.js. Node.js 16 2. Амазон Линукс 2 x86_64, рука64 Node.js 14 2.1055.0 Амазон Линукс 2 x86_64, рука64 Node.js 12 2.1055.0 Амазон Линукс 2 x86_64, рука64 14 ноября 2022 г. Лямбда-функции используют роль выполнения для получения разрешения на
записывать журналы в Amazon CloudWatch Logs и получать доступ к другим сервисам и ресурсам. Для создания роли исполнения Откройте страницу ролей в консоли IAM. Выберите Создать роль . Создайте роль со следующими свойствами. Доверенное лицо – Лямбда . Разрешения – AWSLambdaBasicExecutionRole . Имя роли – Политика AWSLambdaBasicExecutionRole имеет разрешения, необходимые функции для
записывать журналы в журналы CloudWatch. Вы можете добавить разрешения к роли позже или заменить ее на другую роль, относящуюся к одному
функция. Для создания функции Node.js Откройте консоль Lambda. Выберите Создать функцию . Настройте следующие параметры: Имя – Среда выполнения – Node.js 16.x . Роль – Выберите существующую роль . Существующая роль – Выберите Создать функцию . Чтобы настроить тестовое событие, выберите Test . Для Имя события введите Выберите Сохранить изменения . Чтобы вызвать функцию, выберите Test . Консоль создает функцию Lambda с одним исходным файлом с именем Примечание Консоль Lambda использует AWS Cloud9 для предоставления интегрированной среды разработки в браузере. Вы также можете
используйте AWS Cloud9 для разработки функций Lambda в собственной среде. Дополнительные сведения см. в разделе «Работа с лямбда-функциями» в руководстве пользователя AWS Cloud9. Файл При сохранении кода функции консоль Lambda создает пакет развертывания в виде архива в формате .zip.
Когда вы разрабатываете свой код функции вне консоли (используя IDE), вам необходимо создать
пакет развертывания, чтобы загрузить свой код в функцию Lambda. Примечание Чтобы начать разработку приложений в локальной среде, разверните один из примеров
приложения, доступные в репозитории этого руководства на GitHub. Примеры приложений Lambda в Node.js пустых узлов — функция Node.js
который показывает использование ведения журнала, переменных среды, трассировки AWS X-Ray, слоев, модульных тестов и AWS.
SDK. nodejs-apig — функция с
общедоступная конечная точка API, которая обрабатывает событие от шлюза API и возвращает ответ HTTP. rds-mysql — Функция, которая передает
запросы к базе данных MySQL для RDS. Этот пример включает частный VPC и экземпляр базы данных, настроенный с
пароль в AWS Secrets Manager. efs-nodejs — функция, использующая Amazon EFS.
файловая система в Amazon VPC. Этот пример включает в себя VPC, файловую систему, цели подключения и точку доступа. list-manager – Функция обрабатывает
события из потока данных Amazon Kinesis и обновлять сводные списки в Amazon DynamoDB. Функция сохраняет запись каждого
событие в базе данных MySQL для RDS в частном VPC. Этот образец включает частный VPC с конечной точкой VPC для
DynamoDB и экземпляр базы данных. — A Node.js
функция генерирует ошибки для указанного процента запросов. Подписка CloudWatch Logs вызывает вторую функцию.
при записи ошибки. Функция процессора использует AWS SDK для сбора сведений о запросе и сохранения
их в корзине Amazon S3. Среда выполнения функции передает объект контекста обработчику в дополнение к событию вызова. Объект контекста содержит дополнительную информацию о вызове,
функцию и среду выполнения. Дополнительную информацию можно получить из переменных среды. Ваша функция Lambda поставляется с группой журналов CloudWatch Logs. Node.js имеет уникальную модель цикла обработки событий, из-за которой его поведение при инициализации отличается от других сред выполнения.
В частности, Node.js использует неблокирующую модель ввода-вывода, которая поддерживает асинхронные операции.
Эта модель позволяет Node.js эффективно работать с большинством рабочих нагрузок.
Например, если функция Node.js выполняет сетевой вызов, этот запрос может быть обозначен как асинхронная операция и помещен в очередь обратного вызова.
Функция может продолжать обрабатывать другие операции в основном стеке вызовов, не блокируясь ожиданием возврата сетевого вызова.
Как только сетевой вызов возвращается, его обратный вызов выполняется, а затем удаляется из очереди обратного вызова. Некоторые задачи инициализации могут выполняться асинхронно. Эти асинхронные задачи не гарантируют завершения выполнения до вызова.
Например, код, который выполняет сетевой вызов для получения параметра из хранилища параметров AWS, может быть не завершен к тому времени, когда Lambda выполнит функцию обработчика.
В результате переменная может быть нулевой во время вызова.
Чтобы избежать этого, убедитесь, что переменные и другой асинхронный код полностью инициализированы, прежде чем продолжить работу с остальной основной бизнес-логикой функции. Начиная с Node 14, вы можете гарантировать завершение кода асинхронной инициализации до вызова обработчика, назначив свой код модулем ES и используя ожидание верхнего уровня. Пакеты по умолчанию обозначаются как модули CommonJS, а это означает, что вы должны сначала обозначить свой код функции как модуль ES, чтобы использовать ожидание верхнего уровня. В первом сценарии код функции обрабатывает все файлы .js как модули ES, а во втором сценарии только файл, указанный с помощью .mjs, является модулем ES. Вы можете смешивать модули ES и модули CommonJS, назвав их .mjs и .cjs соответственно, поскольку файлы .mjs всегда являются модулями ES, а файлы .cjs всегда являются модулями CommonJS. Дополнительные сведения и пример см. в разделе Использование модулей Node.js ES и Await верхнего уровня в AWS Lambda. Темы
Стоимость продолжительности = (1300 мс /100) * $ 0,0000001042 = 0,0000013546
CERESE $ 0,000001000
9 COST $ 0,0000016166669 COST $ 0,00000166
COST $ 0,00000166
COST = 0,0000013546
.
Общая стоимость вложенного рабочего процесса = 0,20 цента / 1000 выполнений. Заключение

Создание функций Lambda с помощью Node.js
Имя Идентификатор SDK Операционная система Архитектуры Устаревание nodejs16.x  1083.0
1083.0 nodejs14.x nodejs12.x  Если у вас еще нет роли исполнения для
разработка функции, создайте ее.
Если у вас еще нет роли исполнения для
разработка функции, создайте ее. лямбда-роль .
моя функция . лямбда-роль . test . index.js . Вы можете редактировать
этот файл и добавьте дополнительные файлы во встроенный редактор кода. Чтобы сохранить изменения, выберите Сохранить .
Затем, чтобы запустить код, выберите Тест .
Чтобы сохранить изменения, выберите Сохранить .
Затем, чтобы запустить код, выберите Тест . index.js экспортирует функцию с именем обработчик , которая принимает объект события и
объект контекста. Это функция-обработчик, которую Lambda вызывает, когда
вызывается функция. Среда выполнения функции Node.js получает события вызова от Lambda и передает их в
обработчик. В конфигурации функции значение обработчика равно 9.2380 index.handler .
 настроен для использования с Lambda.
настроен для использования с Lambda. Среда выполнения функции отправляет сведения о каждом вызове в
Журналы CloudWatch. Он передает любые журналы, которые ваша функция выводит во время вызова. Если
ваша функция возвращает ошибку, Lambda форматирует ошибку и возвращает ее в
призыватель.
Среда выполнения функции отправляет сведения о каждом вызове в
Журналы CloudWatch. Он передает любые журналы, которые ваша функция выводит во время вызова. Если
ваша функция возвращает ошибку, Lambda форматирует ошибку и возвращает ее в
призыватель.
Назначение обработчика функции в качестве модуля ES
 Сделать это можно двумя способами: указать
Сделать это можно двумя способами: указать типа как модуль в функции package.json или с расширением имени файла .mjs.

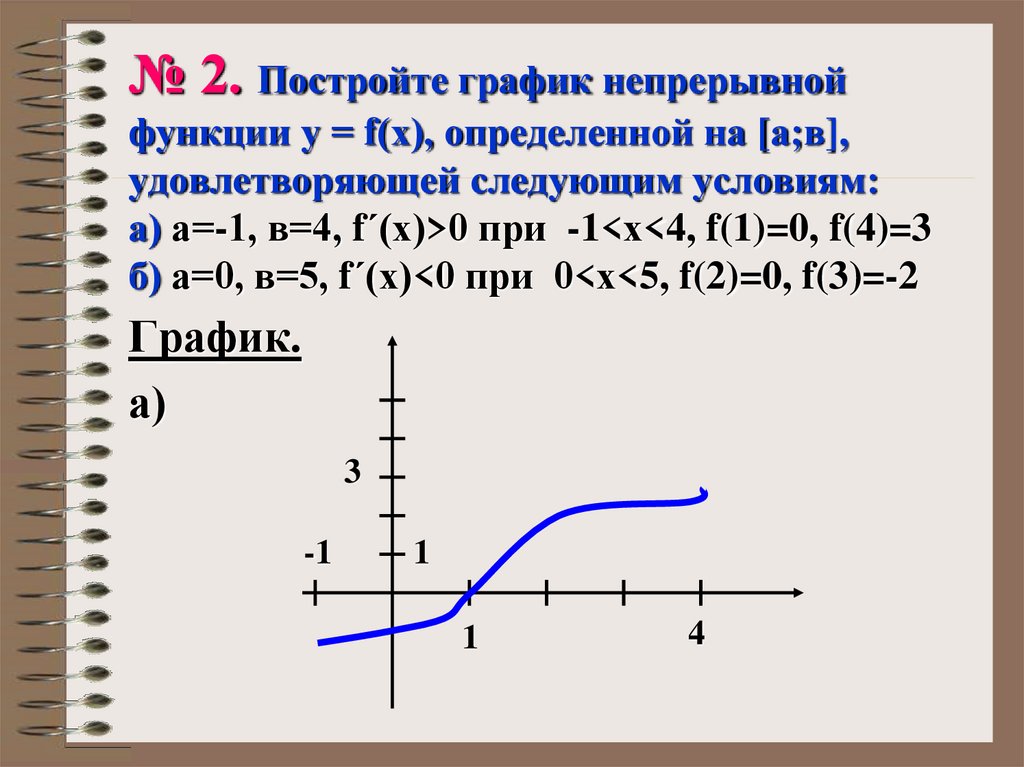
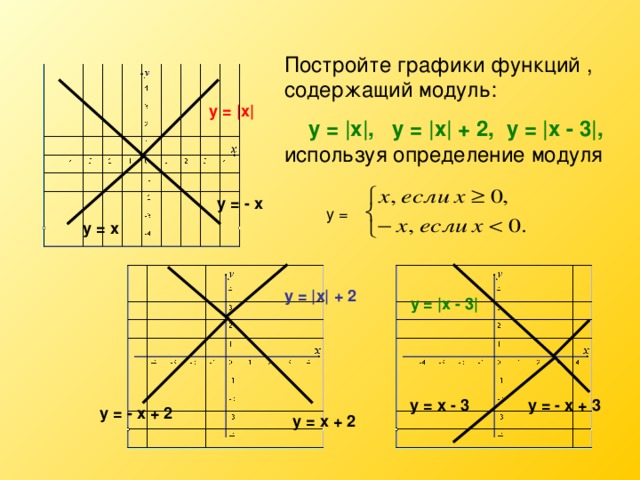 0001 # увеличить аргумент на 0.0001
try:
res1=eval(mass) # посчитать функцию и получить результат
except:
res1=10000 # если функцию нельзя посчитать, то результат число вне координат(знаю, костыль)
dot=Dot(250+i*10,250-res1*10) # dot - точка с координатой(0+x,0+y), так как это дисплей, то вектор "y" направлен вниз
all_sprites.add(dot) # добавить точку в группу спрайтов
0001 # увеличить аргумент на 0.0001
try:
res1=eval(mass) # посчитать функцию и получить результат
except:
res1=10000 # если функцию нельзя посчитать, то результат число вне координат(знаю, костыль)
dot=Dot(250+i*10,250-res1*10) # dot - точка с координатой(0+x,0+y), так как это дисплей, то вектор "y" направлен вниз
all_sprites.add(dot) # добавить точку в группу спрайтов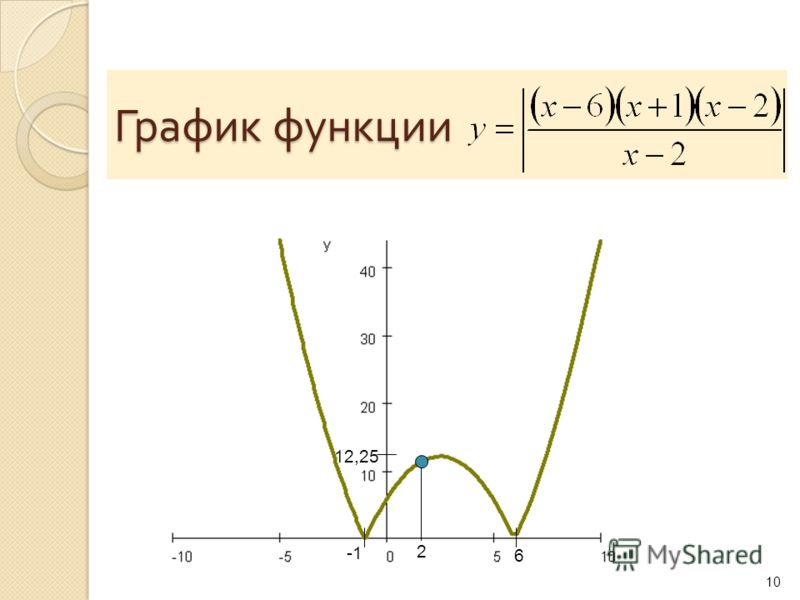 е. наши точки)
pygame.display.flip()
pygame.quit()
е. наши точки)
pygame.display.flip()
pygame.quit()
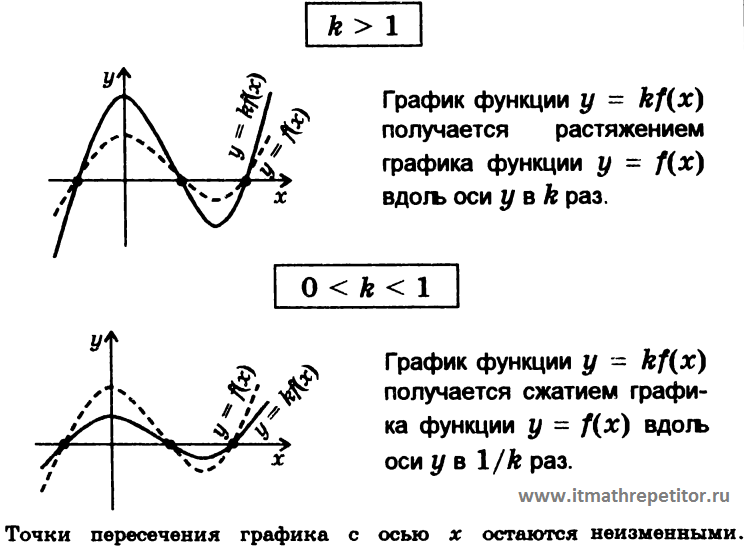 {»}=cosx-sinx\] \[-sinx+cosx=0\] \[x=\frac{\pi }{4}+\pi n,n\in Z\]
{»}=cosx-sinx\] \[-sinx+cosx=0\] \[x=\frac{\pi }{4}+\pi n,n\in Z\]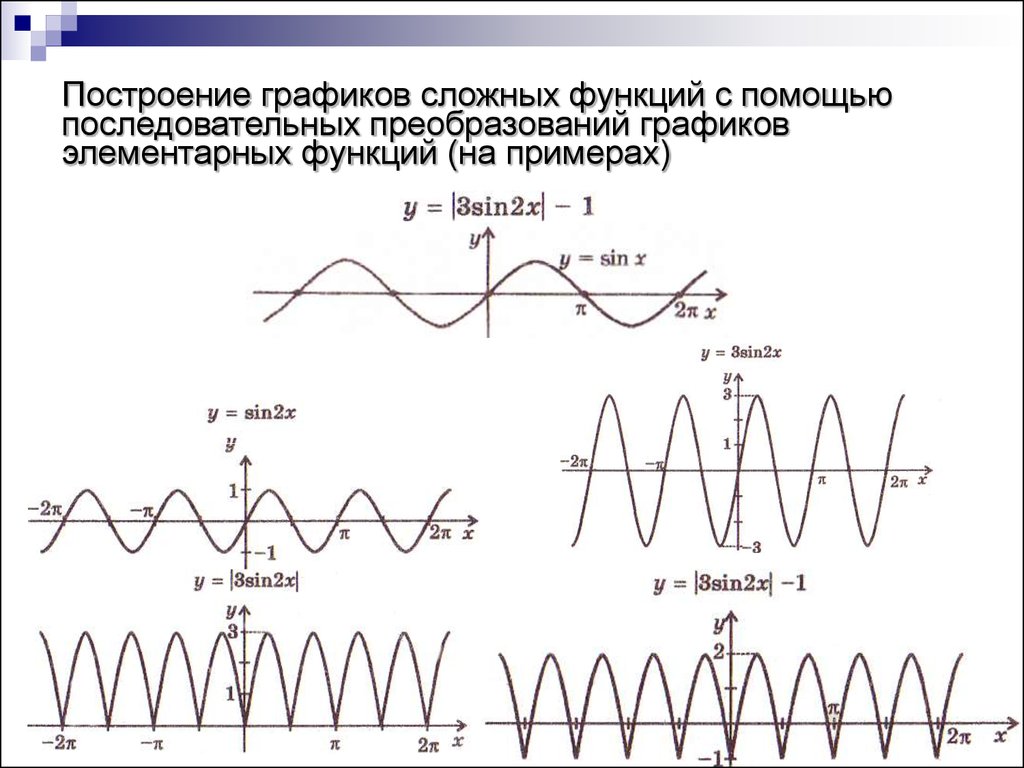 Тем
самым вы можете менять углы обзора
графика и даже заставить график вращаться
в заданном направлении автоматически.
Тем
самым вы можете менять углы обзора
графика и даже заставить график вращаться
в заданном направлении автоматически.
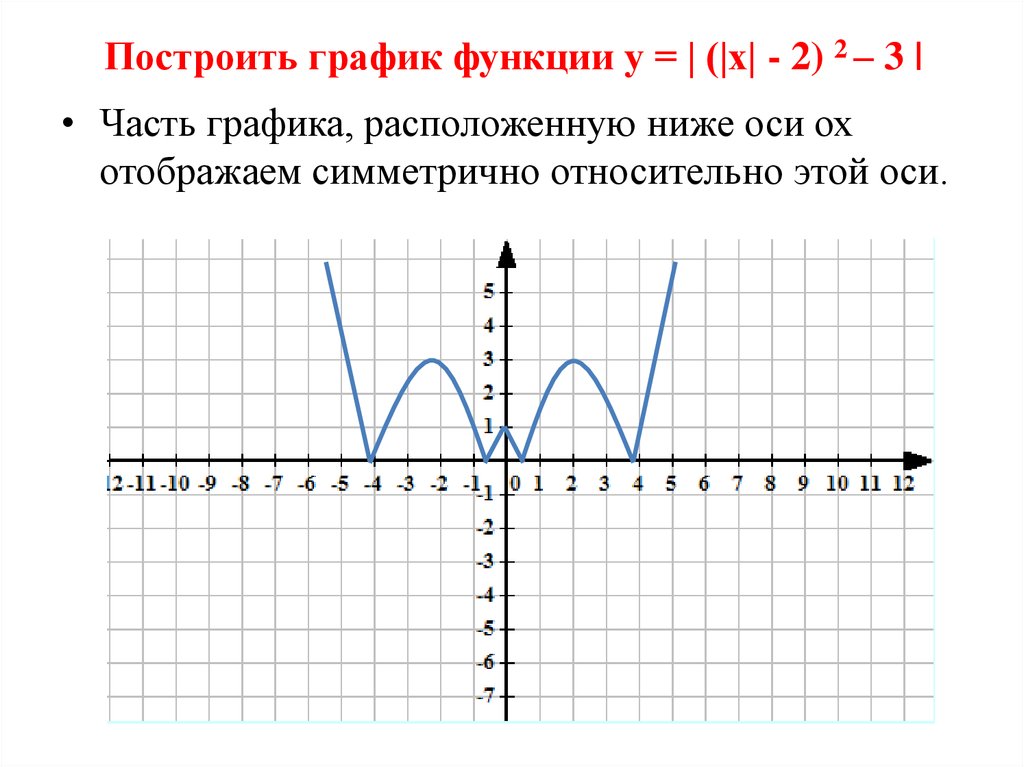 :Питер,2001.
:Питер,2001.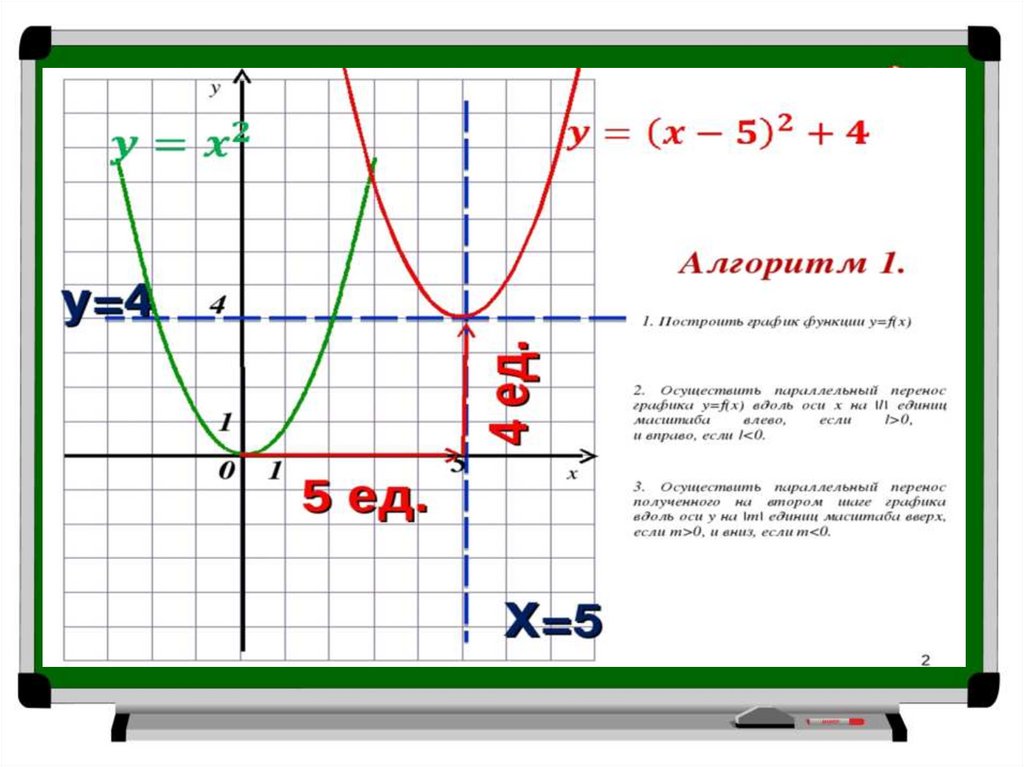 x3.Его внешний вид показан на схеме. 53.As (см. рисунок 57). Разработанное устройство позволяет строить графики локально параметрических заданных функций. x = x (1), y = y (()здесь пара функций x = x ({), y = y {1) равна y = y (x) или x = x( y).Граф параметрической определяемой функции подразумевает объединение графа всех функций в виде формулы x = x (1), Y = Y ({), Y = Cx) и x =§(y).
x3.Его внешний вид показан на схеме. 53.As (см. рисунок 57). Разработанное устройство позволяет строить графики локально параметрических заданных функций. x = x (1), y = y (()здесь пара функций x = x ({), y = y {1) равна y = y (x) или x = x( y).Граф параметрической определяемой функции подразумевает объединение графа всех функций в виде формулы x = x (1), Y = Y ({), Y = Cx) и x =§(y).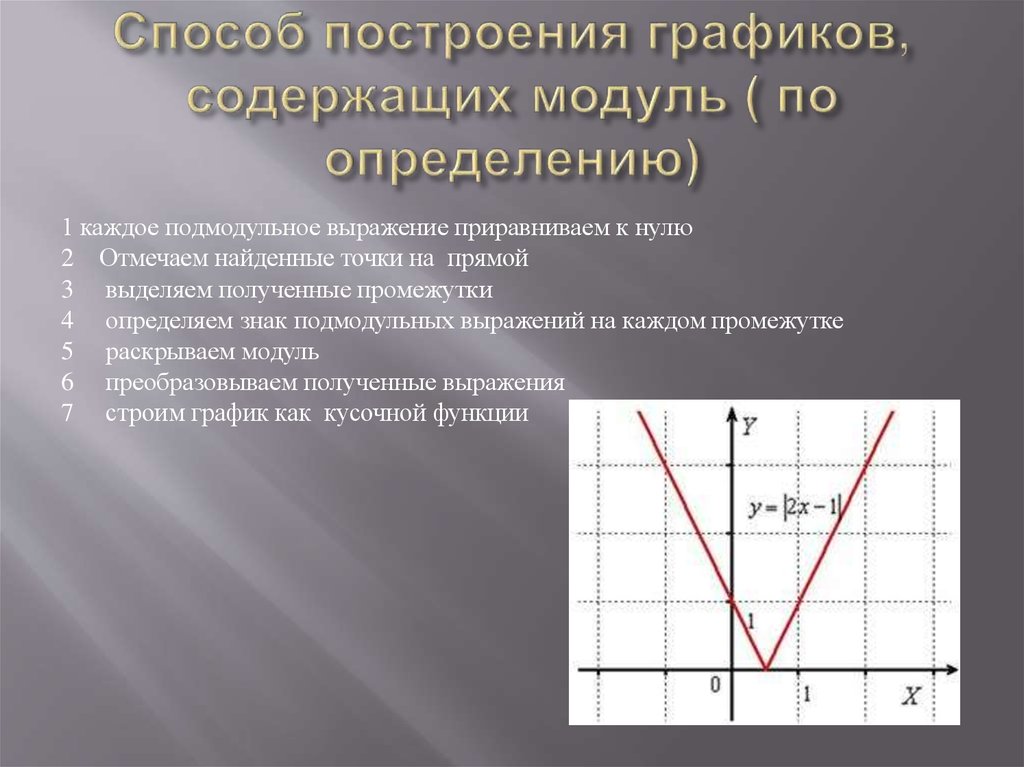 Если окажется, что такое значение 10 существует、 г = Б(14.15) Уравнение асимптоты должно быть найдено. Наконец, чтобы найти асимптоту.
Если окажется, что такое значение 10 существует、 г = Б(14.15) Уравнение асимптоты должно быть найдено. Наконец, чтобы найти асимптоту.

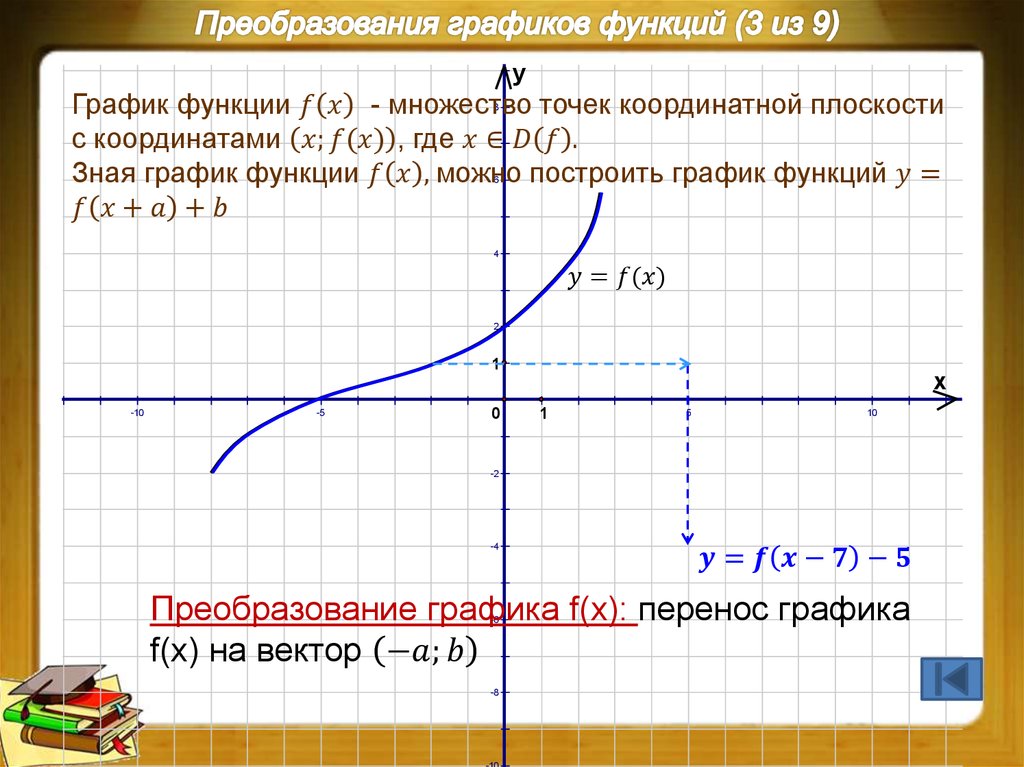

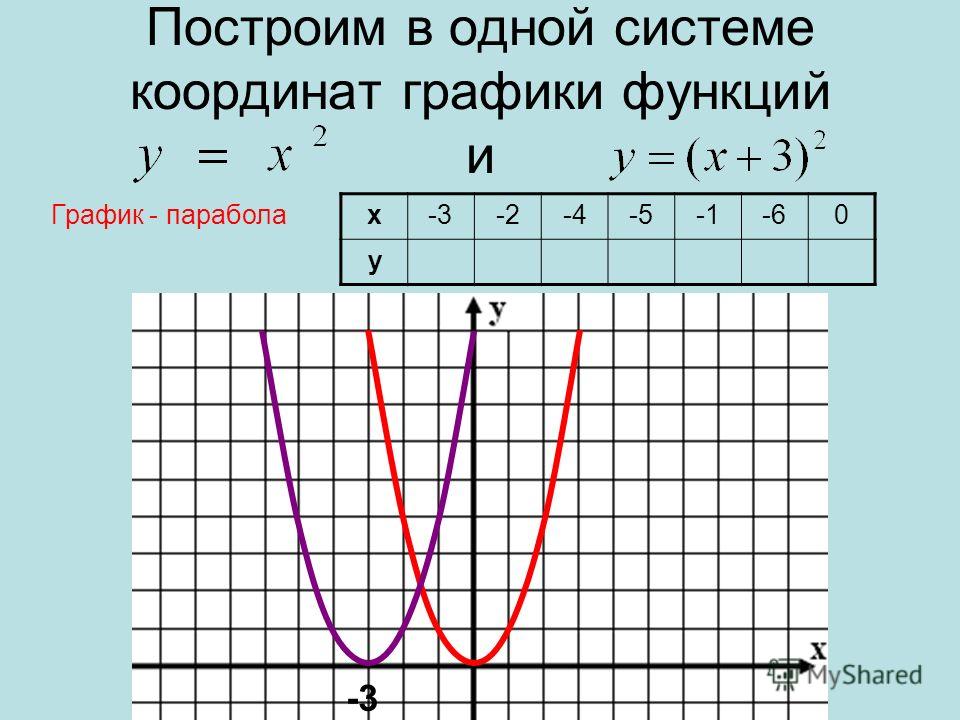
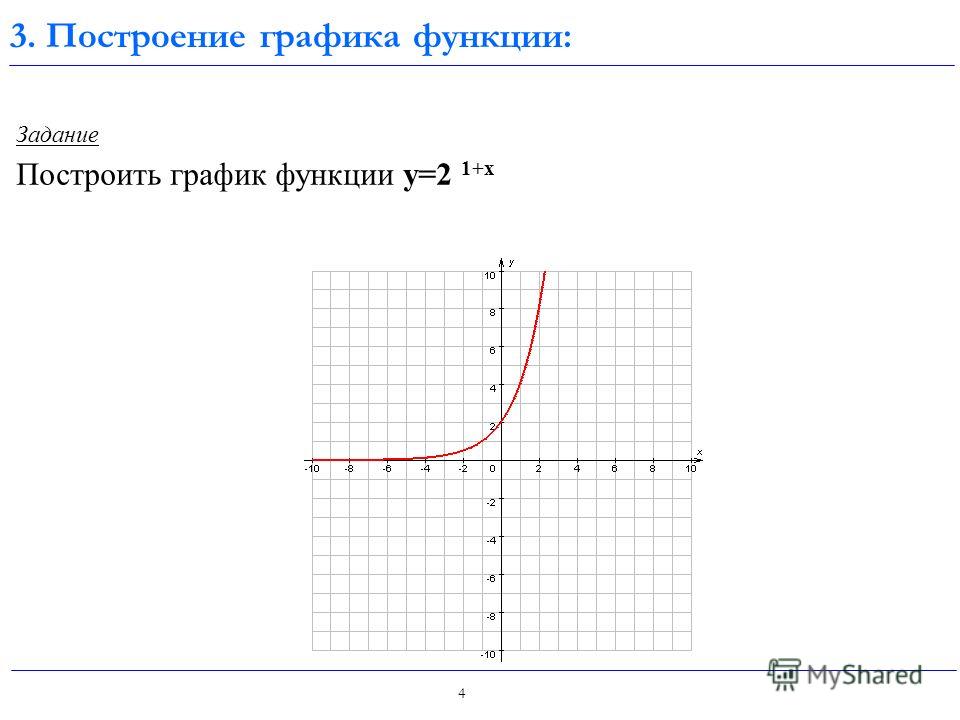 Обзор книги.
Обзор книги.
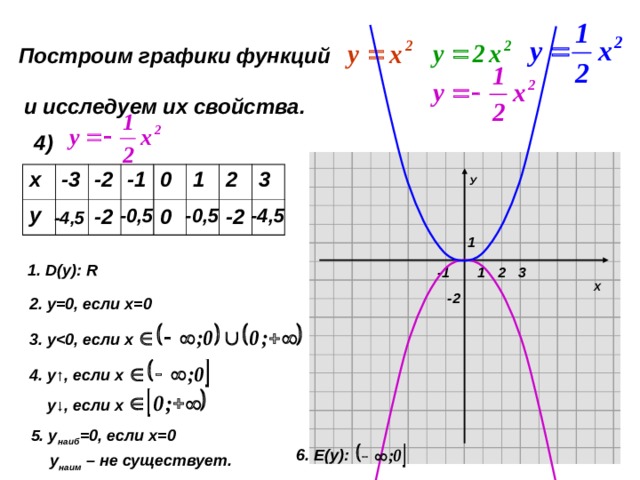 Math.content.HSF.BF.A). Вопросы в этом кластере в значительной степени зависят от построения понимания между реальными жизненными ситуациями, рассматриваемыми с математической точки зрения.
Math.content.HSF.BF.A). Вопросы в этом кластере в значительной степени зависят от построения понимания между реальными жизненными ситуациями, рассматриваемыми с математической точки зрения.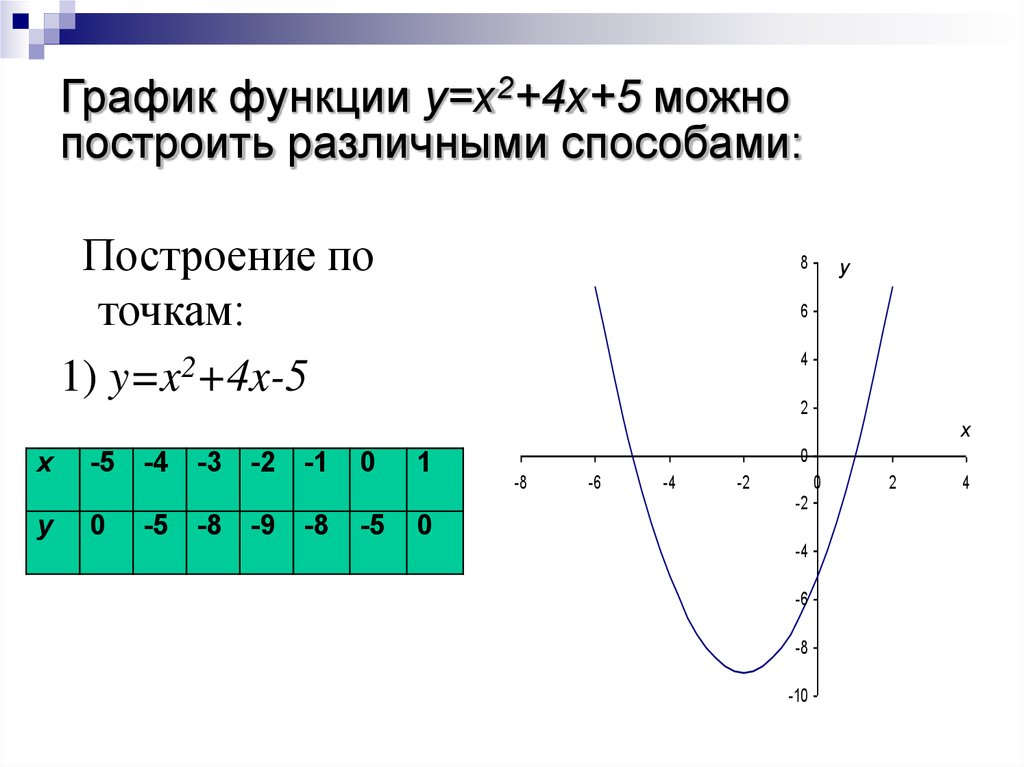
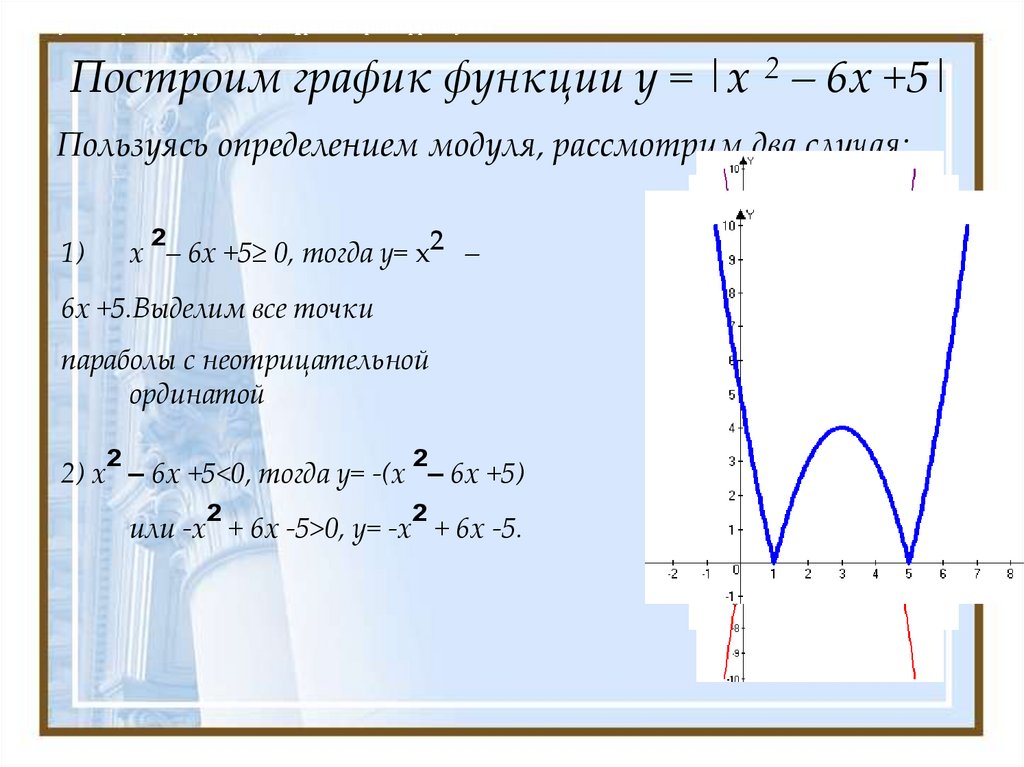
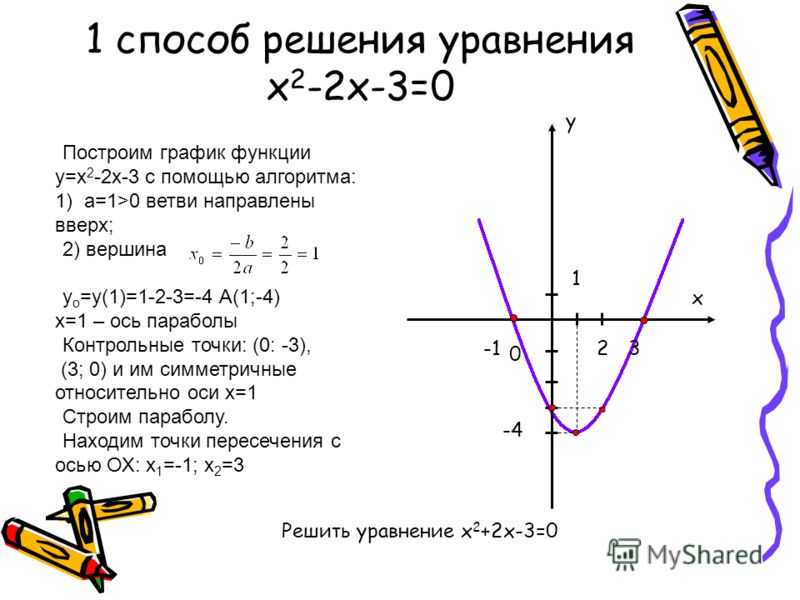
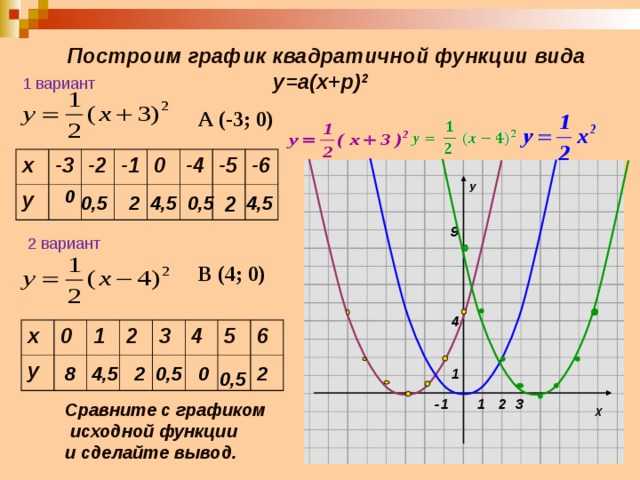
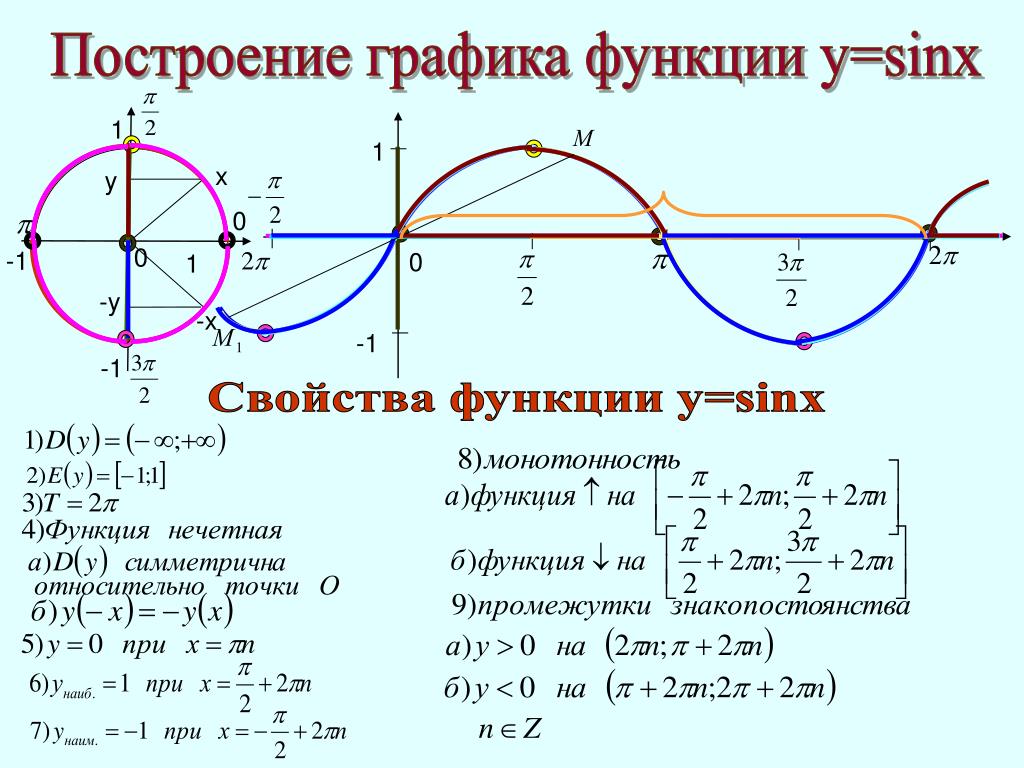 Такой вопрос требует изучения поведения между величинами, будь то явное выражение, рекурсивный процесс или многошаговое вычисление. Это также требует использования алгебраических операций для решения поставленного вопроса, а затем построения функции, моделирующей взаимосвязь.
Такой вопрос требует изучения поведения между величинами, будь то явное выражение, рекурсивный процесс или многошаговое вычисление. Это также требует использования алгебраических операций для решения поставленного вопроса, а затем построения функции, моделирующей взаимосвязь.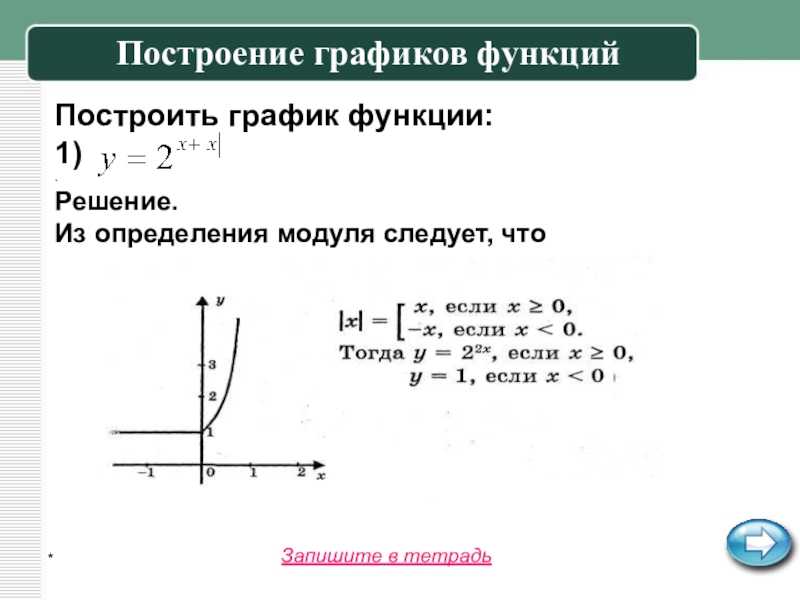

 MATH.CONTENT.HSF.BF.A). Вопросы в этом кластере в значительной степени зависят от построения понимания между реальными жизненными ситуациями, рассматриваемыми с математической точки зрения.
MATH.CONTENT.HSF.BF.A). Вопросы в этом кластере в значительной степени зависят от построения понимания между реальными жизненными ситуациями, рассматриваемыми с математической точки зрения.
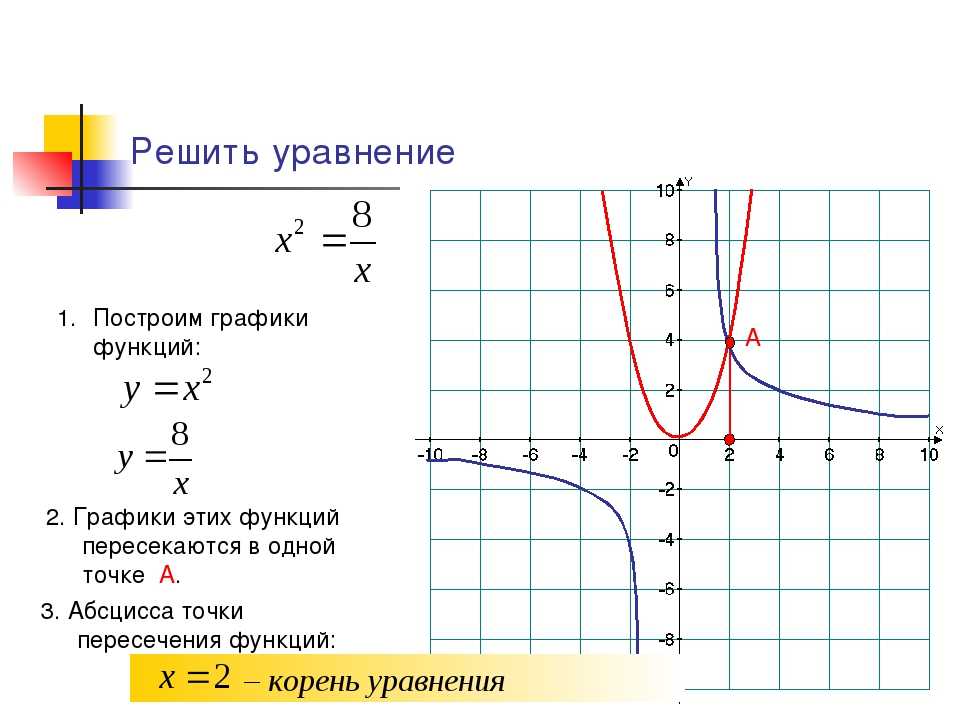
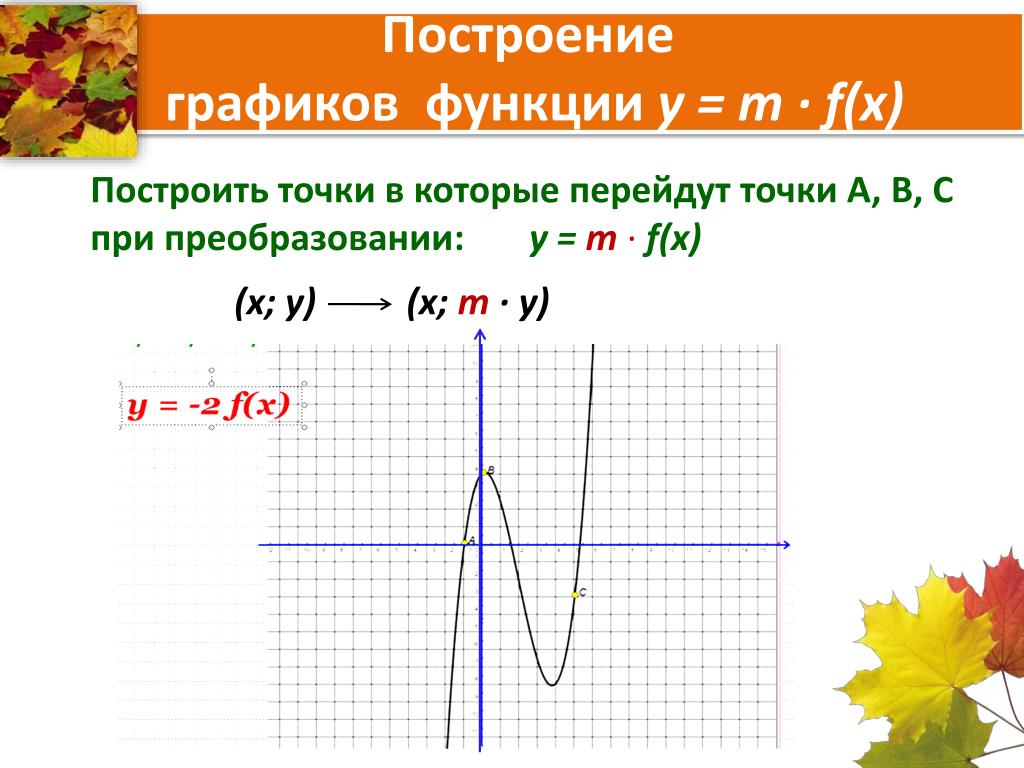

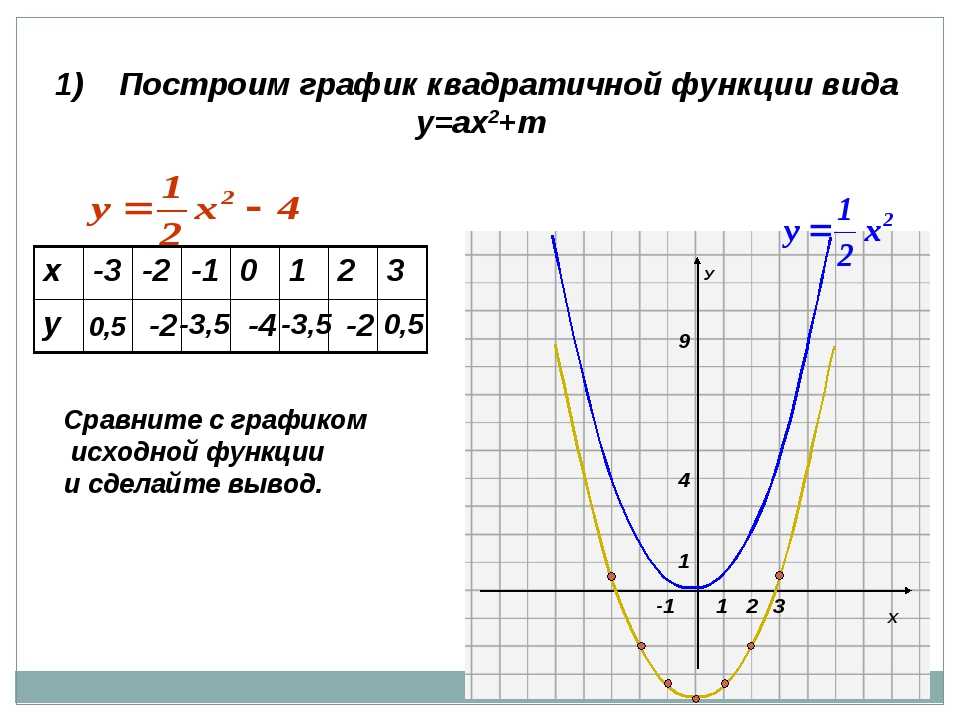

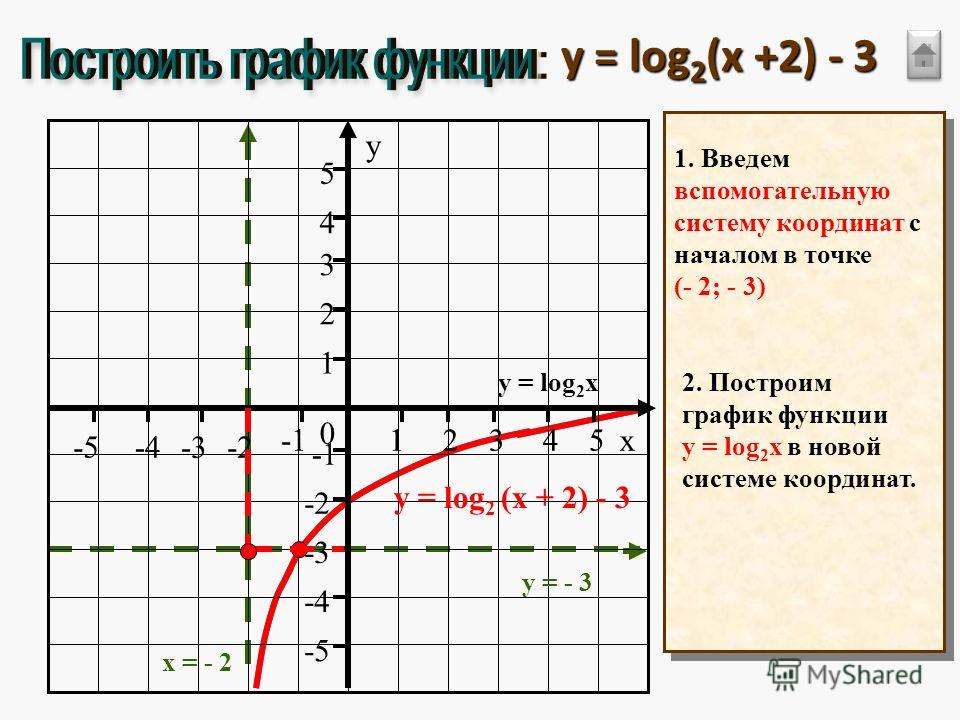
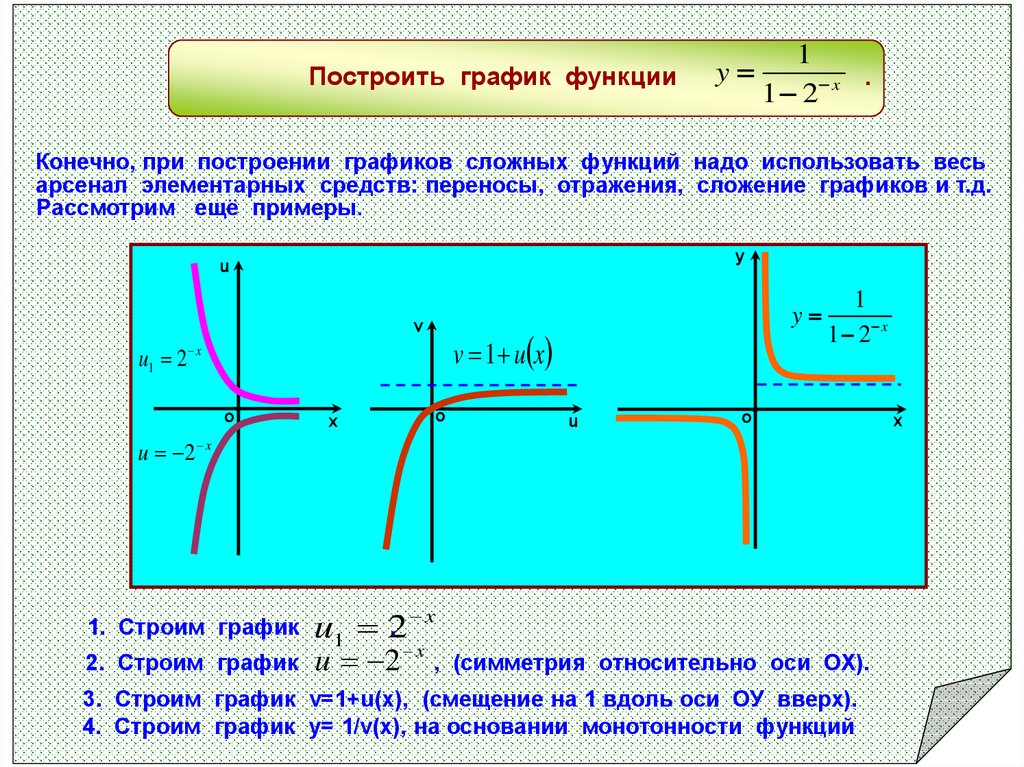 Это также требует использования алгебраических операций для решения поставленного вопроса, а затем построения функции, моделирующей взаимосвязь.
Это также требует использования алгебраических операций для решения поставленного вопроса, а затем построения функции, моделирующей взаимосвязь.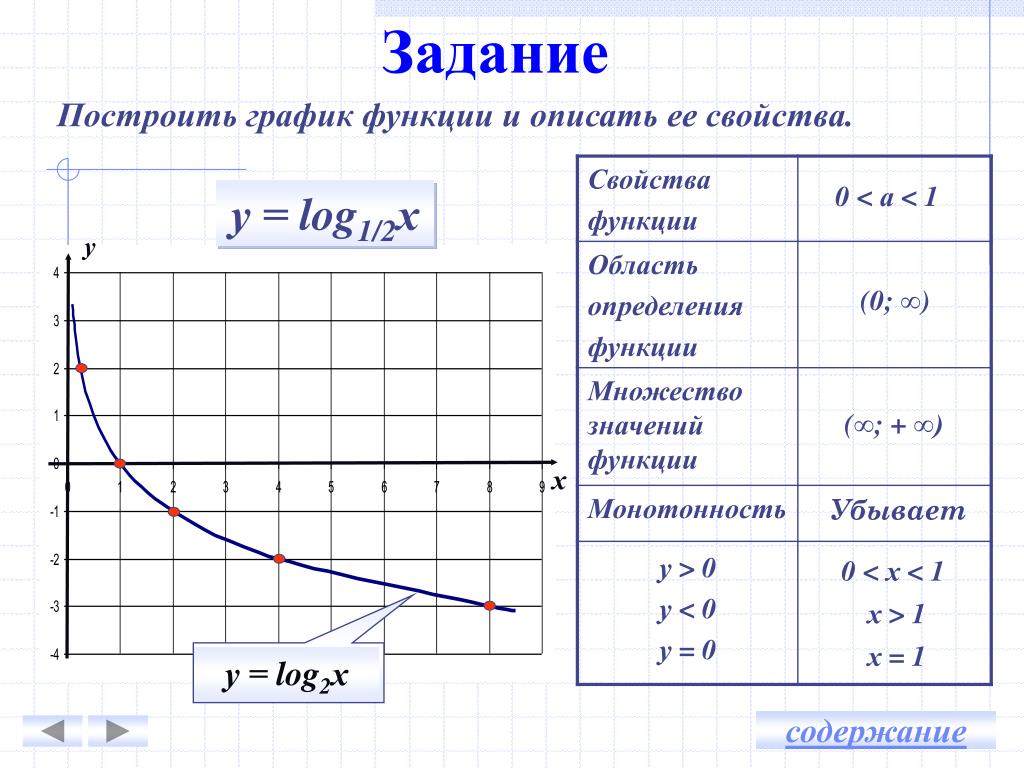

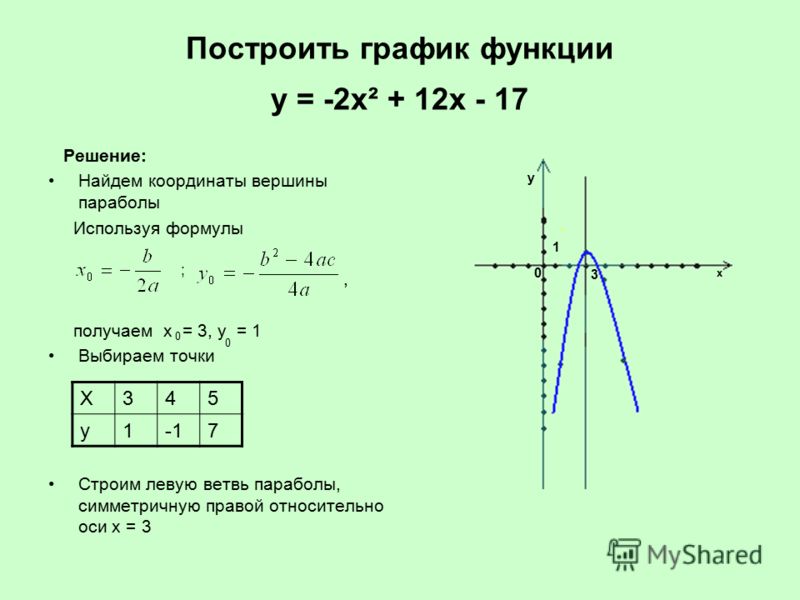 MATH.CONTENT.HSF.BF.A). Вопросы в этом кластере в значительной степени зависят от построения понимания между реальными жизненными ситуациями, рассматриваемыми с математической точки зрения.
MATH.CONTENT.HSF.BF.A). Вопросы в этом кластере в значительной степени зависят от построения понимания между реальными жизненными ситуациями, рассматриваемыми с математической точки зрения.
 Такой вопрос требует изучения поведения между величинами, будь то явное выражение, рекурсивный процесс или многошаговое вычисление. Это также требует использования алгебраических операций для решения поставленного вопроса, а затем построения функции, моделирующей взаимосвязь.
Такой вопрос требует изучения поведения между величинами, будь то явное выражение, рекурсивный процесс или многошаговое вычисление. Это также требует использования алгебраических операций для решения поставленного вопроса, а затем построения функции, моделирующей взаимосвязь.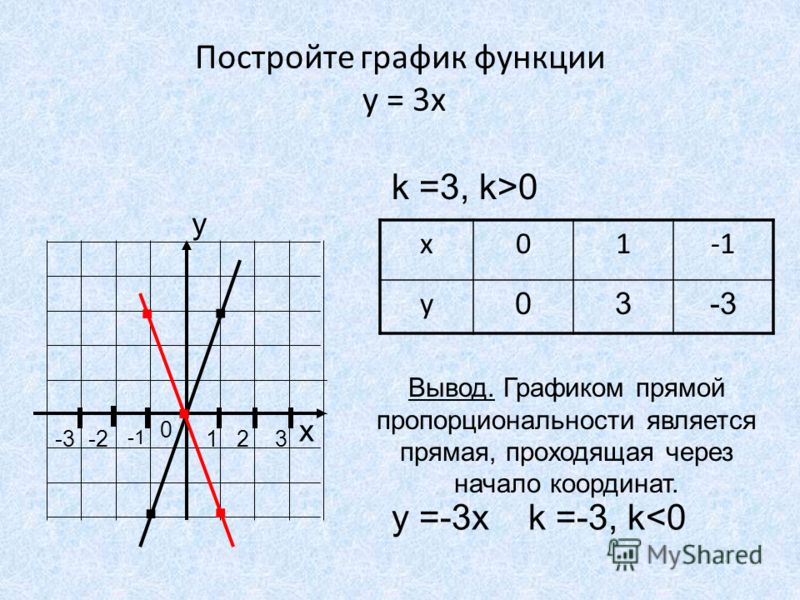

 MATH.CONTENT.HSF.BF.A). Вопросы в этом кластере в значительной степени зависят от построения понимания между реальными жизненными ситуациями, рассматриваемыми с математической точки зрения.
MATH.CONTENT.HSF.BF.A). Вопросы в этом кластере в значительной степени зависят от построения понимания между реальными жизненными ситуациями, рассматриваемыми с математической точки зрения.
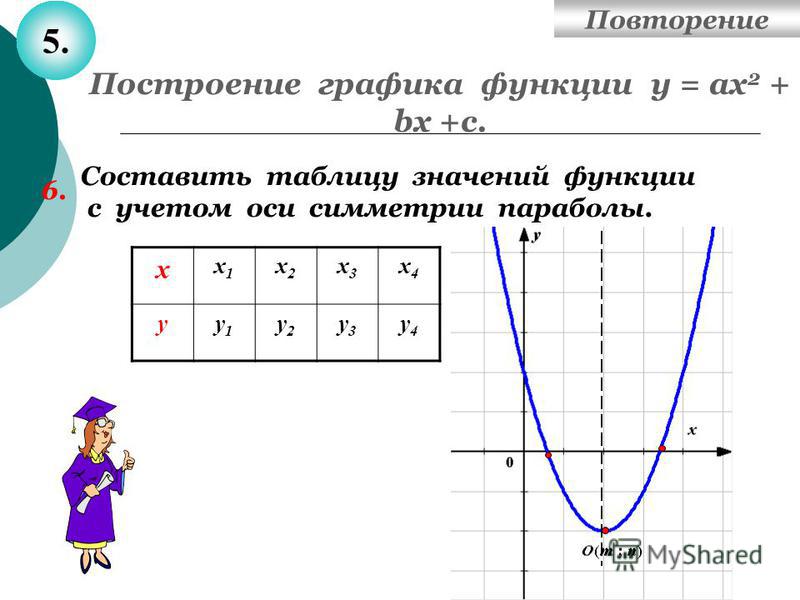 Смотрите все это в этом уроке.
Смотрите все это в этом уроке.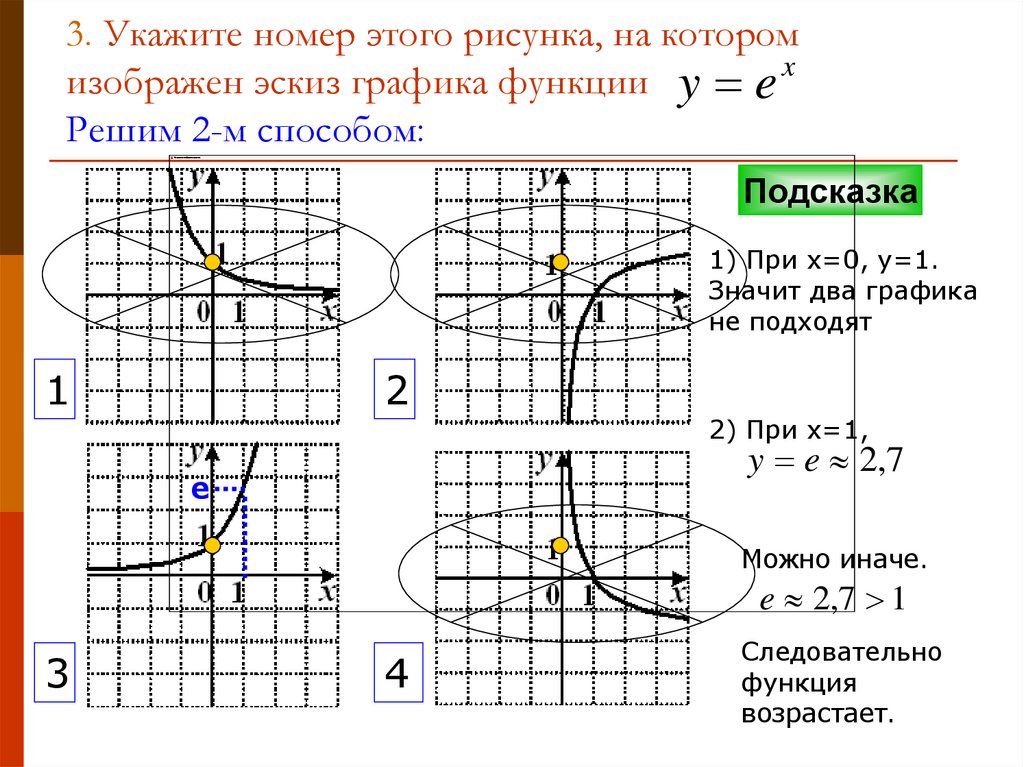
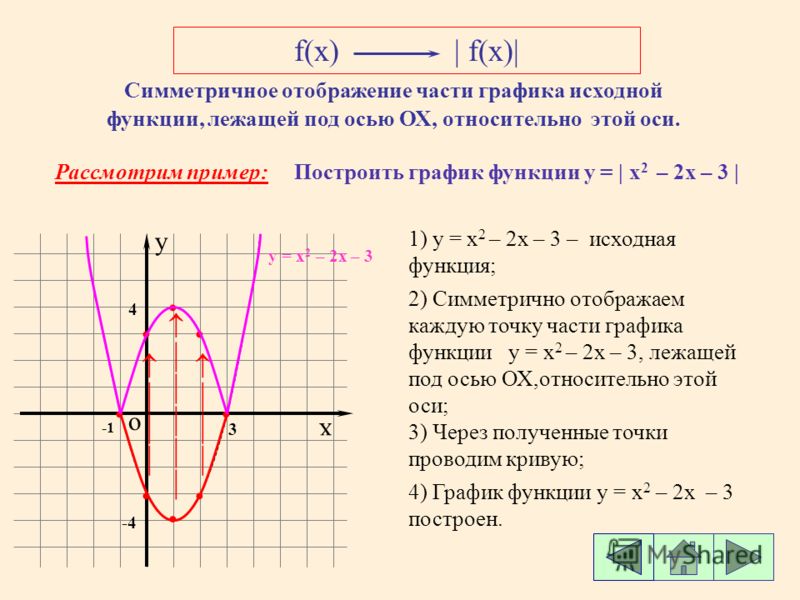 В этом уроке вы узнаете, как превратить текстовую задачу в функцию экспоненциального роста. Затем решите функцию и получите ответ!
В этом уроке вы узнаете, как превратить текстовую задачу в функцию экспоненциального роста. Затем решите функцию и получите ответ! Затем вы можете увидеть, как создать экспоненциальную функцию из данных и решить функцию, чтобы получить ответ!
Затем вы можете увидеть, как создать экспоненциальную функцию из данных и решить функцию, чтобы получить ответ!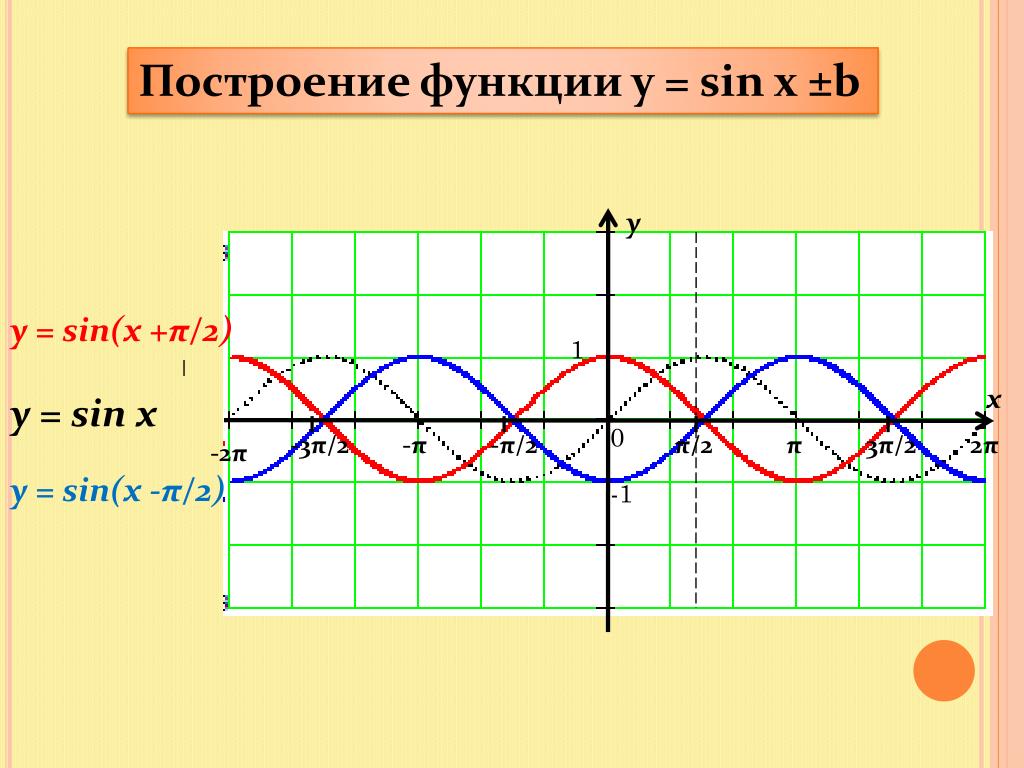 Когда это скорость убывания, у вас есть экспоненциальная функция затухания! Проверьте эти виды экспоненциальных функций в этом уроке!
Когда это скорость убывания, у вас есть экспоненциальная функция затухания! Проверьте эти виды экспоненциальных функций в этом уроке!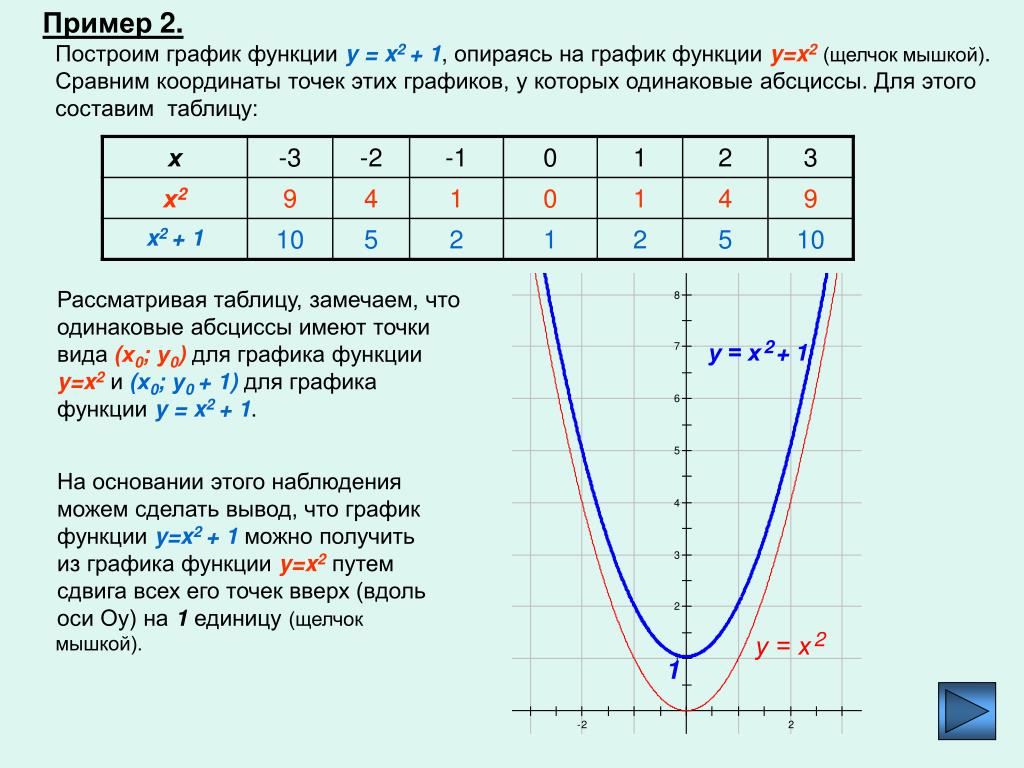 В этом руководстве показано, как написать правило функции для заданного отношения. Проверьте это!
В этом руководстве показано, как написать правило функции для заданного отношения. Проверьте это!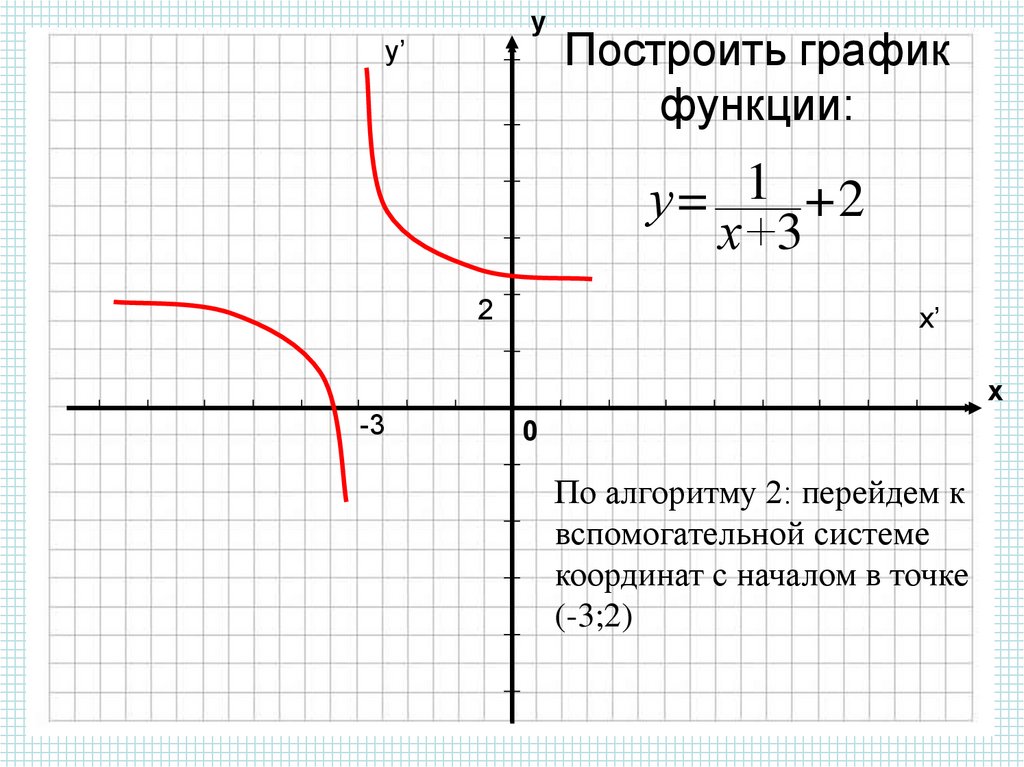 Это проще, чем вы думаете! Посмотрите этот урок и узнайте, как найти общую разность в арифметической прогрессии.
Это проще, чем вы думаете! Посмотрите этот урок и узнайте, как найти общую разность в арифметической прогрессии.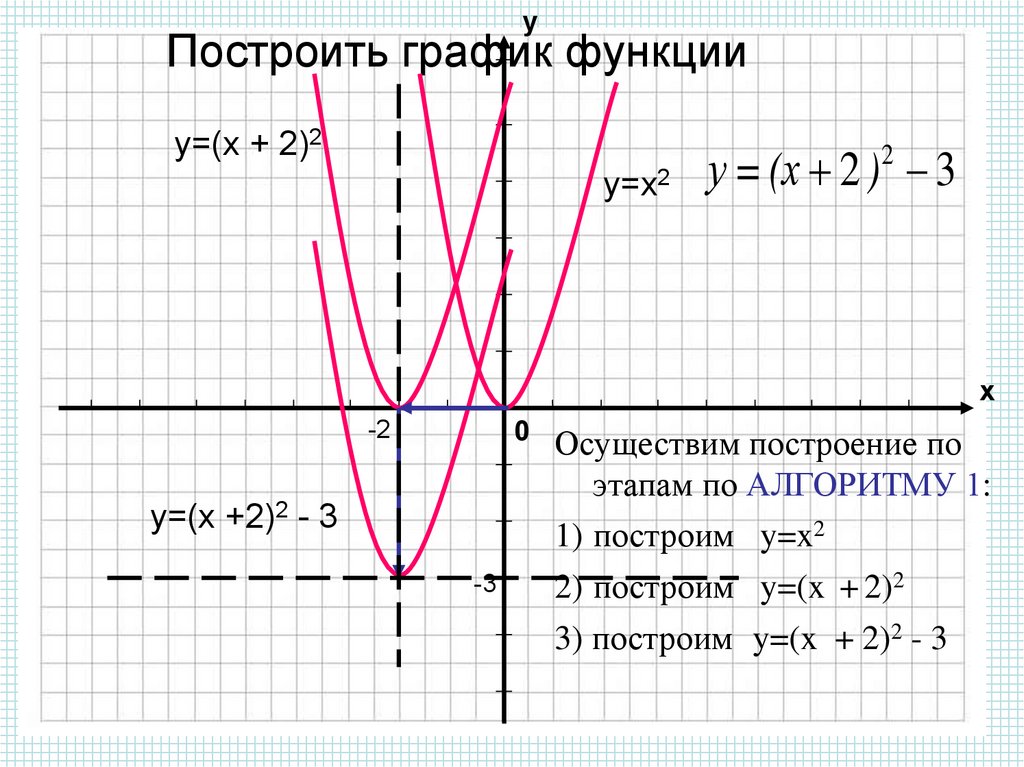 Затем посмотрите, как использовать это уравнение, чтобы найти значение одной из переменных.
Затем посмотрите, как использовать это уравнение, чтобы найти значение одной из переменных.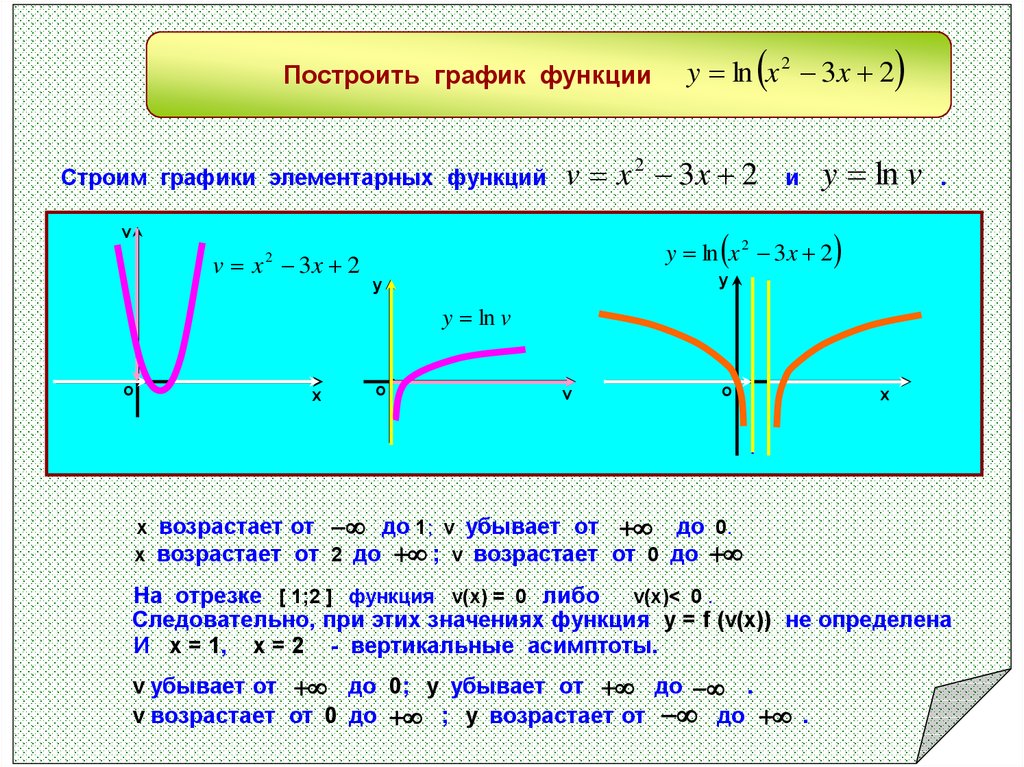 Чтобы найти точку пересечения с осью y, удалите «x» и найдите «y». В этом уроке вы увидите, как найти точки пересечения по осям x и y для заданного линейного уравнения. Проверьте это!
Чтобы найти точку пересечения с осью y, удалите «x» и найдите «y». В этом уроке вы увидите, как найти точки пересечения по осям x и y для заданного линейного уравнения. Проверьте это!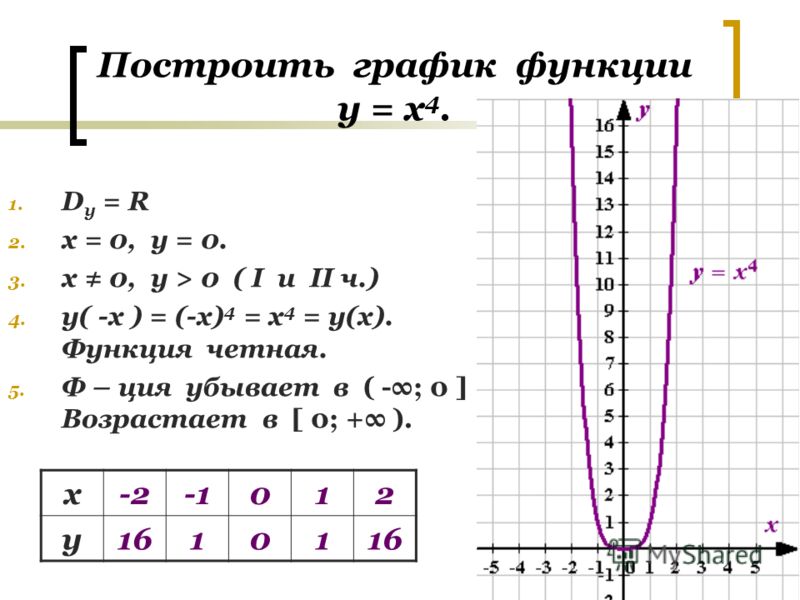 Посмотрите этот урок и узнайте, что нужно сделать, чтобы написать уравнение в форме точка-наклон!
Посмотрите этот урок и узнайте, что нужно сделать, чтобы написать уравнение в форме точка-наклон!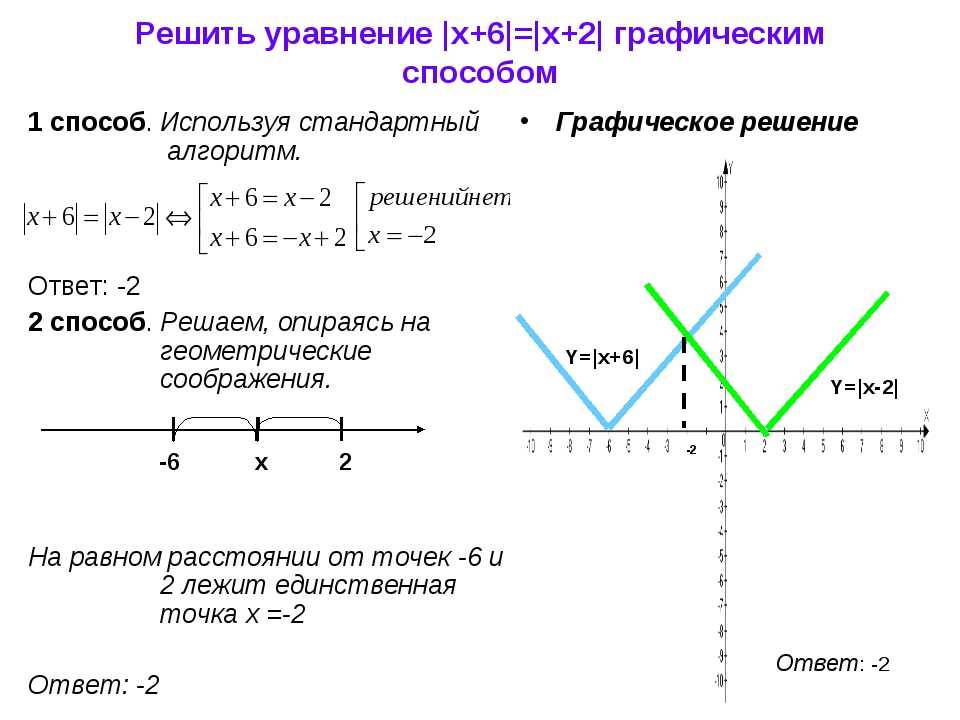 В этом руководстве вы узнаете о x-intercept. Проверьте это!
В этом руководстве вы узнаете о x-intercept. Проверьте это! В этом уроке вы узнаете об y-перехвате. Проверьте это!
В этом уроке вы узнаете об y-перехвате. Проверьте это!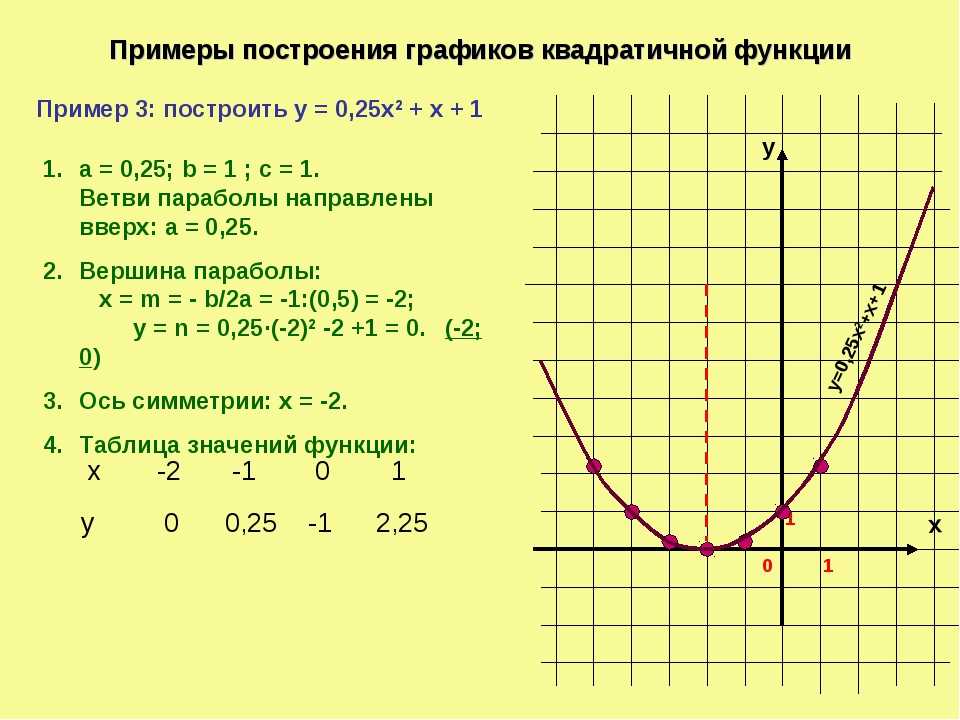 В этом учебном пособии вы пошагово пошагово решаете квадратное уравнение, заполняя квадрат. Проверьте это!
В этом учебном пособии вы пошагово пошагово решаете квадратное уравнение, заполняя квадрат. Проверьте это!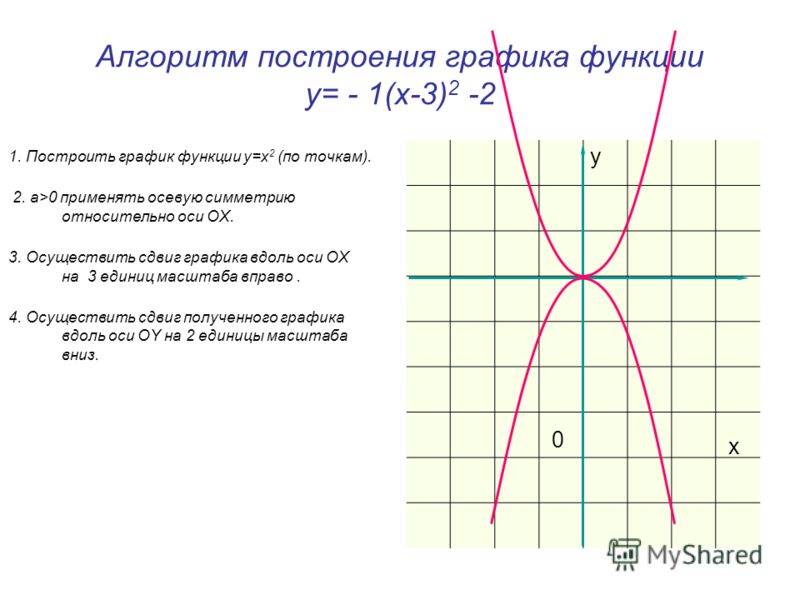 В алгебре чаще всего встречаются три основных типа графиков: линейный, квадратичный и экспоненциальный. Ознакомьтесь с этим руководством и узнайте, как определить, представляет ли график линейную, квадратичную или экспоненциальную функцию!
В алгебре чаще всего встречаются три основных типа графиков: линейный, квадратичный и экспоненциальный. Ознакомьтесь с этим руководством и узнайте, как определить, представляет ли график линейную, квадратичную или экспоненциальную функцию! В этом уроке рассматривается минимум квадратичной функции. Проверьте это!
В этом уроке рассматривается минимум квадратичной функции. Проверьте это!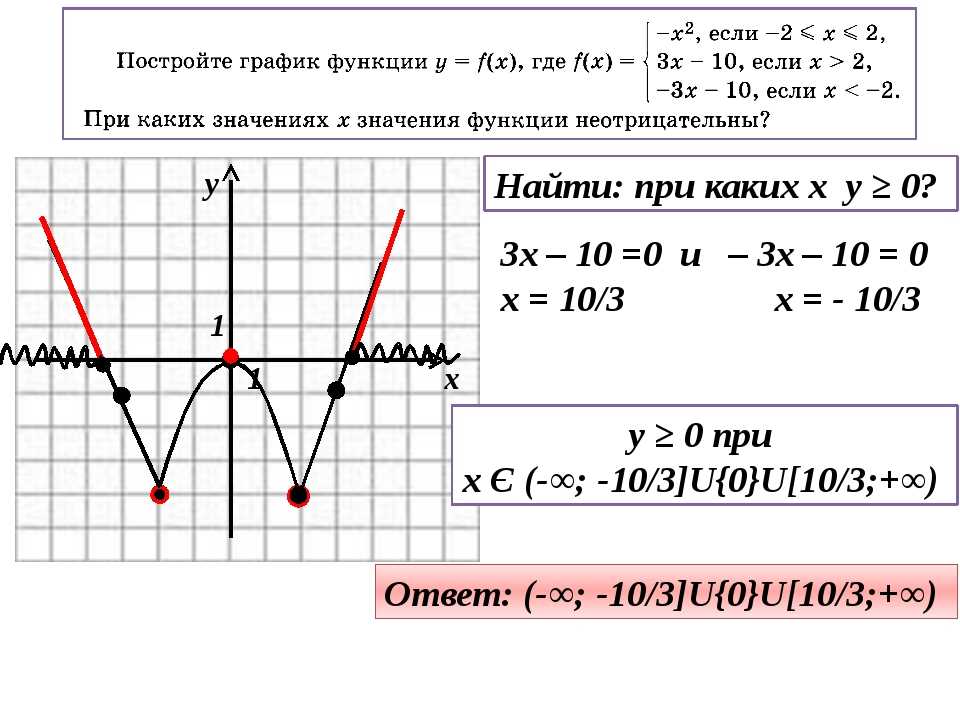
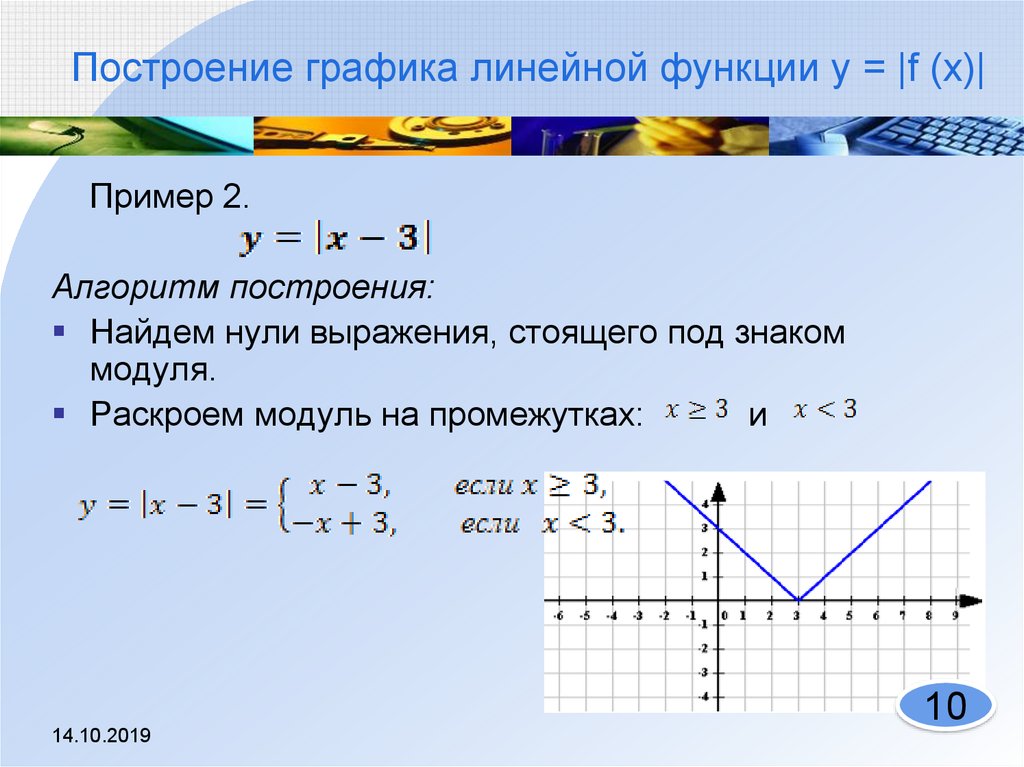 Вы также увидите, как настроить таблицу и график, чтобы помочь найти ответ!
Вы также увидите, как настроить таблицу и график, чтобы помочь найти ответ! Этот учебник определяет домен отношения!
Этот учебник определяет домен отношения! Соберите все это вместе, и вы получите свой график! В этом руководстве показан весь процесс построения графика кусочно-линейной функции.
Соберите все это вместе, и вы получите свой график! В этом руководстве показан весь процесс построения графика кусочно-линейной функции.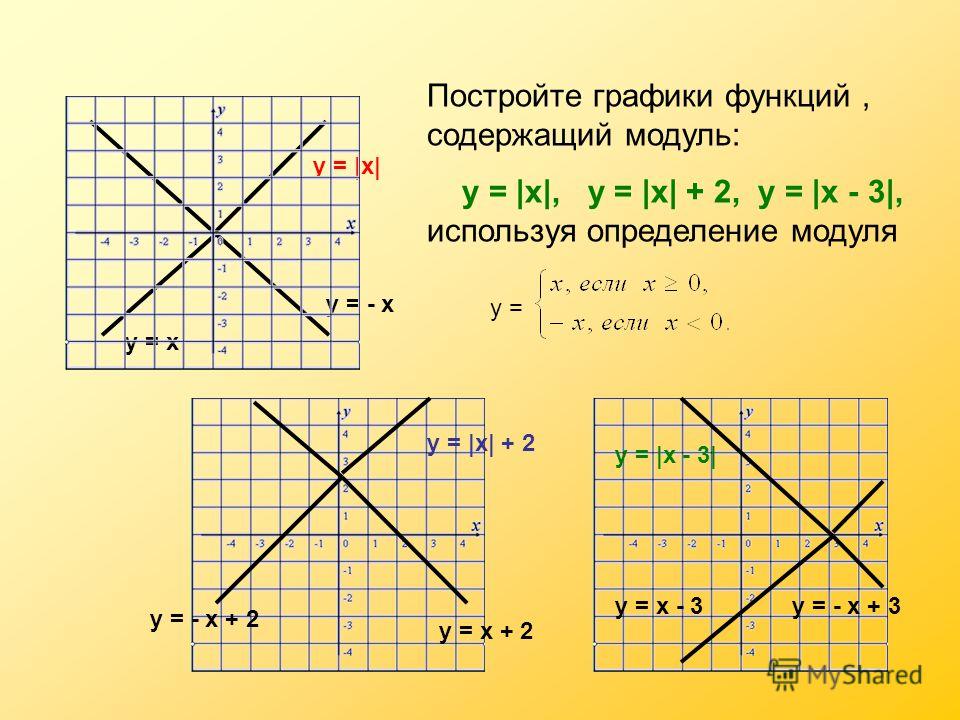
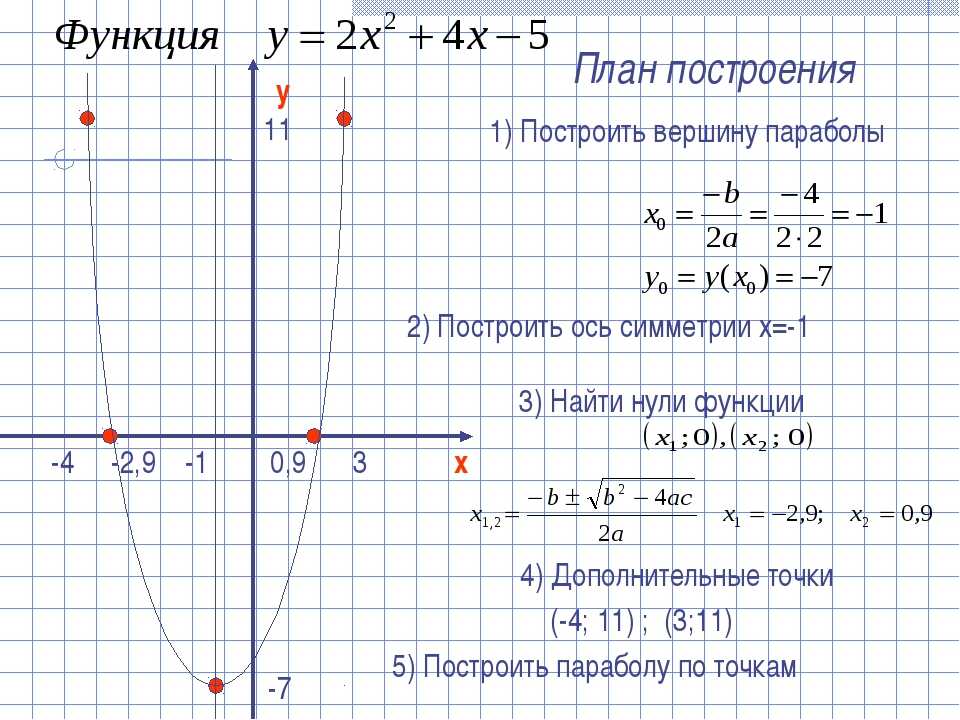
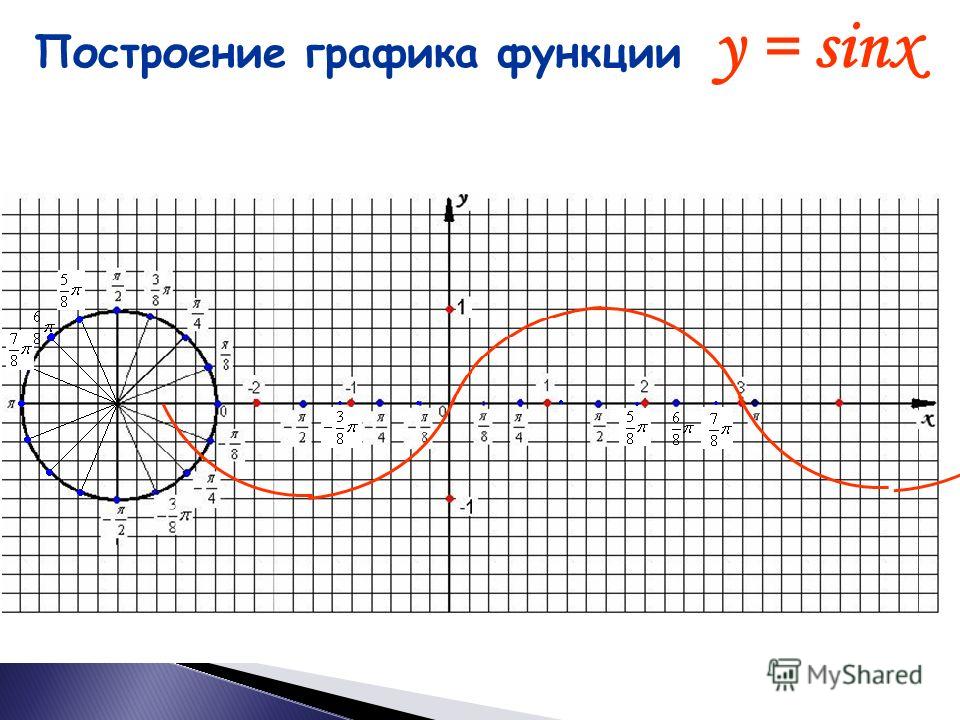
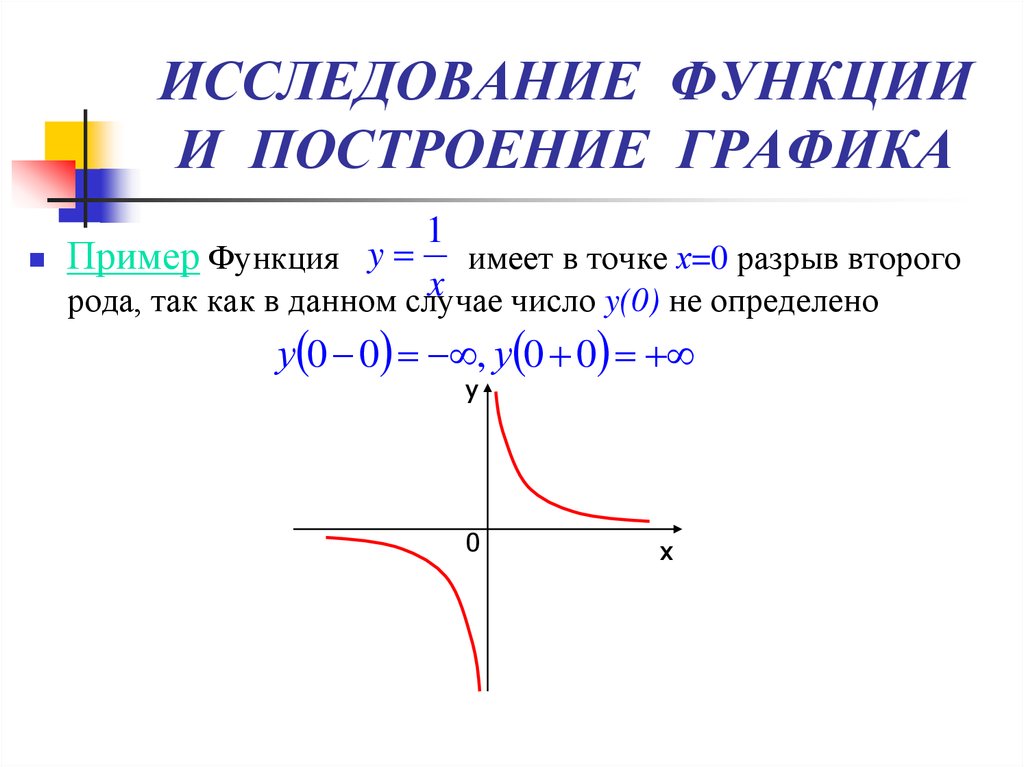
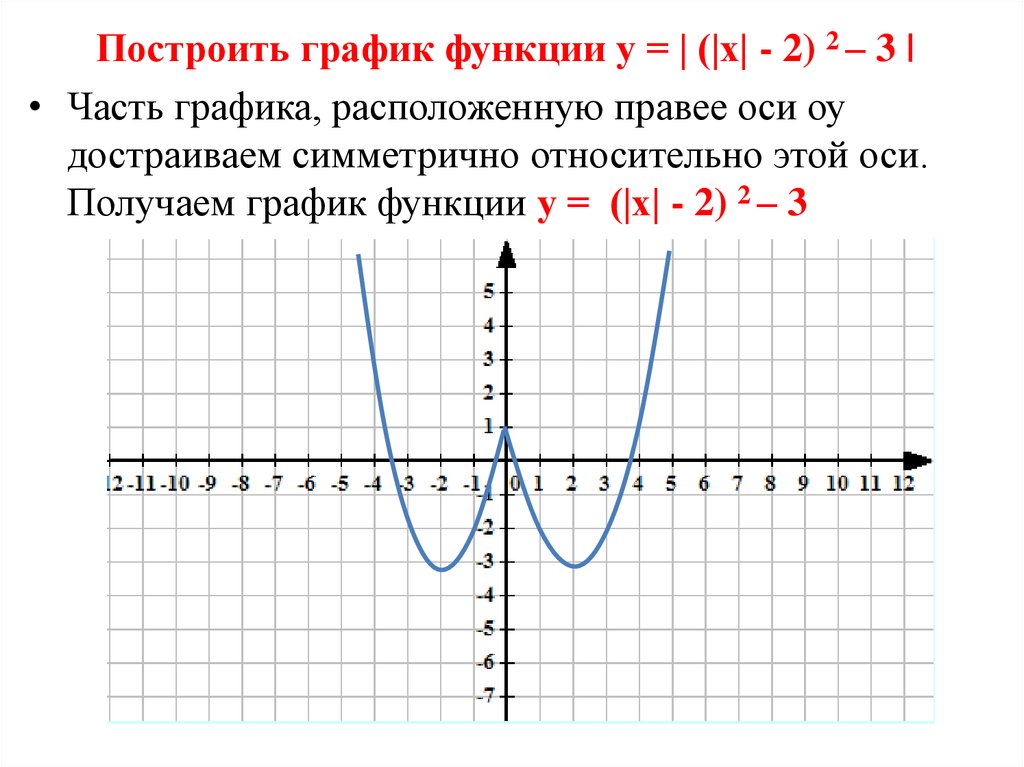

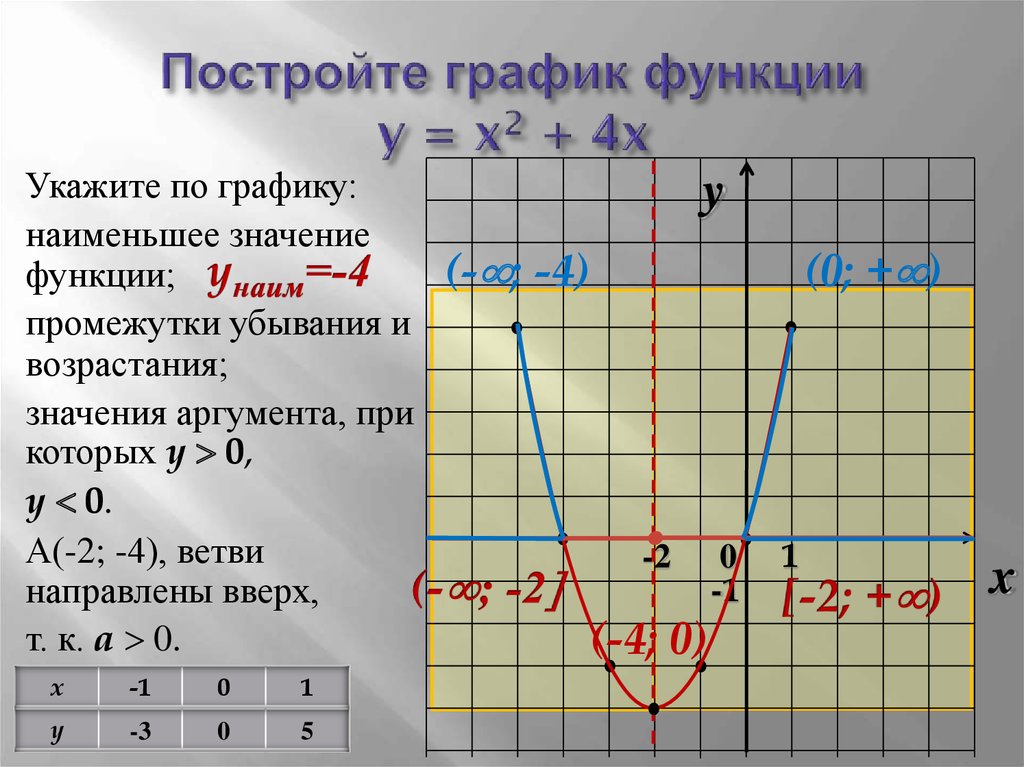 В этом уроке показано, как использовать единичный круг для построения графика касательной!
В этом уроке показано, как использовать единичный круг для построения графика касательной!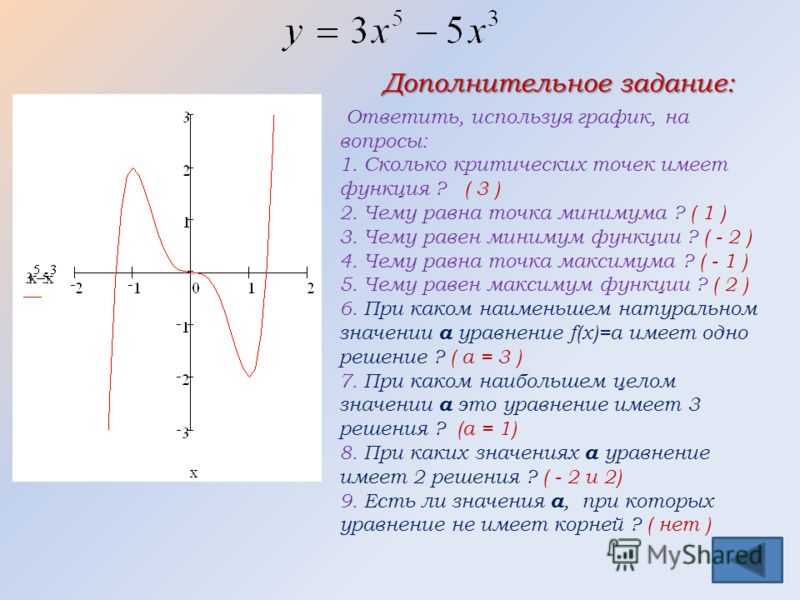
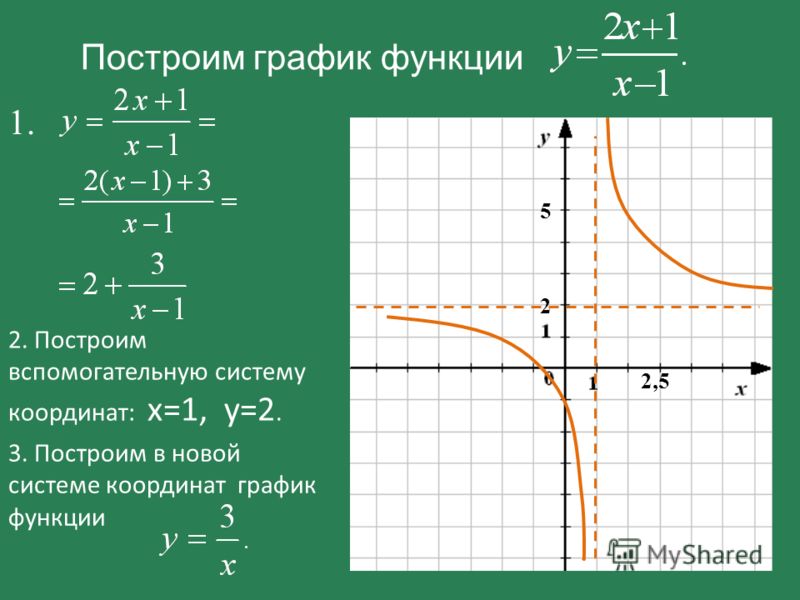 Взглянем!
Взглянем!