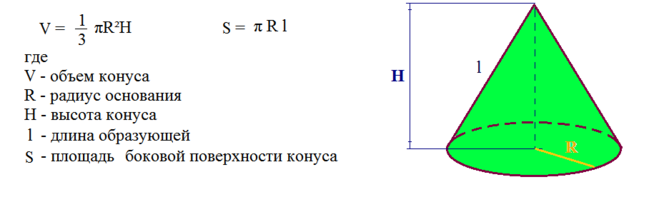
Как найти объем конуса без высоты? – Обзоры Вики
Отсюда, как найти объем конуса без радиуса? Чтобы рассчитать объем конуса, следуйте этим инструкциям:
- Найдите площадь основания конуса а. …
- Найдите высоту конуса h.
- Примените формулу объема конуса: объем = (1/3) * a * h, если известна площадь основания, или объем = (1/3) * π * r² * h в противном случае.
- Поздравляем, вы успешно вычислили объем своего конуса!
Какая формула объема? В то время как основная формула для площади прямоугольной формы — длина × ширина, основная формула для объема — длина × ширина × высота.
Каков объем цилиндра и конуса? Формула объема шара: 4⁄3πr³.
Для цилиндра формула πr²h. Конус составляет ⅓ объема цилиндра, или 1⁄3πr²ч.
Как найти частичный объем конуса?
Формула для расчета объема частичного конуса имеет следующий вид: Объем частичного конуса, V = 1/3 × πh (R2 + Рр + р2), где ‘r’ и ‘R’ — базовые радиусы, такие, что R> r, а ‘h’ — высота усеченной вершины.
Каков объем этого косого конуса? Формула объема косого конуса
Вам нужно π (Пи=~3.14) более 3, затем умножьте на радиус в степени двойки и, наконец, умножьте на высоту.
Как найти объем по площади?
Он дает долю площади поверхности на единицу объема объекта (например, сферы, цилиндра и т. Д.). Следовательно, формула для расчета отношения площади поверхности к объему следующая: SA / VOL = площадь поверхности (x2) / объем (x3) SA / VOL = x–1 , где x — единица измерения.
Также как рассчитать кубический объем? Расчет объема
Формула для определения объема умножает длину на ширину и высоту. Хорошая новость для куба заключается в том, что измерение каждого из этих измерений точно такое же. Следовательно, длину любой стороны можно умножить в три раза. Это приводит к формуле: Объем = сторона * сторона * сторона.
Каков объем конуса на рисунке?
Как найти H конуса? Формула высоты конуса вычисляет высоту конуса. Высота конуса с использованием формул высоты конуса: h = 3V / πr 2 и h = √l2 — р2, где V = объем конуса, r = радиус конуса и l = наклонная высота конуса.
Каков объем этого конуса. Используйте 3.14 для π?
где π∙r2 площадь основания конуса. π определяет отношение длины окружности любого круга к его диаметру и приблизительно равно 3.
141593, однако часто используется значение 3.14. Пример 1: Найдите объем конуса, радиус которого 8 см, а высота 5 см. Таким образом, объем конуса равен 334.93 смXNUMX.3.
Что такое конусная математика?
конус, по математике, поверхность, описываемая движущейся прямой линией (образующей), которая всегда проходит через фиксированную точку (вершину). … Ось этого конуса — это линия, проходящая через вершину и центр окружности, причем эта линия перпендикулярна плоскости окружности.
Какова формула объема прямого конуса с площадью основания B и высотой H? Объем конуса: V = (1/3) πr2h.
Каков объем косого конуса, округленного с точностью до десятых?
Округлите до десятых. Наклонный конус имеет высоту, равную диаметру основания. Объем конуса равен 18π кубических единиц.
Каков объем косого конуса, округленного с точностью до десятых?
Округлите до десятых. Наклонный конус имеет высоту, равную диаметру основания. Объем конуса равен 18π кубических единиц.
Какая единица измерения объема?
Объем — это мера трехмерного пространства, занимаемого материей или ограниченного поверхностью, и измеряется в кубических единицах. Единица объема СИ кубический метр (м3), которая является производной единицей. Литр (L) — это специальное название кубического дециметра (дм3).
Что такое формула площади? Для прямоугольника длиной l и шириной w формула для вычисления площади имеет следующий вид: A = lw (прямоугольник).
То есть площадь прямоугольника — это длина, умноженная на ширину. В качестве особого случая, поскольку l = w в случае квадрата, площадь квадрата со стороной s определяется по формуле: A = s2 (площадь).
Что такое объем прямоугольника?
Уравнение для расчета объема прямоугольника показано ниже: объем=длина×ширина×высота.
Методическая разработка укока «Формулы объема пирамиды и конуса. Формулы площади поверхностей цилиндра и конуса»
Тема: Формулы объема пирамиды и конуса. Формулы площади поверхностей цилиндра и конуса.
· Обучающие:
Создать условия для:
-Закрепления понятий: пирамида, конус,цилиндр, площадь поверхности, объем геометрического тела.
— Выработки умения решать задачи практического содержания, используя формулы объёмов тел.
— Выработки умения использовать приобретенные знания для исследования несложных практических ситуаций на основе изученных формул и свойств фигур
· Воспитательные:
Создать условия для:
—
Формирования культуры учебной деятельности.
— Умения преодолевать трудности.
— Вызова интереса к предмету.
— Воспитания внимания и чувства взаимопомощи.
План занятия
1. Организационный момент
2. Изучение нового материала
3. Закрепление нового материала
4. Подведение итогов занятия и домашнее задание
1. Организационный момент
2. Актуализация знаний.
Вопросы для фронтального опроса:
· Какое геометрическое тело называют многогранником?
· Какое тело называют пирамидой, усеченной пирамидой?
· Какие тела вращения вам известны?
· Как можно получить цилиндр?
· Как можно получить конус?
· Как можно получить усечённый конус?
3. Изучение нового материала
Площадь поверхности пирамиды
Sбок = 1/2pm p — периметр основания; m — апофема.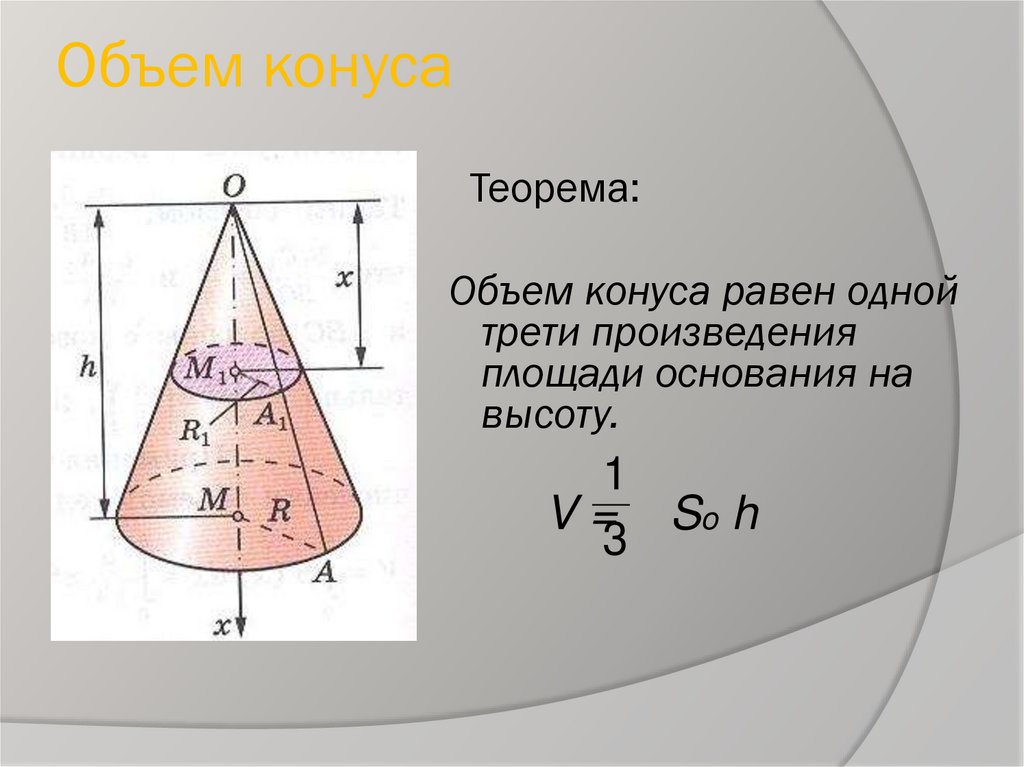
P — периметр нижнего основания, ABCDE
p — периметр верхнего основания, abcde
Формула площади боковой поверхности правильной усеченной пирамиды, (S):
Объем пирамиды
V = | 1 |
So · h |
3 |
Объем пирамиды равен трети от произведения площади ее основания на высоту.
Формула объема пирамиды
где V- объем пирамиды, So— площадь основания пирамиды, h
— длина высоты пирамиды.
h — высота пирамиды
Sниж — площадь нижнего основания, ABCDE
Sверх — площадь верхнего основания, abcde
Объем усеченной пирамиды, (V):
Площадь цилиндра
Площадь боковой поверхности круглого цилиндра равна произведению периметра его основания на высоту.
Формула для вычисления площади боковой поверхности цилиндра S = 2 π R h
Площадь полной поверхности круглого цилиндра равна сумме площади боковой поверхности цилиндра и удвоенной площади основания.
Формула для вычисления площади полной поверхности цилиндра
S = 2 π R h+ 2 π R 2 = 2 π R( R+ h)
где S-
площадь, R- радиус цилиндра, h- высота цилиндра, π = 3.
141592
Объем цилиндра равен произведению площади его основания на высоту.
Формулы объема цилиндра
V = π R2 h V = So h где V- объем цилиндра, So— площадь основания цилиндра, R- радиус цилиндра, h- высота цилиндра, π = 3.141592
Площадь конусаПлощадь боковой поверхности конуса равна произведению его радиуса и образующей умноженному на число π
Формула площади боковой поверхности конуса: S = π R l
Площадь полной поверхности конуса равна сумме площади основания конуса и площади боковой поверхности.
Формула площади полной поверхности конуса: S =π R2 + π R l= π R( R+ l)
где S- площадь, R- радиус основания конуса, l- образующая конуса, π = 3.
R — радиус нижнего основания
r— радиус верхнего основания
L — образующая усеченного конуса
π ≈ 3.14
Формула площади боковой поверхности усеченного конуса, (Sбок):
Формула площади полной поверхности усеченного конуса, (S):
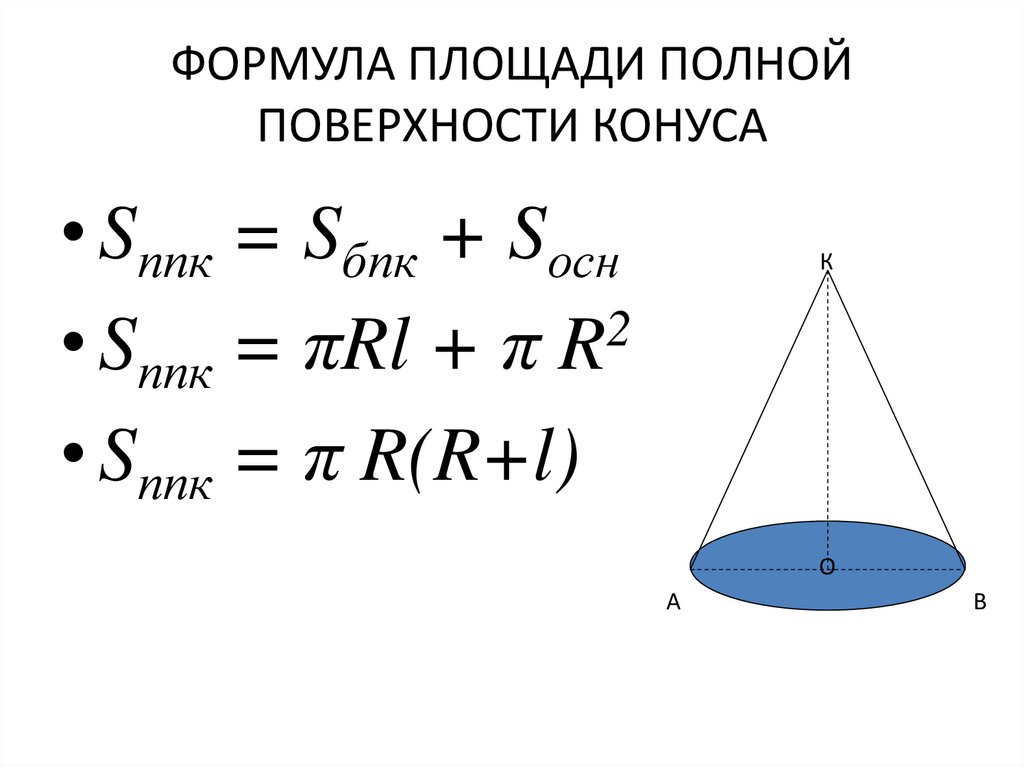
Объем конуса
Объем конуса равен трети от произведению площади его основания на высоту.
Формулы объема конуса
V = | 1 | So h |
3 |
V = | 1 |
πR2h |
3 |
где V- объем конуса,
So— площадь основания конуса, R- радиус основания конуса, h- высота конуса, π = 3.
141592
Формула объема усеченного конуса
R- радиус нижнего основания
r- радиус верхнего основания
h- высота конуса
π ≈ 3,14
Объем усеченного конуса, (V ):
4. Закрепление нового материала
1.Найдите объем цилиндрической мензурки с высотой, равной 3см и диаметром основания – 6см.
2. Площадь осевого сечения цилиндра равна 21см3, площадь основания — 18п см2 Найдите объем цилиндра.
3. Найдите объем конуса, осевое сечение которого представляет собой равнобедренный прямоугольный треугольник с гипотенузой, равной 6 см.
4.Найдите объем конуса, полученного в результате вращения вокруг большего катета прямоугольного треугольника с гипотенузой, равной 2 см, и углом 300.
5. Наибольшая диагональ правильной
шестиугольной призмы равна 8 см и составляет с боковым ребром угол в 300.
Найдите объем призмы.
6. Найти объем правильной треугольной пирамиды, высота которой равна 12 см, а сторона основания равна 13 см.
7. Вода покрывает приблизительно ¾ земной поверхности. Сколько квадратных км занимает суша? (радиус земли считать равным 6375 км)
8. Стаканчик для мороженого конической формы имеет глубину 12 см и диаметр верхней части 5 см. На него сверху положили две ложки мороженого в виде полушарий диаметром 5 см. Переполнит ли мороженое стаканчик, если оно растает?
Работа по УК
5. Тестовые задания для проверки уровня усвоения понятия «Объем»
Инструкция: Выберите правильный ответ из числа предложенных.
Вариант I
1) Не является единицей измерения объёма:
а) см3 б) баррель в) гектар г) м3
2) Развёрткой боковой поверхности цилиндра является:
а) круг б) прямоугольник в) треугольник г) ромб
3) Формула для вычисления объёма призмы:
а)V=1/2 Sосн h б)V=2 Sосн h в) V= Sосн/ h г) V= Sосн
4) Объём какой фигуры вычисляется формулой v=1/3 h (S + S1 +√SS1):
а) пирамиды б) усечённой пирамиды в) цилиндра г) шара?
5) Продолжите утверждение: равные тела…
а) имеют разные объёмы б) имеют равные объёмы в) иногда имеют равные, а иногда разные объёмы
Вариант II
1) Не является единицей измерения объёма:
а) мм3 , б) ар, в) галлон, г) дм3
2) Развёрткой боковой поверхности конуса является:
а) треугольник, б) круг в) круговой сектор, г) прямоугольник
3) Формула для вычисления объёма пирамиды:
а)V=1/3 Sосн h б)V= Sосн h в)V=1/2 Sосн h г) V= Sосн/ h
4) Формула v=1/3 h (S + S 1 +√SS1) позволяет вычислить объём:
а) конуса б) призмы в) цилиндра г) усечённого конуса
5) Продолжите утверждение: если тело составлено из нескольких тел, то его объём равен…
а) сумме объёмов этих тел б) разности объёмов этих тел
в) произведению объёмов этих тел
6.
Решить кроссворд «Объемы тел»
По горизонтали: 1. Фигура на плоскости, все точки которой расположены не далее данного расстояния от одной точки. 2. Прямая, при вращении которой вокруг оси образуется боковая поверхность цилиндра, конуса. 3.Тело, полученное вращением прямоугольника вокруг одной из его сторон . 4. Угол между высотой и плоскостью основания конуса. 5.Тело, полученное вращением круга вокруг оси, лежащей в плоскости круга и не пересекающей его.
По вертикали: 1. Тело, полученное вращением
прямоугольного треугольника вокруг одного из его катетов. 2. Плоская
фигура, при вращении которой образуется усеченный конус. 3. Тело
вращения, являющееся верхней частью архитектурного сооружения. 4. Отрезок, соединяющий две точки сферы и проходящей через центр шара. 5. Тело, полученное вращением полукруга вокруг его диаметра. 6. Тело,
полученное вращением полуокружности вокруг её диаметра.
7. Тело
вращения, об устойчивости движения которого написана известная работа великой
русской женщины-математика.
3 |
|
|
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2 | 5 |
|
|
|
|
|
|
2 |
|
|
|
|
| 7 |
|
|
|
|
|
|
|
|
|
|
| 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| 4 |
|
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 5 |
|
|
|
|
|
|
|
|
7.
Подведение итогов занятия и домашнее задание
Посмотреть
Эталоны ответов
1. Фронтальный опрос
· Какое геометрическое тело называют многогранником?
· Многогранник — замкнутая поверхность, составленная из многоугольников, также называют тело, ограниченное этой поверхностью. Эти многоугольники называются гранями, их стороны — рёбрами, а их вершины — вершинами многогранника
· Какие многогранники называются выпуклыми и невыпуклыми?
Многогранник называется выпуклым, если он весь расположен по одну сторону от плоскости его граней.
· Дайте определение призмы.
Призма -многогранник, у которого две грани — n -угольники (основания
), а остальные n граней (боковых) — параллелограммы.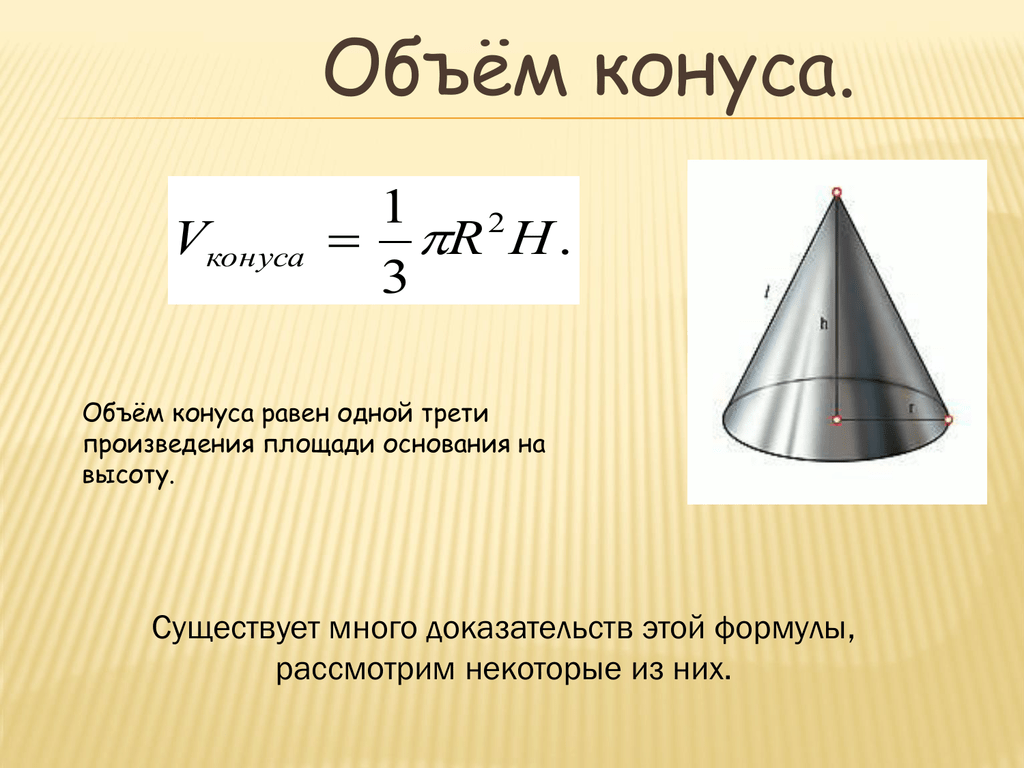
Основания
расположены в параллельных плоскостях. Призма называется прямой, если плоскости
боковых граней перпендикулярны к плоскости основания. Прямую призму называется
правильной, если основанием её служит правильный многоугольник.
· Какое тело называют пирамидой, усеченной пирамидой? Пирами́да — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину. По числу углов основания различают пирамиды треугольные, четырёхугольные и т. д
· Какие тела вращения вам известны?
Цилиндр, конус, усеченный конус, шар.
· Как можно получить цилиндр?
Цилиндр получается вращением прямоугольника вокруг одной из неподвижных сторон.
· Как можно получить конус?
Конус, как тело вращения можно получить вращением прямоугольного треугольника вокруг одного из катетов.
· Как можно получить усечённый конус?
Усеченный конус, как тело вращения
можно получить вращением прямоугольной трапеции.
· Что называем шаром? Сферой?
2. Математический диктант.
1) Написать формулу для вычисления площади поверхности и объёма призмы (куба, параллелепипеда).
Sбок = p*h=p*l; V = So*h
2)Написать формулу для вычисления площади поверхности и объёма пирамиды.
Sбок = 1/2*p*m; V=1/3*So*h
3) Написать формулу для вычисления площади поверхности и объема цилиндра
Sбок = p*h=p*l; V = So*h
V = | 1 |
So h |
3 |
4) Написать формулу для вычисления
площади поверхности и объёма конуса.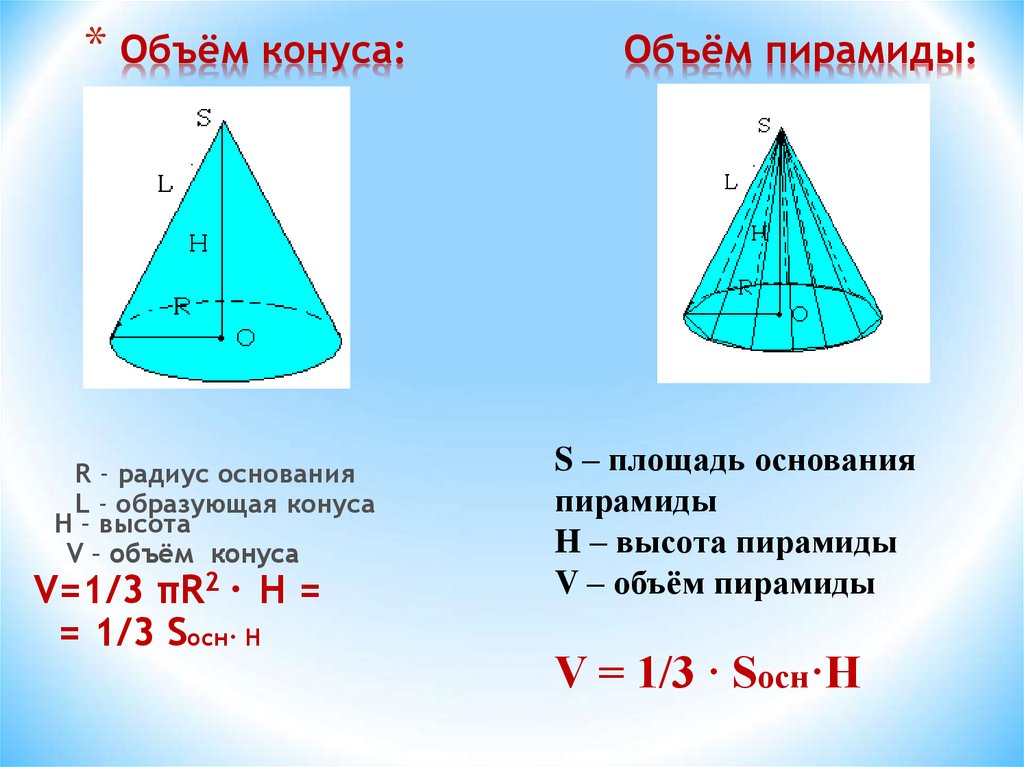
S = πRl
V = | 4 | π R 3 |
3 |
5) Написать формулу для вычисления площади сферы и объема шара.
S = 4 π R2
3. Учебные упражнения.
1. 27п см3
2. 63√2п см3
3. 9п см3
4. √3/3п см3
5. 72 см3
6. 507√3 см3
7. 63752п км2
8. нет
4. Тестовые задания.
1 вариант | 2 вариант | ||
Задание | Правильный ответ | Задание | Правильный ответ |
1 | В | 1 | Б |
2 | Б | 2 | В |
3 | Г | 3 | А |
4 | Б | 4 | Г |
5 | Б | 5 | А |
5.
Кроссворд
3 К |
|
|
|
| 1К | Р | У | Г |
|
У |
|
|
|
| О |
|
|
|
|
П |
| 2Т | 5Ш |
| Н |
|
|
|
|
2О | Б | Р | А | З | У | 7 Ю | Щ | А | Я |
Л |
| А | Р |
| С | Л |
| 6С |
|
|
| П |
|
|
| А |
| Ф |
|
|
| Е | 4Д |
|
|
|
| Е |
|
|
| 3Ц | И | Л | И | Н | Д | Р |
|
|
| И | А |
|
|
|
| А |
|
4П | Р | Я | М | О | Й |
|
|
|
|
|
|
| Е |
|
|
|
|
|
|
|
|
| Т |
|
|
|
|
|
|
| 5Ш | А | Р |
|
|
|
|
|
|
Объем конуса — веб-формулы
r: радиус основания
h: высота
Объем конуса определяется как:
V = π ∙ r 2 ∙ ч / 3,
где π∙ r 2 — площадь основания конуса.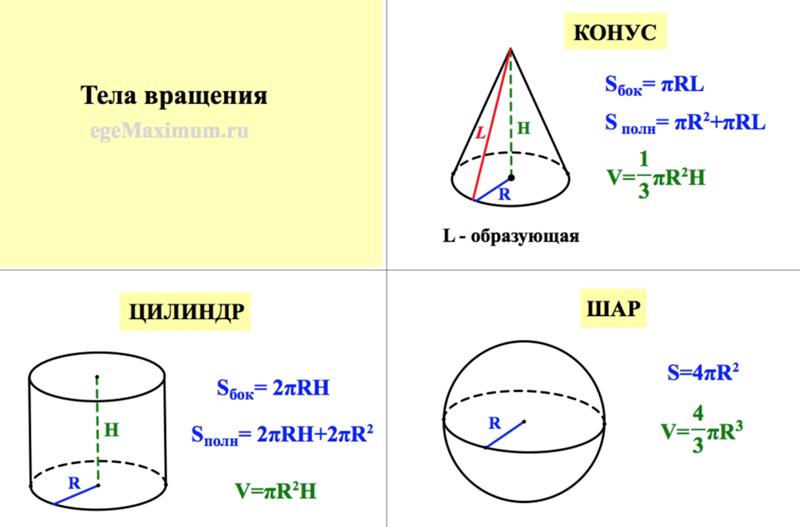
π определяет отношение длины окружности любого круга к его диаметру и приблизительно равно 3,141593, однако часто используется значение 3,14.
Пример 1: Найдите объем конуса, радиус которого 8 см, а высота 5 см.
Решение :
Формула для нахождения объема конуса:
V = π ∙ r 2 ∙ ч / 3
V = π ∙ 8 2 ∙ 5 / 3
V = 1004,8 / 3 = 334,93 см 3
Таким образом, объем конуса равен 334,93 см 3 .
Пример 2: Найдите объем конуса с радиусом основания 2,1 см и высотой 6 см, используя π = 22/7
Решение :
Объем конуса определяется как:
V = π ∙ r 2 ∙ ч / 3
V = 22/7 ∙ 2,1 2 ∙ 6 / 3
V = 27,72 см 3
Итак, объем конуса 27,72 см 3
Пример 3: Найдите объем конуса, диаметр которого 8 см, а высота 11 см.
Решение :
Как и в предыдущих примерах:
V = π ∙ r 2 ∙ h / 3
r определяется как D/2, то есть: 8см / 2 = 4см, вставляем значение r у нас есть:
V = π ∙ 4 2 ∙ 11 / 3
V = 552,64/3 см 3
V = 184,21 см 3
Таким образом, объем конуса равен 184,21 см 3 .
Пример 4: Найдите высоту прямого круглого конуса, объем которого 169 см 3 и радиус 4 см
Решение :
V = 1/3 ∙ π ∙ r 2 ∙ h
V = 169 = 1/3 ∙ 3,14 ∙ 4 2 ∙ ч
V = 169 = 16,75 ∙ ч
V = h = 169/16,75
V = h = 10,09 см
Высота правого кругового конуса 10,09 см.
Пример 5: Найдите высоту конуса, объем которого равен 22 см 3 и радиус конуса = 1 см, используйте π = 22/7
Решение :
V = 1/3 ∙ π ∙ r 2 ∙ ч = 22
V = 1/3 ∙ 22/7 ∙ 1 ∙ 1∙ h = 22
V = h = (22 ∙ 7 ∙ 3)/22
V = h = 21 см.
Пример 6: Окружность основания конической палатки высотой 9 м составляет 44 м. найдите объем воздуха, содержащегося в нем, используя π = 22/7
Решение:
Окружность основания:
P = 2 ∙ π ∙ r = 44 м
r = P / ( 2 ∙ π )
r = 44 / ( 2 ∙ π ) = 7 м
Высота конической палатки = 9м
Объем воздуха = 1/3 ∙ π ∙ r 2 ∙ h = 1/3 ∙22/7 ∙ 7 ∙ 7 ∙ 9 = 462 м 3
Пример 7: Вертикальная высота конической палатки 42 дм, а диаметр основания 5,4 м.
Определить количество человек, которое он может вместить, если каждый человек использует 2916 дм 3 использования площади π = 22/7
Решение :
Высота: h=42 дм
Диаметр: = 5,4 м = 54 дм
Радиус: r = D/2 = 27 дм
Объем = 1/3 ∙ π ∙ r 2 ∙ h
Объем = 1/3 ∙ 22/7 ∙ 27 ∙ 27 ∙ 42 = 32076 дм 3
Пространство на 1 человека =2916 дм 3
Количество человек = 32076 / 2916 = 11 человек.
Объем конуса: формула и примеры
Давайте научимся определять объем конуса .
Что такое конус? Конус представляет собой трехмерный объект, имеющий круглое основание ; вершина или вершина; высота , которая является перпендикулярным расстоянием от вершины до основания; и наклонная высота , которая относится к расстоянию от вершины в сторону и вниз до любой точки на базовой окружности.
Радиус основания конуса важен для нахождения объема конуса, который определяется как количество места, которое занимает объект. Объем измеряется в кубических единицах, таких как кубический дюйм (в 3 ), кубический фут (фут 3 ), кубический сантиметр (см 3 ) или кубический метр (м 3 ).
Чтобы найти объем конуса , умножьте произведение основания и высоты конуса на одну треть по следующей формуле:
V = 1/3 Bh V = 1/3
где B (основание) = π r² и h= высота
Связанные материалы: Объем цилиндра – формула и примеры
Как найти объем конуса :Шаг 1. Запишите указанные цифры. Убедитесь, что для радиуса и высоты используются одни и те же единицы измерения. Если нет, преобразуйте любой из них, чтобы он соответствовал другому.
Шаг 2. Подставьте полученные цифры в формулу.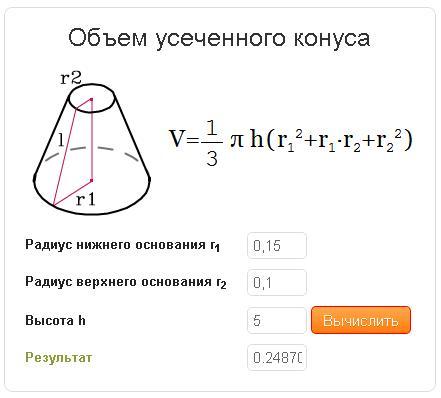
Шаг 3. Выполнить операции: умножение и деление. Запишите кубическую единицу вместе с ответом.
Пример №1: Найдите объем конуса, зная высоту и радиус
Найдите объем конуса ниже .
Решение для примера № 1:
Шаг 1. Запишите данные числа: радиус (r = 8см) и высота (h = 16см) .
Шаг 2. Замените 8 см на r и 16 см на h .
V = 1/3 π r²h
V = 1/3 π (8см)²(16см)
Шаг 3. Упрощение.
В = 1/3 π (64см²)(16см)
V = 1/3 π (1,024 см 3 ) ≈ 1,071,78…см 3
Таким образом, объем конуса равен примерно 9,1024 9 072 см 3 90
Пример 2. Найдите объем конуса, если единицы измерения различны высота
(h=2м) .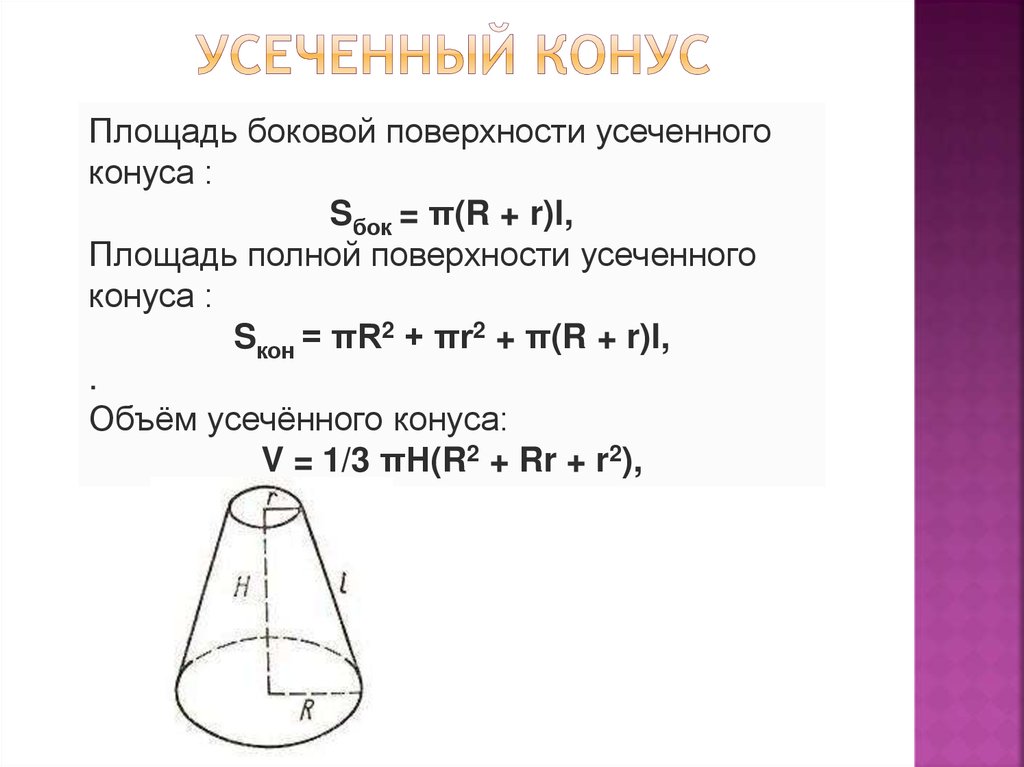
Поскольку они различаются по единицам измерения, преобразуйте любую из них, чтобы она соответствовала другой. Переведем 150 см в метры. Вы, наверное, помните, что 1 м = 100 см
Чтобы преобразовать 150 см в м, умножьте его на дробь:
1 м / r = 100 см / 150 см
Умножьте крест, чтобы найти r
100 см (r) = 150 см (1 м)
r = 150/100 м
r = 1,5 м
Таким образом, преобразованный радиус равен 1,5 м.
Шаг 2. Замените 1,5 м на r и 2 м на ч .
В = 1/3 π r²h
В = 1/3 π (1,5 м)²(2 м)
Шаг 3. Упрощение.
V = 1/3 π (2,25 м²)(2 м)
V = 1/3 π (4,5 м 3 ) ≈ 4,71 м 3
Спасибо, что прочитали. Мы надеемся, что это эффективно! Всегда не стесняйтесь возвращаться на эту страницу, если у вас возникнут какие-либо вопросы об объеме конуса .