Решение различных задач на проценты
Главная » Математика 5-9 класс » Задачи на проценты
Математика 5-9 класс
Автор Ольга Викторовна Опубликовано
Рассмотрим несколько задач на проценты. В целом все задачи решаются по единой схеме, меняются значения и условия. Мы должны хорошо понимать, что такое процент. Поэтому запомните правило.
Процент – это 1/100 часть от всего количества.
Содержание
Важные формулы
Для решения задач важно уметь переводить проценты в десятичные дроби. Это просто – разделите процент на 100. То есть,
10%=0,1 20%=0,2 30%=0,3 40%=0,4 50%= 0,5 60%=0,6 70%=0,7 80%=0,8 90%=0,9 100%=1
А если, например, 35% ? Ничего сложного, получится 35%=0,35. А теперь решим задачки
Задача 1
Задача: на клумбу посадили цветы – розы и тюльпаны.
Тюльпанов посадили 40 штук. А розы составляют 60% всех цветов. Сколько всего цветов посадили на клумбу?
Решение: Если роз 60% от всех цветов, то тюльпанов, значит, 40%.
Тогда пусть всего цветов на клумбе x. Тогда тюльпанов , тогда цветов. Значит, ответ будет 100.
Ответ: 100
Задача 2
В городском парке высадили два вида тюльпанов: белые и красные. Красных было 40% от всех цветов, а белых 126 штук. Сколько еще надо посадить красных тюльпанов, чтобы их было столько же, сколько белых? Сколько сейчас в парке цветов?
Решение: Пусть всего было x цветов. Тогда красных цветов будет 0,4x. Тогда получим уравнение:
Итак, всего 210 цветов, тогда красных цветов .
Чтобы красных цветов стало столько же, сколько и белых цветов: .
Таким образом, чтобы красных цветов было столько же, сколько и белых цветов, надо посадить еще 42 красных цветка.
Ответ: 42 и 210.
Задача 3
Что больше: 2% от 6 или 6% от 2?
Решение: итак 2% от 6 – это , а 6% от 2 – это .
Таким образом получается, что это равные значения.
Ответ: они равны.
Задача 4
В магазин привезли 900 кг картофеля. 45% картофеля продали в первый день. На второй день продали 2/5 от того, что осталось с продажи в первый день. Сколько килограмм картофеля осталось после двух дней торговли?
Решение. В первый день продали 45% картофеля. Посчитаем сколько это кг картофеля. На второй день продали 2/5 от того, что осталось с продажи. Посчитаем сколько осталось с продажи в первый день, для этого от 900 кг отнимем 405 кг , теперь найдем 2/5 от 495: кг. Итак, получается в первый день продали 405 кг картофеля, во второй день продали 198 кг картофеля. Итого, за два дня продали
. Осталось картофеля .
Ответ: 297 кг.
Задача 5
Найди чему равны
- 21% от числа 400
- 8% от числа 5000
Решение:
Ответ: 84; 400.
Задача 6
Найдите число, если
- 15% этого числа равны 60
- 30% этого числа равны 150
Решение:
- Пусть число , тогда , отсюда .
- Пусть число , тогда , отсюда
Ответ: 400; 500.
( 3 оценки, среднее 5 из 5 )
Поделиться с друзьями
Текстовые задачи на проценты — что это, определение и ответ
Для быстрого и верного решения задач на проценты нужно понимание сути процента, умение считать проценты и внимательно читать условие.
С процентами нам постоянно приходится сталкиваться в повседневной жизни. «Скидка 30%», «Кредит без процентов за 5 минут», «Арендная плата выросла на 12%» — со всех сторон на нас сыплются рекламные слоганы и призывы. Но что же значит слово «проценты»? И как ими оперировать?
Проценты являются удобным инструментом. Нужны они для нахождения части от чего-то. Вообще говоря, звучит похоже на определение дроби.
И действительно, проценты очень тесно связаны с дробями, по сути, основываются на них.
Что такое процент?
Процент – это всегда доля какого-то числа.
100% — все число
50% — половина
25% — четверть
Чтобы найти 1%, необходимо поделить всё число на 100.
Один процент – одна сотая доля.
Нахождение процента через деление на 100:
1. Делим изначальное число на 100 (таким образом получаем величину 1 процента от числа).
2. Умножаем на нужное нам количество процентов.
Например, чтобы найти 25% от 200, нужно:
Сначала найти, сколько составляет 1% от 200:
\(200:100 = 2\)
2.Умножить полученное значение на нужное нам количество процентов, то есть на 25:
\(2 \cdot 25 = 50\)
Нахождение процента через умножение на десятичную дробь:
Принцип действия тот же, однако 2 действия объединяем в одно – умножаем исходное число сразу на дробь.
1. Превращаем процент в дробь (отсчитываем 2 символа справа и ставим запятую), например:
\(115\% = 1,15\)
\(82\% = 0,82\)
\(7\% = 0,07\)
\(25\% = 0,25\)
2. Умножаем число на полученную дробь:
25% от \(200 = 200 \cdot 0,25 = 50\)
Нахождение процента упрощённым способом «по кубикам»
Пользуясь правилом перевода процента в десятичную дробь, а затем – правилом перевода десятичной дроби в обыкновенную, можем вывести стандартные соотношения:
\(1\% = \frac{1}{100}\)
\(\ 10\% = \frac{1}{10}\)
\(\ 20\% = \frac{1}{5}\)
\(\ 25\% = \frac{1}{4}\)
\(\ 50\% = \frac{1}{2}\)
\(\ 75\%\ = \frac{3}{4}\)
Тогда работу с дробями мы можем заменить простым умножением или делением.
Например, чтобы найти 25% от 200, можно 200 поделить на 4 и получить 50.
Итак, пользуясь методом кубиков всегда можно найти 50%, 25%, а также 1%,10% и 20%. Например:
Для вычисления 1% нужно поставить запятую после второго символа, а для нахождения 10% поставить запятую после первого символа.
Далее, чтобы получить иной процент, нужно умножить полученное значение на нужное количество процентов. Например:
Как работать с процентами в текстовых задачах?
Для работы с процентами используется пропорция, в которой в одном столбце записываются реальные значения, в другом – соответствующие проценты.
Исходя из правил работы с дробями, получаем правила работы с пропорцией.
1. Внутри одной дроби можно сокращать значения.
2. Произведение накрест лежащих значений равно.
Например, если известно, что всего на прилавке имеется 200 груш, и нужно найти, сколько груш составляет 1%.
Составляем пропорцию:
200 груш – 100 %
x груш – 1 %
Пользуемся правилом произведения накрест лежащих значений:
\(200 \cdot 1 = x \cdot 100\)
Выражаем искомую величину:
\(x = \frac{200 \cdot 1}{100} = 2\)
Получаем готовое соотношение:
200 груш – 100 %
2 груши – 1 %
Итак, 1% от всего количества составляет 2 груши.
Или другая задача: известно, что 20% от всего количества составляет 40 груш. Сколько всего груш на прилавке?
Составляем пропорцию:
x груш – 100 %
40 груш – 20 %
Пользуемся правилом произведения накрест лежащих значений:
\(x \cdot 20 = 40 \cdot 100\)
Выражаем искомую величину:
\(x = \frac{40 \cdot 100}{20} = 200\)
Получаем готовое соотношение:
200 груш – 100 %
40 груш – 20 %
Итак, 100% — это 200 груш.
Видим, что пропорция отражает зависимость величин, по-другому это можно записать в виде двух дробей:
\(\frac{200}{2} = \frac{100}{1}\) или \(\frac{200}{40} = \frac{100}{20}\)
Процентный класс 5 Математика – Рабочий лист
Реклама
Здравствуйте, студенты, добро пожаловать в Net Explanations. На этой странице мы разместили несколько ответов на дополнительные вопросы по математике в процентном классе 5.
процентов класса 5 Математика — Рабочий листГлава 7
Раздел A
1) Конвертируйте следующую фракцию в процентах с Denomator 100: 1). A) 6/9 B) 25/8 C) 15/5 2) Преобразование десятичных дел в процент: A) 1,50 B) 15,79 C) 19.87 3) Преобразование следующего в процент множественного по 100: A) 13/26 B) 3/9 C) 525/25 4) Найдите следующее: а) 10% от 50 б) 80% от 80 в) 16% от 48 г) 56% от 79 5) Преобразуйте следующие проценты в меньшую дробь: а) 195% б) 26%
0008
6) Найдите процент:
A) 30% из 560
B) 19% из 689
C) 93% из 278
Секция BСекция B
. 1) Преобразуйте следующие проценты в дробь в низшей форме: а) 55 9/3% б) 38 11/33% в) 79 26/13% вода б) 53% на 20 кг пшеницы в) 13% на 113 кг риса c) 62% Раздел C 1) Рам купил платье стоимостью рупий. 2) Рини читала книгу, содержащую 1213 страниц, а она прочитала только 300 страниц. Каков процент страниц, которые она прочитала? 3) Человек купил землю стоимостью 2800000 рупий, он заплатил 37% вперед, остальное заплатит позже. Как он должен платить позже? 4) Баран купил 5 кг яблок стоимостью рупий. 500 со скидкой, а продавец требует 800 рупий. Тогда сколько процентов он получил со скидкой? 5) Нидхи получила 327 баллов из 700 на выпускном экзамене. Найдите процент, который она получила? 6) Шьям получил 390 баллов из 500 на выпускном экзамене. Найдите процент, который он получил. 7) Человек купил автомобиль стоимостью 280000 рупий он заплатил 87% вперед а остальное заплатит позже. Как он должен платить позже? Раздел D 1) Рам купил платье стоимостью рупий. 2) Рини читала книгу из 1203 страниц, а она прочитала только 390 страниц. Каков процент страниц, которые она прочитала? 3) Человек купил землю стоимостью 2800000 рупий, он заплатил 37% вперед, остальное заплатит позже. Как он должен платить позже? 4) Рам купил 10 кг апельсинов на рупии. 850 со скидкой, а продавец требует 1000 рупий. Тогда сколько процентов он получил со скидкой? 5) Нидхи получила 527 баллов из 700 на выпускном экзамене. Найдите процент, который она получила? 6) Шьям получил 290 из 500 на выпускном экзамене. Найдите процент, который он получил. 7) Человек купил дом стоимостью 270000 рупий, он заплатил 67% вперед, остальное заплатит позже. Как он должен платить позже? Решение:- ГЛАВА 7 Раздел A 1) A) 66,67% B) 25/8 = 312,5% C) 15/5 = 5 = 25/312,5% C) 300% 2) а) 1,50=150% б) 15,79=1579% c) 19,87 = 1987% 3) Преобразуйте следующее число в проценты, кратные 100: a) 13/26 = 50%b) 3/9 = 33,33% c) 525/25 % 4) а) 10% от 50 = 5 б) 80% от 80 = 64 в) 16% от 48 = 7,68 г) 56% от 79 = а) 195% = 39/20 б) 26% = 13/50 в) 83% = 83/100 г) 67% = 67/100 6) 4 а) 560 = 168 B) 19% из 689 = 130,91 C) 93% из 278 = 258,54 Раздел B 1) A) 559/3% = 55900/3 B) 3811/33%. c) 7926/13% = 792600/13 2) a) 33% на 60 л воды = 99/5 b) 53% на 53 кг пшеницы = 203 /5 c) 13% от 113 кг риса = 1469/100 3) Преобразовать проценты в дроби: а) 60% = 3/5 b) 73% = 73/100 c) 62% = 31/50 РАЗДЕЛ C Х100 = 24,72 ок. 25% страниц прочитано Ринни. 3) Заплатил авансом = (2800000Х37/100) =1036000. Потом заплатит = 2800000-1036000= 1764000 4) (800-500/800) Х100 = 37,5% получил по скидке 05 5) Она получила (327/700) X100=46,71% 6) Он получил. (390/500)Х100=78% 7) 36400 рупий должны быть оплачены им позже. РАЗДЕЛ D 1) (1900/3800) Х100 = 50% получил по скидке 2) (1000-850)/1000) Х100 = 15% получил по скидке 4) Он получил 58% на экзамене 5) 89100 рупий он заплатит позже. Мы предоставляем больше рабочих листов для класса – V. Чтобы увидеть больше рабочих листов, нажмите ниже – Уважаемый студент, я ценю ваши усилия и тяжелую работу, которую вы все вложили. Спасибо за то, что беспокоитесь о нас, и я желаю вам дальнейших успехов. Для тех, кто ищет задачи в процентах в процентах, они прибыли по адресу. Воспользуйтесь доступными задачами на процентное соотношение слов и легко решайте подобные вопросы. Регулярно выполняйте Задачи на проценты с решениями и получайте подробное объяснение, чтобы перепроверить, где вы ошиблись. Обратившись к нашей статье, вы сможете быстро и эффективно решить различные проблемы, связанные с процентами. 1. 10 % книг в публичной библиотеке — это научные книги. Если в библиотеке 90 000 книг, найдите количество доступных книг по естествознанию? Решение: Общее количество книг =
1500 по скидке, а он был отмечен как 2800. Тогда сколько процентов он получил по скидке? 
1900 по скидке, а было отмечено как 3800. Тогда сколько процентов он получил по скидке? 
= 381100/33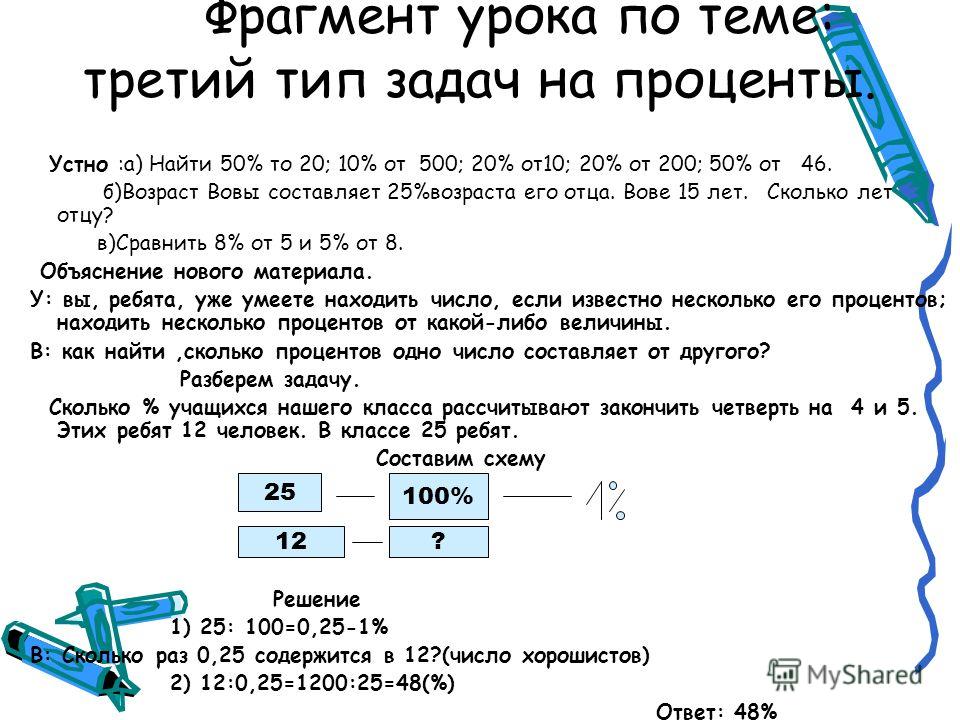
Словесные задачи на проценты | Задачи в процентах с ответами
10% книг составляют научные
, следовательно, 10/100*90,000
= 9000
Общее количество научных книг, доступных в библиотеке 0.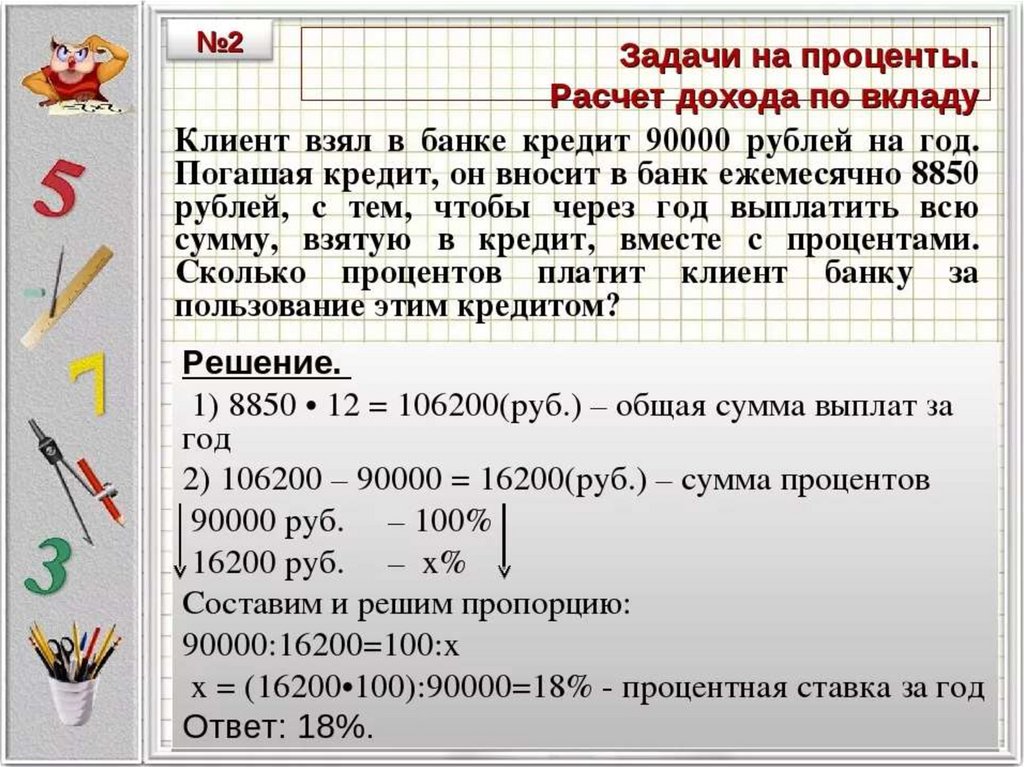
0. 2. Бейсбольный питчер выиграл 70% игр, которые он подавал. Если он провел 40 игр с мячом, сколько игр он выиграл?
Решение:
70/100 =x /40
Умножая на крест, получаем = (70*40)/100
= 28
Следовательно, он выиграл 28 партий.
3. Дэвид прошел тест по математике и получил 25 правильных и 15 неправильных ответов. Каков был процент правильных ответов?
Решение:
Всего ответов = 25+15
= 40
Процент правильных ответов = 25/40*100
= 2500/40
= 62,5%
ответов 6 .
4. В бригаде 45 плотников. В определенный день их было 27. Какой процент вышел на работу?
Решение:
Процент плотников, явившихся на работу = (27/45)*100
= 2700/45
= 60%
Следовательно, 60% плотников явились на работу.
5. Металлический брусок весит 7 кг. 93% слитка — серебро. Сколько кг серебра в слитке?
Решение:
Из предоставленных данных
93% слитка — серебро
= 93% от 7 кг
= 93/100*7
= 651/100
= 6,51 кг
Следовательно, 6,51 кг серебра находится в слитке.