Определители матриц
Для каждой квадратной матриц вводится важная ее числовая характеристика, называемая определителем этой матрицы. Правило, по которому по элементам данной квадратной матрицы произвольного порядка вычисляется ее определитель, достаточно сложно, поэтому будем давать это правило «постепенно», повышая порядок определителя. Пока же ограничимся таким неконструктивным определением.
Каждой квадратной матрице можно по некоторому (вот в чем неконструктивность!) правилу поставить в соответствие число, которое называется определителем данной матрицы. Для определителя квадратной матрицы A, общий вид которой дан в (2), применяются различные обозначения. Укажем наиболее употребительные: или развернутое, в котором перечисляются все элементы данной матрицы:
. Прямые черты, заменяющие круглые (матричные) скобки, указывают на то, что имеется в виду именно определитель матрицы, т.е. единственное число, а не сама матрица
Будем подбираться к строгому определению определителя, рассмотрев это правило последовательно для определителей матриц 1-го, 2-го и 3-го порядков.
Определителем матрицы 1-го порядка называется число, равное единственному имеющемуся у матрицы числу − матричному элементу этой матрицы. Определение настолько простое, что нет необходимости иллюстрировать его примером.
Определитель матрицы второго порядка.
Если , то по определению
Например, .
Рассмотрим определитель матрицы третьего порядка .
Всё, что мы будем далее говорить для
этой матрицы, справедливо и для квадратной
матрицы любого порядка. Определение
определителя матрицы содержит два новых
понятия. Оказывается, для каждого
элемента матрицы (а их всего 9) можно
посчитать 2 числа, которые называются,
соответственно, минором и алгебраическим
дополнением этого элемента.
Минором элемента матрицы (обозначается ) называется значение определителя матрицы, получающейся из данной матрицы вычеркиванием строки и столбца, на пересечении которых стоит данный элемент (т.е. вычеркиванием i-ой строки и j-го столбца).
Алгебраическим дополнением элемента матрицы (обозначается ) называется число, определяемое по формуле
(3) .
Поскольку число (–1) в целой степени принимает всего два значения ( 1 – если показатель степени есть четное число и (–1) – если нечетное), то алгебраическое дополнение элемента матрицы либо ничем не отличается от минора этого элемента (если сумма его нижних индексов – т.е. сумма номеров строки и столбца – есть четное число) или отличается от минора только знаком (если сумма нижних индексов нечетна).
Пример. Найти миноры и алгебраические дополнения всех элементов матрицы
(4) А = .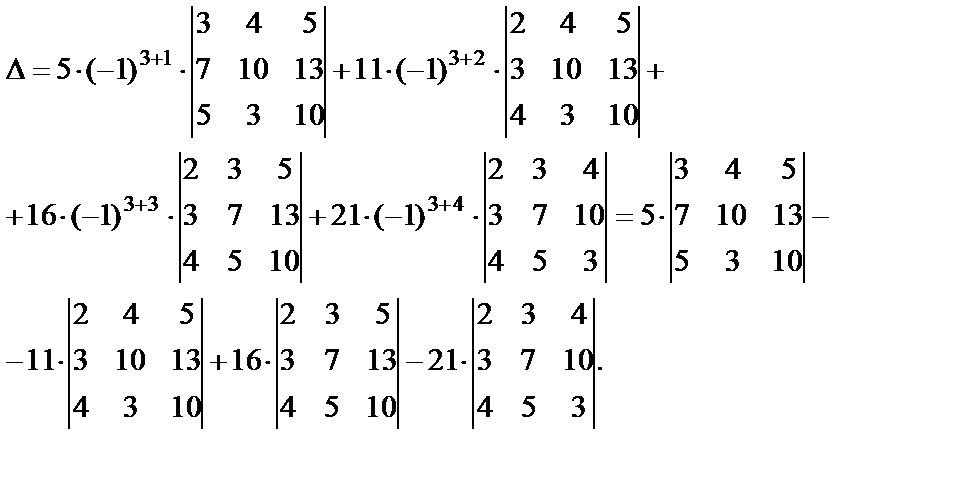
Решение. Сначала ищем миноры всех элементов.
М11= , М12= , М13= ,
М21= , М22= , М23= ,
М31= , М32= , М33= .
Учитывая формулу (3) и приведенные ниже пояснения для этой формулы, получаем следующие алгебраические дополнения
.
Для матрицы (4) для
каждой строки (и столбца) проделаем:
составим сумму попарных произведений
ее (его) элементов на их алгебраические
дополнения. Например, для второго
столбца : .
Взяв любой другой столбец (или строку),
получим то же самое число (для данной
матрицы это (– 4) ). Это общее свойство
всех квадратных матриц − результат
таких вычислений не зависит от того,
какую строчку или столбец матрицы мы
выбрали.
Поэтому корректно следующее
определение.
Определителем квадратной матрицы (любого порядка!) называется число, равное сумме попарных произведений элементов любой строки (столбца) на их алгебраические дополнения.
Поэтому для матрицы (4) по этому определению: D = .
Для вычисления определителя именно третьего порядка есть упрощенная (по сравнению с общим определением) формула
,
которая схематически (для запоминания) записывается так:
( + )
– первые три слагаемые (берутся со знаком +),
– последние 3 слагаемые (берутся со знаком −)
Пример. Найдем по упрощенной схеме определитель матрицы (4).
.
Как и следовало
ожидать, результат получился тот же,
что и ранее.
Для вычисления определителей матриц более высокого (чем третьего) порядка упрощенной схемы нет, поэтому используется только метод, данный в определении: выбирается строка или столбец матрицы и вычисляется сумма попарных произведений соответствующих элементов матрицы на их алгебраические дополнения. При этом вычисление алгебраических дополнений – самый хлопотный этап. Но поскольку строку (или столбец) можно выбирать произвольно (результат от этого не зависит), то проще выбрать ту, среди элементов которой как можно больше нулевых. При этом алгебраические дополнения нулевых элементов можно не считать, так как при составлении упомянутой выше суммы попарных произведений соответствующие слагаемые все равно обратятся в ноль.
Пример. Вычислить определитель 4-го порядка: .
Решение. Самое
большое количество нулей в любой из
строк или столбцов равно 2. Поэтому для
вычисления определителя выбираем любую
строку или столбец с двумя нулями.
.
Появившиеся два определителя 3-го порядка можно считать по приведенной выше упрощенной схеме.
Если среди элементов матрицы нулей мало (или нет вовсе), то можно специальными действиями привести определитель к такому виду, у которого есть строка (или столбец), в которой отличен от нуля только один элемент. После этого определитель легко вычисляется разложением по этой строке (столбцу). Привести определитель к такому виду помогают свойства определителей, рассмотренные ниже.
linear алгебра — Упростите определитель матрицы $4 \times 4$.
Задавать вопрос
спросил
Изменено 4 года, 2 месяца назад
Просмотрено 338 раз
$\begingroup$
Мне нужно найти определитель следующей матрицы 4×4: $\quad A=\begin{bmatrix}3&0&1&0\\0&2&0&0\\1&0&3&0\\0&0&0&-4\end{bmatrix}$
Итак, я применяю исключение Гаусса, чтобы получить матрицу верхнего треугольника: $$det\begin{bmatrix}3&0&1&0\\0&2&0&0\\1&0&3&0\\0&0&0&0&-4\end{bmatrix}=\begin{vmatrix}3&0&1&0\\0&2&0&0\\1&0&3&0\\0&0&0&-4\end{vmatrix}\xrightarrow {3R_3-R_1}\begin{vmatrix}3&0&1&0\\0&2&0&0\\0&0&8&0\\0&0&0&-4\end{vmatrix}$$
Поскольку я знаю из решений, что определитель равен -64, я полагаю, что мне нужно упростить третью строку в приведенной форме до $\quad 0 \quad 0 \quad 2 \quad 0 \quad$ и затем умножить элементы по диагонали сверху слева направо снизу, что действительно равно -64.
Но это не имеет особого смысла, так как есть еще $-4$, которые мы можем упростить. Может ли кто-нибудь объяснить мне фактические правила, которым мы должны следовать?
- линейная алгебра
- матрицы
- определитель
$\endgroup$
5
$\begingroup$
Должно быть: $$\begin{vmatrix}3&0&1&0\\0&2&0&0\\1&0&3&0\\0&0&0&-4\end{vmatrix}\rightarrow \begin{vmatrix}3&0&1&0\\0&2&0&0\\0&0&\color{red}{ 3-{1\over 3}}&0\\0&0&0&-4\end{vmatrix}$$
$\endgroup$
5
$\begingroup$
Вместо применения операций со строками расширьте второстепенные.
$\det A = -4\begin{vmatrix} 3&0&1\\0&2&0\\1&0&3\end{vmatrix} = (-4)(18-2) = -64$
Если вы применяете операции со строками, вы не не хочу, чтобы ваши операции со строками изменяли определитель.
Думаю умножить на элементарную матрицу.
$\begin{vmatrix} 1\\&1\\-\frac 13&&1\\&&&1\end{vmatrix}\begin{vmatrix} 3&0&1&0\\0&2&0&0\\1&0&3&0\\0&0&0&-4\end{vmatrix} = \ begin{vmatrix} 3&0&1&0\\0&2&0&0\\0&0&\frac {8}{3}&0\\0&0&0&-4\end{vmatrix}$
сохраняет определитель без изменений.
в то время как
$\begin{vmatrix} 1\\&1\\-1&&3\\&&&1\end{vmatrix}\begin{vmatrix} 3&0&1&0\\0&2&0&0\\1&0&3&0\\0&0&0&-4\end{vmatrix} = \begin{vmatrix} 3&0&1&0\\0&2&0&0\\0&0&8&0\\0&0&0&-4\end{vmatrix}$
изменит определитель в 3 раза.$
$\endgroup$
$\begingroup$
Просто расширьте первую строку:
\начать{выравнивать}
\begin{vmatrix}3&0&1&0 \\
0&2&0&0 \\
1&0&3&0 \\
0&0&0&-4
\end{vmatrix}&=
3\,\begin{vmatrix}
2&0&0 \\
0&3&0 \\
0&0&-4
\end{vmatrix}+
1\,\begin{vmatrix}
0&2&0 \\
1&0&0 \\
0&0&-4
\end{vmatrix}
=3(2\cdot3\cdot(-4))+1(-1)\begin{vmatrix}
2&0 \\
0&-4
\end{vmatrix}\\
&=-72+8=-64.
$\endgroup$
$\begingroup$
Распространенная ошибка, которую вы допустили, заключается в том, что замена $R_3$ на $3R_3-R_1$ не является элементарной операцией со строками. Вы можете добавить кратное $R_1$ к $R_3$ без изменения определителя, но не наоборот. То, что вы сделали, представляет собой комбинацию двух элементарных операций со строками: $R_3\to3R_3$ и $R_3\to R_3+R_1$. Вторая операция не влияет на определитель, но первая умножает его на $3$, так что вам придется делить на $3$ в конце, когда вы объединяете диагональные записи. После того, как вы учли введенный вами фактор в размере 3 долларов, вы получите правильное значение.
В качестве альтернативы вы могли бы выполнить $R_3\to R_3-\frac13R_1$, чтобы очистить первый столбец без изменения значения определителя. Обратите внимание на разницу между этим и тем, что вы сделали: последняя операция умножает на скаляр отличных строк от заменяемых.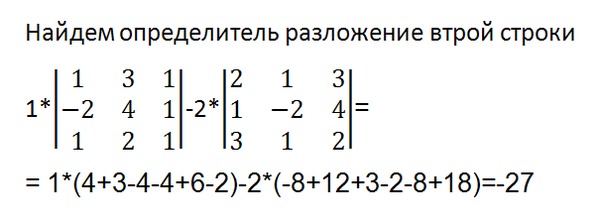
Как уже отмечали другие, гораздо более простой способ вычислить определитель этой матрицы — использовать преимущества всех этих нулей в первой и второй строке/столбце и расширять их по младшим.
$\endgroup$
Определитель матрицы 4×4 – Как вычислить определитель матрицы 4×4?
Знакомство с определителем матрицы 4×4
Определитель — это математическая формула, используемая для вычисления размера определенной матрицы. Определитель также используется, чтобы определить, является ли матрица обратимой или нет. Определитель матрицы 4×4 — это математическая формула, которая используется для вычисления размера конкретной матрицы. Определитель матрицы 4 × 4 также используется для определения того, является ли матрица обратимой или нет. Определитель матрицы 4 × 4 — Как вычислить определитель матрицы 4 × 4?
Зарегистрируйтесь, чтобы получить бесплатный пробный тест и учебные материалы
+91
Подтвердите OTP-код (обязательно)
Я согласен с условиями и политикой конфиденциальности.
Определение определителя
Определитель квадратной матрицы представляет собой скалярное значение, связанное с матрицей. Определитель обычно обозначается символом \mathrm{det} или \mathrm{D}. Определитель можно вычислить, используя комбинацию алгебраических свойств матрицы и суммы ее строк и столбцов.
Что такое Матрица?
Матрица — научно-фантастический боевик 1999 года, написанный и снятый Вачовски, с Киану Ривзом, Лоуренсом Фишбёрном, Кэрри-Энн Мосс, Хьюго Уивингом и Джо Пантолиано в главных ролях. Фильм является адаптацией серии комиксов «Матрица» Вачовски.
«Матрица» рассказывает историю Нео (Ривза), компьютерного хакера, который узнает от таинственных повстанцев об истинной природе своего мира: что это смоделированная реальность, созданная машинами для того, чтобы держать человеческую расу в рабстве. Освободившись из Матрицы, Нео должен сразиться с агентами Матрицы и ее деспотичным правительством.
«Матрица» — культовый и влиятельный фильм, популяризировавший концепцию «Матрицы» и положивший начало карьере сценаристов и режиссеров Вачовски.
Фильм хвалят за новаторские визуальные эффекты, последовательности действий, а также философские и метафизические темы.
Ярлык для определения ранга матрицы
Чтобы найти ранг матрицы, используйте функцию ранга в MATLAB. Эта функция принимает матрицу в качестве входных данных и возвращает ранг матрицы.
Символ определителя
Определитель — это математический символ, который используется для определения размера и формы матрицы. Он представлен маленькой квадратной скобкой, расположенной над и справа от матрицы. Определитель матрицы вычисляется путем умножения диагональных элементов и последующего вычитания произведений недиагональных элементов.
Для матрицы 2×2
Для матрицы 3×3
Для матрицы 2×3
Для матрицы 4×4
Для матрицы 3×4
Для матрицы 5×5
Для матрицы 4×5
Для матрицы 6×6
Для матрицы 5×6
Для матрицы 7×7
Для a Матрица 6×7
Для матрицы 8×8
Для матрицы 7×8
Для матрицы 9×9
Для матрицы 8×9
Определитель для матрицы 2×2
Если A является матрицей 2×2, тогда определитель A равен
A =
Это формула, которую можно использовать для вычисления определителя матрицы 2×2.
Для матрицы 3×3
A =
1 2 3
4 5 6
7 8 9
Как вычислить определитель матрицы 4×4?
Перед вычислением определителя матрицы 4-го порядка проверим несколько условий.
- , если есть какое-либо условие, при котором определитель может быть равен 0 (например, полная строка или полный столбец равны 0)
- , если возможно вынесение на множители любой строки или столбца.
- Если элементы матрицы одинаковы, но переупорядочены в любом столбце или строке.
Если соблюдается любой из трех приведенных выше случаев, используются соответствующие методы вычисления определителя 3*3. Мы преобразуем строку или столбец, чтобы заполнить его 0, за исключением одного элемента. Определитель будет эквивалентен произведению этого элемента и его кофактора. В этой ситуации кофактор представляет собой детерминант 3 × 3, который оценивается по своей конкретной формуле.
Связанный контент
| 1 миллиард рупий – перевод, решенные примеры и часто задаваемые вопросы |
| Класс 12 Математические решения NCERT Solutions — NCERT Solutions для математики класса 12 |
| Введение в 3D Геометрию, координатные системы и формулы |
NCERT Solutions для класса 6. |