Простая линейная регрессия: Введение в простую линейную регрессию

Введение в простую линейную регрессию

---

Простая линейная регрессия — это статистический метод, который можно использовать для понимания связи между двумя переменными, x и y.

Одна переменная x известна как предикторная переменная .

Другая переменная, y , известна как переменная ответа .

Например, предположим, что у нас есть следующий набор данных с весом и ростом семи человек:

Пусть вес будет предикторной переменной, а рост — переменной отклика.

Если мы изобразим эти две переменные с помощью диаграммы рассеяния с весом по оси x и высотой по оси y, вот как это будет выглядеть:

Предположим, нам интересно понять взаимосвязь между весом и ростом. На диаграмме рассеяния мы ясно видим, что по мере увеличения веса рост также имеет тенденцию к увеличению, но для фактической количественной оценки этой взаимосвязи между весом и ростом нам нужно использовать линейную регрессию.

Используя линейную регрессию, мы можем найти линию, которая лучше всего «соответствует» нашим данным. Эта линия известна как линия регрессии наименьших квадратов, и ее можно использовать, чтобы помочь нам понять взаимосвязь между весом и ростом. Обычно вы должны использовать программное обеспечение, такое как Microsoft Excel, SPSS или графический калькулятор, чтобы найти уравнение для этой линии.

Формула линии наилучшего соответствия записывается так:

ŷ = б 0 + б 1 х

где ŷ — прогнозируемое значение переменной отклика, b 0 — точка пересечения с осью y, b 1 — коэффициент регрессии, а x — значение переменной-предиктора.

Связанный: 4 примера использования линейной регрессии в реальной жизни

Поиск «Линии наилучшего соответствия»

Для этого примера мы можем просто подключить наши данные к калькулятору линейной регрессии Statology и нажать « Рассчитать »:

Калькулятор автоматически находит линию регрессии методом наименьших квадратов :

ŷ = 32,7830 + 0,2001x

Если мы уменьшим масштаб нашей диаграммы рассеяния и добавим эту линию на диаграмму, вот как это будет выглядеть:

Обратите внимание, как наши точки данных близко разбросаны вокруг этой линии. Это потому, что эта линия регрессии методом наименьших квадратов лучше всего подходит для наших данных из всех возможных линий, которые мы могли бы нарисовать.

Как интерпретировать линию регрессии методом наименьших квадратов

Вот как интерпретировать эту линию регрессии наименьших квадратов: ŷ = 32,7830 + 0,2001x

б0 = 32,7830.Это означает, что когда предикторная переменная веса равна нулю фунтов, прогнозируемый рост составляет 32,7830 дюйма. Иногда может быть полезно знать значение b 0 , но в этом конкретном примере на самом деле нет смысла интерпретировать b 0 , поскольку человек не может весить ноль фунтов.

б 1 = 0,2001.Это означает, что увеличение x на одну единицу связано с увеличением y на 0,2001 единицы. В этом случае увеличение веса на один фунт связано с увеличением роста на 0,2001 дюйма.

Как использовать линию регрессии наименьших квадратов

Используя эту линию регрессии наименьших квадратов, мы можем ответить на такие вопросы, как:

Какого роста мы ожидаем от человека, который весит 170 фунтов?

Чтобы ответить на этот вопрос, мы можем просто подставить 170 в нашу линию регрессии для x и найти y:

ŷ = 32,7830 + 0,2001 (170) = 66,8 дюйма

Какого роста мы ожидаем от человека, который весит 150 фунтов?

Чтобы ответить на этот вопрос, мы можем подставить 150 в нашу линию регрессии для x и найти y:

ŷ = 32,7830 + 0,2001 (150) = 62,798 дюйма

Предупреждение. При использовании уравнения регрессии для ответа на подобные вопросы убедитесь, что вы используете только те значения переменной-предиктора, которые находятся в пределах диапазона переменной-предиктора в исходном наборе данных, который мы использовали для создания линии регрессии методом наименьших квадратов. Например, вес в нашем наборе данных варьировался от 140 до 212 фунтов, поэтому имеет смысл отвечать на вопросы о прогнозируемом росте только тогда, когда вес составляет от 140 до 212 фунтов.

Коэффициент детерминации

Одним из способов измерения того, насколько хорошо линия регрессии наименьших квадратов «соответствует» данным, является использование коэффициента детерминации , обозначаемого как R 2 .

Коэффициент детерминации — это доля дисперсии переменной отклика, которая может быть объяснена предикторной переменной.

Коэффициент детерминации может варьироваться от 0 до 1. Значение 0 указывает на то, что переменная отклика вообще не может быть объяснена предикторной переменной. Значение 1 указывает, что переменная отклика может быть полностью объяснена без ошибок с помощью переменной-предиктора.

R 2 между 0 и 1 указывает, насколько хорошо переменная отклика может быть объяснена переменной-предиктором. Например, R 2 , равный 0,2, указывает, что 20% дисперсии переменной отклика можно объяснить переменной-предиктором; R 2 , равное 0,77, указывает, что 77% дисперсии переменной отклика можно объяснить переменной-предиктором.

Обратите внимание, что в нашем предыдущем выводе мы получили значение R2, равное 0,9311 , что указывает на то, что 93,11% изменчивости роста можно объяснить предикторной переменной веса:

Это говорит нам о том, что вес является очень хорошим предиктором роста.

Предположения линейной регрессии

Чтобы результаты модели линейной регрессии были достоверными и надежными, нам необходимо проверить выполнение следующих четырех допущений:

1. Линейная зависимость. Существует линейная зависимость между независимой переменной x и зависимой переменной y.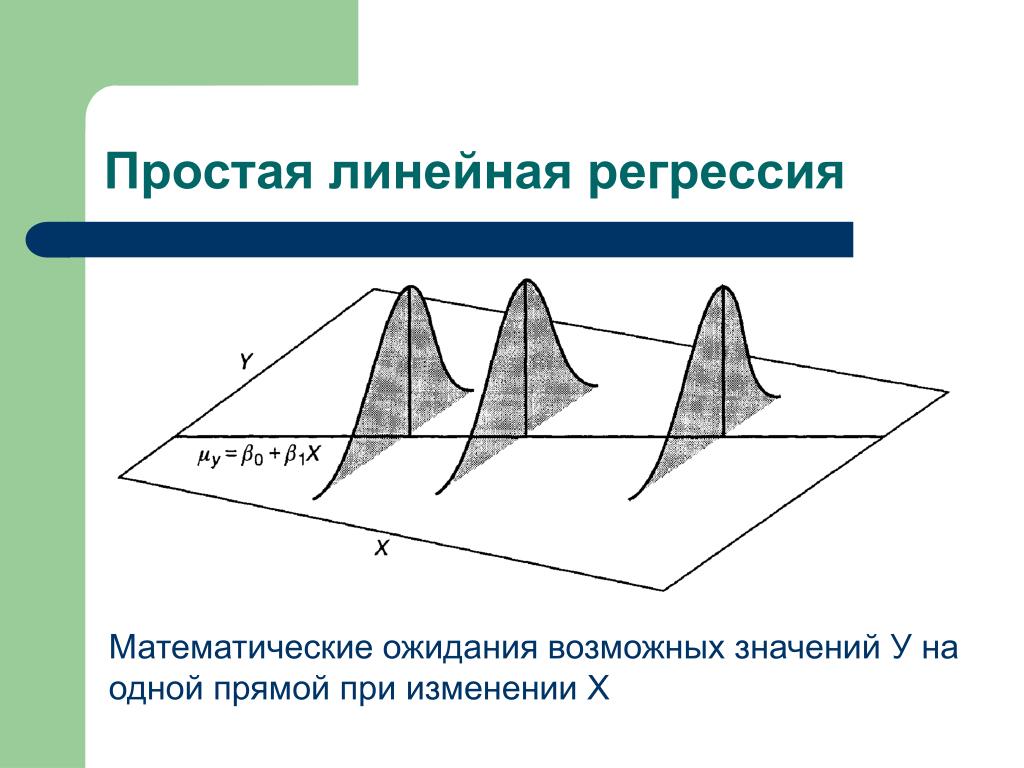

2. Независимость: Остатки независимы. В частности, нет корреляции между последовательными остатками в данных временных рядов.

3. Гомоскедастичность: остатки имеют постоянную дисперсию на каждом уровне x.

4. Нормальность: остатки модели нормально распределены.

Если одно или несколько из этих предположений нарушаются, то результаты нашей линейной регрессии могут быть ненадежными или даже вводящими в заблуждение.

Обратитесь к этому сообщению для объяснения каждого предположения, как определить, выполняется ли предположение, и что делать, если предположение нарушается.

Что такое метод линейной регрессии? – Объяснение модели линейной регрессии – AWS

Что такое линейная регрессия?

Линейная регрессия — это метод анализа данных, который предсказывает ценность неизвестных данных с помощью другого связанного и известного значения данных. Он математически моделирует неизвестную или зависимую переменную и известную или независимую переменную в виде линейного уравнения.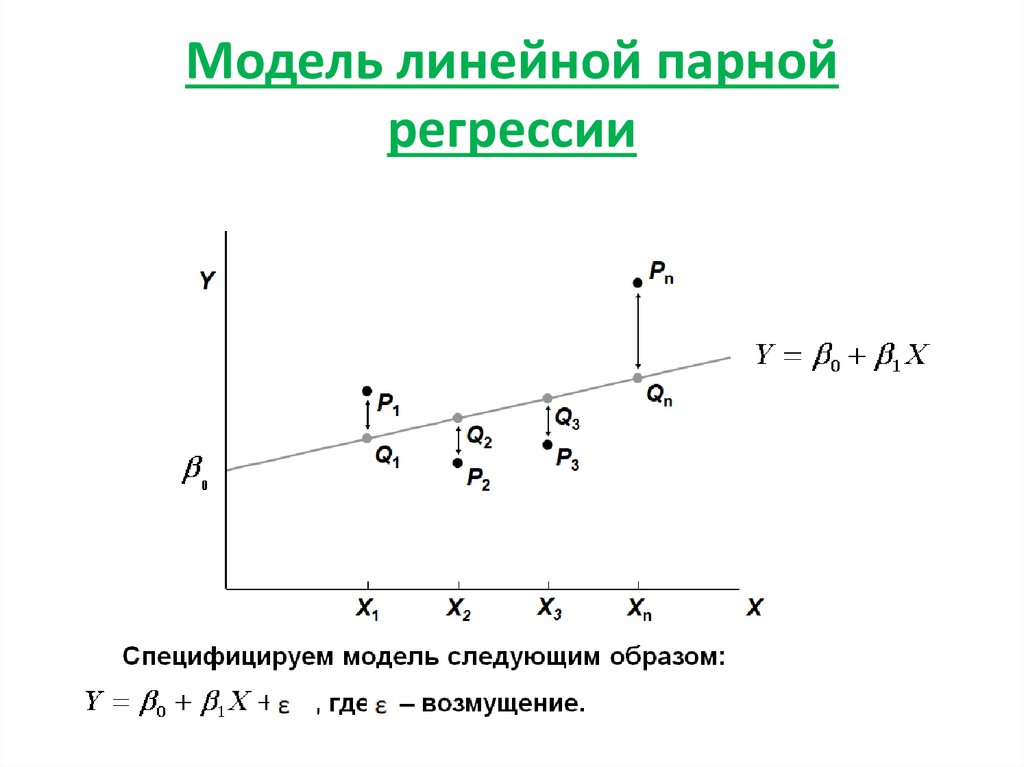 Например, предположим, что у вас есть данные о ваших расходах и доходах за прошлый год. Методы линейной регрессии анализируют эти данные и определяют, что ваши расходы составляют половину вашего дохода. Затем они рассчитывают неизвестные будущие расходы, сокращая вдвое будущий известный доход.

Почему линейная регрессия важна?

Модели линейной регрессии относительно просты и предоставляют легко интерпретируемую математическую формулу для создания прогнозов. Линейная регрессия – это признанный статистический метод, который легко применяется к программному обеспечению и вычислениям. Компании используют его для надежного и предсказуемого преобразования необработанных данных в бизнес-аналитику и полезную аналитику. Ученые во многих областях, включая биологию и поведенческие, экологические и социальные науки, используют линейную регрессию для проведения предварительного анализа данных и прогнозирования будущих тенденций. Многие методы науки о данных, такие как машинное обучение и искусственный интеллект, используют линейную регрессию для решения сложных задач.

Как работает линейная регрессия?

По своей сути простой метод линейной регрессии пытается построить линейный график между двумя переменными данных, x и y. Как независимая переменная x строится вдоль горизонтальной оси. Независимые переменные также называются независимыми переменными или предикторными переменными. Зависимая переменная y нанесена на вертикальную ось. Значения y также можно называть переменными отклика или прогнозируемыми переменными.

Этапы линейной регрессии

Для этого обзора рассмотрим простейшую форму уравнения линейного графика между y и x; y = c*x+m, где c и m постоянны для всех возможных значений x и y. Например, предположим, что входной набор данных для (x, y) был (1,5), (2,8) и (3,11). Чтобы определить метод линейной регрессии, необходимо выполнить указанные ниже шаги.

1. Постройте прямую линию и измерьте корреляцию между 1 и 5.
2. Продолжайте менять направление прямой линии для новых значений (2,8) и (3,11), пока все значения не подойдут.
3. Определите уравнение линейной регрессии как y = 3 * x + 2.
4. Экстраполировать или предсказать, что y равно 14, когда x равно

Что такое линейная регрессия в машинном обучении?

В машинном обучении компьютерные программы, называемые алгоритмами, анализируют большие наборы данных и работают в обратном направлении от этих данных для расчета уравнения линейной регрессии. Специалисты по обработке данных сначала обучают алгоритм на известных или маркированных наборах данных, а затем используют алгоритм для прогнозирования неизвестных значений. Реальные данные сложнее, чем в предыдущем примере. Вот почему линейный регрессионный анализ должен математически изменять или преобразовывать значения данных, чтобы соответствовать указанным ниже четырем предположениям.

Линейная зависимость

Между независимыми и зависимыми переменными должна существовать линейная зависимость. Чтобы определить эту взаимосвязь, специалисты по обработке данных создают точечную диаграмму – случайную коллекцию значений x и y – чтобы увидеть, падают ли они вдоль прямой линии.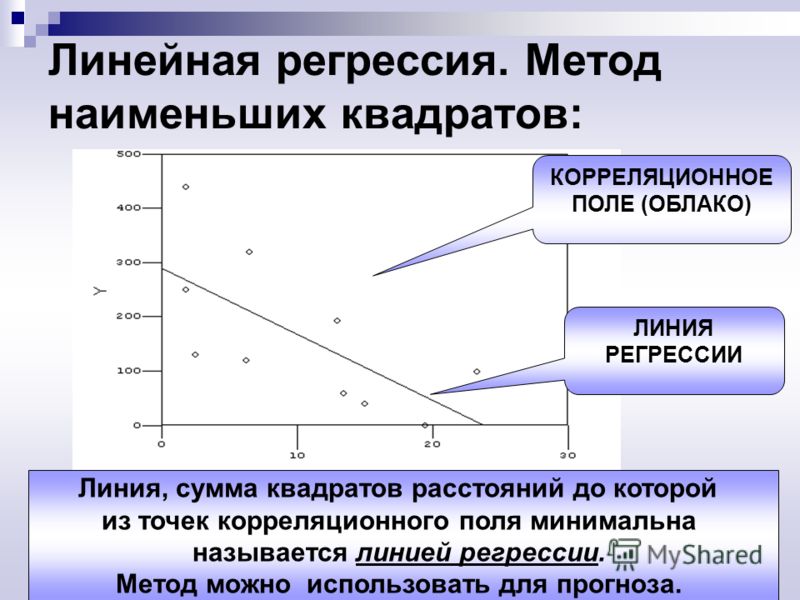 В противном случае можно применить нелинейные функции, такие как квадратный корень или log, для математического создания линейной зависимости между двумя переменными.

Остаточная независимость

Специалисты по обработке данных используют невязки для измерения точности прогнозирования. Невязка – это разница между наблюдаемыми данными и прогнозируемым значением. Остатки не должны иметь идентифицируемой закономерности между ними. Например, вы не хотите, чтобы остатки со временем увеличивались. Для определения остаточной независимости можно использовать различные математические тесты, такие как тест Дурбина-Уотсона. Фиктивные данные можно использовать для замены любых вариаций данных, таких как сезонные данные.

Нормальность

Методы построения графиков, такие как графики Q-Q, определяют, нормально ли распределены невязки. Невязки должны располагаться вдоль диагональной линии в центре графика. Если невязки не нормализованы, можно проверить данные на случайные выбросы или нетипичные значения. Устранение выбросов или выполнение нелинейных преобразований может решить проблему.

Гомоскедастичность

Гомоскедастичность предполагает, что невязки имеют постоянную дисперсию или стандартное отклонение от среднего для каждого значения x. В противном случае результаты анализа могут быть неточными. Если это предположение не выполняется, возможно, придется изменить зависимую переменную. Поскольку дисперсия возникает естественным образом в больших наборах данных, имеет смысл изменить масштаб зависимой переменной. Например, вместо того, чтобы использовать численность населения для прогнозирования количества пожарных частей в городе, можно использовать численность населения для прогнозирования количества пожарных частей на человека.

Какие существуют типы линейной регрессии?

Некоторые типы регрессионного анализа больше подходят для обработки сложных наборов данных, чем другие. Далее приведены некоторые примеры.

Простая линейная регрессия

Простая линейная регрессия определяется линейной функцией:

Y = β0*X + β1 + ε 

β0 и β1 – две неизвестные константы, представляющие наклон регрессии, тогда как ε (эпсилон) – член ошибки.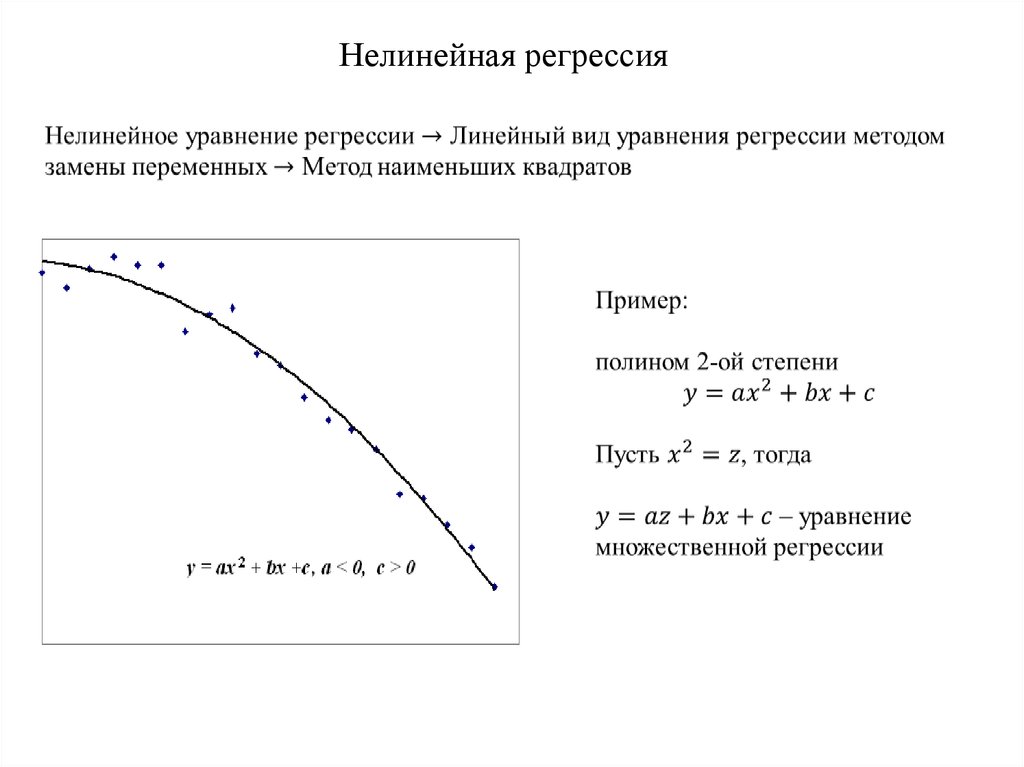

Можно использовать простую линейную регрессию для моделирования взаимосвязи между двумя переменными, например:

• Количество осадков и урожайность
• Возраст и рост у детей
• Температура и расширение металлической ртути в термометре

Несколько линейных регрессий

При множественном линейном регрессионном анализе набор данных содержит одну зависимую переменную и несколько независимых переменных. Функция линии линейной регрессии изменяется и включает в себя большее количество факторов, как указано ниже.

Y = β0*X0 + β1X1 + β2X2+… βnXn + ε 

По мере увеличения количества переменных-предикторов константы β также соответственно увеличиваются.

 Множественная линейная регрессия моделирует несколько переменных и их влияние на результат:

• Количество осадков, температура и использование удобрений на урожайность
• Диета и упражнения при сердечных заболеваниях
• Рост заработной платы и инфляция ставок по жилищным кредитам

Логистическая регрессия

Специалисты по обработке данных используют логистическую регрессию для измерения вероятности возникновения события. Предсказание – это значение от 0 до 1, где 0 означает маловероятное событие, а 1 – максимальную вероятность того, что оно произойдет. Логистические уравнения используют логарифмические функции для вычисления линии регрессии.

Ниже приведены несколько примеров.

• Вероятность победы или поражения в спортивном матче
• Вероятность прохождения или неудачи теста 
• Вероятность того, что изображение будет фруктом или животным

Как AWS может помочь в решении задач линейной регрессии?

Amazon SageMaker – это полностью управляемый сервис, который поможет быстро подготовить, построить, обучить и развернуть высококачественные модели машинного обучения (ML). Amazon SageMaker автопилот – это универсальное автоматическое решение машинного обучения для решения проблем классификации и регрессии, таких как обнаружение мошенничества, анализ оттока и целевой маркетинг. 

Amazon Redshift, быстрое и широко используемое облачное хранилище данных, изначально интегрируется с Amazon SageMaker для машинного обучения. С помощью Amazon Redshift ML можно использовать простые инструкции SQL для создания и обучения моделей машинного обучения на основе данных в Amazon Redshift. Затем эти модели можно использовать для решения всех типов задач линейной регрессии.

Начните работу с Amazon SageMaker JumpStart или создайте аккаунт AWS уже сегодня.

Простая линейная регрессия | Простое введение и примеры

Опубликован в 19 февраля 2020 г. к Ребекка Беванс. Отредактировано 15 ноября 2022 г.

Простая линейная регрессия используется для оценки связи между двумя количественными переменными . Вы можете использовать простую линейную регрессию, когда хотите знать:

1. Насколько сильна взаимосвязь между двумя переменными (например, взаимосвязь между осадками и эрозией почвы).
2. Значение зависимой переменной при определенном значении независимой переменной (например, степень эрозии почвы при определенном уровне осадков).

Модели регрессии описывают взаимосвязь между переменными путем подгонки линии к наблюдаемым данным. В моделях линейной регрессии используется прямая линия, а в моделях логистической и нелинейной регрессии — кривая. Регрессия позволяет оценить, как изменяется зависимая переменная по мере изменения независимой переменной (переменных).

Пример простой линейной регрессии. Вы — социолог, интересующийся взаимосвязью между доходом и счастьем. Вы опрашиваете 500 человек с доходами от 15 до 75 тысяч и просите их оценить свое счастье по шкале от 1 до 10.

Ваша независимая переменная (доход) и зависимая переменная (счастье) являются количественными, поэтому вы можете провести регрессионный анализ, чтобы увидеть, существует ли между ними линейная связь.

Если у вас есть более одной независимой переменной, используйте множественную линейную регрессию.

Содержание

1. Предположения простой линейной регрессии
2. Как выполнить простую линейную регрессию
3. Интерпретация результатов
4. Представление результатов
5. Можете ли вы предсказать значения за пределами диапазона ваших данных?
6. Часто задаваемые вопросы о простой линейной регрессии

Допущения простой линейной регрессии

Простая линейная регрессия — это параметрический тест , что означает, что он делает определенные предположения о данных.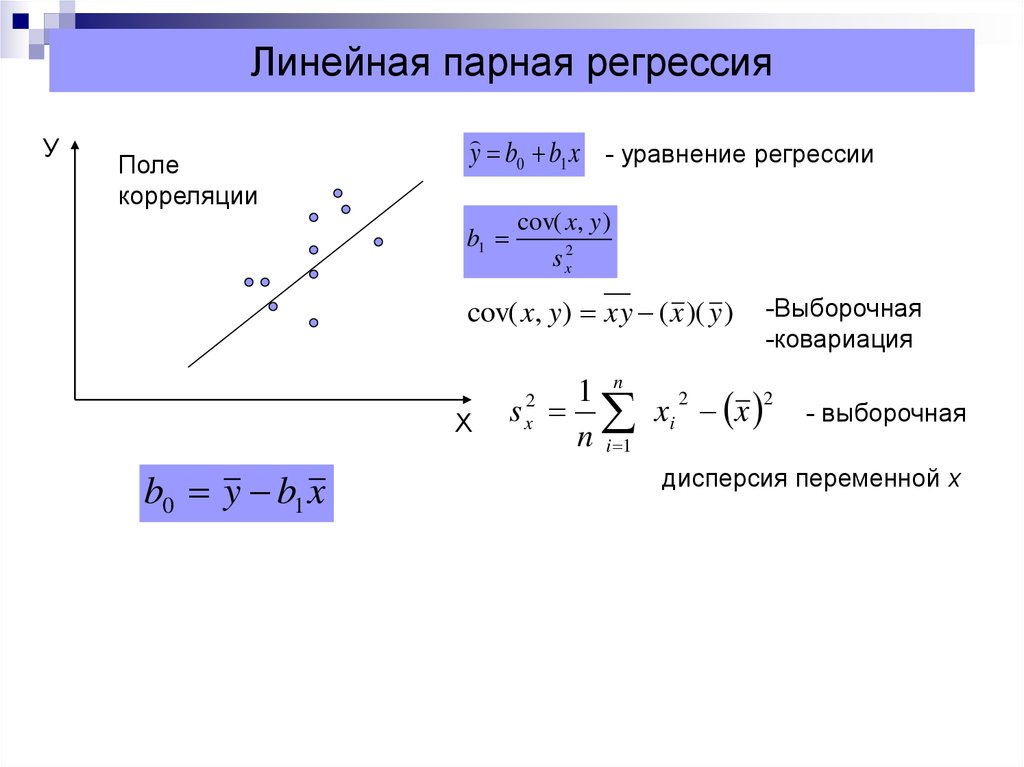 Эти предположения таковы:

1. Однородность дисперсии (гомоскедастичность) : размер ошибки в нашем прогнозе существенно не меняется в зависимости от значений независимой переменной.
2. Независимость наблюдений : наблюдения в наборе данных были собраны с использованием статистически достоверных методов выборки, и между наблюдениями нет скрытых взаимосвязей.
3. Нормальность : Данные имеют нормальное распределение.

Линейная регрессия делает одно дополнительное предположение:

4. Отношение между независимой и зависимой переменной линейное : линия наилучшего соответствия точкам данных является прямой линией (а не кривой или каким-либо группирующим фактором).

Если ваши данные не соответствуют предположениям о гомоскедастичности или нормальности, вы можете вместо этого использовать непараметрический критерий, такой как ранговый критерий Спирмена.

Пример: данные, которые не соответствуют предположениям. Вы считаете, что существует линейная зависимость между потреблением вяленого мяса и заболеваемостью колоректальным раком в США. Однако вы обнаружили, что при высоком уровне потребления мяса было собрано гораздо больше данных, чем при низком. потребления мяса, в результате чего существует гораздо больше различий в оценке показателей заболеваемости раком в низком диапазоне, чем в высоком диапазоне. Поскольку данные нарушают предположение о гомоскедастичности, они не работают для регрессии, но вместо этого вы выполняете ранговый тест Спирмена.

Если ваши данные нарушают предположение о независимости наблюдений (например, если наблюдения повторяются во времени), вы можете выполнить линейную модель смешанных эффектов, которая учитывает дополнительную структуру данных.

Как выполнить простую линейную регрессию

Формула простой линейной регрессии

Формула простой линейной регрессии:

• y — прогнозируемое значение зависимой переменной ( y ) для любого заданного значения независимой переменной ( x ).
• B ₀ — точка пересечения , прогнозируемое значение y , когда x равно 0.
• B ₁ — это коэффициент регрессии — насколько мы ожидаем, что y изменится при увеличении x .
• x — независимая переменная (переменная, которую мы ожидаем, влияет на y ).
• e — это ошибка оценки, или степень вариации в нашей оценке коэффициента регрессии.

Линейная регрессия находит линию наилучшего соответствия вашим данным путем поиска коэффициента регрессии (B ₁ ), который минимизирует общую ошибку (e) модели.

Хотя вы можете выполнить линейную регрессию вручную, это утомительный процесс, поэтому большинство людей используют статистические программы, которые помогают им быстро анализировать данные.

Простая линейная регрессия в R

R — бесплатная, мощная и широко используемая статистическая программа.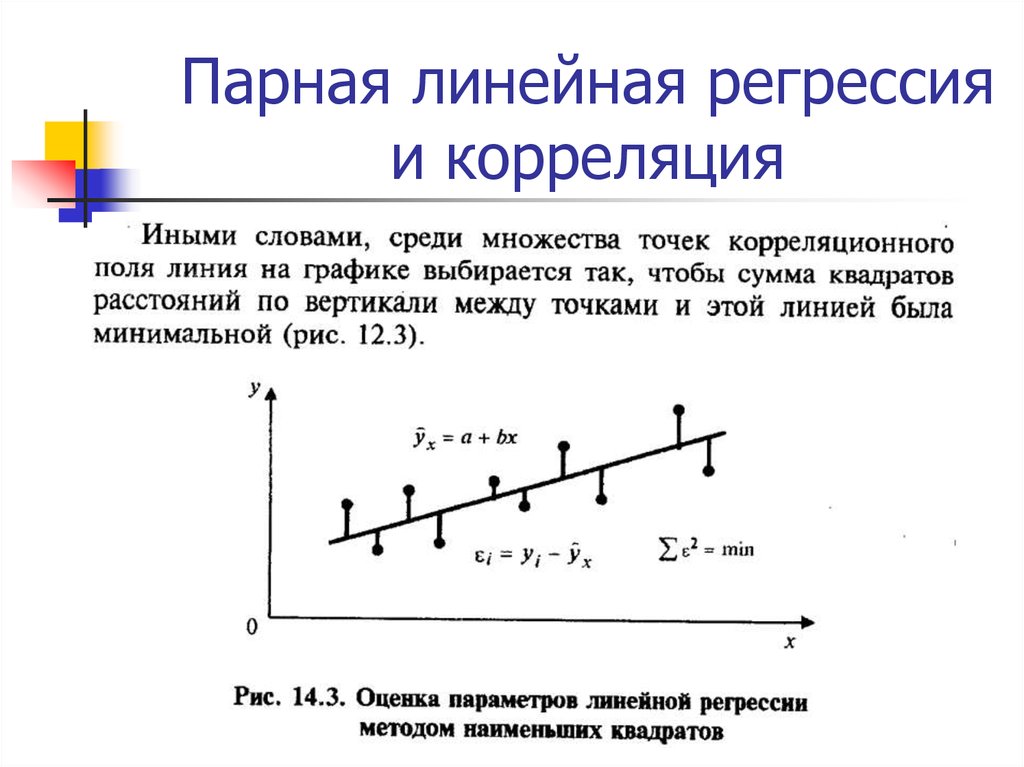

Загрузите набор данных, чтобы попробовать сами, используя наш пример дохода и счастья.

Набор данных для простой линейной регрессии (.csv)

Загрузите набор данных yield.data в среду R, а затем выполните следующую команду, чтобы сгенерировать линейную модель, описывающую взаимосвязь между доходом и счастьем:

Код R для простой линейной регрессии доход.счастье.lm <- lm(счастье ~ доход, данные = доход.данные)

Этот код берет данные, которые вы собрали данные = доход.данные , и вычисляет эффект, который независимая переменная доход оказывает на зависимую переменную счастье , используя уравнение для линейной модели: lm() .

Чтобы узнать больше, следуйте нашему полному пошаговому руководству по линейной регрессии в R.

Интерпретация результатов

Чтобы просмотреть результаты модели, вы можете использовать функцию summary()

в R:

summary(income. happiness.lm)

Эта функция берет наиболее важные параметры из линейной модели и помещает их в таблицу, которая выглядит следующим образом:

В этой выходной таблице сначала повторяется формула, которая использовалась для получения результатов («Вызов»), а затем обобщаются остатки модели («Остатки»), которые дают представление о том, насколько хорошо модель соответствует реальным данным.

Далее идет таблица «Коэффициенты». Первая строка дает оценки y-отрезка, а вторая строка дает коэффициент регрессии модели.

Строка 1 таблицы помечена как (Перехват) . Это y-пересечение уравнения регрессии со значением 0,20. Вы можете включить это в свое уравнение регрессии, если хотите предсказать значения счастья в диапазоне доходов, который вы наблюдали:

счастья = 0,20 + 0,71*доход ± 0,018

Следующая строка в таблице «Коэффициенты» — доход. Это строка, описывающая предполагаемое влияние дохода на сообщаемое счастье:

Столбец Estimate представляет собой оцененное влияние , также называемое коэффициентом регрессии или значением r ² . Число в таблице (0,713) говорит нам о том, что на каждую единицу увеличения дохода (где одна единица дохода = 10 000) соответствует увеличение сообщаемого счастья на 0,71 единицы (где счастье — это шкала от 1 до 10).

Стандартный номер . Столбец Error отображает стандартную ошибку оценки. Это число показывает, насколько сильно различаются наши оценки взаимосвязи между доходом и счастьем.

В столбце t value  отображается статистика теста . Если не указано иное, тестовая статистика, используемая в линейной регрессии, представляет собой значение t из двустороннего теста t . Чем больше статистика теста, тем меньше вероятность того, что наши результаты были получены случайно.

Столбец Pr(>| t |)  отображает значение p . Это число говорит нам, насколько вероятно, что мы увидим оценочное влияние дохода на счастье, если нулевая гипотеза об отсутствии эффекта верна.

Поскольку значение p такое низкое ( p < 0,001), мы можем отклонить нулевую гипотезу и заключить, что доход оказывает статистически значимое влияние на счастье.

Последние три строки сводной информации о модели представляют собой статистические данные о модели в целом. Самое важное, на что следует обратить внимание, это значение модели p . Здесь оно значимо ( p < 0,001), что означает, что эта модель хорошо подходит для наблюдаемых данных.

Представление результатов

При сообщении о результатах включите расчетный эффект (т. е. коэффициент регрессии), стандартную ошибку оценки и значение p . Вы также должны интерпретировать свои цифры, чтобы ваши читатели могли понять, что означает ваш коэффициент регрессии:

Мы обнаружили значимую взаимосвязь ( p < 0,001) между доходом и счастьем (R ² = 0,71 ± 0,018) с увеличением сообщаемого счастья на 0,71 единицы на каждые 10 000 увеличения дохода.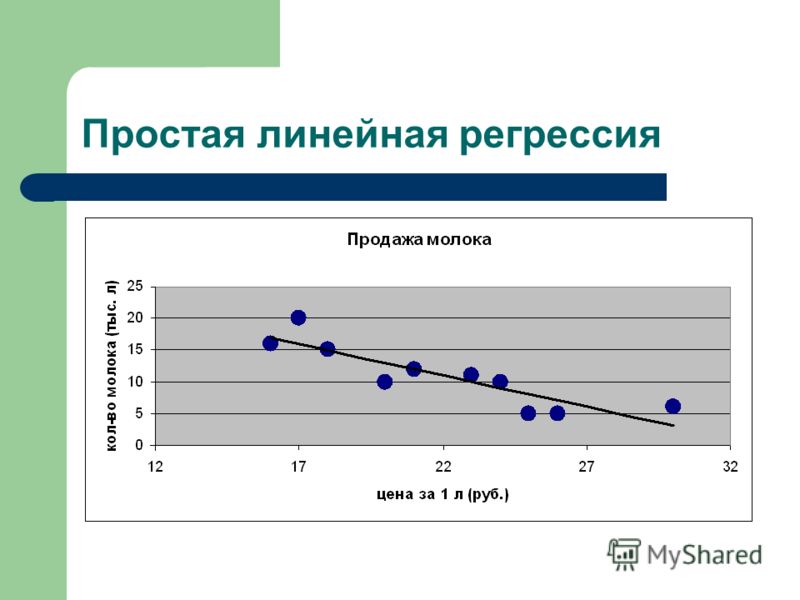

Также может быть полезно приложить к результатам график. Для простой линейной регрессии вы можете просто отобразить наблюдения по осям x и y, а затем включить линию регрессии и функцию регрессии:

Можете ли вы предсказать значения вне диапазона ваших данных?

Нет! Мы часто говорим, что регрессионные модели можно использовать для предсказания значения зависимой переменной при определенных значениях независимой переменной. Однако это верно только для диапазона значений, где мы фактически измерили отклик.

В качестве примера можно использовать наш регрессионный анализ дохода и счастья. Между 15 000 и 75 000 мы обнаружили, что r ² составляет 0,73 ± 0,0193. Но что, если мы проведем второй опрос людей, зарабатывающих от 75 000 до 150 000?

 

r ² для отношения между доходом и счастьем теперь составляет 0,21, или 0,21-единицу увеличения зарегистрированного счастья на каждые 10 000 увеличения дохода.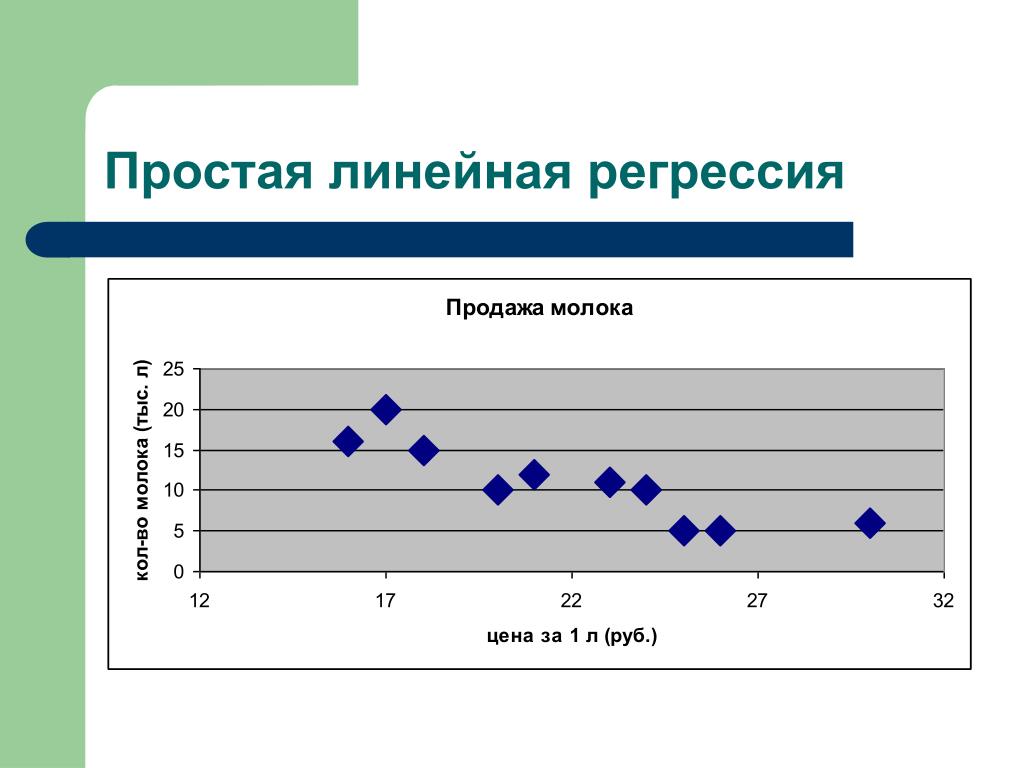 Хотя связь по-прежнему статистически значима (p<0,001), наклон стал намного меньше, чем раньше.

 

 

Что, если бы мы не измеряли эту группу, а вместо этого экстраполировали линию от доходов 15–75 тыс. до доходов 70–150 тыс.?

Как видите, если бы мы просто экстраполировали данные о доходах от 15 до 75 тысяч, мы бы переоценили счастье людей в диапазоне доходов от 75 до 150 тысяч.

 

Если вместо этого мы подгоним кривую к данным, она будет гораздо лучше соответствовать реальному образцу.

Похоже, что счастье на самом деле выравнивается при более высоких доходах, поэтому мы не можем использовать ту же линию регрессии, которую мы рассчитали на основе наших данных о более низких доходах, чтобы предсказать счастье при более высоких уровнях дохода.

 

Даже когда вы видите четкую закономерность в своих данных, вы не можете знать наверняка, сохраняется ли эта закономерность за пределами диапазона фактически измеренных значений. Поэтому важно избегать экстраполяции за пределы того, что на самом деле говорят вам данные.

Часто задаваемые вопросы о простой линейной регрессии

Что такое регрессионная модель?

Регрессионная модель — это статистическая модель, которая оценивает взаимосвязь между одной зависимой переменной и одной или несколькими независимыми переменными с помощью линии (или плоскости в случае двух или более независимых переменных).

Регрессионную модель можно использовать, когда зависимая переменная является количественной, за исключением случая логистической регрессии, когда зависимая переменная является бинарной.

Что такое простая линейная регрессия?

org/Answer">

Простая линейная регрессия — это модель регрессии, которая оценивает взаимосвязь между одной независимой переменной и одной зависимой переменной с помощью прямой линии. Обе переменные должны быть количественными.

Например, зависимость между температурой и расширением ртути в термометре можно смоделировать с помощью прямой линии: при повышении температуры ртуть расширяется. Эта линейная зависимость настолько надежна, что мы можем использовать ртутные термометры для измерения температуры.

Как рассчитывается ошибка в модели линейной регрессии?

Линейная регрессия чаще всего использует среднеквадратичную ошибку (MSE) для расчета ошибки модели. MSE рассчитывается следующим образом:

1. измерение расстояния наблюдаемых значений y от предсказанных значений y при каждом значении x;
2. в квадрате каждого из этих расстояний;
3. вычисление среднего значения каждого из квадратов расстояний.

Линейная регрессия подгоняет линию к данным, находя коэффициент регрессии, который приводит к наименьшему значению MSE.

Процитировать эту статью Scribbr

Если вы хотите процитировать этот источник, вы можете скопировать и вставить цитату или нажать кнопку «Цитировать эту статью Scribbr», чтобы автоматически добавить цитату в наш бесплатный генератор цитирования.

Беванс, Р. (2022, 15 ноября). Простая линейная регрессия | Простое введение и примеры. Скриббр. Проверено 13 марта 2023 г., из https://www.scribbr.com/statistics/simple-linear-regression/

Процитировать эту статью

Полезна ли эта статья?

Вы уже проголосовали. Спасибо 🙂 Ваш голос сохранен 🙂 Обработка вашего голоса...

Ребекка работает над докторской диссертацией по почвенной экологии, а в свободное время пишет. Она очень рада, что может поболтать о статистике со всеми вами.

2.1 - Что такое простая линейная регрессия?

Простая линейная регрессия — это статистический метод, который позволяет нам суммировать и изучать отношения между двумя непрерывными (количественными) переменными:

• Одна переменная, обозначенная x , считается предиктором , объяснительной или независимой переменной.
• Другая переменная, обозначенная y , рассматривается как ответ , результат или зависимая переменная.

Поскольку другие термины сегодня используются реже, мы будем использовать термины « предиктор » и « ответ » для обозначения переменных, встречающихся в этом курсе. Другие термины упоминаются только для того, чтобы вы знали о них, если столкнетесь с ними. Простая линейная регрессия получает прилагательное «простая», потому что она касается изучения только одной переменной-предиктора. Напротив, множественная линейная регрессия, которую мы изучаем позже в этом курсе, получает прилагательное «множественная», потому что она касается изучения двух или более переменных-предикторов.

Типы отношений

Прежде чем продолжить, мы должны уточнить, какие типы отношений мы не будем изучать в этом курсе, а именно, детерминированные (или функциональные ) отношения . Вот пример детерминированной связи.

Обратите внимание, что наблюдаемые ( x , y ) точки данных попадают прямо на линию. Как вы помните, соотношение между градусами Фаренгейта и градусами Цельсия известно как:

\[\text{F} = \frac{9}{5}\text{C}+32\]

То есть, если вы знаете температуру в градусах Цельсия, вы можете использовать это уравнение для определения температуры в градусах по Фаренгейту ровно .

Вот несколько примеров других детерминированных соотношений, которыми поделились студенты предыдущих семестров:

• Окружность = π × диаметр
• Закон Гука: Y = α + β X , где Y = степень растяжения пружины, а X = приложенный вес.
• Закон Ома: I = В / r , где В = приложенное напряжение, r = сопротивление и I = ток.
• Закон Бойля: для постоянной температуры P = α/ V , где P = давление, α = константа для каждого газа, а V = объем газа.

Для каждого из этих детерминированных соотношений уравнение точно описывает взаимосвязь между двумя переменными. В этом курсе не рассматриваются детерминированные отношения. Вместо этого нас интересуют статистических взаимосвязей , в которых взаимосвязь между переменными не идеальна.

Вот пример статистической зависимости. Переменная ответа y представляет собой смертность от рака кожи (количество смертей на 10 миллионов человек), а переменная-предиктор x — это широта (градусы северной широты) в центре каждого из 49 штатов США (skincancer.txt) (данные были собраны в 1950-х годах, поэтому Аляска и Гавайи еще не были штатами, а Вашингтон, округ Колумбия, включен в набор данных, даже если технически это не штат.)

Вы могли бы предположить, что, если бы вы жили в более высоких широтах на севере США, тем меньше вы были бы подвержены вредным солнечным лучам, и, следовательно, тем меньше риск смерти от рака кожи. Диаграмма рассеяния поддерживает такую ​​гипотезу. По-видимому, существует отрицательная линейная зависимость между широтой и смертностью от рака кожи, но эта связь не идеальна. Действительно, в сюжете есть некоторые « тренд », но он также демонстрирует некоторый « разброс ». Таким образом, это статистическая зависимость, а не детерминированная.

No related posts.