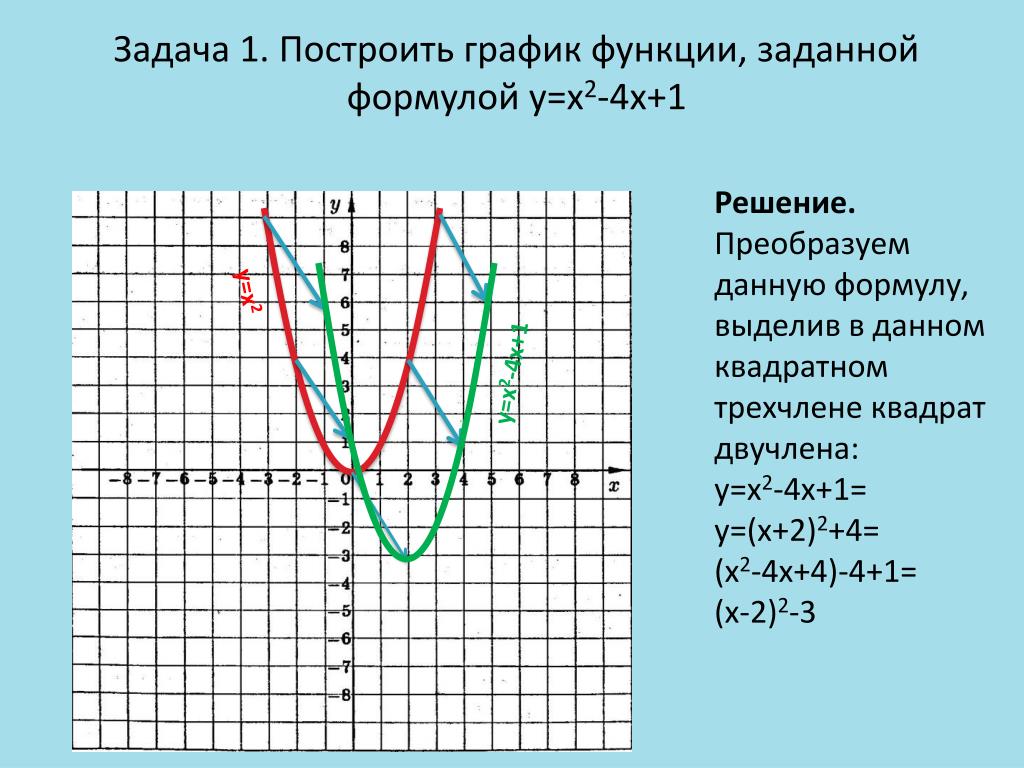
Как построить график функции x y 2: Mathway | Популярные задачи

2

Как построить график функции в Wolfram|Alpha

Как построить график функции в Wolfram|Alpha

Начнем с построения простого 2-мерного графика: plot sin(sqrt(7)x)+19cos(x) для x от -20 до 20

Если заменить 7 на (-7), то получим графики действительной и мнимой частей функции: plot sin(sqrt(-7)x)+19cos(x) для x от -5 до 5

В двух предыдущих примерах мы задавали область значений аргумента х. А что будет, если не задавать область значений х?

Одной из уникальных особенностей Wolfram | Alpha является автоматический выбор подходящего диапазона х для построения графиков функций одной и двух переменных, например, как при построении графика этой функции, содержащей функции Бесселя:

Обращаясь к Wolfram | Alpha, чтобы построить график функции, мы всегда используем префикс plot. Если же мы введем какое-либо одномерное выражение без префикса plot, то получим кроме графика функции в прямоугольных декартовых координатах, еще и много других сведений об этой функции.

3 + 3 x) Во всех рассмотренных выше примерах Wolfram | Alpha строил также и контурные графики (линии уровня) в дополнение к трехмерным графикам (поверхностям). Чтобы увидеть связь между трехмерными и контурными графиками, нужно нажать кнопку “Show contour lines”. Отметим, что и трехмерные и контурные графики используют один и тот же диапазон аргументов.

Все трехмерные графики строятся с помощью функции plot3d системы Mathematica. Контурные графики были сделаны с помощью ContourPlot. В обоих случаях, чтобы увидеть код системы Mathematica для генерации изображения нужно нажать ссылку Copyable planetext в левом нижнем углу нужного изображения.

Источник by Sam Blake

Опубликовано в блоге Web in Math

Следующее Главная страница

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Задавать вопрос

спросил

6 лет, 1 месяц назад

Изменено 6 лет, 1 месяц назад

Просмотрено 2к раз

Может ли кто-нибудь помочь мне с построением трехмерного графика поверхности для уравнения f(x,y) = (x-y)^2

Ось Z должна представлять функцию f(x,y)

У меня есть следующая функция:

 def fnc(X):
    возврат (Х[0] - Х[1]) ** 2
 

Здесь X — массив numpy с первым параметром X и вторым параметром Y. Мне конкретно нужно, чтобы так было. Поэтому, пожалуйста, не предлагайте мне изменить подпись. 😉

Я попробовал следующее из этого решения:

 fig = plt.figure()
топор = fig.add_subplot(111, проекция='3d')
х = у = np.linspace (-5,5,100)
X, Y = np.meshgrid(x, y)
Z = fnc1([np.linspace(-5,5,100) , np.linspace(-6,6,100)])
ax.plot_surface (X, Y, Z)
ax.set_xlabel('Ярлык X')
ax.set_ylabel('Ярлык Y')
ax.set_zlabel('Ярлык Z')
plt.show()
 

Однако я ошибаюсь в сюжете.

• python
• numpy
• matplotlib
• mplot3d

Ваш fnc неверен. Получите свою поверхность так же, как Z=(X-Y)**2 . Это лучшее решение, потому что все вычисления Z будут векторизованы.

 импортировать matplotlib.pylab как plt
из mpl_toolkits.mplot3d импортировать Axes3D
импортировать numpy как np
рис = plt.figure()
топор = fig.add_subplot(111, проекция='3d')
х = у = np.linspace (-5,5,100)
X, Y = np. meshgrid(x, y)
Z = (XY)**2
ax.plot_surface (X, Y, Z)
ax.set_xlabel('Ярлык X')
ax.set_ylabel('Ярлык Y')
ax.set_zlabel('Ярлык Z')
plt.show()
 

3

Массив Z для построения должен быть двумерным массивом, точно так же, как X и Y являются двумерными массивами, так что для каждой пары значений из X и Y вы получаете ровно одну точку в З . Поэтому имеет смысл использовать эти массивы X и Y в качестве входных данных для вашей функции fnc , Z = fnc([X,Y])

Полный код будет выглядеть так:

 импортировать numpy как np
импортировать matplotlib.pylab как plt
из mpl_toolkits.mplot3d импортировать Axes3D
защита fnc(X):
 возврат (Х[0] - Х[1]) ** 2
рис = plt.figure()
топор = fig.add_subplot(111, проекция=Axes3D.name)
х = у = np.linspace (-5,5,100)
X, Y = np.meshgrid(x, y)
Z = fnc([X,Y])
ax.
No related posts.