Как построить график квадратичной функции с модулем: График квадратичной функции с модулем

Содержание

Урок алгебры в 8-м классе по теме: «Модуль и квадратичная функция»

“Великое множество функций
Любой может школьник назвать.
Но лишь о немногих сегодня
Решили мы вам рассказать”

Изучение квадратичной функции с модулем позволяет углубить знания учащихся в преобразовании графиков квадратичной функции. Учащиеся с большим интересом выполняют любые задания с модулем. Рассмотренные приемы построения графиков функции являются общими и применяются не только к квадратичной, но и к другим функциям.

I. Вводное слово учителя

Функция – одно из основных математических и общенаучных понятий, выражающее зависимость между переменными величинами. Математика рассматривает абстрактные переменные величины, изучает законы их взаимосвязи, не углубляясь в природу задачи. Например, в соотношении Y = Х²математик или геодезист увидит зависимость площади квадрата от его стороны, а физик, авиаконструктор или кораблестроитель может увидеть зависимость силы Y сопротивления воздуха или воды от скорости Х движения.

Математика же изучает эту зависимость в отвлеченном виде, и она устанавливает, например, что увеличение Х в 2 раза приведет к увеличению Y в 4 раза, и это заключение может применяться в любой конкретной ситуации.

Модуль и квадратичная функция

Построение графиков функций:

Y = АХ² + ВX + C,
Y = АХ² + ВX + C ,
Y = АХ²+ ВХ + С

II. Устная работа

1) Дать определение модуля числа Х

2) Дать определение квадратичной функции, рассказать все, что известно об этой функции (график, свойства).

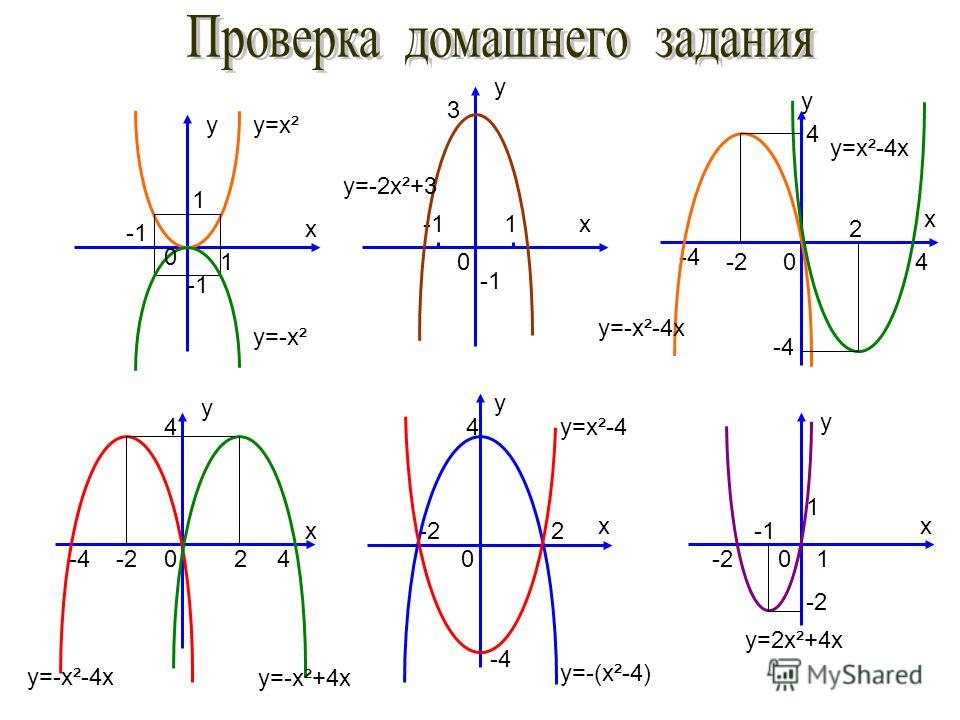
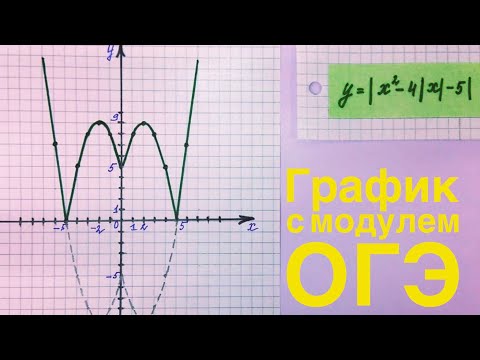
3) Найти на рисунке график функции Y = –Х²+ 4Х – 3.

4) На каком рисунке изображен график функции Y = –(Х + 1)(2 – Х)?

5) Вспомнить, как построить график функции Y = Х

По определению модуля

График функции Y = Х симметричен относительно оси У.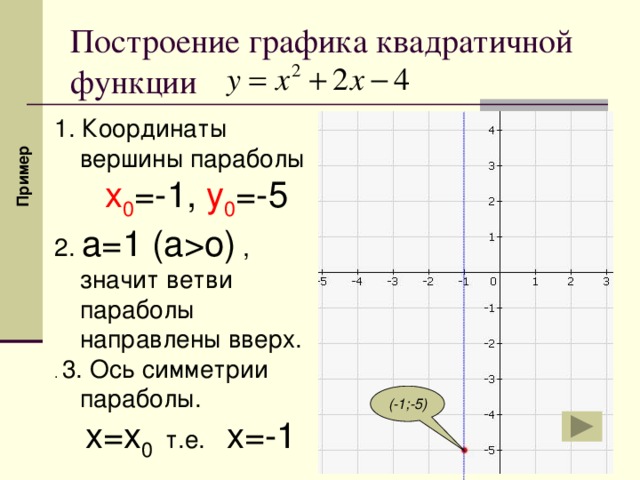

III. Построение графиков функций:

Y = АХ² + ВX + C,

Y = АХ²+ ВХ + С

Работа проводится в группах, т.к. графики в К–1 в) и К–3 в) одинаковы, их необходимо сравнить и сделать вывод (всего 3 группы). Каждой группе выдается карточка, в ней 3 задания. Учащиеся должны построить графики квадратичной функции, содержащей модуль, используя определение модуля и сделать вывод: как построить график данной функции, используя график квадратичной функции и симметрию относительно осей координат.

Работа в группах.

Задание: построить график функции, используя:

а) определение модуля;
б) график функции Y = АХ²+ ВХ + С;
в) симметрию относительно осей координат.

а) Y = Х² – 4 Х + 3
б) Y = Х² – 4 Х + 3
в) Y = Х² – 4 Х + 3

а) Y = Х² + 2 Х – 3
б) Y = Х² + 2 Х – 3
в) Y = Х² + 2 Х – 3

а) Y = –Х² + 4 Х – 3
б) Y = –Х² + 4 Х – 3
в) Y = –Х² + 4 Х – 3

IV.

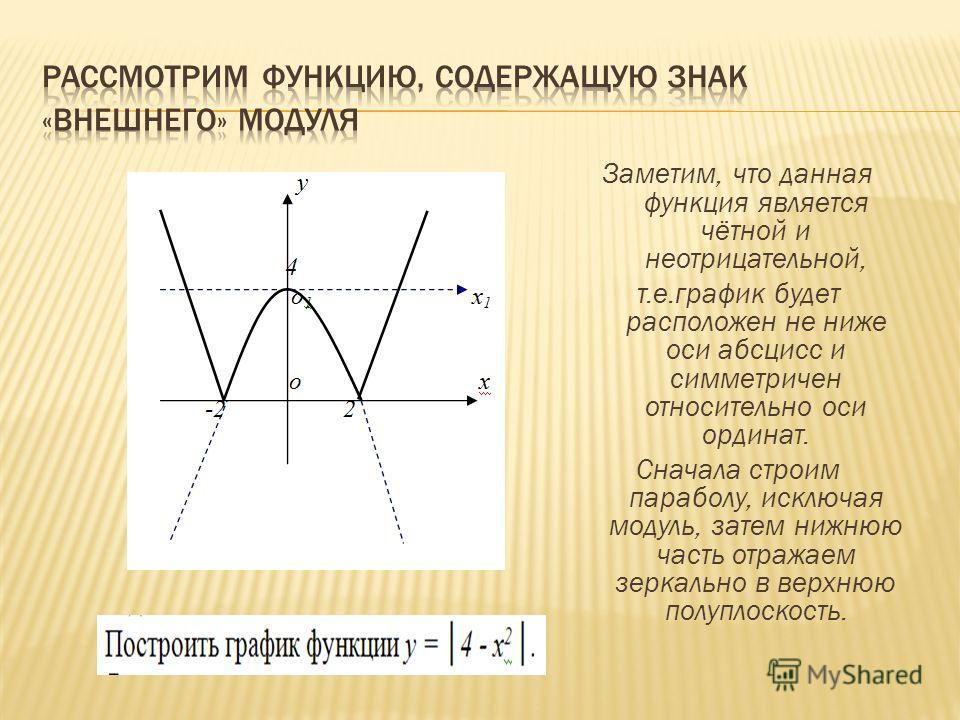
Учащиеся делают вывод о расположении графиков указанных функций

Вопрос: а) Как построить график функции Y = f (X)?

(1 способ. Построить график функции Y = f (X), если Х 0 и Y = f (–Х), если Х< 0.
2 способ. Построить график функции Y = f (X) и отобразить правую часть графика симметрично относительно оси Y).

б) Как построить график функции Y = f (X) ?

(Построить график функции Y = f (X) и точки с отрицательными ординатами симметрично отобразить относительно оси Х).

в) Как построить график функции Y = f (X) ?

(Построить график функции Y = f (X), если Х 0 и эту часть графика симметрично отобразить относительно оси Y, а потом точки с отрицательными ординатами отобразить симметрично относительно оси Х.)

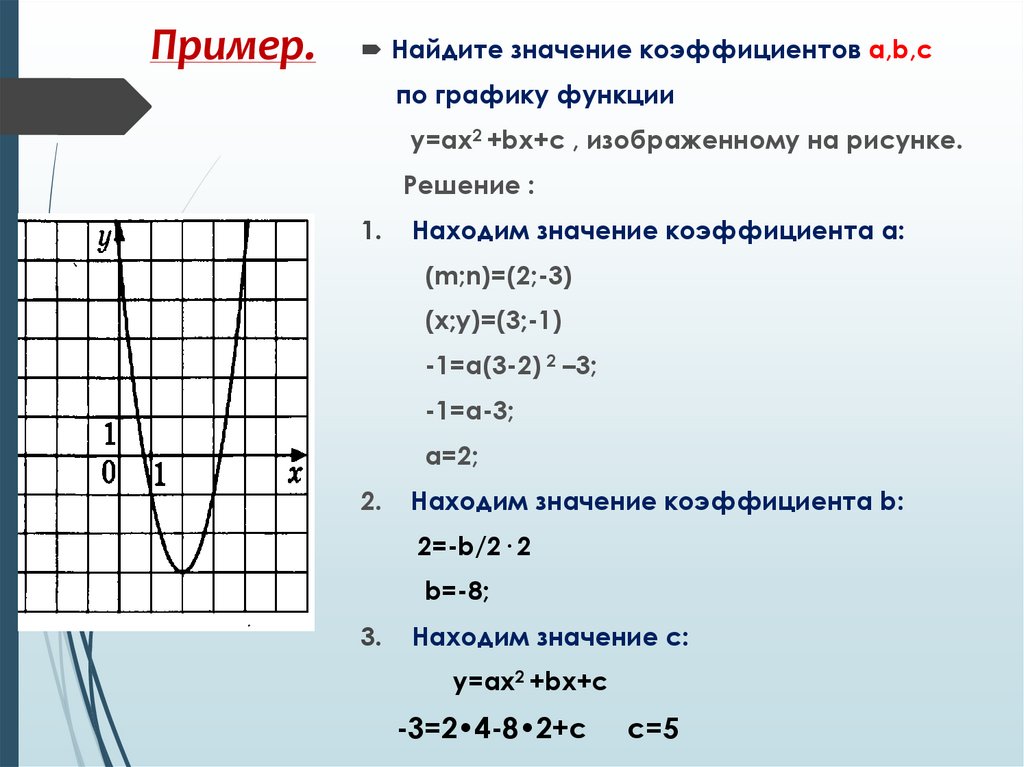
г) Почему графики функций Y = –Х² + 4X – 3 и Y = Х² – 4X + 3 одинаковы?

(Так как А = А , –А = А)

V.

У рассмотренных функций под знаком модуля была независимая переменная.

Теперь рассмотрим функции, где под знаком модуля стоит либо сама функция, либо и функция, и независимая переменная одновременно, т.е. зависимости вида

Y = АХ² + ВX+ C и Y = АХ² + ВX + C

Приведем конкретные примеры.

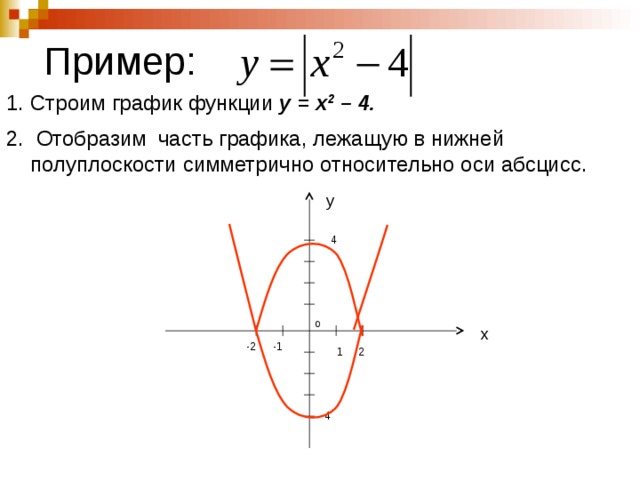
а) Y = Х² – 4X+ 3

По определению

Построим график функции Y = f (X) и берем ту его часть, которая расположена выше оси Х, т.к. Х² – 4X+ 3 0 и добавим к ней ее симметричное отображение относительно оси Х.

б) Y = Х² – 4X+ 3

Сначала строим график функции Y = Х² – 4X+ 3 , а затем множество точек, координаты которых удовлетворяют условию Y = Х² – 4X+ 3 , т.е. график функции Y = Х² – 4X+ 3 отображаем относительно оси Х.

VI. Творческое задание

Дана функция Y = Х² + 2X– 3

Выполнить всевозможные преобразования данной квадратичной функции с модулем.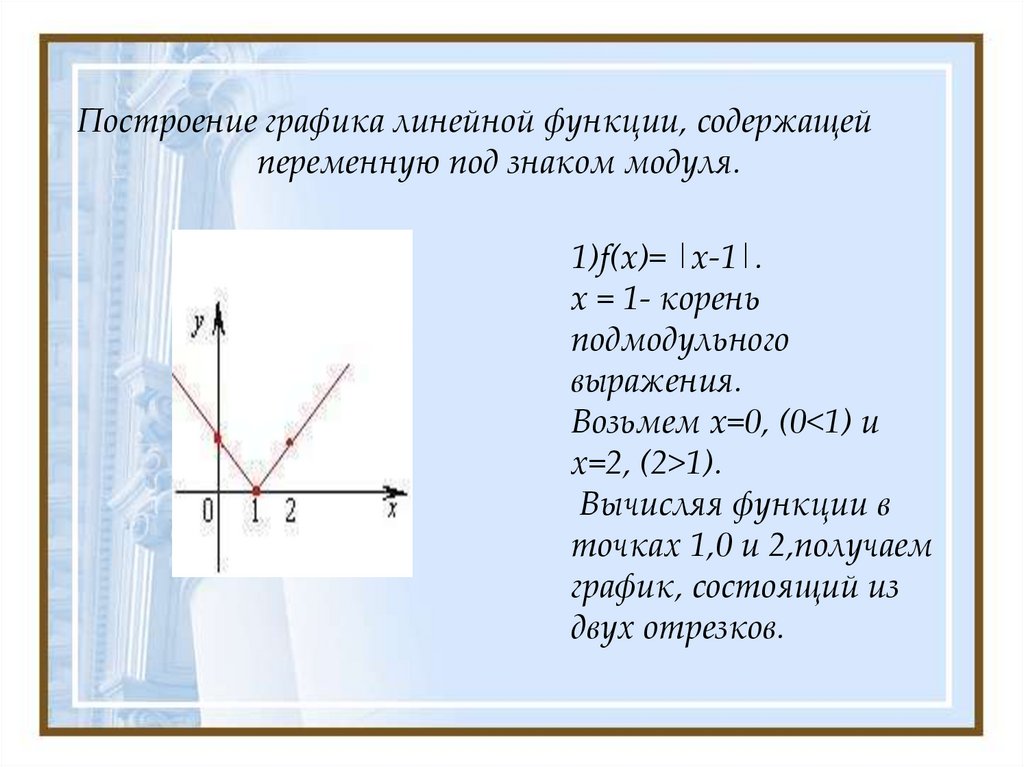

График квадратичной функции, содержащей модуль

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. График квадратичной функции, содержащей модуль

(методическая разработка занятия элективного курса для
9 класса с элементами исследовательской деятельности).
Царевой Елены Борисовны
Рязанская обл., г. Сасово, МБОУ «СОШ №6»
Исследователем можно быть
и перед лицом огромной
неизученной проблемы,
и перед лицом школьной задачи,
миллионы раз решавшейся
другими.

С.Л. Соболев

3. Краткая характеристика работы. Постановка проблемы. Актуальность.

В современном обществе педагог должен не столько давать знания ,
сколько научить эти знания добывать . Дети приходят в школу учиться , то
есть учить себя . Уроки – исследования считаю составной частью в этом
процессе. Необходимо так организовать познавательную деятельность
школьников, чтобы процедура учебного исследования усваивалась ими
вместе с тем содержанием, на котором оно осуществляется.
Под уроком – исследованием я представляю себе деятельность учащихся и
учителя, связанную с решением учащимися (при поддержке учителя)
исследовательской задачи (пусть и с заранее известным решением, но
незнакомым учащимся).
Методическая разработка занятия элективного курса для 9 класса
“Графика квадратичной функции, содержащей модуль”.
является примером организации такой деятельности.

4. Цель и задачи

Цель: Исследовать расположение графика функции на
координатной плоскости в зависимости от модуля.

Задачи:
1. Освоение навыков построения графиков и исследования
функции с помощью компьютерных программ
2. Повышение компетенции учащихся в области умение
анализировать, сравнивать, математически и графически
оформлять результаты деятельности, переносить знания из
области информатики в математику и наоборот
3. Овладение учащимися технологиями учебной
исследовательской деятельности.

5. Вспоминаем то что знаем

6. Обнаружение проблемы

Изобразите схематически графики функций:
а) у = х2 — 6x + 3,
б)у = х2 — 6|x| + 3,
в) у = |х2 — 6х + 3|.
Фиксация затруднения, причины затруднения.
Цель деятельности: узнать как выглядит график (или построить способ
изображения графика функции ) у = ах2 +b|x| + c и у =| ах2 +bx + c |

7. Построение проекта выхода из затруднения

Какие знания, умения, инструменты, способы
деятельности могут помочь при решении проблемы.
(коллективное обсуждение, построение плана
исследования, выбор задания для работы в группе)
Работа выполняется в программе
Advanced Grapher

8.

Примеры заданий учебного исследования 2)Постройте график функции у = -2х2 + 6x + 3,

Сделайте предположение о форме графиков функции у = | -2х2 + 6x + 3 |,
у = -2х2 + 6 | x | + 3.
Проверьте свою гипотезу.
3)Меняя параметры a,b,c, постройте графики функции у = aх2 + bx + c.
Сделайте предположение о форме графиков функции у = | aх2 + bx + c |,
у = aх2 + b | x | + c,
Проверьте свою гипотезу.
4) Постройте график функции
a)у = |x2 — 6|x| + 3|;
б) y = |x2 — 6x + 3| — 3.
При построении графиков данных функций каждая группа исследовала
влияние модуля на вид графика функции и сделала соответствующие
заключения.)
(
Получили сводную таблицу для графиков функций, содержащих модуль.
Таблица построения графиков функций, содержащих модуль.
Вид функции
1. у = f(|x|)
2. у = |f(x)|
3. у = |f(|x|)|
4. у = |f(x)| + a
Способ построения графика
функции
1. Отобразить график функции у = f(x)
симметрично относительно оси Оу.

2. Отобразить график функции у = f(x)
симметрично относительно оси Ох.
3. Последовательно отобразить
график функции у = f(x) симметрично
относительно осей координат.
4. Параллельный перенос перенос
графика функции у = |f(x)|на вектор
{0;а}.
Занимаясь исследованиями, в том числе и на уроке
выпускник получит возможность научиться:
Самостоятельно планировать и выполнять учебное
исследование,
Использовать догадку, озарение, интуицию,
Использовать такие математические приемы и методы, как
перебор логических возможностей, математическое моделирование,
доказательство по аналогии, доказательство от противного,
опровержение, контрпример, индуктивные и дедуктивные
рассуждения, построение и исполнение алгоритма
Для некоторых учеников занятие с элементами исследования – это
первый шаг к началу работы над индивидуальным учебным
исследованием и участию в школьных конференциях.

English Русский Правила

Повторный курс по абсолютным и квадратичным графикам

Прямые линииРадикалы и т. д.

Purplemath

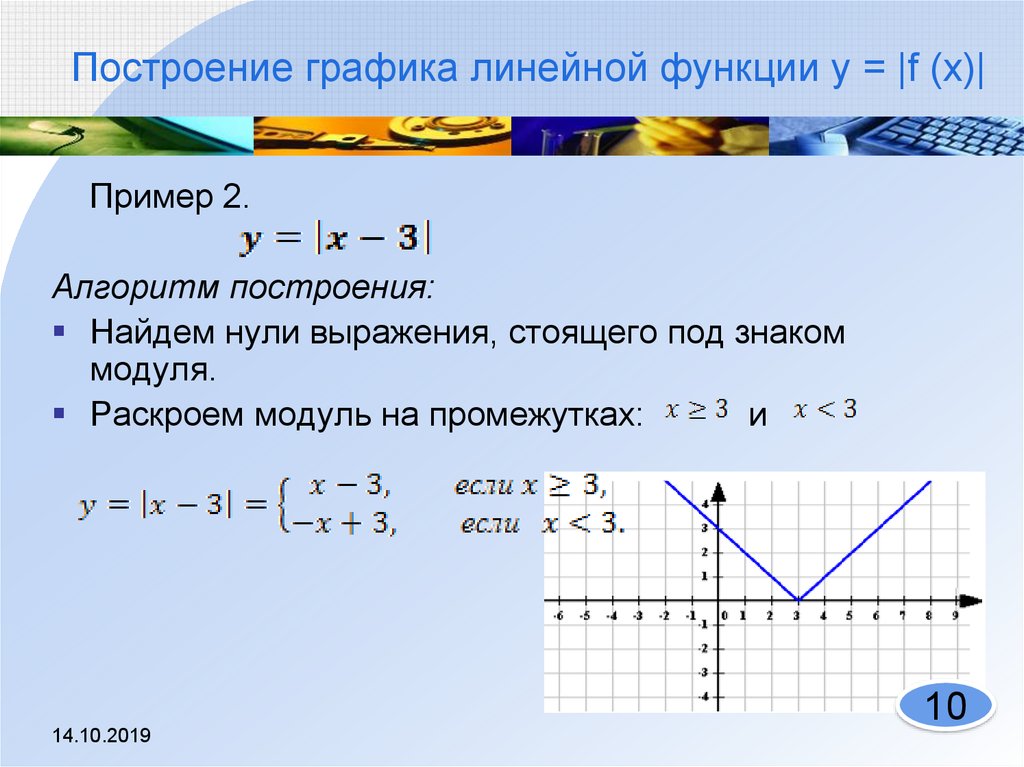
Очевидно, рисовать прямые линии будет проще всего. Но большую часть времени вы будете строить графики для уравнений, которые, по крайней мере, немного сложнее. Первый шаг вверх — это графики абсолютных значений, которые состоят (по крайней мере, когда вы начинаете) из двух прямых линий, образующих своего рода букву «V», либо с правой, либо с обратной стороны.

Содержание продолжается ниже. пример контекста, в котором мы должны быть осторожны, чтобы не забыть выбрать отрицательные значения x для нашей T-диаграммы. В противном случае очень легко забыть, что график абсолютного значения не будет просто одной непрерывной прямой линией.

Например, предположим, что нам дано уравнение y = | x |. И предположим, что мы выбрали только положительные значения x , поэтому наша Т-диаграмма выглядит так:

Тогда наши точки выглядят так:

И мы соединим наши точки так:

Мы только что завалили тест.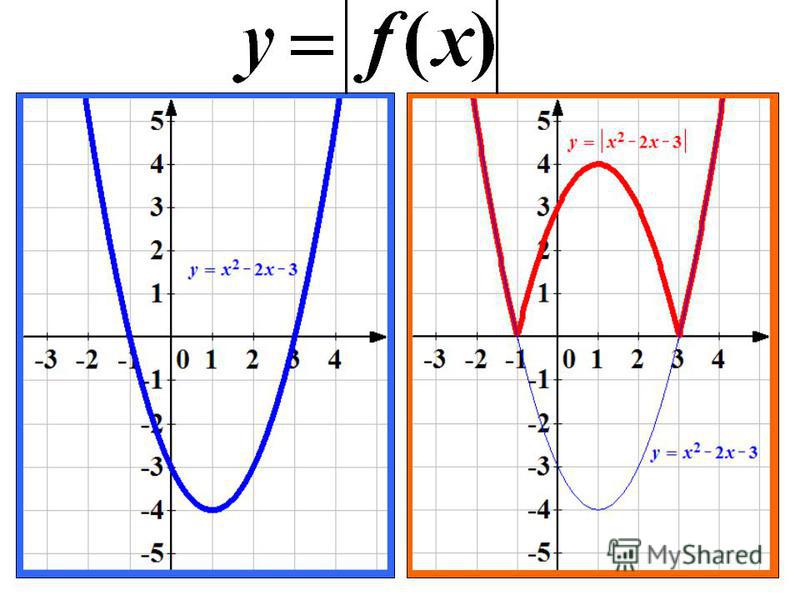

Вместо этого давайте немного разнесем наши значения x и не забудем на этот раз построить отрицательное значение x или два. Наша новая Т-диаграмма выглядит так:

Тогда наши точки выглядят следующим образом:

Поскольку наши точки хорошо разбросаны, и поскольку мы не забыли включить пару «минусовых» x -значений, мы помним, что уравнения абсолютных значений отображаются в виде ломаных линий, поэтому прикладываем нашу линейку дважды, чтобы получилось:

А это и есть правильный график!

(Если вы хотите изучить эту тему более подробно, см. Графики функций абсолютного значения.)

Квадратики

При графическом отображении квадратных уравнений/функций нам нужно нанести не только три точки; Я бы предложил минимум не менее пяти баллов, но от семи до девяти баллов будет лучше, если вы только начинаете. И мы должны ожидать, что нам также потребуется отображать отрицательные значения x . Три точки больше не будут сокращать его, потому что квадратичные графики представляют собой кривые линии, называемые «параболами».

Например, предположим, что они дают нам y = x ² − 6 x + 5. Есть множество вещей, которые мы можем сделать, чтобы помочь себе построить правильный график. Мы можем начать с поиска точек пересечения x и y . (Дополнительную информацию см. в разделе Перехваты.) В этом случае перехваты находятся в точках (1, 0), (5, 0) и (0, 5).

Кроме того, мы можем найти вершину параболы, которая является самой высокой или самой низкой точкой на графике. (Дополнительную информацию см. в разделе Вершина.) В этом случае вершина — это самая нижняя точка на графике, и эта точка находится в точке (3, −4).

Но в основном нам нужно потратить время, чтобы нанести довольно много точек, чтобы мы могли «увидеть» форму, прежде чем начать ее рисовать. Посмотрите, что часто происходит, когда новичок наносит только три точки:

T-диаграмма

Неправильный график

Но приведенный выше график неверен; эта парабола должна выглядеть как «смайлик», а не как прямая линия.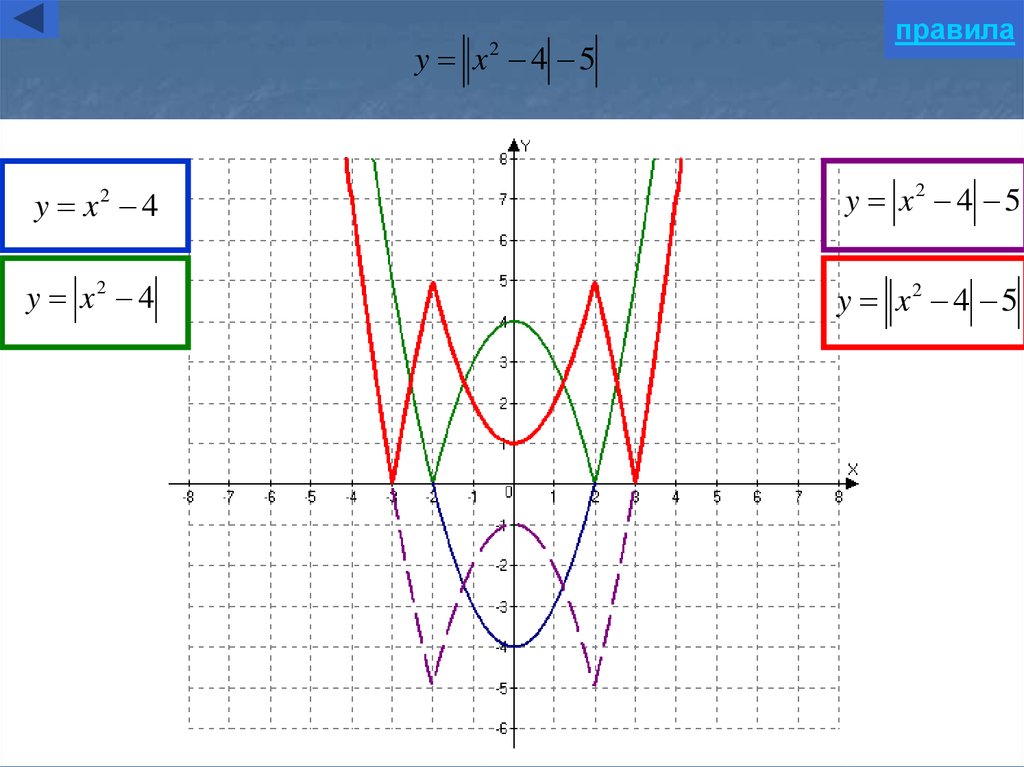 (И, если вы внимательно посмотрите, нанесенные точки на самом деле даже не выстраиваются в прямую линию! Линейка провела линию как бы «между» точками, а не «сквозь» их.)

Итак, нам нужно нанести еще несколько точек. Мы уже нашли точки пересечения и вершину (выше). Добавим к этому еще один пункт, используя x = 6:

Т-диаграмма

Правильный график

Гораздо лучше! Это график, который получит полные баллы!

(Примечание: положительное квадратичное выражение можно рассматривать как графическое изображение «смайлика», а отрицательное квадратичное выражение можно рассматривать как графическое изображение «фрони». Да, это глупый способ выразить это, но вы победите) Забудьте об этом сейчас, хорошо? Если вы хотите изучить эту тему более подробно, пожалуйста, обратитесь к разделу Графики квадратичных функций.)

URL: https://www.purplemath.com/modules/graphing2.htm

Страница 1Страница 3

K20 УЧИТЬСЯ | Трансформеры Часть 1

Резюме

Учащиеся будут использовать инструмент построения графиков для анализа основных преобразований на различных исходных графиках, чтобы создать общие правила преобразования функций.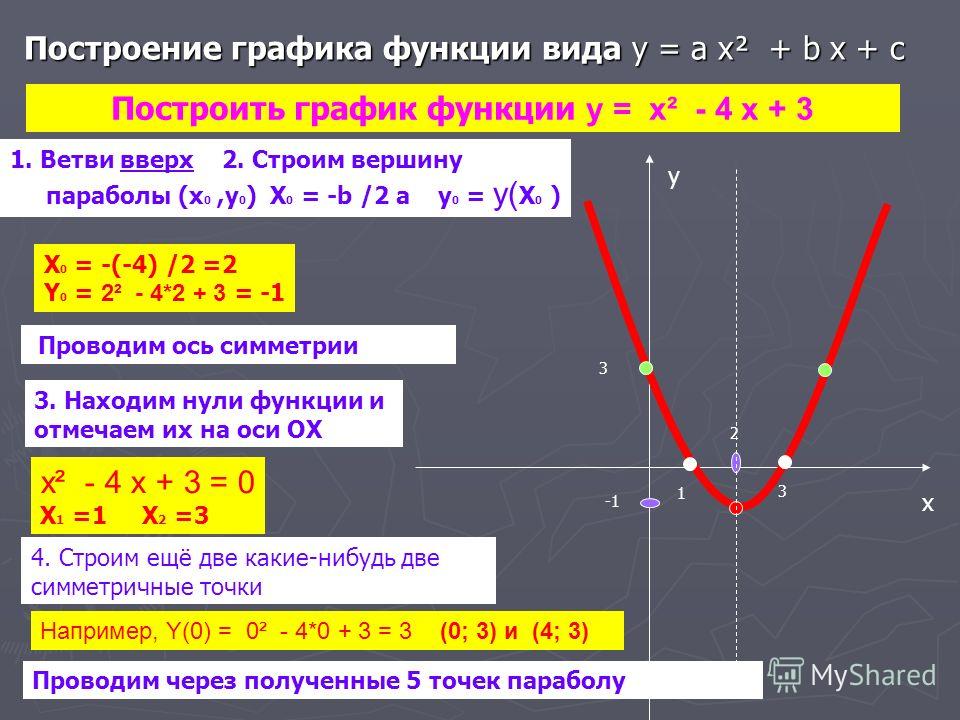

Основные вопросы

Что такое родительские графы? Как связаны преобразования родительских графов? Каковы общие правила преобразования родительского графа?

Снимок

Engage

Учащиеся начинают изучение преобразований функций с анализа линейных функций, с которыми они уже должны быть знакомы.

Изучение

Небольшим группам учащихся выдается раздаточный материал, который поможет им изучить преобразование абсолютного значения и квадратичных функций, чтобы они могли обобщить правила преобразования.

Объяснение

Учащиеся приходят к единому мнению относительно общих правил преобразования в ходе обсуждения в классе.

Расширить

Учащиеся могут создавать свои собственные графики и уравнения, прежде чем перейти к другой группе для определения соответствующих уравнений или графиков.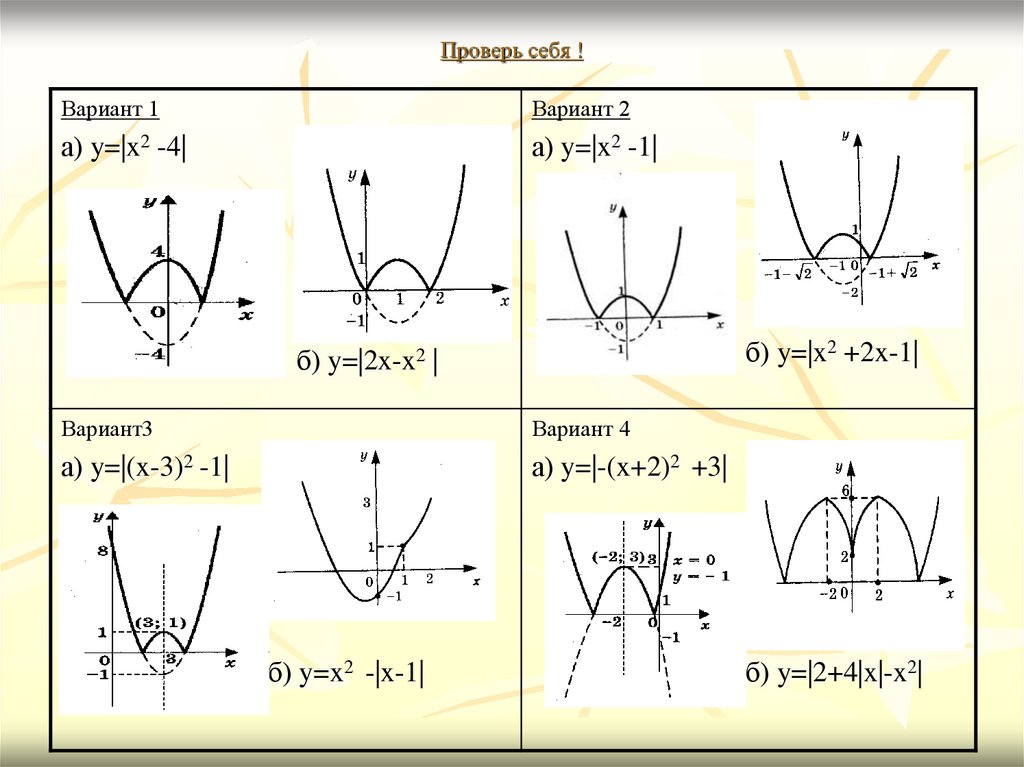

Оценить

Учащимся предоставляется возможность построить соответствующие графики для заданных уравнений, а затем соответствующие уравнения для заданных графиков.

Материалы

бумага для ноутбука
калькулятор
Графический калькулятор (http://www.desmos.com/calculator)
ИССЛЕДОВАНИЕ (ATTDED PER STUDE )
Проекционный экран/документ-камера или другой способ отображения информации

Задействовать

15 минут

Представьте урок, используя прилагаемые слайды урока . Слайд 3 отображает основные вопросы урока: Что такое родительские графики? Как связаны преобразования родительских графов? Каковы общие правила преобразования родительских графов? Слайд 4 определяет цели урока. Обсудите каждый из них со своим классом в той мере, в какой вы считаете это необходимым.

Перед началом занятия попросите учащихся выбрать партнера. Для выполнения задания учащимся необходим графический калькулятор или доступ к сайту desmos.com. Перейти к слайд 5 и покажите учащимся уравнения y = x, y = 2x и y = ½x. Предложите учащимся использовать графический калькулятор для построения графика каждой функции и попросите их сравнить и сопоставить полученные графики. Используя Think-Pair-Share, предложите учащимся поделиться своими ответами. Выберите нескольких учащихся, чтобы поделиться ими с классом.

Перейдите к слайду 6 и задайте тот же вопрос, используя y = x + 1, y = x – 2 и y = x + 3. Обсудите, почему эти изменения привели к другим графикам, чем предыдущие.

Обсудите с учащимися идею родительского графа.

Исследовать

45 минут

Перейдите к слайду 7 и предложите учащимся продолжить работу со своим напарником, чтобы заполнить прилагаемый раздаточный материал Exploring Graphs .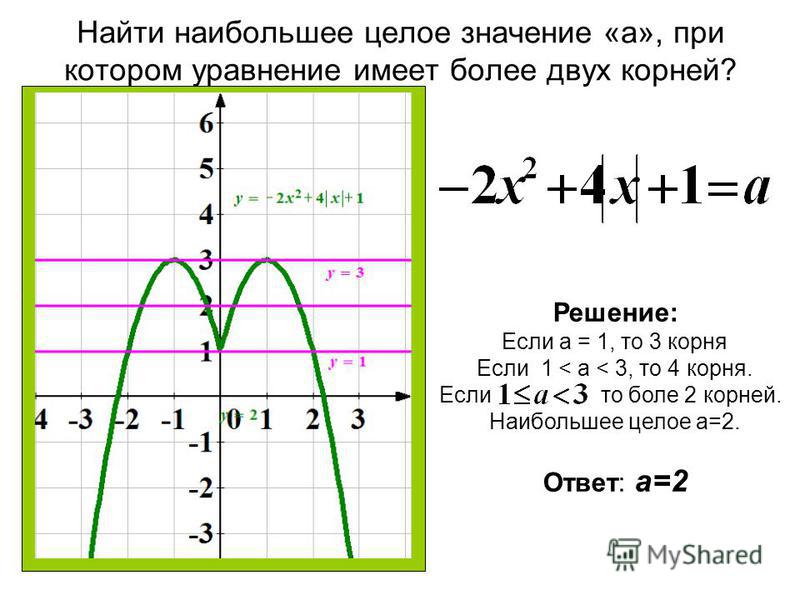 Позвольте учащимся работать в парах независимо друг от друга, но следите за их прогрессом.

Для выполнения задания учащимся необходим графический калькулятор или доступ к сайту desmos.com. Учащиеся должны делать предположения относительно построения графиков и сравнения y = |x|, y = |x-1|, y = |x+3|, y = |x| — 2, а у = |x-2| + 3. Учащиеся делают это снова, но с квадратичными функциями: y = x², y = (x-3)², y = (x+1)², y = x² + 4 и y = (x-2)². + 3.

Учащихся просят сравнить свои абсолютные значения и квадратичные графики, чтобы составить список наблюдений и закономерностей.

Затем каждая группа присоединяется к другой группе, чтобы сравнить то, что они наблюдали.

Объяснение

25 минут

Перейдите к слайду 8 и предложите учащимся поделиться с классом своими наблюдениями из раздаточного материала «Изучение графиков».

Какие изменения произошли в функции абсолютного значения?
Какие изменения произошли в квадратичной функции?
Каковы общие правила преобразований?

Убедитесь, что существует консенсус по общим правилам преобразования.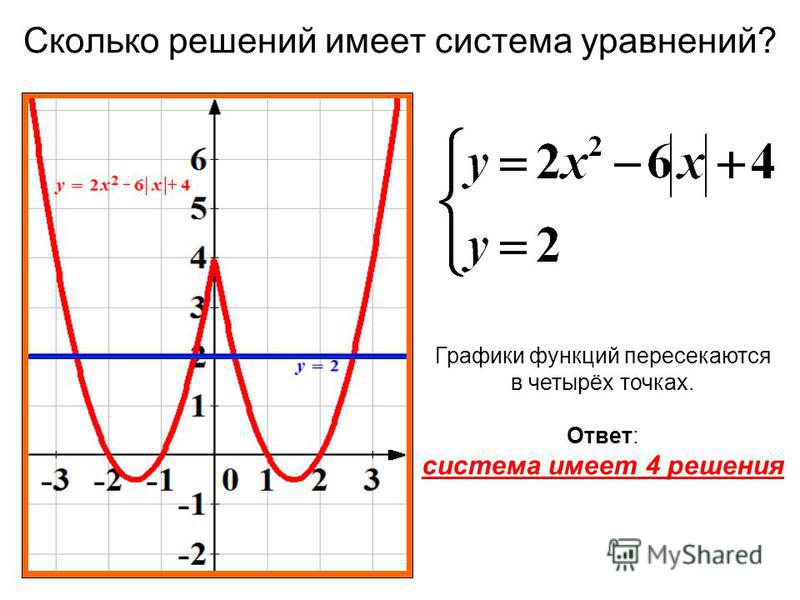

Примечание для учителя: строительные леса

Если учащиеся не могут прийти к единому мнению, им может потребоваться больше времени и примеров для обобщения преобразований. Если учащиеся борются с мыслью о том, что число в скобках имеет противоположный эффект, например, как y = |x-2| сдвигает функцию на 2 единицы вправо, это часто можно уточнить, показав учащимся, что если они приравняют то, что в скобках, к нулю и решат; результат будет описывать сдвиг (т. е. x – 2 = 0 => x = +2 => сдвиг вправо на 2 единицы). *Почему мы устанавливаем его равным нулю? Потому что это минимальное значение родительской функции; минимум там, где мы находим вершину.

Расширение

25 минут

Перейдите к слайду 9 и предложите учащимся создать свои собственные графики и уравнения в парах для торговли с другой парой. Предложите учащимся вместе со своей исходной группой составить:

1 уравнение абсолютного значения (без графика)
1 график абсолютного значения (без уравнения)
1 квадратное уравнение (без графика)
4 квадратичный график (без уравнения)

Затем пусть группы обмениваются своими творениями с другой группой.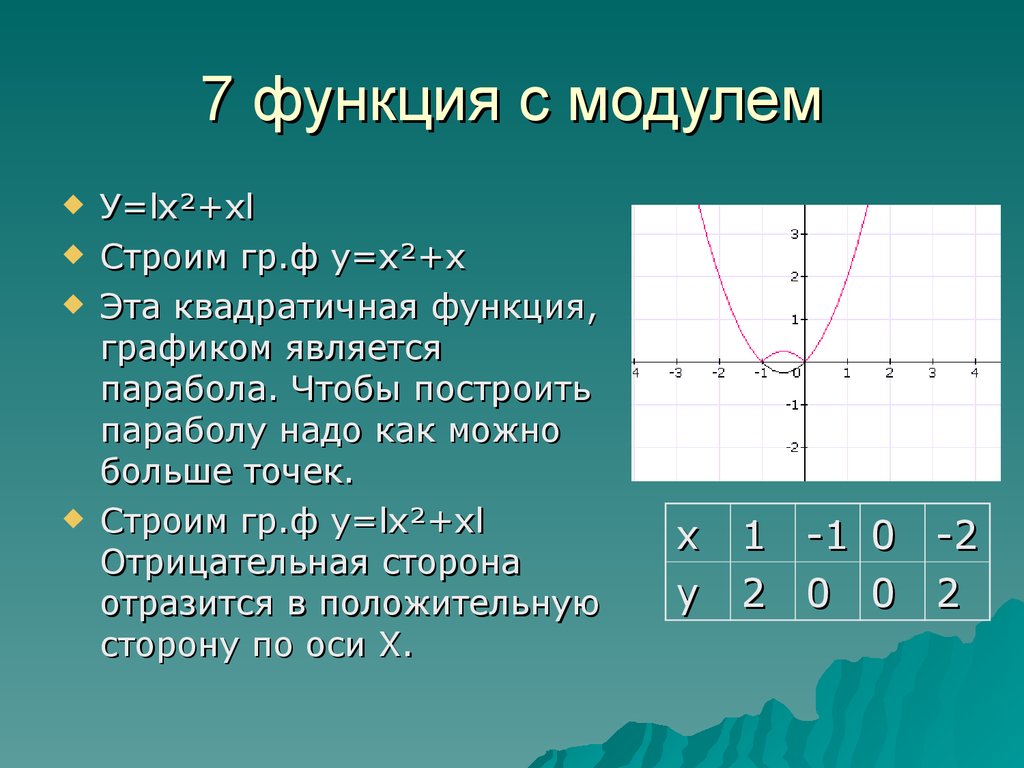 Каждая группа теперь должна найти недостающий график и уравнение для каждого предоставленного уравнения и графика.

Оценка

10 минут

Перейти к слайду 10 . Используя Think-Pair-Share, попросите учащихся предсказать, как график y = -|x+3| — 5 будет отличаться от родительской функции.

Примечание для учителя: создание лесов

Если учащиеся не могут прийти к консенсусу, создайте строительные леса, предложив учащимся построить график y = -|x| и сравнение его с родительской функцией.

Ресурсы

Источник изображения: Pixabay. (9 декабря 2018 г.). Фигурка [Фотография]. Pixabay. https://pixabay.com/images/id-3871893/
Центр К20. (н.д.). Подумай-пари-поделись. Стратегии. https://learn.k20center.ou.edu/strategy/139

Издатель

Загрузки

Скачать PDF

Стандарты

Академические стандарты Оклахомы по математике (9, 10, 11, 12 классы)

A1. F.2.2: Распознавать графики функций f(x) = x и f(x) = |x| и прогнозировать эффекты преобразований [f(x + c) и f(x) + c, где c — положительная или отрицательная константа] алгебраически и графически, используя различные методы и инструменты, которые могут включать графические калькуляторы.

Ресурсы для координаторов

Щелкните значок типа файла, чтобы загрузить вложение .

Урок-Слайды-Трансформеры-Часть-1-Абсолютное-Значение-и-Квадратичные-Функции

Раздаточные материалы для учащихся