График плавления и отвердевания кристаллических тел | 8 класс
Содержание
Если вещество в твердом состоянии будет получать энергию — оно будет нагреваться. При этом с определенной температуры начинает происходить процесс плавления — тело переходит из твердого состояния в жидкое.
Если же жидкость будет отдавать энергию, то с определенной температуры начнется процесс отвердевания (кристаллизации). Жидкость перейдет в твердое состояние.
Процесс плавления кристаллического тела довольно сложный. Для того чтобы более детально его изучить, мы рассмотрим график зависимости температуры твердого тела от времени его последовательного нагревания и охлаждения.
График плавления льда и отвердевания воды
В качестве кристаллического тела будем рассматривать лёд. График плавления льда и отвердевания воды изображен на рисунке 1. Здесь по горизонтальной оси отложено время, а по вертикальной — температура льда. Для нагревания льда будем использовать обычную горелку.
Разберем каждый участок графика.
- Точка A
Это наша начальная точка, начало наблюдения за процессом. Здесь температура льда была равна $-40 \degree C$
- Участок AB
Идет нагревание льда, его температура увеличивается с $-40 \degree C$ до $0 \degree C$
- Точка B
Достигнув температуры $0 \degree C$, лед начинает плавится. Это его температура плавления.
- Участок BC
Лед плавится, но его температура в это время не увеличивается. Процессу плавления соответствует именно этот участок графика.
Отметим, что
В течение всего времени плавления температура льда не меняется, хотя мы продолжаем его нагревать
- Точка C
В этот момент весь лед расплавился и превратился в воду
- Участок CD
На это участке графика идет нагревание воды до $+40 \degree C$
- Точка D
Вода имеет температуру $+40 \degree C$.
В этот момент мы выключаем горелку
В этот момент мы выключаем горелку- Участок DE
Температура воды снижается, она охлаждается
- Точка E
Температуры воды достигает $0 \degree C$. Начинается ее отвердевание (кристаллизация)
- Участок EF
На этом участке графика идет процесс отвердевания (кристаллизации) воды.
Пока вся вода не затвердеет, ее температура не изменится
- Точка F
В этот момент вся вода превратится в лёд
- Участок FK
Температура льда понижается
{"questions":[{"content":"Участки графика BC и EF параллельны оси времени, потому что[[choice-1]]","widgets":{"choice-1":{"type":"choice","options":["они соответствуют плавлению и отвердеванию","во время процессов плавления и отвердевания температура не изменяется","они соответсвуют нагреванию и охлаждению","во время нагревания и охлаждения температура какое-то время не изменяется"],"answer":[0,1]}}}]}Графики плавления олова и свинца
На графиках часто указывают какой-то один процесс (либо отвердевание, либо плавление), но для нескольких веществ.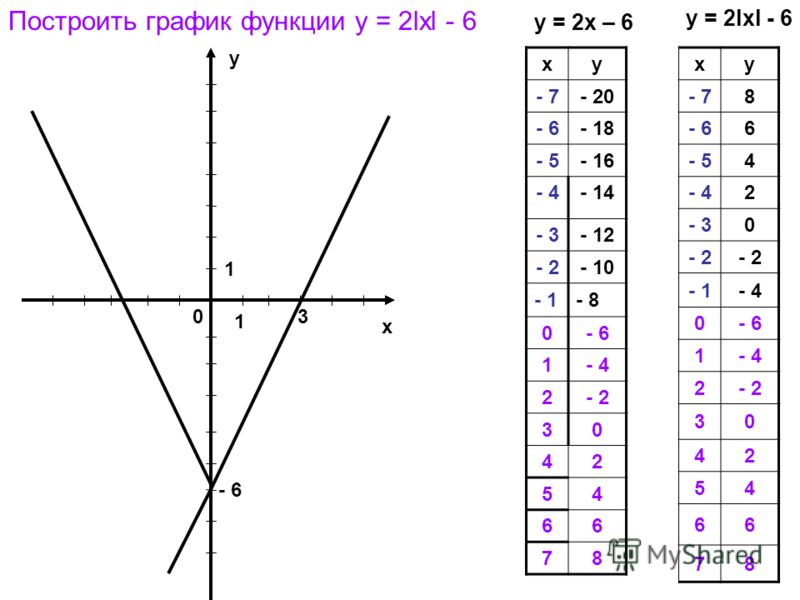
Это делается для наглядного сравнениях их свойств.
Подобный график представлен на рисунке 2.
Рисунок 2. Графики для процесса плавлении олова и свинцаПроцесс плавления олова соответствует участку CD, а процесс плавления свинца — участку AB.
Участок AB находится выше участка CD. Это означает, что свинец имеет большую температуру плавления, чем олово. На графике отмечены эти температуры. Для свинца это $327 \degree C$, а для олова $232 \degree C$.
Также мы можем судить о времени процесса плавления. Участок AB имеет большую длину, чем участок CD. Значит, свинец плавился большее время, чем олово. При этом, свинец начал плавиться раньше.
{"questions":[{"content":"Сколько времени с начала эксперимента мы можем наблюдать свинец в твердом состоянии? [[input-1]] минуты.","widgets":{"input-1":{"type":"input","inline":1,"answer":"4"}}}]}5
Оценить урок
Поделиться уроком →
Что можно улучшить?
Изложение материала
Непонятное объяснение
Урок неполный, не хватает информации
Урок перегружен, слишком много информации
Тесты плохого качества
Тестов недостаточно
Тестов слишком много
Тесты слишком легкие
Тесты слишком сложные
Изображения
Изображения плохого качества
Изображений недостаточно
Изображений слишком много
Другое
Войдите, чтобы оценивать уроки
Что нужно исправить?
Спасибо, что помогаете нам стать лучше!
Проверим знания по теме?
Плавление и отвердевание
Комментарии
График линий с использованием точек пересечения по осям X и Y
Результаты обучения
- Построение графика линейного уравнения с использованием точек пересечения по осям X и Y
Построение линии с использованием точек пересечения
Чтобы построить линейное уравнение путем построения точек, вы можете использовать точки пересечения как две из трех точек.
Найдите две точки пересечения, а затем третью точку, чтобы обеспечить точность, и нарисуйте линию. Этот метод часто является самым быстрым способом построения графика.
Построить линию, используя точки пересечения
- Найдите [латекс]x-[/латекс] и [латекс]\текст{y-intercepts}[/латекс] строки.
- Пусть [латекс]у=0[/латекс] и найдите [латекс]х[/латекс]
- Пусть [латекс]x=0[/латекс] и найдите [латекс]у[/латекс].
- Найдите третье решение уравнения.
- Нанесите три точки и убедитесь, что они совпадают.
- Проведите линию.
пример
График [латекс]-x+2y=6[/латекс] с использованием точек пересечения.
Решение
Сначала найдите [latex]x\text{-intercept}[/latex].
Пусть [латекс]y=0[/латекс],
[латекс]\begin{array}{}\\ -x+2y=6\\ -x+2\left(0\right)=6\\ -x=6\\ x=-6\end{array}[/latex]
[latex]x\text{-intercept}[/latex] равен [latex]\left(-6,0\right)[ /латекс].
Теперь найдите [latex]y\text{-intercept}[/latex].
Пусть [латекс]х=0[/латекс].
[латекс]\begin{массив}{}\\ -x+2y=6\\ -0+2y=6\\ \\ \\ 2y=6\\ y=3\end{массив}[/latex]
[latex]y\text{-intercept}[/latex] равен [latex]\left(0,3\right)[/latex].
Найти третью точку.
Мы будем использовать [латекс]x=2[/латекс],
[латекс]\begin{array}{}\\ -x+2y=6\\ -2+2y=6\\ \\ \\ 2y=8\\ y=4\end{array}[/latex]
Третье решение уравнения: [latex]\left(2,4\right)[/latex].
Суммируйте три точки в таблице, а затем нанесите их на график.
| [латекс]-x+2y=6[/латекс] | ||
|---|---|---|
| х | г | (х, у) |
| [латекс]-6[/латекс] | [латекс]0[/латекс] | [латекс]\влево(-6,0\вправо)[/латекс] |
| [латекс]0[/латекс] | [латекс]3[/латекс] | [латекс]\влево(0,3\вправо)[/латекс] |
| [латекс]2[/латекс] | [латекс]4[/латекс] | [латекс]\влево(2,4\вправо)[/латекс] |
Совпадают ли точки? Да, так что проведите линию через точки.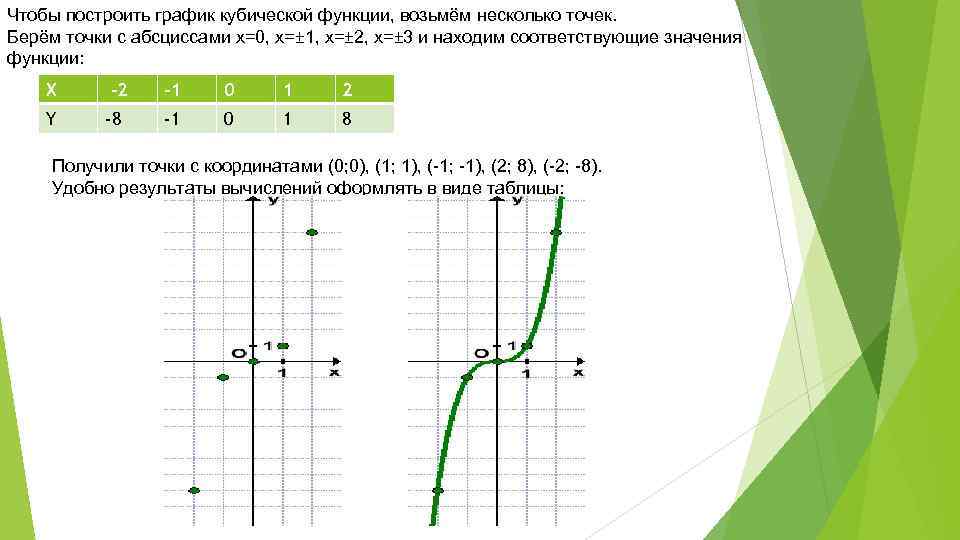
попробуйте
Посмотрите следующее видео, чтобы узнать больше о том, как построить линию с помощью точек пересечения.
попробуйте
В следующем примере есть только одна точка пересечения, потому что линия проходит через точку (0,0).
пример
Постройте график [latex]y=5x[/latex], используя точки пересечения.
Показать раствор
попробуйте
В следующем видео мы покажем еще один пример того, как построить линию, используя точки пересечения линии.
Выбор наиболее удобного способа построения графика линии по заданному уравнению
Хотя мы можем изобразить любое линейное уравнение, нанеся точки, это не всегда самый удобный метод.
| Уравнение | Метод | |
|---|---|---|
| #1 | [латекс]y=2x+1[/латекс] | Точки построения |
| #2 | [латекс]y=\Large\frac{1}{2}\normalsize x+3[/latex] | Точки построения |
| #3 | [латекс]x=-7[/латекс] | Вертикальная линия |
| #4 | [латекс]y=4[/латекс] | Горизонтальная линия |
| #5 | [латекс]2x+y=6[/латекс] | Перехваты |
| #6 | [латекс]4x — 3y=12[/латекс] | Перехваты |
Что такого в форме уравнения, что может помочь нам выбрать наиболее удобный метод построения его линии?
Обратите внимание, что в уравнениях № 1 и № 2 y изолированы в одной части уравнения, а его коэффициент равен 1.
Мы нашли точки, подставив значения x в правую часть уравнения, а затем упростив чтобы получить соответствующие значения y-.
Уравнения №3 и №4 имеют только одну переменную. Помните, что в таком уравнении значение одной переменной постоянно; это не зависит от значения другой переменной. Уравнения этой формы имеют графики, которые представляют собой вертикальные или горизонтальные линии.
В уравнениях №5 и №6 x и y находятся на одной стороне уравнения. Эти два уравнения имеют вид [latex]Ax+By=C[/latex] . Мы заменили [latex]y=0[/latex] и [latex]x=0[/latex], чтобы найти точки пересечения x — и y — , а затем нашли третью точку, выбрав значение для x или и .
Это приводит к следующей стратегии выбора наиболее удобного метода построения линии.
Выберите наиболее удобный способ построения линии
- Если уравнение имеет только одну переменную. Это вертикальная или горизонтальная линия.
- [latex]x=a[/latex] — вертикальная линия, проходящая через [latex]x\text{-ось}[/latex] в точке [latex]a[/latex]
- [latex]y=b[/latex] — это горизонтальная линия, проходящая через [latex]y\text{-ось}[/latex] в точке [latex]b[/latex].
- Если [латекс]у[/латекс] изолирован с одной стороны уравнения. График по точкам.
- Выберите любые три значения для [latex]x[/latex] и затем найдите соответствующие значения [latex]y\text{-}[/latex].
- Если уравнение имеет вид [латекс]Ах+Ву=С[/латекс], найдите точки пересечения.
- Найдите точки пересечения [latex]x\text{-}[/latex] и [latex]y\text{-}[/latex], а затем третью точку.
пример
Определите наиболее удобный способ построения графика каждой линии:
1. [латекс]y=-3[/латекс]
2. [латекс]4x — 6y=12[/латекс]
3. [latex]x=2[/latex]
4. [latex]y=\frac{2}{5}x — 1[/latex]
Решение
1. [latex]y=-3[/latex]
Это уравнение имеет только одну переменную, [latex]y[/latex].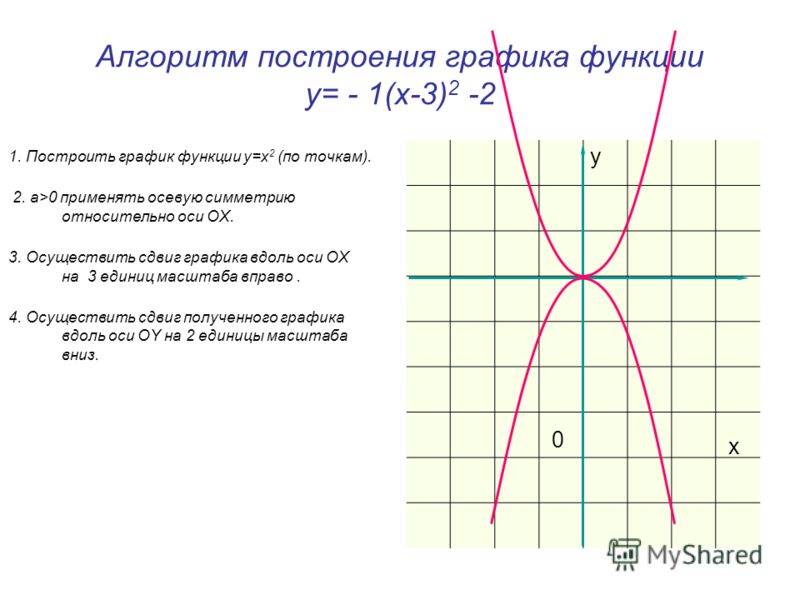
Его график представляет собой горизонтальную линию, пересекающую [латекс]у\текст{-ось}[/латекс] в точке [латекс]-3[/латекс].
2. [латекс]4x — 6y=12[/латекс]
Это уравнение имеет вид [латекс]Ах+Ву=С[/латекс]. Найдите точки пересечения и еще одну точку.
3. [latex]x=2[/latex]
Имеется только одна переменная, [latex]x[/latex]. График представляет собой вертикальную линию, пересекающую [латекс]x\текст{-ось}[/латекс] в точке [латекс]2[/латекс].
Так как [латекс]y[/латекс] изолирован в левой части уравнения, проще всего изобразить эту линию, нанеся три точки.
попробуйте
Внесите свой вклад!
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
Как построить линию с помощью таблицы значений
Что такое таблица значений?
Таблица значений содержит два списка чисел, написанных рядом друг с другом.
Первый список содержит выбранные входные значения, которые часто являются координатами 𝑥. Второй список содержит выходные данные, полученные, когда этот первый список помещается в данное уравнение, часто это координаты y. Вместе пары чисел в обоих списках составляют координаты, которые можно изобразить в виде графика.
В приведенном ниже примере у нас есть таблица значений для y = 2𝑥 + 1.
В таблице значений показаны два списка чисел.
Первый список — это заданные значения 𝑥. Здесь мы выбрали от 0 до 4. Мы можем выбрать любые числа, которые нам нравятся, в ряду 𝑥. Мы выбрали от 0 до 4, потому что их легко подставить в уравнения, потому что это небольшие числа.
Значения y были рассчитаны с использованием уравнения y = 2𝑥 + 1. Это уравнение говорит нам умножить значения 𝑥 на 2, а затем добавить к ним единицу, чтобы найти значения y.
Например, когда × = 3, мы умножаем 3 на 2, а затем прибавляем 1.
3 × 2 + 1 = 7, поэтому мы пишем 7 в строке y под 𝑥 значением 3.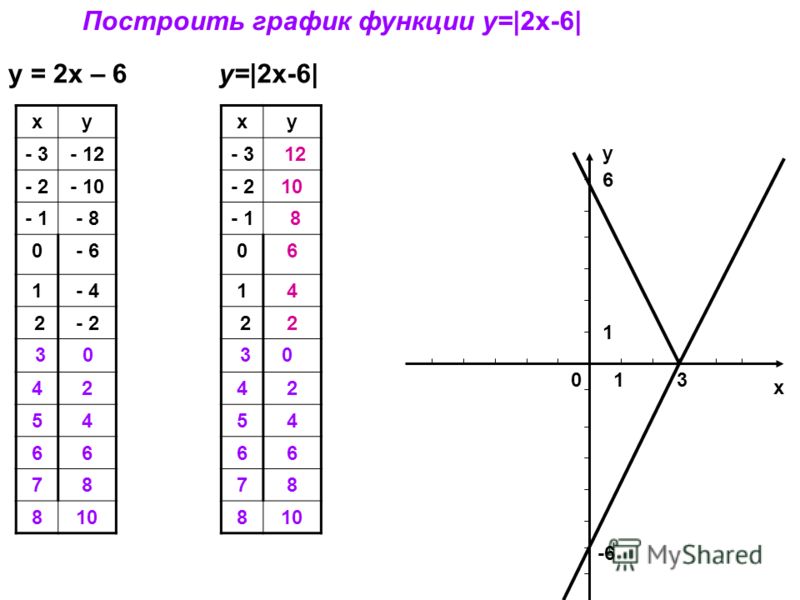
Выполнение этого вычисления для каждого значения 𝑥 приводит к другому числу, которое записывается в строке y рядом со значением 𝑥, из которого оно получено.
Как составить таблицу значений?
Таблица значений состоит из двух строк, первая из которых помечена как 𝑥, а вторая — как y. В строке 𝑥 последовательные числа выбираются из наименьшей и наибольшей 𝑥 координат на заданных осях. Числа в строке y вычисляются путем подстановки этих значений 𝑥 в данное уравнение.
Вот набор осей для построения графика y = 2𝑥 – 3.
Наименьшее значение 𝑥 равно -10, а наибольшее значение 𝑥 равно 10.
Нам нужно всего две точки, чтобы нарисовать прямую линию, но неплохо было бы выбрать от трех до пяти разных значений 𝑥 для таблицы значений. Это позволяет нам лучше замечать любые ошибки и помогает нам провести более точную линию через точки.
Чтобы выбрать, какие значения 𝑥 использовать для таблицы значений, лучше всего выбирать небольшие положительные целые числа, если это возможно.
В этом примере мы выберем 0, 1, 2, 3 и 4.
Числа в строке y рассчитываются путем подстановки этих значений 𝑥 в уравнение y = 2𝑥 – 3. Это говорит нам умножить каждое значение 𝑥 на 2, а затем вычесть 3.
В следующей таблице показаны расчеты для таблицы значений.
| 𝑥 Координата | Расчет для y = 2𝑥 – 3 | г Координата |
|---|---|---|
| 𝑥 = 0 | г = 2 × 0 – 3 | г = -3 |
| 𝑥 = 1 | у = 2 × 1 – 3 | г = -1 |
| 𝑥 = 2 | у = 2 × 2 – 3 | г = 1 |
| 𝑥 = 3 | у = 2 × 3 – 3 | г = 3 |
| 𝑥 = 4 | у = 2 × 4 – 3 | г = 5 |
Как построить линию из таблицы значений
Таблица значений содержит пары значений 𝑥 и y, которые образуют пары координат, которые можно изобразить в виде точек. Координата 𝑥 говорит нам, насколько правее находится точка, а координата y говорит нам, насколько далеко находится точка.
Если координаты отрицательные, то точка находится влево или вниз соответственно. После того, как каждая точка нанесена на график, просто проведите через них линию.
Например, вот таблица значений для y = 3𝑥 – 5.
Имеем следующие координаты:
- (0, -5) из 𝑥 = 0 и y = -5
- (0, -2) из 𝑥 = 1 и y = -2
- (0, 1) из 𝑥 = 2 и y = 1
- (0, 4) из 𝑥 = 3 и y = 4
- (0, 7) из 𝑥 = 4 и y = 7
Координаты нанесены на график, как показано на рисунке.
В следующей таблице объясняется, как наносить координаты на график:
| Координата | Как построить |
|---|---|
| Положительное значение 𝑥 | Двигаться вправо |
| Отрицательное значение 𝑥 | Двигаться влево |
| Положительное значение у | Поднять вверх |
| Отрицательное значение у | Вниз |
- 𝑥 = 0 и y = -5 говорит нам не идти ни влево, ни вправо, а идти на 5 вниз.
- 𝑥 = 1 и y = -2 говорит нам идти 1 вправо и 2 вниз.
- 𝑥 = 2 и y = 1 говорит нам идти вправо и 1 вверх.
- 𝑥 = 3 и y = 4 говорит нам пройти 3 вправо и 4 вверх.
- 𝑥 = 4 и y = 7 говорит нам идти 4 вправо и 7 вверх
Каждое из этих двух чисел описывает одну точку.
После того, как каждая точка нанесена на график, линия изображается путем проведения прямой линии через их все до самого края осей.
Как определить, является ли таблица значений линейной
Таблица значений является линейной, если при увеличении 𝑥 на постоянную величину все значения y увеличиваются на постоянную величину. Если значения y увеличиваются на одинаковую величину от одного числа к другому, то координаты при построении образуют прямую линию. Если значения y каждый раз увеличиваются на разную величину, то таблица значений является нелинейной.
Если что-то линейно, это означает, что оно образует прямую линию.
Например, вот таблица значений, в которой значения y увеличиваются на 2 каждый раз, когда 𝑥 увеличивается на 1.
Поскольку значения y увеличиваются на 2 от одного числа к другому, эта таблица значений создается из линейного выражения.
В качестве альтернативы мы можем нанести значения 𝑥 и y на набор осей и посмотреть на них, чтобы увидеть, образует ли они прямую линию или нет.
Мы видим, что координаты образуют прямую линию, поэтому таблица значений дает линейный график.
Если уравнение, которое создало таблицу значений, содержит только y и 𝑥 в качестве переменных, то оно создаст линейный график. Если оно содержит 𝑥 2 или любые другие степени 𝑥, то оно нелинейно.
Эта таблица значений сформирована из уравнения y = 2𝑥 + 1, и, поскольку нет более высоких степеней 𝑥, уравнение является линейным.
Как найти уравнение прямой из таблицы значений
Уравнение прямой линии имеет вид y = m𝑥 + c, где m — градиент, а c — точка пересечения с осью y. Градиент — это величина y, увеличивающаяся каждый раз, когда 𝑥 увеличивается на 1 в таблице.