Найти функцию обратную к данной: Обратная функция — урок. Алгебра, 10 класс.

Пособие по теме Обратные функции

ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ НОВОСИБИРСКОЙ ОБЛАСТИ «КУПИНСКИЙ МЕДИЦИНСКИЙ ТЕХНИКУМ»

МЕТОДИЧЕСКОЕ ПОСОБИЕ

Для самостоятельной работы студентов

По дисциплине: МАТЕМАТИКА (включая алгебру и начала математического анализа; геометрию)

Тема: «Обратные функции»

Специальность: 34.02.01 Сестринское дело Курс: 1

(базовой подготовки)

Купино

2020

Рассмотрено на заседании предметной цикловой

Методической комиссии по общеобразовательным дисциплинам,

общему гуманитарному и социально-экономическому, математическому и

естественно-научному циклу

Протокол № _____ от «_____» _________20____г.

Автор – составитель: преподаватель математики высшей категории Тюменцева О. Н.

Купино

2020 г

Пояснительная записка к методическому пособию

Методическое пособие предназначено для повторения теоретических и практических знаний по теме.

Цель пособия – повторить понятияобратной функции, определять вид и строить график обратной функции, находить ее область определения и область значений и подготовится к занятию по теме «Обратные функции».

Данное пособие рекомендовано для студентов первого курса специальности 34.02.01 Сестринское дело. Пособие содержит определения, свойства и формулы по теме: Обратные функции, тест для самоконтроля и ключи к тесту.

Пособие направлено на формирование навыков самостоятельной работы с учебным материалом, формирование навыков решения задач, формирование и развитие творческого потенциала, повышение интереса к дисциплине.

Обратные функции

Определение обратной функции

Пусть функция   строго монотонная (возрастающая или убывающая) и непрерывная на области определения  , область значений этой функции  , тогда на интервале   определена непрерывная строго монотонная функция   с областью значений  , которая является обратной для  .

Другими словами, об обратной функции   для функции   на конкретном промежутке имеет смысл говорить, если на этом интервале   либо возрастает, либо убывает.

Функции f и g называют взаимно обратными.

Зачем вообще рассматривать понятие обратных функций?

Это вызвано задачей решения уравнений  . Решения как раз и записываются через обратные функции.

Примеры нахождения взаимнообратных функций.

Например, требуется решить уравнение  .

Решениями являются точки  .

Функции косинус и арккосинус как раз являются обратными на области определения.

Рассмотрим несколько примеров нахождения обратных функций.

Начнем с линейных взаимнообратных функций.

Пример.

Найти функцию обратную для  .

Решение.

Областью определения и областью значений этой функции является все множество действительных чисел. Выразим x через y (другими словами, решим уравнение   относительно x ).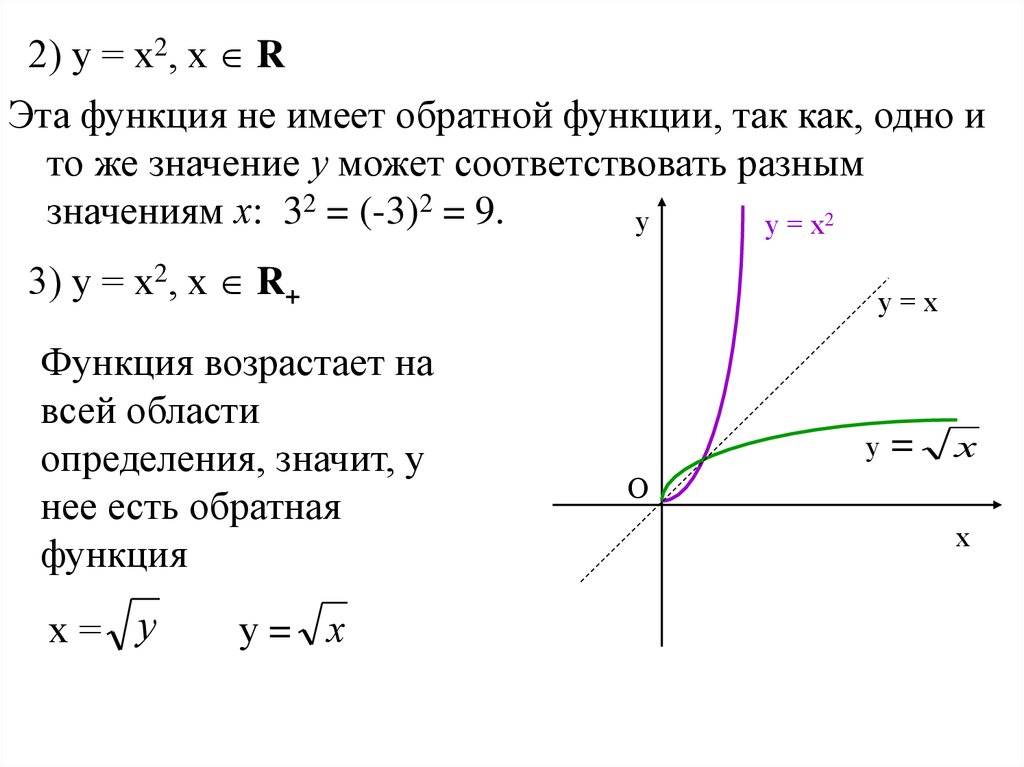

 — это и есть обратная функция, правда здесь y – аргумент, а x – функция этого аргумента. Чтобы не нарушать привычки в обозначениях (это не имеет принципиального значения), переставив буквы x и y , будем писать  .

Таким образом,   и   — взаимно обратные функции.

Приведем графическую иллюстрацию взаимно обратных линейных функций.

Очевидно, что графики симметричны относительно прямой y=x (биссектрисы первого и третьего квадрантов). Это одно из свойств взаимно обратных функций, о которых речь пойдет ниже.

Теперь рассмотрим пример нахождения логарифмической функции, обратной к заданной показательной функции.

Пример.

Найти функцию обратную для  .

Решение.

Областью определения этой функции является все множество действительных чисел, областью значений является интервал  . Выразим x через y(другими словами, решим уравнение   относительно x).

 — это и есть обратная функция. Переставив буквы x и y , имеем  .

Таким образом,   и   — показательная и логарифмическая функции есть взаимно обратные функции на области определения.

График взаимно обратных показательной и логарифмической функций.

Свойства взаимно обратных функций

Перечислим свойства взаимно обратных функций   и  .

•  и  .

• Из первого свойства видно, что область определения функции  совпадает с областью значений функции   и наоборот.

• Графики взаимно обратных функций симметричны относительно прямой y=x.

• Если   возрастает, то и   возрастает, если   убывает, то и   убывает.

Замечание по свойству 1).

Рекомендуем ОЧЕНЬ ВНИМАТЕЛЬНО относиться к области определения и области значений функций.

Например:   и   — взаимно обратные функции. По первому свойству имеем  . Это равенство верно только для положительных y , для отрицательных y логарифм не определен. Так что не спешите с записями вида  , а если уж так написали, то следует добавить фразу «при положительных y».

Равенство   в свою очередь верно для любых действительных x.

Надеемся, Вы уловили этот тонкий момент.

Особенно аккуратными надо быть с тригонометрическими и обратными тригонометрическими функциями.

К примеру,  , так как область значений арксинуса  , а  в нее не попадает.

Правильно будет

В свою очередь   есть верное равенство.

То есть   при   и   при  .

Графики основных элементарных взаимно обратных функций

• Взаимно обратные степенные функции, графики.

Для степенной функции   при   обратной является также степенная функция   Если заменить буквы, то получим пару взаимно обратных функций   и 

Графики для положительных а и отрицательных а.

• Взаимно обратные показательная и логарифмическая функции и , графики.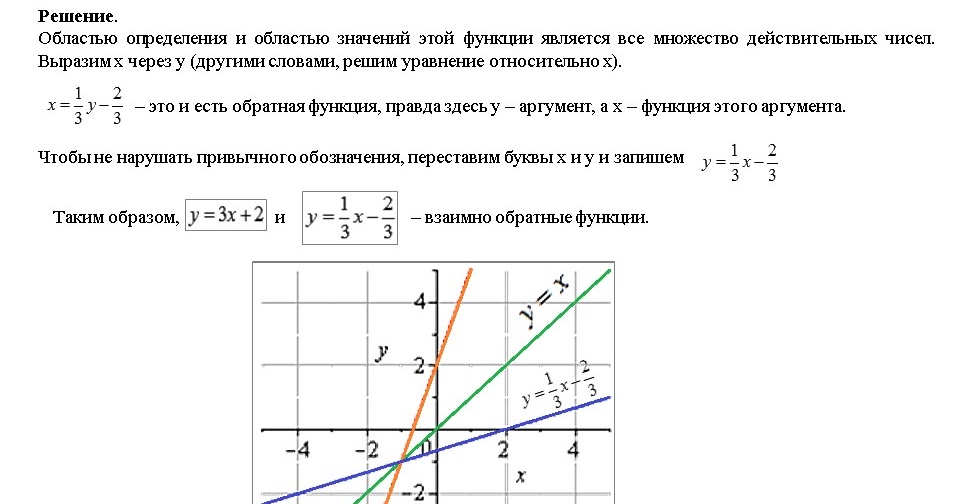

Подразумеваем, что а положительное и не равное единице число.

Графики для   и для 

График главной ветви синуса и арксинуса (светлая область).

График главной ветви косинуса и арккосинуса (светлая область).

График главной ветви тангенса и арктангенса (светлая область).

График главной ветви котангенса и арккотангенса (светлая область).

Если Вам потребуются обратные функции для ветвей тригонометрических функций, отличных от главных, то соответствующую обратную тригонометрическую функцию нужно будет сдвинуть вдоль оси ординат на необходимое количество периодов.

Например, если Вам потребуется обратная функция для ветви тангенса на промежутке   (эта ветвь получается из главной ветви сдвигом на величину  вдоль оси ох ), то ей будет являться ветвь арктангенса, сдвинутая вдоль оси oy на  .

Пока на этом закончим с обратными функциями.

Тест по теме: Обратные функции

1. Как называют функция y = f(х), если она принимает каждое своё значение только при одном значении х?

2. Найдите функцию, обратную к функции у = 5х + 2.

Варианты ответов

• у = 0,2 (х — 2)

• у = 0,5 (х — 2)

• у = 0,2 (2 + х)

• у = (х — 2)²

3. Является ли монотонная функция обратимой?

Варианты ответов

• является

• не является

4.Укажите, какие из перечисленных функций являются обратимыми.

Варианты ответов

• у = 5х + 2

• у = х²

• у = х⁵

• у = х³ + 1

5.Укажите истинные утверждения.
Если g(x) — функция, обратная к функции f(x), то и f(x) — функция, обратная к g(x), при этом …

Варианты ответов

• область определения обратной функции совпадает со множеством значений исходной функции

• множество значений обратной функции совпадает с областью определения исходной функции

• область определения обратной функции совпадает с областью определения исходной функции

• множество значений обратной функции совпадает со множеством значений исходной функции

6. Найдите область значений функции, обратной для f(x) = 4 — 3x.

Варианты ответов

• (-∞;+∞)

• (0;+∞)

• (-∞;4)

• [3;4]

• [-4;-3]

7.Найдите область определения и область значения функции, обратной данной у = 7х — 5.

Варианты ответов

• D(y) = (-∞;+∞)

• E(y) = (-∞;+∞)

• D(y) = (-5;+∞)

• E(y) = (-∞;5)

• D(y) = (-7;+∞)

• E(y) = (-5;7)

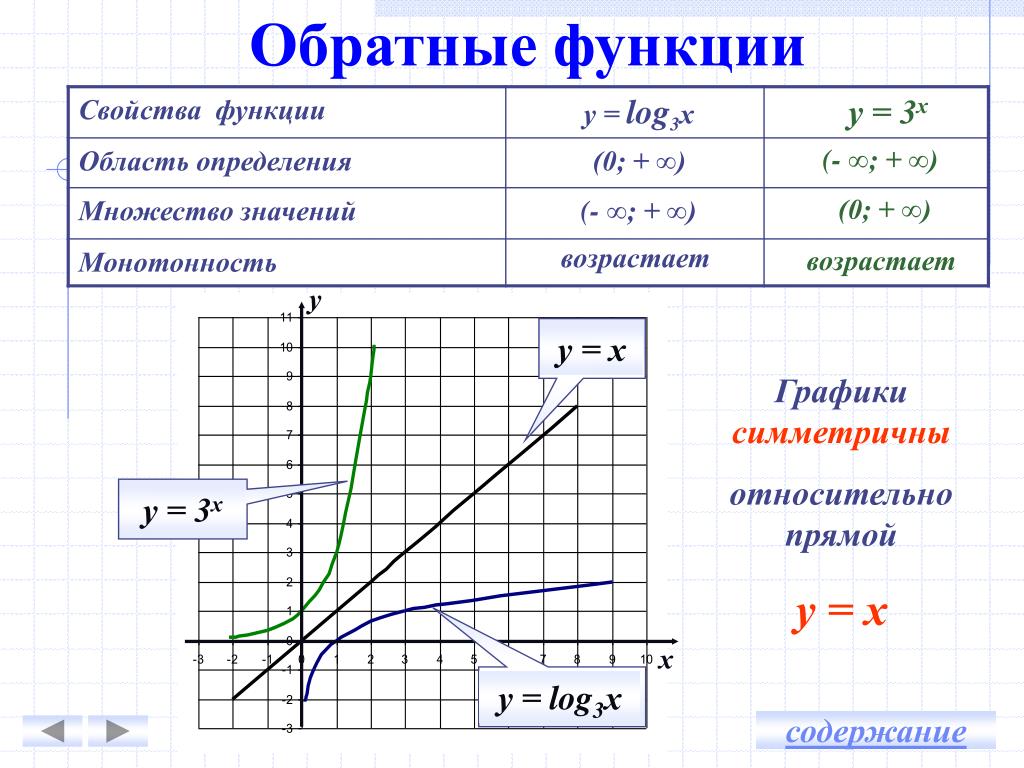
8.Укажите номер рисунка, на котором изображен график обратной функции к функции у = х², при х є [0;+∞).

9.Сопоставьте функции и обратные к ним.

Варианты ответов

• y=x+53

• y=x3

• y=x2

10.Какое значение принимает обратная функция при х = 6 к функции у = 2х — 4.

Эталоны ответов теста по теме: Обратные функции

1. Как называют функция y = f(х), если она принимает каждое своё значение только при одном значении х? Ответ обратимая

2. Найдите функцию, обратную к функции у = 5х + 2.

Варианты ответов

• у = 0,2 (х — 2)

• у = 0,5 (х — 2)

• у = 0,2 (2 + х)

• у = (х — 2)²

3. Является ли монотонная функция обратимой?

Варианты ответов

• является

• не является

4.Укажите, какие из перечисленных функций являются обратимыми.

Варианты ответов

• у = 5х + 2

• у = х²

• у = х⁵

• у = х³ + 1

5.Укажите истинные утверждения.
Если g(x) — функция, обратная к функции f(x), то и f(x) — функция, обратная к g(x), при этом …

Варианты ответов

• область определения обратной функции совпадает со множеством значений исходной функции

• множество значений обратной функции совпадает с областью определения исходной функции

• область определения обратной функции совпадает с областью определения исходной функции

• множество значений обратной функции совпадает со множеством значений исходной функции

6. Найдите область значений функции, обратной для f(x) = 4 — 3x.

Варианты ответов

• (-∞;+∞)

• (0;+∞)

• (-∞;4)

• [3;4]

• [-4;-3]

7.Найдите область определения и область значения функции, обратной данной у = 7х — 5.

Варианты ответов

• D(y) = (-∞;+∞)

• E(y) = (-∞;+∞)

• D(y) = (-5;+∞)

• E(y) = (-∞;5)

• D(y) = (-7;+∞)

• E(y) = (-5;7)

8.Укажите номер рисунка, на котором изображен график обратной функции к функции у = х², при х є [0;+∞).

Ответ 4

9.Сопоставьте функции и обратные к ним.

Варианты ответов

• y=x+53

• y=x3

• y=x2

10.Какое значение принимает обратная функция при х = 6 к функции у = 2х — 4. Ответ 5

Критерии оценивания тестовых заданий

10 вопросов 5 (отлично) (10-9 ответов)

10 вопросов 4 (хорошо) (8 ответов)

10 вопросов 3 (удов) (7 ответов)

Литература

1. Алимов Ш. А. и др. Алгебра и начала анализа. 10 (11) кл. – М.: 2018

2. Башмаков М.И. Сборник задач: учеб. пособие (базовый уровень). 11 кл. – М.: 2012

Интернет-ресурсы

1. http://school-collection.edu.ru – Электронный учебник «Математика в

школе, XXI век».

1. http://fcior.edu.ru — информационные, тренировочные и контрольные материалы.

2. www.school-collection.edu.ru – Единая коллекции Цифровых образовательных ресурсов

1) найти функцию обратную к данной y=-7x+2 2) найти область определения и множество значений функции обратной к данной у=4х-3 — Школьные Знания.net

• Все предметы

• Математика

• Литература

• Алгебра

• Русский язык

• Геометрия

• Английский язык

• Физика

• Биология

• Другие предметы

• История

• Обществознание

• Окружающий мир

• География

• Українська мова

• Информатика

• Українська література

• Қазақ тiлi

• Экономика

• Музыка

• Беларуская мова

• Французский язык

• Немецкий язык

• Психология

• Оʻzbek tili

• Кыргыз тили

• Астрономия

• Физкультура и спорт

Ответ дан

uncl95

Ответ:

Пошаговое объяснение:

1).

у=-7х+2

выразим х через у

-7х= у-2

х=-(у-2)/7

заменим х на у

у= -(х-2)/7 это обратная функция

2).

у=4х-3

найдем обратную функцию

4х=у+3

х=(у+3)/4

заменим х на у

у=(х+3)/4 — это обратная функция

График этой функции прямая линия, соответственно множество будет

D=E=R

Рисунок во вложении

Отмена функции «один к одному»; Обратные функции

Прежде чем читать этот урок, убедитесь, что вы полностью понимаете концепции двух предыдущих уроков:
использование блока функций «назад»
и
функции «один к одному»

Не все функции можно отменить.
«Отменить» означает перейти от вывода обратно к вводу , из которого он был получен — это работает только в том случае, если вывод поступил только из одного места!
То есть, чтобы «отменить» функцию, она должна удовлетворять следующим эквивалентные условия: 9{-1}\,$ переводит $\,y\,$ в $\,x\,$’

Эти два предложения эквивалентны — они одновременно истинны и ложны.

Это определяет связь между функцией и ее обратной функцией: если одна функция что-то делает, другая это отменяет!

Точнее, эквивалентность этих двух предложений дает всю следующую информацию: 93\,.$
Ответьте на следующие вопросы:

1. Является ли $\,f\,$ взаимно однозначным? Приведите причину, подтверждающую ваш ответ.
   Решение: Да. График функции куба проходит тест горизонтальной линии.
2. Есть ли у $\,f\,$ обратный? Приведите причину, подтверждающую ваш ответ. 93\,$ эквивалентно $\,\root 3\of{y} = x\,.$

Нахождение обратной однозначной функции

Предварительный расчет

Белла В.

спросил 31.03.20

Мне нужна помощь в поиске обратной этой однозначной функции. Функция f(x)=2/3+x

Подписаться І 1

Подробнее

Отчет

3 ответа от опытных наставников

Лучший Новейшие Самый старый

Автор: ЛучшиеНовыеСамыеСтарые

Далия П. ответил 31.03.20

Репетитор

Новое в Византе

Помощь учащимся в поиске своего «АГА!» моменты в математике.

Смотрите таких репетиторов

Смотрите таких репетиторов

1. Помните, что f(x) — это то же самое, что и y, поэтому y=2/3+x
2. поменять местами x и y в уравнении x=2/3+y
3. Найти y , y=x-2/3
4. Вы закончили или можете назвать обратную функцию f ^-1 (x)=x-2/3

Голосовать за 1 Голосовать против

Подробнее

Отчет

Кэролайн Х.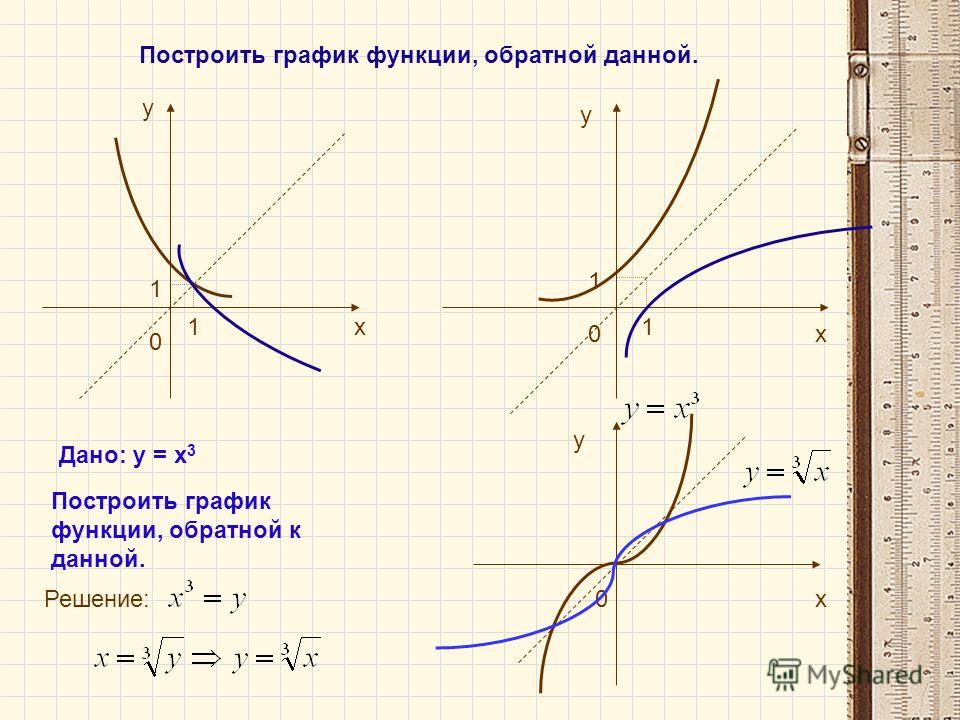 ответил 31.03.20

Репетитор

Новое в Византе

Дружелюбный и опытный репетитор по математике и подготовке к экзаменам

См. таких репетиторов

Смотрите таких репетиторов

Помните определение инверсии:

1. Графически обратная функция будет отражена по диагональной линии y=x и также будет функцией. Напомним также, что область определения исходной функции становится областью значений обратной, а область значений исходной функции — областью значений обратной.
2. Алгебраически, по определению, когда вы составляете функцию с обратной, результатом будет ‘x’. Например:

f(x) = x ² — функция

g(x) = √x — обратная

Итак, f(g(x)) = x и g(f(x)) = x

To решите для обратного алгебраически, вспомните, что f (x) такое же, как y. f(x) буквально означает «значение функции (f(x) или y) является функцией (или зависит) от выбранного вами значения x (независимо).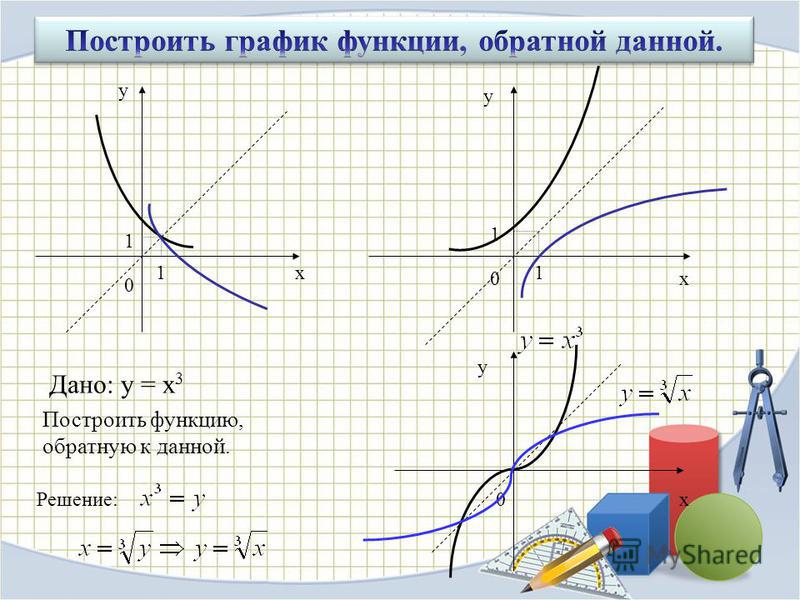 Вы просто:

1. Переписать уравнение функции с y вместо f(x)
2. Переключить x и y (переключить домен и диапазон)
3. Найдите у, чтобы получить обратную

В этом случае:

1. y = 2/(3+x)
2. х = 2/(3+у)
3. x(3+y) = 2 (перекрестное умножение) -> 3x + xy = 2 (распределение) -> xy = 2-3x (вычесть 3x с обеих сторон) ->

y = (2-3x)/x с обеих сторон на x. Если разделить дроби, то получится 9.0273 у = (2/х) — 3

Голосовать за 0 Голосовать против

Подробнее

Отчет

Все еще ищете помощь? Получите правильный ответ, быстро.

Задайте вопрос бесплатно

Получите бесплатный ответ на быстрый вопрос.