Как построить параболу по квадратному уравнению: Квадратичная функция. Как построить параболу?

2+bx_в+с\)
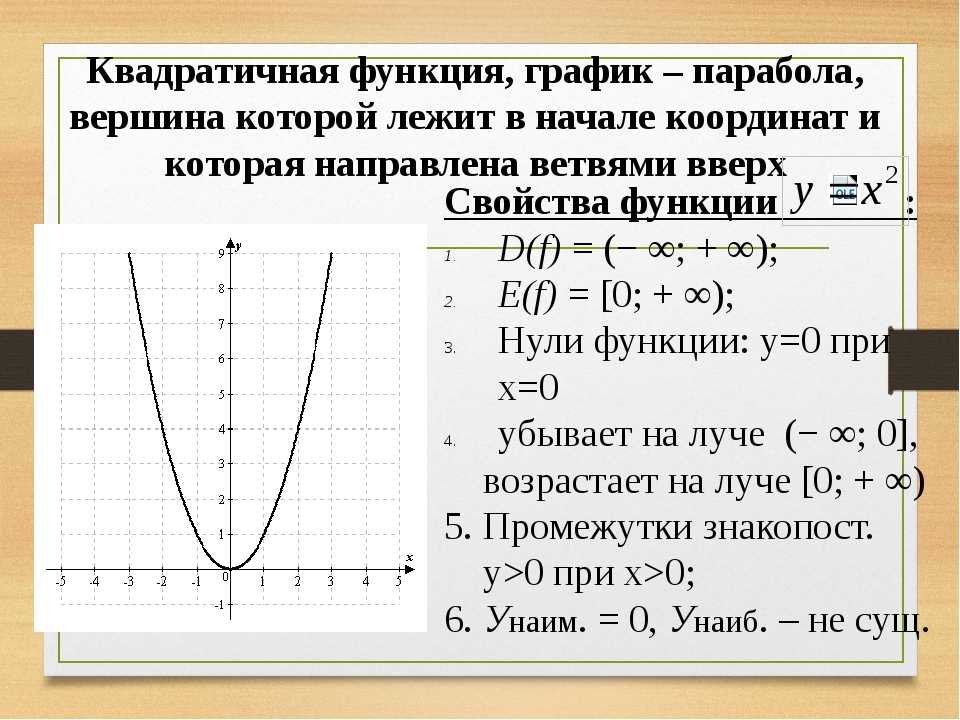
Ось симметрии проходит через вершину параболы и параллельна оси \(y\) (ординат). \(x_1\) и \(x_2\) – нули функции. Их можно найти, приравняв формулу функции к нулю и решив соответствующее квадратное уравнение.

3 параметра позволяющих сопоставить формулу квадратичной функции и график:

1.	\(a>0\) — ветви параболы направлены вверх
	\(a<0\) — ветви параболы направлены вниз
2.	\(c\) равна ординате точки пересечения графика с осью \(y\)
3. 2+5x+1\)      \(x_в= \frac{-5}{2}=-2,5\) так же как на графике 3 Ответ:   А Б В 1 3 2 Как построить график квадратичной функции (параболу)? Квадратичную функцию можно строить, как и все остальные, выбирая точки наугад (подробнее можно прочитать здесь). Но есть способ позволяющий строить параболу быстрее, выбирая точки осмысленно. Найдите координаты вершины параболы. Поставьте точку вершины на координатной плоскости и проведите через неё ось симметрии параболы. 2-4x+5=0\) нет корней, т.к. нету \(x\) при которых y будет равен нулю (функция не пересекает ось \(x\))

Смотрите также:
Линейная функция
Виды графиков функций
Квадратные неравенства

§ Квадратичная функция. Как построить параболу

Квадратичная функция. Как построить параболу Как решать задачи на квадратичную функцию

Прежде чем перейти к разбору квадратичной функции рекомендуем вспомнить, что называют функцией в математике.

Если вы прочно закрепите общие знания о функции (способы задания, понятие графика) дальнейшее изучение других видов функций будет даваться значительно легче.

Запомните!

Квадратичная функция — это функция вида

y = ax² + bx + c,

где a, b и с — заданные числа.

Другими словами можно сказать, что если в функции старшая (то есть самая большая) степень, в которой стоит «x» — это «2», то перед нами квадратичная функция.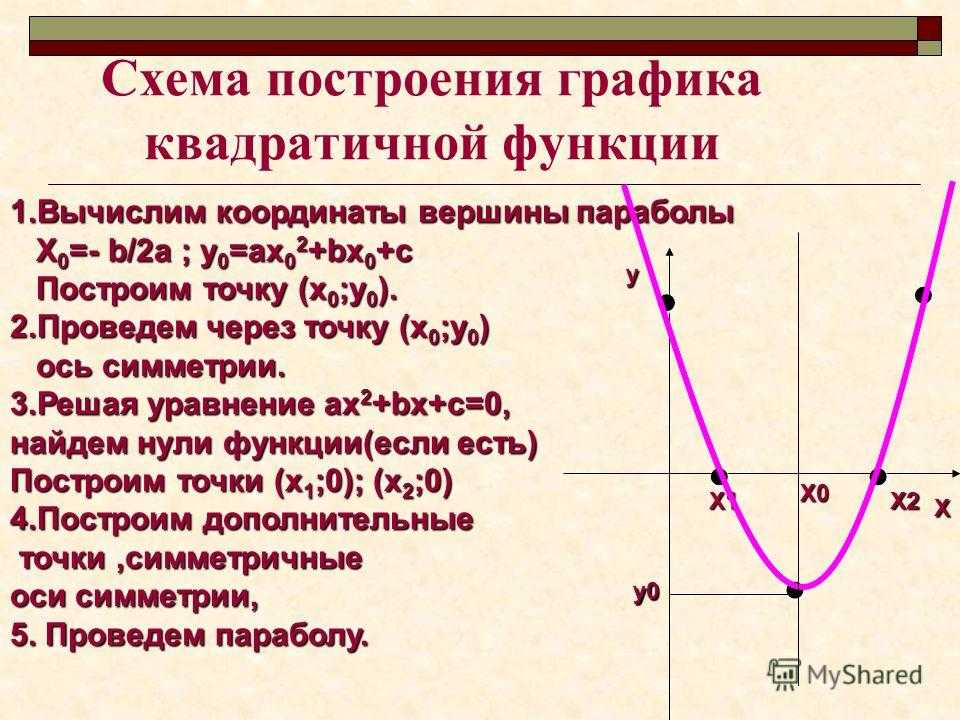

Рассмотрим примеры квадратичных функций и определим, чему в них равны коэффициенты «a», «b» и «с».

Квадратичная функция	Коэффициенты
y = 2x2 − 7x + 9	a = 2 b = −7 с = 9
y = 3x2 − 1	a = 3 b = 0 с = −1
y = −3x2 + 2x	a = −3 b = 2 с = 0

Как построить график квадратичной функции

Запомните!

График квадратичной функции называют параболой.

Парабола выглядит следующим образом.

Также парабола может быть перевернутой.

Существует четкий алгоритм действий при построении графика квадратичной функции. Рекомендуем при построении параболы всегда следовать этому порядку действий, тогда вы сможете избежать ошибок при построении.

Чтобы было проще понять этот алгоритм, сразу разберем его на примере.

Построим график квадратичной функции «y = x² −7x + 10».

1. Направление ветвей параболы

   Запомните!

   Если «a > 0», то ветви направлены вверх.

   Если «a

   В нашей функции «a = 1», это означает, что ветви параболы направлены вверх.

2. Координаты вершины параболы

   Запомните!

   Чтобы найти «x₀» (координата вершины по оси «Ox») нужно использовать формулу:

   x₀ =

   Найдем «x₀» для нашей функции «y = x² −7x + 10».

   x₀ =

   − (−7)

   2 · 1

   = = 3,5

   Теперь нам нужно найти «y₀» (координату вершины по оси «Oy»). Для этого нужно подставить найденное значение «x₀» в исходную функцию. Вспомнить, как найти значение функции можно в уроке «Как решать задачи на функцию» в подразделе «Как получить значение функции».

   y₀(3,5) = (3,5)

   2 − 7 ·3,5 + 10 = 12,25 − 24,5 + 10 = −12,25 + 10 = −2,25

   Выпишем полученные координаты вершины параболы.

   (·) A (3,5; −2,25) — вершина параболы.

   Отметим вершину параболы на системе координат. Проведем через отмеченную точку ось симметрии, так как парабола — это симметричный график относительно оси «Oy».

3. Нули функции

   Для начала давайте разберемся, что называют нулями функции.

   Запомните!

   Нули функции — это точки пересечения графика функции с осью «Ox» (осью абсцисс).

   Наглядно нули функции на графике выглядят так:

   Свое название нули функции получили из-за того, что у этих точек координата по оси «Oy» равна нулю.

   Теперь давайте разберемся, как до построения графика функции рассчитать координаты точек нулей функции.

   Запомните!

   Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо «y = 0».

   Подставим в заданную функцию «y = x² −7x + 10» вместо «y = 0» и решим полученное квадратное уравнение относительно «x» .

   0 = x² −7x + 10
   x² −7x + 10 = 0
   x_1;2 =

   7 ± √49 − 4 · 1 · 10

   2 · 1

   
   x_1;2 =

   7 ± √9

   2

   
   x_1;2 =

   7 ± 3

   2

   
   

   x1 =	x2 = 7 − 3 2
   x1 =	x2 =
   x1 = 5	x2 = 2

   Мы получили два корня в уравнении, значит, у нас две точки пересечения с осью «Ox». Назовем эти точки и выпишем их координаты.

   • (·) B (5; 0)
   • (·) C (2; 0)

   Отметим полученные точки («нули функции») на системе координат.

4. Дополнительные точки для построения графика

   Возьмем четыре произвольные числовые значения для «x». Целесообразно брать целые числовые значения на оси «Ox», которые наиболее близки к оси симметрии. Числа запишем в таблицу в порядке возрастания.

   x	1	3	4	6
   y

   Для каждого выбранного значения «x» рассчитаем «y».

   • y(1) = 1² − 7 · 1 + 10 = 1 − 7 + 10 = 4
   • y(3) = 3² − 7 · 3 + 10 = 9 − 21 + 10 = −2
   • y(4) = 4² − 7 · 4 + 10 = 16 − 28 + 10 = −2
   • y(6) = 6² − 7 · 6 + 10 = 36 − 42 + 10 = 4

   Запишем полученные результаты в таблицу.

   x	1	3	4	6
   y	4	−2	−2	4

   Отметим полученные точки графика на системе координат (зеленые точки).

   Теперь мы готовы построить график. На забудьте после построения подписать график функции.

Краткий пример построения параболы

Рассмотрим другой пример построения графика квадратичной функции. Только теперь запишем алгоритм построения коротко без подробностей.

Пусть требуется построить график функции «y = −3x² − 6x − 4».

1. Направление ветвей параболы
«a = −3» — ветви параболы направлены вниз.
2. Координаты вершины параболы

   x₀ =

   x₀ =

   −(−6)

   2 · (−3)

   =

   = −1

   y₀(−1) = (−3) · (−1)² − 6 · (−1) − 4 = −3 · 1 + 6 − 4 = −1

   (·) A (−1; −1) — вершина параболы.

3. Нули функции

   Точки пересечения с осью «Ox» (y = 0).

   0 = −3x² − 6x − 4

   −3x² − 6x − 4 = 0 |·(−1)

   3x² + 6x + 4 = 0

   x_1;2 =

   −6 ± √62 − 4 · 3 · 4

   2 · 1

   x_1;2 =

   −6 ± √36 − 48

   2

   x_1;2 =

   −6 ± √−12

   2

   Ответ: нет действительных корней.

   Так как корней нет, значит, график функции не пересекает ось «Ox».

4. Вспомогательные точки для: «x = −3»; «x = −2»; «x = 0»; «x = 1». Подставим в исходную функцию «y = −3x² − 6x − 4».
   • y(−3) = −3 · (−3)² − 6 · (−3) − 4 = −3 · 9 + 18 − 4 = −27 + 14 = −13
   
   
   • y(−2) = −3 · (−2)² − 6 · (−2) − 4 = −3 · 4 + 12 − 4 = −12 + 12 − 4 = −4
   
   
   • y(0) = −3 · 0² − 6 · 0 − 4 = −4
   
   
   • y(1) = −3 · 1² − 6 · 1 − 4 = −3 −6 − 4 = −13

   x	−3	−2	0	1
   y	−13	−4	−4	−13

Отметим вспомогательные точки.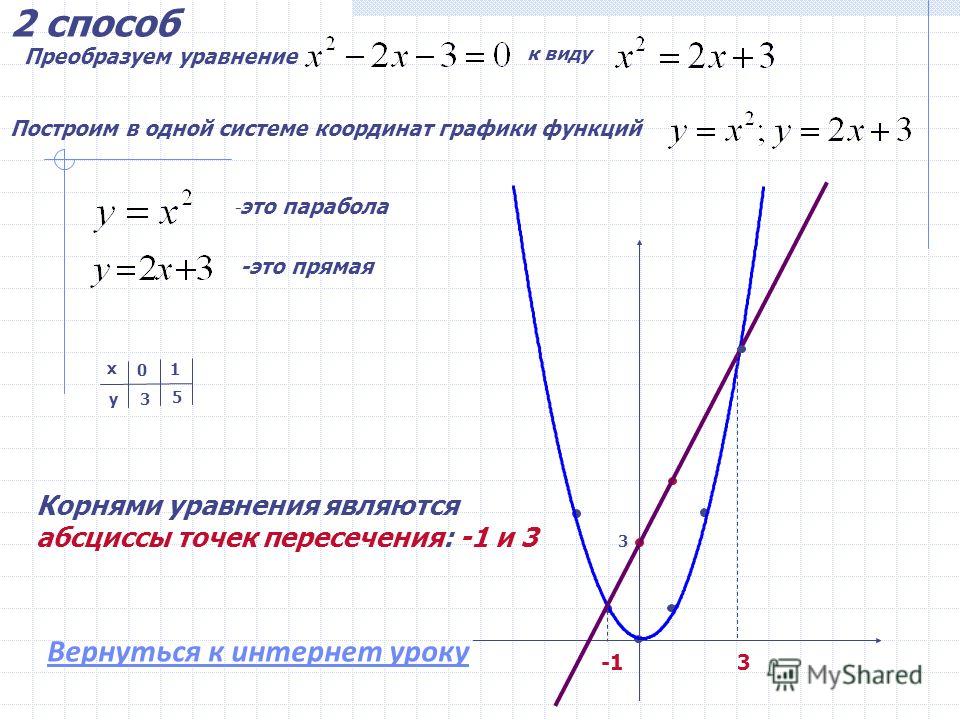 Отмечаем на системе координат только те точки, которые не выходят за масштаб нашей системы координат, то есть точки «(−2; −4)» и «(0; −4)». Построим и подпишем график функции.

Квадратичная функция. Как построить параболу Как решать задачи на квадратичную функцию

---

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи «ВКонтакте».

Оставить комментарий:

Отправить

---

Vertex Form — Как найти уравнение параболы

RadfordMathematics.com

Онлайн-книга по математике

(нахождение уравнения параболы)

---

Узнаем как найти уравнение параболы записав его в вершинную форму

В предыдущем разделе мы узнали , как написать параболу в ее вершинной форме 9.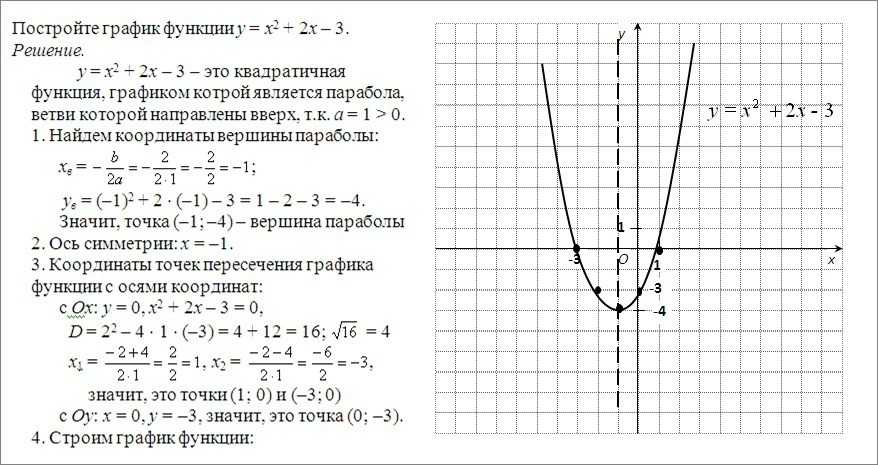 2+к\] где:

• \(h\): горизонтальная координата вершины
• \(k\): вертикальная координата вершины.

Это проиллюстрировано здесь:

Мы можем использовать форму вершины , чтобы найти уравнение параболы . Идея состоит в том, чтобы использовать координат его вершины ( максимальная точка , или минимальная точка 92+k\) (при условии, что мы можем прочитать координаты \(\begin{pmatrix}h,k\end{pmatrix}\) из графика), а затем найти значение коэффициента \(a\).

Это объясняется в пошаговом методе ниже, а также в руководствах .

---

Как найти уравнение параболы, используя ее форму вершины

Учитывая график параболы , для которой мы даны или можем ясно видеть:

• координаты вершины , \(\begin{pmatrix}h,k\end{pmatrix}\), и:
• координаты другой точки \(P\), через которую проходит парабола .

мы можем найти уравнение параболы в вершинной форме после двух шагов :

• Шаг 1: используйте (известные) координаты 92+к\] теперь проблема состоит только в том, чтобы найти значение коэффициента \(а\).
• Шаг 2: Найдите значение коэффициента \(a\), подставив координаты точки \(P\) в уравнение, записанное в шаге 1, и решив для \(a\).

Этот двухэтапный метод лучше/дополнительно объясняется в следующем учебнике , найдите время, чтобы посмотреть его сейчас.

---

Учебник 1

В следующем уроке мы узнаем , как найти параболы, используя координаты ее вершины , а также координаты ее \(y\)-перехвата .

Ваш браузер не поддерживает видео тег.

---

Упражнение 1

Используя двухэтапный метод , который мы только что изучили, найдите уравнение каждой из следующих парабол в следующих двух формах: 92+4х+3\)

Выберите номер вопроса, по которому вы хотите увидеть работу:

Учебник 2

В следующем уроке мы узнаем , как найти параболы, используя координаты ее вершины , а также координаты другой точки вдоль ее длины (это не точка пересечения \(y\)).

Ваш браузер не поддерживает видео тег. 92 — 24х + 31\)

Квадратичные соотношения и конические сечения

Числа: квадратичные соотношения и конические сечения Назад к оглавлению

Числа и их применение — Урок 19?

Обзор урока

• Квадратичные соотношения и Квадратичные функции
• Важная справочная информация (Предположим: B =0.)
• Круг ( А = С .)
• Эллипс ( A C и AC > 0.)
• Парабола ( A = 0 или C = 0, но не оба.)
• Гипербола ( AC < 0.)
• Получение уравнений из описаний
• Термин xy , (B 0)

Конические сечения возникают в результате изучения пересечения между плоскость и конус, в частности конус с двойным ворсом . Под номером с двойным ворсом мы имеем в виду тот факт, что стандарт конус, изучаемый в геометрии с основанием и вершиной, является только однозаходным. Все поверхностные лучи, оканчивающиеся в вершине, должны быть продолжены для создания конуса, задуманного при изучении конических сечений. Таким образом, он больше похож на песочные часы, чем на носовой обтекатель реактивного самолета. Четыре основных конических сечения: круг , эллипс , парабола и гипербола подробно описаны ниже. Для получения этих конических сечений пересекающиеся плоскость не должна проходить через вершину конуса. Если плоскость проходит через вершину, различные вырождения получаются конические сечения, а именно: точка , линия , или две пересекающиеся линии. Конические сечения также известны как квадратичные отношения, потому что уравнения, описывающие их, имеют второй порядок и не всегда функционируют. Эти конические сечения являются прекрасными математическими моделями траекторий движения планеты, метеоры, космические корабли, световые лучи и многие другие объекты. Третий подход определяет коники как местонахождение (коллекция) точек, удовлетворяющих определенным геометрическим свойствам (расстоянию от точки или линии).

Чтобы различать квадратичные отношения и квадратичные функции, общее уравнение квадратичной функции выглядит следующим образом:

у = ах ² + Ьх + в.

Приведенная выше формула имеет форму параболы . Возможно, мы захотим проверить, проходит ли он тест вертикальной линии 9.0332 и на самом деле является функцией. Чтобы выполнить такой тест, просто выберите значение « x » и проведите через него вертикальную линию. Если любая такая строка пересекает график более одного раза, то говорят, что критерий вертикальной линии потерпели неудачу, и отношение не является функцией. Поскольку все многочлены являются функциями, а это многочлен, мы ожидаем, что он пройдет тест вертикальной линии.

Далее рассмотрим соотношение:

года ² = х
Наивно можно было бы переписать это как: у = ( х ). Однако мы потеряли одну ветку и правильно было бы написано: y = ± ( х ), тогда это будет парабола, открывающаяся в направлении x . Но он не проходит тест на вертикальную линию, и это только отношение, а не функция.

Имея это в виду, теперь мы можем рассмотреть квадратичное соотношение, которое указано общее уравнение (или неравенство) вида:

Ax ² + Bxy + Cy ² + Dx + Ey + F = 0
(Буквы A-F являются константами и знак «=» тоже можно заменить со знаком неравенства.) Это общее уравнение может быть преобразовано в различные конкретные уравнения с формой этого уравнения диктуется фактическим типом квадратичной зависимости. Быстрый обзор некоторой важной справочной информации может быть полезен в этот момент.

Формула расстояния :
Формула расстояния выводится из теоремы Пифагора, которая говорит, что сумма квадратов двух сторон прямоугольного треугольника равен квадрату гипотенузы. Таким образом, расстояние ( d ) между двумя известными точками, ( x ₁ , y ₁ ) и ( x ₂ , y ₂ ) является квадратным корнем из следующего:

д ² = (х ₂ — х ₁ ) ² + (у ₂ — у _{1 5 5} ) 2 90. Это соотношение часто будет использоваться для нахождения различных задействованных радиусов.

Завершение квадрата :
Если коэффициент квадратичного члена равен единице, как в x ² +bx , тогда число, которое заполнит квадрат , можно найти, разделив линейный коэффициент вдвое, ( b ), возведя его в квадрат и сложив результат: x ² + bx + (b/2) ² =( x + b /2) ² . Когда коэффициент квадратичного члена не равен единице, вы должны фактор, если out сначала, как показано в некоторых примерах ниже.

Вершина :
В параболе координата вершины x определяется как: h = -(b/2a) . Координата y задается как к = у ( ч ) или k = c — b ² /(4 a ). Уравнение координат x должно быть легко запоминающимся, поскольку корни (нули, x — точки пересечения, решения) квадратичного уравнения симметричны относительно вершины, и эти корни даются квадратичной формулой.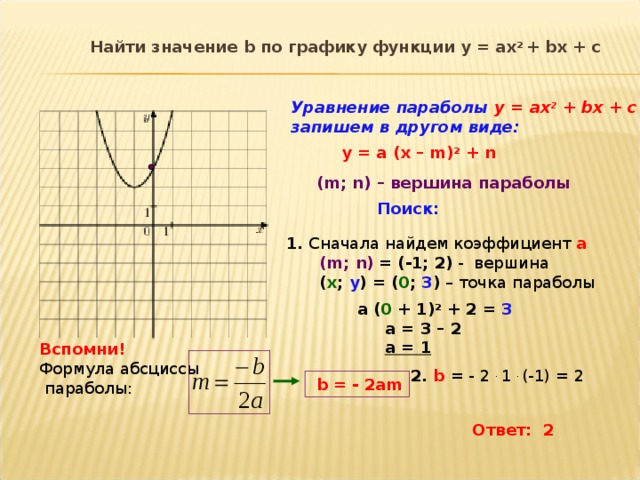 h = -(b/2a) , таким образом, является частью квадратной формулы без части ±. у 9Формула координат 0294 может быть получена путем замены этого h как x в y ( x ).

Неравенства :
» «>» указывает на область вне конического сечения.

Окружность представляет собой набор точек ( x,y ) на координатной плоскости, так что каждая точка равноудалена от фиксированной точки ( h,k ) известен как центр. Для кругов коэффициенты x 2 и y 2 термины в общем квадратичные отношения равны ( т.е. A=C ).

Граф окружности	х 2 + у 2 = 25	Использование окна с квадратным обзором

Уравнение окружности в стандартной форме выглядит следующим образом:

(x-h) ² + (y-k) ² = r ²

Помните:

• ( h,k ) является центральной точкой.
• r — это радиус от центра до координат окружности ( x,y ).

Пример:

x ² + y ² + 6 x — 4 y — 12 = 0

Шаг 1. Совершите поездку и свяжите x и y точки; добавка инверсия -12:

( x ² + 6 x ) + ( y ² — 4 y ) = 12

Шаг 2 — Заполните квадраты (то, что вы делаете с одной стороной, обязательно сделайте с другой стороной):

( х ² + 6 х + 9) + ( у ² — 4 у + 4) = 12 + 9 + 4

Шаг 3 — Фактор:

( x + 3) ² + ( y — 2) ² = 25 = 5 ²

Наблюдения
1. Коническое сечение будет кругом, начиная с x ² и y ² члены имеют одинаковый знак и равные коэффициенты.
2. Центр ( h,k ) равен (-3,2). Обратите внимание, это значения x и y , что делает соответствующий член равным нулю.
3. Радиус окружности будет 5 единиц, так как квадратный корень из 25 это 5.
4. Круг можно нарисовать с помощью циркуля или одной кнопки и веревки.
5. Эксцентриситет окружности равен нулю ( e =0).

Эллипс также является набором точек ( x,y ) на координатной плоскости. Он очень похож на круг, но несколько «некруглый» или овальный. Для эллипса x 2 и y 2 слагаемые имеют неравные коэффициенты, но тот же знак ( А С , и AC > 0). (Множественное число слова эллипс — это эллипсы, что также означает: …. Оба происходят от одного и того же основного корня, означающего «опустить».)

График эллипса		2 х 2 + у 2 = 25		Использование квадратного окна просмотра

Эллипсы имеют следующую стандартную форму:

((x-h)/r _x ) ² + ((y-k)/r _y ) ² = 1

Помните:
• ( h,k ) — центральная точка.
• r _x длина радиуса в ± x — направление.
• r _y — длина радиуса в направлении ± y .

Пример:

x ² + 4 y ² = 16
Шаг 1. Разделите обе стороны на 16: ( x ² )/16 + (4 y ² )/16 = 1.

Шаг 2. Упростите второй член:

( x ² )/16 + ( г ² )/4 = 1.

Этап 3. Фактор/перезапись в стандартной форме:

( x /4) ² + ( y /2) ² = 1.

Наблюдения
1. ОДИНАКОВЫЙ знак, но РАЗНЫЕ коэффициенты для x ² и y ² членов говорят нам, что график будет эллипсом.
2. Два знаменателя, 4 и 2, (расположенные на шаге 3) говорят нам, что эллипс вершина находится в 4 единицах от центра (0,0) в ± x — направление и две другие критические точки расположены 2 единицы от центра в направлении ± y .
3. r _x =4 называется x -радиусом и является расстоянием от центра к эллипсу в направлении x .
4. r _y =2 называется y — радиус и это расстояние от центра к эллипсу в направлении y .
5. Большая полуось больше из r _x и r _y , в данном случае 4.
6. Малая полуось меньше из r _x и r _y , в данном случае 2.
7. Semi- означает половину. Таким образом, большая и второстепенная оси вдвое больше полумажора и малые полуоси.
8. Эллипс можно также описать как множество точек на плоскости, таких, что сумма расстояний каждой точки, d ₁ + d ₂ , из двух фиксированных точек F ₁ и F ₂ постоянна. Таким образом, эллипс можно нарисовать с помощью двух кнопок и веревки.
9. F ₁ и F ₂ это очаги , что каждый является фокусом. Они расположены в точках (h ± c , k ) или ( h , k ± c )
10. Расстояние от центра до фокуса радиус фокуса .
11. Если a — большая полуось, а b — малая полуось, тогда c — радиус фокуса, где d ₁ + d ₂ = 2 а , и c ² =a ² -b ² . В этом случае c ² =16-4=12.
12. эксцентриситет e эллипса определяется соотношением: e=c/a . Так как c a и оба положительны, это будет от 0 до 1. Эксцентриситет, близкий к нулю, соответствует эллипсу в форме круга, тогда как эксцентриситет, близкий к единице, больше соответствует сигаре.
13. Площадь эллипса: A = ab . Окружность обычно должна быть аппроксимирована.
14. latus recta эллипса являются отрезками через фокус с концами на эллипсе и перпендикулярно большой оси. Их длина составляет 2 b ² / a .

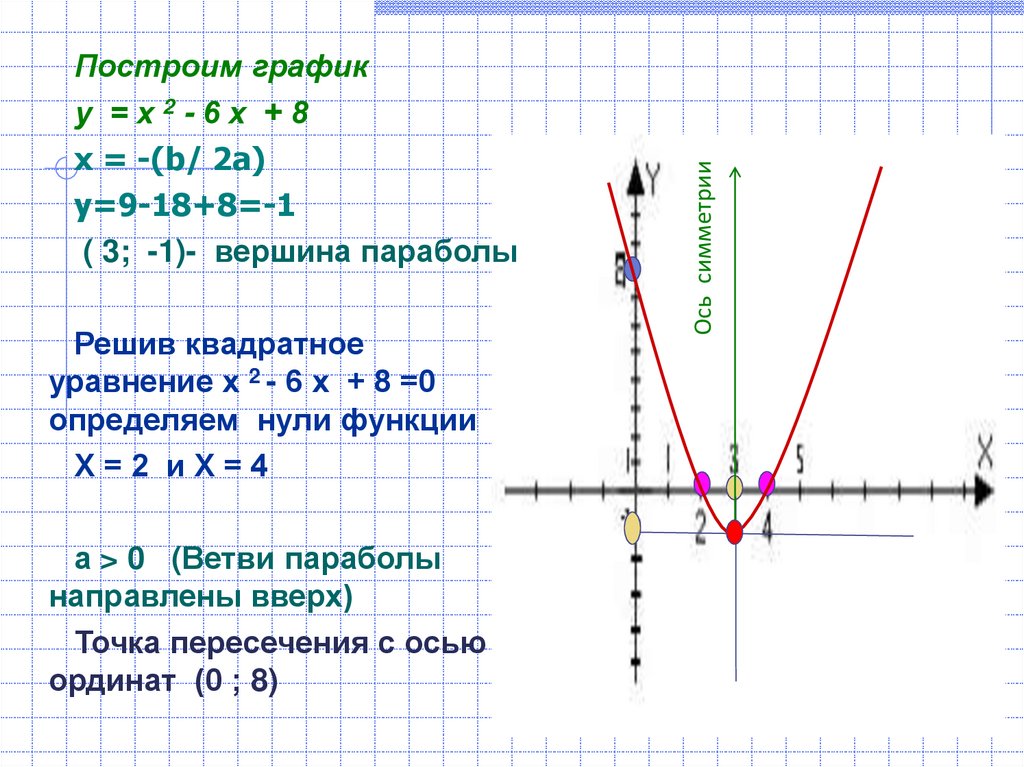
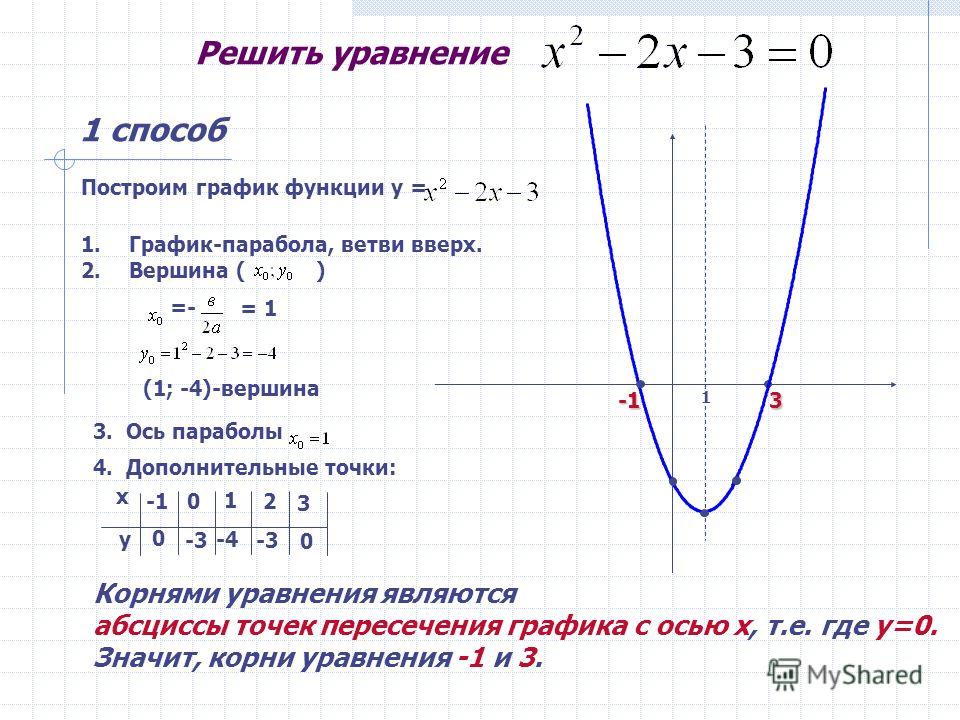
Парабола имеет уравнение, которое содержит только один член в квадрате. Если x 2 исключается, тогда график открывается в направлении x . Если исключить терм y 2 , то график откроется в и -направление. Только графики, которые открываются в направлении ± y являются квадратичными функциями, то есть те, которые открываются в направлении ± x являются квадратичными отношениями.

График параболы	х = у 2 — 25	В искаженном окне просмотра

Параболические функции имеют общее уравнение:

у = топор ² + Ьх + с

Общее параболическое отношение имеет общее квадратичное соотношение уравнение, расположенное на первой странице, кроме A =0 или C =0.

Пример:

x = -2 y ² +12 y -10

Наблюдения
1. Коническое сечение будет параболой, потому что есть только один квадратный член, y ² .
2. Поскольку терм x ² отсутствует, график откроется в x -направление, конкретно — x с C Координата y вершины находится по формуле: к = -b/2а . Так что к = -12/2(-2) = 3.
3. Координата вершины размером x :     h = -2(3 ² ) + 12(3) — 10 = 8.
4. Эксцентриситет параболы равен единице ( e =1).
5. Парабола может быть описана как множество копланарных точек, каждая из которых находится на том же расстоянии от фиксированного фокуса , что и от фиксированного прямая линия называется директриса .
6. Середина между фокусом и директрисой — вершина . Линия, проходящая через фокус и вершину, является осью параболы.
7. A фокальная хорда представляет собой отрезок, проходящий через фокус с концами на параболе.
8. широкая прямая кишка — фокальная хорда, перпендикулярная оси параболы.
9. Еще одна стандартная форма для параболы: ( 9или ( г — к ) ² =4 р ( х — ч )
10. Фокус лежит на оси p единиц от вершины: ( h , k + p ) или ( h + p , k ).
11. Директриса это линия y = k — р или х = ч — р

Гипербола имеет две симметричные разъединенные ветви. Каждая ветвь приближается к диагональным асимптотам * . Гиперболы можно обнаружить по противоположным знакам x 2 и y 2 терм. ( АС

^* ( Асимптоты — это линии, которые на графике сколь угодно близки к, но на самом деле никогда не касается, поскольку переменная продолжает двигаться в положительное или отрицательное направление. )

График гиперболы	— х 2 + у 2 = 25	В искаженном окне просмотра

Гиперболы имеют определенные уравнения:

((x-h)/r _x ) ² — ((y-k)/r _y ) ² = 1 ИЛИ -((x-h)/r _x ) ² + ((y-k)/r _у ) ² = 1
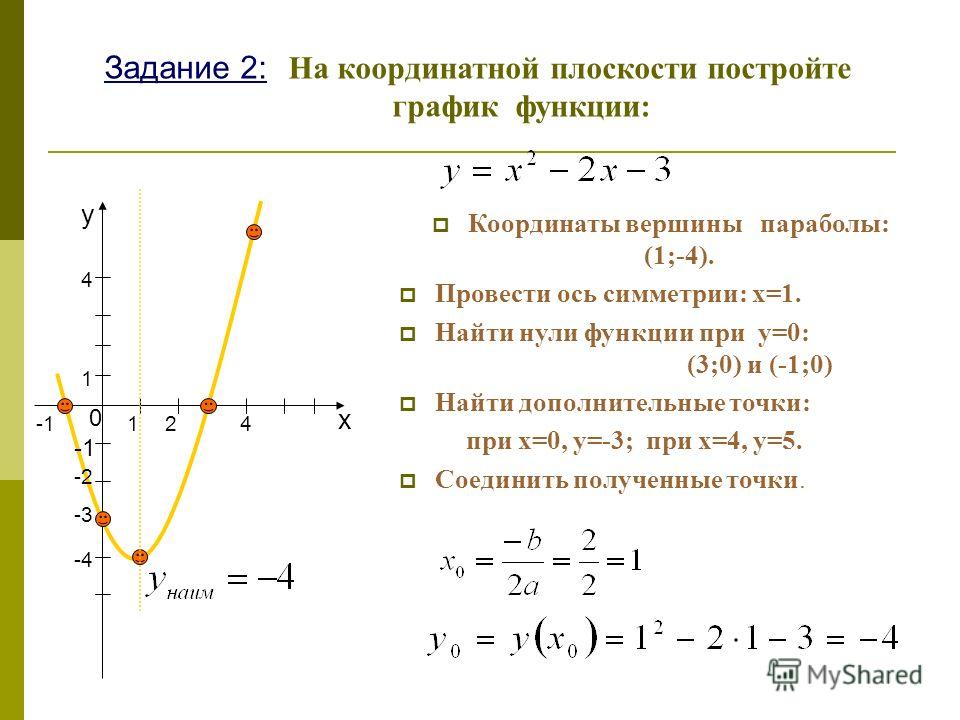
Если знак перед термином x ² ПОЛОЖИТЕЛЬНЫЙ ( A > 0), гипербола откроется в направлении ± x . Но если знак перед y ² термин ПОЛОЖИТЕЛЬНЫЙ ( C > 0), гипербола откроется в направлении ± y .

Помните:
• ( h,k ) — центральная точка.
• r _x — расстояние от центра гиперболы до направления ± x вершина (или асимптота).
• r _y — расстояние от центра до гиперболы ± y — вершина направления (или асимптота).
• асимптоты имеют наклоны r _y /r _x и -( r _y /r _x )
• Гипербола — это множество точек на плоскости, такое что для каждой точки ( x,y ) на гиперболе, разница между его расстоянием от два фиксированных фокуса есть константа.
• Большая полуось, a , является большей из r _x и r _y .
• Малая полуось, b меньшее из r _x и r _y .
• Поперечная ось соединяет две вершины.
• Сопряженная ось перпендикулярен поперечной оси.
• Таким образом, поперечная ось вдвое больше большой полу, a = abs( d ₁ — d ₂ ).
• в ² =а ² +б ² .
• эксцентриситет e гиперболы определяется соотношением: e=c/a . Поскольку c > a и оба положительны, это будет больше 1. Если e близко к единице, гипербола будет узкой и остроконечной; тогда как если e велико, гипербола будет почти плоской.

Пример:

-( x /4) ² + ( y /3) ² = 1

Наблюдения
1. Коническое сечение будет гиперболой, так как x ² и y ² члены имеют разные знаки.
2. Графики открываются в направлении ± y так как знак перед y -член положительный.
3. Асимптоты будут иметь наклон 3/4 или -(3/4).

Предположим, вам поручили найти полиномиальное уравнение для набор компланарных точек, описанный следующим образом: Для каждой точки ее расстояние от фиксированной точки (-3,0) в два раза больше расстояния от фиксированной точки (3,0).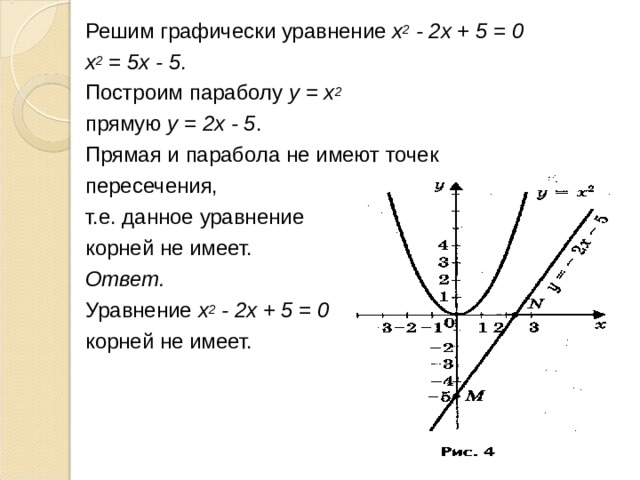 Таким образом: 2 ² (( x -3) ² +( y -0) ² )=( x —3) ² +( y -0) ²

Это происходит от применения формулы расстояния, но обе стороны были возведены в квадрат. This leads to the following relationships:

4( x ² -6 x +9+ y ² )= x ² +6 x +9+ y ² 3 x ² -30 x +27+3 y ² =0    или ( x -5) ² + у ² =4 ² .

Таким образом, у нас есть круг с центром в (5,0) и радиусом 4.

Другой пример может быть следующим: Каждая точка равноудалена от точки (3,-4) и прямой y =2. Таким образом:

( x -3) ² +( y +4) ² = ( x — x ) ² +( и -2) ² . x ² -6 x +9+ Y ² +8 Y +16 = 0 + Y ² +16 = 0 + Y ² .4594. x ² -6 x +12 y +21=0    или    y +1=-( x -3) 5 /

2

2

2

Таким образом, у нас есть парабола с вершиной в точке (3,-1), раскрывающаяся в направлении — y .

Последний пример выглядит следующим образом: Для каждой точки ее расстояние от точки (0,3) равно в 3/2 раза больше расстояния от линии г =-3.

4 ( x -0) ² +( Y -3) ² ) = 9 ( x — x ) ² +( x ) ² 5 +( x ). 2 ) 4( x ² + y ² -6 y +9)=9( y ² +6 y +9) 4 x ² -5 д ² -78 д -45=0

Таким образом, у нас есть открытие гиперболы в x направление.

Несколько шагов были опущены в приведенных выше выводах, и это ученику надлежит проверить их, проверить и освоить, потому что часто встречается несколько распространенных алгебраических ошибок.

xy -терм, вращающий график и его форму, не обсуждается. в любом из приведенных выше уравнений. Однако некоторая информация об этом будет быстро отмечена здесь. Дискриминант ( B ² -4 AC ) используется для определения какое коническое сечение получится.

Если дискриминант меньше нуля, мы имеем круг (если A = C ) или эллипс;
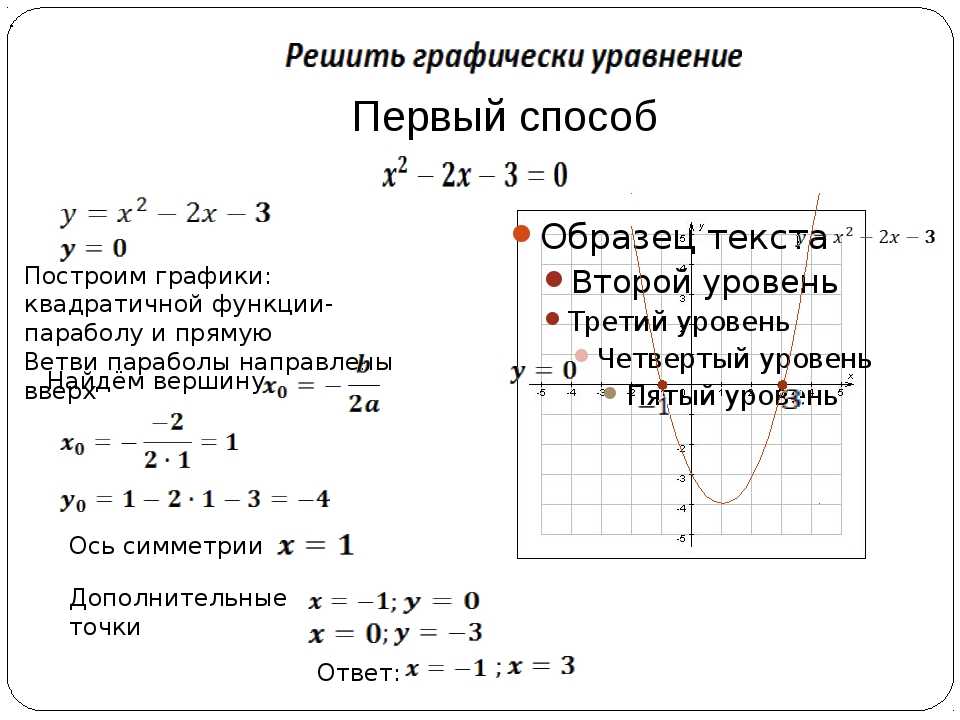
если дискриминант равен нулю, мы имеем параболу;
если дискриминант больше нуля, мы имеем гиперболу.

Наше уравнение можно переписать с B’ = 0 следующим образом: поворот осей координат на угол 0 , где раскладушка(2 0 )=( А — С )/ В . Обратите внимание, что F = F’ инвариантно относительно вращения.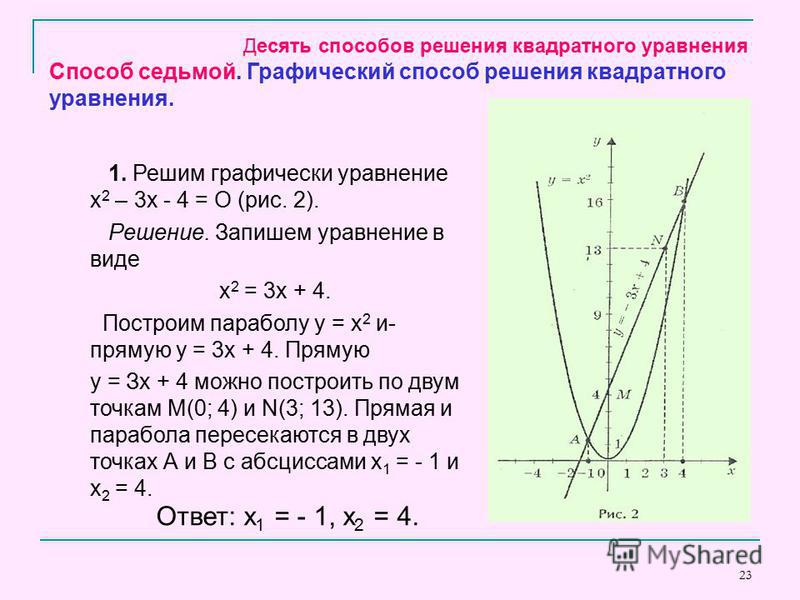 Обратите также внимание на A + C = A’ + C’ и B ² -4 AC = ( B’ ) ² -4 A’C’ . Мы выбираем B’ = 0.

Простейшая гипербола получается из графика: y =1/ x или xy =1. Для этого соотношения заметим, что A = 0, B = 1 и C = 0. Таким образом, кроватка 2 0 =0 или 0 =/4. Таким образом, в системе координат x’y’ , которая повернута на 45° от наша нормальная система координат xy , наше уравнение будет:

( х’ /) ² — ( у’ /) ² =1.

---

Работа над этой веб-страницей была начата осенью 1998 с помощь при вводе данных Салли Грегг, класс BCMSC 2000 г. Основное обновление было сделано в феврале 2001 г.
Эшли поделилась этой ссылкой, которая имеет несколько хороших динамических графиков: http://xahlee.org/SpecialPlaneCurves_dir/specialPlaneCurves.

No related posts.