Как построить сумму и разность векторов: Сложение и вычитание векторов. Умножение вектора на число — урок. Геометрия, 11 класс.

Содержание

Вычитание векторов и правила вычитания

Оглавление

Время чтения: 4 минуты

1 185

Для того, чтобы уяснить, что собой представляет разность векторов, введём понятие откладывания вектора от определённой точки и понятие суммы векторов.

Определение

Если некоторая точка A является началом вектора a, то говорят, что он является отложенным от точки A.

Теорема. От каждой точки можно отложить только один вектор, имеющий заданный модуль и направление. Докажем эту теорему.

Доказательство:

В случае, когда вектор нулевой, то теорема очевидна. Нулевые вектора в одной и той же точки совпадают между собой, т. е. являются одним и тем же вектором.

Сделаем построение. Точкой A обозначим начало вектора a, а точкой B его конец. Пусть у нас имеется некоторая точка K. Проведём через неё прямую b, которая параллельна вектору a. Отложим на данной прямой равные по своей абсолютной величине вектору

a отрезки KL и KM.

Из векторов, образованных этими отрезками искомым можно назвать только сонаправленный с a.

Единственность нашего вектора следует из того, что мы построили и видим.

Теорема доказана.

Определение

Суммой векторов a и b называется вектор с тем же началом, что вектор a и концом, как у вектора b. При этом вектор b должен начинаться в той же самой точке, в которой заканчивается вектор a.

Равные векторы, начинающиеся в разных точках, нередко обозначают одной и той же буквой. Иногда про подобные векторы говорят, как об одном и том же векторе, отложенном из разных мест.

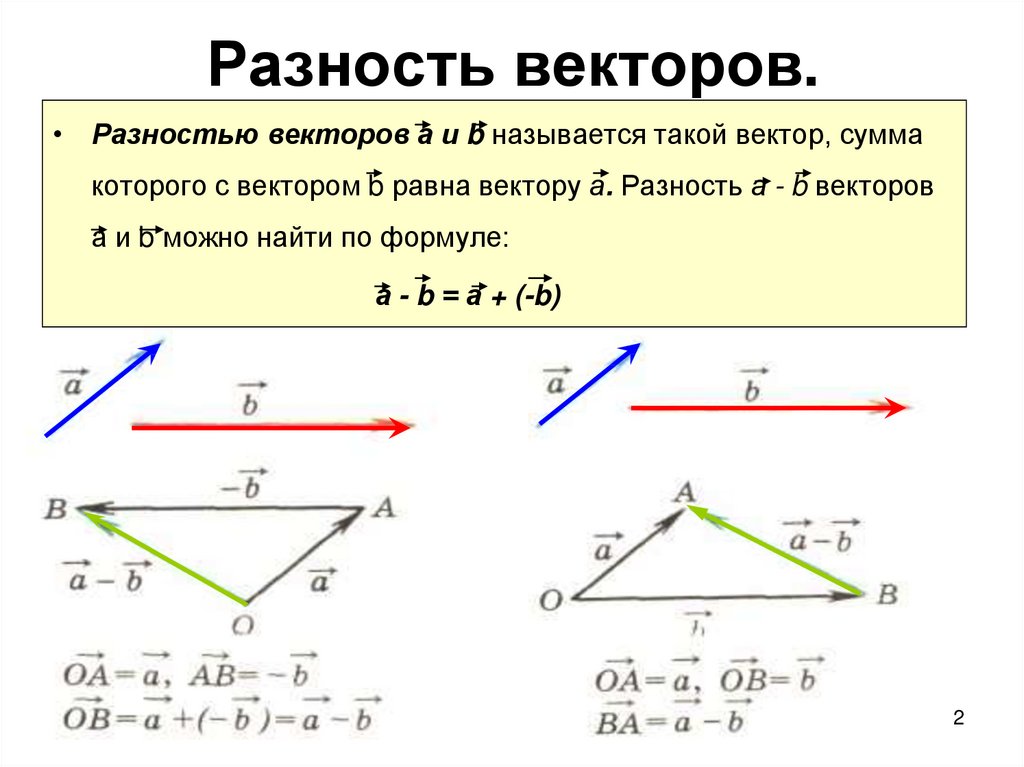
Разность векторов

Определение

Разностью векторов a и b называется сумма вектора a c вектором, который противоположно направлен к вектору b.

По-другому это определение можно сформулировать следующим образом: разностью двух векторов a и b называется вектор c, который при сложении с вычитаемым b образует уменьшаемое, т.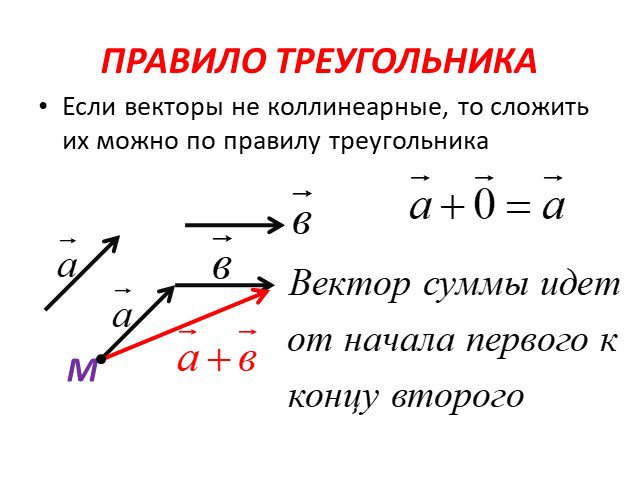 е. вектор a.

Формулами это записывается так:

b + c = a

a – b = c

Как найти разность векторов аналитическим способом

В двухмерном пространстве векторов a {x₁, y₁} и b {x₂, y₂} разность векторов можно вычислить, как показано ниже:

c {x₃, y₃} = {x₁ — x₂, y₁ — y₂}.

Вычитание векторов в 3-мерном пространстве выглядит следующим образом:

c {x₃; y₃; z₃} = {x₁ — x₂, y₂ — y₂, z₁ — z₂}.

Как найти разность векторов графическим способом

Нужно воспользоваться правилом треугольника. Последовательность действий следующая:

Постройте по координатам векторы, для которых требуется найти разность;
Совместите концы построенных векторов. Для этого нужно построить два равных заданным направленных отрезка, концы у которых будут в одной и той же точке;
Соедините начала построенных отрезков и укажите их направление. Вектор c, называемый разностью векторов, будет иметь своё начало в той же точке, где начинается вектор, именуемый уменьшаемым и заканчивается в точке начала вычитаемого. Смотрите рисунок ниже.

Есть ещё один способ графического нахождения разности векторов. Он предусматривает следующий порядок действий:

Постройте исходные направленные отрезки;
Отразите вычитаемый отрезок. Для этого постройте противоположно направленный и равный ему отрезок и затем совместите начало этого отрезка с уменьшаемым;
Постройте сумму, т. е. соедините начало первого отрезка и конец второго.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Примеры вычисления разности векторов

Примеры

Вычислить вектор c, который представляет собой разность вектора a ={1;
2} и вектора

b = {4; 8}.
Решение:
Действуем по выше указанному правилу
a — b = {1 — 4; 2 — 8} = {-3; -6}
Ответ: с{-3; -6}.
Вычислить вектор c, который является разностью векторов a = {1; 2; 5} и
b = {4; 8; 1}.
Решение:
Почти всё делается, как в уже рассмотренном примере, только добавляется третья координата.
a — b = {1 — 4; 2 — 8; 5 — 1} = {-3; -6; 4}
Ответ: c {-3; -6; 4}.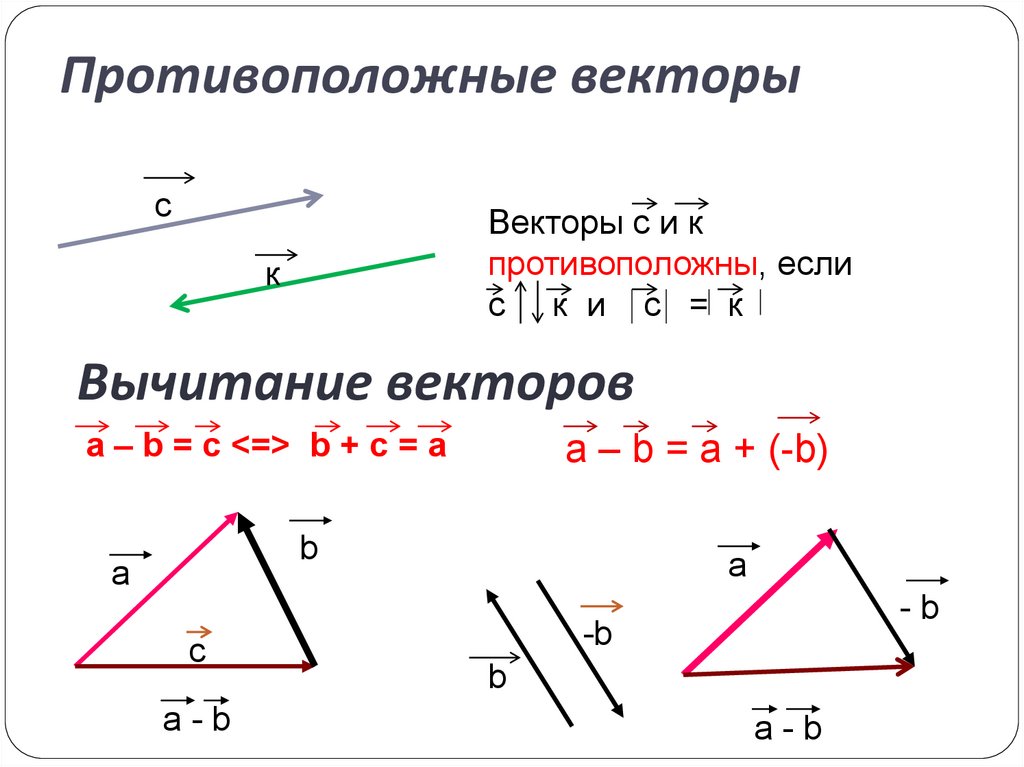
На рисунке векторы
Требуется построить разности: p — n, m —
n,m — n — p
и найти ту из них, которая
имеет наименьший модуль.
Решение:
Для изображения p — n проще всего воспользоваться правилом треугольника. Параллельным переносом
отрезки
следует соединить таким образом, чтобы совпали их конечные точки. Далее нужно соединить начальные точки и
определить направление. В нашем случае вектор разности берёт своё начало там же, где и вычитаемый n.
Для изображения m — n правильнее будет воспользоваться вторым графическим способом нахождения разности
векторов. Сначала построим вектор противоположный n и найдём его суммы с вектором m.
Для нахождения разности m — n — p разобьём это выражение на два действия. Возможны следующие варианты:
m — (n + p). Сначала нужно построить сумму,
затем уже вычесть её из m;
(m — n) — p. Сначала находим m — n,
осле этого от полученной разности отнимаем p;
(m— p) — n. Сначала определяем m — p, затем от
полученного результата отнимаем n.
Из вычислений выше нам известна разность m — n. Для получения решения нам нужно вычесть из неё
p.
Используя определение 3 построим разность векторов на рисунке. На нём изображён окончательный результат
и промежуточный.
Теперь нужно определить наименьший модуль. В нашем случае для этого можно лишь визуально оценить длины p — n,
m — n и m — n — p. Из построения сразу видно, что наименьшим модулем обладает вектор разности m — n —
p.
Оценить статью (34 оценки):
Поделиться
Вычитание векторов / Векторы / Справочник по геометрии 7-9 класс
Главная

Справочники

Справочник по геометрии 7-9 класс

Векторы

Вычитание векторов

Разность векторов и — вектор, сумма которого с вектором равна вектору .
Разность векторов и обозначается так: .
Задача на построение разности векторов (1 способ)
Даны векторы и . Построить вектор .
Дано: и .
Построить: .
Решение:
От произвольной точки О откладываем векторы = и = .
По правилу треугольника + = или + = , то есть сумма векторов и равна . По определению разности векторов это означает, что = , следовательно, вектор — искомый.

Противоположный вектор
Пусть — произвольный ненулевой вектор.
Вектор называется противоположным вектору , если векторы и имеют равные длины и противоположно направлены.
Вектор = является противоположным вектору = . Вектором, противоположным нулевому вектору, считается нулевой вектор.
Вектор, противоположный вектору , обозначается так: .
Сумма противоположных векторов и равна нулевому вектору, т.е. .
Теорема

Для любых векторов и справедливо равенство .
Доказательство
Дано: и .
Доказать: .
Доказательство:
По определению разности векторов . Прибавим к обеим частям этого равенства вектор , получим:
или (т.к. ), следовательно, . Теорема доказана.
Задача на построение разности векторов (2 способ)
Даны векторы и . Построить вектор .
Дано: и .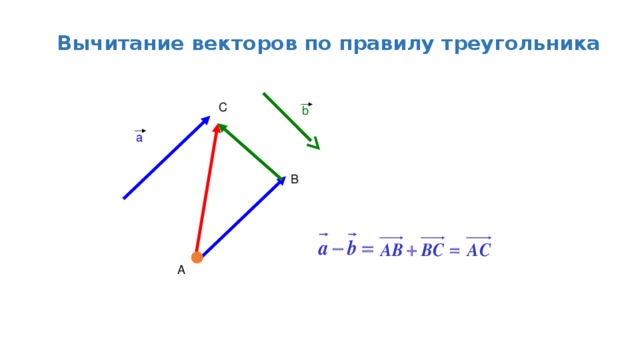
Построить: .
Решение:
От произвольной точки О откладываем векторы = . Затем от точки А отложим =.
По теореме о разности векторов , поэтому , следовательно, вектор — искомый.
Советуем посмотреть:
Понятие вектора
Равенство векторов
Откладывание вектора от данной точки
Сумма двух векторов
Законы сложения векторов. Правило параллелограмма
Сумма нескольких векторов
Произведение вектора на число
Применение векторов к решению задач
Средняя линия трапеции
Векторы
Правило встречается в следующих упражнениях:
7 класс
Задание 757, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 773, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 789, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 792, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 12, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 13, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 802, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 803, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 925, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 10, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Графические методы – College Physics: OpenStax
Глава 3 Двумерная кинематика
Резюме
Понимание правил сложения, вычитания и умножения векторов.
Применять графические методы сложения и вычитания векторов для определения смещения движущихся объектов.
Рисунок 1. Смещение можно определить графически, используя масштабную карту, например, карту Гавайских островов. Путешествие с Гавайев на Молокаи состоит из нескольких этапов или сегментов пути. Эти сегменты могут быть добавлены графически с помощью линейки, чтобы определить общее двухмерное перемещение пути. (кредит: Геологическая служба США).
Вектор — это величина, которая имеет величину и направление. Например, перемещение, скорость, ускорение и сила — все это векторы. В одномерном или прямолинейном движении направление вектора может быть задано просто знаком плюс или минус. Однако в двух измерениях (2-d) мы указываем направление вектора относительно некоторой системы отсчета (т. е. системы координат), используя стрелку, длина которой пропорциональна величине вектора и указывает направление вектора.

На рис. 2 показано такое графическое представление вектора на примере полного перемещения человека, идущего по городу, рассмотренного в главе 3.1 «Кинематика в двух измерениях: введение». Мы будем использовать обозначение, что жирный шрифт, такой как [latex]\textbf{D}[/latex], обозначает вектор. Его величина представлена символом, выделенным курсивом, [латекс]\жирныйсимвол{D},[/латекс], а его направление – [латекс]\жирныйсимвол{\тета}.[/латекс]
ВЕКТОРА В ЭТОМ ТЕКСТЕ
В этом тексте мы будем представлять вектор переменной, выделенной жирным шрифтом. Например, мы представим количественную силу вектором[latex]\textbf{F},[/latex], который имеет как величину, так и направление. Величина вектора будет представлена переменной, выделенной курсивом, например [латекс]\жирныйсимвол{F},[/латекс], а направление переменной будет задано углом[латекс]\жирныйсимвол{\тета} .[/латекс]
Рисунок 2. Человек проходит 9 кварталов на восток и 5 кварталов на север. Водоизмещение 10,3 блока под углом 29.1 ^o к северу от востока. Рисунок 3. Чтобы графически описать результирующий вектор для человека, идущего по городу, показанному на рисунке 2, нарисуйте стрелку, представляющую общий вектор смещения D . С помощью транспортира начертите линию под углом θ относительно оси восток-запад. Длина D стрелки пропорциональна модулю вектора и измеряется линейкой вдоль линии. В этом примере магнитуда D вектора составляет 10,3 единицы, а направление θ равно 29,1 ^o к северу от востока.
Метод «голова к хвосту» представляет собой графический способ добавления векторов, описанный на рис. 4 ниже и в следующих шагах. Конец вектора является начальной точкой вектора, а конец (или кончик) вектора является конечным заостренным концом стрелки.
Рисунок 4. Метод «голова к хвосту»: метод «голова к хвосту» графического сложения векторов проиллюстрирован для двух перемещений человека, идущего по городу, рассмотренного на рисунке 2. (a) Нарисуйте вектор, представляющий перемещение на восток. (b) Нарисуйте вектор, представляющий смещение на север. Хвост этого вектора должен исходить из головы первого вектора, указывающего на восток. (c) Проведите линию от хвоста вектора, указывающего на восток, до начала вектора, указывающего на север, чтобы получить сумму или результирующий вектор D . Длина стрелки D пропорциональна модулю вектора и составляет 10,3 единицы. Его направление, описываемое как угол относительно востока (или горизонтальной оси) θ , измеренное с помощью транспортира, равно 29,1 ⁰ .
Шаг 1. Нарисуйте стрелку, представляющую первый вектор (9 блоков на восток), используя линейку и транспортир .
Рисунок 5.
Шаг 2. Теперь нарисуйте стрелку, представляющую второй вектор (5 кварталов на север). Поместите конец второго вектора в начало первого вектора .
Рисунок 6.
Шаг 3. Если имеется более двух векторов, продолжайте этот процесс для каждого добавляемого вектора. Обратите внимание, что в нашем примере у нас есть только два вектора, поэтому мы закончили размещать стрелки от начала до конца .
Шаг 4. Проведите стрелку от конца первого вектора к началу последнего вектора . Это результат или сумма других векторов.
Рисунок 7.
Шаг 5. Чтобы получить величину равнодействующей, измерьте ее длину линейкой. (Обратите внимание, что в большинстве расчетов мы будем использовать теорему Пифагора для определения этой длины. )
Шаг 6. Чтобы получить направление равнодействующей, измерьте угол, который она образует с системой отсчета, используя транспортир. (Обратите внимание, что в большинстве расчетов мы будем использовать тригонометрические отношения для определения этого угла.)
Точность графического сложения векторов ограничена только точностью, с которой могут быть выполнены чертежи, и точностью измерительных инструментов. Это справедливо для любого количества векторов.
Пример 1. Графическое добавление векторов методом «голова к хвосту»: женщина на прогулке 9о}[/latex]северо-восток. Наконец, она поворачивается и проходит 32,0 м в направлении 68,0° к югу от востока.
Стратегия
Представьте каждый вектор смещения графически со стрелкой, обозначив первый[latex]\textbf{A},[/latex]второй[latex]\textbf{B},[/latex]и третий [latex]\textbf{C},[/latex] делая длины пропорциональными расстоянию и направлениям, указанным относительно линии восток-запад.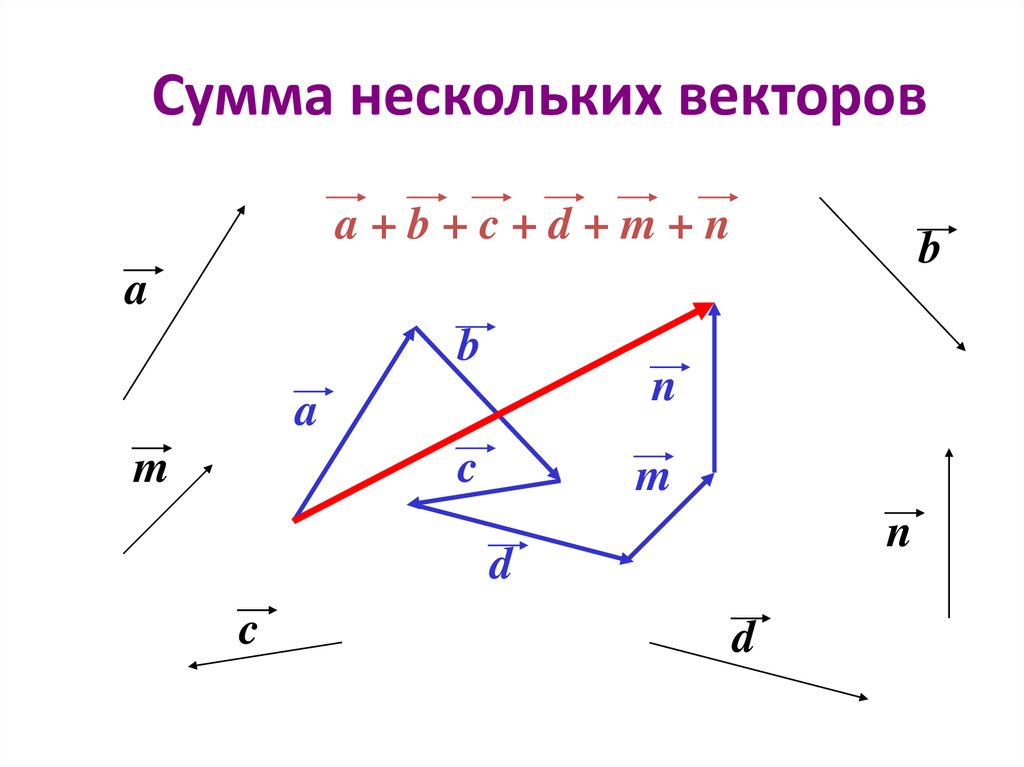 Описанный выше метод «голова к хвосту» позволяет определить величину и направление результирующего смещения, обозначаемого[latex]\textbf{R}.[/latex]
Решение
(1) Нарисуйте три вектора смещения.
Рисунок 8.
(2) Разместите векторы от начала до конца, сохранив их первоначальную величину и направление.
Рисунок 9.
(3) Нарисуйте результирующий вектор,[latex]\textbf{R}.[/latex]
Рисунок 10.
(4) Используйте линейку для измерения величины[latex]\ textbf{R},[/latex]и транспортир для измерения направления[latex]\textbf{R}.[/latex]Хотя направление вектора можно задать разными способами, проще всего измерить угол между вектором и ближайшей горизонтальной или вертикальной осью. Поскольку результирующий вектор находится к югу от оси, направленной на восток, мы переворачиваем транспортир вверх ногами и измеряем угол между осью, направленной на восток, и вектором. 9о}[/latex]юго-восток.
Обсуждение
Графический метод сложения векторов «голова к хвосту» работает для любого количества векторов. Также важно отметить, что результирующая не зависит от порядка добавления векторов. Следовательно, мы можем добавлять векторы в любом порядке, как показано на рис. 12, и все равно получим то же решение.
Рисунок 12.
Здесь мы видим, что при сложении одних и тех же векторов в другом порядке результат будет тот же. Эта характеристика верна в любом случае и является важной характеристикой векторов. Сложение векторов равно коммутативный . Векторы можно добавлять в любом порядке.
[латекс]\boldsymbol{\textbf{A}+\textbf{B}=\textbf{B}+\textbf{A}}.[/latex]
(Это верно для сложения обычных чисел как хорошо — вы получите тот же результат, если вы добавите, например, [латекс]\жирныйсимвол{2+3}[/латекс]или [латекс]\жирныйсимвол{3+2},[/латекс]).
Вычитание векторов — это прямое расширение сложения векторов.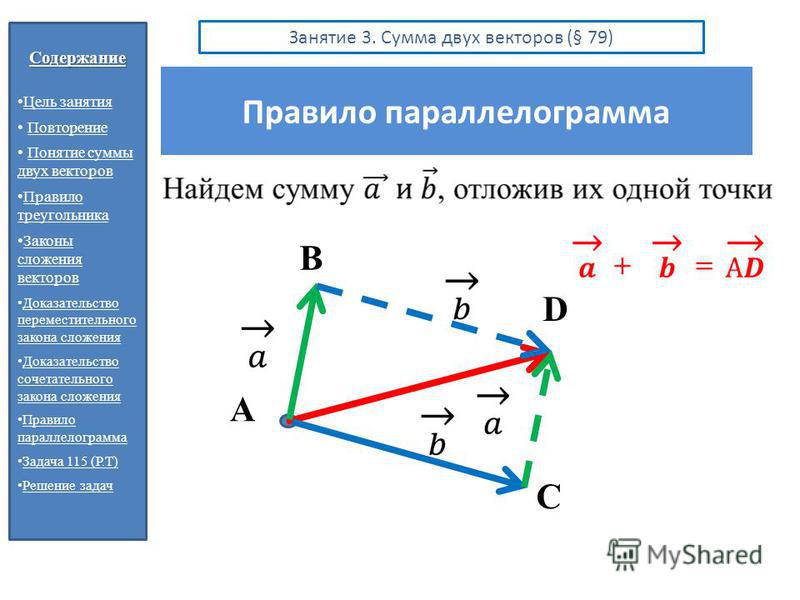 Чтобы определить вычитание (скажем, мы хотим вычесть [латекс]\textbf{B}[/латекс]из [латекс]\текстбф{А},[/латекс]написанного[латекс]\жирныйсимвол{\текстбф{А}-\текстбф {B}}[/latex], мы должны сначала определить, что мы подразумеваем под вычитанием.0021 отрицательный вектора[latex]\textbf{B}[/latex] определяется как [latex]\boldsymbol{-\textbf{B}};[/latex]то есть графически отрицательный для любого вектора имеет ту же величину, но в противоположном направлении , как показано на рисунке 13. Другими словами, [latex]\textbf{B}[/latex] имеет ту же длину, что и [latex]\boldsymbol{-\textbf{B}} ,[/latex], но указывает в противоположном направлении. По сути, мы просто переворачиваем вектор так, чтобы он указывал в противоположном направлении.
Рисунок 13. Отрицательное значение вектора — это просто другой вектор той же величины, но направленный в противоположном направлении. Так B является минусом -B ; он имеет ту же длину, но противоположное направление. o}[/latex]к западу от севера). Если женщина совершает ошибку и путешествует в в противоположном направлении для второго этапа поездки, где она окажется? Сравните это место с расположением дока.
Рисунок 14.
Стратегия
Мы можем представить первый этап поездки с помощью вектора[latex]\textbf{A},[/latex], а второй этап поездки с помощью вектора[latex] \textbf{B}.[/latex]Док расположен в месте[latex]\boldsymbol{\textbf{A}\:+\:\textbf{B}}.[/latex]Если женщина по ошибке путешествует в напротив 9о}[/latex]юго-восток. Мы представляем это как[latex]\boldsymbol{-\textbf{B}},[/latex], как показано ниже. Вектор[latex]\boldsymbol{-\textbf{B}}[/latex] имеет ту же величину, что и [latex]\textbf{B}[/latex], но направлен в противоположном направлении. Таким образом, она окажется в месте [латекс]\boldsymbol{\textbf{A}+(-\textbf{B})},[/latex]или[латекс]\boldsymbol{\textbf{A}-\textbf {B}}.[/latex]
Рисунок 15.
Выполним сложение векторов для сравнения расположения дока,[latex]\boldsymbol{\textbf{A}+\textbf{B}},[/ латекс]с местом, куда по ошибке прибыла женщина,[латекс]\boldsymbol{\textbf{A}+(-\textbf{B})}. [/latex]
Решение
(1) Чтобы определить место, куда случайно попала женщина, нарисуйте векторы[latex]\textbf{A}[/latex]и[latex]\boldsymbol{-\textbf{B}} .[/latex]
(2) Поместите векторы от начала до конца.
(3) Нарисуйте результирующий вектор[latex]\textbf{R}.[/latex]
(4) Используйте линейку и транспортир для измерения величины и направления [latex]\textbf{R}.[/ латекс]
Рисунок 16.
о}[/latex]юго-восток. 9о}[/latex]северо-восток.
Мы видим, что женщина окажется на значительном расстоянии от причала, если она отправится в противоположном направлении на второй этап поездки.
Обсуждение
Поскольку вычитание вектора аналогично сложению вектора с противоположным направлением, графический метод вычитания векторов работает так же, как и сложение.
Если бы мы решили пройти в три раза больше первого этапа пути, рассмотренного в предыдущем примере, то мы бы прошли[latex]\boldsymbol{3 \times 27,5\textbf{ м}},[/latex]или 82,5 м, в направлении[латекс]\boldsymbol{66. o}[/латекс]северо-восток. Это пример умножения вектора на положительное число 9.0014 скаляр . Обратите внимание, что величина меняется, но направление остается прежним.
Если скаляр отрицательный, то умножение вектора на него изменяет величину вектора и дает новому вектору направление, противоположное . Например, если умножить на -2, величина удвоится, но изменится направление. Мы можем обобщить эти правила следующим образом: Когда вектор[латекс]\текстбф{А}[/латекс] умножается на скаляр[латекс]\жирныйсимвол{с},[/латекс]
модуль вектора становится абсолютным значением[latex]\boldsymbol{cA},[/latex]
, если [latex]\boldsymbol{c}[/latex] положительный, направление вектора не меняется,
, если [латекс]\boldsymbol{c}[/латекс]отрицательно, направление меняется на противоположное.
В нашем случае [латекс]\boldsymbol{c=3}[/latex]и[латекс]\boldsymbol{\textbf{A}=27,5\textbf{м}}.[/latex]Вектора умножаются на скаляры во многих ситуациях. Обратите внимание, что деление является обратным умножению. Например, деление на 2 равносильно умножению на значение (1/2). Правила умножения векторов на скаляры такие же, как и при делении; просто рассматривайте делитель как скаляр между 0 и 1.
В приведенных выше примерах мы добавляли векторы для определения результирующего вектора. Однако во многих случаях нам нужно будет сделать обратное. Нам нужно будет взять один вектор и найти, какие другие векторы, сложенные вместе, дают его. В большинстве случаев это включает определение перпендикулярных компонентов одного вектора, например компонентов x – и y , или компонентов север-юг и восток-запад. 9o}[/latex]к северу от востока и хотите узнать, сколько кварталов нужно было пройти на восток и на север. Этот метод называется нахождением компонентов (или частей) смещения в восточном и северном направлениях, и он является обратным процессу, используемому для нахождения полного смещения. Это один из примеров нахождения компонентов вектора. В физике есть много приложений, где это может оказаться полезным. Мы скоро увидим это в главе 3.4 «Движение снаряда» и многое другое, когда мы рассмотрим 9.0014 действует на в главе 4 «Динамика: законы движения Ньютона». Большинство из них включают поиск компонентов вдоль перпендикулярных осей (например, север и восток), так что задействованы прямоугольные треугольники. Аналитические методы, представленные в главе 3.3 Сложение и вычитание векторов: аналитические методы, идеально подходят для нахождения компонент вектора.
PHET EXPLORATIONS: MAZE GAME
Узнайте о положении, скорости и ускорении на «Арене боли». Используйте зеленую стрелку, чтобы переместить мяч. Добавьте больше стен на арену, чтобы усложнить игру. Постарайтесь достичь цели как можно быстрее.
Рисунок 18. Игра «Лабиринт»
Графический метод сложения векторов [latex]\textbf{A}[/latex]и[latex]\textbf{B}[/latex] включает в себя рисование векторов на графике и их сложение с использованием прямого метод хвоста. Результирующий вектор[latex]\textbf{R}[/latex] определяется таким образом, что[latex]\boldsymbol{\textbf{A}+\textbf{B}=\textbf{R}}.[/latex]Величина и направление[latex]\textbf{R}[/latex] затем определяются с помощью линейки и транспортира соответственно.
графический метод вычитания вектора [latex]\textbf{B}[/latex]из [latex]\textbf{A}[/latex]предполагает добавление противоположного вектора[latex]\textbf{B},[/latex] ] который определяется как [латекс]\boldsymbol{-\textbf{B}}.[/latex]В этом случае [латекс]\boldsymbol{\textbf{A}-\textbf{B}=\textbf{A} +(-\textbf{B})=\textbf{R}}.[/latex]Затем обычным методом сложения головы к хвосту получается результирующий вектор[latex]\textbf{R }.[/латекс]
Сложение векторов коммутативно так, что [латекс]\boldsymbol{\textbf{A}+\textbf{B}=\textbf{B}+\textbf{A}}.[/latex]
Метод «голова к хвосту» сложения векторов включает рисование первого вектора на графике, а затем размещение хвоста каждого последующего вектора в начале предыдущего вектора. Затем результирующий вектор рисуется из хвоста первого вектора в начало конечного вектора.
Если вектор[latex]\textbf{A}[/latex] умножается на скалярную величину[latex]\boldsymbol{c},[/latex]величина произведения определяется как[latex]\boldsymbol{cA }.[/latex]Если [латекс]\boldsymbol{c}[/латекс] положителен, направление произведения указывает на то же направление, что и [латекс]\текстбф{А};[/латекс]если[латекс] \boldsymbol{c}[/latex]отрицательно, направление произведения указывает на направление, противоположное [latex]\textbf{A}.[/latex]

компонент (двумерного вектора)
часть вектора, указывающая либо в вертикальном, либо в горизонтальном направлении; каждый двумерный вектор может быть выражен как сумма двух компонент вертикального и горизонтального векторов 90 336
коммутативный
относится к взаимозаменяемости порядка в функции; сложение векторов является коммутативным, потому что порядок сложения векторов не влияет на окончательную сумму 90 336
направление (вектора)
ориентация вектора в пространстве
голова (вектора)
конечная точка вектора; расположение кончика стрелки вектора; также называется «наконечник»
метод «голова к хвосту»
метод сложения векторов, при котором конец каждого вектора помещается в начало предыдущего вектора
величина (вектора)
длина или размер вектора; величина является скалярной величиной
результат
сумма двух или более векторов
результирующий вектор
векторная сумма двух или более векторов
скаляр
количество с величиной, но без направления
хвост
начальная точка вектора; напротив наконечника или наконечника стрелки
Нахождение суммы двух векторов — Криста Кинг Математика
Что значит найти сумму двух векторов?
Когда мы хотим найти комбинацию двух векторов, мы просто совмещаем начальную точку второго вектора с конечной точкой первого вектора, а затем рисуем новый третий вектор из начальной точки первого в конечный пункт второго.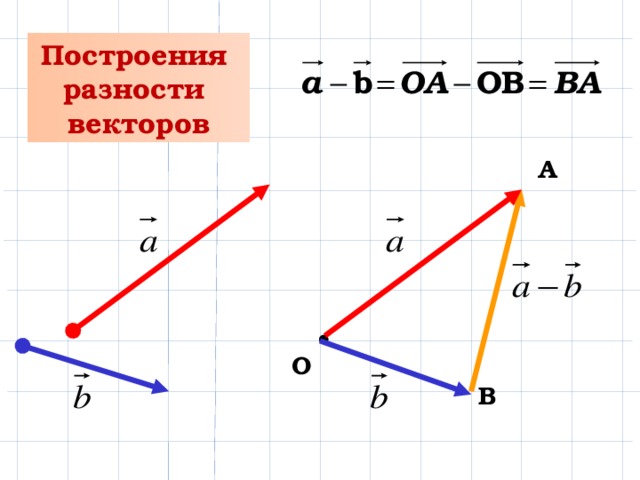
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Другими словами, сочетание серого и синего — фиолетовое:
По сути, объединение двух векторов дает нам тот же результат, что и сложение векторов. В приведенном выше примере серый + синий = фиолетовый. Мы также можем вычитать векторы. Если вычитается вектор, мы движемся точно в направлении, противоположном исходному вектору. В приведенном ниже примере серый — синий = фиолетовый. Сплошной синий вектор — исходный вектор, но поскольку мы вычитаем, мы движемся в противоположном направлении.
Когда нам заданы числовые значения для векторов, мы просто суммируем ???x???-координаты, чтобы получить новую ???x???-координату, и суммируем ???y???? ?-координаты, чтобы получить новую ???y???-координату.
Как найти сумму векторов, в том числе когда векторы заданы в разных формах
Пройти курс
Хотите узнать больше об исчислении 3? У меня есть пошаговый курс для этого.
🙂
Еще два примера суммирования векторов
Пример
Найти сумму векторов.
???u=\langle2,1\rangle??? и ???v=\langle-1,5\rangle???
???u=2i-3j??? и ???v=6i+2j???
Для ???u=\langle2,1\rangle??? и ???v=\langle-1,5\rangle???:
Суммировать векторы ???u=\langle2,1\rangle??? и ???v=\langle-1,5\rangle???, мы просто суммируем ???x???-координаты, чтобы получить новую ???x???-координату, а затем делаем то же самое для ???y???-координат. Мы можем назвать наш новый вектор ???w???.
???w=\langle2+(-1),1+5\rangle???
???w=\langle1,6\rangle???
По сути, объединение двух векторов дает нам тот же результат, что и сложение векторов.
Для ???u=2i-3j??? и ???v=6i+2j???:
Суммировать векторы ???u=2i-3j??? и ???v=6i+2j???, коэффициенты возьмем от нашего ???i??? и ???j??? слагаемых, и складываем их вместе, чтобы найти коэффициенты при этих слагаемых для вектора ???w???.
No related posts.