16. Алгебра событий
Одним из основных понятий теории вероятностей является понятие случайного события. Под событием понимается любое явление, которое происходит в результате осуществления определенного комплекса условий и которые можно неоднократно повторять. Осуществление этого комплекса условий называют экспериментом (опытом, испытанием, наблюдением). Таким образом, любое событие в теории вероятностей рассматриваются как исход некоторого эксперимента. Поэтому события часто называют исходами. Например, бросание кубика можно считать испытанием, которое можно неоднократно повторять, а полученный результат – исходом испытания.
Событие называется случайным, если оно при одних и тех же условиях может как произойти, так и не произойти. Случайными будут, например, события: а) при подбрасывании игрального кубика выпадет 6 очков; б) при выстреле в мишень пуля попадет в «десятку»; в) по пути в школу вы встретите черную кошку.
Чтобы говорить о случайности или неслучайности какого-то события, нужно иметь возможность неоднократно наблюдать за ним.
Случайным экспериментом называют комплекс действий или условий, которые можно многократно повторять, а исход, к которому они приводят, заранее непредсказуем. С примерами случайных экспериментов вы, наверняка, сталкивались и раньше: а) подбрасывание монеты или игрального кубика; б) проведение лотереи; в) стрельба по мишени; г) подъем уровня воды во время весеннего половодья. Последний пример показывает, что случайные эксперименты может совершать и сама природа – в этом случае нам остается лишь наблюдать за их исходами.
Остановимся еще раз на двух важнейших свойствах случайного опыта — непредсказуемости и повторяемости.
Первым важным свойством случайного опыта является его непредсказуемость. Мы не можем заранее предсказать на какую сторону упадет подброшенная вверх монета или кубик; в какую точку мишени попадет пуля.
Вторым важным свойством случайного опыта является его повторяемость: мы (или природа) можем повторять опыт неограниченное число раз в одних и тех же (или очень близких) условиях.
Теория вероятностей не изучает уникальные эксперименты, которые нельзя повторить многократно, даже если их исходы непредсказуемы.
События будем обозначать заглавными буквами латинского алфавита: A, B, C и т. д.
Событие называется невозможными, если при проведении данного случайного эксперимента никогда не происходит. Например, события: а) при подбрасывании игрального кубика выпадет 7 очков; б) при подбрасывании трех монет число орлов окажется равно числу решек, являются, очевидно, невозможными.
Событие называется достоверным, если при проведении данного случайного эксперимента оно обязательно произойдет. Например, события: а) при подбрасывании игрального кубика выпадет меньше 7 очков; б) при подбрасывании трех монет число орлов окажется не равно числу решек, являются, очевидно, достоверными.
События A и B называются несовместными, если наступление одного из них исключает возможность появления другого. Например, при подбрасывании монеты могут наступить два события: выпадет «орел» или «решка». Однако, одновременно эти события, при одном подбрасывании, появится не могут. Если в результате испытания возможно одновременное появление событий A и B, то такие события называются совместными. Например, выпадение чётного числа очков при подбрасывании игральной кости (событие А) и числа очков, кратного трем (событие В) будут совместными, ибо выпадение шести очков означает наступление и события А, и события В.
Возможными исходами случайного эксперимента называются все взаимоисключающие друг друга варианты, одним из которых он должен завершиться. В результате эксперимента всегда происходит один и только один из его исходов. То есть, с одной стороны, в одном эксперименте не могут произойти сразу два исхода, с другой — эксперимент не может завершиться вообще без всякого исхода.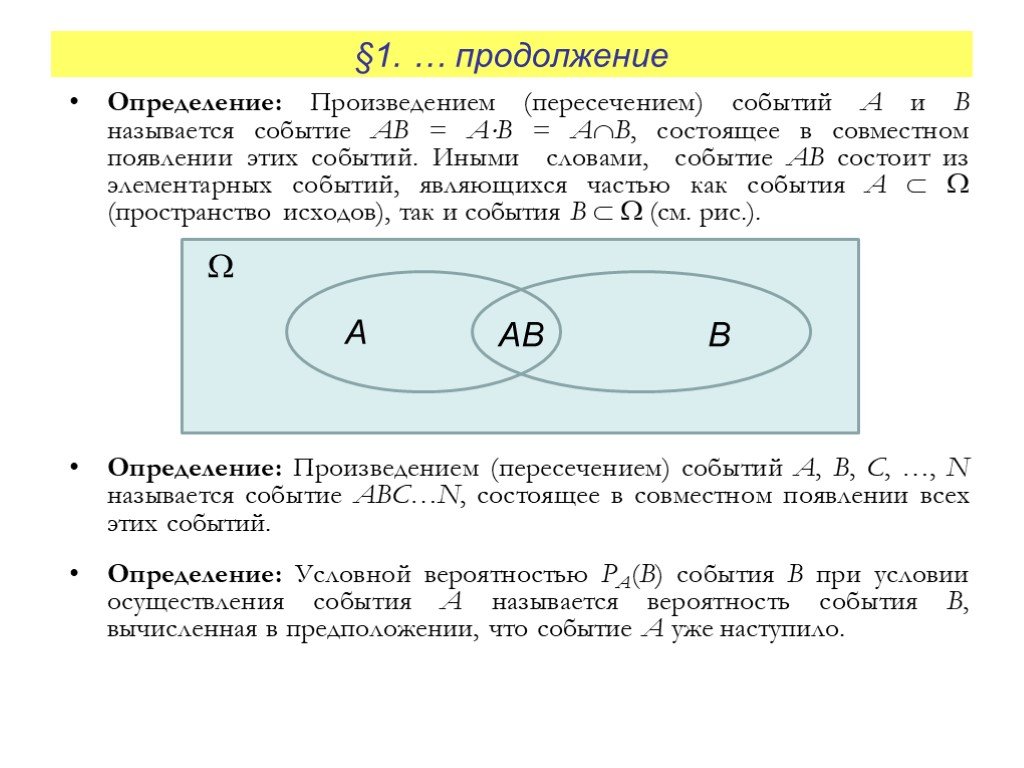 Исходы эксперимента называют элементарными, если их нельзя поделить на более простые. Элементарные исходы в теории вероятностей называют еще элементарными событиями.
Исходы эксперимента называют элементарными, если их нельзя поделить на более простые. Элементарные исходы в теории вероятностей называют еще элементарными событиями.
Заметим, что число возможных исходов случайного опыта может быть любым – от двух до бесконечности. Например, опыт с монетой имеет всего два возможных исхода (орел и решка), а опыт с кубиком – шесть. Но далеко не во всех случаях все возможные исходы опыта столь очевидны.
Из коробки с одним белым и двумя черными шарами вытаскивают наугад один шар. Сколько возможных исходов у этого опыта? Можно сказать два: шар окажется либо белым, либо черным. А можно сказать три: белый, черный-1, черный-2. И то, и другое правильно, просто во втором случае исходы выбраны более элементарными, а сам опыт описывается ими более детально.
Любое неэлементарное событие может наступить при различных исходах опыта. Все такие исходы называют благоприятными для этого события. Благоприятные они в том смысле, что приводят к его наступлению. Например, для случайного события «На кубике выпадет четное число очков» благоприятными исходами будут 2, 4 и 6.
Например, для случайного события «На кубике выпадет четное число очков» благоприятными исходами будут 2, 4 и 6.
Если обозначить множество всех возможных исходов опыта большой греческой буквой (читается омега), то каждый исход можно рассматривать как элемент этого множества , а любое случайное событие A – как его подмножество , состоящее из благоприятных для него исходов.
При этом невозможное и достоверное события получаются как два частных случая таких подмножеств: невозможному событию соответствует пустое множество исходов ; достоверному событию соответствует множество всех исходов опыта .
Итак, для любого случайного события A все исходы эксперимента делятся на два множества: благоприятные для этого события и все остальные, которые можно назвать неблагоприятными для него. Если рассматривать событие A как подмножество в множестве всех возможных исходов, то оно будет состоять из благоприятных исходов.
Например, выниманию из колоды одной карты можно поставить в соответствие множество элементарных событий (карт) W с 36 исходами.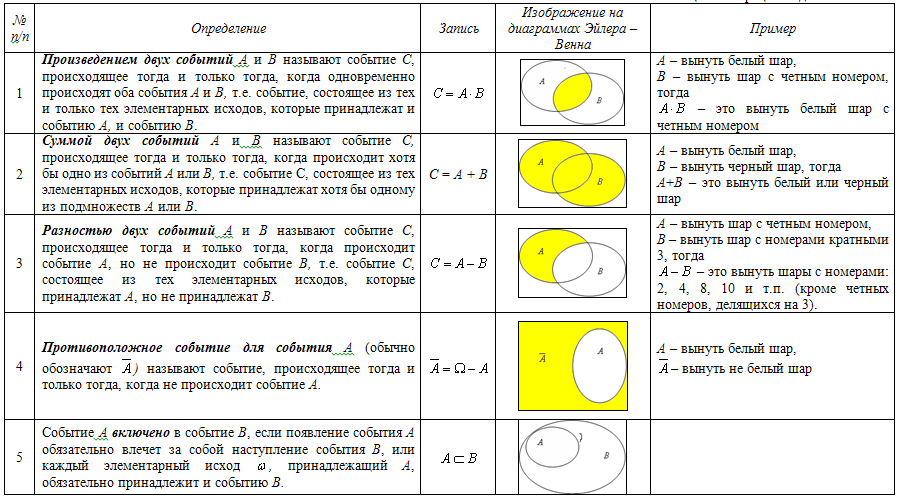 Тогда событию B={вынут туз} соответствует подмножество B={туз пик, туз крести, туз буби, туз червы}.
Тогда событию B={вынут туз} соответствует подмножество B={туз пик, туз крести, туз буби, туз червы}.
Пример 14.1. Пусть эксперимент состоит в подбрасывании один раз игральной кости. Обозначим через X число выпавших очков. Построить пространство элементарных событий и указать состав подмножеств, соответствующих следующим событиям: A={X кратно3}, B={X – нечетно}, C={X < 7}, D={X > 7}.
Решение. Очевидно, что за элементарные события здесь лучше всего взять события: {1}, {2}, {3}, {4}, {5}, {6}, которые образуют полную группу несовместных событий. При помощи этих элементарных событий можно легко описать все перечисленные в задаче события:
A={3;6}, B={1;3;5}, C=, D=Æ.
Над событиями можно совершать те же самые операции, что и для множеств. В частности:
Произведением AB событий A и B называют событие, которое происходит тогда и только тогда, когда имеют место оба события A и B одновременно. Например, событие C={вынут туз черви} является произведением событий A и B, где A={вынута карта червонной масти}, а B={вынут туз}.
Суммой A+B событий A и B называют событие, которое происходит только тогда, когда имеет место либо событие A, либо событие B, либо оба вместе.
Разность A–B событий A и B называют событие, которое происходит только тогда, когда имеет место событие A, но не имеет место событие B.
Событие Называется противоположным к событию, если оно происходит тогда и только тогда, когда не происходит . Другими словами, противоположное событие состоит из тех элементарных исходов множества , при которых событие не происходит, т. е. .
Действия над событиями становятся более наглядными, если придать им геометрическую интерпретацию в виде диаграмм Эйлера-Венна:
|
A+B |
AB |
A–B |
B–A |
Пример 14.
|
A+B={3;5;6;7;9;11;12}, |
A–B={6;12}, |
|
AB={3;9}, |
B–A={5;7;11}. |
Пример 14.3. Пусть имеется колода карт, из которой вынимается одна карта. Описать события AB, , A+B, A–B, , если A={вынутая карта – туз}, B={вынутая карта – черви}.
Ответ:
AB = {вынутая карта – червовый туз},
= {вынутая карта – червовая, но не туз},
A+B = {вынутая карта – либо туз, либо черви},
A–B = {вынутая карта –туз, но не черви},
= {вынутая карта – не туз и не черви}.
Используя операции над событиями, можно описывать более сложные события. Например, пусть A, B, C – три события, наблюдаемые в некотором эксперименте. Используя алгебру событий, опишем событие, произошло только событие А. Это означает, произошло событие A, но события B и С не произошли. Это можно записать следующим образом
Используя алгебру событий, опишем событие, произошло только событие А. Это означает, произошло событие A, но события B и С не произошли. Это можно записать следующим образом
.
Аналогично, можно описать события: произошло только одно событие, не важно какое или: произошло хотя бы одно событие. Все это можно коротко записать так
,
.
Пример 14.4. Пусть ёлочная гирлянда имеет следующий вид
Опишите событие, что: а) цепь будет работать (т. е. загорится хотя бы одна лампочка), б) имеется разрыв цепи (т. е. ни одна лампочка не загорится).
Ответ: а) Для того чтобы цепь работала, нужно чтобы работала лампочка А и (операция умножения) верхняя или нижняя ветка гирлянды (операция сложения). Верхняя ветка будет работать, если будут работать и лампочка B, и лампочка C (операция умножения). Используя алгебру событий всё это можно записать в виде формулы:
.
Б) Для того чтобы цепь не работала, нужно чтобы не работала лампочка А или (операция сложения) верхняя и нижняя ветка гирлянды (операция умножения). Верхняя ветка не будет работать, если не будут работать или лампочка B, или лампочка C (операция сложения). Используя алгебру событий всё это можно записать в виде формулы (для обозначения, что лампочка не работаем мы будем использовать символ противоположного события):
Верхняя ветка не будет работать, если не будут работать или лампочка B, или лампочка C (операция сложения). Используя алгебру событий всё это можно записать в виде формулы (для обозначения, что лампочка не работаем мы будем использовать символ противоположного события):
.
Упражнения
14.1. Имеется колода карт. Вынимается одна карта. Опишите события и если A={карта пиковой масти}, B={карта – дама}.
Ответ: ={вынутая карта – либо не пики, либо не дама}, ={вынутая карта – либо не пики, либо дама}.
14.2. В урне находится 12 шаров. Все они пронумерованы от 1 до 12. Опишите событие и (A–B)+(B–A), если A={шар с номером кратным 3}, B={шар с номером меньше 5}.
Ответ: ={5, 7, 8, 10, 11}, (A–B)+(B–A)={6, 9, 12, 1, 2, 4}.
14.3. В урне находится 12 шаров. Все они пронумерованы от 1 до 12. Опишите событие и , если А={шар, с номером кратным 4}, B={шар, с номером не меньше 6}.
Ответ: ={8, 12, 1, 2, 3, 5}, ={8, 12}.
14.4. Имеется электрическая цепь. Опишите, что: а) цепь будет работать, б) имеется разрыв цепи.
Опишите, что: а) цепь будет работать, б) имеется разрыв цепи.
1) 2) .
Ответ: 1) , ;
2) , .
14.5. Имеется электрическая цепь. Опишите, что: а) цепь будет работать, б) имеется разрыв цепи.
1) 2) .
Ответ: 1) , ;
2) , .
| < Предыдущая | Следующая > |
|---|
1.1.4. Сумма и произведение событий
Определение. Суммой (Объединением) Событий A и B называется событие, которое наступает, когда происходит хотя бы одно из этих событий, и обозначается A+B. При сложении событий множества благоприятствующих исходов складываются (объединяются).
Например, для событий примера 1.6 суммой событий A и C Будет событие A+C ={w1 , w2 , w3 , w4 , w6}, а суммой событий A и B Будет событие A+B = {w1, w2, w3, w4, w5, w6}=W, т. е. достоверное событие.
е. достоверное событие.
Операцию сложения определяют и для бесконечной последовательности событий.
Определение. Суммой (Объединением) Последовательности событий A1, A2, … An,.. называется событие, которое наступает, когда происходит хотя бы одно из событий последовательности и обозначается .
Пусть событие A Состоит из благоприятствующих исходов .
Тогда событие A по определению суммы можно представить в виде
.
Определение. Произведением событий A и B Называется событие, которое происходит при одновременном наступлении этих событий и обозначается AB. При умножении событий множества благоприятствующих исходов умножаются (пересекаются).
Например, для событий примера 1.6 произведением событий A И C будет событие AC = {w1 ,W3}, а произведением событий A и B будет невозможное событие AB =Æ .
Определение. Произведением последовательности событий A1,A2,…An,.. называется событие, которое происходит при одновременном наступлении всех событий последовательности и обозначается .
Определение. Разность событий A и B происходит, когда событие A наступает, а событие B — не наступает, и обозначается A-B.
Используя определения действий над событиями, можно доказать следующие свойства
1) A+B=B+A 2) AB=BA 3) A+(B+C)=(A+B)+C
4) A(B+C)=AB+AC 5) A+Æ=A 6) AÆ=Æ
7) AW=A 8) A+A=A 9) AA=A
10) A+W=W 11) AW=A 12) A+= W
13) A=Æ 14) =A 15) =Æ 16) =W.
Первые семь свойств аналогичны свойствам алгебры, таким как перестановка, сочетание и распределение, при этом невозможное событие Æ можно считать как 0, а достоверное событие W – как 1. Остальные свойства не имеют аналогов в алгебре.
Остальные свойства не имеют аналогов в алгебре.
Для событий А и В справедливы формулы, называемые соотношениями двойственности, если
.
Определение. Класс событий U образует Алгебру событий, если
1) достоверное событие содержится в этом классе, т. е. WÎ U
2) для любых событий AÎ U,BÎ U из этого класса их сумма и произведение также принадлежат этому классу: ABÎ U, A+BÎ U,
3) если событие A из этого класса AÎ U , то и противоположное событие также принадлежит этому классу: АÎ U.
Пример 1.7. Подбрасывают две монеты различного достоинства. Пространство элементарных событий W состоит из четырех элементов
W= {ГГ, ГЦ, ЦГ, ЦЦ }.
Здесь Г означает, что монета выпала гербом вверх, а Ц – цифрой вверх.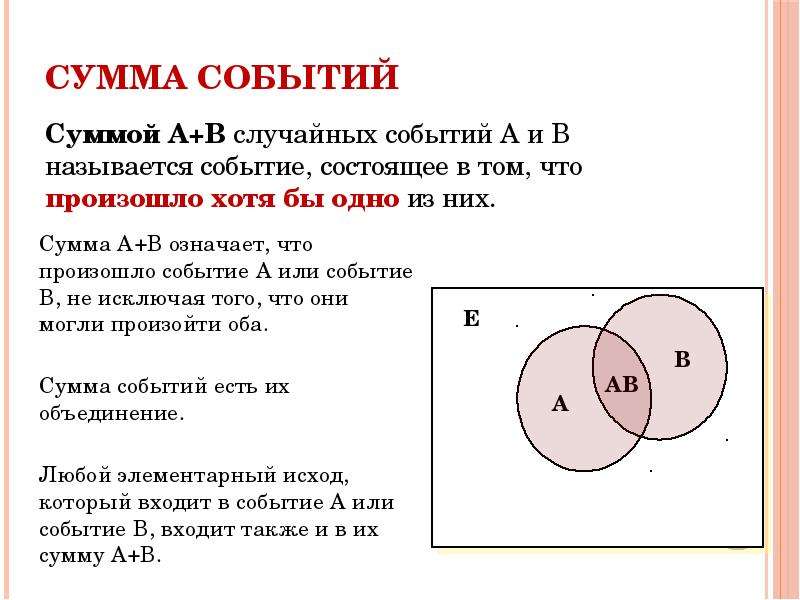
Построим все подмножества пространства элементарных событий W:
Æ , ГГ, ГЦ, ЦГ, ЦЦ, { ГГ, ГЦ }, { ГГ, ЦГ}, {ГГ, ЦЦ}, { ГЦ, ЦГ }
{ ГЦ, ЦЦ }, { ЦГ, ЦЦ }, {ГГ, ГЦ, ЦГ}, {ГГ, ГЦ, ЦЦ }, {ГГ, ЦГ, ЦЦ },
{ГЦ, ЦГ, ЦЦ }, {ГГ, ГЦ, ЦГ, ЦЦ }=W.
Нетрудно проверить, что все 16 событий образуют алгебру событий.
Для точного определения события в произвольном пространстве элементарных событий рассмотрим следующее определение.
Определение. Алгебра событий U образует S-алгебру событий, если для бесконечной последовательности событий Ai Из s-алгебры событий их объединение и пересечение принадлежат s-алгебре
Î U, Î U.
Если задано пространство элементарных событий W и s-алгебра событий U, То говорят, что задано Измеримое пространство { W, U }.
В случае произвольного пространства элементарных событий W, Событиями называют только такие подмножества пространства элементарных событий W, которые образуют s-алгебру событий U. Все остальные подмножества W, не входящие в s-алгебру событий U, событиями не являются.
Вопросы для самопроверки
1. При подбрасывании монеты выпала сторона с изображением герба (условно обозначим это событие буквой А). Какое событие будет являться противоположным событию А?
2. Подбрасываются две монеты, в результате чего видим изображение двух гербов. Что будет являться противоположным событием в этом случае?
3. Написать действие, соответствующее тому факту, что при подбрасывании двух монет на одной будет изображен герб (событие А), а на другой монете – цифра (событие В).
| < Предыдущая | Следующая > |
|---|
Взаимоисключающее событие: определение, примеры, объединения
Вероятность и статистика > Вероятность > Взаимоисключающее событие
Что такое взаимоисключающее событие?
Взаимоисключающие события — это вещи, которые не могут произойти одновременно. Например, вы не можете бежать вперед и назад одновременно. События «бег вперед» и «бег назад» являются взаимоисключающими. Подбрасывание монеты также может дать вам этот тип события. Вы не можете подбросить монетку и выпасть оба орла и хвосты. Так что «выпадение орла» и «выпадение решки» — взаимоисключающие понятия. Вот еще несколько примеров: ваша способность оплачивать аренду, если вам не платят, или смотреть телевизор, если у вас нет телевизора.
Например, вы не можете бежать вперед и назад одновременно. События «бег вперед» и «бег назад» являются взаимоисключающими. Подбрасывание монеты также может дать вам этот тип события. Вы не можете подбросить монетку и выпасть оба орла и хвосты. Так что «выпадение орла» и «выпадение решки» — взаимоисключающие понятия. Вот еще несколько примеров: ваша способность оплачивать аренду, если вам не платят, или смотреть телевизор, если у вас нет телевизора.
Подбрасывание монеты может быть взаимоисключающим.
Посмотрите видео с определением и двумя примерами нахождения вероятностей для взаимоисключающих событий:
Взаимоисключающие события
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Вероятность взаимоисключающего события
Базовая вероятность (P) события (забывая на мгновение о взаимной исключительности) составляет:
P = количество способов, которыми может произойти событие / общее количество исходов.
Пример: Вероятность выпадения «5» при бросании кости равна 1/6, потому что на кубике одна «5» и шесть возможных исходов. Если мы назовем вероятность выпадения 5 «Событием А», то уравнение будет таким:
P(A) = количество способов, которыми может произойти событие / общее количество исходов
P(A) = 1 / 6.
События записываются следующим образом:
P(A и B) = 0
На английском все это означает, что вероятность события A (выпадение 5) и события B (выпадение 6) происходят вместе равна 0.
Однако, когда вы бросаете кубик, вы можете бросить 5 ИЛИ 6 (шансы 1 из 6 для каждого события), и сумма любого события является суммой обеих вероятностей. Вероятность записывается так:
P(A или B) = P(A) + P(B)
P(выпадает 5 или 6) = P(выпадает 5) + P(выпадает 6)
P(выпадает 5 или прокатка 6) = 1/6 + 1/6 = 2/6 = 1/3.
Невозможно выбросить 1 и 2 вместе.
Вероятность взаимно исключающего события: Шаги
Пример задачи: «Если P(A) = 0,20, P(B) = 0,35 и (PA ∪ B) = 0,51, являются ли A и B взаимоисключающими?»
Примечание: объединение (∪) двух происходящих событий означает, что происходит A или B.
Шаг 1: Сложите вероятности отдельных событий (A и B) . В приведенном выше примере:
.20 + .35 = .55
Шаг 2: Сравните свой ответ с данным «союзным» утверждением (A ∪ B) . Если они совпадают, события исключают друг друга. Если они разные, то не исключают друг друга. Почему ? Если они взаимоисключающие (они не могут произойти вместе), то (∪)nion двух событий должен быть суммой обоих, то есть 0,20 + 0,35 = 0,55.
В нашем примере 0,55 не равно 0,51, поэтому события не взаимоисключающие .
Нравится объяснение? Ознакомьтесь с дополнительными пошаговыми примерами — как этот для взаимоисключающих событий — в Справочнике по статистике практического обмана
Ссылки
Beyer, WH CRC Standard Mathematical Tables, 31st ed. Бока-Ратон, Флорида: CRC Press, стр. 536 и 571, 2002 г.
Додж, Ю. (2008 г.). Краткая энциклопедия статистики. Спрингер.
Эверитт, Б.С.; Скрондал, А. (2010), Кембриджский статистический словарь, издательство Кембриджского университета.
Уилан, К. (2014). Голая статистика. W. W. Norton & Company
УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Взаимоисключающее событие: определение, примеры, союзы» От StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/mutually-exclusive-event/
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .
Что такое формула P(A/B)? I Примеры
P(A/B) известна как условная вероятность и означает вероятность события A, которая зависит от другого события B. Она также известна как «вероятность A при данном B». Формула P(A/B) используется для быстрого нахождения этой условной вероятности.
Что такое формула P(A/B)?
Условная вероятность P(A/B) возникает только в случае зависимых событий. Он дает условную вероятность события А при условии, что произошло событие В.
Формула P(A/B)
P(A/B) = P(A∩B) / P(B)
Аналогично, формула P(B/A): P(B/A) ) = P(A∩B) / P(A)
Здесь
P(A) = вероятность события A.
P(B) = Вероятность наступления события B.
P(A ∩ B) = Вероятность наступления событий A и B.
Из этих двух формул мы можем вывести формулы произведения вероятности.
- Р(А∩В) = Р(А/В) × Р(В)
- Р(А∩В) = Р(В/А) × Р(А)
Примечание: Если A и B являются независимыми событиями, то P(A/B) = P(A) или P(B/A) = P(B)
Есть вопросы по основным математическим понятиям ?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами
Забронировать бесплатный пробный урок
Примеры формул P(A/B)
Пример 1: Когда бросается правильная игральная кость, какова вероятность того, что А при заданном В, где А – это событие выпадения нечетного числа и B — это событие получения числа меньше или равного 3?
Решение:
Найти: P(A/B), используя данную информацию.
При броске игральной кости пространство выборки = {1, 2, 3, 4, 5, 6}.
A — событие получения нечетного числа. Итак, А = {1, 3, 5}.
B — это событие получения числа, меньшего или равного 3. Таким образом, B = {1, 2, 3}.
Таким образом, B = {1, 2, 3}.
Тогда А∩В = {1, 3}.
Используя формулу P(A/B):
P(A/B) = P(A∩B) / P(B)
\(P(A/B) = \dfrac{2/6} {3/6} = \dfrac 2 3\)
Ответ: P(A/B) = 2 / 3.
Пример 2: Из колоды в 52 карты берутся две карты, первая карта НЕ заменены перед взятием второй карты. Какова вероятность того, что обе карты короли?
Решение:
Найти: Вероятность того, что обе карты являются королями.
P(карта 1 — король) = 4/52 (так как из 52 карт 4 короля).
P(карта 2 — король/карта 1 — король) = 3/51 (поскольку первый король не заменяется, всего 3 короля из 51 неиспользованной карты).
По формуле условной вероятности
P(карта 1 — король ∩ карта 2 — король) = P(карта 2 — король/карта 1 — король) × P(карта 1 — король)
P (карта 1 — король ∩ карта 2 — король) = 3/51 × 4/52 = 1/221
Ответ: Требуемая вероятность = 1/221.
Часто задаваемые вопросы по формуле P(A/B)
Что такое формула P(A/B)?
Формула P(A/B) — это формула, используемая для расчета условной вероятности, так что мы должны найти вероятность того, что событие ‘A’ произойдет, когда произойдет событие ‘B’.
