Третий признак подобия треугольников — презентация онлайн
Похожие презентации:
ІІ и ІІІ признаки подобия треугольников
2 и 3 признаки подобия треугольников
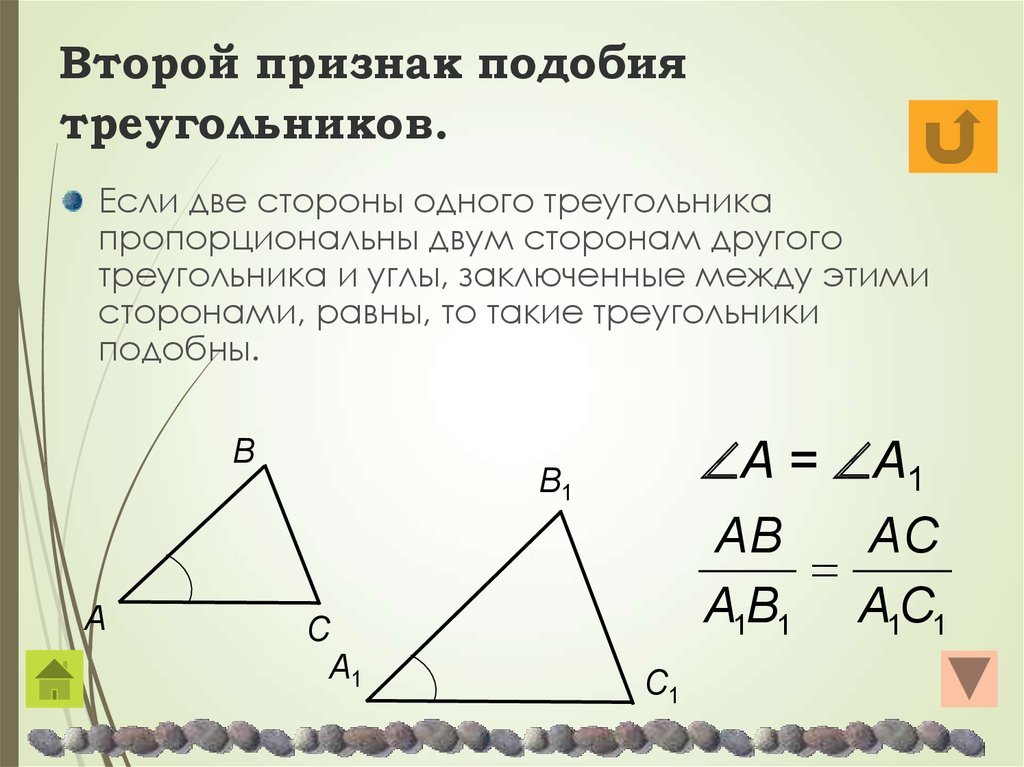
Второй признак подобия треугольников
Второй и третий признаки подобия треугольников
Второй и третий признаки подобия треугольников
Третий признак подобия треугольников
Признаки подобия треугольников. (Упражнение 10. 8 класс)
1 признак подобия треугольников
Второй и третий признаки подобия треугольников
Первый признак подобия треугольников
II
признак подобия треугольников. Если две стороны
одного треугольника пропорциональны двум сторонам
другого треугольника и углы, заключенные между этими
сторонами, равны, то такие треугольники подобны.
АВ
АС
Если ABC, А1В1С1, А А1 ,
А1 В1 А1С1
то
ABC
С1
А1
А1В1С1
С
В1
А
В
Блиц-опрос
Найдите пары подобных
треугольников и докажите их подобие.
L C ,
B
6
M
3
8см
4см
8
=
4
KML
10см
Верно
ABC
по 2 признаку
C
L
3см
6см
K
A
Найдите пары подобных
треугольников и докажите их подобие.
B
69
L C ,
3
C
69
M
115см
92см
4см
5см
L
3
K
A
4
=
92
KML
Верно
ABC
по 2 признаку
Блиц-опрос Найдите пары подобных треугольников и
докажите их подобие.
5
3
Верно
=
В общий
20
12
AВС
B
РВD по 2 признаку
Найти
3
5
12
D
A
P
20
S DBP 1
;
SCBA 16
C
РDBP 1
РCBA 4
Блиц-опрос Найдите пары подобных треугольников и
докажите их подобие.
5
4
Верно
=
ВОС АОD ,
15
12
AОD
?
7
B
4
COD по 2 признаку
С
5
O
15
A
12
21
D
III
признак подобия треугольников. Если три стороны
одного треугольника пропорциональны трем сторонам
другого, то такие треугольники подобны.
Дано: ABC,
Доказать:
А1В1С1,
ABC
Доказательство:
АВ
ВС
АС
А1 В1 В1С1 А1С1
А1В1С1
докажем, что А А1 и применим
2 признак подобия треугольников
С
С1
А1
В1 А
В
С
С1
В1
А1
В
А
1
2
1). Рассмотрим ABC2, у которого
1= А1,
2= В1.
ABC2
А1В1С1
Тогда
по двум углам
АВ ВС 2 АС2
А1 В1 В1С1 А1С1
АВ
ВС
АС
по условию
А1 В1 В1С1 А1С1
АС = АС2
С2
ВС = ВС2
С
С1
В1
А1
В
А
1
2
2).
ABC = АВС2
А = 1,
=
по трем сторонам
1= А1
С2
Блиц-опрос
Найдите пары подобных
треугольников и докажите их подобие.
3
3
=
5
5
3
=
D
3см
3см
B
A
5см
ABC
Докажите по 1 признаку подобия,
по 2 признаку.
5см
5см
DEF
по 3 признаку
5
E
3см
Верно
C
Блиц-опрос
Найдите пары подобных
треугольников и докажите их подобие.

6
4
9
=
6
12
=
Верно
D
4см
6см
F
A
B
12см
9см
ABC
по 3 признаку
8
E
8см
DEF
6см
C
Блиц-опрос
Найдите пары подобных
треугольников и докажите их подобие.
4
8
B
4
=
8
3
=
6
Верно
KML
M
ABC
по 3 признаку
8см
4см
C
L
3см
6см
K
A
Домашнее
задание:
Доказать: КМ II BL
B
10
14
M
C
5
6
7
L
A
3
K
S AMK
S CBL
Найти
РAMK
РCBL
Домашнее
задание:
Найдите пары подобных треугольников и
докажите их подобие. Найдите угол ВАD.
B
10
С
800
91
3
A
14
15
550
21
D
English Русский Правила
Треугольник. Подобие треугольников. Первый признак подобия треугольников.
- org/ListItem»>Альфашкола
- Статьи
- Подобие треугольников
Что такое треугольник? Из школьного определения треугольник:
Также можно сказать, что треугольник – это многоугольник с тремя углами. У треугольника всегда три стороны и три угла, тем больше сторона, чем больше угол и наоборот.
В этой статье мы научимся определять, являются ли подобными треугольники. Различие между подобием и равенством треугольников заключается в том, что в подобных треугольниках длины сторон треугольника умноженные или разделенные на одно и то же число, то есть их стороны имеют одинаковый коэффициент пропорциональности. Равные треугольники имеют равные углы и стороны. Как определить, подобны ли треугольники? Существуют признаки подобия треугольников. В школе изучают три основных признака подобия треугольников.
Второй признак подобия треугольников (по двум сторонам и углу между ними):
Третий признак (по трем сторонам):
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Анастасия Александровна Белая
Репетитор по математике
Стаж (лет)
Образование:
Могилёвский государственный университет имени А. А.Кулешова
А.Кулешова
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Наталья Анатольевна Люфт
Репетитор по математике
Стаж (лет)
Образование:
Новосибирскй педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Александр Николаевич Мельничук
Репетитор по математике
Стаж (лет)
Образование:
Приднестровский государственный университет им.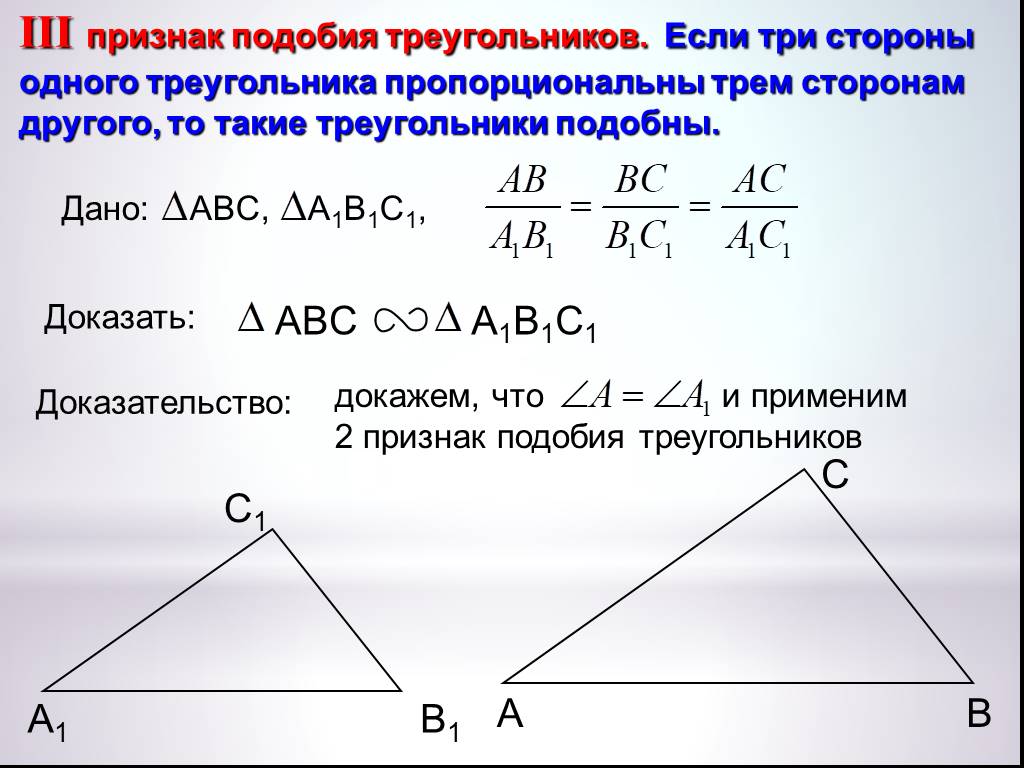
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Предметы
- Математика
- Репетитор по физике
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по английскому языку
- Репетитор по обществознанию
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
Специализации
- Репетитор по геометрии
- Репетитор по химии для подготовки к ЕГЭ
- Подготовка к олимпиадам по химии
- Подготовка к олимпиадам по физике
- Английский язык для начинающих
- Репетитор для подготовки к ЕГЭ по истории
- Репетитор для подготовки к ЕГЭ по обществознанию
- Репетитор по биологии для подготовки к ОГЭ
- Репетитор по географии для подготовки к ОГЭ
- Scratch
Похожие статьи
- Объем куба
- Простейшие уравнения с модулем
- ЕГЭ по математике, базовый уровень.
 Текстовые задачи (вариант 8)
Текстовые задачи (вариант 8) - Преобразование иррациональных выражений
- Зелень в рационе ребенка: когда и какую можно давать
- Наводим красоту: топ-10 простых и красивых причесок для девушек (разного возраста)
- Дети готовят: 10 рецептов простых сладостей
- Ребенок левша: особенности обучения письму
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Текст с ошибкой:
Расскажите, что не так
Подобные треугольники имеют соответствующие стороны и углы — Криста Кинг Математика
Подобные треугольники имеют соответствующие углы и соответствующие стороны
В этом уроке мы рассмотрим отношения подобных треугольников, чтобы найти недостающую информацию о парах подобных треугольников.
В паре подобных треугольников соответствующие стороны пропорциональны и все три угла равны. Это означает, что если вы знаете, что два треугольника похожи друг на друга, вы можете использовать эту информацию для поиска недостающих частей.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Соответствующие углыВ паре подобных треугольников соответствующие углы являются углами одной меры. На схеме подобных треугольников соответствующие углы окрашены в один цвет.
Соответствующие стороныВ паре подобных треугольников соответствующие стороны пропорциональны. Соответствующие стороны касаются одних и тех же двух пар углов.
Когда стороны совпадают, это означает, что при переходе от одного треугольника к другому вы можете умножить каждую сторону на одно и то же число.
На диаграмме подобных треугольников соответствующие стороны одного цвета.
Обозначение подобных треугольниковЧтобы показать, что два треугольника подобны, вы используете символ ???\sim???. Вам нужно сопоставить буквы из первого треугольника с углами с соответствующими вершинами на втором треугольнике.
Здесь можно сказать, что ???\треугольник XYZ\sim \треугольник BCA???.
Когда треугольники подобны, вы можете использовать этот факт для определения значений углов и сторон
Пройти курс
Хотите узнать больше о геометрии? У меня есть пошаговый курс для этого. 🙂
Узнать больше
Нахождение переменной в двух подобных треугольниках
Пример
Если два треугольника на диаграмме подобны, найдите переменную.
В подобных треугольниках соответствующие стороны пропорциональны. На схеме ???x??? соответствует ???8???, а ???42,5??? соответствует ???17???. Итак, мы говорим
???\frac{x}{8}=\frac{42.5}{17}???
???17x=8(42,5)???
???17x=340???
???х=20???
Соответствующие стороны касаются одних и тех же двух пар углов.
Как найти значения в подобных треугольниках
Пример
Если ???\треугольник XVY\sim \треугольник XWZ???, найти ???x???.
В подобных треугольниках соответствующие стороны пропорциональны. На диаграмме ???4x+12??? соответствует ???88???, и ???91??? соответствует ???143???.
???\frac{4x+12}{88}=\frac{91}{143}???
???(4x+12)143=91(88)???
???(4x+12)143=8,008???
???\frac{(4x+12)143}{143}=\frac{8,008}{143}???
???4x+12=56???
???4x=44???
???х=11???
Получить доступ к полному курсу геометрии
Начать
Изучение математикиКриста Кинг математика, изучение онлайн, онлайн-курс, онлайн-математика, геометрия, подобные треугольники, заявления о сходстве треугольников, соответствующие стороны, соответствующие углы, соответствующие пары углов
0 лайковВидео-урок: Подобие треугольников
Стенограмма видео
В этом видео мы научимся идентифицируйте подобные треугольники, используя либо правило AA, либо правило SSS.
Первое, что мы должны сделать, это
Напомним, что у подобных фигур все соответствующие углы равны или равны, и все
соответствующие стороны пропорционально. Обратите внимание, что это отличается от
конгруэнтные фигуры, так как у конгруэнтных фигур соответствующие углы равны и
соответствующие стороны равны. Подобные фигуры будут иметь стороны в
пропорция. Итак, когда дело доходит до идентификации
похожие треугольники, есть несколько кратчайших путей, которые мы можем использовать вместо того, чтобы пытаться
показать, что все углы равны и все соответствующие стороны лежат на
пропорция.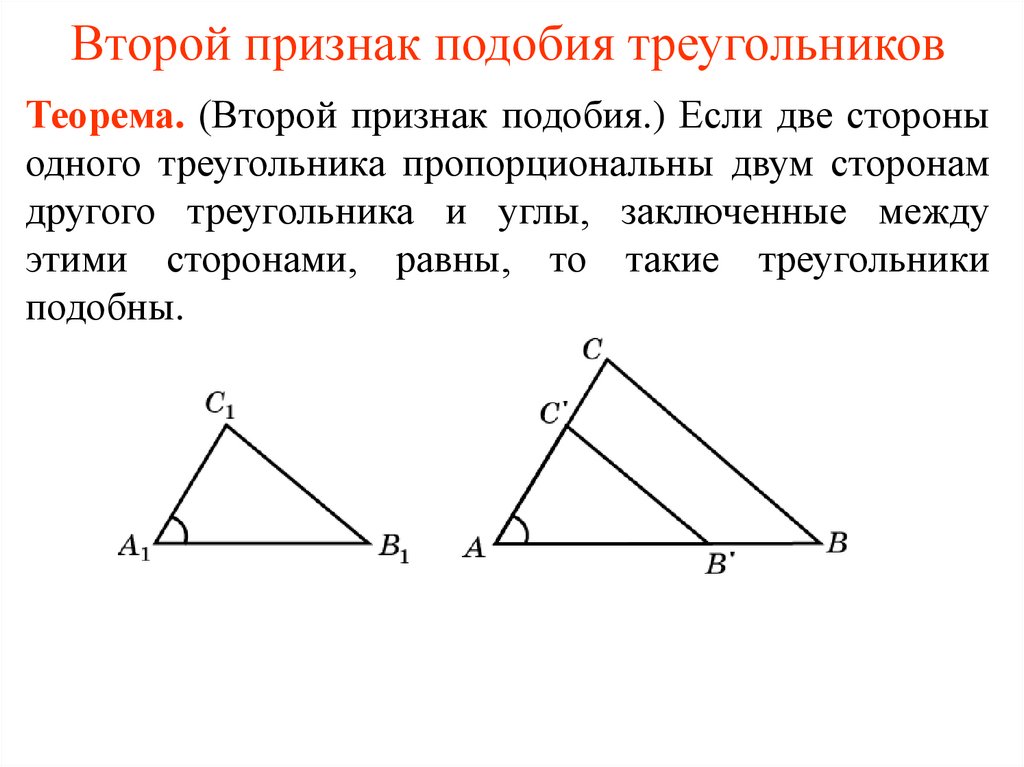 Начнем с того, что сосредоточимся на
углы.
Начнем с того, что сосредоточимся на
углы.
На двух нарисованных здесь треугольниках мы видно, что три пары соответствующих углов равны. Давайте посмотрим на более крупное треугольник. Допустим, мы берем точку на этот больший треугольник имеет ту же длину, что и соответствующая сторона меньшего треугольник и проведите линию, параллельную основанию этого треугольника. Если мы посмотрим на углы, тогда, поскольку у нас есть пара параллельных прямых и две секущие, то у нас будет два пары равных соответственных углов. Пропорциональность треугольника Теорема гласит, что если прямая параллельна одной стороне треугольника и пересекает две другие стороны, то он пропорционально делит эти две стороны.
Итак, если мы пометим вершины
больший треугольник с 𝐴𝐵𝐶 и меньший треугольник с вершинами 𝐷𝐸𝐹, то мы
сказал бы, что сторона 𝐴𝐵 пропорциональна стороне 𝐷𝐸, и это было бы
такая же пропорция, как 𝐴𝐶 к 𝐷𝐹, которая была бы такой же, как пропорция 𝐵𝐶
к 𝐸𝐹. Поэтому, показывая все три угла
конгруэнтны, мы также покажем, что соответствующие стороны находятся в
пропорция.
Поэтому, показывая все три угла
конгруэнтны, мы также покажем, что соответствующие стороны находятся в
пропорция.
На самом деле есть еще проще чем показать, что наши три угла конгруэнтны. И это потому, что если мы только покажем два угла, так как сумма углов треугольника равна 180 градусам, мы знаем, что если если в треугольнике две пары соответственных углов равны, то третья углы тоже должны быть равны. И поэтому, если мы хотим доказать что два треугольника подобны, нам нужно только использовать правило AA, чтобы показать, что два пары соответствующих углов равны.
Теперь давайте подумаем о сторонах
в этих треугольниках. Доля 𝑃𝑄 над 𝐾𝐿
можно записать как шесть на восемь. Отношение 𝑃𝑅 к 𝐾𝑀 может
будет записано как 7,5 на 10. Наконец, 𝑄𝑅 на 𝐿𝑀 будет
пропорция девять к 12. Каждое из этих трех соотношений все
упростить на три четверти.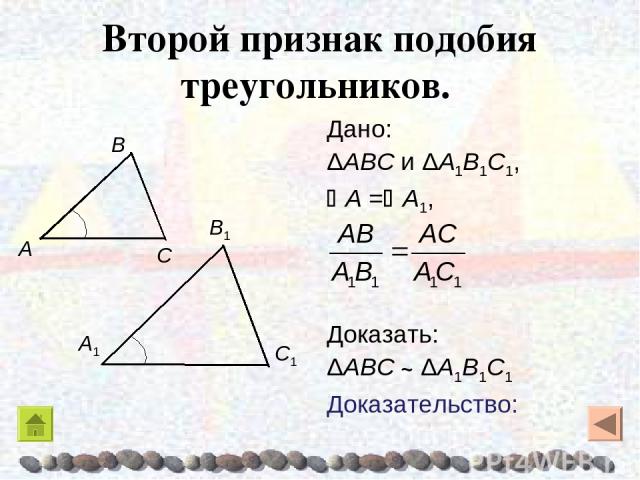 Следовательно, стороны равны
пропорция. Как мы видели выше, если стороны равны
пропорциональны, то соответствующие пары углов будут равны. Это называется правилом SSS, которое
означает, что если мы покажем, что соответствующие пары сторон пропорциональны, то мы
докажите, что у нас есть пара подобных треугольников.
Следовательно, стороны равны
пропорция. Как мы видели выше, если стороны равны
пропорциональны, то соответствующие пары углов будут равны. Это называется правилом SSS, которое
означает, что если мы покажем, что соответствующие пары сторон пропорциональны, то мы
докажите, что у нас есть пара подобных треугольников.
Помните, будьте осторожны и не путайте его с правилом SSS, которое мы могли бы использовать для конгруэнтных треугольников; в этом случае, мы должны были бы показать, что они конгруэнтны. Но для подобных треугольников мы показываем Правило SSS означает, что стороны пропорциональны.
В следующих вопросах мы использовать любое из этих двух правил, чтобы помочь нам идентифицировать подобные треугольники. Давайте посмотрим на нашу первую вопрос.
Учитывая следующие четыре фигуры, какие две похожи?
В этом вопросе нам дается
четыре различных формы, в комплекте с боковыми измерениями.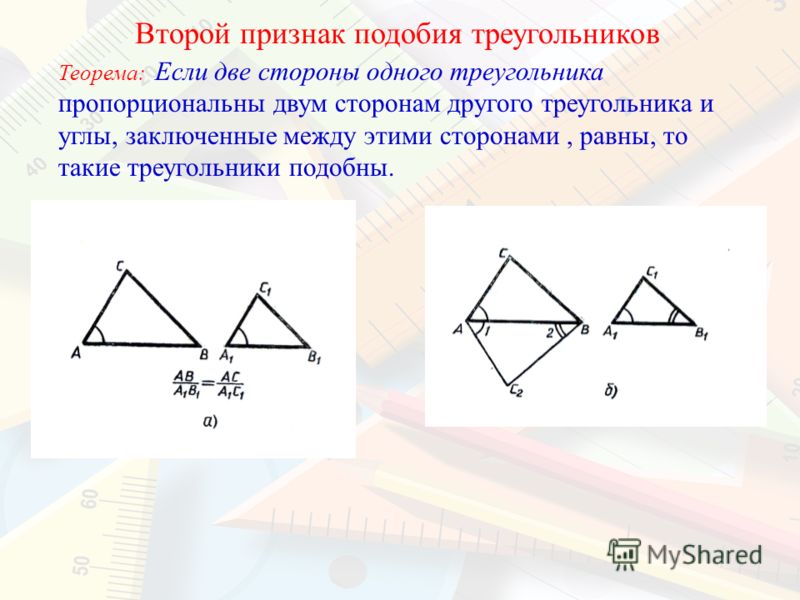 Нас спрашивают, какой из этих
формы похожи. И мы помним, что подобные
фигуры имеют соответствующие углы, равные или равные, и соответствующие стороны в
пропорция. Нам не дают никакой информации
относительно углов в этих четырех треугольниках. Итак, давайте посмотрим на
стороны.
Нас спрашивают, какой из этих
формы похожи. И мы помним, что подобные
фигуры имеют соответствующие углы, равные или равные, и соответствующие стороны в
пропорция. Нам не дают никакой информации
относительно углов в этих четырех треугольниках. Итак, давайте посмотрим на
стороны.
Мы можем заметить, что в этих четыре треугольника, у нас есть два похожих. Форма два и четыре будут обе быть равнобедренными треугольниками, а фигура один и фигура три также выглядят как они похожей формы. Нам нужно проверить каждую пару треугольники, однако, чтобы увидеть, пропорциональны ли соответствующие стороны. Начнем с наших равнобедренных треугольники, то есть фигуры два и четыре. Возьмем соответствующую пару сторон.
Тогда мы бы сказали, что
соотношение здесь было бы 12 в большом треугольнике по сравнению с семью в меньшем
треугольник. Равно ли это отношение
наши другие стороны восемь в большем треугольнике и пять в меньшем
треугольник? Для того, чтобы было легче сравнивать
эти дроби, давайте сделаем знаменатель одинаковым. Чтобы изменить
двенадцать седьмых в дроби больше 35, нам нужно будет умножить числитель
и знаменатель на пять, что даст нам значение 60 в числителе. С правой стороны мы
нужно умножить числитель и знаменатель на семь. Но как мы видим 60 на 35 это не
равно 56 на 35. Таким образом, фигуры два и четыре не являются
похожий.
Равно ли это отношение
наши другие стороны восемь в большем треугольнике и пять в меньшем
треугольник? Для того, чтобы было легче сравнивать
эти дроби, давайте сделаем знаменатель одинаковым. Чтобы изменить
двенадцать седьмых в дроби больше 35, нам нужно будет умножить числитель
и знаменатель на пять, что даст нам значение 60 в числителе. С правой стороны мы
нужно умножить числитель и знаменатель на семь. Но как мы видим 60 на 35 это не
равно 56 на 35. Таким образом, фигуры два и четыре не являются
похожий.
Давайте проверим фигуры один и
три. Запишем наши пропорции с помощью
значение длин меньшего треугольника в качестве числителя и большего
длины треугольника в качестве знаменателя дали бы нам значения четырех восьмых,
три шестых и пять десятых.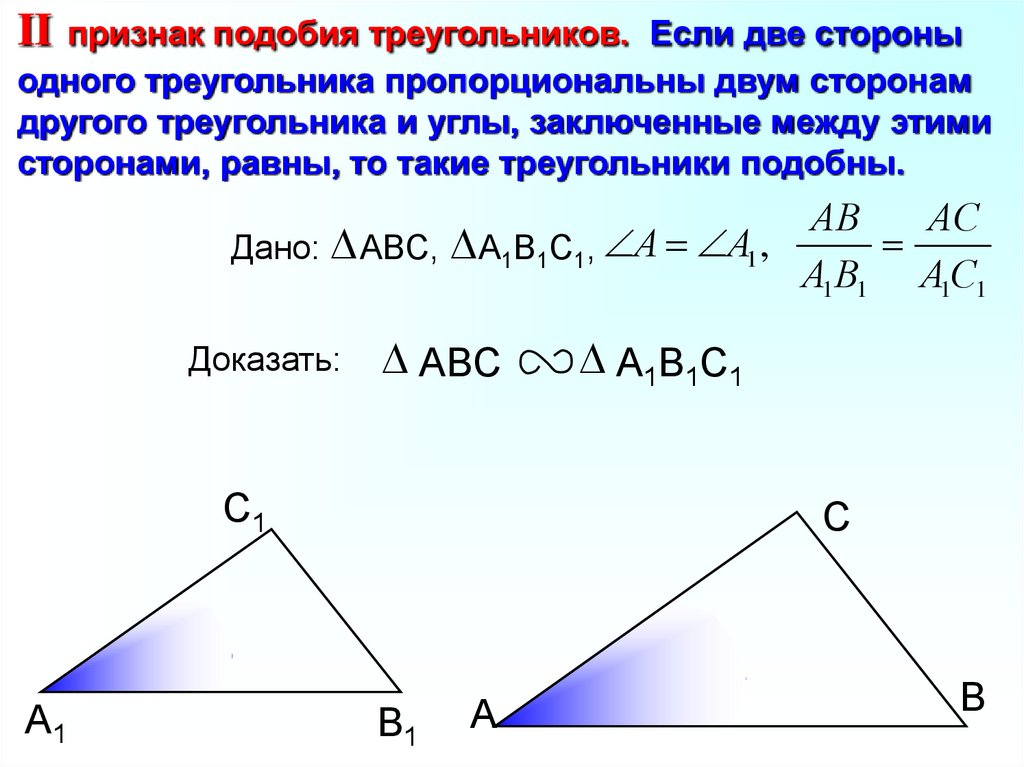 Мы должны заметить, что все
эти дроби упрощаются до половины. Итак, мы продемонстрировали, что
эти три пары соответствующих сторон пропорциональны, и это относится к
SSS правило подобных треугольников. Итак, наш ответ состоит в том, что из
эти четыре формы, форма один и форма три похожи.
Мы должны заметить, что все
эти дроби упрощаются до половины. Итак, мы продемонстрировали, что
эти три пары соответствующих сторон пропорциональны, и это относится к
SSS правило подобных треугольников. Итак, наш ответ состоит в том, что из
эти четыре формы, форма один и форма три похожи.
Посмотрим на другой вопрос.
Два треугольника похожий?
Начнем с того, что вспомним, что
у подобных треугольников соответствующие углы равны и соответственные стороны в
пропорция. Если мы посмотрим на меньшую
треугольник 𝐴𝐷𝐸 и больший треугольник 𝐴𝐵𝐶, не похоже, что эти
два треугольника будут одинаковой формы. Однако давайте посмотрим, сможем ли мы
докажите это математически, на всякий случай, если треугольники нарисованы неправильно. Чтобы показать, что два
треугольники подобны, мы можем помнить, что либо использовали бы правило AA, чтобы
показать, что две пары углов конгруэнтны, или правило SSS, чтобы продемонстрировать, что
есть три пары соответствующих сторон в пропорции.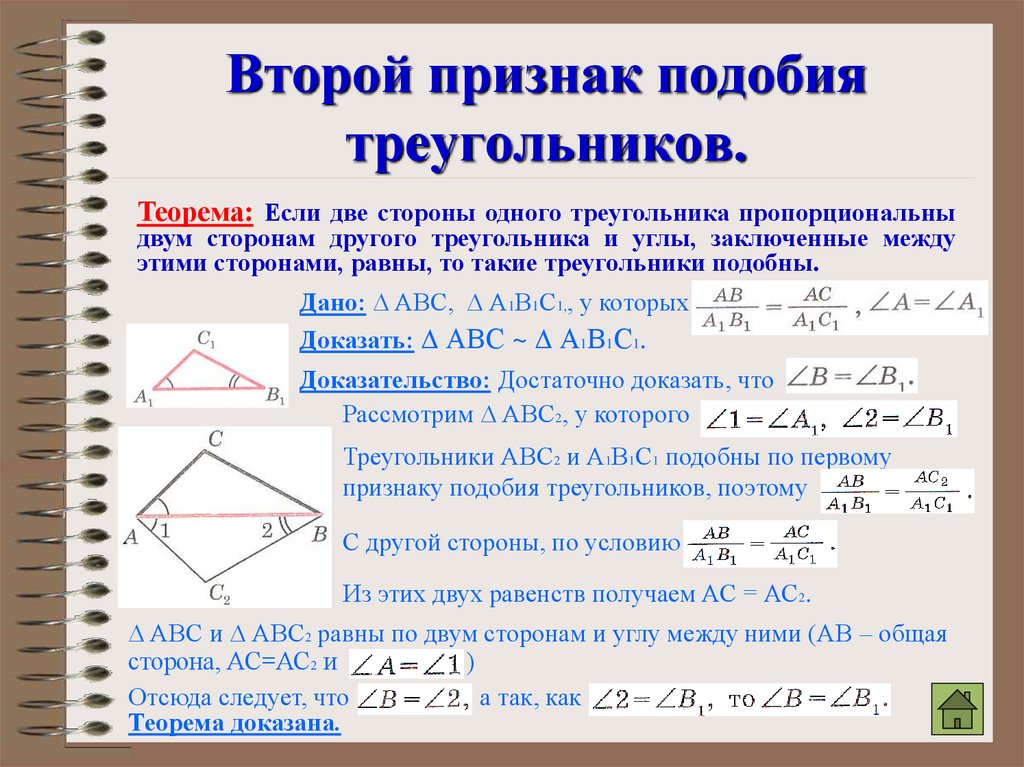 Нам не дано достаточно
информация об углах здесь, поэтому давайте посмотрим, сможем ли мы использовать правило SSS.
Нам не дано достаточно
информация об углах здесь, поэтому давайте посмотрим, сможем ли мы использовать правило SSS.
Нам нужно проверить, есть ли одинаковое соотношение или пропорция между соответствующими сторонами. Например, это сторона 𝐴𝐸 над стороной 𝐴𝐶 в той же пропорции, что и 𝐴𝐷 над 𝐴𝐵 и так же, как 𝐸𝐷 над 𝐶𝐵? Мы можем заполнить числовое значения длины в нашу дополнительную информацию. Но так как у нас нет размеры для сторон 𝐸𝐷 и 𝐶𝐵, мы не сможем доказать два треугольника похожи. Но если пропорции 𝐴𝐸 и 𝐴𝐶 и 𝐴𝐷 и 𝐴𝐵 различны, то мы могли бы доказать, что они не похожий. Давайте взглянем.
Длина 𝐴𝐸 определяется как
46 сантиметров. Но будьте осторожны, так как длина
𝐴𝐶 — это не 32,2, а сумма 46 и 32,2, что равно 78,2. 𝐴𝐷 равно 22, а 𝐴𝐵 — сумма
22 и 24,2 сантиметра, что составляет 46,2 сантиметра. Теперь нам нужно сравнить эти
две дроби, чтобы убедиться, что они эквивалентны. Мы можем начать с удаления этого
десятичной точки от знаменателя. Мы можем сделать это, умножив
как наших числителей, так и знаменателей на 10. Разделив числитель и
знаменатель на 46, тогда 460 на 782 упрощается до 10 на 17. Деление числителя на
знаменатель 220 на 462 на 22 дает дробь 10 на 21. Таким образом, мы можем видеть, что
эти два отношения не равны. Следовательно, стороны не в
пропорция. Если стороны не в
пропорции, то треугольники не были бы подобны. Итак, наш ответ здесь будет
нет.
Теперь нам нужно сравнить эти
две дроби, чтобы убедиться, что они эквивалентны. Мы можем начать с удаления этого
десятичной точки от знаменателя. Мы можем сделать это, умножив
как наших числителей, так и знаменателей на 10. Разделив числитель и
знаменатель на 46, тогда 460 на 782 упрощается до 10 на 17. Деление числителя на
знаменатель 220 на 462 на 22 дает дробь 10 на 21. Таким образом, мы можем видеть, что
эти два отношения не равны. Следовательно, стороны не в
пропорция. Если стороны не в
пропорции, то треугольники не были бы подобны. Итак, наш ответ здесь будет
нет.
Прежде чем мы закончим с этим
вопрос, просто замечание. Если бы мы обнаружили, что 𝐴𝐸 более
𝐴𝐶 было равно 𝐴𝐷 над 𝐴𝐵, то нам также понадобились бы значения для
𝐸𝐷 и 𝐶𝐵. Поскольку недостаточно просто показать
что две стороны пропорциональны, нам нужно показать, что их три
пары соответствующих сторон в пропорции.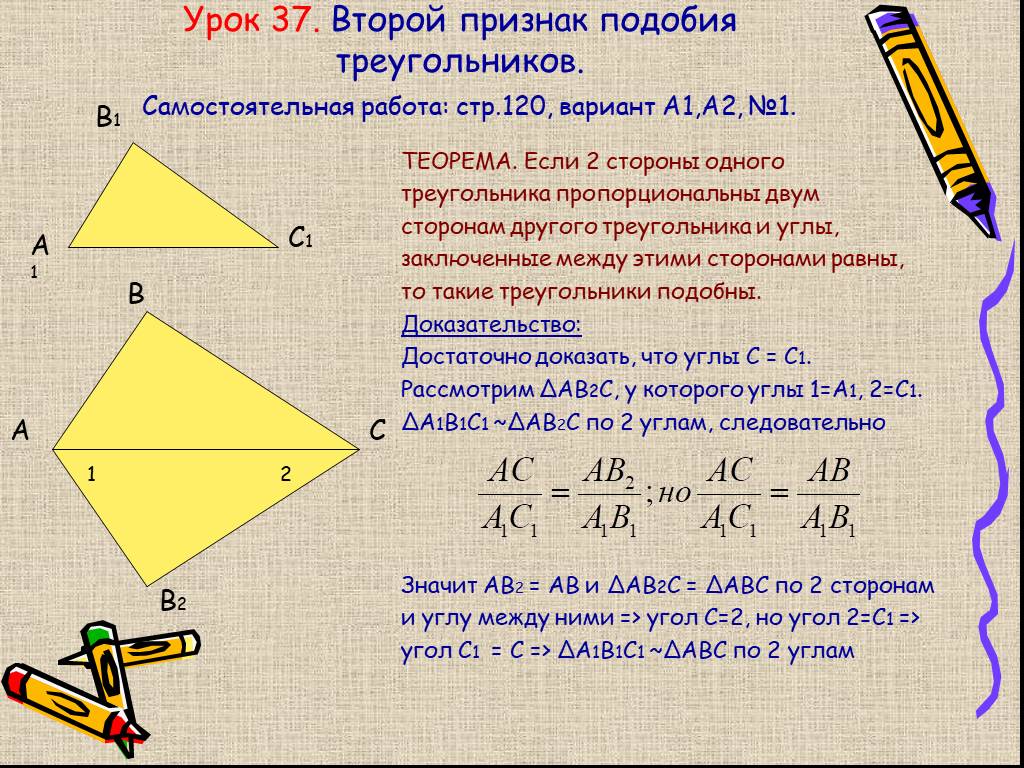 В этом вопросе не было
Дело в том, что у нас не было этих двух других длин, так как этого было достаточно, чтобы показать, что
эти треугольники не были подобны.
В этом вопросе не было
Дело в том, что у нас не было этих двух других длин, так как этого было достаточно, чтобы показать, что
эти треугольники не были подобны.
В следующем вопросе мы посмотрим, мы можем применить правило АА, чтобы продемонстрировать сходство.
На рисунке показаны два треугольники. Два треугольника похожий? Почему?
В этом вопросе нас спрашивают
если эти два треугольника подобны. Мы можем вспомнить подобное
треугольники имеют соответствующие углы равные и соответствующие стороны в
пропорция. Итак, давайте посмотрим на
углы в обоих этих треугольниках. есть прямой угол 90
градусов в каждом треугольнике. И один треугольник имеет
Угол 60 градусов, а другой имеет угол 30 градусов. Однако, если мы помним, что
сумма углов треугольника равна 180 градусам, то мы могли бы вычислить
третий угол в каждом треугольнике.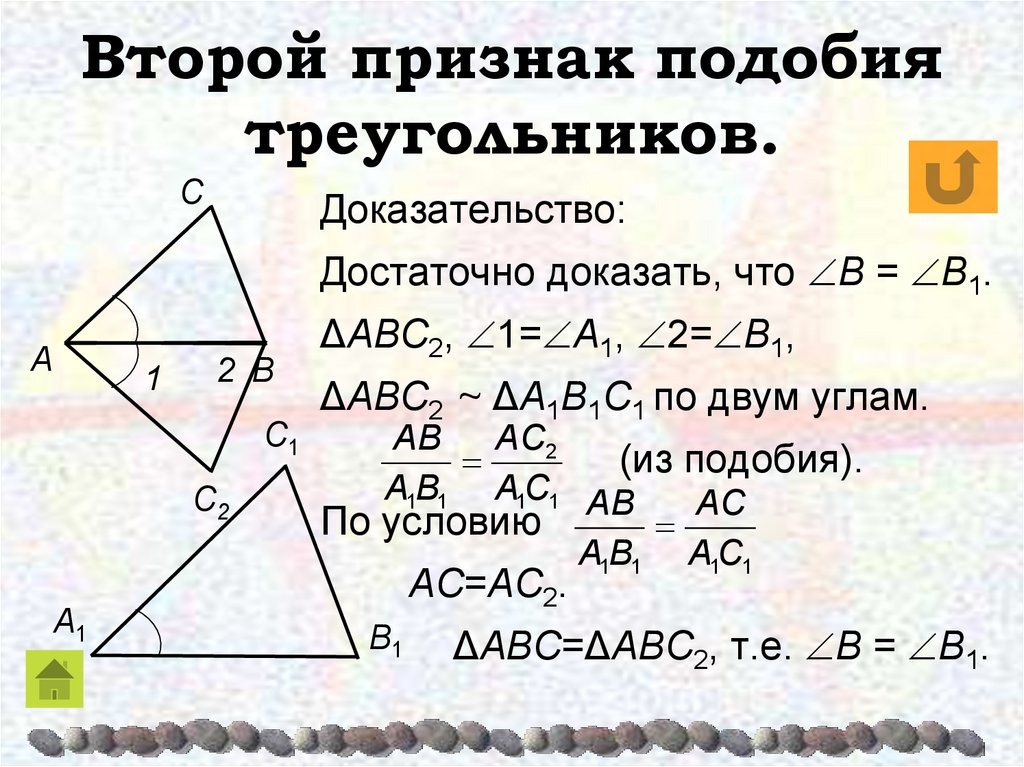
В верхнем треугольнике 60+ прямой угол в 90 градусов даст нам 150 градусов, и вычитая это из 180 градусов у нас останется 30 градусов. В нижнем треугольнике 90 градусов плюс 30 дает нам 120 градусов, оставляя нам третий угол 60 градусов. То, что мы можем видеть, это то, что мы имеют три пары равных углов. У нас есть два угла по 30 градусов, два угла по 60 градусов и два угла по 90 градусов. Мы показали три пары соответствующие углы равны. Но на самом деле нам нужно только показать две пары соответствующих углов, чтобы показать, что два треугольники подобны.
Итак, чтобы ответить на вопрос «есть
два треугольника подобны?» Да. Чтобы ответить на второй вопрос
«почему?», мы могли бы сказать, что если вычислить меру третьего угла за один
треугольников, вы можете видеть, что треугольники имеют два общих угла. Следовательно, по критериям АА
треугольники подобны.
Следовательно, по критериям АА
треугольники подобны.
На рисунке показаны два треугольника, 𝐴𝐵𝐶 и 𝐴 прайм 𝐵 прайм 𝐶 прайм. Определить меру угла 𝐴𝐵𝐶. О чем говорит критерий АА нам об этих двух треугольниках?
В этом вопросе два треугольники, нарисованные на сетке. И первое, что нас спрашивают нужно найти угол 𝐴𝐵𝐶, который находится в меньшем треугольнике. Для того, чтобы сделать это, мы должны Напомним, что сумма углов треугольника составляет 180 градусов. Поэтому нам нужно будет вычислить 180 градусов вычесть два других угла 114,3 градуса и 34,1 градуса градусов, что дает 31,6 градуса. И так, это наш ответ для мера угла 𝐴𝐵𝐶.
Во второй части этого
вопрос, нас спрашивают о критерии АА, который мы используем для
показать, что два треугольника подобны.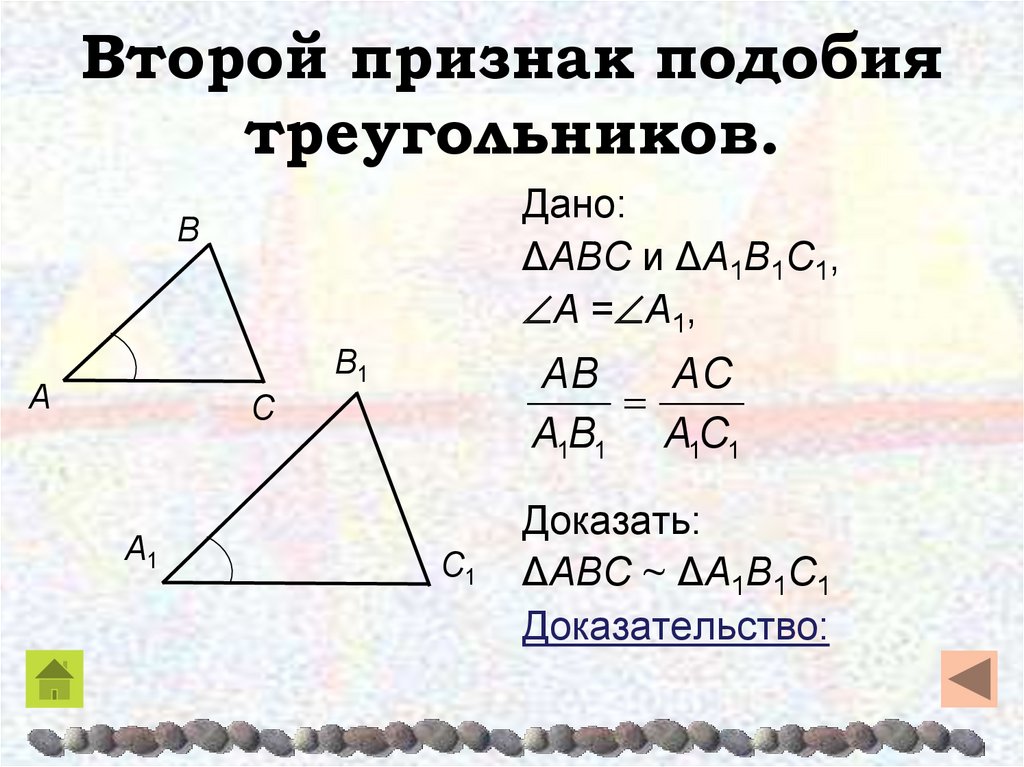 Это то, что у нас есть, когда мы
Докажите, что существуют две пары равных углов. Итак, давайте познакомимся поближе
эти два треугольника. Угол 𝐴𝐵𝐶, который мы
только что получилось, так как 31,6 градуса имеют соответствующий угол при угле 𝐴 простое число 𝐵
простое число 𝐶 простое число того же значения, 31,6 градуса. У нас есть еще одна пара
соответствующие конгруэнтные углы, угол 𝐶 простой 𝐴 простой 𝐵 простой и угол
𝐶𝐴𝐵, обе равны 34,1 градуса. Показывает, что есть два
пары соответствующих конгруэнтных углов или правило AA, мы показываем, что
эти два треугольника подобны.
Это то, что у нас есть, когда мы
Докажите, что существуют две пары равных углов. Итак, давайте познакомимся поближе
эти два треугольника. Угол 𝐴𝐵𝐶, который мы
только что получилось, так как 31,6 градуса имеют соответствующий угол при угле 𝐴 простое число 𝐵
простое число 𝐶 простое число того же значения, 31,6 градуса. У нас есть еще одна пара
соответствующие конгруэнтные углы, угол 𝐶 простой 𝐴 простой 𝐵 простой и угол
𝐶𝐴𝐵, обе равны 34,1 градуса. Показывает, что есть два
пары соответствующих конгруэнтных углов или правило AA, мы показываем, что
эти два треугольника подобны.
Таким образом, мы могли бы ответить на вторая часть этого вопроса с таким утверждением: поскольку оба треугольника разделить двух ангелов равных размеров, они должны быть похожи.
Теперь посмотрим на один последний
вопрос.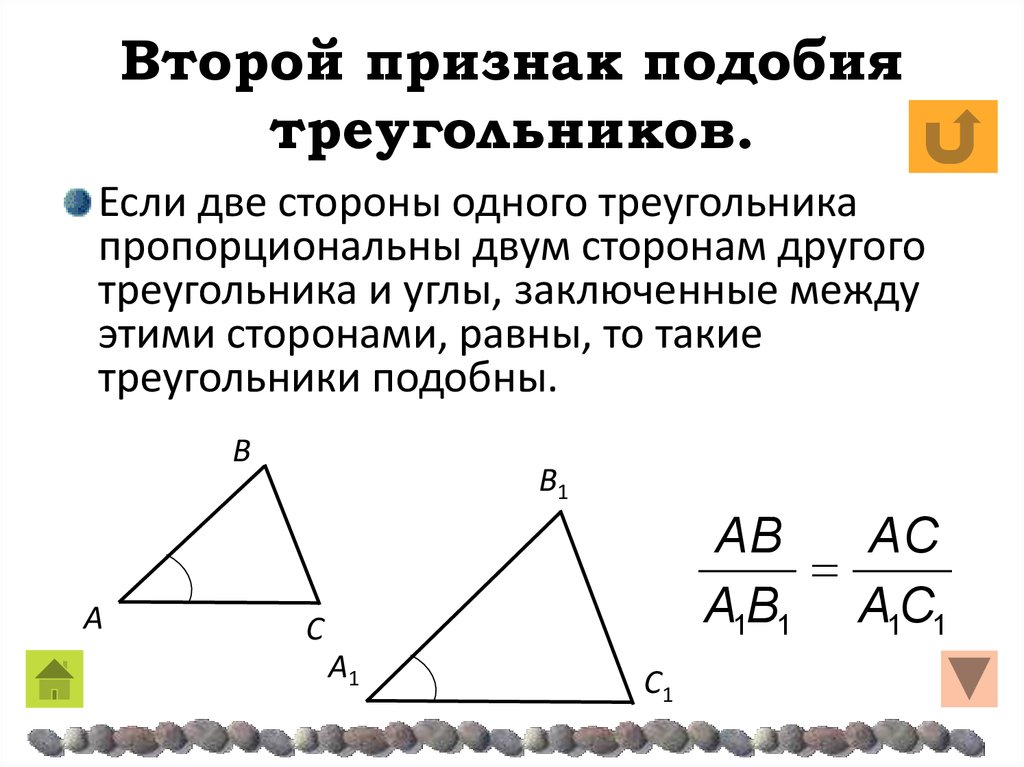
Треугольники 𝐴𝐵𝐶 и 𝐴 простые 𝐵 простых 𝐶 простых чисел на данном рисунке подобны. Определите значение 𝑥.
Нам сказали, что эти два треугольники подобны. Это означает, что соответствующие углы равны и соответствующие стороны пропорциональны. Глядя на треугольники, это будет означать, что угол при 𝐵 будет конгруэнтным углу при 𝐵 простом как эти два угла соответствуют. Угол 𝐶 и 𝐶 простые были бы конгруэнтны, а углы 𝐴 и 𝐴 простые конгруэнтны.
Нам даны размеры для
угол 𝐴 и 𝐴 простые. Итак, мы могли бы написать, что пять 𝑥
плюс 90 больше шести должно быть равно трем 𝑥 плюс 320 больше шести. Затем мы могли бы решить, чтобы найти
значение 𝑥. Умножая оба этих
дроби на шесть дали бы нам, что пять 𝑥 плюс 90 равно трем 𝑥 плюс
320. Вычитание трех 𝑥 из обоих
сторон даст нам два 𝑥 плюс 90 равно 320. Вычитание 90 с обеих сторон
даст нам два 𝑥 равно 230. И, наконец, деление на два
даст нам 𝑥 равно 115. Итак, у нас есть ответ, что
значение 𝑥 будет равно 115. Нам не нужно включать
знак градуса, поскольку он был частью определения угла в простых числах 𝐴 и 𝐴.
Вычитание 90 с обеих сторон
даст нам два 𝑥 равно 230. И, наконец, деление на два
даст нам 𝑥 равно 115. Итак, у нас есть ответ, что
значение 𝑥 будет равно 115. Нам не нужно включать
знак градуса, поскольку он был частью определения угла в простых числах 𝐴 и 𝐴.
Мы можем проверить наш ответ, подставив это значение обратно на 𝑥 и найдем, что угол 𝐵𝐴𝐶 равен 110 и 56 градусов, а также угол 𝐵 простой 𝐴 простой 𝐶 простой.
Теперь мы можем подвести итог тому, что мы
узнал в этом видео. Во-первых, мы видели, что подобные
треугольники имеют соответствующие пары равных углов и соответствующие пары
стороны пропорционально. Мы можем определить подобные треугольники
с помощью правила AA, когда у нас есть две пары соответствующих углов
конгруэнтный. Мы также можем определить похожие
треугольников с использованием критерия SSS, где все три пары соответствующих
стороны находятся в одинаковой пропорции.

 Текстовые задачи (вариант 8)
Текстовые задачи (вариант 8)