Как преобразовать в дробь: Представление десятичной дроби в виде обыкновенной дроби или в виде смешанного числа — урок. Математика, 5 класс.

Общий взгляд на преобразование дробей

Данный обобщенный материал известен из школьного курса математики. Тут рассматриваем дроби общего вида с числами, степенями, корнями, логарифмами, тригонометрическими функция ми или другими объектами. Будут рассмотрены основные преобразования дробей вне зависимости от их вида.

Что такое дробь?

Определение 1

Дробь – это выражение, которое записывается в виде AB или А/В, где A и B являются некоторыми произвольными числами.

Существует еще несколько определений.

Определение 2

Горизонтальная наклонная черта, которая разделяет A и B, называют чертой дроби или дробной чертой.

Определение 3

Выражение, которое находится над чертой дроби, называют числителем,  а под – знаменателем.

От обыкновенных дробей к дробям общего вида

Знакомство с дробью происходит еще в 5 классе, когда проходят обыкновенные дроби. Из определения видно, что числителем и знаменателем являются натуральные числа.

Пример 1

К примеру 15, 26, 127, 31, которые можно записать как 1/5, 2/6, 12/7, 3/1.

После изучения действий с обыкновенными дробями имеем дело с дробями, которые имеют в знаменателе не одно натуральное число, а выражения с натуральными числами.

Пример 2

Например, 1+35, 9-516, 2·79·12.

Когда имеем дело с дробями, где есть буквы или буквенные выражения, то записывается таким образом:

a+bc, a-bc, a·cb·d.

Определение 4

Зафиксируем правила сложения, вычитания, умножения обыкновенных дробей ac+bc=a+bc, ac-bc=a-bc, ab·vd=a·cb·d

Для вычисления зачастую необходимо приходить к переводу смешанных чисел в обыкновенные дроби. Когда целую часть обозначим как a, тогда дробная имеет вид b/c, получаем дробь вида a·c+bc, откуда понятно появления таких дробей 2·11+311, 5·2+12 и так далее.

Черта дроби расценивается как знак деления. Поэтому запись можно преобразовать по-другому:

1:a-(2·b+1)=1a-2·b+1, 5-1,7·3:2·3-4:2=5-1,7·32·3-4:2, где частное 4:2 можно заменить на дробь, тогда получим выражение вида

5-1,7·32·3-42

Вычисления с рациональными дробями занимают особое место в математике, так как в числителе и знаменателе могут быть не просто числовые значения, а многочлены.

Пример 3

Например, 1×2+1, x·y-2·y20,5-2·x+y3.

Рациональные выражения рассматриваются как дроби общего вида.

Пример 4

Например, x·x+14×2·x2-12·x3+3, 1+x2·y·(x-2)1x+3·x1+2-x4·x5+6·x.

Изучение корней, степеней с рациональными показателями, логарифмов, тригонометрических функций говорит о том, что их применение появляется в заданных дробях вида:

Пример 5

anbn, 2·x+x23x13-12·x, 2×2+33×2+3, ln(x-3)ln e5, cos2α-sin2α1-1cos2α.

Дроби могут быть комбинированными, то есть иметь вид  x+1x3log3sin2x+3, lgx+2lgx2-2·x+1.

Виды преобразований дробей

Для ряда тождественных преобразований рассматривают несколько видов:

Определение 5

• преобразование, характерное для работы с числителем и знаменателем;
• изменение знака перед дробным выражением;
• приведение к общему знаменателю и сокращение дроби;
• представление дроби в виде суммы многочленов.

Преобразование выражений в числителе и знаменателе

Определение 6

При тождественно равных выражениях имеем, что полученная дробь является тождественно равной исходной.

Если дана дробь вида A/B, то A и B являются некоторыми выражениями. Тогда при замене получим дробь вида A1/B1_. Необходимо доказать справедливость равенства A/A1=B/B1при любом значении переменных, удовлетворяющих ОДЗ.

Имеем, что A и A1 и B и B1 тождественно равны, тогда их значения тоже равны. Отсюда следует, что при любом их значении A/B и A1/B1 данные дроби будут равны.

Такое преобразование упрощает работу с дробями, если необходимо преобразовывать отдельно числитель и отдельно знаменатель.

Пример 6

Для примера возьмем дробь вида 2/18, которую преобразуем к 22·3·3. Для этого знаменатель раскладываем на простые множители. Дробь x2+x·yx2+2·x·y+y2=x·x+y(x+y)2 имеет числитель вида x2+x·y, означает, что необходимо произвести замену на x·(x+y), которое будет получено при вынесении за скобки общего множителя x. Знаменатель заданной дроби x2+2·x·y+y2

свернуть по формуле сокращенного умножения. Тогда получим, что его тождественно равным выражением является (x+y)2.

Пример 7

Если дана дробь вида sin23·φ-π+cos23·φ-πφ·φ56,тогда для упрощения необходимо числитель заменить 1 по формуле, а знаменатель привести к виду φ1112. Тогда получим, что 1φ1112 равна заданной дроби.

Изменение знака перед дробью,  в ее числителе, знаменателе

Преобразования дробей – это также и замена знаков перед дробью. Рассмотрим некоторые правила:

Определение 7

• при изменении знака числителя получаем дробь, которая равна заданной, причем буквенно это выглядит  как _-A-B=AB, где А и В являются некоторыми выражениями;
• при изменении знака перед дробью и перед числителем, получаем, что —AB=AB;
• при замене знака перед дробью и его знаменателя, получаем, что -A-B=AB.

Доказательство

Знак минуса в большинстве случаев рассматривается как коэффициент со знаком -1, а дробная черта является делением. Отсюда получаем, что -A-B=-1·A:-1·B. Сгруппировав множители, имеем, что

-1·A:-1·B=((-1):(-1)·A:B==1·A:B=A:B=AB

После доказательства первого утверждения, обосновываем оставшиеся. Получим:

—AB=(-1)·(((-1)·A):B)=(-1·-1)·A:B==1·(A:B)=A:B=AB-A-B=(-1)·(A:-1·B)=((-1):(-1))·(A:B)==1·(A:B)=A:B=AB

Рассмотрим примеры.

Пример 8

Когда необходимо выполнить преобразование дроби 3/7 к виду -3-7, —37, -3-7, тогда аналогично выполняется с дробью вида -1+x-x2223-ln(x2+3)x+sin2x·3x.

Преобразования выполняются следующим образом:

1) -1+x-x2223-ln(x2+3)x+sin2x·3x==-(-1+x-x2)-223-lnx2+3x+sin2x·3x==1-x+x2-223+ln(x2+3)x-sin2x·3×2) -1+x-x2223-ln(x2+3)x+sin2x·3x==—(-1+x-x2)223-ln(x2+3)x+sin2x·3x==-1-x+x2223-ln(x2+3)x+sin2x·3×3)-1+x-x2223-ln(x2+3)x+sin2x·3x==—1+x-x2-223-ln(x2+3)x+sin2x·3x==—1+x-x2-223+ln(x2+3)x-sin2x·3x

Приведение дроби к новому знаменателю

При изучении обыкновенных дробей, мы коснулись основного свойства дробей, которое позволяет умножать, делить числитель и знаменатель на одно и то же натуральное число. Это видно из равенства a·mb·m=ab и a:mb:m=ab, где a, b, m являются натуральными числами.

Это равенство действительно для любых значений a, b , m и всех a, кроме b≠0 и m≠0. То есть мы получаем, что если числитель дроби А/В с A и C, которые являются некоторыми выражениями, умножить или разделить на выражение M, не равное 0, тогда получим дробь, тождественно равную начальной. Получаем, что A·MB·M=AB и A:MB:M=AB.

Отсюда видно, что преобразования основываются на 2 преобразованиях: приведении к общему знаменателю,  сокращении.

При приведении к общему знаменателю производится умножение на одно и то же число или выражение числитель и знаменатель. То есть мы переходим к решению тождественной равной преобразованной дроби.

Рассмотрим примеры.

Пример 9

Если взять дробь x+10,5·x3 и умножить на 2, тогда получим, что новый знаменатель получится 2·0,5·x3=x3, а выражение примет вид 2·x+1×3.

Пример 10

Для приведения дроби 1-x2·x23·1+ln x к другому знаменателю вида 6·x·1+ln x3 нужно, чтобы числитель и знаменатель быль умножен на 3·x13·(1+ln x)2. В итоге получаем дробь 3·x13·1+ln x2·1-x6·x·(1+ln x)3

Такое преобразование как избавление от иррациональности в знаменателе также применимо. Оно избавляет от наличия корня в знаменателе, что упрощает процесс решения.

Сокращение дробей

Основное свойство – это преобразование, то есть ее непосредственное сокращение. При сокращении мы получаем упрощенную дробь. Рассмотрим на примере:

Пример 11

Или дробь вида x3·x3·x2·(2×2+1+3)x3·x3·2×2+1+3·3+13·x, где сокращение производится при помощи x3, x3, 2×2+1+3 или на выражение вида x3·x3·2×2+1+3. Тогда получим дробь x23+13·x

Сокращение дроби является простым, когда общие множители сразу явно видны. Практически это встречается не часто, поэтому предварительно необходимо проводить некоторые преобразования выражений такого вида. Бывают случаи, когда необходимо находить общий множитель.

Если имеется дробь вида x223·(1-cos2x)2·sinx2·cosx22·x13, тогда необходимо применять тригонометрические формулы и свойства степеней для того, чтобы можно было преобразовать дробь к виду x13·x213·sin2xsin2x·x13. Это даст возможность сократить ее на x13·sin2x.

Представление дроби в виде суммы

Когда числитель имеет алгебраическую сумму выражений типа A1, A2,…, An, а знаменатель обозначается

B, тогда эта дробь может быть представлена как A1/B, A2/B, …, An/B.

Определение 8

Для этого зафиксируем это A1+A2+…+AnB=A1B+A2B+…+AnB.

Данное преобразование в корне отличается от  сложения дробей с одинаковыми показателями. Рассмотрим пример.

Пример 12

Дана дробь вида sin x-3·x+1+1×2, которую мы представим как алгебраическая сумма дробей. Для этого представим как sin xx2-3·x+1×2+1×2 или sin x-3·x+1×2+1×2 или sin xx2+-3·x+1+1×2.

Любая дробь, имеющая вид А/В представляется  в виде суммы дробей любым способом.  Выражение A в числителе может быть уменьшено или увеличено на любое число или выражение А0, которое даст возможность прейти к A+A0B-A0B.

Разложение дроби на простейшие  является частным случаем для преобразования дроби в сумму. Чаще всего его применяют при сложных вычислениях для интегрирования.

Текст в Фигма. Работа с текстом в Figma

В Фигме есть хорошие возможности для работы с текстом через специальный тип слоёв. Чтобы создать текстовый слой, нажимаем T и кликаем в нужное место, либо растягиваем блок как прямоугольник или фрейм и в нем уже можно писать.

Шрифты из Google Web Fonts

Круто: в Фигме по умолчанию доступна вся библиотека шрифтов Google Fonts,

Не круто: нельзя динамически просматривать как будут выглядеть эти шрифты. Чтобы увидеть, как будет выглядеть шрифт в проекте его обязательно нужно применить. не удобно — факт. Лично я просматриваю шрифты на самом сайте гуглфонтс, копирую название подходящего и применяю его в Figma.

Если ты используешь десктопную версию, то все шрифты с твоего компьютера подтянуться автоматически в фигму. подробно о загрузке локальных шрифтов в браузерную версию программы описано в отдельной статье http://figmaweb.ru/kak-zagruzit-v-figma-shrifty/

Режимы текстового слоя в Figma

• Horizontally — Текстовый блок обволакивает текст по горизонтали( если нет перехода на новую строку — текст выстроится в линию)

• Vertical — обводка текста по вертикали

• Fixed -фиксированный размер текстового блока вне зависимости от количества текста.

Так же ты можешь всегда уменьшить размер текстового блока до размера самого текста дважды кликнув по обводке

Основные настройки текста

Если выделен текстовый слой, справа мы увидим панель работы с текстом.

Справа вверху блока иконка Text Styles — всплывающее меню стилей текста. Подробнее о создании стилей для текста читай в отдельной статье.

Далее идут поля:

• Typeface — само название шрифта

• Weight – выбор начертания

• Size не знаю что это такое))

• Line Height – межстрочное расстояние. В мае 2019 пофиксили баги этой настройки и теперь она работает, как нужно.

• Letter Spacing — трекинг, межбуквенное расстояние или разрядка.

• Paragraph Spacing — отступ между параграфами, разделёнными обрывом строки, Enter

• Paragraph Indentation — красная строка, абзац.

Нравится Figma? — подпишись на нас в вк и инстаграме 

Так же тут у нас есть возможность выравнивать текст по левому краю, центру и по правому краю. Но что более примечательно — есть настройки по вертикальному выравниваю, что просто невероятно круто и полезно.

Настройка текстового блока в фигма

В доп меню за тремя точками скрывается более подробная настройка выравнивания текста внутри блока по вертикали и горизонтали

Красным выделен блок в котором можно настроить все буквы заглавные, строчные, каждое слово с большой буквы, подчеркнутый и зачеркнутый текст.

Блок Font Features

Содержит дополнительные возможности шрифта для…. блин, я не знаю для кого)) Это супер редко используемые фишки.

Discretionary and historical ligatures — использовать ли дискретные и исторические лигатуры.

Fractions – дроби. Соединять ли такие значения как 1/2 в один глиф с дробью.

Выставление степеней и числовых подписей

Numbers

Тут можно выбрать размеры ячейки для каждой буквы. Например, сделать так, чтобы каждая буква занимала определенную ширину или чтобы занимала ширину равную своему размеру. полезно для табличек и перфекционистов, имхо.

Как создать стиль текста в фигме

В начале тебе нужно выставить все настройки текста(выбрать шрифт, его размер, начертание и тд). После этого кликаешь на вот эту иконку (выделена красным) после кликаешь на плюсик и даешь название своему стилю текста в Figma.

Создать стиль текста в фигма

Полезные статьи по типографике для новичков

Термины в типографике

Основа типографики

Горячие клавиши в работе с текстом в Фигма

В начале ответы на популярные вопросы:

Как вставить текст в Фигма? — CTRL+v (удивительно)
Как растянуть текст в Фигме? — выбирай scale tool (K) и растягивай текст, как нужно. Он будет растягиваться пропорционально.

ctrl+с копировать
ctrl+v вставить
ctrl+d сделать дубль (дубль появляется мгновенно поверх копируемого элемента)
ctrl+alt+c копировать свойства текста(цвет, тени, обводку, для  шрифта — размер, начертание, керлинг и тд. )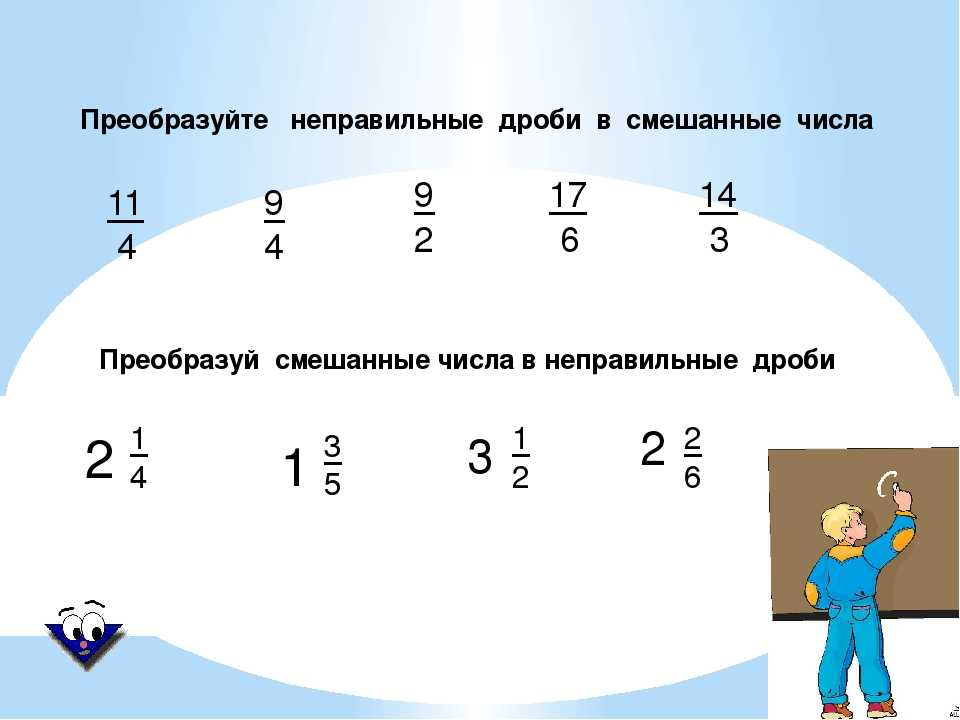
ctrl+alt+v вставить свойства
ctrl+shift+v вставить текст со свойствами текстового блока, в который ты вставляешь сам текст
ctrl+b текст станет жирным
ctrl+i текст станет наклонным
ctrl+u текст станет подчеркнутым

Десятичные числа в дроби — Преобразование, схемы, методы, примеры

Преобразование десятичных чисел в дроби — один из наиболее часто выполняемых шагов в арифметике. Однако, чтобы сделать это, вам нужно иметь основы вашего подразделения. Как только вы это поймете, вы сможете преобразовывать десятичные дроби в дроби, а дроби в десятичные дроби.

Ознакомьтесь с таблицей десятичных дробей в этом уроке, чтобы лучше понять, как можно преобразовать десятичные дроби в дроби.

1.	Как преобразовать десятичную дробь в дробную?
2.	Таблица преобразования десятичных чисел в дроби
3.	Преобразование десятичной дроби в дробь: дюймы
4.	Часто задаваемые вопросы о преобразовании десятичных чисел в дроби

Как преобразовать десятичную дробь в дробную?

Вот простой четырехэтапный процесс преобразования любого десятичного числа в дробь.

Шаги для преобразования:

• Шаг 1 — Определите разрядное значение цифр после запятой в числе.
• Шаг 2 — Используйте это, чтобы определить, каким будет знаменатель дроби.
• Шаг 3- Удалите десятичную точку. Перепишите в виде дроби и упростите.
• Этап 4 — Выразите в виде наименьшей эквивалентной дроби.

Давайте рассмотрим пример, чтобы понять эти шаги.

Пример: Преобразовать 0,5 в дробь.

Решение: Давайте применим шаги, которые мы узнали.

Шаг 1: Определите разрядное значение последней цифры.

0,5 <------------ 5 на десятом месте. (0,5 означает 0,50)

Шаг 2: Знаменатель будет равен 10

Шаг 3: Формат дроби: Числитель/знаменатель = 5/10

Шаг 4: Простейшая форма: 1/2

Таким образом, 0,5=5/10 =1/2.

Просмотрите приведенные ниже разделы, чтобы найти дополнительные примеры преобразования дробей в десятичные. Есть три отдельных случая, с которыми вы можете столкнуться при преобразовании десятичной дроби в дробную, и они перечислены ниже:

• Преобразование повторяющихся десятичных чисел в дроби
• Преобразование десятичных дробей в дроби смешанных чисел
• Преобразование отрицательного десятичного числа в дробь

Давайте подробно разберем каждый случай.

Преобразование повторяющихся десятичных чисел в дроби

Повторяющиеся десятичные числа — это те, которые не заканчиваются после конечного числа десятичных знаков, а некоторые определенные цифры или одна цифра после запятой продолжают повторяться в числе. Чтобы преобразовать любое повторяющееся десятичное число в дробь, необходимо применить определенный метод. Давайте рассмотрим пример, чтобы понять это.

Преобразовать 0,77777… в дробь.

Пусть x = повторяющееся число, т.е.

0,77777….

n= количество повторяющихся цифр, т.е. 7

Умножьте повторяющееся десятичное число на 10, т.е. подразумевает,

10x — x=7
9х=7
∴ x= 7/9

Преобразование десятичных дробей в дроби смешанных чисел

Десятичные дроби со значениями больше 1 можно записать в виде смешанных дробей. Посмотрите на шаги по преобразованию таких десятичных чисел в форму смешанной дроби:

• Шаг 1 — Рассматривать целую часть числа и десятичную часть в заданном десятичном числе отдельно.
• Шаг 2 — Запишите десятичную часть в дробной форме, игнорируя десятичную точку и разделив ее на степень 10, в которой столько же нулей, сколько и десятичных разрядов.
• Шаг 3 — Упростите полученную дробь.
• Шаг 4 — Присоедините целую часть исходного числа к дроби, полученной в шаге 3. Это и будет вашим ответом.

Рассмотрим пример.

Преобразовать 2,5 в смешанную дробь.

• Шаг 1: Рассмотрите 2 и 0,5 как отдельные сущности.
• Шаг 2: 0,5 можно записать как 5/10 (в виде дроби).
• Шаг 3: 5/10 = 1/2 (в упрощенном виде).
• Шаг 4: 2+1/2= \(2\dfrac{1}{2}\)

∴ 2.5 можно записать как дробь \(2\dfrac{1}{2}\).

Преобразование отрицательного десятичного числа в дробь

Чтобы преобразовать любое отрицательное десятичное число в дробь, выполните следующие шаги:

• Шаг 1 : Удалите знак минус из десятичного числа.
• Шаг 2 : Выполните преобразование положительного значения.
• Шаг 3 : Примените знак минус к дробному ответу.

Например, преобразуйте -3,2 в дробь.

• Шаг 1: Удалите знак минус. Считай это 3.2
• Шаг 2: После дроби стоит одна цифра, поэтому умножьте и разделите 3,2 на 10.
• Шаг 3: Преобразуйте 32/10 в наименьшую форму и примените знак минус к ответу дроби.

Таким образом, ответ -16/5.

Таблица преобразования десятичных чисел в дроби

В приведенной ниже таблице преобразования десятичных дробей в дроби показаны некоторые часто используемые дроби и их десятичные эквиваленты.

Десятичный	Дробь Эквивалент	Дробь в простейшей форме
0,1	1/10	1/10
0,2	2/10	1/5
0,3	3/10	3/10
0,4	4/10	2/5
0,5	5/10	1/2
0,6	6/10	3/5
0,75	75/100	3/4
0,125	125/1000	1/8
0,625	625/1000	5/8
1,25	125/100=\(1\dfrac{25}{100}\)	\(1\dfrac{3}{4}\)=7/4

Это табличный способ преобразования десятичной дроби в эквивалентную ей дробь. Теперь посмотрите на приведенную ниже диаграмму и поймите ее визуально.

Преобразование десятичной дроби в дробь: дюймы

Десятичные числа и дроби используются для представления значений в дюймах. Чтобы преобразовать данное измерение в дюймах из десятичных дробей в дроби, мы должны сосредоточиться на дробной части десятичного числа. Например, если нам нужно преобразовать 6,25 дюйма в дробный эквивалент, у него будет 6 в целой части числа и 0,25 в дробной части. 0,25 имеет две цифры после запятой, поэтому его можно записать как 25/100 в виде дроби, которую можно уменьшить до 1/4. Следовательно, мы получаем 6,25 = 6 1/4 дюйма. Вот как мы переводим дюймы из десятичной дроби в дробную.

Десятичные дюймы	Дюймовая доля
36.000	36 дюймов
36.125	36 1/8″
36.250	36 1/4″
36. 375	36 3/8″
36.500	36 1/2 дюйма
36.625	36 5/8″
36.750	36 3/4″

Процесс преобразования десятичной дроби в дюймы

Дробное значение дюйма, такое как 36,125 дюйма, включает 3 фута и дополнительные 0,125 дюйма. После запятой идут три цифры. Следовательно, умножьте и разделите 0,125 на 1000. Для 0,125 оптимальным вариантом будет 1/8 дюйма. Таким образом, высота будет \( 3\dfrac{1}{8} \)» дюймов.

Запомните:

Процедура преобразования десятичной дроби в дробную:

1. Определите разрядное значение последней цифры в числе.
2. Используйте это, чтобы определить, каким будет знаменатель дроби.
3. Удалить десятичную точку. Перепишите в виде дроби и упростите.
4. Выразите в наименьшей эквивалентной дроби.

☛Статьи по теме

Посмотрите еще несколько интересных статей, связанных с преобразованием десятичной дроби в дробную.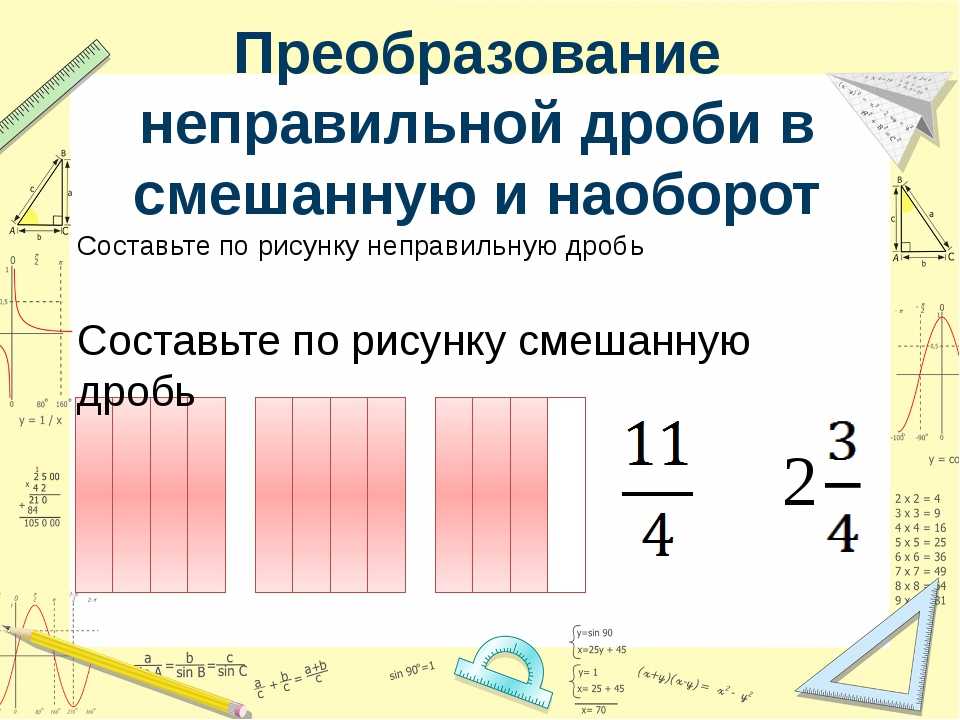

• От дроби до десятичной дроби
• Таблица десятичных дробей
• Калькулятор десятичной дроби

Часто задаваемые вопросы о преобразовании десятичных чисел в дроби

Что такое преобразование десятичной дроби в дробную?

Преобразование десятичных чисел в дробные представляет собой процедуру записи десятичных значений в виде дробных значений и наоборот. Чтобы преобразовать число из десятичной формы в дробную, мы делим число на степень 10 так, чтобы количество нулей в нем было равно количеству знаков после запятой в данном числе, и упрощаем дробь. Например, десятичная форма = 7,5 = 75/10 = 15/2 (дробная форма 7,5).

Как преобразовать десятичную дробь в дробную?

Чтобы преобразовать десятичную дробь в дробь, выполните три основных шага, указанных ниже:

• Перепишите число, игнорируя десятичную точку.
• Разделите число на разрядность последней цифры дробной части числа.
• Упростите дробь.

Как преобразовать дроби в десятичные?

Чтобы преобразовать любую дробь в десятичную форму, достаточно разделить ее числитель на знаменатель.

В чем разница между дробью и десятичной дробью?

Основное различие между дробью и десятичной дробью заключается в том, что дробь представляет собой отношение между двумя, в то время как десятичная дробь может использоваться для записи бесконечных значений и для большей точности.

Как преобразовать смешанную дробь в десятичную?

Чтобы преобразовать смешанную дробь в десятичную, нам сначала нужно преобразовать ее в неправильную дробь. Затем мы можем разделить числитель на знаменатель, чтобы преобразовать его в десятичную.

Какая польза от десятичной дроби?

Когда мы представляем десятичное значение в форме дроби (p/q), мы используем диаграмму десятичной дроби для простых и быстрых вычислений. Это также помогает в обратном преобразовании, которое также преобразует дробь в десятичную.

☛ Проверьте сейчас, чтобы больше попрактиковаться:

• Калькулятор десятичной дроби
• Калькулятор дроби в десятичную дробь
• Преобразование десятичных чисел в рабочие листы

Как записать десятичное значение 0,25 в виде дроби?

Давайте посмотрим, как преобразовать 0,25 в дробь пошагово:

• Шаг 1: Подсчитайте числа после запятой.
• Шаг 2: после запятой две цифры. Следовательно, умножьте и разделите 0,25 на 100.
• Шаг 3: Упростите 25/100 до самой низкой формы, то есть 1/4.

Таким образом, 1/4 является дробной формой числа 0,25.

Что такое повторяющиеся и неповторяющиеся десятичные дроби?

Повторяющиеся десятичные дроби — это те, в которых одна или несколько цифр повторяются снова и снова, например, 1/3=0,333333….., а неповторяющиеся десятичные дроби — это те, которые заканчиваются после определенного количества цифр, например, 1/2=0,5.

Как представляются десятичные числа и дроби?

Дроби записывают в виде p/q, где q≠0, а в десятичных дробях целая часть числа и дробная часть связаны через запятую, например, 0,5.

Преобразование дробей в проценты

Мы открыты — звоните сейчас!

Позвоните сейчас, чтобы записаться на обучение

(888) 736-0920

HotmathMath Домашнее задание. Делай быстрее, учись лучше.

Помните, что процент — это всего лишь особый способ выражения дроби в виде числа из .

Чтобы перевести дробь в проценты, сначала разделите числитель на знаменатель. Затем умножьте десятичную дробь на .

То есть дробь возможно конвертируется в десятичную путем деления к . Его можно преобразовать в проценты, умножив десятичную дробь на .

Итак, дробь эквивалентно .

Пример 1:

Писать как процент.

С больше, чем , чтобы разделить, мы должны добавить десятичную точку и несколько нулей после . Мы можем не знать, сколько нулей добавить, но это не имеет значения. Если мы добавим слишком много, мы можем стереть лишнее; если мы не добавим достаточно, мы можем добавить больше.

Так,

Следовательно, дробь эквивалентно .

Посмотрите на изображение ниже, оно показывает, что дробь такой же, как снаружи , то есть, .

Пример 2:

Писать как процент.

Разделять к .

Так,

Следовательно, дробь эквивалентно .

Пример 3:

Писать как процент.

Разделять к .

Так,

Следовательно, дробь эквивалентно .

Предметы рядом со мной

• Подготовка к сертификационному тесту EMT
• Подготовка к экзамену WPPSI
• Подготовка к экзамену WEST-B
• Предметный тест GRE по курсам и классам по химии
• Серия 79Репетиторы
• Экзамен P — подготовка к вероятностному тесту
• Подготовка к экзамену в штате Миссури
• Курсы и классы CompTIA
• Репетиторы по английскому языку
• Репетиторы по форматированию APA
• Подготовка к тесту CAIA — Совет по клинической патологии Американского общества сертификации
• ASCP 9004 Сертификационное обучение
• Репетиторы по God Of War
• Курсы и классы OAT
• Репетиторы по орнитологии
• Репетиторы по технологиям и кодированию
• Экзамен CDR — повторная сертификация сердечно-сосудистых заболеваний Подготовка к экзамену
• Geometry Tutors
• CLEP Introductory Business Law Courses & Classes
• IB Social and Cultural Anthropology SL Tutors

Popular Cities

• Albuquerque Tutoring
• Austin Tutoring
• Orlando Tutoring
• Phoenix Tutoring
• Madison Tutoring
• Репетиторство в Сакраменто
• Репетиторство в Чикаго
• Репетиторство в Сиэтле
• Репетиторство в Дейтоне
• Репетиторство в Майами

Популярные субъекты

• SSAT-репетиторы в Филадельфии
• Руководители чтения в Денвере
• Учащивания в районе Сан-Франциско.

  No related posts.