| Главная Другое |
страница 1 Пусть дана квадратная матрица А порядка n. Если возможно из каких-либо n собственных векторов матрицы А, принадлежащих собственно числам , как из столбцов построить квадратную невырожденную матрицу S порядка n, то будет выполняться соотношение S-1АS=Λ, где Λ= – диагональная матрица с собственными значениями матрицы А по диагонали. Из соотношения S-1АS=Λ получается соотношение А=SΛS-1 – каноническое разложение матрицы А. Если матрицу S, удовлетворяющую соотношению S 1АS=Λ, построить нельзя, то матрица А не приводится к диагональному виду, и, следовательно, не обладает каноническим разложением. При конструировании матрицы S для соотношений S 1АS=Λ и А=SΛS-1 нужно найти все собственные значения матрицы А и при каждом собственном значении λi построить фундаментальную систему решений (ФСР) однородной системы уравнений (А– λiЕ)Х=0. Для построения ФСР находят общее решение данной однородной системы уравнений: берут любой, отличный от нуля, определитель порядка, равного числу свободных неизвестных в системе; элементы i—й строки (столбца) этого определителя принимают соответственно за значения свободных неизвестных и находят из общего решения значения остальных (главных) неизвестных. Из этого правила вытекает, что построение ФСР однородных системы линейных уравнений неоднозначно. Поэтому будет неоднозначным и построение матрицы S для соотношений S-1АS=Λ и А=SΛS-1. Решение. Характеристический многочлен преобразования имеет вид Так как , то собственные значения таковы: . Составим систему уравнений для нахождения собственных векторов, соответствующих корням : Найдем собственные векторы для : Если , – первое фундаментальное решение и – есть собственный вектор для . Если , – второе фундаментальное решение и – есть собственный вектор для . Легко показать, что векторов недостаточно для конструирования квадратной невырожденной матрицы 3-го порядка. Поэтому матрица не приводится к диагональному виду, вследствие чего не имеет канонического разложения. Пример 2. Выяснить возможность приведения действительной матрицы А к диагональному виду. Решение. Характеристический многочлен имеет вид =(прибавим (1)-й столбец ко (2)-му столбцу)==(умножим (2)-ю строку на (-1) и прибавим к (1)-й строке)==(2–λ)2(1–λ). Корнями характеристического многочлена матрицы А являются числа , λ3=1. Все они действительные и поэтому являются собственными значениями матрицы А. Составим систему уравнений для нахождения собственных векторов, соответствующих корням : Эта система имеет общее решение Х=, в котором два свободных неизвестных. Поэтому возьмём, например, определитель . Полагая в общем решении сначала , , найдём . Затем, положим , , найдём , которые составляют ФСР рассматриваемой однородной системы уравнений: Х1=, Х2=. Составим систему уравнений для нахождения собственных векторов, соответствующих корням : Эта система имеет общее решение Х3=, в котором одно свободное неизвестное. Поэтому ФСР состоит из одного решения, например, Х3=. Из решений Х1, Х2 и Х3, как из столбцов, составляется невырожденная квадратная матрица Поэтому матрица А приводится к диагональному виду S 1АS=Λ = и имеет каноническое разложение А=SΛS-1=. Смотрите также: Приведение матрицы к диагональному виду. Каноническое разложение матрицы 38.46kb. 1 стр. Lu-разложение матрицы 25.9kb. 1 стр. Вопросы к экзамену по курсу «Алгебра и геометрия» 19.74kb. 1 стр. Вопросы к экзамену по оптимизации 12.23kb. 1 стр. Матрицы и определители Числовые матрицы и действия над ними 184.57kb. 1 стр. Мультипликативный метод главных компонент (ммгк) и его применение к сжатию изображений 37.47kb. 1 стр. Решение производим в matlab. Зададим матрицу S=[l 3 1 0]. Функция expm(S) возвращает значение экспоненты от матрицы: a = expm(S). Таким образом 21. 1 стр. Ангелайт Матрицы Жизни. Как достичь желаемого с помощью Матриц Жизни 2527.52kb. 8 стр. Оценка ковариационной матрицы для случая временных рядов различной частотности и приложения для моделей финансовых рынков Cпециальность 08. 00. 13 «Математические и инструментальные методы экономики» 365.89kb. 3 стр. Оптимизация распределения работ и загруженности службы управления персоналом на основе матрицы разу 1843.06kb. 13 стр. Антаков М. А. (Миэт) 1019.49kb. 21 стр. Функции от матриц и операторов 101.98kb. 1 стр. |
Как найти ранг матрицы? расширенной, разными методами
Главная » Математика
Математика
Автор Violetta На чтение 4 мин. Просмотров 644 Опубликовано
Просмотров 644 Опубликовано
Содержание
- Необходимые понятия
- Способы для поиска ранга
- Метод единиц и нулей
- Сведение матрицы к ступенчатому виду
- Метод окаймляющих миноров
- Онлайн-калькуляторы для поиска ранга матрицы
Необходимые понятия
Элементарные преобразования – это преобразования, после которых полученная матрица является эквивалентной для исходной.
Элементарные преобразования означают следующие действия:
- Умножить строку или столбец на число не равное 0;
- Поменять местами любые 2 строки или 2 столбца;
- Прибавить к строке другую строку (или к столбцу другой столбец) соответственно, помноженных на некоторое ненулевое число.
Матрица является ступенчатой, если она содержит хотя бы одну нулевую строку. Кроме этого если 1-й элемент некоторой строки не равный нулю расположен в i-м столбце, то этот элемент следующей строки должен находится в столбце с номером большим за i.
Минор k-го порядка – это определитель матрицы размера k на k, состоящей из k строк и такого же числа столбцов исходной матрицы. Порядок в этих строках и столбцах при этом остаётся прежним.
Способы для поиска ранга
Метод единиц и нулей
После применения элементарных преобразований, каждая матрица может быть приведена к такому виду, при котором все её столбцы будут состоять строго из нулей или иметь в своём составе максимум одну единицу. Посчитав количество единиц, мы сможем определить ранг.
Алгоритм, реализующий данный метод:
- Выполняем элементарные преобразования до тех пор, пока матрица не будет состоять только из нулей и единиц
- Считаем количество единиц
- Количество единиц равно искомому рангу
Пример поиска ранга, используя метод нулей и единиц:
- Первоначально дана матрица такого вида:
- 3-й столбец разделим на 2. 1-ую строку умножим на -2 и сложим с 4-й.
- Умножим 2-й столбец на -2 и сложим его с 4-м столбцом. После этого умножим 2-й столбец на -4 и сложим его с 1-м. Далее прибавим 2-й столбец к 5-му.
- 3-ю строку умножим на -2. Прибавим её ко 2-ой.
- Сложим 5-й столбец с 1-м.

- 3-й столбец умножим на 3 и сложим с 1-м.
- Умножим 3-й столбец на -1 и прибавим к нему 2-й и 4-й.
- Умножим 4-й столбец на -3 и сложим с 5-м. Наконец умножим 4-й столбец на -1. Итоговая матрица принимает следующий вид:
Количество единиц составляет 3, следовательно ранг имеет такое же значение.
Сведение матрицы к ступенчатому виду
Для данного способа также, как и для предыдущего, сперва нужно привести матрицу к определённому виду. Сведение её к ступенчатой позволяет найти ранг матрицы методом элементарных преобразований.
Алгоритм для данного метода:
- Выполняем элементарные преобразования, пока матрица не станет ступенчатой
- Считаем количество строк
- Количество строк равно искомому рангу.
Метод окаймляющих миноров
Чтобы найти ранг матрицы методом окаймляющих миноров нужно рассмотреть большое количество миноров.
Алгоритм, реализующий данный метод:
- Находим наименьшее число из величины матрицы по горизонтали и вертикали.
 Оно будет максимальным возможным значением ранга.
Оно будет максимальным возможным значением ранга. - Далее начинаем поиск миноров от самых меньших.
- Если минор имеет значение 0, то рассматриваем другие миноры этого порядка. Если все они имеют значение 0, то ранг равняется предыдущему порядку.
- Если существует хотя бы один минор не равный 0, то увеличиваем порядок на 1 и рассматриваем окаймляющие миноры. Возвращаемся на 3-й пункт.
Онлайн-калькуляторы для поиска ранга матрицы
Иногда у пользователя нет времени, чтобы самостоятельно изучить методы для поиска ранга. Из-за этого возникает вопрос: «Как найти ранг матрицы для чайников?».
В сети «Интернет» достаточно калькуляторов, которые помогают найти ранг матрицы онлайн с подробным решением. Однако почти все они производят поиск ранга, применяя при этом элементарные преобразования. Найти ранг матрицы методом окаймляющих миноров онлайн чаще всего не предоставляется возможным, так как этот способ не очень удобен и требует большого количества вычисления определителей. *f(x)=\lambda f(x)=0 \Rightarrow f(Ax)=0 \Rightarrow Ax \in \Ker f~\blacksquare$
*f(x)=\lambda f(x)=0 \Rightarrow f(Ax)=0 \Rightarrow Ax \in \Ker f~\blacksquare$
##Теорема Гамильтона-Кэли
Теорема (о приведении матрицы к треугольному виду). Матрицу линейного оператора всегда можно привести к треугольному виду.
$\begin{pmatrix} \lambda_1 & &\huge * \\ & \ddots & \\ \huge 0& & \lambda_n \\ \end{pmatrix}$
$\blacktriangle$ По индукции.
Пусть $A:V \rightarrow V$
По теореме об инвариантной гиперплоскости $V$ содержит инвариантное подпространство $U \subset V,~\codim U=1~(\codim U = \dim V — \dim U)$.
В $U$ существует базис $\{ e_i \}$, такой что $Ae_i=\lambda_i e_i+v_i,~v_i \in \langle e_1,…e_{i-1} \rangle$
Пусть вектор $e_n \notin V$, тогда $V=\langle e_n, U\rangle$.
Пусть $Ae_n=\lambda_n e_n+u,~u \in U$. Тогда в базисе $\langle e_1,..,e_n\rangle$ матрица оператора имеет вид:
$A= \begin{pmatrix} \lambda_1 & &\huge * \\ & \ddots & \\ \huge 0& & \lambda_n \\ \end{pmatrix} ~\blacksquare$
Теорема (Гамильтона-Кэли). n (A-\lambda_i E)V=(A-\lambda_1 E)…(A-\lambda_n E)V_0 \subseteq (A-\lambda_1 E)…(A-\lambda_{n-1} E)V_1 \subseteq … \subseteq (A-\lambda_1 E)V_{n-1}=0$
n (A-\lambda_i E)V=(A-\lambda_1 E)…(A-\lambda_n E)V_0 \subseteq (A-\lambda_1 E)…(A-\lambda_{n-1} E)V_1 \subseteq … \subseteq (A-\lambda_1 E)V_{n-1}=0$
$(A-\lambda_i E)\langle e_1,..,e_i\rangle \subseteq \langle e_1,..,e_{i-1}\rangle$
$Ae_i=\lambda_ie_i+v,~v \in \langle e_1,..,e_{i-1}\rangle$
$(A-\lambda_i E)\langle e_1,..,e_{i-1}\rangle \subseteq \langle e_1,..,e_{i-1}\rangle$
$\chi_A(A)V=0 \Rightarrow \chi_A(A)=O ~\blacksquare$
Следствие. Минимальный многочлен $\mu_A(t)$ оператора $A$ является делителем характеристического многочлена $\chi_A(t)$, и $\mu_A(t)$ делится на все $t-\lambda,~\lambda \in \Spec A$.
$\blacktriangle~ \mu_A(A)=O$ (по определению) и $\chi_A(A)=O$ (по теореме Гамильтона-Кэли) $\Rightarrow \chi_A(t) ~\vdots~ \mu_A(t)$ (т.к. любой аннулирующий многочлен оператора делится без остатка на минимальный многочлен).
Возьмем собственное значение $\lambda \in \mathbb{C}$ оператора $A$
$Av=\lambda v \Rightarrow \mu_A(A)v=\mu_A(\lambda)v=0 \Rightarrow \mu_A(\lambda)=0 \Rightarrow \mu_A(t)$ делится на $t-\lambda$ (по теореме Безу). $\blacksquare$
$\blacksquare$
Вычислить определитель матрицы системы методом гаусса онлайн. Вычисление определителя
Здесь вы сможете бесплатно решить систему линейных уравнений методом Гаусса онлайн больших размеров в комплексных числах с очень подробным решением. Наш калькулятор умеет решать онлайн как обычную определенную, так и неопределенную систему линейных уравнений методом Гаусса, которая имеет бесконечное множество решений. В этом случае в ответе вы получите зависимость одних переменных через другие, свободные. Также можно проверить систему уравнений на совместность онлайн, используя решение методом Гаусса.
Размер матрицы: 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 X 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101О методе
При решении системы линейных уравнений онлайн методом Гаусса выполняются следующие шаги.
- Записываем расширенную матрицу.
- Фактически решение разделяют на прямой и обратный ход метода Гаусса. Прямым ходом метода Гаусса называется приведение матрицы к ступенчатому виду. Обратным ходом метода Гаусса называется приведение матрицы к специальному ступенчатому виду. Но на практике удобнее сразу занулять то, что находится и сверху и снизу рассматриваемого элемента. Наш калькулятор использует именно этот подход.
- Важно отметить, что при решении методом Гаусса, наличие в матрице хотя бы одной нулевой строки с НЕнулевой правой частью (столбец свободных членов) говорит о несовместности системы. Решение линейной системы в таком случае не существует.
Чтобы лучше всего понять принцип работы алгоритма Гаусса онлайн введите любой пример, выберите «очень подробное решение» и посмотрите его решение онлайн.
В ходе решения задач по высшей математике очень часто возникает необходимость вычислить определитель матрицы . Определитель матрицы фигурирует в линейной алгебре, аналитической геометрии, математическом анализе и других разделах высшей математики. Таким образом, без навыка решения определителей просто не обойтись. Также для самопроверки Вы можете бесплатно скачать калькулятор определителей , он сам по себе не научит решать определители, но очень удобен, поскольку всегда выгодно заранее знать правильный ответ!
Таким образом, без навыка решения определителей просто не обойтись. Также для самопроверки Вы можете бесплатно скачать калькулятор определителей , он сам по себе не научит решать определители, но очень удобен, поскольку всегда выгодно заранее знать правильный ответ!
Я не буду давать строгое математическое определение определителя, и, вообще, буду стараться минимизировать математическую терминологию, большинству читателей легче от этого не станет. Задача данной статьи – научить Вас решать определители второго, третьего и четвертого порядка. Весь материал изложен в простой и доступной форме, и даже полный (пустой) чайник в высшей математике после внимательного изучения материала сможет правильно решать определители.
На практике чаще всего можно встретить определитель второго порядка, например: , и определитель третьего порядка, например: .
Определитель четвертого порядка тоже не антиквариат, и к нему мы подойдём в конце урока.
Надеюсь, всем понятно следующее: Числа внутри определителя живут сами по себе, и ни о каком вычитании речи не идет! Менять местами числа нельзя!
(Как частность, можно осуществлять парные перестановки строк или столбцов определителя со сменой его знака, но часто в этом нет никакой необходимости – см. следующий урок Свойства определителя и понижение его порядка)
следующий урок Свойства определителя и понижение его порядка)
Таким образом, если дан какой-либо определитель, то ничего внутри него не трогаем!
Обозначения : Если дана матрица , то ее определитель обозначают . Также очень часто определитель обозначают латинской буквой или греческой .
1) Что значит решить (найти, раскрыть) определитель? Вычислить определитель – это значит НАЙТИ ЧИСЛО. Знаки вопроса в вышерассмотренных примерах – это совершенно обыкновенные числа.
2) Теперь осталось разобраться в том, КАК найти это число? Для этого нужно применить определенные правила, формулы и алгоритмы, о чём сейчас и пойдет речь.
Начнем с определителя «два» на «два» :
ЭТО НУЖНО ЗАПОМНИТЬ, по крайне мере на время изучения высшей математики в ВУЗе.
Сразу рассмотрим пример:
Готово. Самое главное, НЕ ЗАПУТАТЬСЯ В ЗНАКАХ.
Определитель матрицы «три на три» можно раскрыть 8 способами, 2 из них простые и 6 — нормальные.
Начнем с двух простых способов
Аналогично определителю «два на два», определитель «три на три» можно раскрыть с помощью формулы:
Формула длинная и допустить ошибку по невнимательности проще простого. Как избежать досадных промахов? Для этого придуман второй способ вычисления определителя, который фактически совпадает с первым. Называется он способом Саррюса или способом «параллельных полосок».
Суть состоит в том, что справа от определителя приписывают первый и второй столбец и аккуратно карандашом проводят линии:
Множители, находящиеся на «красных» диагоналях входят в формулу со знаком «плюс».
Множители, находящиеся на «синих» диагоналях входят в формулу со знаком минус:
Пример:
Сравните два решения. Нетрудно заметить, что это ОДНО И ТО ЖЕ, просто во втором случае немного переставлены множители формулы, и, самое главное, вероятность допустить ошибку значительно меньше.
Теперь рассмотрим шесть нормальных способов для вычисления определителя
Почему нормальных? Потому что в подавляющем большинстве случаев определители требуется раскрывать именно так.
Как Вы заметили, у определителя «три на три» три столбца и три строки.
Решить определитель можно, раскрыв его по любой строке или по любому столбцу .
Таким образом, получается 6 способов, при этом во всех случаях используется однотипный алгоритм.
Определитель матрицы равен сумме произведений элементов строки (столбца) на соответствующие алгебраические дополнения. Страшно? Все намного проще, будем использовать ненаучный, но понятный подход, доступный даже для человека, далекого от математики.
В следующем примере будем раскрывать определитель по первой строке .
Для этого нам понадобится матрица знаков: . Легко заметить, что знаки расположены в шахматном порядке.
Внимание! Матрица знаков – это мое собственное изобретение. Данное понятие не научное, его не нужно использовать в чистовом оформлении заданий, оно лишь помогает Вам понять алгоритм вычисления определителя.
Сначала я приведу полное решение. Снова берем наш подопытный определитель и проводим вычисления:
И главный вопрос: КАК из определителя «три на три» получить вот это вот:
?
Итак, определитель «три на три» сводится к решению трёх маленьких определителей, или как их еще называют, МИНОРОВ . Термин рекомендую запомнить, тем более, он запоминающийся: минор – маленький.
Термин рекомендую запомнить, тем более, он запоминающийся: минор – маленький.
Коль скоро выбран способ разложения определителя по первой строке , очевидно, что всё вращается вокруг неё:
Элементы обычно рассматривают слева направо (или сверху вниз, если был бы выбран столбец)
Поехали, сначала разбираемся с первым элементом строки, то есть с единицей:
1) Из матрицы знаков выписываем соответствующий знак:
2) Затем записываем сам элемент:
3) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит первый элемент:
Оставшиеся четыре числа и образуют определитель «два на два», который называется МИНОРОМ данного элемента (единицы).
Переходим ко второму элементу строки.
4) Из матрицы знаков выписываем соответствующий знак:
5) Затем записываем второй элемент:
6) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит второй элемент:
Ну и третий элемент первой строки. Никакой оригинальности:
7) Из матрицы знаков выписываем соответствующий знак:
8) Записываем третий элемент:
9) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит третий элемент:
Оставшиеся четыре числа записываем в маленький определитель.
Остальные действия не представляют трудностей, поскольку определители «два на два» мы считать уже умеем. НЕ ПУТАЕМСЯ В ЗНАКАХ!
Аналогично определитель можно разложить по любой строке или по любому столбцу. Естественно, во всех шести случаях ответ получается одинаковым.
Определитель «четыре на четыре» можно вычислить, используя этот же алгоритм.
При этом матрица знаков у нас увеличится:
В следующем примере я раскрыл определитель по четвертому столбцу :
А как это получилось, попробуйте разобраться самостоятельно. Дополнительная информация будет позже. Если кто захочет прорешать определитель до конца, правильный ответ: 18. Для тренировки лучше раскрыть определитель по какому-нибудь другому столбцу или другой строке.
Потренироваться, раскрыть, провести расчёты – это очень хорошо и полезно. Но сколько времени вы потратите на большой определитель? Нельзя ли как-нибудь быстрее и надёжнее? Предлагаю ознакомиться с эффективными методами вычисления определителей на втором уроке – Свойства определителя. Понижение порядка определителя .
Понижение порядка определителя .
БУДЬТЕ ВНИМАТЕЛЬНЫ!
Содержание
Введение…………………………………………………………………………………………….. 2
1. Постановка задачи………………………………………………………………………….. 3
2. Математические и алгоритмические основы решения задачи……………… 5
2.1 Определитель матрицы………………………………………………………………….. 5
2.2 Метод Гаусса для решения систем линейных уравнений…………………… 6
2.3 Метод Гаусса для вычисления определителя……………………………………. 8
3. Функциональные модели и блок-схемы решения задачи…………………….. 9
4. Программная реализация решения задачи………………………………………. 11
5. Пример выполнения программы…………………………………………………….. 16
Заключение……. ………………………………………………………………………………… 18
………………………………………………………………………………… 18
Список использованных источников и литературы……………………………… 19
Введение
Многие проблемы, возникающие в экономических исследованиях, планировании и управлении, будучи сформулированными математически, представляют собой задачи, в которых необходимо решить систему алгебраических уравнений.
Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной.
При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности. Этот метод (который также называют методом последовательного исключения неизвестных) известен в различных вариантах уже более 2000 лет.
Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности. Этот метод (который также называют методом последовательного исключения неизвестных) известен в различных вариантах уже более 2000 лет.
Помимо аналитического решения СЛАУ, метод Гаусса также применяется для нахождения матрицы, обратной к данной, определения ранга матрицы и нахождения определителя.
Целью данной курсовой работы является реализация вычисления определителя методом исключения Гаусса.
1. Постановка задачи
Вычисление определителя матрицы заключается в выполнении над матрицей алгоритма Гаусса для решения систем линейных алгебраических уравнений. В результате выполнения алгоритма получаем диагональную матрицу, её определитель равен произведению элементов, стоящих на диагонали.
. ~. . .
Вычислить определитель матрицы методом A исключения Гаусса.
.
Приведем матрицу к диагональному виду методом Гаусса.
~.
Тогда определитель матрицы равен произведению ее элементов, стоящих на диагонали:
.
Знак определяется количеством обменов строк, следовательно определитель матрицы
.
2. Математические и алгоритмические основы решения задачи
2.1 Определитель матрицы
Введем определение определителя квадратной матрицы любого порядка. Это определение будет рекуррентным, то есть чтобы установить, что такое определитель матрицы порядка n, нужно уже знать, что такое определитель матрицы порядка n-1. Отметим также, что определитель существует только у квадратных матриц.
Определитель квадратной матрицы A будем обозначать
или det A.
Определение. Определителем квадратной матрицы
второго порядка называется число
.
Определителем
квадратной матрицы порядка n,
, называется число
— определитель матрицы порядка n-1, полученной из матрицы A вычеркиванием первой строки и столбца с номером k.
2.2 Метод Гаусса для решения систем линейных уравнений
Пусть дана квадратная матрица A размером NxN. Требуется вычислить её определитель.
Воспользуемся идеями метода Гаусса решения систем линейных уравнений.
Дана система:
a11 x1 + a12 x2 + … + a1n xn = b1
a21 x1 + a22 x2 + … + a2n xn = b2
an1 x1 + an2 x2 + … + ann xn = bn
Выполним следующий алгоритм.
На первом шаге найдём в первом столбце наибольший по модулю элемент, поставим уравнение с этим элементом на первую строчку (обменяв две соответствующие строки матрицы A и два соответствующих элемента вектора B), а затем будем отнимать это уравнение от всех остальных, чтобы в первом столбце все элементы (кроме первого) обратились в ноль. Например, при прибавлении ко второй строке будем домножать первую строку на -a21/a11, при добавлении к третьей — на -a31/a11, и т.д.
На втором шаге найдём во втором столбце, начиная со второго элемента, наибольший по модулю элемент, поставим уравнение с этим элементом на вторую строчку, и будем отнимать это уравнение от всех остальных (в том числе и от первого), чтобы во втором столбце все элементы (кроме второго) обратились в ноль. Понятно, что эта операция никак не изменит первый столбец — ведь от каждой строки мы будем отнимать вторую строку, домноженную на некоторый коэффициент, а во второй строке в первом столбце стоит ноль.
Понятно, что эта операция никак не изменит первый столбец — ведь от каждой строки мы будем отнимать вторую строку, домноженную на некоторый коэффициент, а во второй строке в первом столбце стоит ноль.
Т.е. на i-ом шаге найдём в i-ом столбце, начиная с i-го элемента, наибольший по модулю элемент, поставим уравнение с этим элементом на i-ю строчку, и будем отнимать это уравнение от всех остальных. Понятно, что это никак не повлияет на все предыдущие столбцы (с первого по (i-1)-ый).
В конце концов, мы приведём систему к так называемому диагональному виду:
Т.е. мы нашли решение системы.
Замечание 1. На каждой итерации найдётся хотя бы один ненулевой элемент, иначе система бы имела нулевой определитель, что противоречит условию.
Замечание 2. Требование, что на каждом шаге мы выбираем наибольший по модулю элемент, очень важно в смысле численной устойчивости метода. Если выбирать произвольный ненулевой элемент, то это может привести к гигантской погрешности, когда получившееся решение будет отличаться в разы от правильного.
2.3 Метод Гаусса для вычисления определителя
Будем выполнять те же самые действия, что и при решении системы линейных уравнений, исключив только деление текущей строки на a[i][i] (точнее, само деление можно выполнять, но подразумевая, что число выносится за знак определителя). Тогда все операции, которые мы будем производить с матрицей, не будут изменять величину определителя матрицы, за исключением, быть может, знака (мы только обмениваем местами две строки, что меняет знак на противоположный, или прибавляем одну строку к другой, что не меняет величину определителя).
Но матрица, к которой мы приходим после выполнения алгоритма Гаусса, является диагональной, и определитель её равен произведению элементов, стоящих на диагонали. Знак, как уже говорилось, будет определяться количеством обменов строк (если их нечётное, то знак определителя следует изменить на противоположный). Таким образом, мы можем с помощью алгоритма Гаусса вычислять определитель матрицы за O(N3).
Осталось только заметить, что если в какой-то момент мы не найдём в текущем столбце ненулевого элемента, то алгоритм следует остановить и вернуть 0.
3. Функциональные модели и блок-схемы решения задачи
Блок-схема решения задачи представлена на рисунке 1.
Рисунок 1 – Блок-схема решения задачи для функции DETERMINATE
4 Программная реализация решения задачи
;ФУНКЦИЯ, ВЫЧИСЛЯЮЩАЯ ОПРЕДЕЛИТЕЛЬ
(DEFUN DETERMINANT (MATRIX SIZE)
;ОБЪЯВЛЕНИЕ ПЕРЕМЕННЫХ
;ОПРЕДЕЛИТЕЛЬ
(DECLARE (SPECIAL DET))
;ВСПОМОГАТЕЛЬНЫЕ МАССИВЫ И ПЕРЕМЕННЫЕ
(DECLARE (SPECIAL PAR))
(DECLARE (SPECIAL R))
(DECLARE (SPECIAL T_))
(DECLARE (SPECIAL I))
(DECLARE (SPECIAL II))
;*********************
(SETQ R (MAKE-ARRAY SIZE:ELEMENT-TYPE «FLOAT:INITIAL-ELEMENT 0))
((>= J (- SIZE 1)))
;ИСКЛЮЧАЕМ ДЕЛЕНИЕ НА 0
(IF (= (AREF MATRIX J J) 0)
(SETQ II (+ J 1))
;ИЩЕМ СТРОКУ В КОТОРОЙ J-Й ЭЛЕМЕНТ НЕ 0
((OR (/= (AREF MATRIX II J) 0) (= II (- SIZE 1))))
(SETQ II (+ II 1))
;ЕСЛИ НЕТ ТАКОЙ СТРОКИ ОПРЕДЕЛИТЕЛЬ РАВЕН 0
(IF (AND (= (AREF MATRIX II J) 0) (= II (- SIZE 1))) (SETQ T_ 0))
Вычислим определитель методом Гаусса.
Суть метода состоит в следующем: определитель приводится к треугольному виду с помощью элементарных преобразований, и тогда он равен произведению элементов, стоящих на главной диагонали.
Идея метода состоит в следующем: пусть дан определитель третьего порядка
элементдолжен быть равен
,
для этого первую строку разделим на.
Получим определитель вида
(2)
Обнулим элементы, стоящие в первом
столбце, кроме первого. Для этого из
второй строки вычтем первую, умноженную
на
,
далее из третьей строки вычтем первую,
умноженную на.
Получим определитель вида
.
Обозначим его элементы буквой с, тогда
(3)
Теперь надо обнулить элемент
.
Элемент
должен быть равен
,
для этого вторую строку разделим на
.
Получим определитель вида
.
.
Обозначим его элементы буквой t, тогда
(4)
Вот мы привели определитель к треугольному
виду, теперь он равен
.
Разберем теперь это на конкретном примере.
Пример 4: Вычислить определительметодом Гаусса.
Решение: Поменяем местами первую и третью строки (при замене двух столбцов (строк) определитель меняет знак на противоположный).
Получили
Из второй строки вычтем первую, умноженную
на 2, далее из третьей строки вычтем
первую, умноженную на 3. Получили
Получили —
§2.Матрицы Виды матриц
Определение 7: Если в матрицеmстрок иnстолбцов, то она
называетсяразмерностью mnи пишут
.
Определение 8: Если
,
то матрица называется квадратной.
Определение 9: Матрица, состоящая лишь из одной строки (столбца) называется матрицей-строкой (столбцом).
Определение 10: Матрица, состоящая из нулей, называется нулевой матрицей.
Определение 11: Диагональной матрицей называется квадратная матрица, у которой все элементы, не принадлежащие главной диагонали равны нулю.
Определение 12: Единичной матрицей
называется диагональная матрица, у
которой все элементы, стоящие на главной
диагонали равны единице.
Определение 13: Треугольной называется квадратная матрица, у которой элементы, расположенные по одну сторону от главной диагонали равны нулю.
Действиянад матрицами.
Определение 14: Две матрицы считаются равными, если они имеют одинаковое число строк и столбцов и равные соответствующие элементы.
Пример 5:
Матрицы А и В равны, т.е.
Определение 15: Суммой (разностью)
матриц А и В называется такая матрица
С, у которой каждый элемент равен
.
Пример 6: Найти матрицу
,
если
Решение:
Cвойства сложения
А+В=В+А(переместительное)
2 0 А+О=А, где О-нулевая матрица
3 0 А+(В+С)=(А+В)+С (дистрибутивное)
4 0 А+(-А)=О, где – А противоположная матрица
(т.е. элементы имеют противоположные знаки)
Определение 16: Произведением матрицы
А на число
называется матрица, полученная из
данной умножением всех ее элементов на
число.
Пример 7:
Умножение матиц
Это действие распространяется на так
называемые согласованные матрицы.
Определение 17: Матрица А называетсясогласованной с матрицей В, если число столбцов у матрицы А равно числу строк у матрицы В.
Пример 8:
и
— согласованные
и
— несогласованные
и
несогласованные
Определение 18: Произведением двух матриц А и В называется такая матрица С, каждый элемент которой равен сумме произведений элементовiстроки матрицы А на соответствующие элементыj-го столбца матрицы В.
Если матрица А имеет размерность
,
а матрица В
,
то
.
Пример 9: Умножить матрицы
Решение системы линейных уравнений методом гаусса-жордана
Метод Гаусса-Жордана предназначен для решения систем линейных алгебраических уравнений (СЛАУ). Он является модификацией метода Гаусса . Если метод Гаусса осуществляется в два этапа (прямой ход и обратный) то метод Гаусса-Жордана позволяет решить систему в один этап. Подробности и непосредственная схема применения метода Гаусса-Жордана описаны в примерах.
Во всех примерах $A$ обозначает матрицу системы, $\widetilde{A}$ — расширенную матрицу системы. О матричной форме записи СЛАУ можно прочесть .
Пример №1
Решить СЛАУ $ \left\{ \begin{aligned} & 4x_1-7x_2+8x_3=-23;\\ & 2x_1-4x_2+5x_3=-13;\\ & -3x_1+11x_2+x_3=16. \end{aligned} \right.$ методом Гаусса-Жордана.
Давайте перейдём от последней полученной нами матрице к системе:
$$ \left\{ \begin{aligned} & 0\cdot x_1+1\cdot x_2+0\cdot x_3=1;\\ & 1\cdot x_1+0\cdot x_2+0\cdot x_3=-2;\\ & 0\cdot x_1+0\cdot x_2+1\cdot x_3=-1. \end{aligned} \right. $$
Упрощая полученную систему, имеем:
$$ \left\{ \begin{aligned} & x_2=1;\\ & x_1=-2;\\ & x_3=-1. \end{aligned} \right. $$
Полное решение без пояснений выглядит так:
Хоть этот способ выбора разрешающих элементов вполне допустим, но предпочтительнее выбирать в качестве разрешающих элементов диагональные элементы матрицы системы. Мы рассмотрим этот способ ниже.
Выбор разрешающих элементов на главной диагонали матрицы системы.
Так как этот способ решения полностью аналогичен предыдущему (за исключением выбора разрешающих элементов), то подробные пояснения пропустим. Принцип выбора разрешающих элементов прост: в первом столбце выбираем элемент первой строки, во втором столбце берём элемент второй строки, в третьем столбце — элемент третьей строки и так далее.
Первый шаг
В первом столбце выбираем элемент первой строки, т.е. в качестве разрешающего имеем элемент 4. Понимаю, что выбор числа 2 кажется более предпочтительным, так как это число всё-таки меньше, нежели 4. Для того, чтобы число 2 в первом столбце переместилось на первое место, поменяем местами первую и вторую строки:
$$ \left(\begin{array} {ccc|c} 4 & -7 & 8 & -23\\ 2 & -4& 5 & -13 \\ -3 & 11 & 1 & 16 \end{array} \right)\rightarrow \left(\begin{array} {ccc|c} 2 & -4& 5 & -13\\ 4 & -7 & 8 & -23 \\ -3 & 11 & 1 & 16 \end{array} \right) $$
Итак, разрешающий элемент представлен числом 2. Точно так же, как и ранее, разделим первую строку на 2, а затем обнулим элементы первого столбца:
Точно так же, как и ранее, разделим первую строку на 2, а затем обнулим элементы первого столбца:
$$ \left(\begin{array} {ccc|c} 2 & -4& 5 & -13\\ 4 & -7 & 8 & -23 \\ -3 & 11 & 1 & 16 \end{array} \right) \begin{array} {l} I:2 \\\phantom{0} \\ \phantom{0} \end{array} \rightarrow \left(\begin{array} {ccc|c} 1 & -2& 5/2 & -13/2 \\4 & -7 & 8 & -23\\ -3 & 11 & 1 & 16 \end{array} \right) \begin{array} {l} \phantom{0} \\ II-4\cdot I\\ III+3\cdot I \end{array} \rightarrow \left(\begin{array} {ccc|c} 1 & -2& 5/2 & -13/2\\0 & 1 & -2 & 3\\ 0 & 5 & 17/2 & -7/2 \end{array} \right). $$
Второй шаг
На втором шаге требуется обнулить элементы второго столбца. В качестве разрешающего элемента выбираем элемент второй строки, т.е. 1. Разрешающий элемент уже равен единице, поэтому никаких строк менять местами не будем. Кстати сказать, если бы мы захотели поменять местами строки, то первую строку трогать не стали бы, так как она уже была использована на первом шаге. А вот вторую и третью строки запросто можно менять местами. Однако, повторюсь, в данной ситуации менять местами строки не нужно, ибо разрешающий элемент уже оптимален — он равен единице.
А вот вторую и третью строки запросто можно менять местами. Однако, повторюсь, в данной ситуации менять местами строки не нужно, ибо разрешающий элемент уже оптимален — он равен единице.
$$ \left(\begin{array} {ccc|c} 1 & -2& 5/2 & -13/2\\0 & 1 & -2 & 3\\ 0 & 5 & 17/2 & -7/2 \end{array} \right) \begin{array} {l} I+2\cdot II \\ \phantom{0}\\ III-5\cdot II \end{array} \rightarrow \left(\begin{array} {ccc|c} 1 & 0 & -3/2 & -1/2 \\ 0 & 1 & -2 & 3\\ 0 & 0 & 37/2 & -37/2 \end{array} \right). $$
Второй шаг окончен. Переходим к третьему шагу.
Третий шаг
На третьем шаге требуется обнулить элементы третьего столбца. В качестве разрешающего элемента выбираем элемент третьей строки, т.е. 37/2. Разделим элементы третьей строки на 37/2 (чтобы разрешающий элемент стал равен 1), а затем обнулим соответствующие элементы третьего столбца:
$$
\left(\begin{array} {ccc|c} 1 & 0 & -3/2 & -1/2 \\ 0 & 1 & -2 & 3\\ 0 & 0 & 37/2 & -37/2 \end{array} \right)
\begin{array} {l} \phantom{0}\\ \phantom{0}\\ III:\frac{37}{2} \end{array} \rightarrow
\left(\begin{array} {ccc|c} 1 & 0 & -3/2 & -1/2 \\ 0 & 1 & -2 & 3\\ 0 & 0 & 1 & -1 \end{array} \right)
\begin{array} {l} I+2\cdot III\\II+3/2\cdot III\\ \phantom{0} \end{array} \rightarrow
\left(\begin{array} {ccc|c} 1 & 0 & 0 & -2 \\ 0 & 1 & 0 & 1\\ 0 & 0 & 1 & -1 \end{array} \right). $$
$$
Ответ получен: $x_1=-2$, $x_2=1$, $x_3=-1$. Полное решение без пояснений выглядит так:
Все остальные примеры на этой странице будут решены именно вторым способом: в качестве разрешающих будем выбирать диагональные элементы матрицы системы.
Ответ : $x_1=-2$, $x_2=1$, $x_3=-1$.
Пример №2
Решить СЛАУ $ \left\{ \begin{aligned} & 3x_1+x_2+2x_3+5x_4=-6;\\ & 3x_1+x_2+2x_4=-10;\\ & 6x_1+4x_2+11x_3+11x_4=-27;\\ & -3x_1-2x_2-2x_3-10x_4=1. \end{aligned} \right.$ методом Гаусса-Жордана.
Запишем расширенную матрицу данной системы : $\widetilde{A}=\left(\begin{array} {cccc|c} 3 & 1 & 2 & 5 & -6\\ 3 & 1& 0 & 2 & -10 \\ 6 & 4 & 11 & 11 & -27 \\ -3 & -2 & -2 & -10 & 1 \end{array} \right)$.
В качестве разрешающих элементов станем выбирать диагональные элементы матрицы системы: на первом шаге возьмём элемент первой строки, на втором шаге элемент второй строки и так далее.
Первый шаг
Нам нужно обнулить соответствующие элементы первого столбца. В качестве разрешающего элемента возьмём элемент первой строки, т.е. 3. Соответственно первую строку придётся разделить на 3, чтобы разрешающий элемент стал равен единице. А затем обнулить все элементы первого столбца, кроме разрешающего:
$$
\left(\begin{array}{cccc|c}
3 & 1 & 2 & 5 & -6\\
3 & 1 & 0 & 2 & -10\\
6 & 4 & 11 & 11 & -27\\
-3 & -2 & -2 & -10 & 1\end{array}\right)
\begin{array} {l} I:3\\ \phantom{0}\\\phantom{0}\\\phantom{0}\end{array} \rightarrow
\left(\begin{array}{cccc|c}
1 & 1/3 & 2/3 & 5/3 & -2\\
3 & 1 & 0 & 2 & -10\\
6 & 4 & 11 & 11 & -27\\
-3 & -2 & -2 & -10 & 1\end{array}\right)
\begin{array} {l} \phantom{0}\\ II-3\cdot I\\III-6\cdot I\\IV+3\cdot I\end{array} \rightarrow\\
\rightarrow\left(\begin{array}{cccc|c}
1 & 1/3 & 2/3 & 5/3 & -2\\
0 & 0 & -2 & -3 & -4\\
0 & 2 & 7 & 1 & -15\\
0 & -1 & 0 & -5 & -5\end{array}\right). $$
$$
Второй шаг
Переходим к обнулению соответствующих элементов второго столбца. В качестве разрешающего элемента мы уславливались взять элемент второй строки, но сделать этого мы не в силах, так как нужный элемент равен нулю. Вывод: будем менять местами строки. Первую строку трогать нельзя, так как она уже использовалась на первом шаге. Выбор небогат: или меняем местами вторую и третью строки, или же меняем местами четвёртую и вторую. Так как в четвёртой строке наличествует (-1), то пусть в «обмене» поучавствует именно четвёртая строка. Итак, меняем местами вторую и четвёртую строки:
$$ \left(\begin{array}{cccc|c} 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & 0 & -2 & -3 & -4\\ 0 & 2 & 7 & 1 & -15\\ 0 & -1 & 0 & -5 & -5\end{array}\right)\rightarrow \left(\begin{array}{cccc|c} 1 & 1/3 & 2/3 & 5/3 & -2\\ 0 & -1 & 0 & -5 & -5\\ 0 & 2 & 7 & 1 & -15\\ 0 & 0 & -2 & -3 & -4\end{array}\right) $$
Вот теперь всё в норме: разрешающий элемент равен (-1). Бывает, кстати, что смена мест строк невозможна, но это обговорим в следующем примере №3. А пока что делим вторую строку на (-1), а затем обнуляем элементы второго столбца. Обратите внимание, что во втором столбце элемент, расположенный в четвёртой строке, уже равен нулю, поэтому четвёртую строку трогать не будем.
Бывает, кстати, что смена мест строк невозможна, но это обговорим в следующем примере №3. А пока что делим вторую строку на (-1), а затем обнуляем элементы второго столбца. Обратите внимание, что во втором столбце элемент, расположенный в четвёртой строке, уже равен нулю, поэтому четвёртую строку трогать не будем.
$$
\left(\begin{array}{cccc|c}
1 & 1/3 & 2/3 & 5/3 & -2\\
0 & -1 & 0 & -5 & -5\\
0 & 2 & 7 & 1 & -15\\
0 & 0 & -2 & -3 & -4\end{array}\right)
\begin{array} {l} \phantom{0}\\II:(-1) \\\phantom{0}\\\phantom{0}\end{array} \rightarrow
\left(\begin{array}{cccc|c}
1 & 1/3 & 2/3 & 5/3 & -2\\
0 & 1 & 0 & 5 & 5\\
0 & 2 & 7 & 1 & -15\\
0 & 0 & -2 & -3 & -4\end{array}\right)
\begin{array} {l} I-1/3\cdot II\\ \phantom{0} \\III-2\cdot II\\\phantom{0}\end{array} \rightarrow\\
\rightarrow\left(\begin{array}{cccc|c}
1 & 0 & 2/3 & 0 & -11/3\\
0 & 1 & 0 & 5 & 5\\
0 & 0 & 7 & -9 & -25\\
0 & 0 & -2 & -3 & -4\end{array}\right). $$
$$
Третий шаг
Приступаем к обработке третьего столбца. В качестве разрешающего элемента мы условились брать диагональные элементы матрицы системы. Для третьего шага это означает выбор элемента, расположенного в третьей строке. Однако если мы просто возьмём элемент 7 в качестве разрешающего, то всю третью строку придётся делить на 7. Мне кажется, что разделить на (-2) попроще. Поэтому поменяем местами третью и четвёртую строки, и тогда разрешающим элементом станет (-2):
$$ \left(\begin{array}{cccc|c} 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 7 & -9 & -25\\ 0 & 0 & -2 & -3 & -4\end{array}\right) \rightarrow \left(\begin{array}{cccc|c} 1 & 0 & 2/3 & 0 & -11/3\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & -2 & -3 & -4\\ 0 & 0 & 7 & -9 & -25\end{array}\right) $$
Разрешающий элемент — (-2). Делим третью строку на (-2) и обнуляем соответствующие элементы третьего столбца:
$$
\left(\begin{array}{cccc|c}
1 & 0 & 2/3 & 0 & -11/3\\
0 & 1 & 0 & 5 & 5\\
0 & 0 & -2 & -3 & -4\\
0 & 0 & 7 & -9 & -25\end{array}\right)
\begin{array} {l} \phantom{0}\\ \phantom{0} \\III:(-2)\\\phantom{0}\end{array}\rightarrow
\left(\begin{array}{cccc|c}
1 & 0 & 2/3 & 0 & -11/3\\
0 & 1 & 0 & 5 & 5\\
0 & 0 & 1 & 3/2 & 2\\
0 & 0 & 7 & -9 & -25\end{array}\right)
\begin{array} {l} I-2/3\cdot III\\ \phantom{0} \\ \phantom{0}\\IV-7\cdot III\end{array}\rightarrow\\
\rightarrow\left(\begin{array}{cccc|c}
1 & 0 & 0 & -1 & -5\\
0 & 1 & 0 & 5 & 5\\
0 & 0 & 1 & 3/2 & 2\\
0 & 0 & 0 & -39/2 & -39\end{array}\right). $$
$$
Четвёртый шаг
Переходим к обнулению четвёртого столбца. Разрешающий элемент расположен в четвёртой строке и равен числу $-\frac{39}{2}$.
$$ \left(\begin{array}{cccc|c} 1 & 0 & 0 & -1 & -5\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 1 & 3/2 & 2\\ 0 & 0 & 0 & -39/2 & -39\end{array}\right) \begin{array} {l} \phantom{0}\\ \phantom{0} \\ \phantom{0}\\IV:\left(-\frac{39}{2}\right) \end{array}\rightarrow \left(\begin{array}{cccc|c} 1 & 0 & 0 & -1 & -5\\ 0 & 1 & 0 & 5 & 5\\ 0 & 0 & 1 & 3/2 & 2\\ 0 & 0 & 0 & 1 & 2\end{array}\right) \begin{array} {l} I+IV\\ II-5\cdot IV \\ III-3/2\cdot IV \\ \phantom{0} \end{array}\rightarrow\\ \rightarrow\left(\begin{array}{cccc|c} 1 & 0 & 0 & 0 & -3\\ 0 & 1 & 0 & 0 & -5\\ 0 & 0 & 1 & 0 & -1\\ 0 & 0 & 0 & 1 & 2\end{array}\right). $$
Решение окончено. Ответ таков: $x_1=-3$, $x_2=-5$, $x_3=-1$, $x_4=2$. Полное решение без пояснений:
Полное решение без пояснений:
Ответ : $x_1=-3$, $x_2=-5$, $x_3=-1$, $x_4=2$.
Пример №3
Решить СЛАУ $\left\{\begin{aligned} & x_1-2x_2+3x_3+4x_5=-5;\\ & 2x_1+x_2+5x_3+2x_4+9x_5=-3;\\ & 3x_1+4x_2+7x_3+4x_4+14x_5=-1;\\ & 2x_1-4x_2+6x_3+11x_5=2;\\ & -2x_1+14x_2-8x_3+4x_4-7x_5=20;\\ & -4x_1-7x_2-9x_3-6x_4-21x_5=-9. \end{aligned}\right.$ методом Гаусса-Жордана. Если система является неопределённой, указать базисное решение.
Подобные примеры разбираются в теме «Общее и базисное решения СЛАУ» . Во второй части упомянутой темы данный пример решён с помощью метод Гаусса . Мы же решим его с помощью метода Гаусса-Жордана. Пошагово разбивать решение не станем, так как это уже было сделано в предыдущих примерах.
$$
\left(\begin{array}{ccccc|c}
1 & -2 & 3 & 0 & 4 & -5\\
2 & 1 & 5 & 2 & 9 & -3\\
3 & 4 & 7 & 4 & 14 & -1\\
2 & -4 & 6 & 0 & 11 & 2\\
-2 & 14 & -8 & 4 & -7 & 20\\
-4 & -7 & -9 & -6 & -21 & -9 \end{array}\right)
\begin{array} {l} \phantom{0} \\ II-2\cdot I\\ III-3\cdot I\\ IV-2\cdot I\\ V+2\cdot I\\VI+4\cdot I \end{array} \rightarrow
\left(\begin{array}{ccccc|c}
1 & -2 & 3 & 0 & 4 & -5\\
0 & 5 & -1 & 2 & 1 & 7\\
0 & 10 & -2 & 4 & 2 & 14\\
0 & 0 & 0 & 0 & 3 & 12\\
0 & 10 & -2 & 4 & 1 & 10\\
0 & -15 & 3 & -6 & -5 & -29 \end{array}\right)
\begin{array} {l} \phantom{0} \\ II:5 \\ \phantom{0}\\ \phantom{0}\\ \phantom{0} \\ \phantom{0}\end{array} \rightarrow \\
\left(\begin{array}{ccccc|c}
1 & -2 & 3 & 0 & 4 & -5\\
0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\\
0 & 10 & -2 & 4 & 2 & 14\\
0 & 0 & 0 & 0 & 3 & 12\\
0 & 10 & -2 & 4 & 1 & 10\\
0 & -15 & 3 & -6 & -5 & -29 \end{array}\right)
\begin{array} {l} I+2\cdot II \\ \phantom{0}\\ III-10\cdot II\\ IV:3\\ V-10\cdot II\\VI+15\cdot II \end{array} \rightarrow
\left(\begin{array}{ccccc|c}
1 & 0 & 13/5 & 4/5 & 22/5 & -11/5\\
0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\\
0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 1 & 4\\
0 & 0 & 0 & 0 & -1 & -4\\
0 & 0 & 0 & 0 & -2 & -8 \end{array}\right). $$
$$
Полагаю, что одно из сделанных преобразований всё-таки требует пояснения: $IV:3$. Все элементы четвёртой строки нацело делились на три, поэтому сугубо из соображений упрощения мы разделили все элементы этой строки на три. Третья строка в преобразованной матрице стала нулевой. Вычеркнем нулевую строку:
$$ \left(\begin{array}{ccccc|c} 1 & 0 & 13/5 & 4/5 & 22/5 & -11/5\\ 0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\\ 0 & 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & -1 & -4\\ 0 & 0 & 0 & 0 & -2 & -8 \end{array}\right) $$
Нам пора переходить к третьему шагу, на котором должны быть обнулены элементы третьего столбца. Однако диагональный элемент (третья строка) равен нулю. И смена мест строк ничего не даст. Первую и вторую строки мы уже использовали, поэтому их трогать мы не можем. А четвёртую и пятую строки трогать нет смысла, ибо проблема равенства нулю разрешающего элемента никуда не денется.
В этой ситуации проблема решается крайне незамысловато. Мы не можем обработать третий столбец? Хорошо, перейдём к четвёртому. Может, в четвёртом столбце элемент третьей строки будет не равен нулю. Однако четвёртый столбец «болеет» той же проблемой, что и третий. Элемент третьей строки в четвёртом столбце равен нулю. И смена мест строк опять-таки ничего не даст. Четвёртый столбец тоже не можем обработать? Ладно, перейдём к пятому. А вот в пятом столбце элемент третьей строки очень даже не равен нулю. Он равен единице, что довольно-таки хорошо. Итак, разрешающий элемент в пятом столбце равен 1. Разрешающий элемент выбран, поэтому осуществим дальшейшие преобразования метода Гаусса-Жордана:
$$ \left(\begin{array}{ccccc|c} 1 & 0 & 13/5 & 4/5 & 22/5 & -11/5\\ 0 & 1 & -1/5 & 2/5 & 1/5 & 7/5\\ 0 & 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & -1 & -4\\ 0 & 0 & 0 & 0 & -2 & -8 \end{array}\right) \begin{array} {l} I-22/5\cdot III \\ II-1/5\cdot III \\ \phantom{0}\\ IV+III\\ V+2\cdot III \end{array} \rightarrow \left(\begin{array}{ccccc|c} 1 & 0 & 13/5 & 4/5 & 0 & -99/5\\ 0 & 1 & -1/5 & 2/5 & 0 & 3/5\\ 0 & 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right) \rightarrow \\ \rightarrow\left|\text{Удаляем нулевые строки}\right|\rightarrow \left(\begin{array}{ccccc|c} 1 & 0 & 13/5 & 4/5 & 0 & -99/5\\ 0 & 1 & -1/5 & 2/5 & 0 & 3/5\\ 0 & 0 & 0 & 0 & 1 & 4 \end{array}\right)$$
Мы привели матрицу системы и расширенную матрицу системы к ступенчатому виду. Ранги обеих матриц равны $r=3$, т.е. надо выбрать 3 базисных переменных. Количество неизвестных $n=5$, поэтому нужно выбрать $n-r=2$ свободных переменных. Так как $r данная система является неопределённой (т.е. имеет бесконечное количество решений). Для нахождения решений системы составим «ступеньки»:
Ранги обеих матриц равны $r=3$, т.е. надо выбрать 3 базисных переменных. Количество неизвестных $n=5$, поэтому нужно выбрать $n-r=2$ свободных переменных. Так как $r данная система является неопределённой (т.е. имеет бесконечное количество решений). Для нахождения решений системы составим «ступеньки»:
На «ступеньках» стоят элементы из столбцов №1, №2, №5. Следовательно, базисными будут переменные $x_1$, $x_2$, $x_5$. Свободными переменными, соответственно, будут $x_3$, $x_4$. Столбцы №3 и №4, соответствующие свободным переменным, перенесём за черту, при этом, конечно, не забыв сменить им знаки.
$$
\left(\begin{array}{ccccc|c}
1 & 0 & 13/5 & 4/5 & 0 & -99/5\\
0 & 1 & -1/5 & 2/5 & 0 & 3/5\\
0 & 0 & 0 & 0 & 1 & 4 \end{array}\right)\rightarrow
\left(\begin{array}{ccc|ccc}
1 & 0 & 0 & -99/5 & -13/5 & -4/5\\
0 & 1 & 0 & 3/5 & 1/5 & -2/5\\
0 & 0 & 1 & 4 & 0 & 0\end{array}\right). $$
$$
Из последней матрицы получим общее решение: $\left\{\begin{aligned} & x_1=-\frac{99}{5}-\frac{13}{5}x_3-\frac{4}{5}x_4;\\ & x_2=\frac{3}{5}+\frac{1}{5}x_3-\frac{2}{5}x_4;\\ & x_3 \in R;\\ & x_4\in R;\\ & x_5=4. \end{aligned}\right.$. Базисное решение найдём, приняв свободные переменные равными нулю, т.е. $x_3=0$, $x_4=0$:
$$ \left\{\begin{aligned} & x_1=-\frac{99}{5};\\ & x_2=\frac{3}{5};\\ & x_3=0;\\ & x_4=0;\\ & x_5=4. \end{aligned}\right. $$
Задача решена, осталось лишь записать ответ.
Ответ : Общее решение: $\left\{\begin{aligned} & x_1=-\frac{99}{5}-\frac{13}{5}x_3-\frac{4}{5}x_4;\\ & x_2=\frac{3}{5}+\frac{1}{5}x_3-\frac{2}{5}x_4;\\ & x_3 \in R;\\ & x_4\in R;\\ & x_5=4. \end{aligned}\right.$, базисное решение: $\left\{\begin{aligned} & x_1=-\frac{99}{5};\\ & x_2=\frac{3}{5};\\ & x_3=0;\\ & x_4=0;\\ & x_5=4. \end{aligned}\right.$.
Здесь вы сможете бесплатно решить систему линейных уравнений методом Гаусса онлайн больших размеров в комплексных числах с очень подробным решением. Наш калькулятор умеет решать онлайн как обычную определенную, так и неопределенную систему линейных уравнений методом Гаусса, которая имеет бесконечное множество решений. В этом случае в ответе вы получите зависимость одних переменных через другие, свободные. Также можно проверить систему уравнений на совместность онлайн, используя решение методом Гаусса.
Наш калькулятор умеет решать онлайн как обычную определенную, так и неопределенную систему линейных уравнений методом Гаусса, которая имеет бесконечное множество решений. В этом случае в ответе вы получите зависимость одних переменных через другие, свободные. Также можно проверить систему уравнений на совместность онлайн, используя решение методом Гаусса.
О методе
При решении системы линейных уравнений онлайн методом Гаусса выполняются следующие шаги.
- Записываем расширенную матрицу.
- Фактически решение разделяют на прямой и обратный ход метода Гаусса. Прямым ходом метода Гаусса называется приведение матрицы к ступенчатому виду. Обратным ходом метода Гаусса называется приведение матрицы к специальному ступенчатому виду. Но на практике удобнее сразу занулять то, что находится и сверху и снизу рассматриваемого элемента. Наш калькулятор использует именно этот подход.
- Важно отметить, что при решении методом Гаусса, наличие в матрице хотя бы одной нулевой строки с НЕнулевой правой частью (столбец свободных членов) говорит о несовместности системы. Решение линейной системы в таком случае не существует.
Чтобы лучше всего понять принцип работы алгоритма Гаусса онлайн введите любой пример, выберите «очень подробное решение» и посмотрите его решение онлайн.
Однажды немецкий математик Вильгельм Йордан (мы неверно транскрибируем с немецкого Jordan как Жордан) сел решать очередную систему уравнений. Он любил этим заниматься и в свободное время совершенствовал свои навыки. Но вот настал момент, когда ему наскучили все методы решения и метод Гаусса в том числе…
Он любил этим заниматься и в свободное время совершенствовал свои навыки. Но вот настал момент, когда ему наскучили все методы решения и метод Гаусса в том числе…
Предположим, дана система с тремя уравнениями, тремя неизвестными и записана её расширенная матрица . В наиболее распространенном случае получаются стандартные ступеньки , и так каждый день…. Одно и то же – как беспросветный ноябрьский дождь.
На некоторое время развевает тоску другой способ приведения матрицы к ступенчатому виду: , причём он совершенно равноценен и может быть неудобен только по причине субъективного восприятия. Но всё рано или поздно приедается…. И подумал тогда Жо рдан – а зачем вообще мучиться с обратным ходом гауссовского алгоритма? Не проще ли сразу получить ответ с помощью дополнительных элементарных преобразований?
…да, такое бывает только по любви =)
Для освоения данного урока «чайникам» придётся пойти путём Жо рдана и прокачать элементарные преобразования хотя бы среднего уровня, прорешав, минимум, 15-20 соответствующих заданий. Поэтому если вы смутно понимаете, о чём идёт разговор и/или у вас возникнет недопонимание чего-либо по ходу занятия, то рекомендую ознакомиться с темой в следующем порядке:
Поэтому если вы смутно понимаете, о чём идёт разговор и/или у вас возникнет недопонимание чего-либо по ходу занятия, то рекомендую ознакомиться с темой в следующем порядке:
Ну, и совсем замечательно, если отработано понижение порядка определителя .
Как все поняли, метод Гаусса-Жордана представляет собой модификацию метода Гаусса и с реализацией основной, уже озвученной выше идеи, мы встретимся на ближайших экранах. Кроме того, в число немногочисленных примеров данной статьи вошло важнейшее приложение – нахождение обратной матрицы с помощью элементарных преобразований .
Не мудрствуя лукаво:
Пример 1
Решить систему методом Гаусса-Жордана
Решение : это первое задание урока Метод Гаусса для чайников , где мы 5 раз трансформировали расширенную матрицу системы и привели её к ступенчатому виду:
Теперь вместо обратного хода в игру вступают дополнительные элементарные преобразования. Сначала нам необходимо получить нули на этих местах: ,
а потом ещё один ноль вот здесь: .
Идеальный с точки зрения простоты случай:
(6) Ко второй строке прибавили третью строку. К первой строке прибавили третью строку.
(7) К первой строке прибавили вторую строку, умноженную на –2.
Не могу удержаться от иллюстрации итоговой системы:
Ответ :
Предостерегаю читателей от шапкозакидательского настроения – это был простейший демонстрационный пример. Для метода Гаусса-Жордана характерны свои специфические приёмы и не самые удобные вычисления, поэтому, пожалуйста, настройтесь на серьёзную работу.
Не хочу показаться категоричным или придирчивым, но в подавляющем большинстве источников информации, которые я видел, типовые задачи рассмотрены крайне плохо – нужно обладать семью пядями во лбу и потратить массу времени/нервов на тяжёлое неуклюжее решение с дробями. За годы практики мне удалось отшлифовать, не скажу, что самую лучшую, но рациональную и достаточно лёгкую методику, которая доступна всем, кто владеет арифметическими действиями:
Пример 2
Решить систему линейных уравнений методом Гаусса-Жордана.
Решение : первая часть задания хорошо знакома:
(1) Ко второй строке прибавили первую строку, умноженную на –1. К третьей строке прибавили первую строку, умноженную на 3. К четвертой строке прибавили первую строку, умноженную на –5.
(2) Вторую строку разделили на 2, третью строку разделили на 11, четвёртую строку разделили на 3.
(3) Вторая и третья строки пропорциональны, 3-ю строку удалили. К четвёртой строке прибавили вторую строку, умноженную на –7
(4) Третью строку разделили на 2.
Очевидно, что система имеет бесконечно много решений, и наша задача – привести её расширенную матрицу к виду .
Как действовать дальше? Прежде всего, следует отметить, что мы лишились вкусного элементарного преобразования – перестановки строк. Точнее говоря, переставить-то их можно, но в этом нет смысла (просто выполним лишние действия). И далее целесообразно придерживаться следующего шаблона:
Находим наименьшее общее кратное чисел третьего столбца (1, –1 и 3), т. е. – наименьшее число, которое бы делилось без остатка и на 1, и на –1 и на 3. В данном случае, это, конечно же, «тройка». Теперь в третьем столбце нам нужно получить одинаковые по модулю числа , и этими соображениями обусловлено 5-е преобразование матрицы:
е. – наименьшее число, которое бы делилось без остатка и на 1, и на –1 и на 3. В данном случае, это, конечно же, «тройка». Теперь в третьем столбце нам нужно получить одинаковые по модулю числа , и этими соображениями обусловлено 5-е преобразование матрицы:
(5) Первую строку умножаем на –3, вторую строку умножаем на 3. Вообще говоря, первую строку можно было умножить тоже на 3, но это было бы менее удобно для следующего действия. К хорошему привыкаешь быстро:
(6) Ко второй строке прибавили третью строку. К первой строке прибавили третью строку.
(7) Во втором столбце два ненулевых значения (24 и 6) и нам снова нужно получить одинаковые по модулю числа . В данном случае всё сложилось довольно удачно – наименьшее кратное 24, и эффективнее всего умножить вторую строку на –4.
(8) К первой строке прибавили вторую.
(9) Заключительный штрих: первую строку разделили на –3, вторую строку разделили на –24 и третью строку разделили на 3. Это действие выполняется В ПОСЛЕДНЮЮ ОЧЕРЕДЬ! Никаких преждевременных дробей!
В результате элементарных преобразований получена эквивалентная исходной система:
Элементарно выражаем базисные переменные через свободную:
и записываем:
Ответ : общее решение:
В подобных примерах применение рассмотренного алгоритма чаще всего оправдано, поскольку обратный ход метода Гаусса обычно требует трудоёмких и неприятных вычислений с дробями.
И, разумеется, крайне желательна проверка, которая выполняется по обычной схеме, рассмотренной на уроке Несовместные системы и системы с общим решением .
Для самостоятельного решения:
Пример 3
Найти базисное решение с помощью элементарных преобразований
Такая формулировка задачи предполагает использование метода Гаусса-Жордана, и в образце решения матрица приводится к стандартному виду с базисными переменными . Однако всегда держите на заметке, что в качестве базисных можно выбрать и другие переменные . Так, например, если в первом столбце громоздкие числа, то вполне допустимо привести матрицу к виду (базисные переменные ), или к виду (базисные переменные ), или даже к виду с базисными переменными . Существуют и другие варианты.
Но всё-таки это крайние случаи – не стОит лишний раз шокировать преподавателей своими знаниями, техникой решения и уж тем более не надо выдавать экзотических жордановсих результатов вроде . Впрочем, бывает трудно удержаться от нетипового базиса, когда в исходной матрице, скажем, в 4-м столбце есть два готовых нуля.
Примечание : термин «базис» имеет алгебраический смысл и понятие геометрического базиса здесь не при чём!
Если в расширенной матрице данных размеров вдруг обнаруживается пара линейно зависимых строк, то её следует попытаться привести к привычному виду с базисными переменными . Образец такого решения есть в Примере №7 статьи об однородных системах линейных уравнений , причём там выбран другой базис .
Продолжаем совершенствовать свои навыки на следующей прикладной задаче:
Как найти обратную матрицу методом Гаусса?Обычно условие формулируют сокращённо, но, по существу, здесь также работает алгоритм Гаусса-Жордана. Более простой метод нахождения обратной матрицы для квадратной матрицы мы давным-давно рассмотрели на соответствующем уроке, и суровой поздней осенью тёртые студенты осваивают мастерский способ решения.
Краткое содержание предстоящих действий таково: сначала следует записать квадратную матрицу в тандеме с единичной матрицей: . Затем с помощью элементарных преобразований необходимо получить единичную матрицу слева, при этом (не вдаваясь в теоретические подробности) справа нарисуется обратная матрица. Схематически решение выглядит следующим образом:
Затем с помощью элементарных преобразований необходимо получить единичную матрицу слева, при этом (не вдаваясь в теоретические подробности) справа нарисуется обратная матрица. Схематически решение выглядит следующим образом:
(Понятно, что обратная матрица должна существовать)
Демо-пример 4
Найдём обратную матрицу для матрицы с помощью элементарных преобразований. Для этого запишем её в одной упряжке с единичной матрицей, и понеслась «двойка скакунов»:
(1) Ко второй строке прибавили первую строку, умноженную на –3.
(2) К первой строке прибавили вторую строку.
(3) Вторую строку разделили на –2.
Ответ :
Сверьтесь с ответом первого примера урока Как найти обратную матрицу?
Но то была очередная заманивающая задачка – в действительности решение гораздо более длительно и кропотливо. Как правило, вам будет предложена матрица «три на три»:
Пример 5
Решение : присоединяем единичную матрицу и начинаем выполнять преобразования, придерживаясь алгоритма «обычного» метода Гаусса :
(1) Первую и третью строки поменяли местами. На первый взгляд, перестановка строк кажется нелегальной, но на самом деле переставлять их можно – ведь по итогу слева нам нужно получить единичную матрицу, а справа же «принудительно» получится именно матрица (вне зависимости от того будем ли мы переставлять строки в ходе решения или нет) . Обратите внимание, что здесь вместо перестановки можно организовать «шестёрки» в 1-м столбце (наименьшее общее кратное (НОК) чисел 3, 2 и 1) . Решение через НОК особенно удобно, когда в первом столбце отсутствуют «единицы».
На первый взгляд, перестановка строк кажется нелегальной, но на самом деле переставлять их можно – ведь по итогу слева нам нужно получить единичную матрицу, а справа же «принудительно» получится именно матрица (вне зависимости от того будем ли мы переставлять строки в ходе решения или нет) . Обратите внимание, что здесь вместо перестановки можно организовать «шестёрки» в 1-м столбце (наименьшее общее кратное (НОК) чисел 3, 2 и 1) . Решение через НОК особенно удобно, когда в первом столбце отсутствуют «единицы».
(2) Ко 2-й и 3-й строкам прибавили 1-ю строку, умноженную на –2 и –3 соответственно.
(3) К 3-й строке прибавили 2-ю строку, умноженную на –1
Вторая часть решения проводится по уже известной из предыдущего параграфа схеме: перестановки строк становятся бессмысленными, и мы находим наименьшее общее кратное чисел третьего столбца (1, –5, 4): 20. Существует строгий алгоритм нахождения НОК, но здесь обычно хватает подбора. Ничего страшного, если взять бОльшее число, которое делится и на 1, и на –5, и на 4, например, число 40. Отличие будет в более громоздких вычислениях.
Отличие будет в более громоздких вычислениях.
К слову о вычислениях. Для решения задачи совсем не зазорно вооружиться микрокалькулятором – числа здесь фигурируют немалые, и будет очень обидно допустить вычислительную ошибку.
(4) Третью строку умножаем на 5, вторую строку на 4, первую строку на «минус двадцать»:
(5) К 1-й и 2-й строкам прибавили третью строку.
(6) Первую и третью строки разделили на 5, вторую строку умножили на –1.
(7) Наименьшее общее кратное ненулевых чисел второго столбца (–20 и 44) равно 220. Первую строку умножаем на 11, вторую строку – на 5.
(8) К первой строке прибавили вторую строку.
(9) Первую строку умножили на –1, вторую строку разделили «обратно» на 5.
(10) Теперь на главной диагонали левой матрицы целесообразно получить наименьшее общее кратное чисел диагонали (44, 44 и 4). Совершенно понятно, что это число 44. Третью строку умножаем на 11.
(11) Каждую строку делим на 44. Данное действие выполняется в последнюю очередь!
Таким образом, обратная матрица:
Внесение и вынесение -й, в принципе, лишние действия, но того требует протокол оформления задачи.
Ответ :
Проверка выполняется по обычной схеме, рассмотренной на уроке об обратной матрице .
Продвинутые люди могут несколько сократить решение, но должен предупредить, спешка тут чревата ПОВЫШЕННЫМ риском допустить ошибку.
Аналогичное задание для самостоятельного решения:
Пример 6
Найти обратную матрицу методом Гаусса-Жордана.
Примерный образец оформления задачи внизу страницы. И ради того, чтобы вы «не проехали мимо с песнями» я оформил решение в уже упомянутом стиле – исключительно через НОК столбцов без единой перестановки строк и дополнительных искусственных преобразований. По моему мнению, эта схема – если и не самая, то одна из самых надёжных .
Иногда бывает удобно более короткое «модернистское» решение, которое заключается в следующем: на первом шаге всё как обычно: .
На втором шаге накатанным приёмом (через НОК чисел 2-го столбца) организуются сразу два нуля во втором столбце: . Перед данным действием особенно трудно устоять, если во 2-м столбце нарисовались одинаковые по модулю числа, например, те же банальные «единицы».
И, наконец, на третьем шаге точно так же получаем нужные нули в третьем столбце: .
Что касается размерности, то в большинстве случаев приходится разруливать матрицу «три на три». Однако время от времени встречается лайт-версия задачи с матрицей «два на два» и хард… – специально для всех читателей сайт:
Пример 7
Найти обратную матрицу с помощью элементарных преобразований
Это задание из моей собственной физматовской контрольной работы по алгебре, …эх, где мой первый курс =) Пятнадцать лет назад (листочек на удивление ещё не пожелтел) , я уложился в 8 шагов, а сейчас – всего лишь в 6! Матрица, кстати, весьма творческая – на первом же шаге просматривается несколько заманчивых путей решения. Моя поздняя версия внизу страницы.
И заключительный совет – после таких примеров очень полезна гимнастика для глаз и какая-нибудь хорошая музыка для релаксации =)
Желаю успехов!
Решения и ответы:
Пример 3: Решение : запишем расширенную матрицу системы и с помощью элементарных преобразований получим базисное решение:
(1) Первую и вторую строки поменяли местами.
(2) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на 5.
(3) Третью строку разделили на 3.
(4) К третьей строке прибавили вторую строку, умноженную на 2.
(5) Третью строку разделили на 7.
(6) Наименьшее кратное чисел 3-го столбца (–3, 5, 1) равно 15. Первую строку умножили на 5, вторую строку умножили на –3, третью строку умножили на 15.
(7) К первой строке прибавили 3-ю строку. Ко второй строке прибавили 3-ю строку.
(8) Первую строку разделили на 5, вторую строку разделили на –3, третью строку разделили на 15.
(9) Наименьшее кратное ненулевых чисел 2-го столбца (–2 и 1) равно: 2. Вторую строку умножили на 2
(10) К первой строке прибавили вторую строку.
(11) Вторую строку разделили на 2.
Выразим базисные переменные через свободные переменные :
Ответ : общее решение:
Пример 6: Решение : обратную матрицу найдём с помощью элементарных преобразований:
(1) Первую строку умножили на –15, вторую строку умножили на 3, третью строку умножили на 5.
(2) Ко 2-й и 3-й строкам прибавили первую строку.
(3) Первую строку разделили на –15, вторую строку разделили на –3, третью строку разделили на –5.
(4) Вторую строку умножили на 7, третью строку умножили на –9.
(5) К третьей строке прибавили вторую строку.
(6) Вторую строку разделили на 7.
(7) Первую строку умножили на 27, вторую строку умножили на 6, третью строку умножили на –4.
(8) К первой и второй строкам прибавили третью строку.
(9) Третью строку разделили на –4. К первой строке прибавили вторую строку, умноженную на –1.
(10) Вторую строку разделили на 2.
(11) Каждую строку разделили на 27.
В результате:
Ответ :
Пример 7: Решение : найдём обратную матрицу методом Гаусса-Жордана:
(1) К 1-й и 4-й строкам прибавили 3-ю строку.
(2) Первую и четвёртую строки поменяли местами.
(3) Ко 2-й строке прибавили 1-ю строку. К 3-й строке прибавили 1-ю строку, умноженную на 2:
(4) К 3-й строке прибавили 2-ю строку, умноженную на –2. К 4-й строке прибавили 2-ю строку.
(5) К 1-й и 3-й строкам прибавили 4-ю строку, умноженную на –1.
(6) Вторую строку умножили на –1, третью строку разделили на –2.
Ответ :
В данной статье мы рассмотрим метод Жордана-Гаусса для решения систем линейных уравнений, отличие метода Гаусса от метода Жордана-Гаусса, алгоритм действий, а также приведем примеры решений СЛАУ.
Yandex.RTB R-A-339285-1
Основные понятия
Определение 1
Метод Жордана-Гаусса — один из методов, предназначенный для решения систем линейных алгебраических уравнений.
Этот метод является модификацией метода Гаусса — в отличие от исходного (метода Гаусса) метод Жордана-Гаусса позволяет решить СЛАУ в один этап (без использования прямого и обратного ходов).
Примечание
Матричная запись СЛАУ: вместо обозначения А в методе Жордана-Гаусса для записи используют обозначение Ã — обозначение расширенной матрицы системы.
Пример 1
4 x 1 — 7 x 2 + 8 x 3 = — 23 2 x 1 — 4 x 2 + 5 x 3 = — 13 — 3 x 1 + 11 x 2 + x 3 = 16
Как решить?
Записываем расширенную матрицу системы:
à = 4 — 7 8 | — 23 2 — 4 5 | — 13 — 3 11 1 | 16
Напоминаем, что слева от черты записывается матрица системы А:
A = 4 — 7 8 2 — 4 5 — 3 11 1
Замечание 1
На каждом шаге решения необходимо выбирать разрешающие элементы матрицы. Процесс выбора может быть различным — в зависимости от того, как выбираются элементы, решения будут отличаться. Можно выбирать в качестве разрешающих элементов диагональные элементы матрицы, а можно выбирать произвольно.
В этой статье мы покажем оба способа решения.
Произвольный способ выбора разрешающих элементов
- Первый этап:
Следует обратиться к 1-му столбцу матрицы Ã — необходимо выбрать ненулевой (разрешающий) элемент.
В 1-ом столбце есть 3 ненулевых элемента: 4, 2, -3. Можно выбрать любой, но, по правилам, выбирается тот, чей модуль ближе всего к единице. В нашем примере таким числом является 2.
Цель: обнулить все элементы, кроме разрешающего, т.е. необходимо обнулить 4 и -3:
4 — 7 8 2 — 4 5 — 3 11 1
Произведем преобразование: необходимо сделать разрешающий элемент равным единице. Для этого делим все элементы 2-ой строки на 2. Такое преобразование имеет обозначение: I I: 2:
4 — 7 8 | — 23 2 — 4 5 | — 13 — 3 11 1 | 16 I I ÷ 2 → 4 — 7 8 | — 23 2 — 4 5 / 2 | — 13 / 2 — 3 11 1 | 16
Теперь обнуляем остальные элементы: 4 и -3:
4 — 7 8 | — 23 2 — 4 5 / 2 | — 13 / 2 — 3 11 1 | 16 I — 4 × I I I I I — (- 3) × I I
Необходимо выполнить преобразования:
I — 4 × I I и I I I — (- 3) × I I = I I I + 3 × I I
Запись I — 4 × I I означает, что от элементов 1-ой строки вычитаются соответствующие элементы 2-ой строки, умноженные на 4.
Запись I I I + 3 × I I означает, что к элементам 3-ей строки прибавляются соответствующие элементы 2-ой строки, умноженные на 3.
I — 4 × I I = 4 — 7 8 — 23 — 4 1 — 2 5 / 2 — 13 / 2 = = 4 — 7 8 — 23 — 4 — 8 10 — 26 = 0 1 — 2 3
Записываются такие изменения следующим образом:
4 — 7 8 | — 23 2 — 4 5 / 2 | — 13 / 2 — 3 11 1 | 16 I — 4 × I I I I I — (- 3) × I I → 0 1 — 2 | 3 1 — 2 5 / 2 | — 13 / 2 0 5 17 / 2 | — 7 / 2
- Второй этап
Необходимо обнулить 2-ой столбец, следовательно, нужно выбрать разрешающий элемент: 1, -2, 5. Однако 2-ую строку матрицы мы использовали в первом этапе, так что элемент -2 не может быть использован.
Поскольку необходимо выбирать число, чей модуль ближе всего к единице, то выбор очевиден — это 1. Обнуляем остальные элементы 2-го столбца:
0 1 — 2 | 3 1 — 2 5 / 2 | — 13 / 2 0 5 17 / 2 | — 7 / 2 I I — (- 2) × I I I I — 5 × I
0 1 — 2 | 3 1 — 2 5 / 2 | — 13 / 2 0 5 17 / 2 | — 7 / 2 I I + 2 × I I I I — 5 × I → 0 1 — 2 | 3 1 0 — 3 / 2 | — 1 / 2 0 0 37 / 2 | — 37 / 2
- Третий этап
Теперь требуется обнулить элементы 3-го столбца. Поскольку первая и вторая строки уже использованы, поэтому остается только один вариант: 37 / 2 . Обнуляем с его помощью элементы третьего столбца:
Поскольку первая и вторая строки уже использованы, поэтому остается только один вариант: 37 / 2 . Обнуляем с его помощью элементы третьего столбца:
0 1 — 2 | 3 1 0 — 3 / 2 | — 1 / 2 0 0 37 / 2 | — 37 / 2
Выполнив преобразования
I — (- 2) × I I I = I + 2 × I I I и I I — (- 3 2) × I I I = I I + 3 2 × I I
получим следующий результат:
0 1 — 2 | 3 1 0 — 3 / 2 | — 1 / 2 0 0 1 | — 1 I + 2 × I I I I I + 3 / 2 × I I I → 0 1 0 | 1 1 0 0 | — 2 0 0 1 | — 1
Ответ : x 1 = — 2 ; x 2 = 1 ; x 3 = — 1 .
Полное решение:
4 — 7 8 | — 23 2 — 4 5 | — 13 — 3 11 1 | 16 I I ÷ 2 → 4 — 7 8 | — 23 2 — 4 5 / 2 | — 13 / 2 — 3 11 1 | 16 I — 4 × I I I I I — (- 3) × I I →
→ 0 1 — 2 | 3 1 — 2 5 / 2 | — 13 / 2 0 5 17 / 2 | — 7 / 2 I I — (- 2) × I I I I — 5 × I → 0 1 — 2 | 3 1 0 — 3 / 2 | — 1 / 2 0 0 37 / 2 | — 37 / 2 I I I ÷ 37 2 →
→ 0 1 — 2 | 3 1 0 — 3 / 2 | — 1 / 2 0 0 1 | — 1 I + 2 × I I I I I + 3 / 2 × I I I → 0 1 0 | 1 1 0 0 | — 2 0 0 1 | — 1 .
Выбор разрешающих элементов на главной диагонали матрицы системы
Определение 2
Принцип выбора разрешающих элементов строится на простом отборе соответствующих элементов: в 1-ом столбце выбирается элемент 1-го столбца, во 2-ом — второй, в 3-ем — третий и т.д.
- Первый этап
В первом столбце необходимо выбрать элемент первой строки, т.е. 4. Но поскольку в первом столбце есть число 2, чей модуль ближе к единице, чем 4, то можно поменять местами первую и вторую строку:
4 — 7 8 | — 23 2 — 4 5 | — 13 — 3 11 1 | 16 → 2 — 4 5 | — 13 4 — 7 8 | — 23 — 3 11 1 | 16
Теперь разрешающий элемент — 2. Как показано в первом способе, делим первую строку на 2, а затем обнуляем все элементы:
4 — 7 8 | — 23 2 — 4 5 | — 13 — 3 11 1 | 16 I ÷ 2 → 2 — 4 5 / 2 | — 13 / 2 4 — 7 8 | — 23 — 3 11 1 | 16 I I — 4 × I I I I + 3 × I → 1 — 2 5 / 2 | — 13 / 2 0 1 — 2 | 3 0 5 17 / 2 | — 7 / 2
- Второй этап
На втором этапе требуется обнулить элементы второго столбца. Разрешающий элемент — 1, поэтому никаких изменений производить не требуется:
Разрешающий элемент — 1, поэтому никаких изменений производить не требуется:
0 1 — 2 | 3 1 — 2 5 / 2 | — 13 / 2 0 5 17 / 2 | — 7 / 2 I + 2 × I I I I I — 5 × I I → 0 1 — 2 | 3 1 0 — 3 / 2 | — 1 / 2 0 0 37 / 2 | — 37 / 2
- Третий этап
На третьем этапе необходимо обнулить элементы третьего столбца. Разрешающий элемент — 37/2. Делим все элементы на 37/2 (чтобы сделать равными 1), а затем обнуляем:
0 1 — 2 | 3 1 0 — 3 / 2 | — 1 / 2 0 0 37 / 2 | — 37 / 2 I I I ÷ 37 2 → 1 0 — 3 / 2 | — 1 / 2 0 1 — 2 | 3 0 0 1 | — 1 I + 2 × I I I I I + 3 / 2 × I I I → 1 0 0 | — 2 0 1 0 | 1 0 0 1 | — 1
Ответ: x 1 = — 2 ; x 2 = 1 ; x 3 = — 1 .
4 — 7 8 | — 23 2 — 4 5 | — 13 — 3 11 1 | 16 I ÷ 2 → 2 — 4 5 / 2 | — 13 / 2 4 — 7 8 | — 23 — 3 11 1 | 16 I I — 4 × I I I I + 3 × I → 0 1 — 2 | 3 1 — 2 5 / 2 | — 13 / 2 0 5 17 / 2 | — 7 / 2 I + 2 × I I I I I — 5 × I I →
→ 0 1 — 2 | 3 1 0 — 3 / 2 | — 1 / 2 0 0 37 / 2 | — 37 / 2 I I I ÷ 37 2 → 1 0 — 3 / 2 | — 1 / 2 0 1 — 2 | 3 0 0 1 | — 1 I + 2 × I I I I I + 3 / 2 × I I I → 1 0 0 | — 2 0 1 0 | 1 0 0 1 | — 1
Пример 2
Решить СЛАУ методом Жордана-Гаусса:
3 x 1 + x 2 + 2 x 3 + 5 x 4 = — 6 3 x 1 + x 2 + 2 x 4 = — 10 6 x 1 + 4 x 2 + 11 x 3 + 11 x 4 = — 27 — 3 x 1 — 2 x 2 — 2 x 3 — 10 x 4 = 1
Как решить?
Записать расширенную матрицу данной системы Ã :
3 1 2 5 | — 6 3 1 0 2 | 10 6 4 11 11 | — 27 — 3 — 2 — 2 — 10 | 1
Для решения используем второй способ: выбор разрешающих элементов на главной диагонали системы. На первом этапе выбираем элемент первой строки, на втором — второй строки, на третьем — третьей и т.д.
На первом этапе выбираем элемент первой строки, на втором — второй строки, на третьем — третьей и т.д.
- Первый этап
Необходимо выбрать разрешающий элемент первой строки, т.е. 3. Затем обнуляем все элементы столбца, разделяя на 3 все элементы:
3 1 2 5 | — 6 3 1 0 2 | — 10 6 4 11 11 | — 27 — 3 — 2 — 2 — 10 | 1 I ÷ 3 → 1 1 / 3 2 / 3 5 / 3 | — 2 3 1 0 2 | — 10 6 4 11 11 | — 27 — 3 — 2 — 2 — 10 | 1 I I — 3 × I I I I — 6 × I I V + 3 × I →
→ 1 1 / 3 2 / 3 5 / 3 | — 2 0 0 — 2 — 3 | — 4 0 2 7 1 | — 15 0 — 1 0 — 5 | — 5
- Второй этап
Необходимо обнулить элементы второго столбца. Для этого выделяем разрешающий элемент, но элемент первой строки второго столбца равен нулю, поэтому необходимо менять строки местами.
Поскольку в четвертой строке есть число -1, то меняем местами вторую и четвертую строки:
1 1 / 3 2 / 3 5 / 3 | — 2 0 0 — 2 — 3 | — 4 0 2 7 1 | — 15 0 — 1 0 — 5 | — 5 → 1 1 / 3 2 / 3 5 / 3 | — 2 0 — 1 0 — 5 | — 5 0 2 7 1 | — 15 0 0 — 2 — 3 | — 4
Теперь разрешающий элемент равен -1. Делим элементы второго столбца на -1, а затем обнуляем:
Делим элементы второго столбца на -1, а затем обнуляем:
1 1 / 3 2 / 3 5 / 3 | — 2 0 — 1 0 — 5 | — 5 0 2 7 1 | — 15 0 0 — 2 — 3 | — 4 I I ÷ (- 1) → 1 1 / 3 2 / 3 5 / 3 | — 2 0 1 0 5 | 5 0 2 7 1 | — 15 0 0 — 2 — 3 | — 4 I — 1 / 3 × I I I I I — 2 × I →
→ 1 0 2 / 3 0 | — 11 / 3 0 1 0 5 | 5 0 0 7 — 9 | — 25 0 0 — 2 — 3 | — 4
- Третий этап
На третьем этапе необходимо также обнулить элементы третьего столбца. Для этого находим разрешающий элемент в третьей строке — это 7. Но на 7 делить неудобно, поэтому необходимо менять строки местами, чтобы разрешающий элемент стал -2:
1 0 2 / 3 0 | — 11 / 3 0 1 0 5 | 5 0 0 7 — 9 | — 25 0 0 — 2 — 3 | — 4 → 1 0 2 / 3 0 | — 11 / 3 0 1 0 5 | 5 0 0 — 2 — 3 | — 4 0 0 7 — 9 | — 25
Теперь делим все элементы третьего столбца на -2 и обнуляем все элементы:
1 0 2 / 3 0 | — 11 / 3 0 1 0 5 | 5 0 0 — 2 — 3 | — 4 0 0 7 — 9 | — 25 I I I ÷ (- 2) → 1 0 2 / 3 0 | — 11 / 3 0 1 0 5 | 5 0 0 1 3 / 2 | 2 0 0 0 — 9 | — 25 I — 2 / 3 × I I I I V — 7 × I I I →
1 0 0 — 1 | — 5 0 1 0 5 | 5 0 0 1 3 / 2 | 2 0 0 0 — 39 / 2 | — 39
- Четвертый этап
Обнуляем четвертый столбец. Разрешающий элемент — — 39 2:
Разрешающий элемент — — 39 2:
1 0 0 — 1 | — 5 0 1 0 5 | 5 0 0 1 3 / 2 | 2 0 0 0 — 39 / 2 | — 39 I V ÷ (- 39 2) → 1 0 0 — 1 | — 5 0 1 0 5 | 5 0 0 1 3 / 2 | 2 0 0 0 1 | 2 I + I V I I — 5 × I V I I I — 3 / 2 × I V →
→ 1 0 0 0 | — 3 0 1 0 0 | — 5 0 0 1 0 | — 1 0 0 0 1 | 2 .
Ответ : x 1 = — 3 ; x 2 = — 5 ; x 3 = — 1 ; x 4 = 2
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
4. Метод Жордана — Гаусса.
Схема с выбором главного элемента состоит в том, что требование неравенства нулю диагональных элементов akk, на которые происходит деление в процессе исключения, заменятся более жестким: из всех элементов К-го столба выбрать наибольший по модулю и переставить уравнения так, чтобы этот элемент оказался на месте элемента акк. Выбор главного элемента и связанная с ним перестановка строк необходимы в тех случаях, когда на каком-либо i-ом шаге акк=0 либо же акк очень мало по остальными элементами i- го столбца: при делении на такое «малое» акк будут получаться большие числа с большими абсолютными погрешностями, в результате чего решение может сильно исказиться.
Ниже излагается алгоритм полного исключения неизвестных или метод Жордана – Гаусса. Суть метода состоит в том, что, рассмотрев первое уравнение, в нем неизвестное с коеффициэнтом, отличным от нуля (в дальнейшем разрешающий элемент), и разделив первое уравнение на этот коэффициент, с помощью первого уравнения исключают это неизвестное из всех уравнений, кроме первого. Выбрав во втором уравнении неизвестное с коэффициентом, отличным от нуля, и разделив на него второе уравнение, с помощью второго исключают другие неизвестные из всех уравнений, кроме второго и т.д., т.е. с помощью одного уравнения производят полное исключение одного неизвестного. Процесс продолжается до тех пор, пока не будут использованы все уравнения.
Как известно, системы линейных алгебраических уравнений могут имеет одно решение, множество решений или системы несовместны. При элементарных преобразованиях элементов матрицы системы эти случаи выявляются в следующем:
1. В процессе исключений левая часть I –го уравнения системы обращается в нуль, а правая часть равна некоторому числу, отличному от нуля. т.е. 02+=bc0.
т.е. 02+=bc0.
Это означает, что система не имеет решений, так как I – му уравнению не могут удовлетворять никакие значения неизвестных;
2. Левая и правая части I – го уравнения обращаются в нуль. Это означает, что I – ое уравнение является линейной комбинацией остальных, ему удовлетворяет любое найденное решение системы, поэтому оно может быть отброшено. В системе количество неизвестных больше количества уравнений и, следовательно, такая система имеет множество решений;
3. После того как все уравнения использованы для исключения неизвестных получено решение системы.
Таким образом, конечной целью преобразований Жордана-Гаусса является получение из заданной линейной системы
| a11x1 + a12x2 + … + a1nxn = b1,n+1 |
a21x1 + a22x2 + … + a2nxn = b2,n+1 |
| am1x1 + am2x2 + … + amnxn = bm.n+1 |
Здесь x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно.
Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно.
Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной.
Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.
Решение системы (1) — совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все ее уравнения в тождества.
Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее нет ни одного решения.
Совместная система вида (1) может иметь одно или более решений.
Решения c1(1), c2(1), …, cn(1) и c1(2), c2(2), …, cn(2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:
c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2).
Совместная система вида (1) называется определенной, если она имеет единственное решение; если же у нее есть хотя бы два различных решения, то она называется неопределенной. Если уравнений больше, чем неизвестных, она называется переопределённой.
Если уравнений больше, чем неизвестных, она называется переопределённой.
Решим следующую систему уравнений:
Запишем её в виде матрицы 3×4, где последний столбец является свободным членом:
Проведём следующие действия:
· К строке 2 добавим: -4 * Строку 1.
· К строке 3 добавим: -9 * Строку 1.
· К строке 3 добавим: -3 * Строку 2.
· Строку 2 делим на -2
· К строке 1 добавим: -1 * Строку 3.
· К строке 2 добавим: -3/2 * Строку 3.
· К строке 1 добавим: -1 * Строку 2.
В правом столбце получаем решение:
.
В методе Ньютона наблюдается ускорение сходимости процесса приближений. 5. Метод касательных (метод Ньютона)
Метод касательных, связанный с именем И. Ньютона, является одним из наиболее эффективных численных методов решения уравнений. Идея метода очень проста. Возьмём производную точку x0 и запишем в ней уравнение касательной к графику функции f(x): y=f(x0)+ f ¢(x) (x-x0) (1. 5) Графики…
5) Графики…
Решения от численных методов расчёта. Для определения корней уравнения не требуется знания теорий групп Абеля, Галуа, Ли и пр. и применения специальной математической терминологии: колец, полей, идеалов, изоморфизмов и т.д. Для решения алгебраического уравнения n — ой степени нужно только умение решать квадратные уравнения и извлекать корни из комплексного числа. Корни могут быть определены с…
Математики тригонометрической подстановки и проверка эффективности разработанной методики преподавания. Этапы работы: 1. Разработка факультативного курса на тему: «Применение тригонометрической подстановки для решения алгебраических задач» с учащимися классов с углубленным изучением математики. 2. Проведение разработанного факультативного курса. 3. Проведение диагностирующей контрольной…
… «проявляется» лишь в процессе преобразований. Очевидность и «завуалированность» новой переменной мы рассмотрим на конкретных примерах во второй главе данной работы. 2. Возможности применения метода замены неизвестного при решении алгебраических уравнений В этой главе выявим возможности применения метода замены неизвестного при решении алгебраических уравнений в стандартных и нестандартных…
2. Возможности применения метода замены неизвестного при решении алгебраических уравнений В этой главе выявим возможности применения метода замены неизвестного при решении алгебраических уравнений в стандартных и нестандартных…
Матрицы. Операции над матрицами. Элементарные преобразования. Приведение к ступенчатому виду. Ранг матрицы презентация, доклад
Матрицы. Операции над матрицами. Элементарные преобразования. Приведение к ступенчатому виду. Ранг матрицы. Решение систем линейных алгебраических уравнений методом Гаусса
Калабухова Галина Валентиновна,
к.социол.н., доцент
Тема 4
Вопросы темы:
Матрицы: терминология и обозначения.
Операции над матрицами: сложение, умножение матрицы на число. Умножение матриц. Транспонирование матрицы.
Элементарные преобразования матрицы. Приведение к ступенчатому виду.
Ранг матрицы.
Решение систем линейных алгебраических уравнений методом Гаусса.
Матрицы:
терминология и обозначения
Определение
Матрицей размера m x n называется прямоугольная таблица, состоящая из m строк и n столбцов, заполненная некоторыми элементами
Обозначения:
Amxn – матрица
aij – элемент матрицы, расположенный на пересечении i-той строки и j-ого столбца
m x n – размер матрицы
Применение матриц
Матрицы широко применяются в математике для компактной записи систем линейных алгебраических уравнений или систем дифференциальных уравнений. Тогда количество строк матрицы соответствует количеству уравнений системы, а количество столбцов равно количеству неизвестных
Другие определения
Если все элементы матрицы равны нулю, то матрица называется нулевой. Обозначается: Θ
Обозначается: Θ
Если n = m, то матрица называется квадратной, а n – порядком матрицы.
Другие определения
Строка (столбец) матрицы называется нулевой, если все ее (его)элементы равны нулю.
Если хотя бы один из элементов строки (столбца) не равен нулю, то строка (столбец) называется ненулевой
Пример:
нулевой
столбец
ненулевой
столбец
нулевая строка
ненулевая строка
Другие определения
Главной диагональю матрицы называется диагональ, проведённая из левого верхнего угла матрицы в правый нижний.
Побочной диагональю матрицы называется диагональ, проведённая из левого нижнего угла матрицы в правый верхний.
Пример:
главная диагональ
побочная диагональ
Другие определения
Матрица, состоящая из одной строки, называется вектор-строкой, а матрица, состоящая из одного столбца, — вектор-столбцом.
Примеры:
вектор-строка
вектор-столбец
Другие определения
Квадратная матрица называется диагональной, если все ее элементы, стоящие вне главной диагонали, равны нулю.
Скалярной называется диагональная матрица S, у которой все диагональные элементы равны между собой.
Единичной матрицей En называется скалярная матрица порядка n, диагональные элементы которой равны 1.
Другие определения
Матрица называется верхней треугольной матрицей, если все элементы ниже главной диагонали равны нулю.
Матрица называется нижней треугольной матрицей, если все элементы выше главной диагонали равны нулю.
Примеры:
верхнетреугольная
матрица
Другие определения
Ступенчатой называется матрица, которая содержит m строк и у которой первые r ≤ m диагональных элементов ненулевые, а элементы, лежащие ниже главной диагонали и элементы последних (m — r) строк равны нулю, то есть это матрица вида:
Главным элементом некоторой строки матрицы A называется ее первый ненулевой элемент
Другие определения
Матрица А называется ступенчатой, если:
все ее нулевые строки стоят после ненулевых;
в каждой ненулевой строке, начиная со второй, ее главный элемент стоит правее (в столбце с большим номером) главного элемента предыдущей строки.
Примеры ступенчатых матриц:
НЕ ЯВЛЯЕТСЯ СТУПЕНЧАТОЙ:
Другие определения
Две матрицы называются равными, если они имеют одинаковые размеры и их соответствующие элементы равны:
Anxm = Bnxm aij = bij, i = 1,n, j = 1,m
Операции над матрицами
Произведением матрицы на число
называется матрица, полученная из исходной умножением каждого ее элемента на заданное число
B = λA, bij = λaij, i = 1,n, j = 1,m
Суммой матриц
A и B одного размера называется матрица C = A + B, такого же размера, получаемая из исходных путем сложения соответствующих элементов
C = A + B, cij = aij+bij, i = 1,n, j = 1,m
Свойства линейных операций
Умножение матрицы на число
Сумма матриц
Ассоциативность: (A + B) + C = A + (B + C)
A + Θ = Θ + A, где Θ – нулевая матрица
A – A = Θ
Коммуникативность: A + B = B + A
Дистрибутивность: λ * (A + B) = λ * A + λ * B
(λ + μ) * A = λ * A + μ * A
(λ * μ) * A = λ * (μ * A)
— линейные операции
Произведением матриц
Amxn на матрицу Bnxk называется матрица Cmxk такая, что элемент матрицы С, стоящий в i-той строке и j-том столбце (т. е. элемент cij) равен сумме произведений элементов i-той строки матрицы A на соответствующие элементы j-го столбца матрицы B
е. элемент cij) равен сумме произведений элементов i-той строки матрицы A на соответствующие элементы j-го столбца матрицы B
C = A * B, cij = Σail*blj, l = 1,n
Свойства произведения матриц
Ассоциативность: (A * B) * C = A * (B * C)
Ассоциативность по умножению: (μ * A) * B = μ * (A * B)
Дистрибутивность: A * (B + C) = A * B + A * C;
(A + B) * C = A * C + B * C
Умножение на единичную матрицу: E * A = A * E = A
Некоммуникативно: A * B ≠ B * A
Транспонирование матрицы
это операция над матрицей, когда ее строки становятся столбцами с теми же номерами.
Обозначается AT
Свойства операции транспонирования матриц
(AT)T = A
(λ * A)T = λ * AT
(A + B)T = AT + BT
(A * B)T = BT * AT
Элементарные преобразования матрицы
Эквивалентные преобразования над строками матрицы
называют следующие преобразования строк:
умножение строки на ненулевое число;
перестановка двух строк;
прибавление к одной строке матрицы другой ее строки, умноженной на некоторое ненулевое число.
Если от матрицы к матрице перешли с помощью эквивалентных преобразований над строками, то такие матрицы называются эквивалентными и обозначают
A ~ B.
Ранг матрицы
Определения
Линейной комбинацией (ЛК) строк s1, s2, …, sm матрицы A называется выражение λ1s1 + λ2s2 +…+λmsm.
ЛК называется тривиальной, если все коэффициенты λi равны нулю одновременно.
ЛК называется нетривиальной, если хотя бы один из коэффициентов λi отличен от нуля.
Система строк называется линейно зависимой (ЛЗ), если существует их нетривиальная ЛК, равная нулевой строке
Система строк называется линейно независимой (ЛНЗ), если только тривиальная ЛК равна нулевой строке
Рангом системы строк
называется максимальное количество линейно независимых строк этой системы
В каждой матрице может быть два ранга: строчный ранг (ранг системы строк) и столбцовый ранг (ранг системы столбцов).
Теорема: Строчный ранг матрицы равен её столбцовому рангу
Рангом матрицы
называется ранг её системы строк или столбцов
Обозначается: rang A.
Элементарные преобразования над строками (столбцами) матрицы не меняют её ранга.
Ранг ступенчатой матрицы равен количеству её ненулевых строк.
На практике для нахождения ранга матрицы используют следующее утверждение: ранг матрицы равен количеству ненулевых строк после приведения матрицы к ступенчатому виду.
Решение систем линейных алгебраических уравнений методом Гаусса
Системой линейных алгебраических уравнений (СЛАУ)
называется система вида:
Упорядоченный набор значений {x01, x02, …, x0n} называется решением системы, если при подстановке в уравнения все уравнения превращаются в тождество
Определения
СЛАУ называется совместной, если она имеет хотя бы одно решение.
В противном случае система называется несовместной.
Система называется определённой, если она совместна и имеет единственное решение.
В противном случае (т.е. если система совместна и имеет более одного решения) система называется неопределённой.
Система называется однородной, если все правые части уравнений, входящих в нее, равны нулю одновременно.
Система называется квадратной, если количество уравнений равно количеству неизвестных.
Определения
Расширенной матрицей системы A = (A|B) называется матрица, полученная из матрицы системы A, дописыванием справа после вертикальной черты столбца свободных членов B.
Принцип метода Гаусса
Метод Гаусса включает в себя прямой (приведение расширенной матрицы к ступенчатому виду) и обратный (получение нулей над главной диагональю расширенной матрицы) ходы. Прямой ход и называется методом Гаусса, обратный — методом Гаусса-Жордана, который отличается от первого только последовательностью исключения переменных.
Метод Гаусса идеально подходит для решения систем содержащих больше трех линейных уравнений, для решения систем уравнений, которые не являются квадратными, т.о. метод Гаусса — наиболее универсальный метод для нахождения решения любой системы линейных уравнений, он работает в случае, когда система имеет бесконечно много решений или несовместна
Скачать презентацию
Echelon Transform
Матрица имеет форму эшелона строк (ссылка) когда он удовлетворяет следующим условиям.
- Первый ненулевой элемент в каждой строке, называемый ведущая запись , равна 1.
- Каждая ведущая запись находится в столбце справа от ведущая запись в предыдущей строке.
- Строки со всеми нулевыми элементами, если таковые имеются, находятся ниже строк, имеющих ненулевой элемент.
Матрица в сокращенной ступенчатой форме строки (ссылка) когда он удовлетворяет следующим условиям.
- Матрица имеет эшелонированную форму (т.
 е. удовлетворяет условию
три условия, перечисленные выше).
е. удовлетворяет условию
три условия, перечисленные выше). - Первая запись в каждой строке является единственной ненулевой записью в его столбец.
Матрица в ступенчатой форме называется ступенчатой матрицей . Матрица A и матрица B являются примерами ступенчатых матриц.
|
| |||||||||||||||||||||||||||||||||||||
| A | B |
Matrix A находится в форме эшелона строк, а матрица B находится в форме редуцированного эшелонированного ряда.
Реклама
Как преобразовать матрицу в ее ступенчатую форму
Любую матрицу можно преобразовать в ступенчатую форму, используя ряд элементарные операции со строками. Вот как.
- Свести матрицу
- Найти точку разворота , первую ненулевую запись в первый столбец матрицы.
- Поменять ряды местами, перемещая основной ряд в первый ряд.
- Умножить каждый элемент в сводной строке на величину, обратную
- Прибавьте кратные значения сводной строки к каждой из нижних строк, поэтому каждый элемент в сводном столбце нижнего rows равно 0.
- Чтобы получить матрицу в виде эшелона строк, повторите разворот
- Повторите процедуру, начиная с шага 1 выше, игнорируя предыдущий сводные ряды.
- Продолжайте до тех пор, пока не закончатся опорные точки. обработанный.
- Чтобы получить матрицу в уменьшенной строковой ступенчатой форме, обработайте ненулевой
записи над каждым сводом.

- Определите последнюю строку, имеющую опорную точку, равную 1, и пусть это будет сводная строка.
- Добавьте кратные значения сводной строки в каждую из верхних строк, пока каждый элемент над опорной точкой не будет равен 0.
- Перемещаясь вверх по матрице, повторите этот процесс для каждой строки.
Преобразование матрицы в ее эшелонированные формы: пример
Чтобы проиллюстрировать процесс преобразования, преобразуем Matrix A в рядный эшелон форме и к форме редуцированного эшелонированного ряда.
| ⇒ |
| ⇒ |
| |||||||||||||||||||||||||||||||||
| A | A 1 | A 2 |
| ⇒ |
| ⇒ |
| ||||||||||||||||||||||
| A ref | A rref |
Для преобразования матрицы A в ее эшелонные формы мы реализовали
следующую серию элементарных операций над строками.
Мы нашли первую ненулевую запись в первом столбце матрицы в строке 2; поэтому мы поменяли местами ряды 1 и 2, в результате чего в матрице A 1 .
Работа с матрицей А 1 , мы умножили каждый элемент строки 1 на -2 и добавили результат к Строка 3. Получилось A 2 .
Работа с матрицей А 2 , мы умножили каждый элемент строки 2 на -3 и добавили результат к Ряд 3. Получилось A исх. . Заметь Номер ref находится в форме эшелона строк, потому что он удовлетворяет следующим требованиям: (a) первая ненулевая запись каждого строка равна 1, (b) первая ненулевая запись находится справа от первой ненулевой элемент в предыдущей строке и (c) строки, полностью состоящие из нули находятся внизу матрицы.
И, наконец, работа с матрицей A ref , мы умножили вторую строку на -2 и добавили ее к первый ряд.
 Это произвело A rref .
Обратите внимание, что A rref в уменьшено эшелонированную форму строки, так как она удовлетворяет требованиям к
форма эшелона строки плюс каждая ведущая ненулевая запись является единственной ненулевой
запись в своей колонке.
Это произвело A rref .
Обратите внимание, что A rref в уменьшено эшелонированную форму строки, так как она удовлетворяет требованиям к
форма эшелона строки плюс каждая ведущая ненулевая запись является единственной ненулевой
запись в своей колонке.
Примечание: Эшелонная матрица строк, полученная из ряда элементарные операции со строками не обязательно уникальны. Другой набор строк операции могут привести к другой ступенчатой матрице строк. Однако, уменьшенная рядная эшелонированная матрица уникальна; каждая матрица имеет только один уменьшенная ступенчатая матрица строк.
Проверьте свое понимание
Задача 1
Рассмотрим матрицу X , показанную ниже.
| X = |
|
Какая из следующих матриц является редуцированной эшелонированной формой строк матрица X ?
|
|
|
| ||||||||||||||||||||||||||||||||
| A | B | C | D |
(a) Матрица A
(B) Матрица B
(C) Матрица C
(D) Матрица D
(E). Ни один из вышеупомянутых
Ни один из вышеупомянутых
Solade Alge.
Правильный ответ (Б). Элементарные операции со строками, используемые для изменения Показана матрица X в ее уменьшенной эшелонированной форме строк. ниже.
| ⇒ |
| ⇒ |
| ⇒ |
| ||||||||||||||||||||||||||||||||
| X | X 1 | x 2 | x RREF |
на изменение x 9004. следующие шаги:
следующие шаги:
- Поменять местами ряды 1 и 2, получив X 1 .
- В Х 1 , умножьте 2-й ряд на -5 и прибавьте его к 3-му ряду, получив Х 2 .
- В Х 2 , умножьте 2-й ряд на -2 и прибавьте его к 1-му ряду, получив X rref .
Примечание: Matrix A не имеет сокращенной ступенчатой формы, потому что ведущая запись в строке 2 находится слева от ведущей записи в Ряд 3; он должен быть справа. Матрица С не находится в форме редуцированного эшелона строк, потому что столбец 2 имеет больше чем одна ненулевая запись. И, наконец, матрица D не в сокращенной эшелонированной форме строки, потому что следует строка 2 со всеми нулями по строке с ненулевым элементом; все нулевые строки должны следовать за ненулевыми строками.
Последний урок Следующий урок
Эшелонированная форма рядов и Сокращенная эшелонированная форма рядов
Содержание (Нажмите, чтобы перейти к этому разделу:
- Что такое эшелонированная форма?
- Форма эшелона рядов
- Форма эшелона с уменьшенным рядом
- Исключение Гаусса
- Ранг матрицы
Посмотрите видео с определениями эшелона, рядного эшелона и уменьшенного рядного эшелона:
Рядный эшелон и уменьшенный рядный эшелон
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Что такое Форма Эшелона?
Эшелонная форма означает, что матрица находится в одном из двух состояний:
- Рядно-эшелонная форма.
- Эшелонная форма уменьшенного ряда.
Это означает, что матрица удовлетворяет следующим трем требованиям:
- Первое число в строке (называемое старшим коэффициентом) равно 1. Примечание: некоторые авторы не требуют, чтобы старший коэффициент был равен 1; это может быть любое число. Вы можете уточнить у своего инструктора, какой версии этого правила он придерживается).
- Каждая ведущая 1 находится справа от той, что над ней.
- Любые ненулевые строки всегда выше строк со всеми нулями.
Следующие примеры относятся к матрицам в эшелонированной форме:
Следующие примеры представляют собой , а не в эшелонированной форме:
Матрица A не имеет нулевых строк ниже ненулевых строк.
Матрица B имеет 1 на 2-й позиции в третьей строке. Для эшелонированной формы строки он должен быть справа от ведущего коэффициента над ним. Другими словами, он должен быть на четвертой позиции вместо 3.
Матрица C имеет 2 в качестве старшего коэффициента вместо 1.
Матрица D имеет -1 в качестве ведущего коэффициента вместо 1. матрица подверглась исключению по методу Гаусса, который представляет собой серию операций со строками.
Уникальность и эшелонированные формы
Эшелонная форма матрицы не уникальна, а это означает, что при сокращении строк возможно бесконечное количество ответов. Эшелонная форма уменьшенного ряда находится на другом конце спектра; это — это уникальное число , что означает, что сокращение строк в матрице даст один и тот же ответ независимо от того, как вы выполняете одни и те же операции со строками.
Наверх.
Что такое форма эшелонирования строк?
Матрица имеет ступенчатую форму, если она удовлетворяет следующим требованиям:
- Первое ненулевое число слева («старший коэффициент») всегда находится справа от первого ненулевого числа в строке выше.

- Строки, состоящие только из нулей, находятся внизу матрицы.
Технически старший коэффициент может быть любым числом. Однако в большинстве учебников по линейной алгебре указывается, что старший коэффициент должен быть числом 1. Чтобы добавить путаницы, некоторые определения эшелонированной формы строк утверждают, что нули должны быть как выше , так и ниже старшего коэффициента. Поэтому лучше всего следовать определению, данному в учебнике, которому вы следуете (или тому, что дал вам ваш профессор). Если вы не уверены (например, сегодня воскресенье, ваша домашняя работа должна быть сделана, а вы не можете дозвониться до преподавателя), безопаснее всего использовать 1 в качестве старшего коэффициента в каждой строке.
Если старший коэффициент в каждой строке является только ненулевым числом в этом столбце, говорят, что матрица имеет форму сокращенного эшелона строк.
Эшелонированные формы строк часто встречаются в линейной алгебре, когда вас иногда просят преобразовать матрицу в эту форму. Форма эшелона строк может помочь вам увидеть, что представляет собой матрица, а также является важным шагом к решению систем линейных уравнений.
Онлайн-калькулятор формы эшелона строк
Этот онлайн-калькулятор преобразует любую матрицу, и обеспечивает операции со строками, которые помогут вам перейти от шага к шагу. На следующем изображении (из калькулятора Old Dominion University Calculator показано, как матрица [01, 00, 59] сводится к форме эшелона строк с помощью двух простых операций со строками:
Вернуться к началу.
Что такое сокращенная форма эшелона строк?
Сокращенная ступенчатая форма строки — это тип матрицы, используемой для решения систем линейных уравнений.Сокращенная ступенчатая форма строки имеет четыре требования:
- Первое ненулевое число в первой строке ( первая запись ) — это число 1.

- Вторая строка также начинается с цифры 1, которая находится правее первой записи в первой строке. В каждой последующей строке цифра 1 должна быть правее.
- Начальная запись в каждой строке должна быть единственным ненулевым числом в своем столбце.
- Любые ненулевые строки помещаются в конец матрицы.
Преобразование матрицы в форму редуцированного эшелона строк
Любую матрицу можно преобразовать в форму редуцированного эшелона строк, используя метод, называемый методом исключения Гаусса. Это особенно полезно для решения систем линейных уравнений. Большинство графических калькуляторов (таких как TI-83) имеют функцию rref, которая преобразует матрицу в сокращенную ступенчатую форму строк. См.: В этой статье на веб-сайте Университета штата Колорадо приведены инструкции по использованию TI-89 и TI-83 для расчета формы сокращенного эшелона строк.
Этот онлайн-калькулятор на веб-сайте Университета Олд Доминион преобразует матрицу, которую вы вводите, в сокращенную форму эшелона строк.
Расчет вручную требует знания элементарных операций со строками, а именно:
- Замена одной строки на другую.
- Умножить одну строку на ненулевую константу.
- Заменить одну строку на: одну строку плюс константу, умноженную на другую строку.
Кроме того, недостаточно просто знать правила, нужно уметь смотреть на матрицу и принимать логические решения о том, какое правило и когда использовать. Вы пытаетесь преобразовать матрицу в уменьшенную эшелонированную форму строк, поэтому вам также потребуется обратиться к четырем требованиям, изложенным в начале этой статьи. Если вам нужно преобразовать матрицу в сокращенную ступенчатую форму вручную, рекомендуется использовать один из калькуляторов выше, чтобы проверить свою работу. Фактически, если вы используете онлайн-калькулятор ODU, он даже предоставит вам операции со строками. На изображении ниже показано преобразование калькулятором матрицы [204,923]:
Наверх.
Что такое исключение Гаусса?
Исключение Гаусса — это способ найти решение системы линейных уравнений. Основная идея заключается в том, что вы выполняете математическую операцию над строкой и продолжаете до тех пор, пока не останется только одна переменная. Например, некоторые возможные операции со строками:
Основная идея заключается в том, что вы выполняете математическую операцию над строкой и продолжаете до тех пор, пока не останется только одна переменная. Например, некоторые возможные операции со строками:
- Замена любых двух строк местами
- Сложите две строки вместе.
- Умножить одну строку на ненулевую константу (например, 1/3, -1, 5)
Вы также можете выполнять более одной операции со строками одновременно. Например, умножьте одну строку на константу, а затем добавьте результат к другой строке.
После этого цель состоит в том, чтобы в конечном итоге получить матрицу в форме сокращенного эшелона строк, где старший коэффициент a 1 в каждой строке находится справа от старшего коэффициента в строке над ним. Другими словами, вам нужно получить 1 в верхнем левом углу матрицы. В следующей строке должен быть 0 в позиции 1 и 1 в позиции 2. Это дает вам решение системы линейных уравнений.
Исключение Гаусса Пример
Решите следующую систему линейных уравнений, используя исключение Гаусса:
- x + 5y = 7
- -2x – 7y = -5
Шаг 1: Преобразуйте уравнение в форму матрицы коэффициентов . Другими словами, просто возьмите коэффициент для чисел и забудьте пока о переменных:
Другими словами, просто возьмите коэффициент для чисел и забудьте пока о переменных:
Шаг 2: Превратите числа в нижней строке в положительные, добавив 2 раза первую строку:
Шаг 3: Умножьте вторую строку на 1/3. Это дает вам второй ведущий 1:
Шаг 4: Умножьте строку 2 на -5, а затем добавьте это к строке 1:
Вот и все!
В первой строке у вас есть x = -8, а во второй строке y = 3. Обратите внимание, что x и y находятся в тех же позициях, что и при преобразовании уравнения на шаге 1, поэтому все, что вам нужно сделать, это прочитать решение:
Вернуться к началу.
Каков ранг матрицы?
Ранг матрицы равен количеству линейно независимых строк. Линейно независимая строка — это строка, которая не является комбинацией других строк.
Следующая матрица имеет две линейно независимые строки (1 и 2). Однако, когда в смесь добавляется третья строка, вы можете видеть, что первая строка теперь равна сумме второй и третьей строк. Следовательно, ранг этой конкретной матрицы равен 2, так как есть только две линейно независимые строки.
Следовательно, ранг этой конкретной матрицы равен 2, так как есть только две линейно независимые строки.
Ранг матрицы всегда будет на меньше, чем на количество ненулевых строк или количество столбцов в матрице. Если все строки в матрице линейно независимы, матрица имеет полный ранг строки . Для квадратной матрицы она имеет полный ранг только в том случае, если ее определитель отличен от нуля.
Выяснение ранга матрицы, пытаясь визуально определить только количество линейно независимых строк или столбцов, может оказаться практически невозможным. Более простым (и, возможно, очевидным) способом является преобразование в эшелонированную форму строк.
Как найти ранг матрицы
Найти ранг матрицы просто, если вы знаете, как найти ступенчатую матрицу строк. Чтобы найти ранг любой матрицы:
- Найдите ступенчатую матрицу строк.
- Подсчитать количество ненулевых строк.

Приведенная выше матрица была преобразована в ступенчатую форму строк с двумя ненулевыми строками. Следовательно, ранг матрицы равен 2.
Вы также можете найти отличный инструмент конвертации на сайте Университета Старого Доминиона.
Наверх.
Ссылки
Everitt, B.S.; Скрондал, А. (2010), Кембриджский статистический словарь, издательство Кембриджского университета.
Гоник, Л. (1993). Мультяшный путеводитель по статистике. HarperPerennial.
Сирл, С. (2017). Матричная алгебра, полезная для статистики (серия Wiley по теории вероятностей и статистике), 2-е издание. Уайли.
УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Форма эшелона ряда и уменьшенная форма эшелона ряда» Из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/matrices-and-matrix-алгебра/reduced-row-echelon-form-2/
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .
Создание многошаговой пользовательской формы :: Документация Squiz (Матрица)
В этом учебном пособии показано, как создать онлайн-форму заявления о приеме на работу с помощью актива «Пользовательская форма».
Пользователь может заполнить форму на нескольких страницах, включая загрузку вложенного файла на одном из шагов. Перед отправкой формы пользователь может подтвердить свои ответы на странице подтверждения формы.
Содержание
- Перед началом работы
- Настройка пользовательской формы
- Добавить вопросы формы
- Создать папку для отправки файлов
- Настройка раскладки
- Настройка макета содержимого страницы
- Настройка макета страницы подтверждения
- Настройка макета «Спасибо»
- О неполных представлениях
- Резюме
Прежде чем начать
В этом руководстве предполагается, что у вас уже есть базовые знания и понимание ресурса Custom Form.
| Чтобы увидеть работающее решение для этого учебного пособия, вы можете загрузить учебные ресурсы , используемые в этом учебном пособии, и импортировать их в свою систему Matrix с помощью инструмента «Импортировать активы из XML». |
Настройка пользовательской формы
Начните с создания и настройки актива пользовательской формы, используемого для питания нашей формы заявления о приеме на работу. Эта форма состоит из трех основных шагов, которые необходимо выполнить пользователю, поэтому мы создадим раздел для каждого шага.
Начните с создания нового актива пользовательской формы с именем «Приложение о приеме на работу» в месте, где вы можете просмотреть его на внешнем интерфейсе.
Щелкните правой кнопкой мыши ресурс «Содержимое формы» и выберите экран содержимого формы.
Добавьте в форму три раздела: «Личная информация», «Загрузить резюме» и «Заключительные комментарии».

На том же экране прокрутите вниз до раздела «Форматирование» и установите параметр «Использовать страницу подтверждения?». вариант «Да».
Найдите поле «Использовать основной текст» и выберите «Содержимое страницы», «Содержимое страницы подтверждения» и «Спасибо».
Мы настроим эти макеты позже в этом руководстве, но сейчас нам нужно сделать их видимыми. Прокрутите вниз до раздела «Параметры нескольких страниц из» и установите параметр «Многостраничный?». выберите значение Да, чтобы каждый из разделов, созданных на предыдущем шаге, представлял собой отдельную страницу пользовательской формы.
Добавьте вопросы формы
Добавьте несколько полевых вопросов в каждый раздел. Для нашего примера мы добавим следующие вопросы:
В разделе личной информации:
Текстовый вопрос под названием Имя.

Текстовый вопрос под названием «Контактный номер».
Вопрос об адресе электронной почты под названием «Адрес электронной почты».
В разделе «Загрузить резюме»:
В разделе «Заключительные комментарии»:
Создать папку для отправки файлов
Нам нужно определить место для хранения любых файлов, загруженных соискателями с помощью нашей формы.
Создайте новый актив «Папка» в активе «Пользовательская форма заявления о приеме на работу» и назовите его «CV».
Перейти к экрану сведений о вопросе резюме.
В поле «Создать местоположения» выберите папку CV в качестве выбора активов и сохраните экран.
Передовая практика
На этом этапе вы можете добавить правила проверки файлов, чтобы кандидаты загружали только те типы файлов, которые вы принимаете (например,.и pdf
pdf .doc) и ограничения на размер файлов, которые они могут загружать.
Теперь актив вашей пользовательской формы в дереве должен выглядеть примерно так:
Настройка макета
Уточните макет презентации для различных шагов, включая форматы страниц подтверждения и благодарности.
Настройка макета содержимого страницы
Начните с макета содержимого страницы формы. Нам нужно добавить пару дополнительных функций, таких как кнопка «Предыдущая страница», для лучшей навигации при заполнении формы.
Щелкните правой кнопкой мыши ресурс «Содержимое страницы» и выберите экран «Редактировать содержимое».
Откройте всплывающее окно Изменить свойства компонента и измените компонент на Код, сохраните экран.
Вставьте следующую базовую разметку HTML с заменой ключевых слов:
Введите значения ниже:
(1) %form_errors_message% (2) %current_page_contents% (3) <дел> %previous_page_button% %submit_button% (4)1 Этот статический текст появляется вверху каждого шага формы. 
2 %form_errors_message%печатает сообщение, если отправка шага формы не удалась.3 %current_page_contents%выводит содержимое каждого шага (раздела) формы.4 %previous_page_button%и%submit_button%печатать кнопки «Предыдущий шаг» и «Следующий шаг» динамически. Эти ключевые слова интеллектуальны тем, что если мы находимся на шаге 1 формы,%previous_page_button%не отображается. Если мы находимся на странице подтверждения формы,%submit_button%говорит «Отправить» вместо «Следующая страница».
При предварительном просмотре актива Custom Form во внешнем интерфейсе вы должны увидеть похожие макеты, описанные на следующих рисунках:
Рисунок 1. Экран личной информации
Рисунок 2. Экран загрузки файлов
Экран загрузки файлов
Рисунок 3. Закрытие экрана комментариев
Настройка макета страницы подтверждения
Далее мы настроим макет страницы подтверждения.
Перейдите на экран «Редактировать содержимое» актива «Контент страницы подтверждения».
Преобразование компонента в Код .
Вставьте следующую базовую HTML-разметку с заменой ключевых слов:
Подтвердите свои данные:
(1) %form_summary% (2) <дел> %previous_page_button% %submit_button% (3)1 Статический текст, уникальный только для этой страницы. 2 %form_summary%выводит сводку всех ответов формы, сгруппированных по каждому шагу (разделу) формы.3 %previous_page_button%и%submit_button%печатает кнопку «Предыдущая страница» (позволяя пользователю вернуться назад и изменить значения) и кнопку «Отправить».
Макет страницы подтверждения имеет аналогичный формат для внешнего интерфейса:
Настройка макета «Спасибо»
Наконец, мы настроим макет страницы «Спасибо», который показывает пользователю сообщение после того, как он успешно подали заявление о приеме на работу.
Перейдите на экран «Редактировать содержимое» актива «Спасибо».
Преобразование компонента в Код .
Вставьте следующую базовую разметку HTML с заменой ключевых слов:
Спасибо, %response_10154_q1%, за отправку.
(1)Ниже представлена информация, которую вы нам предоставили. Если что-то из этого неверно, свяжитесь с нами и укажите следующий ссылочный номер:
(2) %form_summary% (3)
%form_submission_id%1 Первый абзац состоит из некоторого статического текста, а также замены ключевого слова для ответа на вопрос «Имя» в разделе «Личная информация».  Замените идентификатор актива
Замените идентификатор актива 10154на тот, который соответствует вашему примеру.2 Распечатайте идентификатор актива отправки формы, созданного как часть отправки. Ключевое слово %form_submission_id%— отличный выбор для идентификатора ссылки, поскольку это уникальное значение хранится в Matrix.3 %form_summary%`выводит ту же сводку, которую мы видели на странице подтверждения.
О незавершенных отправках
При использовании многостраничной формы Matrix необходимо временно хранить ресурсы отправки формы, пока пользователь выполняет шаги. Хранение этой информации является ролью папки незавершенных представлений .
Папка незавершенных отправок создается Matrix автоматически при первой загрузке формы пользователем и переходе с шага 1 на шаг 2.
| Поскольку вы, вероятно, протестировали форму перед ее публикацией, эта папка уже должна быть доступна в ресурсе «Содержимое формы» в дереве: |
После того, как пользователь заполнит форму и выполнит все шаги, актив отправки формы перемещается из этой папки в папку отправки. Идентификатор актива доступен в области «Журналы отправки» актива «Содержимое формы».
Идентификатор актива доступен в области «Журналы отправки» актива «Содержимое формы».
Дополнительные сведения об этой функции см. в документации по журналам отправки.
Резюме
Теперь вы понимаете основные шаги, необходимые для создания многостраничной формы и настройки макетов для различных экранов. Вы также понимаете, как частично заполненные данные формы хранятся в Matrix.
Создание матричного визуального элемента в Power BI — Power BI
- Статья
- 12 минут на чтение
ПРИМЕНЯЕТСЯ К: ✔️ Power BI Desktop ✔️ Служба Power BI
Визуальное представление матрицы похоже на таблицу. Таблица поддерживает два измерения, а данные являются плоскими, то есть повторяющиеся значения отображаются, а не агрегируются. Матрица упрощает осмысленное отображение данных в нескольких измерениях — она поддерживает ступенчатый макет. Матрица автоматически агрегирует данные и позволяет выполнять детализацию.
Матрица упрощает осмысленное отображение данных в нескольких измерениях — она поддерживает ступенчатый макет. Матрица автоматически агрегирует данные и позволяет выполнять детализацию.
Вы можете создавать матричные визуальные элементы в отчетах Power BI и перекрестно выделять элементы в матрице с другими визуальными элементами на этой странице отчета. Например, вы можете выбирать строки, столбцы и даже отдельные ячейки и выделять их перекрестно. Кроме того, отдельные ячейки и выбор нескольких ячеек можно копировать и вставлять в другие приложения.
С матрицей связано множество функций, и мы рассмотрим их в следующих разделах этой статьи.
Примечание
Чтобы поделиться своим отчетом с коллегой по Power BI, необходимо, чтобы у вас обоих были отдельные лицензии Power BI Pro или чтобы отчет был сохранен в емкости Premium.
Понимание того, как Power BI вычисляет итоги
Прежде чем перейти к использованию визуального элемента матрицы, важно узнать, как Power BI вычисляет итоговые и промежуточные значения в таблицах и матрицах. Для итоговых и промежуточных строк Power BI оценивает меру по всем строкам в базовых данных — это не просто добавление значений в видимых или отображаемых строках. Это означает, что вы можете получить значения в итоговой строке, отличные от ожидаемых.
Для итоговых и промежуточных строк Power BI оценивает меру по всем строкам в базовых данных — это не просто добавление значений в видимых или отображаемых строках. Это означает, что вы можете получить значения в итоговой строке, отличные от ожидаемых.
Взгляните на следующие изображения матрицы.
В этом примере каждая крайняя справа строка в визуальной матрице показывает Сумма для каждой комбинации продавец/дата. Однако, поскольку продавец появляется с несколькими датами, числа могут появляться более одного раза. Таким образом, точная сумма из базовых данных и простое добавление видимых значений не равны. Это распространенный шаблон, когда значение, которое вы суммируете, находится на стороне «один» отношения «один ко многим».
Когда вы смотрите на итоги и промежуточные итоги, помните, что эти значения основаны на базовых данных. Они основаны не только на видимых значениях.
Существует два способа расширения заголовков строк. Первый — через контекстное меню. Вы увидите параметры для расширения выбранного вами заголовка строки, всего уровня или всего, вплоть до самого последнего уровня иерархии. У вас также есть аналогичные параметры для свертывания заголовков строк.
Вы увидите параметры для расширения выбранного вами заголовка строки, всего уровня или всего, вплоть до самого последнего уровня иерархии. У вас также есть аналогичные параметры для свертывания заголовков строк.
Вы также можете добавить кнопки +/- в заголовки строк через панель форматирования под Заголовки строк карточка. По умолчанию значки будут соответствовать форматированию заголовка строки, но при желании вы можете настроить цвета и размеры значков отдельно.
Когда значки включены, они работают так же, как значки сводных таблиц в Excel.
Состояние раскрытия матрицы будет сохранено вместе с вашим отчетом. Матрицу можно прикрепить к развернутой или свернутой панели мониторинга. Когда эта плитка панели мониторинга выбрана и отчет открывается, состояние раскрытия по-прежнему можно изменить в отчете.
Примечание
Если вы строите отчет на основе многомерной модели служб Analysis Services, необходимо учитывать некоторые особенности развертывания/свертывания, если в модели используется функция элемента по умолчанию. Дополнительные сведения см. в статье Работа с многомерными моделями в Power BI.
Дополнительные сведения см. в статье Работа с многомерными моделями в Power BI.
Использование действий детализации с визуальным представлением матрицы
С помощью визуального представления матрицы можно выполнять все виды интересных действий детализации, которые раньше были недоступны. Это включает в себя возможность детализации по строкам, столбцам и даже по отдельным разделам и ячейкам. Давайте посмотрим, как работает каждый из них.
На панели визуализаций, когда вы добавляете несколько полей в раздел Rows лунки Fields , вы включаете действия по детализации строк матричного визуального элемента. Это похоже на создание иерархии, которая затем позволяет выполнять детализацию (а затем резервное копирование) этой иерархии и анализировать данные на каждом уровне.
На следующем изображении раздел Rows содержит Этап продаж и Размер возможной сделки , создавая группировку (или иерархию) в строках, которые мы можем детализировать, чтобы увидеть подробности.
Когда визуальный элемент имеет группу, созданную в разделе Rows , сам визуальный элемент отображает значки сверления и расширения в верхнем углу визуального элемента.
Аналогично действиям детализации и развертывания в других визуальных элементах, выбор этих кнопок позволяет нам детализировать (или выполнить резервное копирование) иерархию. В этом случае мы можем перейти от Этап продаж к Размер возможной сделки , как показано на следующем рисунке, где детализация на один уровень выбрана иконка (вилы).
Помимо использования этих значков, вы можете выбрать любой из этих заголовков строк и развернуть его, выбрав в появившемся меню.
Обратите внимание, что в появившемся меню есть несколько параметров, которые дают разные результаты:
Выбор Развертка расширяет матрицу для уровня строки , исключая все остальные заголовки строк, кроме выбранного заголовка строки. . На следующем изображении Предложение > Было выбрано Детализация . Обратите внимание, что другие строки верхнего уровня больше не отображаются в матрице. Этот способ детализации является полезной функцией и становится особенно интересным, когда мы добираемся до раздела перекрестного выделения.
. На следующем изображении Предложение > Было выбрано Детализация . Обратите внимание, что другие строки верхнего уровня больше не отображаются в матрице. Этот способ детализации является полезной функцией и становится особенно интересным, когда мы добираемся до раздела перекрестного выделения.
Выберите значок Детализация , чтобы вернуться к предыдущему представлению верхнего уровня. Если вы затем выберете Proposal > Show Next Level , вы получите восходящий список всех элементов следующего уровня (в данном случае Размер возможной сделки ), без иерархической категоризации более высокого уровня.
Выберите значок Детализация в верхнем углу, чтобы в матрице отображались все категории верхнего уровня, затем выберите Предложение > Расширить до следующего уровня , чтобы просмотреть все значения для обоих уровней иерархии — Этап продаж и Размер возможной сделки .
Вы также можете использовать пункт меню Expand для дальнейшего управления дисплеем. Например, выберите Разверните значок . Затем выберите Proposal > Expand > Selection . Power BI отображает одну итоговую строку для каждого этапа продаж и всех вариантов размера возможности для предложения .
Детализация заголовков столбцов
Подобно возможности детализации строк, вы также можете детализировать столбцы. На следующем изображении в поле Columns есть два поля, что создает иерархию, подобную той, что мы использовали для строк ранее в этой статье. В Столбцы поле ну у нас регион и сегмент . Как только второе поле было добавлено в Columns , на визуальном элементе отображается новое раскрывающееся меню ( Drill on ), в настоящее время оно показывает Rows .
Чтобы развернуть столбцы, выберите Столбцы в меню Детализация , которое находится рядом со значками детализации и развертывания. Выберите регион East и выберите Drill Down 9.0004 .
При выборе Детализация отображается следующий уровень иерархии столбцов для Регион > Восток , в данном случае это Количество возможностей . Другой регион скрыт.
Остальные пункты меню работают со столбцами так же, как и со строками (см. предыдущий раздел, Детализация заголовков строк ). Вы можете Показать следующий уровень и Расширить до следующего уровня со столбцами точно так же, как со строками.
Примечание
Значки детализации и детализации применяются только к строкам. Чтобы развернуть столбцы, вы должны использовать контекстное меню.
Ступенчатый макет с матричными визуальными элементами
Матричный визуальный элемент автоматически устанавливает отступы для подкатегорий в иерархии под каждым родительским элементом, что называется ступенчатым макетом.
В исходной версии матричного визуального элемента подкатегории отображались в совершенно другом столбце, занимая гораздо больше места в визуальном элементе. На следующем изображении показана таблица в исходном матричном визуальном представлении. обратите внимание на подкатегории в отдельном столбце.
На следующем изображении вы видите матричный визуал со ступенчатой компоновкой в действии. Обратите внимание, что категория Qualify имеет подкатегории (Small, Medium и Large) с небольшим отступом, что обеспечивает более чистое и более сжатое изображение.
Вы можете легко изменить настройки ступенчатого макета. Выбрав матричный визуальный элемент, в разделе Формат (значок кисти) панели Визуализации разверните раздел заголовков строк. У вас есть два варианта: Переключатель Stepped layout (включает или выключает его) и Stepped layout indentation (указывает величину отступа в пикселях).
Если отключить ступенчатый макет, Power BI отображает подкатегории в другом столбце, а не с отступом под родительской категорией.
Промежуточные итоги и общие итоги с матричными визуальными элементами
Вы можете включить или выключить промежуточные итоги в матричных визуальных элементах как для строк, так и для столбцов. На следующем изображении вы можете видеть, что промежуточные итоги строк установлены на 9.0003 На и настроить отображение внизу.
Когда вы включаете Промежуточные итоги строки и добавляете метку, Power BI также добавляет строку и ту же метку для общего итогового значения. Чтобы отформатировать общую сумму, выберите вариант формата для Строка общей суммы .
Если вы хотите отключить промежуточные итоги и общий итог, в разделе форматирования панели визуализаций разверните карточку Строка промежуточных итогов . Поверните ползунок промежуточных итогов строки на Выкл. . При этом промежуточные итоги не отображаются.
. При этом промежуточные итоги не отображаются.
Тот же процесс применяется для промежуточных итогов столбца.
Добавление условных значков
Добавьте визуальные подсказки к таблице или матрице с помощью условных значков .
В разделе формата панели Визуализации разверните карточку Элементы ячейки . Переместите ползунок Icons в положение On и выберите значок определений.
Настройте условия, значки и цвета для вашей матрицы и выберите ОК . В этом примере мы использовали красный флажок для низких значений, фиолетовый кружок для высоких значений и желтый треугольник для всего, что между ними.
Перекрестное выделение с помощью матричных визуальных элементов
С помощью матричного визуального представления можно выбрать любые элементы в матрице в качестве основы для перекрестного выделения. Выберите столбец в матрице, и Power BI выделит столбец, как и любые другие визуальные элементы на странице отчета. Этот тип перекрестного выделения был общей чертой других визуальных элементов и выбора точек данных, поэтому теперь матричный визуальный элемент предлагает ту же функцию.
Этот тип перекрестного выделения был общей чертой других визуальных элементов и выбора точек данных, поэтому теперь матричный визуальный элемент предлагает ту же функцию.
Кроме того, использование Ctrl+щелчок также работает для перекрестного выделения. Например, на следующем изображении коллекция подкатегорий была выбрана из матричного визуального элемента. Обратите внимание, что элементы, которые не были выбраны в визуальном элементе, отображаются серым цветом, а другие визуальные элементы на странице отражают выбор, сделанный в матричном визуальном элементе.
Копирование значений из Power BI для использования в других приложениях
Ваша матрица или таблица может иметь содержимое, которое вы хотели бы использовать в других приложениях: Dynamics CRM, Excel и другие отчеты Power BI. Щелкнув правой кнопкой мыши Power BI, вы можете скопировать одну ячейку или набор ячеек в буфер обмена. Затем вставьте их в другое приложение.
Чтобы скопировать значение одной ячейки, выберите ячейку, щелкните правой кнопкой мыши и выберите Копировать значение .
 Имея в буфере обмена неформатированное значение ячейки , теперь вы можете вставить его в другое приложение.
Имея в буфере обмена неформатированное значение ячейки , теперь вы можете вставить его в другое приложение.Чтобы скопировать несколько ячеек, выберите диапазон ячеек или используйте клавишу CTRL, чтобы выбрать одну или несколько ячеек. Копировать выбор гарантирует, что меры будут отформатированы в соответствии с правилами форматирования столбца, в отличие от неформатированного Команда копирования значения .
Копия будет включать заголовки столбцов и строк.
Чтобы создать копию самого визуального элемента, содержащего только выбранные ячейки, выберите одну или несколько ячеек с помощью клавиши CTRL, щелкните правой кнопкой мыши и выберите Копировать визуальный элемент .
Если затем использовать Ctrl + V для вставки данных на холст, появится копия матричной визуализации, но она будет содержать только ваши скопированные данные.

Установка значения матрицы в качестве пользовательского URL-адреса
Если у вас есть столбец или мера, содержащие URL-адреса веб-сайтов, вы можете использовать условное форматирование, чтобы применить эти URL-адреса к полям в качестве активных ссылок. Вы найдете эту опцию под карточкой Cell elements на панели форматирования.
Включите Web URL и выберите поле, которое будет использоваться в качестве URL-адреса для столбца. После применения значения в этом поле (столбце) становятся активными ссылками. Наведите указатель мыши, чтобы увидеть ссылку, и выберите для перехода на эту страницу.
Дополнительные сведения см. в разделе Условное форматирование таблиц.
Затенение и цвета шрифта с визуальными элементами матрицы
С помощью визуального элемента матрицы можно применять условное форматирование (цвета, заливку и гистограммы) к фону ячеек в матрице, а также применять условное форматирование к тексту и самим значениям .
Чтобы применить условное форматирование, выберите визуализацию матрицы и откройте панель Формат . Развернуть карту Cell elements и на Цвет фона , Цвет шрифта или Панели данных , переведите ползунок на Вкл. . Включение одного из этих параметров делает доступным значок его определений. Когда вы выбираете этот значок, вы можете настроить цвета и значения для цветового форматирования.
Выберите значок определений, чтобы отобразить диалоговое окно, которое можно использовать для внесения изменений. В этом примере показано диалоговое окно для столбцов данных .
Рваная иерархия
Неоднородная иерархия имеет уровни без данных. Хорошим примером является матрица сотрудников компании. В компании много уровней, от генерального директора и ниже. Генеральный директор является высшим уровнем в иерархии и не подчиняется другим сотрудникам. С другой стороны, любой другой сотрудник компании может подчиняться цепочке менеджеров, которые подчиняются вице-президенту, который подчиняется генеральному директору. В зависимости от их уровня в иерархии и того, как организован их отдел, сотрудники могут иметь данные для одного, двух, пяти или десяти уровней в иерархии. И для любого данного сотрудника может не быть данных для определенных уровней иерархии.
С другой стороны, любой другой сотрудник компании может подчиняться цепочке менеджеров, которые подчиняются вице-президенту, который подчиняется генеральному директору. В зависимости от их уровня в иерархии и того, как организован их отдел, сотрудники могут иметь данные для одного, двух, пяти или десяти уровней в иерархии. И для любого данного сотрудника может не быть данных для определенных уровней иерархии.
В настоящее время невозможно скрыть пустые строки или идентичные родительские и дочерние значения. И вы не можете контролировать, какие уровни иерархии можно и нельзя расширять. Тем не менее, есть несколько шагов, которые вы можете предпринять, чтобы сделать внешний вид более привлекательным.
Выключить ступенчатую компоновку. На панели Формат разверните карточку Заголовки строк . Затем откройте раздел карты Options и установите переключатель Stepped layout в положение Off 9.0004 .
 Все пустые значения для уровня иерархии теперь будут отображаться в одной строке.
Все пустые значения для уровня иерархии теперь будут отображаться в одной строке.Отключить промежуточные итоги для строк и столбцов матрицы. На панели Формат установите ползунок Промежуточные итоги строк и ползунок Промежуточные итоги столбцов в положение Выкл. .
Соображения и устранение неполадок
Если текстовые данные в ячейках или заголовках вашей матрицы содержат символы новой строки, эти символы будут игнорироваться, пока вы не включите параметр «Перенос слов» на соответствующей карточке панели форматирования элемента.
Появятся полосы прокрутки, помогающие прокручивать ячейки тела, которые не все сразу помещаются на визуальном элементе, но столбцы заголовков строк фиксируются на матричном визуальном элементе и не будут прокручиваться. Если вы включите в матрицу слишком много заголовков строк, так что ячейки тела будут скрыты, прокрутка не покажет ячейки тела.
 Вместо этого уменьшите количество заголовков строк в визуальном элементе, отрегулируйте ширину столбца, уменьшите размер шрифта или иным образом обеспечьте видимость ячеек тела матрицы для доступа к вашим данным значения.
Вместо этого уменьшите количество заголовков строк в визуальном элементе, отрегулируйте ширину столбца, уменьшите размер шрифта или иным образом обеспечьте видимость ячеек тела матрицы для доступа к вашим данным значения.
Следующие шаги
Визуальный элемент Power Apps для Power BI
Типы визуализации в Power BI
Транспонирование, умножение, примеры массивов NumPy
Что такое Python Matrix?
Матрица Python — это специализированный двумерный прямоугольный массив данных, хранящихся в строках и столбцах. Данные в матрице могут быть числами, строками, выражениями, символами и т. д. Матрица — одна из важных структур данных, которую можно использовать в математических и научных расчетах.
Из этого руководства по Python вы узнаете:
- Что такое матрица Python?
- Как работают матрицы Python?
- Создание матрицы Python с использованием типа данных вложенного списка
- Чтобы прочитать данные внутри Python Matrix, используя список.

- Пример 2: Чтобы прочитать последний элемент из каждой строки.
- Пример 3: Печать строк в матрице
- Добавление матриц с использованием вложенного списка
- Умножение матриц с использованием вложенного списка
- Создание матрицы Python с использованием массивов из пакета Python Numpy
- Матричная операция с использованием Numpy.Array()
- Доступ к матрице NumPy
Как работают матрицы Python?
Данные внутри двумерного массива в матричном формате выглядят следующим образом:
Шаг 1)
Он показывает матрицу 2×2. Он имеет две строки и 2 столбца. Данные внутри матрицы являются числами. Строка1 имеет значения 2,3, а строка2 имеет значения 4,5. Столбцы, т. е. col1, имеют значения 2,4, а col2 — значения 3,5.
Шаг 2)
Показывает матрицу 2×3. Он имеет две строки и три столбца. Данные внутри первой строки, т. е. row1, имеют значения 2, 3, 4, а row2 — значения 5, 6, 7. Столбцы col1 имеют значения 2,5, col2 имеют значения 3,6, а col3 имеют значения 4,7.
Столбцы col1 имеют значения 2,5, col2 имеют значения 3,6, а col3 имеют значения 4,7.
Точно так же вы можете хранить свои данные внутри матрицы nxn в Python. Многие операции могут быть выполнены с матричным сложением, вычитанием, умножением и т. д.
В Python нет простого способа реализации матричного типа данных.
Матрица Python использует массивы, и то же самое можно реализовать.
- Создайте матрицу Python, используя тип данных вложенного списка
- Создание матрицы Python с использованием массивов из пакета Python Numpy
Создание матрицы Python с использованием типа данных вложенного списка
В Python массивы представляются с использованием типа данных списка. Итак, теперь мы будем использовать список для создания матрицы Python.
Мы создадим матрицу 3×3, как показано ниже:
- Матрица имеет 3 строки и 3 столбца.
- Первая строка в формате списка будет следующей: [8,14,-6]
- Вторая строка в списке будет: [12,7,4]
- Третья строка в списке будет: [-11,3,21]
Матрица внутри списка со всеми строками и столбцами показана ниже:
Список = [[Row1],
[Ряд 2],
[Строка 3]
. ..
[РядN]]
..
[РядN]]
Таким образом, в соответствии с приведенной выше матрицей тип списка с матричными данными выглядит следующим образом:
М1 = [[8, 14, -6], [12,7,4], [-11,3,21]]
Для чтения данных внутри Python Matrix с помощью списка.
Мы будем использовать матрицу, определенную выше. Пример будет читать данные, печатать матрицу, отображать последний элемент из каждой строки.
Пример: для печати матрицы
M1 = [[8, 14, -6],
[12,7,4],
[-11,3,21]]
#Чтобы распечатать матрицу
печать(M1)
Вывод:
Матрица M1 = [[8, 14, -6], [12, 7, 4], [-11, 3, 21]]
Пример 2: Для чтения последнего элемента из каждой строки.
М1 = [[8, 14, -6],
[12,7,4],
[-11,3,21]]
длина_матрицы = длина (M1)
#Чтобы прочитать последний элемент из каждой строки.
для i в диапазоне (matrix_length):
печать (M1[i][-1])
Вывод:
-6 4 21
Пример 3: Печать строк в матрице
M1 = [[8, 14, -6],
[12,7,4],
[-11,3,21]]
длина_матрицы = длина (M1)
#Чтобы напечатать строки в матрице
для i в диапазоне (matrix_length):
печать (M1 [я])
Вывод:
[8, 14, -6] [12, 7, 4] [-11, 3, 21]
Добавление матриц с помощью вложенного списка
Мы можем легко добавить две заданные матрицы. Матрицы здесь будут в виде списка. Давайте поработаем над примером, который позаботится о добавлении данных матриц.
Матрицы здесь будут в виде списка. Давайте поработаем над примером, который позаботится о добавлении данных матриц.
Матрица 1:
М1 = [[8, 14, -6],
[12,7,4],
[-11,3,21]]
Матрица 2 :
M2 = [[3, 16, -6],
[9,7,-4],
[-1,3,13]]
Последняя инициализирует матрицу, в которой будет храниться результат M1 + M2.
Матрица 3 :
M3 = [[0,0,0],
[0,0,0],
[0,0,0]]
Пример: добавление матриц
Для добавления матриц будет использоваться цикл for, который будет проходить по обеим заданным матрицам.
М1 = [[8, 14, -6],
[12,7,4],
[-11,3,21]]
М2 = [[3, 16, -6],
[9,7,-4],
[-1,3,13]]
М3 = [[0,0,0],
[0,0,0],
[0,0,0]]
длина_матрицы = длина (M1)
#Чтобы добавить матрицы M1 и M2
для i в диапазоне (len (M1)):
для k в диапазоне (len (M2)):
M3[i][k] = M1[i][k] + M2[i][k]
#Распечатать матрицу
print("Сумма матриц M1 и M2 = ", M3)
Вывод:
Сумма матриц M1 и M2 = [[11, 30, -12], [21, 14, 0], [-12, 6, 34]]
Умножение матриц с использованием вложенного списка
Чтобы умножить матрицы, мы можем использовать цикл for для обеих матриц, как показано в коде ниже:
M1 = [[8, 14, -6],
[12,7,4],
[-11,3,21]]
М2 = [[3, 16, -6],
[9,7,-4],
[-1,3,13]]
М3 = [[0,0,0],
[0,0,0],
[0,0,0]]
длина_матрицы = длина (M1)
#Для умножения матриц M1 и M2
для i в диапазоне (len (M1)):
для k в диапазоне (len (M2)):
M3[i][k] = M1[i][k] * M2[i][k]
#Распечатать матрицу
print("Умножение матриц M1 и M2 = ", M3)
Вывод:
Умножение матриц M1 и M2 = [[24, 224, 36], [108, 49, -16], [11, 9, 273]]
Создание матрицы Python с использованием массивов из пакета Python Numpy
Библиотека Python Numpy помогает работать с массивами. Numpy обрабатывает массив немного быстрее, чем список.
Numpy обрабатывает массив немного быстрее, чем список.
Для работы с Numpy его необходимо сначала установить. Следуйте инструкциям ниже, чтобы установить Numpy.
Шаг 1)
Команда для установки Numpy:
pip install NumPy
Шаг 2)
Чтобы использовать Numpy в своем коде, его необходимо импортировать.
import NumPy
Шаг 3)
Вы также можете импортировать Numpy, используя псевдоним, как показано ниже:
import NumPy as np
матрица питона.
Пример: массив в Numpy для создания матрицы Python
импортировать numpy как np M1 = np.массив([[5, -10, 15], [3, -6, 9], [-4, 8, 12]]) печать(M1)
Вывод:
[[ 5 -10 15] [ 3 -6 9] [-4 8 12]]
Матричная операция с использованием Numpy.Array()
Матричная операция, которую можно выполнить, — это сложение, вычитание, умножение, транспонирование, чтение строк, столбцов матрицы, нарезка матрицы и т. д. Во всех примерах мы собирается использовать метод array().
д. Во всех примерах мы собирается использовать метод array().
Сложение матрицы
Чтобы выполнить сложение матрицы, мы создадим две матрицы с помощью numpy.array() и добавим их с помощью оператора (+).
Пример:
импортировать numpy как np M1 = np.array([[3, 6, 9], [5, -10, 15], [-7, 14, 21]]) M2 = np.array([[9, -18, 27], [11, 22, 33], [13, -26, 39]]) М3 = М1 + М2 печать(M3)
Вывод:
[[ 12 -12 36] [ 16 12 48 ] [ 6 -12 60]]
Вычитание матрицы
Чтобы выполнить вычитание матрицы, мы создадим две матрицы с помощью numpy.array() и вычтем их с помощью оператора (-).
Пример:
импортировать numpy как np M1 = np.array([[3, 6, 9], [5, -10, 15], [-7, 14, 21]]) M2 = np.array([[9, -18, 27], [11, 22, 33], [13, -26, 39]]) М3 = М1 - М2 печать(M3)
Вывод:
[[ -6 24 -18] [-6-32-18] [-20 40 -18]]
Умножение матриц
Сначала создадим две матрицы, используя numpy. arary(). Чтобы умножить их, вы можете использовать метод numpy dot(). Numpy.dot() — это точечный продукт матриц M1 и M2. Numpy.dot() обрабатывает двумерные массивы и выполняет умножение матриц.
arary(). Чтобы умножить их, вы можете использовать метод numpy dot(). Numpy.dot() — это точечный продукт матриц M1 и M2. Numpy.dot() обрабатывает двумерные массивы и выполняет умножение матриц.
Пример:
импортировать numpy как np M1 = np.массив ([[3, 6], [5, -10]]) M2 = np.массив ([[9, -18], [11, 22]]) М3 = М1.точка(М2) печать(M3)
Вывод:
[[ 93 78] [-65-310]]
Транспонирование матрицы
Транспонирование матрицы вычисляется путем преобразования строк в столбцы и столбцов в строки. Функцию transpose() из Numpy можно использовать для вычисления транспонирования матрицы.
Пример:
импортировать numpy как np M1 = np.массив([[3, 6, 9], [5, -10, 15], [4,8,12]]) M2 = M1.транспонировать() печать(М2)
Вывод:
[[ 3 5 4] [ 6 -10 8] [ 9 15 12]]
Нарезка матрицы
Нарезка вернет вам элементы из матрицы на основе заданного начального/конечного индекса.
- Синтаксис для нарезки – [начало:конец]
- Если начальный индекс не указан, он считается равным 0.
 Например, [:5], это означает как [0:5].
Например, [:5], это означает как [0:5]. - Если конец не передан, он будет считаться длиной массива.
- Если начало/конец имеют отрицательные значения, нарезка будет выполняться с конца массива.
Прежде чем мы приступим к срезу матрицы, давайте сначала разберемся, как применить срез к простому массиву.
импортировать numpy как np массив = np.массив ([2,4,6,8,10,12,14,16]) print(arr[3:6]) # напечатает элементы с 3 по 5 print(arr[:5]) # напечатает элементы от 0 до 4 print(arr[2:]) # напечатает элементы от 2 до длины массива. print(arr[-5:-1]) # будет печатать с конца, т.е. от -5 до -2 print(arr[:-1]) # будет печатать с конца, т.е. от 0 до -2
Вывод:
[8 10 12] [ 2 4 6 8 10 ] [ 6 8 10 12 14 16] [ 8 10 12 14 ] [ 2 4 6 8 10 12 14]
Теперь реализуем нарезку матрицы. Для выполнения среза матрицы
синтаксис будет M1[начало_строки:конец_строки, начало_столбца:конец_столбца]
- Первое начало/конец будет для строки, т.
 е. для выбора строк матрицы.
е. для выбора строк матрицы. - Второе начало/конец будет для столбца, т.е. для выбора столбцов матрицы.
Матрица M1 t, которую мы собираемся использовать, выглядит следующим образом:
M1 = np.массив([[2, 4, 6, 8, 10],
[3, 6, 9, -12, -15],
[4, 8, 12, 16, -20],
[5, -10, 15, -20, 25]])
Всего 4 ряда. Индекс начинается с 0 до 3. 0 -й -й ряд — это [2,4,6,8,10], 1 -й -й ряд — это [3,6,9,-12,-15], за которыми следуют 2 -й и 3 -й .
Матрица M1 имеет 5 столбцов. Индекс начинается от 0 до 4. Столбец 0 th имеет значения [2,3,4,5], столбцы 1 st имеют значения [4,6,8,-10], за которыми следуют 2 -й , 3-й -й , 4-й -й и 5-й -й -й.
Вот пример, показывающий, как получить данные строк и столбцов из матрицы с помощью срезов. В примере мы печатаем строки 1 st и 2 nd , а для столбцов нам нужны первый, второй и третий столбцы. Чтобы получить этот вывод, мы использовали: M1[1:3, 1:4]
Чтобы получить этот вывод, мы использовали: M1[1:3, 1:4]
Пример:
import numpy as np
M1 = np.массив([[2, 4, 6, 8, 10],
[3, 6, 9, -12, -15],
[4, 8, 12, 16, -20],
[5, -10, 15, -20, 25]])
print(M1[1:3, 1:4]) # Для 1:3 это даст первую и вторую строку.
#Столбцы будут взяты с первого по третий.
Вывод:
[[ 6 9 -12] [ 8 12 16]]
Пример: для печати всех строк и третьих столбцов
импортировать numpy как np
M1 = np.массив([[2, 4, 6, 8, 10],
[3, 6, 9, -12, -15],
[4, 8, 12, 16, -20],
[5, -10, 15, -20, 25]])
print(M1[:,3]) # Это напечатает все строки и данные третьего столбца.
Вывод:
[8-12 16-20]
Пример: для печати первой строки и всех столбцов
импортировать numpy как np
M1 = np.массив([[2, 4, 6, 8, 10],
[3, 6, 9, -12, -15],
[4, 8, 12, 16, -20],
[5, -10, 15, -20, 25]])
print(M1[:1,]) # Будет напечатана первая строка и все столбцы
Вывод:
[[ 2 4 6 8 10]]
Пример: для печати первых трех строк и первых двух столбцов
импортировать numpy как np M1 = np.массив([[2, 4, 6, 8, 10], [3, 6, 9, -12, -15], [4, 8, 12, 16, -20], [5, -10, 15, -20, 25]]) печать (M1 [: 3,: 2])
Вывод:
[[2 4] [3 6] [4 8]]
Доступ к матрице NumPy
Мы видели, как работает нарезка. Принимая это во внимание, мы узнаем, как получить строки и столбцы из матрицы.
Для печати строк матрицы
В примере будут напечатаны строки матрицы.
Пример:
импортировать numpy как np M1 = np.массив([[3, 6, 9], [5, -10, 15], [4,8,12]]) print(M1[0]) # первая строка print(M1[1]) # вторая строка print(M1[-1]) # -1 напечатает последнюю строку
Вывод:
[3 6 9] [ 5 -10 15] [ 4 8 12]
Чтобы получить последнюю строку, вы можете использовать индекс или -1. Например, матрица имеет 3 строки:
, поэтому M1[0] даст вам первую строку,
M1[1] даст вам вторую строку
M1[2] или M1[-1] даст вам третий ряд или последний ряд.
Для печати столбцов матрицы
импортировать numpy как np M1 = np.массив([[2, 4, 6, 8, 10], [3, 6, 9, -12, -15], [4, 8, 12, 16, -20], [5, -10, 15, -20, 25]]) print(M1[:,0]) # Будет напечатан первый столбец print(M1[:,3]) # Будет напечатан третий столбец print(M1[:,-1]) # -1 даст вам последний столбец
Вывод:
[2 3 4 5] [ 8 -12 16 -20] [ 10 -15 -20 25]
Сводка:
- Матрица Python представляет собой специализированный двумерный прямоугольный массив данных, хранящихся в строках и столбцах. Данные в матрице могут быть числами, строками, выражениями, символами и т. д. Матрица — одна из важных структур данных, которую можно использовать в математических и научных расчетах.
- В Python нет простого способа реализовать матричный тип данных. Матрица Python может быть создана с использованием типа данных вложенного списка и библиотеки numpy.
- Библиотека Python Numpy помогает работать с массивами. Numpy обрабатывает массив немного быстрее, чем список.
- Матричная операция, которую можно выполнять, — это сложение, вычитание, умножение, транспонирование, чтение строк, столбцов матрицы, разрезание матрицы и т.
 д.
д. - Чтобы добавить две матрицы, вы можете использовать numpy.array() и добавить их с помощью оператора (+).
- Чтобы умножить их, вы можете использовать метод numpy dot(). Numpy.dot() — это точечный продукт матриц M1 и M2. Numpy.dot() обрабатывает двумерные массивы и выполняет умножение матриц.
- Транспонирование матрицы вычисляется путем преобразования строк в столбцы и столбцов в строки. Функцию transpose() из Numpy можно использовать для вычисления транспонирования матрицы.
- Нарезка матрицы вернет вам элементы на основе заданного начального/конечного индекса.
Как создать матрицу в Excel
1. Как сделать матрицу в Excel
Многие люди могут захотеть создать матрицу в Excel, но процесс сложный и может не дать хорошего результата. Пользователь должен знать как создать матричную диаграмму в Excel для создания матричной диаграммы профессионального уровня. Чтобы создать матричную диаграмму Excel, пользователям необходимо выполнить следующие шаги:
Шаг 1. Откройте Excel и упорядочите данные
Откройте Excel и упорядочите данные
При создании матрицы пользователю необходимо упорядочить все необходимые данные перед началом работы. Затем им нужно расположить данные внутри листа Excel соответствующим образом.
Шаг 2: выберите пузырьковую диаграмму
На следующем шаге пользователь должен выбрать текст, а затем перейти к «Вставить» и нажать «Другие диаграммы». Из других диаграмм они должны перейти к пузырьковой диаграмме, чтобы создать матричную диаграмму в Excel .
Шаг 3. Стилизация матрицы
Они могут щелкнуть вкладку «Дизайн» и выбрать желаемый дизайн для своей матрицы пузырьковой диаграммы, чтобы она выглядела привлекательно. На вкладке «Дизайн» пользователи могут перейти на вкладку «Формат», чтобы задать цвет фона для матрицы пузырьковой диаграммы или создать эффект тени. Пользователи также могут придать диаграмме трехмерный эффект, стилизовав фигуры. Тем самым делая его привлекательным как никогда.
Шаг 4. Сохраните матрицу
Пользователи могут добавлять новые значения, чтобы изменить высоту и ширину полей группы размера и, наконец, сохранить рабочий лист для будущего использования и совместного использования.
2. Как сделать матрицу проще
Пользователь может рассмотреть возможность использования Excel для создания своей матричной диаграммы, но создание матричной диаграммы в Excel сложно и требует много времени. Это также требует знаний о функциях Excel, если пользователь хочет создать высококачественный матричная диаграмма excel . Пользователи должны использовать онлайн-инструмент EdrawMax, который упрощает создание матричных диаграмм профессионального уровня. Вот несколько простых шагов, которые пользователь может выполнить, чтобы создать свою матричную диаграмму:
Шаг 1. Выберите шаблон матрицы
Пользователю необходимо найти параметр [ Marketing ] в онлайн-приложении EdrawMax, а затем выбрать [ Matrix Diagrams ] в соответствии с этой классификацией, как показано на рисунке.
Источник: EdrawMax Online
Шаг 2. Настройте матрицу
Откроется страница с знаком плюс , чтобы начать с нового шаблона. Пользователь может выбрать редактируемые шаблоны в соответствии со своими требованиями. Они должны учитывать цель своей матрицы при выборе шаблона. Они могут изменять шаблон и добавлять детали для создания своей матрицы. Если пользователь не хочет использовать редактируемые шаблоны для создания матрицы, он может работать вручную.
Источник: EdrawMax Online
Шаг 3. Сохраните и поделитесь
После того, как пользователь заполнит свои шаблоны, он может сохранить файл в нескольких форматах по своему выбору. Наконец, пользователь может вставить в Word, чтобы завершить свою матрицу.
Источник: EdrawMax Online
3. Матричные шаблоны Excel
Иногда очень сложно выполнить шаги по созданию матрицы в Excel или EdrawMax Online и создать идеальную диаграмму. В настоящее время есть примеры матриц из галереи шаблонов EdrawMax, которые вы можете редактировать немедленно или для получения дополнительных ссылок. Примеры матриц не только помогают глубже понять матрицу и ее классификацию, но и помогают рисовать матрицы без усилий.
В настоящее время есть примеры матриц из галереи шаблонов EdrawMax, которые вы можете редактировать немедленно или для получения дополнительных ссылок. Примеры матриц не только помогают глубже понять матрицу и ее классификацию, но и помогают рисовать матрицы без усилий.
Шаблон матрицы Excel
Характер человека состоит из всех качеств, которые делают его отличным от других. Человек с хорошим характером думает, чувствует и действует в соответствии с некоторыми общепринятыми чертами. Есть несколько черт характера, таких как упорство, любопытство, самоконтроль, социальный интеллект, энтузиазм, оптимизм и благодарность.
Источник: EdrawMax Online
Шаблон онлайн-матрицы
Это базовая модель матрицы Ансоффа с друзьями в сообществе! Цель этой матрицы Ансоффа — помочь компаниям планировать и выбирать свои продукты и стратегии роста рынка.
Источник: EdrawMax Online
Шаблон матрицы
Матричная диаграмма — это инструмент управления проектом, который может сравнивать и определять отношения между различными наборами данных. Это графические наборы данных, которые упрощают сложные отношения между программами и функциями.
Это графические наборы данных, которые упрощают сложные отношения между программами и функциями.
Источник: EdrawMax Online
4. Онлайн-конструктор матриц
Чтобы создать матрицу без каких-либо проблем, пользователь должен воспользоваться помощью онлайн-инструмента EdrawMax. Инструмент прост в использовании, что сделало его фаворитом многих пользователей. Вот некоторые из его уникальных особенностей, которые сделали его надежным компаньоном для построения диаграмм многих людей.
Почему стоит выбрать EdrawMax Online
- Создайте более 280 типов диаграмм
- Поддерживает совместную работу в команде
- Персональное облако и защита данных
- Распечатайте, поделитесь и загрузите
- Мощное сообщество шаблонов
5. Основные выводы
Матрица является необходимым инструментом для бизнеса, поскольку помогает визуализировать взаимосвязь между процессом, событиями и программами.

 Из решений всех таких ФСР, как из столбцов, составить матрицу S. Причём в матрице S столбцами записываются решения по каждому λi в порядке нумерации собственных значений (одинаковые λi считаются столько раз, какова их кратность). Если матрица S окажется квадратной, то она будет удовлетворять соотношениям
Из решений всех таких ФСР, как из столбцов, составить матрицу S. Причём в матрице S столбцами записываются решения по каждому λi в порядке нумерации собственных значений (одинаковые λi считаются столько раз, какова их кратность). Если матрица S окажется квадратной, то она будет удовлетворять соотношениям  Так поступают для всех строк (столбцов) выбранного определителя. Полученные при этом частные решения составляют ФСР рассматриваемой однородной системы уравнений. Свободным неизвестным можно придавать значения из строк (столбцов) выбранного определителя в самой системе уравнений и находить соответствующие значения главных неизвестных из системы.
Так поступают для всех строк (столбцов) выбранного определителя. Полученные при этом частные решения составляют ФСР рассматриваемой однородной системы уравнений. Свободным неизвестным можно придавать значения из строк (столбцов) выбранного определителя в самой системе уравнений и находить соответствующие значения главных неизвестных из системы.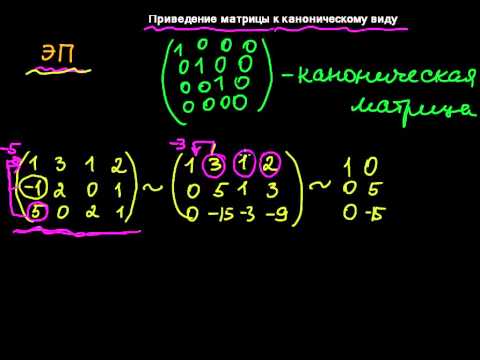


 38kb.
38kb.
 Оно будет максимальным возможным значением ранга.
Оно будет максимальным возможным значением ранга.