Высшая математика системы линейных уравнений: Элементы высшей математики: Решение систем линейных уравнений

Содержание

Элементы высшей математики: Решение систем линейных уравнений

Решение систем линейных уравнений

7.1.

Системы линейных алгебраических уравнений

Сегодня вы изучите вопросы

Методы решения систем линейных алгебраических уравнений (СЛАУ)
Метод обратной матрицы
Метод Крамера
Метод Гаусса
Условия разрешимости данных систем
Критерий совместности

Изучив тему занятия, вы сможете

решать СЛАУ методом обратной матрицы, по формулам Крамера, методом Гаусса;
решать произвольные системы линейных уравнений и системы однородных уравнений.

Основные понятия

7.1.1.

Системы линейных алгебраических уравнений

Системой линейных алгебраических уравнений (СЛАУ) называется система вида

(4. 1)

Решением системы (4.1) называется такая совокупность n чисел

, при подстановке которых каждое уравнение системы обращается в верное равенство.

Решить систему означает найти все ее решения или доказать, что ни одного решения нет.

СЛАУ называется совместной, если она имеет хотя бы одно решение, и несовместной, если она решений не имеет.

Если совместная система имеет только одно решение, то она называется определенной, и неопределенной, если она имеет более чем одно решение.

Например, система уравнений совместная и определенная, так как имеет единственное решение ; система

несовместная, а система совместная и неопределенная, так как имеет более одного решения .

Две системы уравнений называются равносильными или эквивалентными, если они имеют одно и то же множество решений. В частности, две несовместные системы считаются эквивалентными.

Основной матрицей СЛАУ (4.1) называется матрица А размера , элементами которой являются коэффициенты при неизвестных данной системы, то есть

Матрицей неизвестных СЛАУ (4.1) называется матрица-столбец Х, элементами которой являются неизвестные системы (4.1):

Матрицей свободных членов СЛАУ (4.1) называется матрица-столбец В, элементами которой являются свободные члены данной СЛАУ:

С учетом введенных понятий СЛАУ (4.1) можно записать в матричном виде или

. (4.2)

7.1.2.

Решение систем линейных уравнений. Метод обратной матрицы

Перейдем к изучению СЛАУ (4.1), которой соответствует матричное уравнение (4.2). Сначала рассмотрим частный случай, когда число неизвестных равно числу уравнений данной системы () и , то есть основная матрица системы A невырождена. В этом случае, согласно предыдущему пункту, для матрицы существует единственная обратная матрица A

-1. Ясно, что она согласована с матрицами и . Покажем это. Для этого умножим слева обе части матричного уравнения (4.2) на матрицу :

Следовательно, с учетом свойств умножения матриц получаем

Так как , а , тогда

. (4.3)

Убедимся, что найденное значение является решением исходной системы. Подставив (4.3) в уравнение (4.2), получим , откуда имеем .

Покажем, что это решение единственное. Пусть матричное уравнение (4.2) имеет другое решение , которое удовлетворяет равенству

Покажем, что матрица равна матрице

С этой целью умножим предыдущее равенство слева на матрицу A^-1.

В результате получим

Такое решение системы уравнений с неизвестными называется решением системы (4.1) методом обратной матрицы.

Пример. Найти решение системы

Выпишем матрицу системы:

Для этой матрицы ранее мы уже нашли обратную:

или

Здесь мы вынесли общий множитель , так как нам в дальнейшем нужно будет произведение .

Ищем решение по формуле: .

Найденные значения переменных подставляем в уравнения системы и убеждаемся, что они являются ее решением.

Упражнение. Проверку этого факта сделайте самостоятельно.

7.1.3.

Правило и формулы Крамера

Рассмотрим систему линейных уравнений с неизвестными

От матричной формы (4.3) перейдем к более удобным и в ряде случаев более простым при решении прикладных задач формулам для нахождения решений системы линейных алгебраических уравнений.

Учитывая равенство , или в развернутом виде

Таким образом, после перемножения матриц получаем:

или

Заметим, что сумма есть разложение определителя

по элементам первого столбца, который получается из определителя путем замены первого столбца коэффициентов столбцом из свободных членов.

Таким образом, можно сделать вывод, что

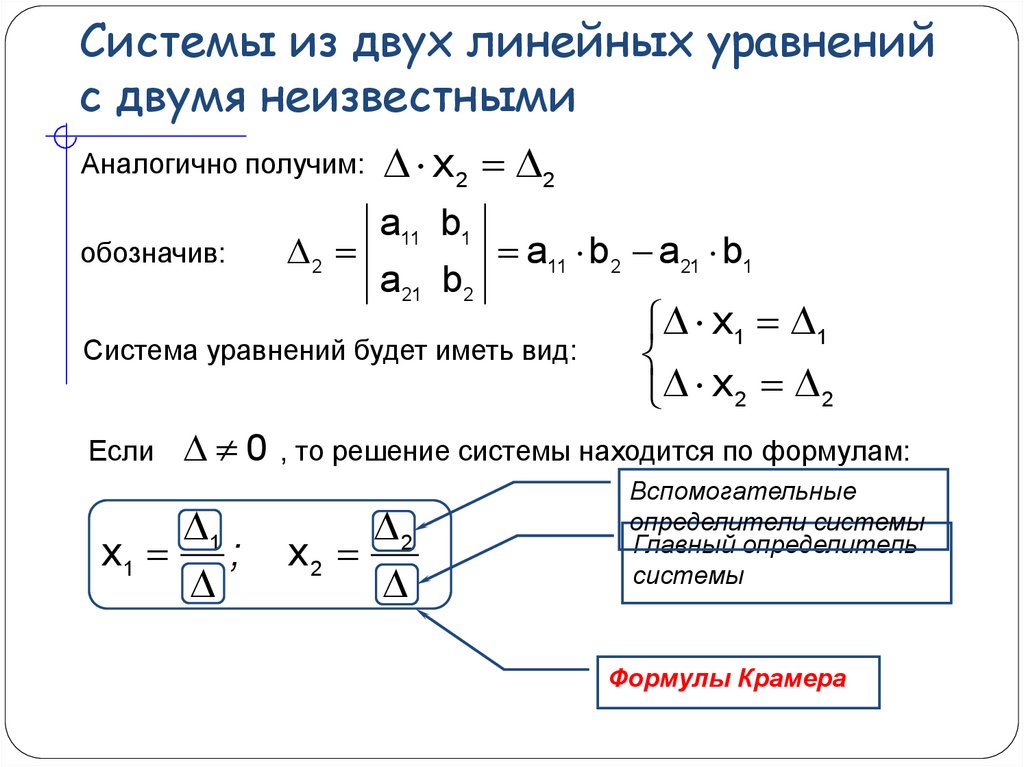
Аналогично: , где получен из путем замены второго столбца коэффициентов столбцом из свободных членов, .

Следовательно, нами найдено решение заданной системы по равенствам

, , ,

известным и как формулы Крамера.

Для нахождения решения СЛАУ, последние равенства можно записать в общем виде следующим образом:

. (4.4)

Согласно этим формулам, имеем правило Крамера для решения СЛАУ:

по матрице системы вычисляется определитель системы ;
если , то в матрице системы каждый столбец последовательно заменяется столбцом свободных членов и вычисляются определители получаемых при этом матриц;
решение системы находится по формулам Крамера (4.4).

Пример. С помощью формул Крамера решить систему уравнений

Решение. Определитель данной системы

Так как , то формулы Крамера имеют смысл, то есть система имеет единственное решение. Находим определители:

, , .

Следовательно, по формулам (4.4) получаем:

, , .

Найденные значения переменных подставляем в уравнения системы и убеждаемся, что они являются ее решением.

Упражнение. Проверку этого факта сделайте самостоятельно.

Критерий совместности СЛАУ (теорема Кронекера-Капелли)

Расширенной матрицей системы (4. 1) называется матрица, получаемая добавлением к основной матрице А справа столбца свободных членов с отделением его вертикальной чертой, то есть матрица

Заметим, что при появлении у матрицы новых столбцов ранг может увеличиться, следовательно . Расширенная матрица играет очень важную роль в вопросе совместности (разрешимости) системы уравнений. Исчерпывающий ответ на этот вопрос дает теорема Кронекера-Капелли.

Сформулируем теорему Кронекера-Капелли (без доказательства).

Система линейных алгебраических уравнений (4.1) совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы . Если — число неизвестных системы, то система имеет единственное решение, а если , то система имеет бесчисленное множество решений.

Опираясь на теорему Кронекера-Капелли, сформулируем алгоритм решения произвольной системы линейных уравнений.

Вычисляют ранги основной и расширенной матриц СЛАУ. Если , то система не имеет решений (несовместна).
Если , система совместна. В этом случае берут любой отличный от нуля минор основной матрицы порядка и рассматривают уравнений, коэффициенты которых входят в этот базисный минор, а остальные уравнения отбрасывают. Неизвестные коэффициенты, которые входят в этот базисный минор, объявляют главными или базисными, а остальные свободными (неосновными). Новую систему переписывают, оставляя в левых частях уравнений только члены, содержащие базисных неизвестных, а все остальные члены уравнений, содержащих неизвестных, переносят в правые части уравнений.
Находят выражения базисных неизвестных через свободные. Полученные решения новой системы с базисными неизвестными называются общим решением СЛАУ (4.1).
Придавая свободным неизвестным некоторые числовые значения, находят так называемые частные решения.

Проиллюстрируем применение теоремы Кронекера-Капелли и вышеприведенного алгоритма на конкретных примерах.

Пример. Определить совместность системы уравнений

Решение. Запишем матрицу системы и определим ее ранг.

Имеем:

Так как матрица имеет порядок , то наивысший порядок миноров равен 3. Число различных миноров третьего порядка Нетрудно убедиться, что все они равны нулю (проверьте самостоятельно). Значит, . Ранг основной матрицы равен двум, так как существует отличный от нуля минор второго порядка этой матрицы, например,

Ранг расширенной матрицы этой системы равен трем, так как существует отличный минор третьего порядка этой матрицы, например,

Таким образом, согласно критерию Кронекера-Капелли, система несовместна, то есть не имеет решений.

Пример. Исследовать совместность системы уравнений

Решение. Ранг основной матрицы этой системы равен двум, так как, например, минор второго порядка равен

а все миноры третьего порядка основной матрицы равны нулю. Ранг расширенной матрицы также равен двум, например,

а все миноры третьего порядка расширенной матрицы равны нулю (убедиться самостоятельно). Следовательно, система совместна.

Возьмем за базисный минор, например . В этот базисный минор не входят элементы третьего уравнения, поэтому ее отбрасываем.

Неизвестные и объявляем базисными, так как их коэффициенты входят в базисный минор, неизвестную объявляем свободной.

В первых двух уравнениях члены, содержащие переменную , перенесем в правые части. Тогда получим систему

Решаем эту систему с помощью формул Крамера.

Таким образом, общим решением исходной системы является бесконечное множество наборов вида ,

где — любое действительное число.

Частным решением данного уравнения будет, например, набор , получающийся при .

7.1.4.

Решение систем линейных алгебраических уравнений методом Гаусса

Одним из наиболее эффективных и универсальных методов решений СЛАУ является метод Гаусса. Метод Гаусса состоит из однотипных циклов, позволяющих последовательно исключать неизвестные СЛАУ. Первый цикл направлен на то, чтобы во всех уравнениях, начиная со второго, обнулить все коэффициенты при . Опишем первый цикл. Полагая, что в системе коэффициент (если это не так, то следует на первое место поставить уравнение с отличным от нуля коэффициентом при x₁ и переобозначить коэффициенты), преобразуем систему (4.1) следующим образом: первое уравнение оставляем без изменения, а из всех остальных уравнений исключаем неизвестную x₁ с помощью элементарных преобразований. Для этого умножим обе части первого уравнения на и сложим почленно со вторым уравнением системы. Затем умножим обе части первого уравнения на и сложим с третьим уравнением системы. Продолжая этот процесс, на последнем шаге цикла умножим обе части первого уравнения на и сложим с последним уравнением системы. Первый цикл завершен, в результате получим эквивалентную систему

(4.5)

Замечание. Для удобства записи обычно используют расширенную матрицу системы. После первого цикла данная матрица принимает следующий вид:

(4.6)

Второй цикл является повторением первого цикла. Предположим, что коэффициент . Если это не так, то перестановкой уравнений местами добьемся того, что . Первое и второе уравнение системы (4.5) перепишем в новую систему (в дальнейшем будем оперировать только расширенной матрицей).

Умножим второе уравнение (4.5) или вторую строку матрицы (4.6) на , сложим с третьим уравнением системы (4.5) или третьей строкой матрицы (4.6). Аналогично поступаем с остальными уравнениями системы. В результате получим эквивалентную систему:

(4.7)

Продолжая процесс последовательного исключения неизвестных, после k — 1-го шага, получим расширенную матрицу

(4.8)

Последние m — k уравнений для совместной системы (4.1) являются тождествами . Если хотя бы одно из чисел не равно нулю, то соответствующее равенство противоречиво, следовательно, система (4.1) несовместна. В совместной системе при ее решении последние m — k уравнений можно не рассматривать. Тогда полученная эквивалентная система (4.9) и соответствующая расширенная матрица (4.10) имеют вид

(4. 9)

(4.10)

После отбрасывания уравнений, являющихся тождествами, число оставшихся уравнений может быть либо равно числу переменных , либо быть меньше числа переменных. В первом случае матрица имеет треугольный вид, а во втором — ступенчатый. Переход от системы (4.1) к равносильной ей системе (4.9) называется прямым ходом метода Гаусса, а нахождение неизвестных из системы (4.9) — обратным ходом.

Пример. Решить систему методом Гаусса:

Решение. Расширенная матрица этой системы имеет вид

Проведем следующие преобразования расширенной матрицы системы: умножим первую строку на и сложим со второй строкой, а также умножим первую строку на и сложим с третьей строкой. Результатом будет расширенная матрица первого цикла (в дальнейшем все преобразования будем изображать в виде схемы)

Полученная расширенная матрица соответствует системе уравнений

которая эквивалентна исходной системе. Далее последовательно находим:

, , .

Пример. Решить систему методом Гаусса:

Преобразуем расширенную матрицу системы по методу Гаусса:

Последняя строка последней матрицы соответствует не имеющему решения уравнению .

Следовательно, исходная система несовместна.

Системы однородных уравнений

Система линейных алгебраических уравнений называется однородной, если она тождественными преобразованиями приводится к виду:

(4.11)

Ясно, что однородная система всегда совместна, хотя бы потому, что она всегда имеет тривиальное решение x₁ = x₂ = … = x_n = 0.

Сплошь нулевое решение часто называют тривиальным решением системы.

Содержательным вопросом, очевидно, является следующий: при каких условиях однородная система имеет и ненулевые решения? Ответом служит следующая теорема.

Теорема. Для того чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг r ее основной матрицы был меньше числа n неизвестных, .

Необходимость.

Так как ранг не может превосходить размера матрицы, то, очевидно, . Пусть . Тогда один из миноров размера отличен от нуля. Поэтому соответствующая система линейных уравнений имеет единственное решение:

. Значит, других, кроме тривиальных, решений нет. Итак, если есть нетривиальное решение, то .

Достаточность.

Пусть r < n. Тогда однородная система, будучи совместной, является неопределенной. Значит, она имеет бесчисленное множество решений, т.е. имеет и ненулевые решения.

В заключении выделим частный случай последней теоремы.

Пусть дана однородная система n линейных уравнений с n неизвестными (4.11).

Теорема. Для того чтобы однородная система n линейных уравнений с n неизвестными имела ненулевые решения, необходимо и достаточно, чтобы ее определитель ∆ был равен нулю, т.е. ∆ = 0.

Если система имеет ненулевые решения, то ∆ = 0, так как при ∆ ≠ 0 система имеет единственное, нулевое решение. Если же ∆ = 0, то ранг r основной матрицы системы меньше числа неизвестных, то есть r < n. Это означает, что система имеет бесконечное множество ненулевых решений.

Пример. Решить систему

Решение.

Так как r < n, то система имеет бесчисленное множество решений. Найдем их.

Стало быть, — общее решение.

Положив х₃ = 0, получаем одно частное решение: х₁ = 0, х₂ = 0, х₃ = 0. Положив х₃ = 1, получаем второе частное решение: х₁ = 2, х₂ = 3, х₃ = 1, и т.д.

Контрольные вопросы

Что понимается под системой линейных алгебраических уравнений?
Запишите в общем виде СЛАУ. Каков смысл величин, входящих в уравнения системы?
Дайте определение решения системы, определения совместной, несовместной системы.
При каких условиях СЛАУ имеет единственное решение?
К какой СЛАУ применим метод обратной матрицы?
К какой СЛАУ применимо правило Крамера?
Сформулируйте теорему Кронекера-Капелли.
Сформулируйте алгоритм решения произвольной системы линейных уравнений.
Какая система линейных алгебраических уравнений называется однородной?
При каких условиях система однородных уравнений имеет ненулевое решение?

Задания для самостоятельной работы

Задание 1. Примеры для самоподготовки

(решение систем линейных уравнений)

Решить следующие системы уравнений по формулам Крамера
Ответ. x = α, y = 3,5 —0,5α, где α — произвольное действительное число.

1.4.

Ответ. .
Решить систему уравнений с применением теории матриц:

Задание 2. Примеры для самопроверки

(отметьте правильный вариант ответа)

Решить следующую систему уравнений
Решить следующую систему уравнений
Решить следующую систему уравнений
Решить следующую систему уравнений
Решить следующую систему уравнений
Решить следующую систему уравнений

ТЕМА 3. Системы линейных уравнений — Высшая математика: лекционный курс — ВЫСШАЯ МАТЕМАТИКА, ТВ и МС, МАТ. МЕТОДЫ — Учебно-методические материалы для студентов всех ВУЗов: — std72.ru

Пусть дана система n линейных уравнений с n неизвестными
(1)

1. Правило Крамера

     Пусть составленный из коэффициентов при неизвестных определитель:
     .
     Тогда система (1) имеет единственное решение
     ,
     где определитель Δ_k (k=1,2,…n) получен из определителя Δ путем замены k-го столбца столбцом свободных членов системы (1).
     Пример. Решить систему линейных уравнений по правилу Крамера:

     Решение. Вычислим определители Δ, Δ₁ , Δ₂ , Δ_3.





     Тогда .
     Ответ: х₁=1, х₂=0, х₃= -1.

2. Метод Гаусса

     Пусть дана система уравнений (1).
     Предположим, что среди коэффициентов при неизвестном х₁ имеются коэффициенты, отличные от нуля. Пусть одним из таких коэффициентов является а₁₁. Разделим первое уравнение системы (1) на а₁₁, получим:
                                              (2)
     Это уравнение умножим на (–а₂₁) и сложим его со вторым уравнением системы (1), затем уравнение (2) умножим на (-а₃₁) и сложим его с третьим уравнением и т. д. С помощью таких операций исключим неизвестное х₁ из всех уравнений системы, начиная со второго. Оставляем неизменным первое уравнение системы (1), а к оставшимся применяем тот же прием, т.е. в n-2 уравнениях исключаем неизвестное х₂ и т.д.
     Систему уравнений (1) приведем к треугольному виду:
                                              (3)
     Пусть . Из последнего уравнения системы (3) найдем х_n. Подставляя затем это значение в предыдущее уравнение, найдем х_n_-1 и т.д. Продолжая эту процедуру, дойдем до первого уравнения, из которого путем подстановки уже найденных значений х₂, х₃, …, х_n получим неизвестное х₁.
     Пример . Решить систему уравнений методом Гаусса:
                                                              (4)
     Решение. Заметим, что во втором уравнении системы коэффициент при х₁ равен 1. Поменяв местами первое и второе уравнения, получим систему:
                                                                 (5)
     Умножим первое уравнение системы (5) на (–2) и сложим его со вторым уравнением. Затем умножим первое уравнение на (–3) и сложим его с третьим уравнением. Получим следующую систему уравнений:
                                                            (6)
     Разделим второе уравнение системы (6) на (-5), затем полученное уравнение умножим на 9 и сложим с третьим уравнением системы (6). В результате придем к системе (7)
                                                         (7)
     Из третьего уравнения находим х₃=-1. Подставим это значение во второе уравнение системы (7) и найдем х₂:
     .
     Подставляя полученные значения х₂ = 0 и х₃ = -1 в первое уравнение системы (7), найдем х₁:
    х₁ + 2*0-1*(-1)=2, или х₁ = 1.
     Ответ: х₁ = 1, х₂= 0, х₃ = -1.

3. Решение системы линейных уравнений с использованием обратной матрицы.

     Введем для системы линейных уравнений (1) следующие матрицы:
     .
     Систему (1) представим в матричной форме А* Х = В, которая эквивалентна исходной. Действительно, если перемножить матрицы А и Х и приравнять элементы матрицы-произведения к соответствующим элементам матрицы В, то получим систему уравнений (1).
     Умножим обе части уравнения А*Х = В слева на матрицу А^-1, получим А^-1 * (А Х) = А^-1 В или (А^-1 А) Х= А^-1 В.
     Так как А^-1* А = Е, то Е*Х = А^-1 * В или Х = А^-1* В.
     Эта формула дает решение системы в матричной форме.
     Пример. Решить систему
           используя обратную матрицу.
     Решение. Найдем обратную матрицу к матрице системы .
     Определитель матрицы А:
     .
     Так как определитель матрицы А отличен от 0, то обратная матрица существует. Найдем ее по формуле , вычислив предварительно алгебраические дополнения. Получим:
     .
     Найдем матричное решение системы:
     .
     Ответ: х₁ = 1; х₂ = 1; х₃ = 1.

Лекция Системы линейных алгебраических уравнений

Скачать с Depositfiles

Лекция № 2. Тема 2 : Системы линейных алгебраических уравнений

2.1. Правило Крамера

Рассмотрим систему трёх линейных алгебраических уравнений, когда число неизвестных равно числу уравнений, т. е. систему вида

(1)

где  коэффициенты системы,  свободные члены ,  неизвестные.

Будем считать, что определитель системы, составленный из коэффи-циентов системы (главный определитель), отличен от нуля, т.е.

Предположим, что система (1) совместна, т.е. имеет решение. Тогда умножим первое уравнение системы на , второе – на , третье – на и сложим полученные выражения

(2)

Первое выражение в скобках в левой части полученного соотношения (2) представляет собой разложение главного определителя системы по элементам первого столбца. Остальные выражения в скобках равны нулю, так как представляют собой разложение определителя, имеющего два одинаковых столбца (см. свойство 4). Например,

Тогда из выражения (2) получаем , где

Аналогично можно получить

(3)

где

Определители называются вспомогательными опреде-лителями системы (1).

Покажем теперь, что полученные значения неизвестных (3) на самом деле удовлетворяют системе уравнений (1).

Подставляя выражения (3) в систему (1), получим на примере первого уравнения

Аналогично можно показать и для двух оставшихся уравнений системы.

Таким образом, получаем следующий результат (правило Крамера).

Теорема. Система уравнений (1) с главным определителем имеет единственное решение, определяемое по формулам

где определители получаются из главного определителя системы уравнений заменой соответствующего столбца на столбец свобод-ных членов.

Замечание 1. Для системы линейных однородных уравнений

(4)

все и тогда, если , то система (4) имеет единст-венное нулевое решение Отсюда следует: если система (4) обладает ненулевым решением, то её определитель равен нулю.

Замечание 2. Если же главный определитель системы (1) , тогда возможны следующие два случая:

1. Система несовместна, если, по крайней мере, один из вспомога-тельных определителей отличен от нуля;

2. Если же все определители системы равны нулю, то система либо имеет бесконечное множество решений, что возможно из равенств

либо такая система несовместна, например, в системе уравнений

все определители равны нулю, но система несовместна, что следует из ее вида. В этом случае для решения системы уравнений более целесообразно применить метод Гаусса, который будет рассмотрен далее.

Замечание 3. Правило Крамера справедливо для любого числа уравнений системы, т.е. системы вида

Здесь, если то

Пример 1. Используя правило Крамера, решить систему уравнений

Здесь

откуда получаем

2.2. Метод Гаусса (метод последовательного исключения неизвестных)

Рассмотрим ту же систему уравнений (1). Пусть коэффициент , чего всегда можно достигнуть, переставляя уравнения системы или меняя нумерацию неизвестных. Первое уравнение системы (1) умножим на и сложим со вторым. Затем первое уравнение умножим на и сложим с третьим, тогда получим

(5)

Здесь  новые значения коэффициентов, полу-ченные после таких преобразований. Пусть , чего можно достигнуть, переставляя два последних уравнения системы. В противном случае, т.е. когда , сразу определяем неизвестную z, или получаем несов-местную систему. При таком условии второе уравнение системы (5) умно-жим на и сложим с третьим уравнением, тогда получим

(6)

В системе уравнений (6)  новые значения коэффициентов и здесь возможны следующие случаи:

1. Затем найденное значение z подставляем во второе уравнение системы (6) и определяем у. Из первого уравнения, уже зная у и z, находим х.

2. а . Тогда система (6) решений не имеет, т.е. система несовместна.

3. и . В этом случае система (6) принимает вид

(7)

Число уравнений в системе (7) меньше числа неизвестных. Оставим два неизвестных слева, например, х и у, а z перенесем в правую часть системы уравнений (7) и будем считать его произвольным числом. Получим

(8)

Из системы (8) х и у выражаются через z и система имеет беско-нечное множество решений.

Пример 2. Систему уравнений из примера 1 решить методом Гаусса

Первое уравнение умножим на 2 и сложим со вторым уравнением, затем первое уравнение сложим с третьим, получим

или

Второе уравнение умножим на 3 и сложим с третьим:

Из третьего уравнения получим, из второго и из пер-вого уравнения

Пример 3. Методом Гаусса решить систему однородных уравнений

Первое уравнение умножим на 2 и сложим со вторым, затем первое уравнение умножим на 3 и сложим с третьим, получим

откуда

Система имеет бесконечное множество решений. Поэтому в этом случае (см. замечание 1) определитель данной системы уравнений должен быть равен нулю. Проверьте!

Скачать с Depositfiles

Системы линейных уравнений — основные понятия с примерами решений

Содержание:

Системы линейных уравнений. Понятия линейного уравнения и системы линейных уравнений
Метод Гаусса решения систем линейных уравнений

Системы линейных уравнений. Понятия линейного уравнения и системы линейных уравнений

Напомним, что линейным уравнением с неизвестными называют уравнение вида

. (1)

Числа называют коэффициентами при неизвестных, число b — свободным членом.

Определение 1. Систему алгебраических уравнений, каждое из которых имеет вид (1), называют системой линейных уравнений или линейной системой.

Система линейных уравнений с неизвестными (далее система х ) записывается в общем виде так:

(2)

Коэффициенты уравнений нумеруют двумя индексами, первый из которых — номер уравнения, а второй — номер неизвестного.

Систему (2) удобно записывать в виде таблицы:

Решением системы (2) является любой набор значений неизвестных

удовлетворяющий всем уравнениям системы. Система, не имеющая ни одного решения, называется несовместной.

Две системы уравнений с одними и теми же неизвестными называются равносильными, если они имеют одно и то же множество решений.

Для любой системы (2) возможны три случая:

1) система не имеет ни одного решения;

2) система имеет единственное решение;

3) система имеет бесконечное множество решений.

Множество всех решений системы (2) называют ее общим решением. Решить систему означает найти ее общее решение.

Над системой (2) можно совершать элементарные преобразования:

1) перестановка уравнений;

2) вычеркивание из системы уравнения вида

или, проще говоря, 0 = 0;

3) умножение обеих частей уравнения системы на число ;

4) прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на одно и то же число.

Пример №15

Решить систему уравнений

Решение:

1) Если не выходить за рамки школьной математики, то можно в одном из уравнений выразить одно неизвестное через другое и подставить в оставшееся уравнение:

2) Если же использовать элементарные преобразования над системой, то можно ко второму уравнению, умноженному на 2, прибавить первое и, т.о., исключить из второго уравнения переменную :

Продолжая дальше заниматься теорией линейных систем, заметим, что при выполнении элементарных преобразований может возникнуть уравнение вида

где. Это уравнение не имеет решений и мы будем называть его противоречивым. Система, содержащая противоречивое уравнение, несовместна.

Метод Гаусса решения систем линейных уравнений

Для нахождения общего решения линейных систем вида (2) имеется универсальный метод Гаусса — метода последовательного исключения неизвестных. Суть метода заключается в том, что с помощью элементарных преобразований системы (2) либо получают систему, содержащую противоречивое уравнение (и тогда система оказывается несовместной), либо система (2) приводится к некоторому специальному виду. Особенность этого вида заключается в том, что для каждого уравнения имеется неизвестное, которое входит в это уравнение с коэффициентом, не равным нулю, а в остальные уравнения — с коэффициентом 0. Если для каждого уравнения зафиксировано такое неизвестное, то оно называется базисным, а весь набор базисных неизвестных — базисом неизвестных. Остальные неизвестные (если они есть) называются свободными.

Пример №16

Рассмотрим систему линейных уравнений

Решение:

Здесь — базисные неизвестные (они выделены квадратными скобками), a — свободные. Заметим, что коэффициенты при базисных неизвестных равны 1. Этого можно добиться с помощью элементарных преобразований 3), 4).

Перепишем нашу систему в виде:

Базисные переменные помещены в левых частях уравнений, свободные — в правых. В итоге получено общее решение системы. Подставляя вместо свободных неизвестных любые числа, находим значения базисных неизвестных . Взяв, например, , вычислим , а значит получим частное (т.е. конкретное) решение: .

Замечание. При наличии хотя бы одного свободного неизвестного система имеет бесконечное множество решений. Если же свободных неизвестных нет (все неизвестные — базисные), то решение единственно.

Опишем алгоритм метода Гаусса.

Шаг первый. Одно из уравнений (например, первое) выбирается за разрешающее уравнение и одно из неизвестных (например, ) за разрешающее неизвестное. Коэффициент при разрешающем неизвестном должен быть отличен от нуля (удобно, когда он равен единице). Этот коэффициент называют разрешающим элементом. Из всех уравнений, кроме разрешающего, исключаем разрешающее неизвестное. Для этого к каждому из этих уравнений прибавляем разрешающее уравнение, умноженное на подходящее число. Из полученной системы удаляем уравнения 0 = 0. Если в системе имеется хотя бы одно противоречивое уравнение, то система несовместна и работа с ней прекращается.

Шаг второй. Какое-то другое уравнение выбирается за разрешающее и одно из неизвестных в нем выбирается за разрешающее неизвестное. К этому выбору предъявляются два требования: 1) на предыдущих шагах это уравнение не было разрешающим; 2) в разрешающем уравнении коэффициент при разрешающем неизвестном должен быть отличен от нуля. Остальные действия такие же, как в шаге первом…

Процесс заканчивается, если ни одно из уравнений уже нельзя выбрать за разрешающее (т.е. все уравнения уже были в этой роли). Тогда для каждого уравнения имеется свое базисное неизвестное, входящее в это уравнение с коэффициентом, отличным от нуля, а в остальные уравнения — с коэффициентом 0. Т.о., процесс прекращается после получения базиса неизвестных. Т.е. мы нашли общее решение системы.

Пример №17

Найти общее решение системы линейных уравнений

Решение:

Последовательность действий будем записывать в виде таблиц. Разрешающие элементы отмечаются квадратными скобками. Конкретные действия комментируются в крайнем правом столбце таблицы. Например, запись {3}*(-2)+{1} означает, что третье уравнение системы, умноженное на число (-2), прибавлено к первому уравнению.

Последней таблице соответствует система

Подстановкой в исходную систему убеждаемся в правильности решения.

Ответ: система имеет единственное решение .

Пример №18

Найти общее решение системы линейных уравнений

Решение:

Последней таблице соответствует система

Таким образом, — базисные неизвестные, — свободное неизвестное. Поэтому общее решение задается формулами

Ответ: система имеет бесконечное множество решении , где — любое действительное число.

Эта лекция взята из раздела о предмете высшая математика, там вы найдёте другие лекци по всем темам высшей математики:

Высшая математика: полный курс лекций

Другие темы которые вам помогут понять высшую математику:

Линии второго порядка

Арифметические n-мерные векторные пространства

Решение разных задач методом гаусса

Матрицы

Открытый урок по дисциплине «Основы высшей математики» на тему «Методы решения систем линейных алгебраических уравнений»

Открытый урок по дисциплине «Основы высшей математики» на тему «Методы решения систем линейных алгебраических уравнений»

Тип и вид занятия:занятие обобщения и систематизации знаний (ЗОСЗ)

Цель занятия:Обеспечить закрепление знаний и способов деятельности студентовпо данной теме, создать содержательные и организационные условия для самостоятельного применения студентамикомплекса знаний и способов деятельности по теме: «Методы решения систем линейных алгебраических уравнений».

Задачи:

— Образовательная — повторить и обобщить понятия решения систем уравнений, показать применение определителей, обратной матрицы и метода Гаусса, закрепить умения и навыки математического моделирования при решении задач, характерных для будущей профессиональной деятельности

— Развивающая — продолжить отрабатывать вычислительные навыки при решении задач по специальности, продолжить развитие умений обобщать, систематизировать, делать выводы, сравнивать.

— Воспитательная — продолжить формирование необходимости повышения профессионального уровня, продолжить формирование умения принимать решения и отвечать за принятые решения.

Межпредметная связь: Языки программирования, Математическое моделирование экономических и производственных процессов

Материально-техническое обеспечение занятия: интерактивная доска, презентация к занятию

Методическая литература:

1. Письменный Д.Г. Конспект лекций по высшей математике. 1 часть. — М.: Айрис-пресс, 2002 — 288с.

2. Лунгу К.Н. Сборник задач по высшей математике. 1 курс. – М.: Айрис-пресс, 2013.-576с.

ХОД ЗАНЯТИЯ

1. Организационный момент.

Взаимное приветствие, проверка состава студентов, сообщение темы, цели и задач занятия проводится в форме беседы.

— Почему именно системы уравнений?

Математика – наука молодых. Иначе и не может быть.

Занятия математикой – это такая гимнастика ума, для

которой нужны вся гибкость и вся выносливость молодости.

Н. Винер

К решению систем линейных алгебраических уравнений сводятся многочисленные практические задачи (по некоторым оценкам более 75% всех задач). Можно с полным основанием утверждать, что решение линейных систем является одной из самых распространенных и важных задач вычислительной математики. Конечно, существует много методов и современных пакетов прикладных программ для решения СЛАУ, но для того, чтобы их успешно использовать, необходимо разбираться в основах построения методов и алгоритмов, иметь представления о недостатках и преимуществах используемых методов.

2.Основная часть занятия:

2.1 Актуализация и коррекция опорных знаний и умений.

С целью повторения необходимых теоретических сведений по теме, развития умений говорить и слушать проводится проверка теоретических знаний по теме «Матрицы и действия над ними».

Сопоставьте строки таблицы:

Прямоугольная таблица чисел называется		образуют элементы с равными индексами
Матрица называется квадратной, если		матрица
Единичной называется		число столбцов первой матрицы равно числу строк второй матрицы
В квадратной матрице главную диагональ		матрица, в которой строки и столбцы поменялись местами с сохранением порядка.
Суммой двух матриц		нужно умножить на это число все элементы матрицы.
Вектор-столбец, это		если у них одинаковое число строк и столбцов и все соответствующие элементы совпадают
Две матрицы можно перемножить, если		число строк в ней равно числу столбцов
Транспонированная матрица		матрица, состоящая из одного столбца
Матрицы называются равными		квадратная матрица, элементы главной диагонали которой единицы, а остальные нули
Чтобыумножить матрицу на число		называется матрица той же размерности, каждый элемент которой равен сумме соответствующих элементов слагаемых.

Наиболее часто матрицы используются при проведении экономических расчетов. С их помощью можно легко и быстро обработать большой объем информации. При этом конечный результат будет представлен в удобном для восприятия виде.

Еще одна сфера человеческой деятельности, в которой матрицы также нашли большое применение – это моделирование 3D-изображений. Подобные инструменты интегрированы в современные пакеты для реализации 3D-моделей и позволяют конструкторам производить быстро и точно необходимые расчеты.

2.2 Актуализация и обобщение отдельных фактов, событий, явлений.

Определение СЛАУ

Системой m линейных уравнений с n неизвестными называется система вида

где a_ij и b_i(i=1,…,m; b=1,…,n) – некоторые известные числа, а x₁,…,x_n – неизвестные.

Преподаватель проводит фронтальный опрос и проверку навыков вычисления определителя второго и третьего порядков.

— Что является решением системы?

— В каком случае СЛАУ имеет одно единственное решение?

— Что такое главный определитель системы?

— Каким образом находят определители второго и третьего порядков?

Нахождение определителя третьего порядка проводится у доски преподавателем вместе со студентами.

2.3 Повторение, обобщение и систематизациясоответствующей системы знаний.

Метод решения хорош, если с самого начала

мы можем предвидеть — и далее подтвердить это,

— что, следуя этому методу, мы достигнем цели.

Г. Лейбниц

Студенты вместе с преподавателем повторяют метод Крамера для решения СЛАУ.

Затем самостоятельно находят дополнительные определители системы и значения неизвестных.

отсюда по формулам Крамера (4): x = Dx / D = 0 / 32 = 0;

y = Dy / D = 32 / 32 = 1; z = Dz / D = 64 / 32 = 2 .

Повторение метода Гаусса решения СЛАУ.

Повторение метода обратной матрицы для решения систем линейных уравнений.

— Какую формулу применяют для данного метода?

— По какой формуле находят обратную матрицу?

— Как найти алгебраические дополнения?

— Что такое минор?

— Каким образом умножают матрицу на вектор — столбец?

3. Закрепление знаний.

Проводится в форме самостоятельной работы студентов.

3.1 Решить систему методом обратной матрицы. При этом алгебраические дополнения студенты перепроверяют «морским боем».

А₁₁₌3	А₂₁₌5	А₃₁₌1
А₁₂₌-11	А₂₂₌3	А₃₂₌7
А₁₃₌-7	А₂₃₌-1	А₃₃₌19

Дальнейшие расчеты студенты выполняют самостоятельно.

3.2 Решить систему методом Гаусса.

Студенты сдают работы и переходят к обсуждению достоинств и недостатков методов решения.

4. Подведение итогов занятия:

4.1Формирование профессиональной направленности.

Решение СЛАУ средствами языка программирования PascalABC.

Примеры использования систем линейных уравнений.

4.2 Оценивание знаний.

4.3 Домашнее задание.

Составить систему линейных уравнений. Решить её тремя методами.

Из некоторого листового материала необходимо выкроить 360 заготовок типа А, 300 заготовок типа Б и 675 заготовок типа В. При этом можно применять три способа раскроя. Количество заготовок, получаемых из каждого листа при каждом способе раскроя, указано в таблице:

Тип заготовки	Способ раскроя
заготовки	1	2	3
А	3	2	1
Б	1	6	2
В	4	1	5

Письменный Д. Г. Конспект лекций по высшей математике. 1 часть. — М.: Айрис-пресс, 2002 — 288с.

Разработка урока по алгебре в 7 классе по теме «Нестандартный способ решения систем линейных уравнений с двумя переменными»

Автор: Бородина Марина Юрьевна

Рубрика: Математика

Опубликовано в Молодой учёный №33 (167) август 2017 г.

Дата публикации: 22.08.2017 2017-08-22

Статья просмотрена: 1062 раза

Скачать электронную версию

Скачать Часть 1 (pdf)

Библиографическое описание:

Бородина, М. Ю. Разработка урока по алгебре в 7 классе по теме «Нестандартный способ решения систем линейных уравнений с двумя переменными» / М. Ю. Бородина. — Текст : непосредственный // Молодой ученый. — 2017. — № 33 (167). — С. 1-4. — URL: https://moluch.ru/archive/167/45372/ (дата обращения: 19.09.2022).

В данной статье предлагается разработка урока алгебры в 7 классе по учебнику А. Г. Мордковича. Школьникам скоро предстоит сдавать экзамены, и многие из них хотят, как можно хорошо и быстро научиться решать задачи. И в таких случаях можно применять нестандартные решения. Задания: «Решить систему уравнений» входят в задания экзамена как после 9 класса, так и после 11 класса. Данное изучение лучше применить на втором уроке в теме «Решение систем уравнений способ сложения».

Цель: Познакомиться с нестандартным решением систем линейных уравнений.

Задача: Научиться решать системы линейных уравнений методом Крамера и сравнить с другими методами решения.

Ход урока

Сегодня на уроке мы рассмотрим нестандартный способ решения систем уранений с двумя переменными и сравним данный способ решения с другими решенями. Но сначала повторим темы прошлых уроков:

– Что значит «решить систему линейных уравнений»? (Найти все его корни, или показать, что их нет.)

– Что является решением системы с двумя переменными? (Пара значений переменных, обращающая каждое уравнение системы в верное равенство.)

– Какие способы решения систем уравнений мы применяли? (способ сравнения; графический способ; способ подстановки; способ сложения)

К доске вызываются четыре ученика и решают систему различными способами, а остальные по вариантам. После решения ученики рассказывают алгоритм решения, в случае затруднения помогает класс.

При решении систем уравнений с двумя переменными можно применить еще один способ, применяя метод Крамера. Габриэль Крамер (Gabriel Cramer) (31. 07.1704 — 04.01.1752). Швейцарский математик, один из создателей линейной алгебры.

Данный метод значительно ускоряет процесс решения систем линейных уравнений и очень удобно применять его для систем с громоздкими вычислениями.

Метод Крамера применяется в Высшей математике при решении системы линейных уравнений с тремя неизвестными или решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Вам будет интересно научиться применять решение, не просто школьного курса, а решение, которые применяют студенты первых курсов высших заведений.

В данном методе при решении используют понятие определителя системы:

Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается Δ(дельта) и вычисляется по формуле.

где, _, — заданные числа_; х и у- неизвестные, числа — называются коэффициентами, а числа — свободными членами.

Δ = = а₁₁ · а₂₂ — а₁₂ · а₂₁.

Для нахождения неизвестных н6ам нужно найти еще два определителя и , путём замены коэффициентов при соответствующих неизвестных свободными членами:

= = в₁ · а₂₂ — а₁₂ · в₂.

= а₁₁ · в₂ — в₁ · а₂₁.

Формула Крамера для нахождения неизвестных: х = ; у = .

Найти значения неизвестных можно только при условии, когда определитель не равен нулю (Δ≠0).

Замечание: если определитель системы равен нулю, то система может иметь бесконечно много решений или не имеет решений.

Пример:

Δ = = 3·4–2·5 = 12–10=2≠0

Найдем еще два определителя и , путём замены коэффициентов при соответствующих неизвестных свободными членами:

= 2;

Формула Крамера для нахождения неизвестных: х = ; у = . Ответ: (1;-2).

Решите систему уравнений способ сложения и методом Крамера:

а) ; б) ; в)

Решив системы, сделаем вывод: какой способ решается быстрее и легче?

– способ сравнения: выразим переменную у через х, решим уравнение через х, приравняв правые части уравнения, и найдем переменную у;

– графический способ: выразим переменную у через х, построим график. Но на графике не всегда можно увидеть точное решение;

– способ подстановки: выразим одну переменную через другую, подставим и решим уравнение, найдем другую переменную;

– способ сложения: умножим уравнения системы на такие множители, чтобы коэффициенты при одной из переменных стали противоположными; сложим левые и правые части уравнений системы; решим получившееся уравнение с одной переменной и найдем другую переменную;

– методом Крамера: по формулам найдем три определителя и переменные.

При рассмотрении решений несколькими способами ученики убеждаются, что метод Крамера упрощает время и трудности вычисления для нахождения неизвестных в решении систем уравнений.

Итоги урока:

— Сегодня на уроке мы обобщили все методы решения систем линейных уравнений с двумя переменными.

— Какие способы решения вы знаете?

— Каким бы способом вы решали системы уравнений и почему?

— А какой способ решения вы бы применили на экзамене?

Домашнее задание: 1225(а, б), 1226.

Литература:

1. Ю. Н. Макарычев, Н. Г. Миндюк, К.И. и др. Алгебра 7 класс. Учебник. –М.: Просвещение 3-е изд. — М.: 2014. — 256 с.

Письменный Д. Т. Конспект лекций по высшее математике. 1 часть.- второе издание, испр.- М: Айрис-пресс, 2003.-288с.: ил.
Лисичкин В. Т., Соловейчик И. Л. математика: учебное пособие для техникумов. -М.: Высшая школа, 1991 480 с: ил.
Пичурин Л. Ф. За страницами учебника алгебры. — М: Просвещение, 1990–224с., ил.

Основные термины (генерируются автоматически): нахождение неизвестных, переменная, определитель системы, решение систем уравнений, решение системы, способ сложения, уравнение, графический способ, замена коэффициентов, какой способ решения.

Системы линейных уравнений

Линейное уравнение представляет собой уравнение для линии .

Линейное уравнение не всегда имеет форму y = 3,5 − 0,5x ,

Оно также может иметь вид y = 0,5(7 − x)

Или y + 0,5x = 3,5

7
Или как у + 0,5х — 3,5 = 0 и больше.
(Примечание: это одно и то же линейное уравнение!)

A Система линейных уравнений — это когда у нас есть два или более линейных уравнения , работающих вместе.
Пример: Вот два линейных уравнения:
2x + г = 5
−x + г = 2
Вместе они представляют собой систему линейных уравнений.
Можете ли вы найти значения х и у сами? (Просто попробуйте, поиграйте с ними немного.)
Давайте попробуем построить и решить пример из реального мира:
Пример: Вы против Лошади
Это гонка!
Вы можете пробежать 0,2 км каждую минуту.
Лошадь может пробежать 0,5 км каждую минуту. Но чтобы оседлать лошадь, нужно 6 минут.
Как далеко ты уедешь, прежде чем тебя догонит лошадь?

Мы можем составить два уравнения ( d = расстояние в км, t = время в минутах)
Вы бежите со скоростью 0,2 км каждую минуту, поэтому d = 0,2t
Лошадь бежит со скоростью 0,5 км в минуту, но мы уменьшаем ее время на 6: d = 0,5(t−6)

Итак, у нас есть система уравнений ( линейных ):
d = 0,2t
d = 0,5(t−6)
Решим на графике:
Видите, как лошадь стартует через 6 минут, а потом бежит быстрее?
Кажется, тебя поймали через 10 минут. .. ты проехал всего 2 км.
В следующий раз беги быстрее.
Итак, теперь вы знаете, что такое система линейных уравнений.
Продолжаем узнавать о них больше….
Решение
Способов решения линейных уравнений может быть много!
Давайте посмотрим на другой пример:
Пример: Решите эти два уравнения:
x + y = 6
-3х + у = 2
На этом графике показаны два уравнения:
Наша задача — найти место пересечения двух линий.
Ну, мы можем видеть, где они пересекаются, так что это уже решено графически.
А теперь давайте решим ее с помощью алгебры!

Хммм… как это решить? Способов может быть много! В этом случае в обоих уравнениях есть «y», поэтому давайте попробуем вычесть все второе уравнение из первого:
х + у — (-3х + у) = 6 — 2
Теперь упростим это: теперь мы знаем, что линии пересекаются в точке x=1 .
И мы можем найти соответствующее значение y , используя любое из двух исходных уравнений (потому что мы знаем, что они имеют одно и то же значение при x=1). Воспользуемся первым (второй можете попробовать сами):
x + y = 6
1 + y = 6
y = 5
И решение:
x = 1 и y = 5
И график показывает нам, что мы правы!
Линейные уравнения
В линейных уравнениях допускаются только простые переменные. no x ², Y ³, √x и т. Д. :

Линейный против нелинейного
Размеры
A Line Equation CAN BR 2 DIMENTIONAION IN 2 DIMENTIONIONS IRI DIMENTIONAINS 9000. как х и у )
… или в 3-х измерениях …
(составляет самолет)
… или 4 размера …
… или больше!
Общие переменные
Чтобы уравнения «работали вместе», они используют одну или несколько переменных:
Система уравнений имеет два или более уравнений в одна или несколько переменных
много переменных
Таким образом, система уравнений может иметь много уравнений и много переменных.
Пример: 3 уравнения с 3 переменными
2x + г — 2з = 3
х − г — г = 0
х + г + 3з = 12
Может быть любая комбинация:
2 уравнения с 3 переменными,
6 уравнений с 4 переменными,
9000 уравнений с 567 переменными,
и т. д.
Решения
Когда количество уравнений равно тому же , что и количество переменных, то вероятно будут решением. Не гарантировано, но вероятно.
На самом деле возможны только три случая:
Нет решения
Один раствор
Бесконечное множество решений
Когда есть нет решения уравнения называются «несовместимыми» .
One или бесконечно многие растворов называются «Последовательные»
Вот диаграмма для 2 Уравнения в 2 переменных :
Независимые
«
. уравнение дает новую информацию.
В противном случае они «Зависимые» .
Также называется «линейная независимость» и «линейная зависимость»
Пример:
х + у = 3
2х + 2у = 6
Эти уравнения «зависимы» , потому что они на самом деле то же самое уравнение , просто умноженное на 2.
Итак, второе уравнение не дало никакой новой информации .
Где уравнения верны
Хитрость заключается в том, чтобы найти, где все уравнений верны одновременно .
Правда? Что это значит?
Пример: Вы против Лошади
Строка «вы» истинна по всей своей длине (но больше нигде).
В любом месте этой линии d равно 0,2t
при t=5 и d=1 уравнение верно верно)
при t=5 и d=3 уравнение , а не верно (d = 0,2t? Нет, так как 3 = 0,2×5 неверно )
Точно так же линия «лошадь» также истинна по всей своей длине (но больше нигде).
Но только в точке, где они пересекают (при t=10, d=2), оба истинны .
Таким образом, они должны быть верными одновременно …
… поэтому некоторые люди называют их «Одновременными линейными уравнениями»
Решить с помощью алгебры их.
Вот пример «Лошадь», решенный с помощью алгебры:
Пример: Вы против Лошади
Система уравнений:
d = 0,2t
d = 0,5(t−6)
В этом случае проще всего приравнять их: Расширить 0,5(t−6) :0,2t = 0,5t − 3
Вычесть 0,5t с обеих сторон: −0,3t = −3
Разделить обе стороны на −0,3 :t = −3/−0,3 = 10 минут
Теперь мы знаем , когда тебя поймают!
Знание T Мы можем рассчитать D : D = 0,2t = 0,2 × 10 = 2 км
, а наше решение:
T = 10 минут и D = 2 км
Algebra.
против графиков
Зачем использовать алгебру, когда графики так просто? Потому что:
Более 2 переменных не могут быть решены с помощью простого графика.
Итак, алгебра приходит на помощь с двумя популярными методами:
Решение путем подстановки
Решение методом исключения
Мы рассмотрим каждый из них с примерами в 2 переменных и в 3 переменных. Вот…
Решение путем подстановки
Вот шаги:
Напишите одно из уравнений в таком стиле «переменная =…»
Заменить (т. е. заменить) эту переменную в другом уравнении (уравнениях).
Решить другое уравнение(я)
(Повторите при необходимости)
Вот пример с 2 уравнения с 2 переменными :
Пример:
3x + 2y = 19
х + у = 8
Мы можем начать с любого уравнения и любой переменной .
Используем второе уравнение и переменную «y» (выглядит простейшим уравнением).

Напишите одно из уравнений в стиле «переменная = …»:
Мы можем вычесть x из обеих частей x + y = 8, чтобы получить y = 8 − x . Теперь наши уравнения выглядят так:
3x + 2y = 19
у = 8 — х

Теперь замените «y» на «8 − x» в другом уравнении:
3x + 2 (8 − x) = 19
у = 8 — х

Решите, используя обычные алгебраические методы:
Разверните 2(8−x) :
3x + 16 − 2x = 19
у = 8 — х
Тогда 3x−2x = x :
x + 16 = 19
у = 8 — х
И, наконец, 19−16=3
х = 3
у = 8 — х

Теперь мы знаем, что такое x , мы можем поместить его в y = 8 − x уравнение:
x = 3
у = 8 — 3 = 5
и ответ:
x = 3
y = 5
Примечание. Потому что есть A Решение. Уравнения «Последовательные»
Проверка: почему вы проверить, работает ли x = 3 и y = 5 в обоих уравнениях?

Решение методом замены: 3 уравнения с 3 переменными
ОК! Давайте перейдем к более длинному примеру : 3 уравнения с 3 переменными .
Это не сложно сделать… просто долго !
Пример:
x + z = 6
г — 3у = 7
2x + у + 3z = 15
Мы должны аккуратно выстроить переменные, иначе мы можем потерять представление о том, что делаем:

x + г = 6
— 3 года + г = 7
2x + г + 3з = 15

Мы можем начать с любого уравнения и любой переменной. Давайте используем первое уравнение и переменную «x».

Напишите одно из уравнений так, чтобы оно было в стиле «переменная =…»:
х = 6 − я
— 3 года + г = 7
2x + г + 3з = 15

Теперь замените «x» на «6 − z» в других уравнениях:
(К счастью, есть только одно уравнение с x в нем)
х = 6 — я
— 3 года + г = 7
2 (6-з) + г + 3з = 15

Решите, используя обычные алгебраические методы:
2(6−z) + y + 3z = 15 упрощается до y + z = 3 :
x = 6 — я
— 3 года + г = 7
г + г = 3
Хорошо. Мы добились некоторого прогресса, но еще не все.

Теперь повторите процесс , но только для двух последних уравнений.

Напишите одно из уравнений так, чтобы оно было в стиле «переменная =…»:
Выберем последнее уравнение и переменную z:
x = 6 — я
— 3 года + г = 7
я = 3 − у

Теперь замените «z» на «3 − y» в другом уравнении:
x = 6 — я
— 3 года + 3 − у = 7
г = 3 − у
Решение с использованием обычных методов алгебры:
−3y + (3 -y) = 7 упрощает до −4y = 4 , или в других словах y = −1
4166 y = −1
414166 y = −1
414166 y = −1
41419 6.
х = 6 — я
г = −1
г = 3 − у
Почти готово!

Зная, что y = −1 , мы можем вычислить, что z = 3−y = 4 :
x = 6 — я
г = −1
я = 4
Зная, что z = 4 , мы можем вычислить, что x = 6−z = 2 :
x = 2
г = −1
г = 4

И ответ:
x = 2
y = −1
z = 4

Проверьте сами.
Мы можем использовать этот метод для 4 или более уравнений и переменных… просто повторяйте одни и те же шаги снова и снова, пока не решите.
Вывод: Замена работает хорошо, но требует много времени.

Решение путем исключения
Исключение может быть быстрее… но оно должно быть аккуратным.
«Устранить» означает удалить : этот метод работает путем удаления переменных до тех пор, пока не останется только одна.
Идея в том, что мы можем безопасно :
умножить уравнение на константу (кроме нуля),
добавить (или вычесть) уравнение из другого уравнения
Как в этих примерах:
ПОЧЕМУ мы можем складывать уравнения друг с другом?
Представьте два очень простых уравнения:
x — 5 = 3
5 = 5
Мы можем добавить «5 = 5» к «x — 5 = 3»:
x — 5 + 5 = 3 + 5
x = 8
Попробуйте сделать это сами, но используйте 5 = 3+2 в качестве второго уравнения
Оно по-прежнему будет работать нормально, потому что обе части равны (для этого и нужен знак =!)

Мы также можем поменять местами уравнения , так что 1-й может стать 2-м и т. д., если это поможет.

Хорошо, время для полного примера. Давайте воспользуемся 2 уравнениями с 2 переменными пример из предыдущего:
Пример:
3x + 2y = 19
х + у = 8
Очень важно поддерживать порядок:
3x + 2 года = 19
х + г = 8

Теперь… наша цель исключить переменную из уравнения.
Сначала мы видим, что есть «2y» и «y», так что давайте поработаем над этим.
Умножьте второе уравнение на 2:
3x + 2 года = 19
2 х + 2 у = 16
Вычесть второе уравнение из первого уравнения:
x = 3
2x + 2 года = 16
Ура! Теперь мы знаем, что такое х!

Далее мы видим, что второе уравнение имеет «2x», поэтому давайте уменьшим его вдвое, а затем вычтем «x»:
Умножьте второе уравнение на ½ (т. е. разделите на 2):
x = 3
х + г = 8
Вычесть первое уравнение из второго уравнения:
x = 3
г = 5
Готово! А вот и график: где x + y = 8 верно
При x=3, y=5 (где линии пересекаются) они равны оба верно. Ответ: .
Вот еще один пример:
Пример:
2x − y = 4
6х — 3у = 3
Аккуратно разложите:
2x — г = 4
6x — 3 года = 3
Умножьте первое уравнение на 3:
6x — 3 года = 12
6x — 3 года = 3
Вычесть второе уравнение из первого уравнения:
0 — 0 = 9
6x — 3 года = 3
0 − 0 = 9 ???
Что здесь происходит?

Проще говоря, решения нет.

На самом деле это параллельные линии:
И, наконец:
Пример:
2x − y = 4
6х — 3у = 12
Аккуратно:
2x — г = 4
6x — 3 года = 12
Умножьте первое уравнение на 3:
6x — 3 года = 12
6x — 3 года = 12
Вычесть второе уравнение из первого уравнения:
0 — 0 = 0
6x — 3 года = 3
0 − 0 = 0
Что ж, это действительно ПРАВДА! Ноль действительно равен нулю. ..

… потому что на самом деле это одно и то же уравнение…

… так что существует бесконечное количество решений
Это одна и та же строка:
Итак, теперь мы рассмотрели пример каждого из трех возможных случаев:
Нет решение
Один раствор
Бесконечное множество решений
Решение методом исключения: 3 уравнения с 3 переменными
Прежде чем мы приступим к следующему примеру, давайте рассмотрим улучшенный способ работы.
Следуйте этому методу, и мы с меньшей вероятностью допустим ошибку.
Прежде всего, исключить переменные по порядку :
Сначала исключить x с (из уравнения 2 и 3, по порядку)
затем исключить y (из уравнения 3)
Итак, вот как мы их устраняем:
Получим вот такую «форму треугольника»:
Теперь начните снизу и вернитесь к (так называемая «обратная подстановка»)
(вставьте z , чтобы найти y , затем z и y , чтобы найти) :
И мы решаем:
ТАКЖЕ, мы обнаружим, что некоторые расчетов в уме или на бумаге легче делать, чем всегда работать в рамках системы уравнений:
Пример:
х + у + г = 6
2г + 5г = -4
2x + 5y — z = 27
Написано аккуратно:
x + г + г = 6
2 года + 5з = −4
2x + 5 лет — г = 27

Сначала исключите x из второго и третьего уравнений.
Во 2-м уравнении нет x… переходим к 3-му уравнению:
Вычтем 2 раза 1-е уравнение из 3-го уравнения (просто сделайте это в уме или на бумаге):
И получаем:
х + г + г = 6
2 года + 5з = −4
3 года — 3з = 15

Затем исключите y из третьего уравнения.
Мы могли бы вычесть 1½ раза 2-е уравнение из 3-го уравнения (потому что 1½ умножить на 2 равно 3) …
… но мы можем избежать дробей , если мы:
умножим 3-е уравнение на 2 и
умножить второе уравнение на 3
и затем делаем вычитание… вот так:
И в итоге получаем:
x + г + г = 6
2 года + 5з = −4
я = −2
Теперь у нас есть «треугольная форма»!

Теперь снова вернитесь наверх, «обратно подставив»:
Мы знаем z , поэтому 2y+5z = −4 становится 2y -10 = -4 , затем 2y = 6 , так что y = 3 :
x + г + г = 6
г = 3
г = −2
Тогда x+y+z=6 становится x+3−2=6 , поэтому x=6−3+2=5
x = 5
г = 3
г = −2

Ответ:
x = 5
y = 3
z = −2

Проверьте: проверьте сами.
Общий совет
Как только вы привыкнете к методу исключения, он станет проще, чем замена, потому что вы просто выполняете шаги, и ответы появляются.
Но иногда Замена может дать более быстрый результат.
Замена часто проще для небольших случаев (например, 2 уравнения, а иногда и 3 уравнения)
Устранение проще для больших ящиков
И всегда полезно сначала просмотреть уравнения, чтобы увидеть, нет ли простого сокращения … так что опыт помогает.

Головоломка с карандашами и баночками

Решение систем линейных уравнений
Горячая математика
А система линейные уравнения представляет собой просто набор из двух или более линейных уравнений.
В двух переменных ( Икс а также у ) , график системы двух уравнений представляет собой пару прямых на плоскости.
Есть три возможности:
Линии пересекаются в нулевых точках. (Прямые параллельны.)
Линии пересекаются ровно в одной точке. (Большинство случаев.)
Прямые пересекаются в бесконечном числе точек. (Два уравнения представляют одну и ту же прямую.)
Нулевые решения:
у знак равно − 2 Икс + 4 у знак равно − 2 Икс − 3
Одно решение:
у знак равно 0,5 Икс + 2 у знак равно − 2 Икс − 3
Бесконечное множество решений:
у знак равно − 2 Икс − 4 у + 4 знак равно − 2 Икс
Существует несколько различных методов решения систем линейных уравнений:
Графический метод . Это полезно, когда вам просто нужен грубый ответ, или вы уверены, что пересечение происходит в целочисленных координатах. Просто нарисуйте две линии и посмотрите, где они пересекаются!
См. второй график выше. Решение находится там, где две линии пересекаются, точка ( − 2 , 1 ) .
Метод замены . Сначала решим одно линейное уравнение относительно у с точки зрения Икс . Затем подставьте это выражение вместо у в другом линейном уравнении. Вы получите уравнение в Икс . Решите это, и вы получите Икс -координата перекрестка. Затем подключите Икс к любому уравнению, чтобы найти соответствующее у -координата. (Если это проще, вы можете начать с решения уравнения для Икс с точки зрения у , тоже – такая же разница!)
Пример 1:
Решите систему { 3 Икс + 2 у знак равно 16 7 Икс + у знак равно 19
Решите второе уравнение для у .
у знак равно 19 − 7 Икс
Заменять 19 − 7 Икс за у в первом уравнении и решить Икс .
3 Икс + 2 ( 19 − 7 Икс ) знак равно 16 3 Икс + 38 − 14 Икс знак равно 16 − 11 Икс знак равно − 22 Икс знак равно 2
Заменять 2 за Икс в у знак равно 19 − 7 Икс и решить для у .
у знак равно 19− 7 ( 2 ) у знак равно 5
Решение ( 2 , 5 ) .
Метод линейной комбинации , он же Метод добавления , он же Метод ликвидации. Прибавьте (или вычтите) число, кратное одному уравнению, к другому уравнению (или из него) таким образом, чтобы Икс -термины или у -термины отменяются. Затем решите для Икс (или же у , в зависимости от того, что осталось) и подставьте обратно, чтобы получить другую координату.
Пример 2:
Решите систему { 4 Икс + 3 у знак равно − 2 8 Икс − 2 у знак равно 12
Умножьте первое уравнение на − 2 и добавьте результат ко второму уравнению.
− 8 Икс − 6 у знак равно 4 8 Икс − 2 у знак равно 12 _ − 8 у знак равно 16
Решить для у .
у знак равно − 2
Замена для у в любом из исходных уравнений и решить для Икс .
4 Икс + 3 ( − 2 ) знак равно − 2 4 Икс − 6 знак равно − 2 4 Икс знак равно 4 Икс знак равно 1
Решение ( 1 , − 2 ) .
Матричный метод . На самом деле это просто метод линейной комбинации, упрощенный сокращённой записью.
11.1: Системы линейных уравнений — две переменные
Последнее обновление
Сохранить как PDF
Идентификатор страницы
2669
OpenStax
OpenStax
Цели обучения
Решать системы уравнений с помощью графиков.
Решите системы уравнений подстановкой.
Решайте системы уравнений методом сложения.
Определите противоречивые системы уравнений, содержащие две переменные.
Выразите решение системы зависимых уравнений, содержащей две переменные.
Производитель скейтбордов представляет новую линейку досок. Производитель отслеживает свои затраты, которые представляют собой сумму, которую он тратит на производство плат, и свой доход, который представляет собой сумму, которую он зарабатывает на продаже своих плат. Как компания может определить, получает ли она прибыль от своей новой линии? Сколько скейтбордов нужно произвести и продать, чтобы можно было получить прибыль? В этом разделе мы рассмотрим линейные уравнения с двумя переменными, чтобы ответить на эти и подобные вопросы.
Рисунок $\PageIndex{1}$
Введение в системы уравнений
Чтобы исследовать такие ситуации, как ситуация с производителем скейтборда, нам нужно признать, что мы имеем дело с более чем одной переменной и, вероятно, с более чем одним уравнением . Система линейных уравнений состоит из двух или более линейных уравнений, состоящих из двух или более переменных, так что все уравнения в системе рассматриваются одновременно. Чтобы найти единственное решение системы линейных уравнений, мы должны найти числовое значение для каждой переменной в системе, которое будет удовлетворять всем уравнениям в системе одновременно. Некоторые линейные системы могут не иметь решения, а другие могут иметь бесконечное число решений. Чтобы линейная система имела единственное решение, в ней должно быть не меньше уравнений, чем переменных. Тем не менее, это не гарантирует уникальности решения.
В этом разделе мы рассмотрим системы линейных уравнений с двумя переменными, которые состоят из двух уравнений, содержащих две разные переменные. Например, рассмотрим следующую систему линейных уравнений с двумя переменными.
\[\begin{align*} 2x+y &= 15 \\ 3x–y &= 5 \end{align*}\]
Решение системы линейных уравнений с двумя переменными является любым упорядоченным пара, удовлетворяющая каждому уравнению независимо. В этом примере упорядоченная пара $(4,7)$ является решением системы линейных уравнений. Мы можем проверить решение, подставив значения в каждое уравнение, чтобы увидеть, удовлетворяет ли упорядоченная пара обоим уравнениям. Вскоре мы исследуем методы нахождения такого решения, если оно существует.
\[\begin{align*} 2(4)+(7) &=15 \text{ True} \\ 3(4)−(7) &= 5 \text{ True} \end{align*} \]
Помимо рассмотрения количества уравнений и переменных, мы можем классифицировать системы линейных уравнений по количеству решений. Непротиворечивая система уравнений имеет хотя бы одно решение. Непротиворечивая система считается независимой системой , если она имеет единственное решение, как в примере, который мы только что рассмотрели. Две линии имеют разные наклоны и пересекаются в одной точке плоскости. Непротиворечивая система считается зависимая система , если уравнения имеют одинаковый наклон и одинаковые и -перехваты. Другими словами, прямые совпадают, поэтому уравнения представляют одну и ту же прямую. Каждая точка на прямой представляет собой пару координат, удовлетворяющую системе. Таким образом, существует бесконечное множество решений.
Другим типом системы линейных уравнений является противоречивая система , в которой уравнения представляют собой две параллельные прямые. Линии имеют одинаковый наклон и разные г- перехватов. Нет общих точек для обеих прямых; следовательно, система не имеет решения.
ТИПЫ ЛИНЕЙНЫХ СИСТЕМ
Существует три типа систем линейных уравнений с двумя переменными и три типа решений.
Независимая система имеет ровно одну пару решений $(x,y)$. Точка пересечения двух прямых является единственным решением.
Несовместная система не имеет решения. Обратите внимание, что две линии параллельны и никогда не пересекаются.
Зависимая система имеет бесконечно много решений. Линии совпадают. Это одна и та же линия, поэтому каждая пара координат на линии является решением обоих уравнений.
На рисунке $\PageIndex{2}$ сравниваются графические представления каждого типа системы.
Рисунок $\PageIndex{2}$
Для заданной системы линейных уравнений и упорядоченной пары определите, является ли упорядоченная пара решением
Подставьте упорядоченную пару в каждое уравнение системы.
Определить, верны ли утверждения в результате замены в обоих уравнениях; если да, то упорядоченная пара является решением.
Пример $\PageIndex{1}$: определение того, является ли упорядоченная пара решением системы уравнений
Определить, является ли упорядоченная пара $(5,1)$ решением данной системы уравнений уравнения.
\[\begin{align*} x+3y &= 8 \\ 2x−9 &= y \end{align*}\]
Решение
Подставить упорядоченную пару $(5,1) $ в оба уравнения.
\[ \begin{align*} (5)+3(1) &= 8 \\ 8 &= 8 \text{ True} \\ 2(5)−9 &= (1) \\ 1 &= 1 \text{ True} \end{align*}\]
Упорядоченная пара $(5,1)$ удовлетворяет обоим уравнениям, поэтому является решением системы.
Анализ
Мы можем ясно увидеть решение, построив график каждого уравнения. Поскольку решение представляет собой упорядоченную пару, удовлетворяющую обоим уравнениям, это точка на обеих прямых и, следовательно, точка пересечения двух прямых. См. рисунок $\PageIndex{3}$.
Рисунок $\PageIndex{3}$
Упражнение $\PageIndex{1}$
Определите, является ли упорядоченная пара $(8,5)$ решением следующей системы.
\[\begin{align*} 5x−4y &= 20 \\ 2x+1 &= 3y \end{align*}\]
Ответ
Не решение.
Решение систем уравнений с помощью графика
Существует несколько методов решения систем линейных уравнений. Для системы линейных уравнений с двумя переменными мы можем определить как тип системы, так и решение, изобразив систему уравнений на одном и том же наборе осей.
Пример $\PageIndex{2}$: Решение системы уравнений с двумя переменными с помощью графика
Решите следующую систему уравнений с помощью графика. Определите тип системы.
\[\begin{align*} 2x+y &= −8 \\ x−y &= −1 \end{align*}\]
Решение
Решите первое уравнение для $y\ ).
\[\begin{align*} 2x+y &= −8 \\ y &= −2x−8 \end{align*}\]
Решите второе уравнение для \(y$.
\[\begin{align*} x−y &= −1 \\ y &= x+1 \end{align*}\]
Постройте график обоих уравнений на том же наборе осей, что и на рисунке $\PageIndex{4}$.
Рисунок $\PageIndex{4}$
Линии пересекаются в точке $(−3,−2)$. Мы можем убедиться, что это решение системы, подставив упорядоченную пару в оба уравнения.
\[\begin{align*} 2(−3)+(−2) &= −8 \\ −8 &= −8 \text{ True} \\ (−3)−(−2) &= −1 \\ −1 &= −1 \text{ True} \end{align*}\]
Решением системы является упорядоченная пара $(−3,−2)$, поэтому система независимый.
Упражнение $\PageIndex{2}$
Решите следующую систему уравнений, построив график.
\[\begin{align*} 2x−5y &= −25 \\ −4x+5y &= 35 \end{align*}\]
Ответ
Решением системы является упорядоченная пара $(−5,3)$.
Рисунок $\PageIndex{5}$
Вопросы и ответы
Можно ли использовать графики, если система непоследовательна или зависима?
Да, в обоих случаях мы можем построить график системы, чтобы определить тип системы и решения. Если две прямые параллельны, то система не имеет решений и несовместна. Если две линии идентичны, система имеет бесконечные решения и является зависимой системой.
Решение систем уравнений путем подстановки
Решение линейной системы с двумя переменными с помощью графика хорошо работает, когда решение состоит из целых чисел, но если наше решение содержит десятичные числа или дроби, это не самый точный метод. Рассмотрим еще два метода решения системы линейных уравнений , которые являются более точными, чем построение графика. Одним из таких методов является решение системы уравнений методом подстановки , в котором мы решаем одно из уравнений для одной переменной, а затем подставляем результат во второе уравнение для решения второй переменной. Напомним, что мы можем решать только для одной переменной за раз, поэтому метод подстановки ценен и практичен.
Как: Дана система из двух уравнений с двумя переменными, решить методом подстановки.
Решите одно из двух уравнений для одной из переменных относительно другой.
Подставьте выражение для этой переменной во второе уравнение, затем найдите оставшуюся переменную.
Подставьте это решение в любое из исходных уравнений, чтобы найти значение первой переменной. Если возможно, запишите решение в виде упорядоченной пары.
Проверьте решение обоих уравнений.
Пример $\PageIndex{3}$: решение системы уравнений с двумя переменными с помощью замены
Решите следующую систему уравнений с помощью замены.
\[\begin{align*} −x+y &= −5 \\ 2x−5y &= 1 \end{align*}\]
Решение
Сначала решим первое уравнение для $у$.
\[\begin{align*} −x+y &=−5 \\ y &= x−5 \end{align*}\]
Теперь мы можем заменить выражение $x−5$ на $y$ во втором уравнении.
\[\begin{align*} 2x−5y &= 1 \\ 2x−5(x−5) &= 1 \\ 2x−5x+25 &= 1 \\ −3x &= −24 \\ x &= 8 \end{align*}\]
Теперь подставим $x=8$ в первое уравнение и найдем $y$.
\[\begin{align*} −(8)+y &= −5 \\ y &= 3 \end{align*}\]
Наше решение: $(8,3)$.
Проверьте решение, подставив $(8,3)$ в оба уравнения.
\[\begin{align*} −x+y &= −5 \\ −(8)+(3) &= −5 \text{ True} \\ 2x−5y &= 1 \\ 2(8 )−5(3) &= 1 \text{ True} \end{align*}\]
Упражнение $\PageIndex{3}$
Решите следующую систему уравнений методом замены.
\[\begin{align*} x &= y+3 \\ 4 &= 3x−2y \end{align*}\]
Ответ
$(−2,−5)$
Вопросы и ответы
Можно ли использовать метод подстановки для решения любой линейной системы с двумя переменными?
Да, но метод работает лучше всего, если одно из уравнений содержит коэффициент $1$ или $–1$, чтобы нам не приходилось иметь дело с дробями.
Решение систем уравнений с двумя переменными методом сложения
Третий метод решения систем линейных уравнений — метод сложения. В этом методе мы добавляем два слагаемых с одной и той же переменной, но с противоположными коэффициентами, так что сумма равна нулю. Конечно, не во всех системах два члена одной переменной имеют противоположные коэффициенты. Часто нам приходится корректировать одно или оба уравнения путем умножения, чтобы исключить одну переменную путем сложения.
Как: Имея систему уравнений, решить ее методом сложения.
Напишите оба уравнения с x — и y -переменными слева от знака равенства и константами справа.
Напишите одно уравнение над другим, выстраивая соответствующие переменные. Если одна из переменных в верхнем уравнении имеет противоположный коэффициент той же переменной в нижнем уравнении, сложите уравнения вместе, исключив одну переменную. Если нет, используйте умножение на ненулевое число, чтобы одна из переменных в верхнем уравнении имела коэффициент, противоположный той же переменной в нижнем уравнении, затем добавьте уравнения, чтобы исключить переменную.
Решите полученное уравнение для оставшейся переменной.
Подставьте это значение в одно из исходных уравнений и найдите вторую переменную.
Проверьте решение, подставив значения в другое уравнение.
Пример $\PageIndex{4}$: Решение системы методом сложения
Решите данную систему уравнений методом сложения.
\[\begin{align*} x+2y &= −1 \\ −x+y &=3 \end{align*}\]
Решение
Оба уравнения уже установлены равными константе. Обратите внимание, что коэффициент $x$ во втором уравнении, $–1$, противоположен коэффициенту $x$ в первом уравнении, $1$. Мы можем сложить два уравнения, чтобы исключить $x$ без необходимости умножения на константу.
\[\begin{align*} x+2y &= -1 \\ \underline{-x+y}& = \underline{3} \\ 3y&= 2 \\ \end{align*}\]
Теперь, когда мы исключили $x$, мы можем решить полученное уравнение относительно $y$.
\[\begin{align*} 3y &= 2 \\ y &=\dfrac{2}{3} \end{align*}\]
Затем мы подставляем это значение для $y$ в одно из исходных уравнений и решить относительно $x$.
\[\begin{align*} −x+y &= 3 \\ −x+\dfrac{2}{3} &= 3 \\ −x &= 3−\dfrac{2}{3} \\ −x &= \dfrac{7}{3} \\ x &= −\dfrac{7}{3} \end{align*}\]
Решением этой системы является $\left(−\dfrac {7}{3},\dfrac{2}{3}\right)$.
Проверьте решение первого уравнения.
\[\begin{align*} x+2y &= −1 \\ \left(−\dfrac{7}{3}\right)+2\left(\dfrac{2}{3}\right) &= \\ −\dfrac{7}{3}+\dfrac{4}{3} &= −\dfrac{3}{3} \\ −1 &= −1 \;\;\;\;\ ;\;\;\; \text{True} \end{align*}\]
Анализ
Мы получаем важный взгляд на системы уравнений, глядя на графическое представление. См. рисунок $\PageIndex{6}$, чтобы убедиться, что уравнения пересекаются в решении. Нам не нужно спрашивать, может ли быть второе решение, потому что наблюдение за графиком подтверждает, что система имеет ровно одно решение.
Рисунок $\PageIndex{6}$
Пример $\PageIndex{5}$: Использование метода сложения, когда требуется умножение одного уравнения
Решите данную систему уравнений методом сложения.
\[\begin{align*} 3x+5y &= −11 \\ x−2y &= 11 \end{align*}\]
Решение
Добавление этих уравнений в представленном виде не приведет к удалению переменной . Однако мы видим, что в первом уравнении есть $3x$, а во втором уравнении есть $x$. Итак, если мы умножим второе уравнение на $−3$, x — слагаемые добавятся к нулю.
\[\begin{align*} x−2y &= 11 \\ −3(x−2y) &=−3(11) \;\;\;\;\;\;\;\; \text{Умножьте обе части на }−3. \\ −3x+6y &= −33 \;\;\;\;\;\;\;\;\; \text{Используйте свойство дистрибутива.} \end{align*}\]
Теперь добавим их.
\[\begin{align*} 3x+5y &= -11 \\ \underline{-3x+6y }& = \underline{-33} \\ 11y&= -44 \\ y&= -4 \end{ align*}\]
На последнем этапе мы подставляем $y=−4$ в одно из исходных уравнений и находим $x$.
\[\begin{align*} 3x+5y &= −11 \\ 3x+5(−4) &= −11 \\ 3x−20 &= −11 \\ 3x &= 9 \\ x &= 3 \end{align*}\]
Наше решение — упорядоченная пара $(3,−4)$. См. рисунок $\PageIndex{7}$. Проверьте решение в исходном втором уравнении.
\[\begin{align*} x−2y &= 11 \\ (3)−2(−4) &= 3+8 \\ &= 11 \;\;\;\;\;\;\ ;\;\;\; \text{True} \end{align*}\]
Рисунок $\PageIndex{7}$
Упражнение $\PageIndex{4}$
Решите систему уравнений сложением.
\[\begin{align*} 2x−7y &= 2 \\ 3x+y &= −20 \end{align*}\]
Ответ
$(−6,−2)$
Пример $\PageIndex{6}$: Использование метода сложения, когда требуется умножение обоих уравнений
Решите данную систему уравнений с двумя переменными методом сложения.
\[\begin{align*} 2x+3y &= −16 \\ 5x−10y &= 30 \end{align*}\]
Решение
Одно уравнение имеет $2x$ и другой имеет $5x$. Наименьшее общее кратное равно $10x$, поэтому нам придется умножить оба уравнения на константу, чтобы исключить одну переменную. Удалим $x$, умножив первое уравнение на $−5$, а второе уравнение на $2$.
\[\begin{align*} −5(2x+3y) &= −5(−16) \\ −10x−15y &= 80 \\ 2(5x−10y) &= 2(30) \\ 10x−20y &= 60 \end{align*}\]
Затем мы складываем два уравнения вместе.
\[\begin{align*} -10x-15y &= 80 \\ \underline{10x-20y}& = \underline{60} \\ -35y&= 140 \\ y&= -4 \end{align* }\]
Подставить $y=−4$ в исходное первое уравнение.
\[ \begin{align*} 2x+3(−4) &=−16 \\ 2x−12 &= −16 \\ 2x &= −4 \\ x &=−2 \end{align*} \]
Решение: $(−2,−4)$. Проверьте это в другом уравнении.
\[\begin{align*} 5x−10y &= 30 \\ 5(−2)−10(−4) &= 30 \\ −10+40 &= 30 \\30 &=30 \end{ align*}\]
См. рисунок $\PageIndex{8}$.
Рисунок $\PageIndex{8}$
Пример $\PageIndex{7}$: Использование метода сложения в системах уравнений, содержащих дроби
Решите данную систему уравнений с двумя переменными методом сложения.
\[ \begin{align*} \dfrac{x}{3}+\dfrac{y}{6} &= 3 \\ \dfrac{x}{2}-\dfrac{y}{4} & = 1 \end{выравнивание*}\]
Решение
Сначала очистите каждое уравнение дробей, умножив обе части уравнения на наименьший общий знаменатель.
\[\begin{align*} 6\left(\dfrac{x}{3}+\dfrac{y}{6}\right) &= 6(3) \\ 2x+y &= 18 \\ 4\left(\dfrac{x}{2}−\dfrac{y}{4}\right) &= 4(1) \\ 2x−y &= 4 \end{align*}\]
Теперь умножьте второе уравнение на $−1$, так что мы можем исключить x -переменную.
\[\begin{align*} −1(2x−y) &= −1(4) \\ −2x+y &= −4 \end{align*}\]
Сложите два уравнения, чтобы исключить переменную $x$, и решите полученное уравнение.
\[\begin{align*} 2x+y &= 18 \\ −2x+y &= −4 \\ 2y &= 14 \\ y &=7 \end{align*}\]
Замена \ (y=7\) в первое уравнение.
\[\begin{align*} 2x+(7) &= 18 \\ 2x &= 11 \\ x &= \dfrac{11}{2} \\ &= 7.5 \end{align*}\]
Решение: $\left(\dfrac{11}{2},7\right)$. Проверьте это в другом уравнении.
\[\begin{align*} \dfrac{x}{2}-\dfrac{y}{4} &= 1 \\ \dfrac{\dfrac{11}{2}}{2}-\dfrac {7}{4} &=1 \\ \dfrac{11}{4}-\dfrac{7}{4} &=1 \\ \dfrac{4}{4} &=1 \end{align*} \]
Упражнение $\PageIndex{5}$
Решите систему уравнений сложением.
\[\begin{align*} 2x+3y &= 8 \\ 3x+5y &= 10 \end{align*}\]
Ответ
$(10,−4)$
Идентификация несовместных систем уравнений, содержащих две переменные
Теперь, когда у нас есть несколько методов решения систем уравнений, мы можем использовать эти методы для выявления несовместных систем. Напомним, что несогласованная система состоит из параллельных прямых, имеющих одинаковый наклон, но разные точки пересечения по оси y. Они никогда не пересекутся. При поиске решения несогласованной системы мы придем к ложному утверждению, например $12=0$.
Пример $\PageIndex{8}$: Решение противоречивой системы уравнений
Решите следующую систему уравнений.
\[\begin{align*} x &= 9−2y \\ x+2y &= 13 \end{align*}\]
Решение
Мы можем решить эту задачу двумя способами. Поскольку одно уравнение уже решено для $x$, наиболее очевидным шагом является использование подстановки.
\[\begin{align*} x+2y &= 13 \\ (9−2y)+2y &= 13 \\ 9+0y &= 13 \\ 9&= 13 \end{align*}\]
Ясно, что это утверждение является противоречием, потому что $9≠13$. Следовательно, система не имеет решений.
Второй подход заключается в том, чтобы сначала манипулировать уравнениями так, чтобы они оба были в форме пересечения наклона. Поработаем с первым уравнением следующим образом.
\[\begin{align*} x &= 9−2y \\ 2y &= −x+9 \\ y &= −\dfrac{1}{2}x+\dfrac{9}{2} \end {align*}\]
Затем мы преобразуем второе уравнение, выраженное в форму пересечения наклона.
\[\begin{align*} x+2y &= 13 \\ 2y &= −x+13 \\ y &= −\dfrac{1}{2}x+\dfrac{13}{2} \end {align*}\]
Сравнивая уравнения, мы видим, что они имеют одинаковый наклон, но разные $y$-перехваты. Следовательно, прямые параллельны и не пересекаются.
\[\begin{align*} y &= −\dfrac{1}{2}x+\dfrac{9}{2} \\ y &= −\dfrac{1}{2}x+\dfrac{13 }{2} \end{align*}\]
Анализ
Запись уравнений в форме наклон-пересечение подтверждает, что система несовместима, поскольку все прямые в конечном итоге пересекутся, если они не параллельны. Параллельные линии никогда не пересекутся; таким образом, две прямые не имеют общих точек. Графики уравнений в этом примере показаны на рисунке $\PageIndex{9}$.
Рисунок $\PageIndex{9}$
Упражнение $\PageIndex{6}$
Решите следующую систему уравнений с двумя переменными.
\[\begin{align*} 2y-2x &= 2 \\ 2y-2x &= 6 \end{align*}\]
Ответ
Нет решения. Это непоследовательная система.
Выражение решения системы зависимых уравнений с двумя переменными
Напомним, что зависимая система уравнений с двумя переменными — это система, в которой два уравнения представляют одну и ту же прямую. Зависимые системы имеют бесконечное число решений, потому что все точки на одной прямой находятся также и на другой прямой. После использования подстановки или сложения результирующее уравнение будет тождеством, например $0=0$.
Пример $\PageIndex{9}$: поиск решения зависимой системы линейных уравнений
Найдите решение системы уравнений с помощью метода сложения .
\[\begin{align*} x+3y &= 2 \\ 3x+9y &= 6 \end{align*}\]
Решение
С помощью метода сложения мы хотим исключить один из переменные путем добавления уравнений. В этом случае давайте сосредоточимся на устранении $x$. Если мы умножим обе части первого уравнения на $−3$, то мы сможем исключить переменную x.
\[\begin{align*} x+3y &= 2 \\ (−3)(x+3y) &= (−3)(2) \\ −3x−9y &= −6 \end{align *}\]
Теперь добавим уравнения.
\[\begin{align*} -3x-9y &= -6 \\ \underline{+\space 3x+9y}& = \underline{6} \\ 0&= 0 \\ \end{align*} \]
Мы видим, что будет бесконечное число решений, удовлетворяющих обоим уравнениям.
Анализ
Если бы мы переписали оба уравнения в форме пересечения наклона, мы могли бы знать, как будет выглядеть решение перед добавлением. Давайте посмотрим, что происходит, когда мы преобразуем систему в форму пересечения наклона.
\[ \begin{align*} x+3y &= 2 \\ 3y &= −x+2 \\ y &= −\dfrac{1}{3}x+\dfrac{2}{3} \\ 3x+9y &= 6 \\ 9y &=−3x+6 \\ y &= −\dfrac{3}{9}x+\dfrac{6}{9} \\ y &= −\dfrac{1}{ 3}x+\dfrac{2}{3} \end{align*}\]
См. рисунок $\PageIndex{10}$. Обратите внимание, что результаты одинаковы. Общее решение системы: $\left(x, −\dfrac{1}{3}x+\dfrac{2}{3}\right)$.
Рисунок $\PageIndex{10}$
Упражнение $\PageIndex{7}$
Решите следующую систему уравнений с двумя переменными.
\[\begin{align*} y−2x &= 5 \\ −3y+6x &= −15 \end{align*}\]
Ответ
Система зависима, поэтому существует бесконечное количество решений вида $(x,2x+5)$.
Используя то, что мы узнали о системах уравнений, мы можем вернуться к проблеме изготовления скейтборда в начале раздела. Функция дохода производителя скейтборда — это функция, используемая для расчета суммы денег, поступающей в бизнес. Его можно представить уравнением $R=xp$, где $x$=количество и $p$=цена. Функция дохода показана оранжевым цветом на рисунке $\PageIndex{11}$.
Функция затрат — это функция, используемая для расчета затрат на ведение бизнеса. Он включает постоянные затраты, такие как арендная плата и заработная плата, и переменные затраты, такие как коммунальные услуги. Функция стоимости показана синим цветом на рисунке $\PageIndex{11}$. Ось $x$ представляет количество в сотнях единиц. Ось $y$ представляет либо затраты, либо доход в сотнях долларов.
Рисунок $\PageIndex{11}$
Точка, в которой пересекаются две линии, называется точкой безубыточности. Из графика видно, что если произведено $700$ единиц, то себестоимость составит $3300$$, а выручка также составит $3300$$. Другими словами, компания безубыточна, даже если она производит и продает $700$ единиц. Они не зарабатывают и не теряют деньги.
Заштрихованная область справа от точки безубыточности представляет объемы, при которых компания получает прибыль. Заштрихованная область слева представляет объемы, по которым компания несет убытки. Функция прибыли представляет собой функцию дохода за вычетом функции затрат, записанную как $P(x)=R(x)−C(x)$. Очевидно, что знание количества, при котором затраты равны выручке, имеет большое значение для бизнеса.
Пример $\PageIndex{10}$: нахождение точки безубыточности и функции прибыли с помощью подстановки
Зная функцию затрат $C(x)=0,85x+35 000$ и функцию дохода $R(x)=1,55x$, найди точку безубыточности и функцию прибыли.
Решение
Напишите систему уравнений, используя $y$ вместо обозначения функции.
\[\begin{align*} y &= 0.85x+35,000 \\ y &= 1,55x \end{align*}\]
Подставим выражение $0,85x+35,000$ из первого уравнения в второе уравнение и решить относительно $x$.
\[\begin{align*} 0,85x+35 000 &= 1,55x \\ 35 000 &= 0,7x \\ 50 000 &= x \end{align*}\]
Затем мы подставляем $x=50 000$ либо в функцию затрат, либо в функцию дохода.
$1,55(50 000)=77 500$
Точка безубыточности равна $(50 000 77 500)$.
Функция прибыли находится по формуле $P(x)=R(x)−C(x)$.
\[\begin{align*} P(x) &= 1,55x−(0,85x+35 000) \\ &=0,7x−35 000 \end{align*}\]
Функция прибыли равна $P (х)=0,7х-35000$.
Анализ
Затраты на производство $50 000$ единиц составляют $77 500 долларов США$, а доход от продажи $50 000$ единиц также составляет $77 500 долларов США$. Чтобы получать прибыль, бизнес должен производить и продавать более $50 000$ единиц. См. рисунок $\PageIndex{12}$.
Рисунок $\PageIndex{12}$
Из графика на рисунке $\PageIndex{13}$ видно, что функция прибыли имеет отрицательное значение до $x=50 000$, когда график пересекает $x$-ось. Затем график выходит на положительные $y$-значения и продолжается по этому пути, так как функция прибыли представляет собой прямую линию. Это показывает, что точка безубыточности для предприятий возникает, когда функция прибыли равна $0$. Область слева от точки безубыточности представляет собой работу в убыток.
Рисунок $\PageIndex{13}$
Пример $\PageIndex{11}$: Написание и решение системы уравнений с двумя переменными
Стоимость билета в цирк составляет $$25.00$ для детей и $$50.00$ для взрослых. В определенный день посещаемость цирка составляет $2000$, а общий доход от продажи билетов составляет $70000$$. Сколько детей и сколько взрослых купили билеты?
Решение
Пусть $c$ = количество детей, а $a$ = количество присутствующих взрослых.
Общее количество людей $2000$. Мы можем использовать это, чтобы написать уравнение для количества людей в цирке в тот день.
$c+a=2,000$
Доход от всех детей можно найти, умножив $25.00$$ на количество детей, $25c$. Доход от всех взрослых можно найти, умножив $$50.00$ на количество взрослых, $50a$. Общий доход составляет $$70,000$. Мы можем использовать это, чтобы написать уравнение для дохода.
$25c+50a=70 000$
Теперь у нас есть система линейных уравнений с двумя переменными.
$с+а=2000$
$25с+50а=70000$
В первом уравнении коэффициент обеих переменных равен $1$. Мы можем быстро решить первое уравнение либо для $с$, либо для $а$. Мы будем решать для $а$.
\[\begin{align*} c+a &= 2,000 \\ a &= 2,000−c \end{align*}\]
Подставим выражение $2,000−c$ во второе уравнение для a и решить для \ (с \).
\[\begin{align*} 25c+50(2000−c) &= 70000 \\ 25c+100000−50c &= 70000 \\ −25c &= −30000 \\ c &= 1200 \end{align* }\]
Подставьте $c=1,200$ в первое уравнение, чтобы найти $a$.
\[\begin{align*} 1,200+a &= 2,000 \\ a &= 800 \end{align*}\]
Мы находим, что $1,200$ детей и $800$ взрослых купили билеты в цирк в этот день.
Упражнения $\PageIndex{8}$
Билеты в цирк стоят $4 доллара США$ для детей и $12 долларов США$ для взрослых. Если было куплено $1650$ талонов на питание на общую сумму $14 200 долларов США$, сколько детей и сколько взрослых купили талоны на питание?
Ответить
$700$ дети, $950$ взрослые
Средства массовой информации
Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с системами линейных уравнений.
Решение систем уравнений с помощью замены
Решение систем уравнений методом исключения
Применение систем уравнений
Ключевые понятия
Система линейных уравнений состоит из двух или более уравнений, состоящих из двух или более переменных, так что все уравнения в системе рассматриваются одновременно.
Решением системы линейных уравнений с двумя переменными является любая упорядоченная пара, удовлетворяющая каждому уравнению независимо. См. пример $\PageIndex{1}$.
Системы уравнений классифицируются как независимые с одним решением, зависимые с бесконечным числом решений и несовместные без решения.
Одним из методов решения системы линейных уравнений с двумя переменными является построение графика. В этом методе мы наносим уравнения на один и тот же набор осей. См. пример $\PageIndex{2}$.
Другой метод решения системы линейных уравнений — подстановка. В этом методе мы находим одну переменную в одном уравнении и подставляем результат во второе уравнение. См. пример $\PageIndex{3}$.
Третий метод решения системы линейных уравнений — сложение, в котором мы можем исключить переменную, добавляя противоположные коэффициенты соответствующих переменных. См. пример $\PageIndex{4}$.
Часто бывает необходимо умножить одно или оба уравнения на константу, чтобы облегчить исключение переменной при сложении двух уравнений. См. Пример $\PageIndex{5}$, Пример $\PageIndex{6}$ и Пример $\PageIndex{7}$.
Любой метод решения системы уравнений приводит к ложному утверждению о несовместимых системах, поскольку они состоят из параллельных линий, которые никогда не пересекаются. См. пример $\PageIndex{8}$.
Решение системы зависимых уравнений всегда будет верным, поскольку оба уравнения описывают одну и ту же прямую. См. пример $\PageIndex{9}$.
Системы уравнений можно использовать для решения реальных задач, включающих более одной переменной, например связанных с доходом, затратами и прибылью. См. пример $\PageIndex{10}$ и пример $\PageIndex{11}$.
Эта страница под названием 11.1: Системы линейных уравнений — две переменные распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
Наверх
Была ли эта статья полезной?
Тип изделия
Раздел или страница
Автор
ОпенСтакс
Лицензия
СС BY
Версия лицензии
4,0
Программа ООР или издатель
ОпенСтакс
Показать страницу TOC
нет
Теги
Система линейных уравнений
зависимая система
несогласованная система
независимая система
источник@https://openstax. org/details/books/precalculus
метод замены
Преподавание линейных уравнений по математике
Назад к фигурным
Математика
Фигурный посох
29 марта 2020 г.
Чтение через 10 мин
Для многих учащихся 8-х классов и старше числа и фигуры, которые они узнали, действительно начинают складываться воедино, когда они составляют и решают линейные уравнения. Эта тема объединяет идеи об алгебре, геометрии и функциях, и многим детям — и взрослым! — может быть трудно усвоить ее. В этой статье объясняется, что такое линейное уравнение, и рассматриваются различные примеры. Затем он предлагает уроки для введения и развития концепции линейных уравнений с одной переменной для ваших студентов.
Что такое линейное уравнение?
Как и любое другое уравнение, линейное уравнение состоит из двух равных друг другу выражений. Есть некоторые ключевые особенности, общие для всех линейных уравнений:
Линейное уравнение имеет только одну или две переменные.
Ни одна переменная в линейном уравнении не возводится в степень больше 1 и не используется в качестве знаменателя дроби.
Когда вы находите пары значений, которые делают линейное уравнение верным, и наносите эти пары на координатную сетку, все точки лежат на одной линии. График линейного уравнения представляет собой прямую линию.
Линейное уравнение с двумя переменными может быть описано как линейная зависимость между х и y , то есть двумя переменными, в которых значение одной из них (обычно y ) зависит от значение другого (обычно x ). В этом случае х является независимой переменной, а х зависит от нее, поэтому х называется зависимой переменной.
Независимо от того, помечено ли это значение x , независимая переменная обычно откладывается по горизонтальной оси. Большинство линейных уравнений являются функциями. Другими словами, каждому значению x соответствует только одно значение y . Когда вы присваиваете значение независимой переменной x , вы можете вычислить значение зависимой переменной y . Затем вы можете нанести точки, названные каждой парой ( x , y ) на координатной сетке.
Описание линейных отношений
Учащиеся уже должны знать, что любые две точки определяют линию. Таким образом, для построения графика линейного уравнения на самом деле требуется только найти две пары значений и провести линию через точки, которые они описывают. Все остальные точки на линии дадут значения x и y , которые удовлетворяют уравнению.
Графики линейных уравнений всегда являются линиями. Однако важно помнить, что не каждая точка на линии, описываемой уравнением, обязательно будет решением задачи, описываемой уравнением. Например, задача может не иметь смысла для отрицательных чисел (скажем, если независимой переменной является время) или очень больших чисел (скажем, для чисел больше 100, если зависимой переменной является оценка в классе).
Как выглядит линейное уравнение?
Пример 1: расстояние = скорость × время
В этом уравнении для любой фиксированной скорости зависимость между расстоянием и временем будет линейной. Однако расстояние обычно выражается положительным числом, поэтому на большинстве графиков этого отношения точки отображаются только в первом квадранте. Обратите внимание, что направление линии на графике ниже — снизу слева направо вверх. Линии, стремящиеся в этом направлении, имеют положительные уклон . Положительный наклон указывает на то, что значения по обеим осям увеличиваются слева направо.
Пример 2: количество воды в негерметичном ведре = скорость утечки × время первый квадрант. Обратите внимание, что направление линии на этом графике — сверху слева вниз справа. Линии, стремящиеся в этом направлении, имеют отрицательный наклон. А отрицательный наклон указывает на то, что значения на оси y- уменьшаются по мере увеличения значений на оси x-.
Пример 3: количество углов многоугольника = количеству сторон этого многоугольника
Опять же, на этом графике мы связываем значения, которые имеют смысл только в том случае, если они положительны, поэтому мы показываем точки только в первом квадранте. Кроме того, в этом случае, поскольку ни один многоугольник не имеет менее 3 сторон или углов, а количество сторон или углов многоугольника должно быть целым числом, мы показываем график, начинающийся с (3,3), и указываем пунктирной линией, что точки между нанесенными на график не имеют отношения к задаче.
Пример 4: градусы Цельсия = 5/9 × (градусы Фаренгейта – 32)
Поскольку совершенно разумно иметь как положительные, так и отрицательные температуры, мы наносим точки на этом графике на полной координатной сетке. (Хотя это и не видно на графике, самая низкая возможная физическая температура составляет около –460° по Фаренгейту, поэтому не каждое решение на графике полезно!) линия относится к y- ось и наклон линии вверх или вниз, если смотреть на нее слева направо. С технической точки зрения, наклон показывает скорость, с которой зависимая переменная изменяется по отношению к изменению независимой переменной.
Расчет уклона
Выберите любые две точки на линии. Чтобы найти скорость изменения y , вычтите значение y первой точки из значения y второй точки: ( y ₂ – y ₁). Чтобы узнать, как быстро изменяется x , вычтите значение x первой точки из значения x второй точки: ( x ₂ – x ₁ ). Чтобы найти скорость, с которой y изменяется по отношению к изменению х , рассчитайте отношение: х ₁ ).
Если мы обозначим точку A в качестве первой точки и Point B в качестве второй точки, наклон линии равен (–2 – 4)/(–1 – 2) = –6/–3 или 2. Не имеет значения какие точки вдоль линии вы обозначили как A и B , до тех пор, пока мы согласны с тем, какая точка является «первой» ( x ₁ , y ₁ ), а какая «второй» ( x ₂ , y ₂ ). Если мы обозначим точку B как первую точку, а точку A в качестве второй точки, значение наклона такое же: (4 – -2)/(2 – -1) = 6/3 или 2. Это также то же значение, которое вы получите, если выберете любую другую пару точек на линии для вычисления уклона.
Формула линейного уравнения
Уравнение прямой можно записать в форме, которая делает уклон очевидным и позволяет рисовать линию без каких-либо вычислений. Если учащимся удобно решать простое линейное уравнение, состоящее из двух шагов, они могут написать линейные уравнения в форме пересечения наклона. Форма линейного уравнения с пересечением наклона: y = m x + b . В уравнении x и y являются переменными. Числа м и b дают наклон линии ( м ) и значение y , когда x равно 0 ( b ). Значение y , когда x равно 0, называется y -перехватом , потому что (0, y ) — это точка пересечения прямой с осью y .
Вы можете нарисовать линию для уравнения, соответствующего этой линейной формуле, построив график (0, b ), а затем используя м , чтобы найти другую точку. Например, если м равно 1/2, вы можете интерпретировать это как разницу в 1 среди и координат для каждой разницы в 2 среди x координат (то есть ( y ₂ – y ₁ )/( x ₂ – x ₁ ) = 1/2). Отсчитайте +2 по оси x-, затем +1 по оси y-, чтобы добраться до другой точки: (2, b + 1).
Уравнение этой прямой: y + 3 = 2 x . В форме пересечения уклона уравнение имеет вид y = 2 x – 3. В этой форме вы можете легко увидеть, что уклон м = 2. Глядя на график, уклон действительно равен 2, так как для каждого + 2 изменение в г , есть +1 изменение в x . Теперь посмотрите на b в уравнении: -3 должно быть там, где линия пересекает ось y , и это так.
Положительный наклон
Когда линия наклоняется вверх слева направо, она имеет положительный наклон. Это означает, что положительное изменение х связано с положительным изменением х . Чем круче наклон, тем больше скорость изменения y по отношению к изменению х . Уклон 6 круче, чем уклон 1, который, в свою очередь, круче, чем уклон 1/6. Когда линия представляет точки реальных данных, нанесенные на координатную плоскость, положительный наклон указывает на положительную корреляцию, и чем круче наклон, тем сильнее положительная корреляция.
Рассмотрим линейное уравнение, в котором независимая переменная g — это количество использованного газа в галлонах, а зависимая переменная d — пройденное расстояние в милях. Если вы водите большую старую машину, у вас будет плохой расход бензина. Количество пройденных миль мало по сравнению с количеством израсходованного газа, поэтому значение м — это малое число. Наклон линии достаточно плавный. Если вместо этого вы едете на легком экономичном автомобиле, вы увеличиваете расход бензина. Вы проезжаете больше миль относительно того же количества потребляемого газа, поэтому значение м больше, а линия круче. Обе ставки положительны, потому что вы по-прежнему проезжаете положительное количество миль на каждый галлон бензина, который вы потребляете.
Отрицательный наклон
Когда линия наклонена вниз слева направо, она имеет отрицательный наклон. Это означает, что отрицательное изменение и связаны с положительным изменением х . Когда линия представляет точки реальных данных, нанесенные на координатную плоскость, отрицательный наклон указывает на отрицательную корреляцию, и чем круче наклон, тем сильнее отрицательная корреляция.
Рассмотрим линию, представляющую количество перцев, оставшихся для посадки после нескольких минут, проведенных в саду. Если в саду может поместиться 18 кустов перца, и вы сажаете 1 куст перца в минуту, то скорость, с которой садовая квартира опустеет, довольно высока, поэтому абсолютное значение м — число больше, а линия круче. Если вместо этого вы сажаете только 1 растение перца каждые 2 минуты, вы все равно опустошите садовую квартиру, но скорость, с которой вы это делаете, будет ниже. Абсолютное значение м ниже (1/2 вместо 1), и линия не такая крутая.
Нулевой наклон
Когда и не изменяются при изменении x , график линии горизонтален. Горизонтальная линия имеет нулевой наклон.
Undefined Slope
Когда x не изменяются при изменении y , график линии является вертикальным. Вы не можете вычислить наклон этой линии, потому что вам нужно разделить на 0. Обратите внимание, что вы можете думать об этих линиях как о «бесконечно крутых», либо положительно , либо отрицательно. Наклон вертикальной линии не определяется.
Линии с одинаковым уклоном
Две линии с одинаковым уклоном имеют одинаковую крутизну. Это означает одно из двух: либо линии параллельны, либо они являются одной и той же линией.
Во всех этих трех строках каждое изменение на 1 единицу в y связано с изменением на 1 единицу в x . Все три имеют наклон 1.
Решение двухшаговых линейных уравнений с рациональными числами
Когда линейное уравнение имеет две переменные (как это обычно и бывает), оно имеет бесконечное число решений. Каждое решение представляет собой пару чисел ( x , y ), которые делают уравнение верным. Решение линейного уравнения обычно означает нахождение значения y для заданного значения x .
When the Equation Is Already in Slope-Intercept Form
If the equation is already in the form y = mx + b , with x and y variables and m and b рациональных чисел, решение для конкретных значений не представляет сложности. Выберите значение для x, и вычислите соответствующее значение для y . Вы заметите, что легко выбрать значение x равно 0, потому что в этом случае y = b . Студентам может быть предложено составить таблицы значений для линейных уравнений. Это просто T-таблицы со списками значений для x с соответствующими значениями для y .
Двухшаговые уравнения включают поиск значений для выражений, содержащих более одного члена . Терм может быть числом, переменной или числами и переменными, перемноженными вместе. Члены выражения разделяются символами сложения или вычитания. 2 x — это выражение с одним членом. 2 x + 6 имеет два члена. Чтобы найти значение y по заданному значению x , подставьте в выражение значение x .
Рассмотрим уравнение y = 2 x + 6. Найдите значение для y , когда x = 5:
Подставьте значение для . у = 2(5) + 6
Умножить. у = 10 + 6
Доп. y = 16
Когда уравнение не имеет форму пересечения наклона
+ b ), учащиеся все еще могут составить таблицу значений, чтобы найти решения уравнения, но может быть проще сначала представить уравнение в форме пересечения наклона. Это требует зеркального отображения операций с каждой стороны уравнения до y само по себе находится на одной стороне уравнения и равно линейному выражению, включающему x . Вы можете манипулировать уравнением таким образом из-за свойств равенства:
Если a = b , то a + c = b + c.
Если a = b , то a – c = b – c.
Если а = б г., затем г. н.э. = г. до н.э.
Если a = b , то a ÷ c = b ÷ c (пока c
≥).
Рассмотрим 2 x + y – 6 = 0. Это уравнение не в форме пересечения наклона, но вы можете использовать свойства равенства, чтобы получить y на одной стороне уравнения.
Вы можете вычесть y из обеих частей уравнения, чтобы получить 2 х – 6 = – у . Затем умножьте обе части уравнения на –1, чтобы получить –2 x + 6 = лет.
Кроме того, вы можете вычесть 2 x и добавить 6 к обеим частям уравнения, чтобы получить y = –2 x + 6. = y и y = 6 – 2 x эквивалентны. Вы можете превратить одно в другое, используя коммутативное свойство сложения, которое гласит, что a + b = b + a и симметричное свойство равенства, которое утверждает, что если a = b , то b = a .
Переместительное свойство сложения –2x + 6 = y эквивалентно 6 – 2 x = y .
Симметричное свойство равенства 6 – 2 x = y эквивалентно y = 6 – 2 х .
Линейные уравнения: знакомство с концепцией
Материалы: Координатная сетка, которую могут видеть все учащиеся (сетка должна идти как минимум от –10 до +10 по обеим осям), инструмент для разметки сетки точками и линии
Подготовка: Поскольку учащиеся будут считывать точки с графиков и строить линии из списков точек, они (и вы) должны быть готовы использовать линейку для создания точных прямых линий. При онлайн-обучении используйте цифровой инструмент, способный генерировать точки и линии.
Необходимые навыки и понятия: Учащиеся должны уметь наносить точки на координатную плоскость и должны быть знакомы с различными способами обозначения умножения и деления в уравнении. Они также должны быть знакомы с порядком операций и свойствами равенства.
Аккуратно проведите линию через (0,0) и (2,2) на сетке. Не забудьте расширить его в обоих направлениях, чтобы на нем было много точек, которые легко назвать.
Произнесите: Назовите несколько точек на этой прямой. Учащиеся должны составить список точек с целочисленными координатами. Если нет, потратьте некоторое время на присвоение имен точкам на сетке, прежде чем продолжить этот урок. Если учащиеся называют нецелые точки, например (1,5, 1,5), уделите время объяснению, почему они тоже находятся на прямой.
Ask: Можете ли вы дать мне правило, как найти y, когда мы знаем x в этой строке? Обсудите, как связаны координаты, затем попросите учащихся записать правило в виде уравнения. Уравнение этой линии равно х = х .
Скажем: Это была линия для уравнения y = x. H Как бы вы нарисовали линию для уравнения y = x + 3? Предложите учащимся самостоятельно провести линию. Если это возможно, попросите их объединиться в пары и сравнить их линии. Организуйте обсуждение различных линий, нарисованных учащимися, выделяя сходства и различия. Затем покажите один из способов рисования линии: подставьте несколько значений вместо 9.2947 x в уравнение, найдите соответствующие значения для y , а затем постройте эти пары координат. Две точки дают вам достаточно информации для проведения линии, но поскольку возможны ошибки, а человеческий рисунок не идеален, безопаснее создать по крайней мере три точки. Отобразите T-таблицу со связанными значениями x и y и нарисуйте график линии.
Скажем: Теперь, как бы вы нарисовали линию для уравнения у = 2 х + 3? Учащиеся, скорее всего, будут использовать стратегию составления Т-таблицы и вычисления баллов. Если они забудут умножить свои значения x на 2 перед добавлением 3, напомните им о порядке операций (умножение или деление слева направо, затем сложение или вычитание слева направо). Попросите разных учащихся сформулировать разные точки зрения, обсуждая их рассуждения по ходу дела.
Спросите: Кто-нибудь может дать мне число от –5 до 5? А как насчет числа от –10 до 10? : Используйте эти числа для создания линейных уравнений. Первое число будет коэффициентом х , а второе будет добавлено к терму х . Создавайте уравнения, находите точки, затем рисуйте линии. Вы можете сделать это упражнение более похожим на игру, попросив учащихся бросать кубики с реальными или виртуальными числами. Если вы работали с наклоном, эти задачи также дадут вам возможность укрепить эту концепцию. (Спросите: как вы думаете, будет ли наклон этой линии положительным или отрицательным? Как вы думаете, будет ли он очень крутым или не таким крутым? Пройдет ли эта линия через начало координат?)
Линейные уравнения: развитие концепции
Материалы: Координатная сетка, которую могут видеть все учащиеся (сетка должна идти не менее от –10 до +10 по обеим осям), инструмент для разметки сетки точками и линиями
Произнесите Когда мы создавали точки для линий на прошлом уроке, наши уравнения всегда выглядели одинаково. Другими словами, они всегда были в одной и той же форме. Сегодня мы рассмотрим, как они могут выглядеть по-разному.
Скажем, Может кто-нибудь описать, как найти некоторые пары координат для линейного уравнения, 2 x + y = 15? Это двухшаговое уравнение. Решения включают присвоение значения x , затем умножение этого значения на 2, прежде чем попытаться выяснить, какое значение y удовлетворяет уравнению. Учащиеся могут использовать метод проб и ошибок или преобразовать уравнение, используя свойства равенства:
Напишите уравнение. 2 x + y = 15
Присвойте значение x . 2(3) + y = 15
Умножить. 6 + y = 15
Вычесть 6 с каждой стороны. 6 – 6 + y = 15 – 6
Вычесть. y = 9
Это решение дает нам точку (3,9). Продолжайте находить решения или согласовывать пары для этого уравнения до тех пор, пока вы не будете удовлетворены тем, что учащиеся довольны процессом. Затем нанесите точки на сетку и нарисуйте линию.
Скажем, Может кто-нибудь описать, как найти некоторые точки на линии, описываемой уравнением y + x/3 = 5?
Напишите уравнение. y + x /3 = 5
Присвойте значение x . у + 3/3 = 5
Разделить. y + 1 = 5
Вычтите по 1 с каждой стороны. г + 1 – 1 = 5 – 1
Вычесть. y = 4
Это решение дает нам точку (3,4). Студенты могут заметить, что это не похоже на предыдущие линейные уравнения. Объясните, что, поскольку x /3 — это то же самое, что (1/3) x , x /3 по-прежнему является обычным термином. Продолжайте находить решения или согласовывать пары для этого уравнения до тех пор, пока вы не будете удовлетворены тем, что учащиеся довольны процессом. Затем нанесите точки на сетку и нарисуйте линию.
Скажем, Может кто-нибудь описать, как найти некоторые точки на линии, описываемой уравнением y – 6 = 2x? Напишите уравнение. г – 6 = 2 x
Присвойте значение x .
y – 6 = 2(3)
Умножить. y – 6 = 6
Добавьте по 6 с каждой стороны. лет – 6 + 6 = 6 + 6
Доп. y = 12
Это решение дает нам точку (3,12).
К настоящему времени учащиеся должны были заметить, что простая замена x равна 0. Эта замена даст вам точку, в которой линия пересекает ось y . Предложите учащимся прийти к этому пониманию, если они не делают этого самостоятельно.
Советы по оценке
Когда учащиеся решают многошаговые уравнения, обратите особое внимание на то, соблюдают ли они порядок операций. Это важное алгебраическое понятие.
Кроме того, следите за тем, действительно ли учащиеся понимают, что свойства равенства говорят о том, что если вы делаете что-то с одной частью уравнения, вы ДОЛЖНЫ сделать то же самое с другой частью уравнения. То, что вы делаете, определяется действием, указанным уравнением. Если число вычитается из и , и вы хотите и , чтобы быть сами по себе, добавьте это число к каждой части уравнения, и его противоположное число «переместится» на другую часть уравнения. Точно так же, если y умножить на число, деление поможет вам получить y само по себе.
***
Ищете решение для учащихся 5-х классов и старше, которое поможет разблокировать изучение уравнений и формул линейных отношений и не только? Исследуйте Math 180 , революционный подход к математическому вмешательству.
Математика Мероприятия и уроки 6-8 классы 9-12 классы Вмешательство
Связанные материалы
Ричард Бланкман
Фасонный Редактор
15 сентября 2022 г.
Дженнифер Прескотт
Форма Участник
09 сентября 2022 г.
Дженнифер Прескотт
Форма Участник
09 сентября 2022 г.
Математика Мероприятия и уроки 6-8 классы 9 класс-12 Вмешательство
Подпишитесь на нашу рассылку новостей
Будьте первым, кто прочитает последние новости от Shaped .
Подписаться
Системы линейных уравнений: определения
Графики. Особые случаи. Подстановка. Исключение/сложение.0147 Purplemath
«Система» уравнений — это набор или набор уравнений, с которыми вы работаете одновременно. Линейные уравнения (те, которые представляют собой прямые линии) проще, чем нелинейные уравнения, а простейшая линейная система — это система с двумя уравнениями и двумя переменными.
Вспомните, когда вы впервые узнали о линейных уравнениях с двумя переменными, которые часто формулируются в форме « y = m x + b ». Например, рассмотрим линейное уравнение y = 3 x — 5. «Решением» этого уравнения была любая ( x , y ) точка, которая «работала» в уравнении.
Содержание продолжается ниже
MathHelp.com
Решение систем путем сложения
Так, например, точка (2, 1) является решением уравнения, поскольку подстановка 2 вместо x возвращает правильное значение для y , как показано ниже:
3 x — 5 = 3(2) — 5 = 6 — 5 = 1 = y
С другой стороны, точка (1, 2) не является решением уравнения, потому что подстановка 1 вместо x приводит к значению, которое равно , а не данному y -значению, поскольку мы можно увидеть:
3 x — 5 = 3(1) — 5 = 3 — 5 = -2
Это значение, -2, не является значением y , которое мы получили; а именно +2. Таким образом, точка не может быть решением уравнения.
Конечно, с практической точки зрения, вы не найдете решения уравнения, выбирая случайные точки, подставляя их и проверяя, «работают» ли они в уравнении. Вместо этого вы выбрали x значений, а затем вычислить соответствующие значения y . И вы использовали эту же процедуру для построения графика уравнения. Это указывает на важный факт: каждая точка на графике была решением уравнения, и любое решение уравнения было точкой на графике.
Теперь рассмотрим следующую систему линейных уравнений с двумя переменными: иметь дело с ними вместе в то же время. В частности, мы можем изобразить их вместе на одной системе координат, например:
Решением одного уравнения является любая точка, лежащая на прямой этого уравнения. Решением системы уравнений является любая точка, лежащая на каждой прямой этой системы. Например, красная точка на приведенном ниже графике не является решением системы, поскольку она не находится ни на одной из прямых:
Синяя точка на приведенном ниже графике не является решением системы, поскольку она лежит только на одной из линии, а не на обе из них:
Фиолетовая точка на графике ниже является решением системы, поскольку она лежит на обеих линиях:
В частности, эта фиолетовая точка отмечает пересечение двух линий. Поскольку эта точка находится на обеих линиях, она, таким образом, решает оба уравнения, следовательно, решает всю систему уравнений.
Это соотношение всегда верно: для систем уравнений «решения» систем — это «пересечения» линий. И вы можете подтвердить, что точка пересечения является решением системы, подставив эту точку обратно в каждое из уравнений системы и подтвердив, что точка работает в каждом уравнении.
Определите, является ли любая из точек (−1, −5) и (0, −2) решением данной системы уравнений.
у = 3 х — 2
у = — х — 6
Чтобы проверить данные возможные решения, я просто подставляю координаты x и y в уравнения и проверяю, работают ли они.
проверка (-1, -5):
(−5) ?=? 3(−1) − 2
−5 ?=? −3 − 2
−5 = −5
(проверки решений)
(−5) ?=? −(−1) − 6
−5 ?=? 1 − 6
−5 = −5
(проверки решения)
Поскольку данная точка работает в каждом уравнении, она является решением системы. Теперь я проверю другую точку (которая, как мы уже знаем, глядя на график, не является решением):
проверка (0, −2):
(−2) ?=? 3(0) − 2
−2 ?=? 0 − 2
−2 = −2
(проверки решения)
Итак, решение работает в одном из уравнений. Но чтобы быть решением системы уравнений, оно должно работать в обоих уравнениях этой системы. Продолжаем проверку:
Но -2 не равно -6, так что это «решение» не проверяет. Тогда ответ:
только точка (−1, −5) является решением системы
URL: https://www.purplemath.com/modules/systlin1.htm
Страница 2Страница 3Страница 4Страница 5Страница 6Страница 7
Вы можете использовать виджет Mathway ниже, чтобы проверить, является ли данная точка решением данной системы. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway.
Пожалуйста, примите куки-файлы настроек, чтобы включить этот виджет.
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления. )
Страница 2Страница 3Страница 4Страница 5Страница 6Страница 7
Математика B.A./B.S. Описание курсов | Duquesne University
Просмотрите блок-схему рекомендуемой последовательности курсов.
Курсы математики (*Курсы статистики)
MATH 101 College Algebra** — 3 кредита
Темы включают действительные числа, факторинг, рациональные выражения, показатели степени и радикалы, решение уравнений и неравенств (включая линейные, квадратичные, дробные, радикальные, и абсолютное значение), нетригонометрические функции (линейные, полиномиальные, рациональные, корневые, абсолютное значение, экспоненциальные, логарифмические, композиция) и построение графиков. Учащиеся должны одновременно зарегистрироваться на раздел МАТЕМАТИКА 101R. Подготавливает студентов к математике 111 — Исчисление для студентов, не изучающих естественные науки. Недостаточная подготовка к математике 115 — Исчисление I.
MATH 101R Реферат по алгебре в колледже — необходимо сдавать вместе с математикой 101
Основные принципы и концепции лекции по алгебре в колледже MATH 101 закрепляются на этом занятии посредством решения задач. Оценивается работа как в лекции, так и в чтении. Этот курс необходимо изучать одновременно с MATH 101.
MATH 104 Исчисление с алгеброй и тригонометрией колледжа I — прекращено осенью 2018 г.** — 4 кредита
Исходные темы MATH 115 с темами из алгебры и тригонометрии, интегрированными по мере необходимости. Зачет не разрешен одновременно для МАТЕМАТИКА 104/101, МАТЕМАТИКА 104/111 или МАТЕМАТИКА 104/115.
MATH 105 Колледж Алгебра и тригонометрия – начало осени 2018 г.** – 4 кредита
Темы включают действительные числа, факторинг, рациональные выражения, показатели степени и радикалы, решение уравнений и неравенств (включая линейные, квадратичные, дробные, радикальные и абсолютные значения). ), функции (в том числе линейные, полиномиальные, рациональные, корневые, абсолютное значение, экспоненциальные, логарифмические, тригонометрические, композиция) и построение графиков. Подготавливает учащихся к математике 115 — Исчисление I. Зачеты не допускаются как по МАТЕМАТИКЕ 101, так и по МАТЕМАТИКЕ 105.
МАТЕМАТИКА 111 Исчисление для студентов, не занимающихся естественными науками** — 3 кредита
Пределы, непрерывность и дифференцирование алгебраических, экспоненциальных и логарифмических функций. Формулы суммы, произведения, частного и цепного правила для дифференцирования. Логарифмическое и неявное дифференцирование. График с использованием первой и второй производной. Применение производной к задачам оптимизации и связанных с ними задач. Неопределенные и определенные интегралы. Применение определенного интеграла к задачам о площадях. Зачет не разрешен одновременно для МАТЕМАТИКА 111/104, МАТЕМАТИКА 111/114 или МАТЕМАТИКА 111/115. Требование: оценка «C» или выше по MATH 101 или подтверждение владения навыками алгебры в колледже.
МАТЕМАТИКА 114 Исчисление с Колледж Алгебра и Тригонометрия II — прекращено Весна 19** — 4 кредита
Остальные темы МАТЕМАТИКА 115 с интегрированными темами из алгебры и тригонометрии по мере необходимости. Зачет не разрешен как для MATH 114/111, так и для MATH 114/115.
МАТЕМАТИКА 115 Исчисление I — 4 кредита
Пределы, непрерывность и дифференцирование алгебраических, экспоненциальных, логарифмических, тригонометрических и обратных тригонометрических функций. Формулы суммы, произведения, частного и цепного правила для дифференцирования. Логарифмическое и неявное дифференцирование. Линеаризация и дифференциалы. Неопределенные формы и правило Лопиталя. График с использованием первой и второй производной. Применение производной к задачам оптимизации и связанных с ними задач. Неопределенные и определенные интегралы. Правило подстановки для интегрирования. Применение определенного интеграла к задачам о площадях. Зачет не разрешен одновременно для МАТЕМАТИКА 115/104, МАТЕМАТИКА 115/114 или МАТЕМАТИКА 115/111. Требование: оценка «C» или выше по MATH 105 или подтверждение владения навыками алгебры и тригонометрии в колледже
МАТЕМАТИКА 116 Исчисление II — 4 кредита
Применение интегрирования (площадь, объем, работа, длина дуги, площадь поверхности), дополнительные методы интегрирования, несобственные интегралы, бесконечные последовательности и ряды, включая тесты сходимости, степенные ряды, Тейлора и серии Маклорена. Требование: оценка «C» или выше по МАТЕМАТИКЕ 114 ИЛИ МАТЕМАТИКЕ 115.
МАТЕМАТИКА 125 Основы статистики ** — 3 кредита
Исследовательский анализ данных и статистические выводы, включая графические сводки данных, распределения выборок, доверительные интервалы и гипотезы тестирование. Кредит не разрешен как для MATH 125, так и для MATH 225.
МАТЕМАТИКА 135 Дискретная математика* — 3 кредита
Множества, функции, отношения, частичный порядок, методы логики высказываний, введение в логику предикатов, подсчет, рекуррентные отношения, асимптотический анализ, приемы корректуры, включая индукцию.
МАТЕМАТИКА 210 Алгебра матриц* Курс прекращен — 3 кредита
Вычислительные аспекты систем линейных уравнений, матричные операции, определители, векторные пространства и подпространства, линейные преобразования, замена базиса, собственные значения и собственные векторы, диагонализация и ортогональность. Условие: оценка «C» или выше по МАТЕМАТИКЕ 116. Зачет не допускается ни по МАТЕМАТИКЕ 210, ни по МАТЕМАТИКЕ 310.
МАТЕМАТИКА 215 Исчисление III — 4 кредита
Параметрические уравнения, полярные координаты, исчисление функций многих переменных и вектор-функций, включая двойные и тройные интегралы с использованием различных систем координат. Предварительное требование: оценка «C» или выше по МАТЕМАТИКЕ 116.
МАТЕМАТИКА 225 Введение в биостатистику * — 3 кредита
Классификация данных и план эксперимента, графическое обобщение данных, описательная статистика, основные понятия вероятности, приложения вероятности. (чувствительность, специфичность, относительный риск, отношение шансов), распределения вероятностей, выборочные распределения, доверительные интервалы, одновыборочная проверка гипотез. Кредит не допускается для обоих МАТЕМАТИКА 125/225. Требование: Свидетельство о навыках алгебры на уровне колледжа.
МАТЕМАТИКА 250 Основы высшей математики — 3 кредита
Введение в высшую математику. Темы включают математическую логику, множества, отношения, функции, системы счисления и счетность. Курс делает упор на овладение методами написания доказательств, включая условные, биусловные, противоречивые, индукционные, теоретико-множественные доказательства, а также доказательства существования и уникальности. Требование: оценка «C» или выше по МАТЕМАТИКЕ 116.
МАТЕМАТИКА 301 Введение в теорию вероятностей и статистику I — 3 кредита
Одномерные и многомерные распределения вероятностей дискретных и непрерывных случайных величин, математическое ожидание, предельные теоремы, преобразования случайных величин, производящие функции моментов. Требование: оценка «C» или выше по МАТЕМАТИКЕ 116.
МАТЕМАТИКА 302W Введение в теорию вероятностей и статистику II – 3 кредита
Выборочные распределения случайных величин, доверительные интервалы и проверка гипотез для одной и двух выборочных настроек. Дисперсионный анализ, простая линейная регрессия, методы оценки, свойства оценок, критерий отношения правдоподобия. Условие: оценка «C» или выше по МАТЕМАТИКЕ 301. Зачет не допускается как по МАТЕМАТИЧЕСКОЙ 302W, так и по МАТЕМАТИЧЕСКОЙ 335.
МАТЕМАТИКА 308 Численный анализ — 3 кредита
Линейные системы, интерполяция, функциональная аппроксимация, численное дифференцирование и интегрирование, решения нелинейных уравнений. Может считаться либо математикой, либо информатикой, но не тем и другим одновременно. Требования: оценка «C» или выше по COSC 150, COSC 160 или COSC 170 и по математике 116. Предлагается только весной.
МАТЕМАТИКА 310 Линейная алгебра — 3 кредита
Системы линейных уравнений, матричные операции, определители, векторные пространства и подпространства, линейные преобразования, замена базиса, собственные значения и собственные векторы, диагонализация и ортогональность. Требования: оценка «C» или выше по МАТЕМАТИКЕ 116.
МАТЕМАТИКА 311 Теория чисел — 3 кредита
Делимость, сравнения, квадратичные вычеты, диофантовы уравнения и арифметические функции. Требование: оценка «C» или выше по МАТЕМАТИКЕ 250.
МАТЕМАТИКА 314 Дифференциальные уравнения — 3 кредита
Обыкновенные дифференциальные уравнения первого порядка, теория и решения линейных обыкновенных дифференциальных уравнений высшего порядка, преобразование Лапласа, численные решения дифференциальных уравнения, приложения к физическим наукам и технике. Требование: оценка «С» или выше по МАТЕМАТИКЕ 116.
МАТЕМАТИКА 317 Математическое моделирование — 1 кредита
Цель этого курса состоит в том, чтобы студенты могли решить важную проблему в обществе, используя математику и вычисления. Учащиеся определят конкретную проблему, представляющую интерес для партнера по сообществу, и определят соответствующие математические или вычислительные инструменты, необходимые для поиска решений. В небольших группах и под руководством преподавателя учащиеся будут подходить к проблеме сообщества, собирая необходимые данные, создавая соответствующую модель и анализируя результаты модели способами, значимыми для сообщества. Все группы представят свои результаты в официальной презентации в конце семестра. Кроме того, у студентов будет возможность представить свои работы на местных исследовательских симпозиумах. Требования: оценка «C» или выше по MATH 314 (этот курс можно изучать одновременно с MATH 314) и по одному из следующих курсов программирования COSC 150, COSC 160, COSC 170 или BMED 110.
МАТЕМАТИКА 325W Прикладная статистика с регрессией — 3 кредита
TЭтот курс начинается с обзора статистики вывода. Акцент делается на методах сбора данных, формулировании гипотез, доверительных интервалах и методах начальной загрузки для оценки параметров. Для проверки гипотез демонстрируются как традиционные методы, так и методы повторной выборки. Дополнительные темы включают графические методы исследования распределений и определения выбросов, односторонний и двусторонний анализ моделей дисперсии с использованием подхода линейных моделей, а также методы линейной и множественной регрессии. Программное обеспечение JMP используется для демонстрации методов. Требования: оценка «С» или выше по МАТЕМАТИКЕ 225 или по МАТЕМАТИКЕ 301.
МАТЕМАТИКА 330W Основы геометрии — 3 кредита
Евклидова и неевклидова геометрия как с синтетическим, так и с метрическим аксиоматическим подходом. Требование: оценка «C» или выше по МАТЕМАТИКЕ 250.
МАТЕМАТИКА 335 Биостатистика II * — 3 кредита
Этот курс является продолжением МАТЕМАТИКА 225 (Введение в биостатистику). Темы включают проверку гипотез с двумя выборками, дисперсионный анализ, методы корреляции, простую линейную регрессию, множественную регрессию, логистическую регрессию, тесты хи-квадрат и непараметрические статистические процедуры. Условие: оценка «C» или выше по МАТЕМАТИКЕ 225. Зачет не допускается как по МАТЕМАТИЧЕСКОЙ 302W, так и по МАТЕМАТИЧЕСКОЙ 335.
МАТЕМАТИКА 340 Семинар по решению задач — 1 кредит
Решение и обсуждение задач из экзамена Патнэма и других источников. Завершение или одновременная регистрация в MATH 215 или разрешение инструктора.
МАТЕМАТИКА 350W История математики — 3 кредита
Мультикультурный обзор истории математики от развития систем счисления до развития исчисления. Подчеркивается вклад древнегреческой и западной математики, но также обсуждаются вклады египетской, вавилонской, исламской, индуистской и китайской культур. Условие: оценка «C» или выше по MATH 311.
PHYS 350 Математические методы в физике – 3 кредита
Разнообразные теоретические методы, полезные для решения общих задач в углубленных научных и инженерных курсах: комплексные числа и функции комплексной переменной, ряды и преобразования Фурье, преобразования Лапласа, Полиномы Лежандра, Лагерра и Эрмита, вариационное исчисление, специальные функции и тензорный анализ или другое содержание, которое определено как подходящее для поддержки курсовой работы по физике верхнего уровня. Предпосылки: МАТЕМАТИКА 215, МАТЕМАТИКА 310 (можно сдавать одновременно) и МАТЕМАТИКА 314 (можно сдавать одновременно).
МАТЕМАТИКА 366 Исследование операций — 3 кредита
Курс предоставит введение в историю операций, включая примеры задач и краткую историю. Последует подробное обсуждение теории и применения линейного программирования. Другие темы будут включать нелинейное программирование, непрерывные и дискретные вероятностные модели, динамическое программирование, теорию игр и модели транспортных и сетевых потоков. Требование: оценка «C» или выше по МАТЕМАТИКЕ 310.
МАТЕМАТИКА 380 Исследования по математике 0-3 кредита
Этот курс дает студентам возможность участвовать в исследовательских проектах с преподавателями факультета математики и статистики. Проекты могут носить вычислительный и/или теоретический характер. Обязанности и ожидания различаются и должны быть обсуждены с наставником факультета студента до регистрации.
Для регистрации требуется одобрение наставника факультета. Курс может быть повторен для получения кредита максимум на 3 кредита.
МАТЕМАТИКА 390 Стажировка – от 1 до 3 кредитов
Стажировка, соответствующим образом связанная с программой, определенной консультантом факультета и в зависимости от одобрения кафедры. Может повторяться в общей сложности до трех кредитов. Предварительные требования: оценка «C» или выше по МАТЕМАТИКЕ 215 и МАТЕМАТИКЕ 310.
МАТЕМАТИКА 410 Расширенный курс линейной алгебры – 3 кредита
Это второй курс линейной алгебры, который обеспечивает углубленное изучение фундаментальных понятий предмета. . Темы включают общие векторные пространства, собственные значения и собственные векторы, скалярные произведения и ортогональность, процесс Грама-Шмидта, QR-факторизацию, разложение по сингулярным числам, спектральную теорему, наименьшие квадраты и обобщенное обратное. Требования: оценка «С» или выше по МАТЕМАТИКА 250 и МАТЕМАТИКА 310.
МАТЕМАТИКА 411W Абстрактная алгебра I – 3 кредита
Введение в алгебраические структуры с упором на группы, включая подгруппы, абелевы и циклические группы, группы перестановок, смежные классы и факторгруппы, а также гомоморфизмы и изоморфизмы. Предварительные требования: оценка «C» или выше по МАТЕМАТИКЕ 215, МАТЕМАТИКЕ 250 и МАТЕМАТИКЕ 310.
МАТЕМАТИКА 412W Абстрактная алгебра II — 3 кредита
Более глубокое изучение алгебраических структур, включая кольца, идеалы, области целостности, поля, и другие избранные темы. Требование: оценка «C» или выше по MATH 411W.
МАТЕМАТИКА 415W Введение в действительный анализ I — 3 кредита
Свойства действительных чисел, мощность, последовательности и ряды, свойства множеств, функциональные ограничения и непрерывность. Предварительные требования: оценка «C» или выше по МАТЕМАТИКЕ 215, МАТЕМАТИКЕ 250 и МАТЕМАТИКЕ 310.
МАТЕМАТИКА 416W Введение в реальный анализ II — 3 кредита
Продолжение МАТЕМАТИКА 415W, включая дифференцирование, последовательности и ряды функций, теория интеграции и продвинутые темы анализа. Условие: оценка «C» или выше по MATH 415W.
МАТЕМАТИКА 420 Введение в комплексные переменные — 3 кредита
Плоскость комплексных чисел, аналитические функции, интегрирование комплексных функций, последовательности и ряды, а также конформные отображения. Предварительные требования: оценка «C» или выше по МАТЕМАТИКА 215, МАТЕМАТИКА 250 и МАТЕМАТИКА 310.
МАТЕМАТИКА 423W Топология — 3 кредита
Топологические пространства, гомеоморфизмы, связность, компактность, регулярные и нормальные пространства, метрические пространства, сходимость и аксиомы разделения. Требования: оценка «С» или выше по МАТЕМАТИКЕ 411W или по 415W.
МАТЕМАТИКА 435 Клинические испытания: дизайн и анализ — 3 кредита
Этот курс охватывает основные и дополнительные элементы, связанные с дизайном клинического исследования. Темы включают типы и свойства клинических испытаний, этические вопросы, процедуры рандомизации, оценку размера выборки, варианты исходной оценки, соблюдение требований и работу с отсутствующими данными. Статистические темы включают анализ линейной модели, продольный анализ данных, анализ стратифицированных данных, множественные сравнения и множественные конечные точки, ковариатную корректировку, анализ подгрупп, адаптивные планы, анализ не меньшей эффективности и методы условного исчисления. Требование: оценка «C» или выше по MATH 325 или MATH 525.
МАТЕМАТИКА 445 Прогнозирование и моделирование классификации – 3 кредита
Коэффициенты классификации, кривые ROC, методы перекрестной проверки, современные методы регрессии, сокращение данных/принципиальные компоненты, этапы разработки биомаркеров, а также вопросы дизайна исследования рака и профессиональных исследований. Условие: степень «C» или выше по MATH 325W или по MATH 525W.
МАТЕМАТИКА 471 Оптимизация — 3 кредита
Линейное программирование, транспортная задача, сетевой поток, нелинейное выпуклое программирование, динамическое программирование, геометрическое программирование, теория игр и градиентные методы. Требования: оценка «C» или выше по МАТЕМАТИКЕ 215 или эквивалентной и МАТЕМАТИКА 310.
МАТЕМАТИКА 473 Статистические вычисления — 3 кредита
Генерация псевдослучайных чисел, интегрирование Монте-Карло, моделирование, байесовский вывод, выборка Гиббса, выборка Метрополиса, выборка Метрополиса-Гастингса, алгоритм Э-М, многомерная максимизация Ньютона-Рафсона. Предварительное условие: оценка «C» или выше по MATH 302W и одна из оценок COSC 150, COSC 160 или COSC 170.
MATH 481 Applied Math Capstone Project — 3 кредита
Этот курс предлагает учащимся возможность использовать свои навыки прикладной математики изучать проблемы, возникающие в реальных условиях, в рамках индивидуального или группового проекта. Учащиеся будут изучать стратегии решения, реализовывать стратегию, интерпретировать свои выводы и сообщать о своих результатах в письменной и/или устной форме.
Предварительные требования: Старший статус и оценка «c» или выше по МАТЕМАТИКА 301, МАТЕМАТИКА 314 или МАТЕМАТИКА 308 или МАТЕМАТИКА 302 или МАТЕМАТИКА 325W, МАТЕМАТИКА 410
МАТЕМАТИКА 491 Избранные темы по математике I — 1 кредит
Выбранные темы по согласованию с консультантом.
МАТЕМАТИКА 492 Избранные темы по математике II — 2 кредита
Темы, выбранные по согласованию с консультантом.
МАТЕМАТИКА 493 Избранные темы по математике III — 3 кредита
Темы выбраны по согласованию с консультантом.
No related posts.