Четность и нечетность функций
Вопросы занятия:
· повторить такое свойство функции, как чётность и нечётность.
Материал урока
Прежде давайте вспомним свойства функций, о которых мы уже говорили. Это: область определения функции, область значений функции, нули функции, промежутки знакопостоянства функции, промежутки монотонности функции.
Для того чтобы мы могли говорить о чётности, еще раз давайте повторим, что мы понимаем под областью определения функции.
Определение.
Область определения функции – это все значения, которые может принимать аргумент.
Теперь вспомним, что
Теперь
давайте разберёмся с этим определением по подробней. Первым условием является
то, что область определения функции должна быть симметрична относительно икс
равного нулю. Что это значит? Это значит, что если число А принадлежит области
определения, то и число минус А тоже принадлежит области определения этой
функции.
Выполним задание:
Пример.
Второе условие чётности говорит о том, что:
Если посмотреть на график чётной функции, то можно увидеть, что он будет симметричен относительно оси ординат.
Если же нарушается первое условие, то есть область определения функции – не симметричное относительно x = 0 множество, то такая функция не обладает свойством чётности.
Теперь давайте вспомним какую функцию называют нечётной.
Если мы посмотрим на график нечётной функции, то нетрудно увидеть, что он симметричен относительно начала координат.
Мы с вами уже рассмотрели некоторые элементарные функции, их свойства и графики. А теперь давайте попробуем определить какие из этих функций являются чётными, нечётными, ни чётными, ни нечётными.
Итак,
начнём с прямой пропорциональности. Область определения прямой
пропорциональности – вся числовая прямая, то есть говорить о чётности или нечётности,
мы можем.
Если мы посмотрим на графики прямой пропорциональности, то увидим, что эти графики симметричны относительно начала координат.
Теперь давайте рассмотрим обратную пропорциональность.
Область определения этой функции – симметричная относительно x = 0 область, то есть говорить о чётности или нечётности этой функции можно.
Подставим вместо х -х и получим, что y(-x) = —y(x), то есть обратная пропорциональность – нечётная функция
Следующей мы рассмотрим линейную функцию.
Область определения функции – вся числовая прямая, то есть область определения – симметричное множество. Подставим вместо х -х, тогда получим что:
То
есть линейная функция не является ни чётной, ни нечётной.
Рассмотрим функцию y = │x│.
Область определения этой функции – вся числовая прямая. То есть можно проверить эту функцию на чётность и нечётность. Подставим вместо х -х. По свойству модуля:
Тогда получим, что функция игрек равно модуль икс – чётная функция.
Теперь поговорим о функции у = х2.
Область определения – вся числовая прямая.
Подставим вместо х -х. По свойству квадрата выражения, получим, что:
то есть функция чётная.
Рассмотрим квадратичную функцию.Область определения – вся числовая прямая.
Подставим вместо х -х и получим, что:
то есть квадратичная функция не является ни чётной, ни нечётной.
Теперь давайте рассмотрим функцию:
Область
определения функции – промежуток [0; + ∞) – это не симметричное
относительно точки x
= 0
множество, то есть мы сразу можем написать, что о чётности или нечётности этой
функции говорить нельзя.
Теперь давайте рассмотрим функцию y = x3. Область определения – вся числовая прямая. Подставим вместо x —x и получим, что:
то есть перед нами нечётная функция.
Теперь давайте решим несколько заданий.
Пример.
Рассмотрим ещё один пример.
Пример.
Пример.
Итоги урока
Сегодня на уроке мы повторили такое свойство функций как чётность. Вспомнили какая функция называется чётной, а какая – нечётной.
Как проверить четное ли число в php? Очень просто!
Привет!
Заметил, что многие не знают, как можно узнать четное ли число или нечетное в php. А ведь делается это очень просто! Конечно, было бы проще, если бы разработчики подготовили для нас самостоятельную функцию, но сотворить такую самому — тоже плевое дело.
Итак, для того, чтобы решить поставленную задачу, легче всего будет использовать деление по модулю.
Думаю со школьной скамьи многие помнят, как происходит деление по модулю. Вы делите число, и смотрите, есть ли остаток. Если мы делим четное число, например, на 2, то остатка не будет. А вот если мы поделим 7 на 2, тогда будет остаток.
Исходя из этого можно проследить алгоритм определения четности числа. Если остаток есть — число нечетное. Если остатка нет — число четное. Разберем пример на конкретном практическом уроке.
Как проверить четное ли число в php?
Для этого мы будем использовать следующий код:
$val%2 //если число в переменной $val четное, результат будет 0 $val%2 //если число в переменной $val не четное, результат будет 1 |
Как Вы поняли, все, что нам осталось — использовать условие.
|
1 2 3 4 5 6 |
if($val%2 == 0) { echo ‘Это четное число!’; } else { echo ‘Число не четное’; } |
Практический пример определения четности числа php
Многие, в том числе и я, любят выделять в таблицах четные колонки.
Сами строки будем выводить через цикл foreach. Зададим еще и счетчик. Это будет переменная, значение которой устанавливаем до цикла, а внутри цикла эта переменная будет увеличиваться на 1. Так же внутри цикла будем проверять, если значение переменной четное, тогда к выводимой строке добавим стиль с фоном. Если же значение нечетное, тогда ничего добавлять не будем.
$val = 0; foreach ($table as $tbl) { $val++; $val%2 == 0 ? print ‘<tr>’ : print <tr>; } |
Кто не понял последнюю строку, это обычное условие if/else, просто написанное более быстрым и удобным способом. В результате выполнения этого кода у нас будут нечетные строки стандартного цвета, а четные блоки получат класс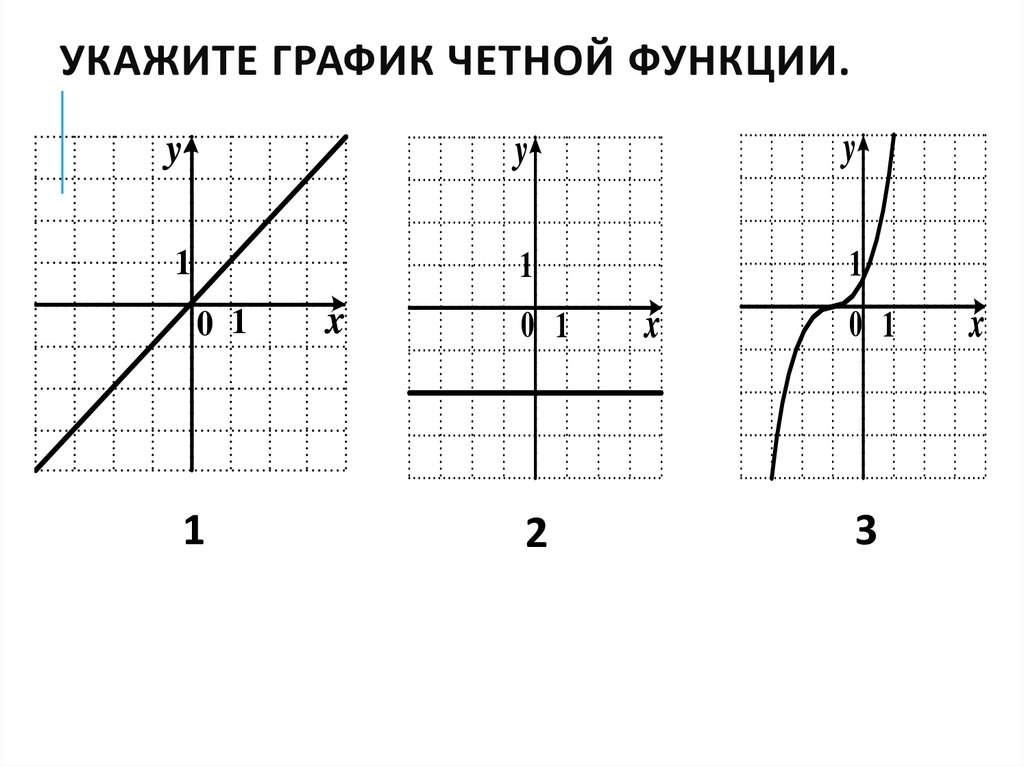 
Вот и все! Теперь мы узнали, как можно легко определить четное ли число в php.
До скорых встреч!
Heilmittel gibt es in verschiedenen Formen und wir nehmen sie auf unterschiedliche Weise. Es gibt Medikamente, die nur für Frauen bestimmt sind. Informationen über die Vor- und Nachteile von Drogen können aus vielen Quellen stammen, darunter aus dem Internet, den Medien und der Familie. Eine kürzlich durchgeführte Studie ergab, dass bestimmte Arzneimittel vielfältig sind und von Tag zu Tag schädlicher werden. Aber es gibt verschiedene Fragen, die damit einhergehen. Was müssen Patienten immer den Apotheker um professionelle Beratung bitten, wie man Viagra kauft? Aber ist das eigentlich eine gute Idee für Sie? Hier haben wir wichtige Informationen besprochen, die Sie berücksichtigen sollten, sowie Möglichkeiten, wie Sie gesund bleiben können. Es könnte sein, dass Sie darüber lesen. Wirst du Medikamente aus dem Internet bestellen? Sicher gibt es auch andere wichtige Fragen.
Was sind die wichtigsten Informationen, an die Sie denken sollten, wenn Sie Arzneimittel bestellen? Viele Männer halten verschreibungspflichtige Medikamente für sicher, weil sie von einem Arzt verschrieben wurden. Typische häufige Nebenwirkungen sind Gesichtsrötungen. Laut der Royal Pharmaceutical Society sind diese Mittel normalerweise sicher, wenn sie wie vorgeschrieben angewendet werden, und haben vergleichsweise wenige gefährliche Nebenwirkungen. Wir werden uns jede dieser Nebenwirkungen in zukünftigen Artikeln genauer ansehen. Trotzdem kann nur Ihr Arzt entscheiden, ob das Arzneimittel für Sie geeignet ist. Nehmen Sie zum Schluss Kontakt mit Ihrer Gesundheit auf und bleiben Sie ein Leben lang gesund. In diesem Sinne können Sie jetzt einfach ohne Probleme beginnen.
diese Website ausprobieren
Obwohl einige Mittel auf ähnliche Weise wirken, hat jedes Medikament eine leicht unterschiedliche chemische Zusammensetzung. Ihr Arzt wird viele Faktoren sowie mögliche Wechselwirkungen mit anderen Medikamenten, die Sie einnehmen, berücksichtigen. Viele Arzneimittel mit demselben Wirkstoff sind in unterschiedlichen Stärken erhältlich. Wenn es Gruppen von Rezepten gibt, die alle ähnliche Aufgaben erfüllen, sind sie bei der Behandlung einer bestimmten Krankheit ungefähr so wirksam wie die anderen. Sie können zwar Geld sparen, indem Sie günstigere Produkte nehmen, dies ist jedoch nicht immer eine gute Idee. Die Ärzte sind darin geschult, wie Sie sicher Abhilfe schaffen können. Gegenwärtig gibt es verschiedene Optionen für viagra generika für diejenigen, die an einem solchen Gesundheitsproblem leiden.
Verbraucher können nützliche Informationen dazu aus evidenzbasierten Quellen wie dem Internet, den sozialen Netzwerken und sogar der Familie finden. Wissen Sie, was für Sie am besten ist? Dies ist ein Mittel zur Behandlung zahlreicher Infektionen. Was muss noch besprochen werden? Wo finden Sie korrekte Informationen dazu?
Wie auch immer, die Umstände, die Ihre Entscheidung vorbestimmen können, können unterschiedlich sein. Dies sind wichtige Möglichkeiten, um sich um Ihren Körper zu kümmern, an die Sie möglicherweise nicht von Natur aus denken. Wenn Sie sich jedoch Ziele setzen, um diese Ideen in Ihrem Leben Wirklichkeit werden zu lassen, werden Sie den Unterschied sofort spüren, aber in den kommenden Monaten auch in mehreren Bereichen Ihres Lebens Ergebnisse sehen.sein Kommentar ist hier
{Wie kaufe ich cialis generika?
Medikamente könnten Teil Ihrer täglichen Routine sein, um Ihre Gesundheit gut zu verwalten. Internet-Drogerien kombinieren garantiert niedrige Preise mit schnellem Versand. Wenn es darum geht, privat verschriebene Medikamente zu kaufen, bieten Ihnen Online-Drogerien mehr Auswahl beim Eingang Ihrer Bestellung. Da immer mehr Patienten online gehen, um ihre Gesundheitsprobleme zu verstehen, gehen einige auch online, um generische Mittel zu kaufen. Natürlich sollte jeder von uns Zugang zu wichtigen und kostengünstigen Mitteln haben, die zur Bekämpfung von Infektionen beitragen oder einfach die allgemeine Gesundheit verbessern.
Der Online-Kauf von Generika kann eine gute Idee sein, solange Sie dies verantwortungsbewusst tun. Zugegeben, sobald das Generikum verfügbar ist, werden die Kosten sowohl für das ursprüngliche Markenprodukt als auch für das Generikum erheblich gesenkt. Sie haben sie natürlich im Supermarkt gesehen. Generische Versionen von Arzneimitteln sind in vielen ausländischen Märkten, einschließlich Kanada und den meisten Ländern Europas, legal. Generika sind grundsätzlich nur deshalb billiger, weil die Hersteller nicht die Kosten für die Entwicklung eines neuen Arzneimittels hatten. Generika sind im Allgemeinen etwas günstiger und meist genauso wirksam wie Markenmedikamente. Jeder weiß, dass es wichtig ist, darüber Bescheid zu wissen.Wenn Sie cialis generika kaufen, erkundigen Sie sich bei einem qualifizierten Gesundheitsdienstleister, ob diese unschuldig sind, wenn Sie sie mit Ihren anderen Generika einnehmen.
|Wenn Sie online über Medikamente nachdenken, möchten Sie vielleicht mehr über dieses Problem erfahren.
Zweifellos haben Sie bereits etwas darüber gehört, wie man cialis generika kauft. Viele gesundheitsbezogene Websites bieten mehr Inhalte und dies könnte die Patienten zum Thema führen.Vielleicht wissen Sie bereits etwas über das Problem. Lassen Sie uns nun über verschiedene Medikamente sprechen, die Sie online kaufen können. Es ist wichtig, über sichere Wege zum Kauf von Medikamenten informiert zu bleiben. Wenn Sie über Ihre Behandlungsoption nachdenken, kann es hilfreich sein, einige wichtige Fakten darüber zu kennen, wo Sie cialis generika kaufen können.
Diejenigen, die Rabattmedikamente und Nahrungsergänzungsmittel in Betracht ziehen, werden häufig eine Reihe von Optionen zur Auswahl finden. Es ist verlockend, Medikamente und Kräuterergänzungen online zu kaufen, wenn dieselben Produkte so viel billiger sind. Vieles, was darüber gesagt wurde, gilt auch für natürliche Gesundheits- und Wellnessprodukte und alltägliche wichtige Toilettenartikel. Wenn Sie cialis generika kaufen, sollten Sie einige wesentliche Details kennen.
|Wenn Sie die Anziehungskraft auf einen bestimmten Partner verloren haben, ist es normalerweise unwahrscheinlich, dass Behandlungsoptionen zur Verbesserung der Potenz ihm helfen. Als die Mehrheit der Einzelhändler online ging, stiegen die Erwartungen und eine überwältigende Anzahl von Kunden erwartete, online die Mittel zu finden, die sie benötigen. Illegale Online-Apotheken versuchen möglicherweise, illegale «generische» Versionen dieser Originalmarkenmedikamente zu verkaufen. Fragen Sie Ihren Apotheker nach Informationen, wenn Sie sich über den Online-Kauf von Generika nicht sicher sind. Darüber hinaus machen Generika die überwiegende Mehrheit der landesweit verschriebenen Rezepte aus. Das Medikament ist verschreibungspflichtig und muss unter Aufsicht eines Arztes angewendet werden. Aber ist es wirklich das richtige Feld für Sie, cialis generika zu kaufen? Es gibt verschiedene ernsthafte Fragen zu diesem Thema. Darüber hinaus kann es auch zur Behandlung einiger anderer von Ihrem Arzt festgelegter Erkrankungen verwendet werden.
Wenn Sie sicher sind, dass diese gesetzlichen Anforderungen erfüllt werden können und Sie wissen, dass die von Ihnen ausgewählte Apotheke sicher ist, ist es möglicherweise an der Zeit, Ihre verschreibungspflichtigen Medikamente aus einer Online-Apotheke zu beziehen. Während sich alle Symptome bessern können, bevor die Krankheit vollständig behandelt ist, nehmen Sie das Mittel für den gesamten vorgeschriebenen Zeitraum ein. Auf dieser Website finden Sie einige nützliche Informationen zu den Risiken von Arzneimitteln und deren Erforschung.Was ist ein kostengünstiges Medikament, um Patienten bei der Aufrechterhaltung einer Erektion zu helfen? Der Rat ist unkompliziert, kann aber den Unterschied ausmachen, wenn Sie Informationen zu diesem Thema benötigen. Obwohl der Missbrauch verschreibungspflichtiger Medikamente viele Familien betrifft, können bestimmte Bevölkerungsgruppen wie Jugendliche einem besonderen Risiko ausgesetzt sein. Für die meisten Menschen, die keine Erektion bekommen, die fest genug für Sex ist, funktionieren Arzneimittel gut, verursachen aber manchmal schwerwiegende Nebenwirkungen.
Und die Pillen gelten allgemein als sehr sicher. Häufige unerwünschte Effekte können das sogenannte blaue Sehen sein, aber es ist sicherlich häufiger, wenn Sie mehr als die vorgeschriebene Menge einnehmen. Sie können eine Checkliste für Nebenwirkungen verwenden, um den Überblick zu behalten und Informationen schnell mit Ihrem medizinischen Fachpersonal zu teilen. Nehmen Sie dieses Generikum nicht in kleineren Mengen ein. Der Rat ist üblich, kann aber den Unterschied ausmachen, wenn Sie Informationen über Pillen benötigen. Normalerweise erfordert die Behandlung Geduld, um eine erwartbare Wirkung zu erzielen. Verbraucher sollten die online gefundenen Informationen jedoch immer objektiv behandeln. Schließlich können Sie Zeit bei Ihren Rabattmedikamenten und Kräutern sparen, indem Sie sie online bestellen.}Sie könnten es versuchen hier
{Wie cialis generika?
Der ideale Zeitpunkt für den Beginn der Behandlung ist, bevor sichtbare Anzeichen auftreten. Die zunehmende Nachfrage nach Informationen im täglichen Leben von Millionen von Menschen hat dazu geführt, dass immer mehr pharmazeutische Gesundheitsdienstleister versuchen, ihre Gesundheitsprodukte vor ihren Konkurrenten zu positionieren.
Wie finde ich Medikamente online? Die Verschreibung und Verwendung von Medikamenten ist jedoch Vertrauenssache. Für Kunden wird es immer einfacher, Medikamente online zu bekommen. Es gibt viele Online-Apotheken im Internet, daher sollte es kein Problem sein, eine vertrauenswürdige Drogerie zu finden. Sie bieten Kunden mit eingeschränkter Mobilität und Kunden in abgelegenen Gebieten Zugang. Die reduzierten Transaktionskosten werden in Form weitaus niedrigerer Preise an die Patienten weitergegeben. In beiden Fällen ist es nicht alles. Dieser Leitfaden behandelt alles von der Sicherung Ihres Computers bis zur Überprüfung und Bestellung von Viagra in zuverlässigen Online-Apotheken.10 Möglichkeiten, gefälschte Medikamente zu erkennen.
|Deshalb interessieren sich viele für dieses Thema. Ist es für Sie aktuell, wie man cialis generika?
Lassen Sie uns Antworten auf Ihre wichtigsten Fragen zu diesem Thema finden. Das Bestellen von Rezepten im Internet kann eine kostengünstige Methode sein, solange Sie dies verantwortungsbewusst tun.
Lassen Sie uns darüber sprechen, wie Sie sicher sein können, dass online bestellte Medikamente den Qualitätsstandards entsprechen. Ziemlich cialis generika oder andere Medikamente, die von einer virtuellen Drogerie angeboten werden, sind sehr elementar.Es gibt viele gültige Internet-Drogerien, die legitime Rabatte anbieten. Wenn Sie Medikamente online kaufen möchten, tun Sie dies in einer legalen Apotheke. Die Lieferanten bieten Tausende von Arzneimitteln an, zu denen sowohl generische als auch bekannte Marken gehören. Es gibt Varianten von renommierten virtuellen Drogerien, in denen Patienten Viagra bestellen können.
|Zu wissen, wonach zu suchen ist, kann eine Herausforderung sein, insbesondere bei allen verfügbaren Optionen. Normalerweise sind viele Medikamente zu berücksichtigen. Können Sie verschreibungspflichtige Medikamente legal online bekommen? Es ist wichtig, die Vorteile verschriebener Medikamente sowie deren mögliche unerwünschte Wirkungen zu kennen und mit Ihrem Apotheker über mögliche Bedenken zu sprechen.
Wenn Sie besprechen, wie Sie Viagra bestellen können, ist es viel wahrscheinlicher, dass Sie einen Plan entwickeln, der für Sie gut funktioniert. Wir alle können verlässliche Informationen aus vertrauenswürdigen Quellen wie dem Internet, den Medien und sogar Freunden finden. Dies sind sicherlich nur die Grundregeln. Wenn Sie Arzneimittel bestellen, sollten Sie darüber nachdenken. Seit Jahrzehnten helfen diese Medikamente, viele Störungen zu verhindern. Der ideale Zeitpunkt für den Beginn der Behandlung ist, wenn nur Symptome auftreten. Themen zur Bestellung von Viagra sind im letzten Jahr sehr beliebt. Einige Forscher achten auf solche Angelegenheiten. Haben Sie etwas über Nebenwirkungen gelernt?Höchstwahrscheinlich hat jeder Mann zumindest etwas davon gehört. Wenn Sie Medikamente in Online-Apotheken bestellen möchten, erhalten Sie normalerweise zuerst ein gültiges Rezept. Es ist wichtig zu verstehen, dass nicht alle Medikamente wirklich nützlich sind. Wie alle Arzneimittel hat das Arzneimittel unterschiedliche unerwünschte Wirkungen.
2+7\) четной и нечетной функцией или ни четной, ни нечетной функцией.Решение
Нам нужно упростить формулу для \(f(-x)\text{.}\) Если она идентична формуле для \(f(x)\text{,}\), мы можем объявить, что \(f\) — четная функция. Если нет, нам нужно упростить формулу для \(-f(x)\) и сравнить ее с упрощенной формулой для \(f(-x)\text{.}\). Если две формулы одинаковы, мы можно утверждать, что \(f\) — нечетная функция. Если эти две последние формулы не идентичны, мы утверждаем, что \(f\) не является ни четной, ни нечетной функцией. 96-16x \end{align*}
Заметим, что формула для \(f(-x)\) также не совпадает с формулой для \(f(-x)\) (знаки коэффициентов на втором не совпадают), поэтому мы можем с уверенностью утверждать, что \(f\) не является ни четной, ни нечетной функцией.
Возможно, вы заметили, а могли и не заметить, что в первом примере все члены имели четную степень (степень над \(x\)) и функция оказалась четной. Точно так же во втором примере все члены имели нечетную степень и функция оказалась нечетной.
Наконец, в третьем примере были как члены с четной степенью, так и члены с нечетной степенью, и функция оказалась ни четной, ни нечетной. Это может показаться довольно большим совпадением, но я подозреваю, что это явление является основным стимулом для терминов четная функция и нечетная функция, потому что для 95-6x}
\end{align*}
Мы видим, что формула для \(f(-x)\) идентична формуле для \(f(x)\), и заключаем, что \(f\) является четной функцией. Заметим, что \(f\) оказалась четной функцией, несмотря на то, что каждый член имеет нечетную степень. Это, однако, не противоречит сказанному выше, поскольку анализируемая нами функция не была полиномиальной функцией.
Графики нечетных и четных функций.
Графики четных и нечетных функций имеют свои уникальные графические свойства.
Функция \(y=f(x)\text{,}\) является четной функцией тогда и только тогда, когда ее график симметричен относительно оси \(y\) . Это связано с тем, что для каждой точки на графике \((a,b)\text{,}\) точка \((-a,b)\) также лежит на графике.
Таким образом, если мы сложим график по оси \(y\), каждая точка функции, лежащая слева от оси, будет лежать поверх своего близнеца, лежащего справа от оси \(y\).
Функция, показанная на рисунке 5.7.5, симметрична относительно оси \(y\), и поэтому мы знаем, что это четная функция, 9{\circ}\) и положил его поверх копии B, две кривые будут лежать друг над другом — это то, что подразумевается под симметрией относительно начала координат.
Функция, показанная на рис. 5.7.6, симметрична относительно начала координат, поэтому мы знаем, что это нечетная функция.
Рисунок 5.7.6. График нечетной функцииУпражнения Упражнения
Определить, является ли каждая заданная функция нечетной функцией, четной функцией или ни четной, ни нечетной функцией.
1.
94} \end{align*}Формула для \(f(-x)\) идентична формуле для \(f(x)\text{,}\), поэтому \(f\) является четной функцией.
7.
Функция, показанная на рисунке 5.7.7.
Рисунок 5.
7.7. Нечетное, четное или ни то, ни другое?Решение
Функция симметрична относительно оси \(y\), поэтому является четной функцией.
8.
Функция, показанная на рисунке 5.7.8.
Рисунок 5.7.8. Нечетное, четное или ни то, ни другое?Решение
Функция симметрична относительно начала координат, поэтому является нечетной функцией.
9.
Функция, показанная на рисунке 5.7.9.
Рисунок 5.7.9. Нечетное, четное или ни то, ни другое?Решение
Функция симметрична относительно оси \(y\), поэтому является четной функцией.
10.
Функция, показанная на рисунке 5.7.10.
Рисунок 5.7.10. Нечетное, четное или ни то, ни другое?Решение
Хотя функция обладает вертикальной симметрией, она не является специфически симметричной относительно оси \(y\), поэтому она не является четной функцией.
Функция также явно не симметрична относительно начала координат, поэтому она также не является нечетной функцией. Таким образом, функция не является ни четной, ни нечетной.
11.
Функция, показанная на рисунке 5.7.11.
Рисунок 5.7.11. Нечетное, четное или ни то, ни другое?Решение
Функция не симметрична относительно оси \(y\) и не симметрична относительно начала координат, поэтому она не является ни четной, ни нечетной.
Четные и нечетные триггерные функции
Home > Math > Trigonometry > Четные и нечетные триггерные функции
Все функции, включая триггерные, могут быть описаны как четные, нечетные или никакие. Функция нечетное тогда и только тогда, когда f(-x) = — f(x) и симметрично относительно начала координат. Функция равна даже тогда и только тогда, когда f(-x) = f(x) и симметрична оси y. Полезно знать, является ли функция четной или нечетной, когда вы пытаетесь упростить выражение, когда переменная внутри тригонометрической функции отрицательна.
грех(-х) = — грех х | csc (-x) = — csc х |
потому что (-х) = потому что х | сек (-х) = сек х |
загар (-х) = — загар х | загар (-x) = — детская кроватка x |
Пример 1: найти значение (4 · sin (-60)) 2
= (-4 · sin (60)) 2 sin(-x) = — sin x
=
=
= 12
Пример 2: Определите, является ли следующая функция четной или нечетной
f(x) = x 3 sin x
Найти f(-x) f(-x) = -(-x) 3 sin (x) заменив x на -x и sin (-x) = — sin x
f(-x) = x 3 грех х
f(x) = f(-x), следовательно, функция четная.