Как проверить коллинеарны ли векторы: Онлайн калькулятор. Коллинеарность векторов

Как определить коллинеарность векторов плоскости?



Ортогональность векторов мы проверяли с помощью скалярного произведения, и вот теперь коллинеарность.

Для того чтобы два вектора плоскости  были коллинеарны, необходимо и достаточно, чтобы их соответствующие координаты были пропорциональны: , где  – константа.

По существу, это покоординатная детализация очевидного соотношения .

Задача 37

а) Проверить, коллинеарны ли векторы .
б) Образуют ли базис векторы ?

Решение:

а) Выясним, существует ли для векторов  коэффициент пропорциональности , такой, чтобы выполнялись равенства :
 – из обоих уравнений следует, что , значит, данные векторы коллинеарны.

И обязательно расскажу о «пижонской» разновидности применения данного правила, которая вполне работает на практике. Идея состоит в том, чтобы сразу составить пропорцию  и посмотреть, будет ли она верной:

сокращаем обе части:
 – в результате получено верное равенство, таким образом, соответствующие координаты пропорциональны, следовательно,  .

Отношение можно было составить и наоборот, это равноценный вариант:
 – верное равенство.

Для проверки можно использовать тот факт, что коллинеарные векторы линейно выражаются друг через друга. В данном случае имеют место равенства , и их справедливость легко проверяется через элементарные действия с векторами:

б) Два вектора плоскости образуют базис, если они не коллинеарны (линейно независимы). Исследуем на коллинеарность векторы . Составим систему:

Из первого уравнения следует, что , а из второго уравнения следует, что , значит, система

несовместна (решений нет). Таким образом, соответствующие координаты векторов не пропорциональны.

Вывод: векторы линейно независимы и образуют базис.

Упрощённая версия решения выглядит так:

Составим пропорцию из соответствующих координат векторов :
, значит, данные векторы линейно независимы и образуют базис.

Обычно такой вариант не бракуют рецензенты, но он не применим в тех случаях, когда некоторые координаты равны нулю: . Или так: . Или так: . Как тут действовать через пропорцию? (на ноль же делить нельзя). Именно по этой причине я и назвал упрощенное решение «пижонским».

Ответ: а) ,        б) образуют.

Небольшое творческое задание для самостоятельного решения:

Задача 38

При каком значении параметра  векторы  будут коллинеарны?

В образце решения параметр найден через пропорцию .

Но это ещё не всё. Помимо рассмотренных, существует изящный алгебраический способ проверки векторов на коллинеарность, систематизируем наши знания и пятым пунктом как раз добавим этот способ:

Для двух векторов плоскости эквивалентны следующие утверждения:

1) векторы линейно независимы;
2) векторы образуют базис;
3) векторы не коллинеарны;
4) векторы нельзя линейно выразить друг через друга;
+ 5) определитель, составленный из координат данных векторов, отличен от нуля.
– далее нам потребуются некоторые алгебраические навыки, и по ходу изложения

я буду проставлять гиперссылки на соответствующие статьи mathprofi.ru.

и, соответственно, эквивалентны следующие противоположные утверждения:
1) векторы линейно зависимы;
2) векторы не образуют базиса;
3) векторы коллинеарны;
4) векторы можно линейно выразить друг через друга;
+ 5) определитель, составленный из координат данных векторов, равен нулю.

! Проконтролируйте , всё ли вам понятно в терминах и утверждениях?

Я очень и очень надеюсь, что на данный момент вы уже эльфы 4-го уровня 🙂

Рассмотрим более подробно новый, пятый пункт: два вектора плоскости ,  коллинеарны тогда и только тогда, когда определитель, составленный из координат данных векторов, равен нулю: .

Решим Задачу 37 вторым способом:

а) Вычислим определитель, составленный из координат векторов :
, значит, данные векторы коллинеарны.

б) Два вектора плоскости образуют базис, если они не коллинеарны. Вычислим определитель, составленный из координат векторов :
, значит, векторы  линейно независимы и образуют базис.

Ответ: а) ,        б) образуют.

Выглядит значительно компактнее и симпатичнее, чем решение с пропорциями.

С помощью рассмотренных методов можно устанавливать не только коллинеарность векторов, но и доказывать параллельность отрезков, прямых. Разберём пару задач с конкретными геометрическими фигурами:

Задача 39

Даны вершины четырёхугольника . Доказать, что четырёхугольник  является параллелограммом.

Перед доказательством вспомним, что это за геометрическая фигура: параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны (см. Приложение Школьные Материалы).Таким образом, нужно доказать:

1) параллельность противоположных сторон  и ;

2) параллельность противоположных сторон  и .

Доказываем:

1) Найдём векторы:

Вычислим определитель, составленный из координат векторов :
, значит, данные векторы  коллинеарны, откуда следует параллельность соответствующих сторон: .

2)

Найдём векторы:

Получился один и тот же вектор («по школьному» – равные векторы), но решение таки лучше оформить с толком, с расстановкой. Вычислим определитель, составленный из координат векторов :
, значит, данные векторы  коллинеарны, и .

Вывод: противоположные стороны четырёхугольника  попарно параллельны, значит, он является параллелограммом по определению, что и требовалось доказать.

Обратите внимание, что чертёж здесь не нужен – решение чисто аналитическое.

Больше фигур хороших и разных:

Задача 40

Даны вершины четырёхугольника . Доказать, что четырёхугольник  является трапецией.

Это задание для самостоятельного решения.

А теперь пора потихонечку перебираться из плоскости в пространство:

1.8.3. Как определить коллинеарность векторов пространства?

1. 8.1. Базис и система координат на плоскости

| Оглавление |



Автор: Aлeксaндр Eмeлин

Условие коллинеарности векторов, когда векторы параллельны, свойства коллинеарных векторов

В статье ниже рассмотрим условия, при которых векторы считаются коллинеарными, а также разберем тему на конкретных примерах. И, прежде чем приступить к обсуждению, напомним некоторые определения.

Определение 1

Коллинеарные векторы – ненулевые векторы, лежащие на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому.

Данное определение дает возможность убедиться в коллинеарности векторов в их геометрическом отображении, однако точность такого способа может иметь погрешности, например, в зависимости, от качества самого чертежа. Поэтому обратимся к алгебраическому толкованию: сформируем условие, которое будет явным признаком коллинеарности.

Согласно схемам операций над векторами умножение вектора на некоторое заданное число приводит к соответствующему сжатию или растяжению вектора при сохранении или смене направления.

Тогда вектор b→=λ·a→ коллинеарен вектору a→ , где λ – некоторое действительное число. Справедливым будет и обратное утверждение: если вектор b→ коллинеарен вектору a→, его можно представить в виде λ·a→. Это является необходимым и достаточным условием коллинеарности двух ненулевых векторов.

Определение 2

Для коллинеарности двух векторов необходимо и достаточно, чтобы они были связаны равенствами: b→=λ·a→ или a→=μ·b→,   μ∈R

Исходные данные: вектор a→ задан в некоторой прямоугольной системе координат на плоскости и имеет координаты (ax, ay), тогда, согласно полученному выше условию, вектор b→=λ·a→ имеет координаты (λ·ax, λ·ay).

По аналогии: если вектор a→ задан в трехмерном пространстве, то он будет представлен в виде координат a=(ax, ay, az) , а вектор b→=λ·a→ имеет координаты (λ·ax, λ·ay, λ·az). Из полученных утверждений следуют условия коллинеарности двух векторов в координатном толковании.

Определение 3

1.   ​​​Для коллинеарности двух ненулевых векторов на плоскости необходимо и достаточно, чтобы их координаты были связаны соотношениями:  bx=λ·axby=λ·ay  или ax=μ·bxay=μ·by
2. Для коллинеарности двух ненулевых векторов в пространстве необходимо и достаточно, чтобы их координаты были связаны соотношениями:   bx=λ·axby=λ·ay bz=λ·azили ax=μ·bxay=μ·by az=μ·bz

Мы можем также получить еще одно условие коллинеарности векторов, опираясь на понятие их произведения.

Если ненулевые векторы a→=(ax, ay, az) и b→=(bx, by, bz) коллинеарны, то согласно векторному определению произведения a→×b→=0→. И это также соответствует равенству: i→j→k→axayazbxbybz=0→, что, в свою очередь, возможно только тогда, когда заданные векторы связаны соотношениями b→=λ·a→ и a→=μ·b→ , где μ — произвольное действительное число (на основании теоремы о ранге матрицы), что указывает на факт коллинеарности векторов.

Определение 4

Два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.

Рассмотрим применение условия коллинеарности на конкретных примерах.

Пример 1

Исходные данные: векторы  a→=(3-22, 1) и b→=(12+1, 2+1) . Необходимо определить, коллинеарны ли они.

Решение

Выполним задачу, опираясь на условие коллинеарности векторов на плоскости в координатах: bx=λ·axby=λ·ay Подставив заданные значения координат, получим: bx=λ·ax⇔12+1=λ·(3-22)⇒λ=1(2+1)·(3-22)=132-4+3-22=12-1by=λ·ay⇔2+1=12-1·1⇔(2+1)·(2-1)=1 ⇔1≡1

Т. е. b→=12-1·a→, следовательно, заданные векторы коллинеарны.

Ответ: заданные векторы коллинеарны.

Пример 2

Исходные данные: векторы a→=(1, 0, -2) и b→=(-3, 0, 6) . Необходимо убедиться в их коллинеарности.

Решение

Т.к. bx=λ·axby=λ·ay bz=λ·az⇔-3=-3·10=-3·06=-3·(-2) , то верным будет равенство: b→=-3·a→ , что является необходимым и достаточным условием коллинеарности. Таким образом, заданные векторы коллинеарны.

Найдем также векторное произведение заданных векторов и убедимся, что оно равно нулевому вектору: a→×b→=i→j→k→axayazbxbybz=i→j→k→10-2-306=i→·0·6+j→·(-2)·(-3)+k→·1·0-k→·0·(-3)-j→·1·6-i→·(-2)·0=0→Ответ: заданные векторы коллинеарны.

Пример 3

Исходные данные: векторы a→=(2, 7) и b→=(p, 3) . Необходимо определить, при каком значении pзаданные векторы будут коллинеарны.

Решение

Согласно выведенному выше условию, векторы коллинеарны, если

b→=λ·a→⇔bx=λ·axby=λ·ay⇔p=λ·23=λ·7

тогда λ=37, а p=λ·2⇔p=67 .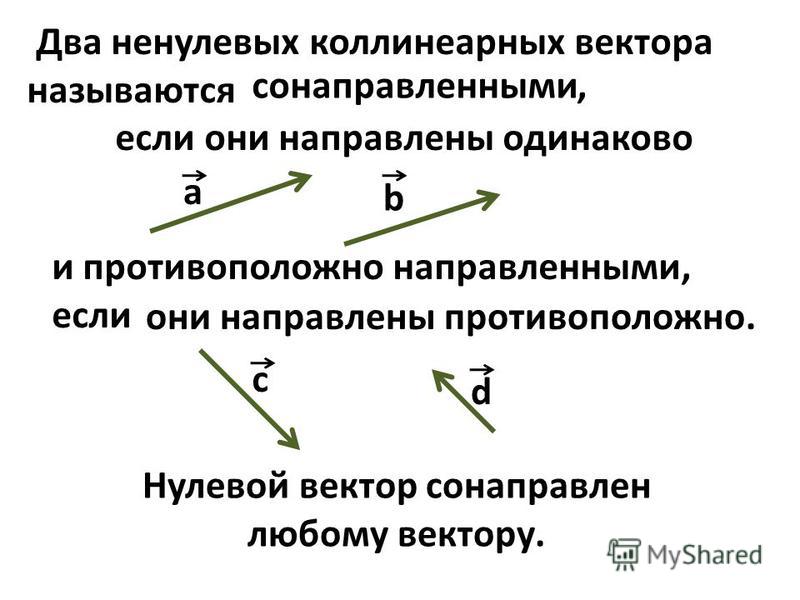  

 Ответ: при p=67 заданные векторы коллинеарны.

Также распространены задачи на нахождения вектора, коллинеарного заданному. Решаются они без затруднений, основываясь на условии коллинеарности: : достаточным будет взять произвольное действительное число λ и определить вектор, коллинеарный данному.

Пример 4

Исходные данные: вектор a→=(2, -6) . Необходимо найти любой ненулевой вектор, коллинеарный заданному.

Решение

Ответом может послужить, например, 12·a→=(1, -3) или вектор 3·a→=(6, -18) .

Ответ: вектор, коллинеарный заданному имеет координаты (1, -3).

Пример 5

Исходные данные: вектор a→=(3, 4, -5) . Необходимо определить координаты вектора единичной длины, коллинеарного заданному.

Решение

Вычислим длину заданного вектора по его координатам: a→=ax2+bx2+cx2=32+42+(-5)2=52 Разделим каждую из заданных координат на полученную длину и получим единичный вектор, коллинеарный данному: 1a→·a→=(352, 452,- 12)

Ответ: (352, 452,- 12)

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

аффинная геометрия — Докажите, что 3 вектора коллинеарны

спросил 6 лет, 8 месяцев назад

Изменено 6 лет, 8 месяцев назад

Просмотрено 2к раз

$\begingroup$

Меня просят доказать коллинеарность A(2,4), B(8,6), C(11,7) с помощью векторов.

Я могу вычислить AB, вычитая A из B, и BC, вычитая B из C в векторной форме.

Могу сказать, что ВС = 2АВ.

Но я не понимаю, почему это доказывает, что они коллинеарны.

• векторы
• аффинная геометрия

$\endgroup$

2

$\begingroup$

Если $A=(2,4), \; В=(8,6), \; С=(11,7)$, тогда $$ \vec{AB} = B — A = (6,2) \quad ; \четверка \vec{BC} = C — B = (3,1) $$ Таким образом, $\vec{AB} = 2 \vec{BC}$, что отличается от вашего вывода.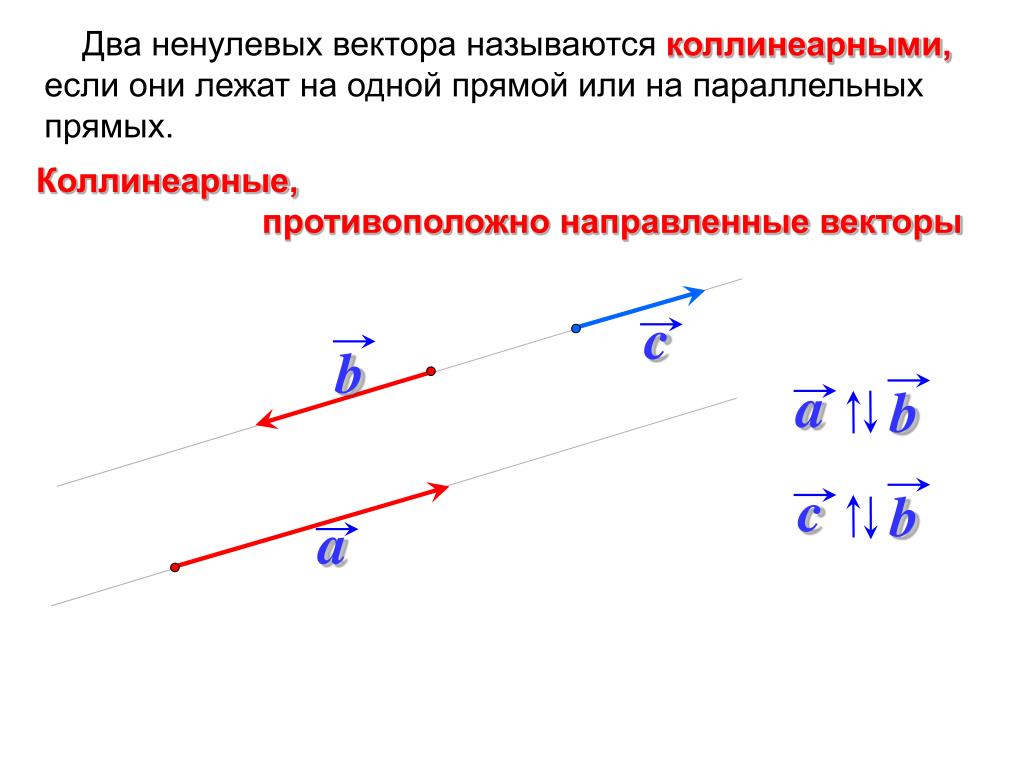

Во всяком случае, это говорит о том, что $\vec{AB}$ и $\vec{BC}$ параллельны, поскольку одно просто кратно другому. Таким образом, чтобы попасть из $B$ в $C$, вы идете в том же направлении, что и из $A$ в $B$ (поворот не требуется). Это означает, что $A$, $B$, $C$ должны лежать на одной прямой.

$\endgroup$

$\begingroup$

Потому что теперь вы можете параметризовать:

$$A=B-BA$$

$$B=B$$

$$C=B-BC=B+\frac12 BA$$

Теперь вы видите, что они находятся на одной линии?

$\endgroup$

$\begingroup$

Я думаю, что проще всего это проверить по наклонам: три точки на плоскости коллинеарны тогда и только тогда, когда наклоны между любыми двумя из них равны, и здесь у вас есть

$$m_{AB}=m_{ AC}=m_{BC}=\frac13$$

$\endgroup$

$\begingroup$

Они действительно коллинеарны.

9n$, эти точки коллинеарны тогда и только тогда, когда размерность $\{A_1-A_0,\cdots,A_{n-1}-A_0\}$ не превосходит $1$.

Итак, начнем с вычисления $B-A$ и $C-A$:

$$B-A = (6,2), \qquad C-A = (9,3)$$

Теперь вы можете использовать линейную алгебру, чтобы узнать размерность размаха двух вышеуказанных векторов; на самом деле это всего лишь $1$, поскольку они скалярно кратны друг другу. Следовательно, исходная тройка действительно коллинеарна.

Конечно, есть версии большего размера. Например: 9n$, эти точки компланарны тогда и только тогда, когда отрезок $\{A_1-A_0,\cdots,A_{n-1}-A_0\}$ имеет размерность не более $2$.

Вывод: мы часто можем ответить на вопросы об аффинной геометрии, сначала вычитая соответствующий вектор, так что теперь мы просто занимаемся линейной алгеброй.

$\endgroup$

2

$\begingroup$

Два вектора являются коллинеарными (и, следовательно, вашими конечными точками), если и только если один из них кратен другому.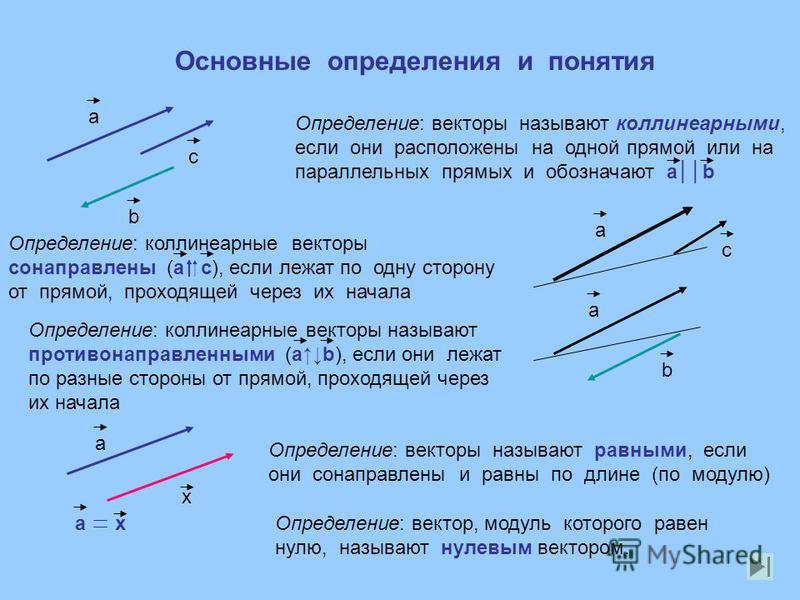

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Почему нельзя доказать коллинеарность двух векторов, если у них есть разностные знаки с помощью предположений?

спросил 1 год, 7 месяцев назад

Изменено 1 год, 7 месяцев назад

Просмотрено 65 раз

$\begingroup$

Векторы $A = xi + 2j + zk$ и $B = 2i + yj + 1k$

Вопрос состоит в том, чтобы проверить, являются ли они ($A$ и $B$) параллельными или коллинеарными.

Итак, в моей книге написано, что $x= 2 , y = 2$ и $z = 1$. Тогда они параллельны. Это тоже выглядит довольно очевидным.

Теперь еще один $Q$ с отрицательными значениями. $A = 2i + 3j -4k$ и $B = 3i-aj +bk$.

Здесь не предполагалось, что $a = -3$ и $b = 4$. Но решается другим методом, т. е. что их соотношение коэффициентов должно быть равным.

$\frac{2}{ 3} $= $\frac {3}{-a}$= $\frac {-4}{b}$. Итак,

$b \times 2 = -4 \times 3$ , $b = -6$. Теперь здесь значения были решены по-другому и имеют разные ответы. Почему это ? Я думаю из-за отрицательного знака, но для 1-го $Q$. Я не уверена.

$\frac{x}{2} = \frac{2}{y} =\frac{z}{1}$ . Здесь мы не можем решить это так, как мы сделали 2nd $Q$. Так как есть 3 переменных. Тогда как решить это

• векторов

$\endgroup$

2

$\begingroup$

Вам не нужно проверять параллельность векторов. Вас просят найти значения неизвестных, которые делают их такими.

1. $$\frac{x}{2}=\frac{2}{y}=\frac{z}{1}.$$ Для удобства можно предположить, что обыкновенный коэффициент равен $1$.

2. $$\frac{2}{3}=\frac{3}{-a}=\frac{-4}{b}.

   No related posts.