Как проверить на монотонность функцию: Исследование функций на монотонность — урок. Алгебра, 11 класс.

Монотонность функции, урок — 10 класс, алгебра

Дата публикации: 09 апреля 2017.

Урок и презентация по алгебре в 10 классе на тему: «Исследование функции на монотонность. Алгоритм исследования»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.

---

Скачать:Исследование функции на монотонность (PDF)

---

Что будем изучать:
1. Убывающие и возрастающие функции.
2. Связь производной и монотонности функции.
3. Две важные теоремы о монотонности.
4. Примеры.

Ребята, ранее мы с вами рассмотрели множество различных функций и строили их графики. Теперь давайте введем новые правила, которое работают для всех функций, которые мы рассматривали и еще будем рассматривать.

Убывающие и возрастающие функции

Давайте рассмотрим понятие возрастающей и убывающей функции. Ребята, а что такое функция?

Функцией называется соответствие y= f(x), в котором каждому значению x ставится в соответствие единственное значение y.

Посмотрим на график некоторой функции:

На нашем графике видно: чем больше x, тем меньше y. Итак, давайте дадим определение убывающей функции. Функция называется убывающей, если большему значению аргумента соответствует меньшее значение функции.

Если x2 > x1, то f(x2) Теперь давайте рассмотрим график такой функции:
На этом графике видно: чем больше x, тем больше y. Итак, давайте дадим определение возрастающей функции. Функция называется возрастающей, если большему значению аргумента соответствует большее значения функции.
Если x2 > x1, то f(x2 > f(x1) или: чем больше x, тем больше y.

Если функция возрастает или убывает на некотором промежутке, то говорят, что она монотонна на данном промежутке

.

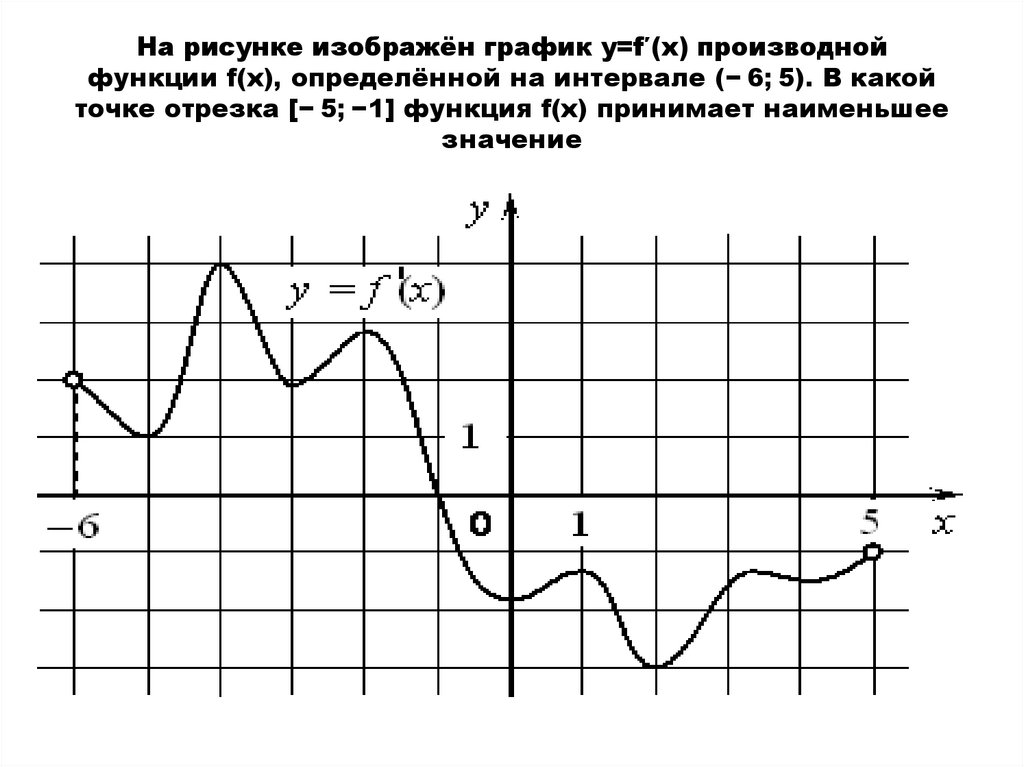
Связь производной и монотонности функции

Ребята, а теперь давайте подумаем, как можно применять понятие производной при исследовании графиков функций. Нарисуем график возрастающей дифференцируемой функции и проведем пару касательных к нашему графику.

Если посмотреть на наши касательные или зрительно провести любую другую касательную, то можно заметить, что угол между касательной и положительным направлением оси абсцисс будет острым. Значит, касательная имеет положительный угловой коэффициент. Угловой коэффициент касательной равен значению производной в абсциссе точки касания. Таким образом, значение производной положительно во всех точках нашего графика. Для возрастающей функции выполняет следующее неравенство: f'(x) ≥ 0, для любой точки x.

Ребята, теперь давайте посмотрим на график некоторой убывающей функции и построим касательные к графику функции.

Посмотрим на касательные и зрительно проведем любую другую касательную. Мы заметим, что угол между касательной и положительным направлением оси абсцисс — тупой, а значит касательная имеет отрицательный угловой коэффициент.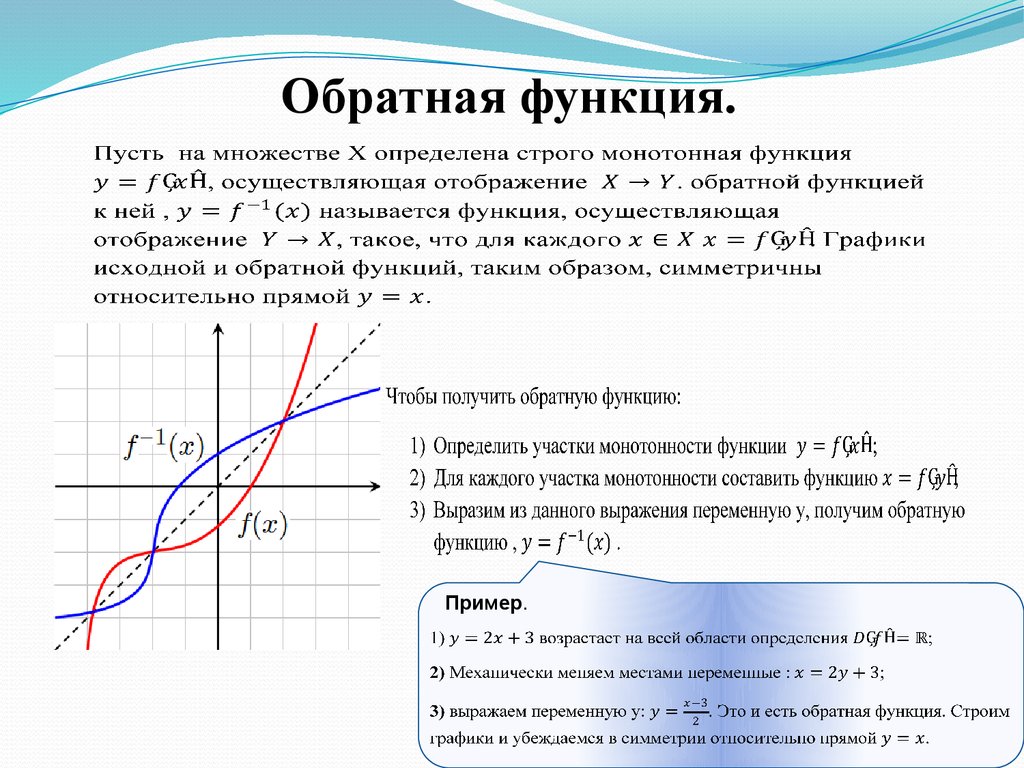

Таким образом, значение производной отрицательно во всех точках нашего графика. Для убывающей функции выполняет следующее неравенство: f'(x) ≤ 0, для любой точки x.

Итак, монотонность функции зависит от знака производной:

Если функция возрастает на промежутке и имеет производную на этом промежутке, то эта производная будет не отрицательна.

Если функция убывает на промежутке и имеет производную на этом промежутке, то эта производная будет не положительна.

Важно, чтобы промежутки, на которых мы рассматриваем функцию были открытыми!

Две важные теоремы о монотонности

Теорема 1. Если во всех точках открытого промежутка Х выполняется неравенство f’(x) ≥ 0 (причем равенство производной нулю либо не выполняется, либо выполняется, но лишь в конечном множестве точек), то функция y= f(x) возрастает на промежутке Х.

Теорема 2. Если во всех точках открытого промежутка Х выполняется неравенство f’(x) ≤ 0 (причем равенство производной нулю либо не выполняется, либо выполняется, но лишь в конечном множестве точек), то функция y= f(x) убывает на промежутке Х.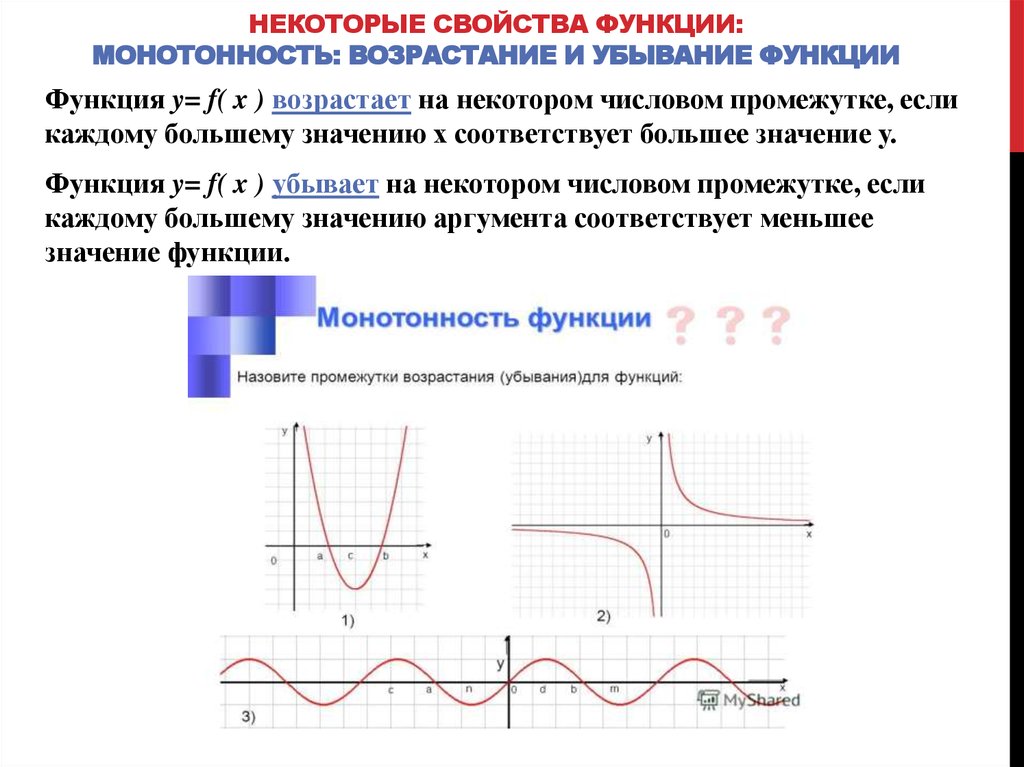

Теорема 3. Если во всех точках открытого промежутка Х выполняется равенство
f’(x)= 0, то функция y= f(x) постоянна на этом промежутке.

Примеры исследования функции на монотонность

1) Доказать, что функция y= x⁷ + 3x⁵ + 2x — 1 возрастает на всей числовой прямой.

Решение: Найдем производную нашей функции: y’= 7⁶ + 15x⁴ + 2. Т.к. степень при x четная, то степенная функция принимает только положительные значения. Тогда y’ > 0 для любого x, а значит по теореме 1, наша функция возрастает на всей числовой прямой.

2) Доказать, что функция убывает: y= sin(2x) — 3x.

Найдем производную нашей функции: y’= 2cos(2x) — 3.
Решим неравенство:
2cos(2x) — 3 ≤ 0,
2cos(2x) ≤ 3,
cos(2x) ≤ 3/2.
Т.к. -1 ≤ cos(x) ≤ 1, значит наше неравенство выполняется для любых x, тогда по теореме 2 функция y= sin(2x) — 3x убывает.

3) Исследовать на монотонность функцию: y= x² + 3x — 1.

Решение: Найдем производную нашей функции: y’= 2x + 3.
Решим неравенство:
2x + 3 ≥ 0,
x ≥ -3/2.
Тогда наша функция возрастает при x ≥ -3/2, а убывает при x ≤ -3/2.
Ответ: При x ≥ -3/2 — функция возрастает, при x ≤ -3/2 — функция убывает.

4) Исследовать на монотонность функцию: y= $\sqrt{3x — 1}$.

Решение: Найдем производную нашей функции: y’= $\frac{3}{2\sqrt{3x — 1}}$.
Решим неравенство: $\frac{3}{2\sqrt{3x — 1}}$ ≥ 0.

Наше неравенство больше либо равно нуля:
$\sqrt{3x — 1}$ ≥ 0,
3x — 1 ≥ 0,
x ≥ 1/3.
Решим неравенство:
$\frac{3}{2\sqrt{3x-1}}$ ≤ 0,

$\sqrt{3x-1}$ ≤ 0,
3x — 1 ≤ 0.
Но это невозможно, т.к. квадратный корень определен только для положительных выражений, значит промежутков убывания у нашей функции нет.
Ответ: при x ≥ 1/3 функция возрастает.

Задачи для самостоятельного решения

а) Доказать, что функция y= x⁹ + 4x³ + 1x — 10 возрастает на всей числовой прямой.
б) Доказать, что функция убывает: y= cos(5x) — 7x.
в) Исследовать на монотонность функцию: y= 2x³ + 3x² — x + 5. {3}$ возрастает на всей действительной оси.

Читать дальше: понятие экстремума функции.

Как определить, является ли функция монотонной

Определение:

Функция, которая полностью возрастает или полностью убывает на данном интервале, называется монотонной на данном интервале.

Обычно, глядя на график функции, можно сказать, является ли функция возрастающей или убывающей, или ни тем, ни другим.

График возрастающей функции не падает при движении слева направо, а график убывающей функции не растет при движении слева направо.

Но если нам не дан график, как мы можем решить, является ли данная функция монотонной или нет?

Проверка монотонных функций :

Пусть I открытый интервал. Пусть f : I → R дифференцируема. Тогда

(i) Функция f возрастает тогда и только тогда, когда f ′(x) ≥ 0 для всех x в I.

(ii) Функция f убывает тогда и только тогда, когда f ′(x) ≤ 0 для все x в I.

Примечание:

Если функция меняет знаки в разных точках области (интервала), тогда функция не является монотонной в этой области.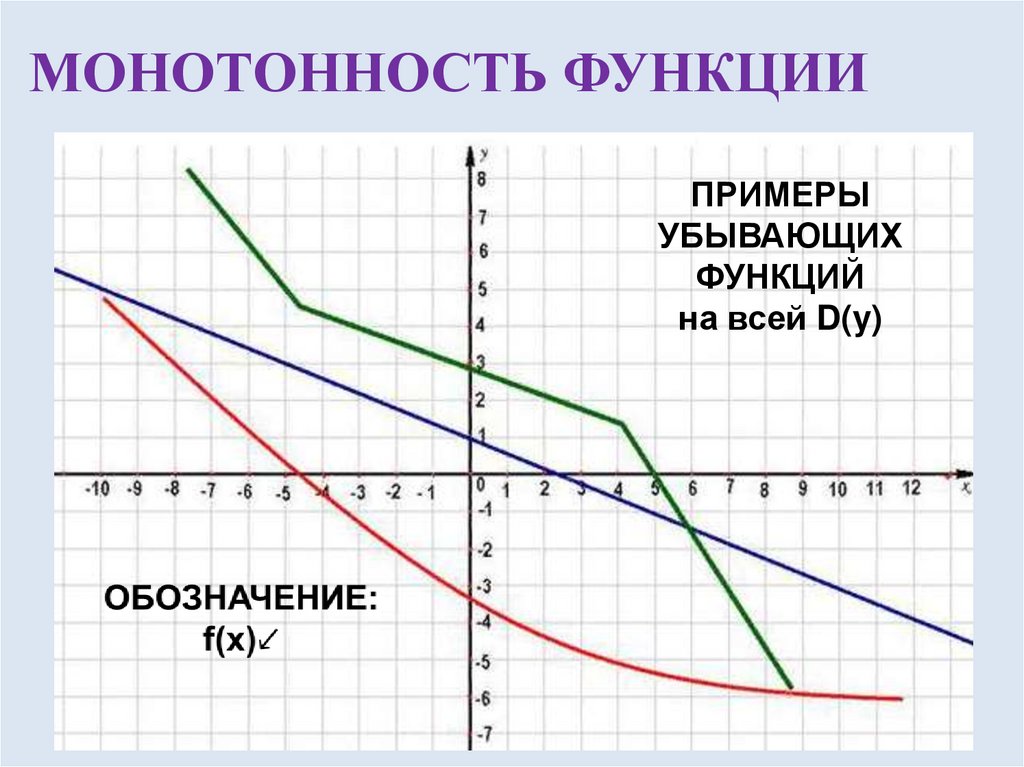 Итак, чтобы доказать немонотонность функции, достаточно доказать, что f ′ имеет разные знаки в разных точках.

Пример 1 :

Проверить, является ли функция

y = sin x + cos 2x

монотонной на интервале [0, Π/4]

Решение:

f(x)  = sin x + cos 2x

f'(x) = cos x — sin 2x [2 (1)]

f'(x) = cos x — 2 sin 2x

Применяя x = 0, мы получаем

f'(0) = cos 0 — 2 sin 2(0)

f'(0)  =  1-2 (0)

f'(0)  =  1 — 0

f'(0)  =  1 > 0 

Применяя x = Π/4, мы получаем

f'(Π/4) = cos Π/4 — 2 sin 2(Π/4)

f'(Π/4)  = 1/√2 — 2 sin (П/2)

f'(П/4)  =  1/√2 — 2 (1)

f'(П/4)  =  1/√2 — 2

f'(П/ 4) = 0,707 — 2

f'(Π/4) = -1,292 < 0

Таким образом, f’ имеет разные знаки при 0 и π/4. Итак, данная функция не является монотонной на отрезке [0, Π/4].

Пример 2:

Проверить, работает ли функция

y = x sin x

монотонно на интервале [Π/2, Π]

Решение:

f(x)  =  x sin x

f'(x)  =  x (cos x) + sin x (1)

f'(x) =   x (cos x) + sin x

Применяя x = Π/2

f'(0)  =  Π/2 (cos Π/2) + sin Π/2

f'(0) = Π/2 (0) + 1

f'(0) = 1 > 0

Применяя x = Π

f'(Π) = Π (cos Π ) + sin Π

f'(0) = Π (-1) + 0

f'(0)  =   — Π < 0

Таким образом, функция не является монотонной функцией.

Пример 3 :

Обсудите монотонность функции

(i) e ^x для всех действительных чисел.

(ii) log x на (0, ∞)

Решение:

(i) f(x) = e ^x  

Пусть f(x) = e ^{x 9 0128}

ф'( x) = e ^x

• Если x > 0, то f′(x) > 0. Функция строго возрастает для всех положительных значений x.
• Если x < 0, то f′(x) > 0. Функция строго возрастает для всех отрицательных значений x.
• Если x = 0, то f'(x) = 1, мы получаем положительное значение для f'(x).

Итак, функция монотонна на действительных числах.

(ii) f(x) = log x на (0, ∞)

Пусть f(x) = log x

f'(x) = 1/x

Если x > 0, то f'( x) > 0. Функция строго возрастает при всех положительных значениях x.

Итак, функция монотонна на (0, ∞). 9{2}-2x-1$

спросил

6 лет, 6 месяцев назад

Изменено 6 лет, 6 месяцев назад

Просмотрено 4к раз

$\begingroup$

В домашнем задании я должен показать, что эта функция монотонна или монотонна ли она вообще:

$$f(x)=x^{2}-2x-1$$

Я сделал это так, но я совсем не уверен, что это правильный способ сделать, мне нужно подтверждение или мой учитель злится, я сделал неправильно, пожалуйста:

$$f'(x)=0$$

$$f'(x)=2x-2$$

$$0=2x-2|+2$$

$$2x=2|:2$$

$$x=1$$

Поскольку $1>0$ функция монотонно возрастает?

Скажите, пожалуйста, правильно ли я не хочу, чтобы учитель меня ругал в классе, а другие снова смеялись.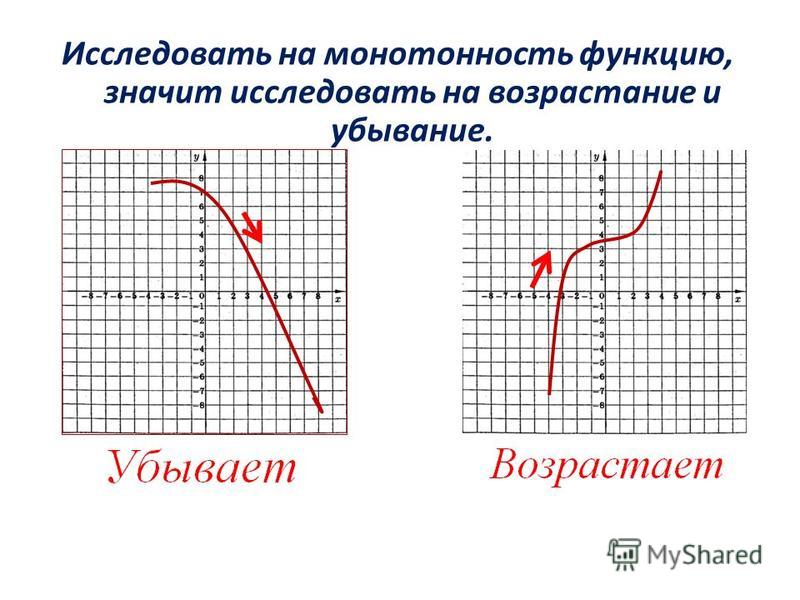 .. Мне нужен подарок завтра в классе 🙁

92-2$.

$\endgroup$

$\begingroup$

Для монотонности (по крайней мере возрастающей) нам нужна везде положительная производная. Это не вариант. Вы должны проверить, что при $x > 1$ (обратите внимание на строгое неравенство) производная положительна. При $x < 1$ производная отрицательна. Таким образом, $f$ монотонна либо на $(1, \infty)$, либо на $(-\infty, 1)$.

Вы сделали это, просто нужно немного больше. Ничего страшного, все будет хорошо.

$\endgroup$

5

$\begingroup$

Функция не монотонна в $\mathbb{R}$, это U-образная функция с точкой минимума при $x = 1$. Он монотонен в интервалах $[ — \infty, 1[$ и $]1 , +\infty]$.

Не волнуйся, твой учитель будет тобой гордиться.

No related posts.