Как раскрыть две скобки со знаком умножения между ними: Как правильно раскрывать скобки?

Раскрытие скобок при умножении и делении. Правило раскрытия скобок при произведении

сформировать способность к раскрытию скобок с учетом знака, стоящего перед скобками;

развивающие:

развивать логическое мышление, внимание, математическую речь, умение анализировать, сравнивать, обобщать, делать выводы;

воспитывающие:

формирование ответственности, познавательного интереса к предмету

Ход урока

I. Организационный момент.

Проверь-ка дружок
Ты готов на урок?
Всё ли на месте? Всё в порядке?
Ручка, книжка и тетрадка.
Все ли правильно сидят?
Все ль внимательно глядят?

Начать урок я хочу с вопроса к вам:

Как вы думаете, что самое ценное на Земле? (Ответы детей.)

Этот вопрос волновал человечество не одну тысячу лет. Вот какой ответ дал известный ученый Аль-Бируни: “Знание – самое превосходное из владений. Все стремятся к нему, само же оно не приходит”.

Пусть эти слова станут девизом нашего урока.

II. Актуализация прежних знаний, умений, навыков:

Устный счет:

1.1. Какое сегодня число?

2. Расскажите, что вы знаете о числе 20?

3. А где расположено это число на координатной прямой?

4. Назовите число ему обратное.

5. Назовите число ему противоположное.

6. Как называется число – 20?

7. Какие числа называются противоположными?

8. Какие числа называются отрицательными?

9. Чем равен модуль числа 20? – 20?

10. Чему равна сумма противоположных чисел?

2. Объясните следующие записи:

а) Гениальный математик древности Архимед родился в 0 287 г.

б) Гениальный русский математик Н.И.Лобаческий родился в 1792 г.

в) Первые олимпийские игры состоялись в Греции в – 776 г.

г) Первые Международные олимпийские игры состоялись в 1896 г.

д) XXII Олимпийские зимние игры состоялись в 2014 году.

3. Узнайте, какие числа крутятся на “математической карусели” (все действия выполняются устно).

II.

Формирование новых знаний, умений, навыков.

Вы научились выполнять разные действия с целыми числами. Чем же будем заниматься дальше? Как будем решать примеры и уравнения?

Давайте найдем значение данных выражений

7 + (3 + 4) = -7 + 7 = 0
-7 + 3 + 4 = 0

Какой порядок действий в 1 примере? Сколько получилось в скобках? Порядок действий во втором примере? Результат первого действия? Что можно сказать об этих выражениях?

Конечно результаты первого и второго выражений одинаковы, значит между ними можно поставить знак равенства: -7 + (3 + 4) = -7 + 3 + 4

Что же мы сделали со скобками? (Опустили.)

Как вы думаете чем мы будем заниматься сегодня на уроке? (Дети формулируют тему урока.) В нашем примере, какой знак стоит перед скобками. (Плюс.)

И так мы подошли к следующему правилу:

Если перед скобками стоит знак +, то можно опустить скобки и этот знак +, сохраняя знаки слагаемых, стоящих в скобках. Если первое слагаемое в скобках записано без знака, то его надо записать со знаком +.

А как быть, если перед скобками стоит знак минус?

В этом случае нужно рассуждать так же как при вычитании: необходимо прибавить число противоположное вычитаемому:

7 – (3 + 4) = -7 + (-7) = -7 + (-3) + (-4) = -7 – 3 – 4 = -14

– Итак, мы раскрыли скобки, когда перед ними стоял знак минус.

Правило раскрытия скобок, когда перед скобками стоит знак “-“.

Чтобы раскрыть скобки, перед которыми стоит знак -, надо заменить этот знак на +, поменяв знаки всех слагаемых в скобках на противоположные, а потом раскрыть скобки.

Давайте послушаем правила раскрытия скобок в стихах:

Перед скобкой плюс стоит.
Он о том и говорит
Что ты скобки опускай
Да все знаки выпускай!
Перед скобкой минус строгий

Загородит нам дорогу
Чтобы скобки убирать
Надо знаки поменять!

Да ребята знак минус очень коварный, это “ сторож” у ворот(скобки), он выпускает числа и переменные только тогда, когда они поменяют “ паспорта”, то есть свои знаки.

Зачем вообще нужно раскрывать скобки? (Когда есть скобки, есть момент какой-то элемент незавершенности, какой-то тайны. Это – как закрытая дверь, за которой находится что-то интересное.) Вот сегодня мы изведали эту тайну.

Небольшой экскурс в историю:

Фигурные скобки появляются в сочинениях Виета (1593). Широкое применение скобки получили лишь в первой половине XVIII века, благодаря Лейбницу и ещё больше Эйлеру.

Физкультминутка.

III. Закрепление новых знаний, умений, навыков.

Работа по учебнику:

№ 1234 (раскройте скобки) – устно.

№ 1236(раскройте скобки) – устно.

№ 1235 (найдите значение выражения) – письменно.

№ 1238 (упростите выражения) – работа в парах.

IV. Подведение итогов урока.

1. Объявляются оценки.

2. Дом. задание. п.39 №1254 (а, б, в),1255 (а, б, в),1259.

3. Чему мы сегодня научились?

Что нового узнали?

И завершить урок я хочу пожеланиями каждому из вас:

“К математике способность проявляй,
Не ленись, а ежедневно развивай.
Умножай, дели, трудись, соображай,
С математикой дружить не забывай”.

Раскрытие скобок является одним из видов преобразования выражения. В этом разделе мы опишем правила раскрытия скобок, а также рассмотрим наиболее часто встречающиеся примеры задач.

Yandex.RTB R-A-339285-1

Что называется раскрытием скобок?

Скобки используются для указания на порядок выполнения действий в числовых и буквенных выражениях, а также в выражениях с переменными. От выражения со скобками удобно перейти к тождественно равному выражению без скобок. Например, заменить выражение 2 · (3 + 4) на выражение вида

2 · 3 + 2 · 4 без скобок. Этот прием носит название раскрытия скобок.

Определение 1

Под раскрытием скобок подразумевают приемы избавления от скобок и рассматривают его обычно в отношении выражений, которые могут содержать:

• знаки « + » или « — » перед скобками, в которые заключены суммы или разности;
• произведение числа, буквы или нескольких букв и суммы или разности, которая помещена в скобки.

Так мы привыкли рассматривать процесс раскрытия скобок в курсе школьной программы. Однако никто не мешает нам посмотреть на это действие шире. Мы можем назвать раскрытием скобок переход от выражения, которое содержит отрицательные числа в скобках, к выражению, не имеющему скобок. К примеру, мы можем перейти от 5 + (− 3) − (− 7) к 5 − 3 + 7 . Фактически, это тоже раскрытие скобок.

Точно также мы можем заменить произведение выражений в скобках вида (a + b) · (c + d) на сумму a · c + a · d + b · c + b · d . Такой прием также не противоречит смыслу раскрытия скобок.

Вот еще один пример. Мы можем допустить, что в выражениях вместо чисел и переменных могут быть использованы любые выражения. Например, выражению x 2 · 1 a — x + sin (b) будет соответствовать выражение без скобок вида x 2 · 1 a — x 2 · x + x 2 · sin (b) .

Отдельного внимания заслуживать еще один момент, который касается особенностей записи решений при раскрытии скобок. Мы можем записать начальное выражение со скобками и полученный после раскрытия скобок результат как равенство. Например, после раскрытия скобок вместо выражения 3 − (5 − 7) мы получаем выражение

3 − 5 + 7 . Оба этих выражения мы можем записать в виде равенства 3 − (5 − 7) = 3 − 5 + 7 .

Проведение действий с громоздкими выражениями может потребовать записи промежуточных результатов. Тогда решение будет иметь вид цепочки равенств. Например, 5 − (3 − (2 − 1)) = 5 − (3 − 2 + 1) = 5 − 3 + 2 − 1 или 5 − (3 − (2 − 1)) = 5 − 3 + (2 − 1) = 5 − 3 + 2 − 1 .

Правила раскрытия скобок, примеры

Приступим к рассмотрению правил раскрытия скобок.

У одиночных чисел в скобках

Отрицательные числа в скобках часто встречаются в выражениях. Например, (− 4) и 3 + (− 4) . Положительные числа в скобках тоже имеют место быть.

Сформулируем правило раскрытия скобок, в которых заключены одиночные положительные числа. Предположим, что а – это любое положительное число. Тогда (а) мы можем заменить на а, + (а) на + а, — (а) на – а. Если вместо а взять конкретное число, то согласно правилу: число (5) запишется как 5 , выражение 3 + (5) без скобок примет вид 3 + 5 , так как + (5) заменяется на + 5 , а выражение 3 + (− 5) эквивалентно выражению

3 − 5 , так как + (− 5) заменяется на − 5 .

Положительные числа обычно записываются без использования скобок, так как скобки в этом случае излишни.

Теперь рассмотрим правило раскрытия скобок, внутри которых содержится одиночное отрицательное число. + (− a) мы заменяем на − a , − (− a) заменяется на + a . Если выражение начинается с отрицательного числа (− a) , которое записано в скобках, то скобки опускаются и вместо (− a) остается − a .

Приведем примеры: (− 5) можно записать как − 5 , (− 3) + 0 , 5 принимает вид − 3 + 0 , 5 , 4 + (− 3) превращается в 4 − 3 , а − (− 4) − (− 3) после раскрытия скобок принимает вид 4 + 3 , так как − (− 4) и − (− 3) заменяется на + 4 и + 3 .

Следует понимать, что записать выражение 3 · (− 5) как 3 · − 5 нельзя. Об этом речь пойдет в следующих пунктах.

Давайте посмотрим, на чем основываются правила раскрытия скобок.

Согласно правилу разность a − b равна a + (− b) . На основе свойств действий с числами мы можем составить цепочку равенств (a + (− b)) + b = a + ((− b) + b) = a + 0 = a , которая будет справедлива. Эта цепочка равенств в силу смысла вычитания доказывает, что выражение a + (− b) — это разность a − b .

Основываясь на свойствах противоположных чисел и правил вычитания отрицательных чисел мы можем утверждать, что − (− a) = a , a − (− b) = a + b .

Встречаются выражения, которые составляются из числа, знаков минуса и нескольких пар скобок. Использование приведенных выше правил позволяет последовательно избавляться от скобок, продвигаясь от внутренних скобок к наружным или в обратном направлении. Примером такого выражения может быть − (− ((− (5)))) . Раскроем скобки, продвигаясь изнутри наружу: − (− ((− (5)))) = − (− ((− 5))) = − (− (− 5)) = − (5) = − 5 . Также этот пример можно разобрать и в обратном направлении:

− (− ((− (5)))) = ((− (5))) = (− (5)) = − (5) = − 5 .

Под a и b можно понимать не только числа, но также произвольные числовые или буквенные выражения со знаком « + » впереди, которые не являются суммами или разностями. Во всех этих случаях можно применять правила точно также, как мы делали это в отношении одиночных чисел в скобках.

К примеру, после раскрытия скобок выражение − (− 2 · x) − (x 2) + (− 1 x) − (2 · x · y 2: z) примет вид 2 · x − x 2 − 1 x − 2 · x · y 2: z . Как мы это сделали? Мы знаем, что − (− 2 · x) есть + 2 · x , а так как это выражение стоит вначале, то + 2 · x можно записать как 2 · x , − (x 2) = − x 2 , + (− 1 x) = − 1 x и − (2 · x · y 2: z) = − 2 · x · y 2: z .

В произведениях двух чисел

Начнем с правила раскрытия скобок в произведении двух чисел.

Предположим, что a и b – это два положительных числа. В этом случае произведение двух отрицательных чисел − a и − b вида (− a) · (− b) мы можем заменить на (a · b) , а произведения двух чисел с противоположными знаками вида (− a) · b и a · (− b) заменить на (− a · b) . Умножение минуса на минус дает плюс, а умножение минуса на плюс, как и умножение плюса на минус дает минус.

Верность первой части записанного правила подтверждается правилом умножения отрицательных чисел. Для подтверждения второй части правила мы можем использовать правила умножения чисел с разными знаками.

Рассмотрим несколько примеров.

Пример 1

Рассмотрим алгоритм раскрытия скобок в произведении двух отрицательных чисел — 4 3 5 и — 2 , вида (- 2) · — 4 3 5 . Для этого заменим исходное выражение на 2 · 4 3 5 . Раскроем скобки и получим 2 · 4 3 5 .

А если мы возьмем частное отрицательных чисел (− 4) : (− 2) , то запись после раскрытия скобок будет иметь вид 4: 2

На месте отрицательных чисел − a и − b могут быть любые выражения со знаком минус впереди, которые не являются суммами или разностями. К примеру, это могут быть произведения, частные, дроби, степени, корни, логарифмы, тригонометрические функции и т.п.

Раскроем скобки в выражении — 3 · x x 2 + 1 · x · (- ln 5) . Согласно правилу, мы можем произвести следующие преобразования: — 3 · x x 2 + 1 · x · (- ln 5) = — 3 · x x 2 + 1 · x · ln 5 = 3 · x x 2 + 1 · x · ln 5 .

Выражение (− 3) · 2 можно преобразовать в выражение (− 3 · 2) . После этого можно раскрыть скобки: − 3 · 2 .

2 3 · — 4 5 = — 2 3 · 4 5 = — 2 3 · 4 5

Деление чисел с разными знаками также может потребовать предварительного раскрытия скобок: (− 5) : 2 = (− 5: 2) = − 5: 2 и 2 3 4: (- 3 , 5) = — 2 3 4: 3 , 5 = — 2 3 4: 3 , 5 .

Правило может быть использовано для выполнения умножения и деления выражений с разными знаками. Приведем два примера.

1 x + 1: x — 3 = — 1 x + 1: x — 3 = — 1 x + 1: x — 3

sin (x) · (- x 2) = (- sin (x) · x 2) = — sin (x) · x 2

В произведениях трех и большего количества чисел

Перейдем к произведенимя и частным, которые содержат большее количество чисел. Для раскрытия скобок здесь будет действовать следующее правило. При четном количестве отрицательных чисел можно опустить скобки, заменив числа противоположными. После этого необходимо заключить полученное выражение в новые скобки. При нечетном количестве отрицательных чисел, опустив скобки, заменить числа на противоположные. После этого полученное выражение необходимо взять в новые скобки и поставить перед ним знак минус.

Пример 2

Для примера, возьмем выражение 5 · (− 3) · (− 2) , которое представляет собой произведение трех чисел. Отрицательных чисел два, следовательно, мы можем записать выражение как (5 · 3 · 2) и затем окончательно раскрыть скобки, получив выражение 5 · 3 · 2 .

В произведении (− 2 , 5) · (− 3) : (− 2) · 4: (− 1 , 25) : (− 1) пять чисел являются отрицательными. поэтому (− 2 , 5) · (− 3) : (− 2) · 4: (− 1 , 25) : (− 1) = (− 2 , 5 · 3: 2 · 4: 1 , 25: 1) . Окончательно раскрыв скобки, получаем −2,5·3:2·4:1,25:1 .

Обосновать приведенное выше правило можно следующим образом. Во-первых, такие выражения мы можем переписать как произведение, заменив умножением на обратное число деление. Представляем каждое отрицательное число как произведение множительного числа и — 1 или — 1 заменяем на (− 1) · a .

Используя переместительное свойство умножения меняем местами множители и переносим все множители, равные − 1 , в начало выражения. Произведение четного числа минус единиц равно 1 , а нечетного – равно − 1 , что позволяет нам использовать знак минус.

Если бы мы не использовали правило, то цепочка действий по раскрытию скобок в выражении — 2 3: (- 2) · 4: — 6 7 выглядела бы следующим образом:

2 3: (- 2) · 4: — 6 7 = — 2 3 · — 1 2 · 4 · — 7 6 = = (- 1) · 2 3 · (- 1) · 1 2 · 4 · (- 1) · 7 6 = = (- 1) · (- 1) · (- 1) · 2 3 · 1 2 · 4 · 7 6 = (- 1) · 2 3 · 1 2 · 4 · 7 6 = = — 2 3 · 1 2 · 4 · 7 6

Приведенное выше правило может быть использовано при раскрытии скобок в выражениях, которые представляют собой произведения и частные со знаком минус, не являющихся суммами или разностями. Возьмем для примера выражение

x 2 · (- x) : (- 1 x) · x — 3: 2 .

Его можно привести к выражению без скобок x 2 · x: 1 x · x — 3: 2 .

Раскрытие скобок, перед которыми стоит знак +

Рассмотрим правило, которое можно применить для раскрытия скобок, перед которыми стоит знак плюс, а «содержимое» этих скобок не умножается и не делится на какое-либо число или выражение.

Согласно правилу скобки вместе со стоящим перед ними знаком опускаются, при этом знаки всех слагаемых в скобках сохраняются. Если перед первым слагаемым в скобках не стоит никакого знака, то нужно поставить знак плюс.

Пример 3

Для примера приведем выражение (12 − 3 , 5) − 7 . Опустив скобки, мы сохраняем знаки слагаемых в скобках и ставим перед первым слагаемым знак плюс. Запись будет иметь вид (12 − 3 , 5) − 7 = + 12 − 3 , 5 − 7 . В приведенном примере знак перед первым слагаемым ставить не обязательно, так как + 12 − 3 , 5 − 7 = 12 − 3 , 5 − 7 .

Пример 4

Рассмотрим еще один пример. Возьмем выражение x + 2 a — 3 x 2 + 1 — x 2 — 4 + 1 x и проведем с ним действия x + 2 a — 3 x 2 + 1 — x 2 — 4 + 1 x = = x + 2 a — 3 x 2 + 1 — x 2 — 4 + 1 x

Вот еще один пример раскрытия скобок:

Пример 5

2 + x 2 + 1 x — x · y · z + 2 · x — 1 + (- 1 + x — x 2) = = 2 + x 2 + 1 x — x · y · z + 2 · x — 1 — 1 + x + x 2

Как раскрываются скобки, перед которыми стоит знак минус

Рассмотрим случаи, когда перед скобками стоит знак минус, и которые не не умножаются (или делятся) на какое-либо число или выражение. Согласно правилу раскрытия скобок, перед которыми стоит знак « — », скобки со знаком « — » опускаются, при этом знаки всех слагаемых внутри скобок меняются на противоположные.

Пример 6

К примеру:

1 2 = 1 2 , — 1 x + 1 = — 1 x + 1 , — (- x 2) = x 2

Выражения с переменными могут быть преобразованы с использованием того же правила:

X + x 3 — 3 — — 2 · x 2 + 3 · x 3 · x + 1 x — 1 — x + 2 ,

получаем x — x 3 — 3 + 2 · x 2 — 3 · x 3 · x + 1 x — 1 — x + 2 .

Раскрытие скобок при умножении числа на скобку, выражения на скобку

Здесь мы рассмотрим случаи, когда нужно раскрыть скобки, которые умножаются или делятся на какое-либо число или выражение. Тут применимы формулы вида (a 1 ± a 2 ± … ± a n) · b = (a 1 · b ± a 2 · b ± … ± a n · b) или b · (a 1 ± a 2 ± … ± a n) = (b · a 1 ± b · a 2 ± … ± b · a n) , где a 1 , a 2 , … , a n и b – некоторые числа или выражения.

Пример 7

Например, проведем раскрытие скобок в выражении (3 − 7) · 2 . Согласно правилу, мы можем провести следующие преобразования: (3 − 7) · 2 = (3 · 2 − 7 · 2) . Получаем 3 · 2 − 7 · 2 .

Раскрыв скобки в выражении 3 · x 2 · 1 — x + 1 x + 2 , получаем 3 x 2 · 1 — 3 · x 2 · x + 3 · x 2 · 1 x + 2 .

Умножение скобки на скобку

Рассмотрим произведение двух скобок вида (a 1 + a 2) · (b 1 + b 2) . Это поможет нам получить правило для раскрытия скобок при проведении умножения скобки на скобку.

Для того, чтобы решить приведенный пример, обозначим выражение (b 1 + b 2) как b . Это позволит нам использовать правило умножения скобки на выражение. Получим (a 1 + a 2) · (b 1 + b 2) = (a 1 + a 2) · b = (a 1 · b + a 2 · b) = a 1 · b + a 2 · b . Выполнив обратную замену b на (b 1 + b 2) , снова применим правило умножения выражения на скобку: a 1 · b + a 2 · b = = a 1 · (b 1 + b 2) + a 2 · (b 1 + b 2) = = (a 1 · b 1 + a 1 · b 2) + (a 2 · b 1 + a 2 · b 2) = = a 1 · b 1 + a 1 · b 2 + a 2 · b 1 + a 2 · b 2

Благодаря ряду несложных приемов мы можем прийти к сумме произведений каждого из слагаемых из первой скобки на каждое из слагаемых из второй скобки. Правило можно распространить на любое количество слагаемых внутри скобок.

Сформулируем правила умножения скобки на скобку: чтобы перемножить между собой две суммы, необходимо каждое из слагаемых первой суммы перемножить на каждое из слагаемых второй суммы и сложить полученные результаты.

Формула будет иметь вид:

(a 1 + a 2 + . . . + a m) · (b 1 + b 2 + . . . + b n) = = a 1 b 1 + a 1 b 2 + . . . + a 1 b n + + a 2 b 1 + a 2 b 2 + . . . + a 2 b n + + . . . + + a m b 1 + a m b 1 + . . . a m b n

Проведем раскрытие скобок в выражении (1 + x) · (x 2 + x + 6) Оно представляет собой произведение двух сумм. Запишем решение: (1 + x) · (x 2 + x + 6) = = (1 · x 2 + 1 · x + 1 · 6 + x · x 2 + x · x + x · 6) = = 1 · x 2 + 1 · x + 1 · 6 + x · x 2 + x · x + x · 6

Отдельно стоит остановиться на тех случаях, когда в скобках присутствует знак минус наряду со знаками плюс. Для примера возьмем выражение (1 − x) · (3 · x · y − 2 · x · y 3) .

Сначала представим выражения в скобках в виде сумм: (1 + (− x)) · (3 · x · y + (− 2 · x · y 3)) .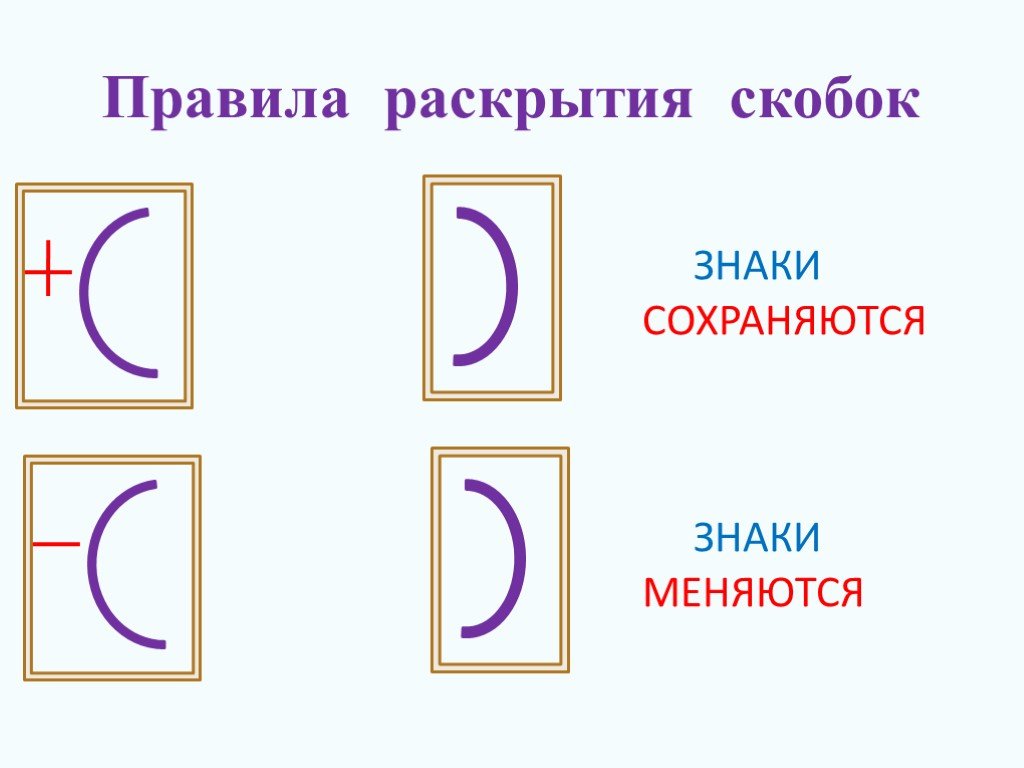 Теперь мы можем применить правило: (1 + (− x)) · (3 · x · y + (− 2 · x · y 3)) = = (1 · 3 · x · y + 1 · (− 2 · x · y 3) + (− x) · 3 · x · y + (− x) · (− 2 · x · y 3))

Раскроем скобки: 1 · 3 · x · y − 1 · 2 · x · y 3 − x · 3 · x · y + x · 2 · x · y 3 .

Раскрытие скобок в произведениях нескольких скобок и выражений

При наличии в выражении трех и более выражений в скобках, раскрывать скобки необходимо последовательно. Начать преобразование необходимо с того, что два первых множителя берут в скобки. Внутри этих скобок мы можем проводить преобразования согласно правилам, рассмотренным выше. Например, скобки в выражении (2 + 4) · 3 · (5 + 7 · 8) .

В выражении содержится сразу три множителя (2 + 4) , 3 и (5 + 7 · 8) . Будем раскрывать скобки последовательно. Заключим первые два множителя еще в одни скобки, которые для наглядности сделаем красными: (2 + 4) · 3 · (5 + 7 · 8) = ((2 + 4) · 3) · (5 + 7 · 8) .

В соответствии с правилом умножения скобки на число мы можем провести следующие действия: ((2 + 4) · 3) · (5 + 7 · 8) = (2 · 3 + 4 · 3) · (5 + 7 · 8) .

Умножаем скобку на скобку: (2 · 3 + 4 · 3) · (5 + 7 · 8) = 2 · 3 · 5 + 2 · 3 · 7 · 8 + 4 · 3 · 5 + 4 · 3 · 7 · 8 .

Скобка в натуральной степени

Степени, основаниями которых являются некоторые выражения, записанные в скобках, с натуральными показателями можно рассматривать как произведение нескольких скобок. При этом по правилам из двух предыдущих пунктов их можно записать без этих скобок.

Рассмотрим процесс преобразования выражения (a + b + c) 2 . Его можно записать в виде произведения двух скобок (a + b + c) · (a + b + c) . Произведем умножение скобки на скобку и получим a · a + a · b + a · c + b · a + b · b + b · c + c · a + c · b + c · c .

Разберем еще один пример:

Пример 8

1 x + 2 3 = 1 x + 2 · 1 x + 2 · 1 x + 2 = = 1 x · 1 x + 1 x · 2 + 2 · 1 x + 2 · 2 · 1 x + 2 = = 1 x · 1 x · 1 x + 1 x · 2 · 1 x + 2 · 1 x · 1 x + 2 · 2 · 1 x + 1 x · 1 x · 2 + + 1 x 2 · 2 + 2 · 1 x · 2 + 2 · 2 · 2

Деление скобки на число и скобки на скобку

Деление скобки на число предполагает, что необходимо разделить на число все заключенные в скобки слагаемые. Например, (x 2 — x) : 4 = x 2: 4 — x: 4 .

Деление можно предварительно заменить умножением, после чего можно воспользоваться подходящим правилом раскрытия скобок в произведении. Это же правило применимо и при делении скобки на скобку.

Например, нам необходимо раскрыть скобки в выражении (x + 2) : 2 3 . Для этого сначала заменим деление умножением на обратное число (x + 2) : 2 3 = (x + 2) · 2 3 . Умножим скобку на число (x + 2) · 2 3 = x · 2 3 + 2 · 2 3 .

Вот еще один пример деления на скобку:

Пример 9

1 x + x + 1: (x + 2) .

Заменим деление умножением: 1 x + x + 1 · 1 x + 2 .

Выполним умножение: 1 x + x + 1 · 1 x + 2 = 1 x · 1 x + 2 + x · 1 x + 2 + 1 · 1 x + 2 .

Порядок раскрытия скобок

Теперь рассмотрим порядок применения правил, разобранных выше в выражениях общего вида, т.е. в выражениях, которые содержат суммы с разностями, произведения с частными, скобки в натуральной степени.

Порядок выполнения действий:

• первым делом необходимо выполнить возведение скобок в натуральную степень;
• на втором этапе производится раскрытие скобок в произведениях и частных;
• заключительным шагом будет раскрытие скобок в суммах и разностях.

Рассмотрим порядок выполнения действий на примере выражения (− 5) + 3 · (− 2) : (− 4) − 6 · (− 7) . Намнем преобразование с выражений 3 · (− 2) : (− 4) и 6 · (− 7) , которые должны принять вид (3 · 2: 4) и (− 6 · 7) . При подстановке полученных результатов в исходное выражение получаем: (− 5) + 3 · (− 2) : (− 4) − 6 · (− 7) = (− 5) + (3 · 2: 4) − (− 6 · 7) . Раскрываем скобки: − 5 + 3 · 2: 4 + 6 · 7 .

Имея дело с выражениями, которые содержат скобки в скобках, удобно проводить преобразования, продвигаясь изнутри наружу.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Основная функция скобок – менять порядок действий при вычислениях значений . Например , в числовом выражении \(5·3+7\) сначала будет вычисляться умножение, а потом сложение: \(5·3+7 =15+7=22\). А вот в выражении \(5·(3+7)\) сначала будет вычислено сложение в скобке, и лишь потом умножение: \(5·(3+7)=5·10=50\).

Пример. Раскройте скобку: \(-(4m+3)\).
Решение : \(-(4m+3)=-4m-3\).

Пример. Раскройте скобку и приведите подобные слагаемые \(5-(3x+2)+(2+3x)\).
Решение : \(5-(3x+2)+(2+3x)=5-3x-2+2+3x=5\).

Пример. Раскройте скобки \(5(3-x)\).
Решение : В скобке у нас стоят \(3\) и \(-x\), а перед скобкой — пятерка. Значит, каждый член скобки умножается на \(5\) — напоминаю, что знак умножения между числом и скобкой в математике не пишут для сокращения размеров записей .

Пример. Раскройте скобки \(-2(-3x+5)\).
Решение : Как и в предыдущем примере, стоящие в скобке \(-3x\) и \(5\) умножаются на \(-2\).

Пример. Упростить выражение: \(5(x+y)-2(x-y)\).
Решение : \(5(x+y)-2(x-y)=5x+5y-2x+2y=3x+7y\).

Осталось рассмотреть последнюю ситуацию.

При умножении скобки на скобку, каждый член первой скобки перемножается с каждым членом второй:

\((c+d)(a-b)=c·(a-b)+d·(a-b)=ca-cb+da-db\)

Пример. Раскройте скобки \((2-x)(3x-1)\).
Решение : У нас произведение скобок и его можно раскрыть сразу по формуле выше. Но чтобы не путаться, давайте сделаем всё по шагам.
Шаг 1. Убираем первую скобку — каждый ее член умножаем на скобку вторую:

Шаг 2. Раскрываем произведения скобки на множитель как описано выше:
— сначала первое…

Потом второе.

Шаг 3. Теперь перемножаем и приводим подобные слагаемые:

Так подробно расписывать все преобразования совсем необязательно, можно сразу перемножать. Но если вы только учитесь раскрывать скобок – пишите подробно, меньше будет шанс ошибиться.

Примечание ко всему разделу. На самом деле, вам нет необходимости запоминать все четыре правила, достаточно помнить только одно, вот это: \(c(a-b)=ca-cb\) . Почему? Потому что если в него вместо c подставить единицу, получиться правило \((a-b)=a-b\) . А если подставить минус единицу, получим правило \(-(a-b)=-a+b\) . Ну, а если вместо c подставить другую скобку – можно получить последнее правило.

Скобка в скобке

Иногда в практике встречаются задачи со скобками, вложенными внутрь других скобок. Вот пример такого задания: упростить выражение \(7x+2(5-(3x+y))\).

Чтобы успешно решать подобные задания, нужно:
— внимательно разобраться во вложенности скобок – какая в какой находиться;
— раскрывать скобки последовательно, начиная, например, с самой внутренней.

При этом важно при раскрытии одной из скобок не трогать все остальное выражение , просто переписывая его как есть.
Давайте для примера разберем написанное выше задание.

Пример. Раскройте скобки и приведите подобные слагаемые \(7x+2(5-(3x+y))\).
Решение:

Пример. Раскройте скобки и приведите подобные слагаемые \(-(x+3(2x-1+(x-5)))\).
Решение :

\(-(x+3(2x-1\)\(+(x-5)\) \())\)		Здесь тройная вложенность скобок. Начинаем с самой внутренней (выделено зеленым). Перед скобкой плюс, так что она просто снимается.
\(-(x+3(2x-1\)\(+x-5\) \())\)		Теперь нужно раскрыть вторую скобку, промежуточную. Но мы перед этим упростим выражение привидением подобный слагаемых в этой второй скобке.
\(=-(x\)\(+3(3x-6)\) \()=\)		Вот сейчас раскрываем вторую скобку (выделено голубым). Перед скобкой множитель – так что каждый член в скобке умножается на него.
\(=-(x\)\(+9x-18\) \()=\)
		И раскрываем последнюю скобку. Перед скобкой минус – поэтому все знаки меняются на противоположные.

Раскрытие скобок — это базовое умение в математике. Без этого умения невозможно иметь оценку выше тройки в 8 и 9 классе. Поэтому рекомендую хорошо разобраться в этой теме.

Правило раскрытия скобок при делении.

Решение простых линейных уравнений

В данной статье мы подробно рассмотрим основные правила такой важной темы курса математики, как раскрытие скобок. Знать правила раскрытия скобок нужно для того, чтобы верно решать уравнения, в которых они используются.

Как правильно раскрывать скобки при сложении

Раскрываем скобки, перед которыми стоит знак « + »

Эта самый простой случай, ибо если перед скобками стоит знак сложения, при раскрытии скобок знаки внутри них не меняются. Пример:

(9 + 3) + (1 — 6 + 9) = 9 + 3 + 1 — 6 + 9 = 16.

Как раскрыть скобки, перед которыми стоит знак « — »

В данном случае нужно переписать все слагаемые без скобок, но при этом сменить все знаки внутри них на противоположные. Знаки меняются только у слагаемых из тех скобок, перед которыми стоял знак « — ». Пример:

(9 + 3) — (1 — 6 + 9) = 9 + 3 — 1 + 6 — 9 = 8.

Как раскрыть скобки при умножении

Перед скобками стоит число-множитель

В данном случае нужно умножить каждое слагаемое на множитель и раскрыть скобки, не меняя знаков. 2) * 12 = 1728.

Как раскрыть 3 скобки

Бывают уравнения, в которых перемножаются сразу 3 скобки. В таком случае нужно сначала перемножить между собой слагаемые первых двух скобок, и затем сумму этого перемножения умножить на слагаемые третьей скобки. Пример:

(1 + 2) * (3 + 4) * (5 — 6) = (3 + 4 + 6 + 8) * (5 — 6) = — 21.

Данные правила раскрытия скобок одинаково распространяются для решения как линейных, так и тригонометрических уравнений.

Скобки используются для указания на порядок выполнения действий в числовых и буквенных выражениях, а также в выражениях с переменными. От выражения со скобками удобно перейти к тождественно равному выражению без скобок. Этот прием носит название раскрытия скобок.

Раскрыть скобки означает избавить выражение от этих скобок.

Отдельного внимания заслуживает еще один момент, который касается особенностей записи решений при раскрытии скобок. Мы можем записать начальное выражение со скобками и полученный после раскрытия скобок результат как равенство. Например, после раскрытия скобок вместо выражения
3−(5−7) мы получаем выражение 3−5+7. Оба этих выражения мы можем записать в виде равенства 3−(5−7)=3−5+7.

И еще один важный момент. В математике для сокращения записей принято не писать знак плюс, если он стоит в выражении или в скобках первым. Например, если мы складываем два положительных числа, к примеру, семь и три, то пишем не +7+3, а просто 7+3, несмотря на то, что семерка тоже положительное число. Аналогично если вы видите, например, выражение (5+x) – знайте, что и перед скобкой стоит плюс, который не пишут, и перед пятеркой стоит плюс +(+5+x).

Правило раскрытия скобок при сложении

При раскрытии скобок, если перед скобками стоит плюс, то этот плюс опускается вместе со скобками.

Пример. Раскрыть скобки в выражении 2 + (7 + 3) Перед скобками плюс, значит знаки перед числами в скобках не меняем.

2 + (7 + 3) = 2 + 7 + 3

Правило раскрытия скобок при вычитании

Если перед скобками стоит минус, то этот минус опускается вместе со скобками, но слагаемые, которые были в скобках, меняют свой знак на противоположный. Отсутствие знака перед первым слагаемым в скобках подразумевает знак +.

Пример. Раскрыть скобки в выражении 2 − (7 + 3)

Перед скобками стоит минус, значит нужно поменять знаки перед числами из скобок. В скобках перед цифрой 7 знака нет, это значит, что семерка положительная, считается, что перед ней знак +.

2 − (7 + 3) = 2 − (+ 7 + 3)

При раскрытии скобок убираем из примера минус, который был перед скобками, и сами скобки 2 − (+ 7 + 3) , а знаки, которые были в скобках, меняем на противоположные.

2 − (+ 7 + 3) = 2 − 7 − 3

Раскрытие скобок при умножении

Если перед скобками стоит знак умножения, то каждое число, стоящее внутри скобок, умножается на множитель, стоящий перед скобками. При этом умножение минуса на минус дает плюс, а умножение минуса на плюс, как и умножение плюса на минус дает минус.

Таким образом, сскобки в произведениях раскрываются в соответствии с распределительным свойством умножения.

Пример. 2 · (9 — 7) = 2 · 9 — 2 · 7

При умножении скобки на скобку, каждый член первой скобки перемножается с каждым членом второй скобки.

(2 + 3) · (4 + 5) = 2 · 4 + 2 · 5 + 3 · 4 + 3 · 5

На самом деле, нет необходимости запоминать все правила, достаточно помнить только одно, вот это: c(a−b)=ca−cb. Почему? Потому что если в него вместо c подставить единицу, получится правило (a−b)=a−b. А если подставить минус единицу, получим правило −(a−b)=−a+b. Ну, а если вместо c подставить другую скобку – можно получить последнее правило.

Раскрываем скобки при делении

Если после скобок стоит знак деления, то каждое число, стоящее внутри скобок, делится на делитель, стоящий после скобок, и наоборот.

Пример. (9 + 6) : 3=9: 3 + 6: 3

Как раскрыть вложенные скобки

Если в выражении присутствуют вложенные скобки, то их раскрывают по порядку, начиная с внешних или внутренних.

При этом важно при раскрытии одной из скобок не трогать остальные скобки, просто переписывая их как есть. 3 \)

Произведение одночлена и многочлена тождественно равно сумме произведений этого одночлена и каждого из членов многочлена.

Этот результат обычно формулируют в виде правила.

Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый из членов многочлена.

Мы уже неоднократно использовали это правило для умножения на сумму.

Произведение многочленов. Преобразование (упрощение) произведения двух многочленов

Вообще, произведение двух многочленов тождественно равно сумме произведении каждого члена одного многочлена и каждого члена другого.

Обычно пользуются следующим правилом.

Чтобы умножить многочлен на многочлен, надо каждый член одного многочлена умножить на каждый член другого и сложить полученные произведения.

Формулы сокращенного умножения. Квадраты суммы, разности и разность квадратов

С некоторыми выражениями в алгебраических преобразованиях приходится иметь дело чаще, чем с другими. Пожалуй, наиболее часто встречаются выражения \((a + b)^2, \; (a — b)^2 \) и \(a^2 — b^2 \), т. 2 = (a — b)(a + b) \) — разность квадратов равна произведению разности на сумму.

Эти три тождества позволяют в преобразованиях заменять свои левые части правыми и обратно — правые части левыми. Самое трудное при этом — увидеть соответствующие выражения и понять, чем в них заменены переменные а и b. Рассмотрим несколько примеров использования формул сокращенного умножения.

На этом уроке вы узнаете, как из выражения, содержащего скобки, путем преобразования получить выражение, в котором скобок нет. Вы научитесь раскрывать скобки, перед которыми стоит знак плюс и знак минус. Мы вспомним, как раскрывать скобки, используя распределительный закон умножения. Рассмотренные примеры позволят связать новый и ранее изученный материал в единое целое.

Тема: Решение уравнений

Урок: Раскрытие скобок

Как раскрыть скобки, перед которыми стоит знак «+». Использование сочетательного закона сложения.

Если к числу нужно прибавить сумму двух чисел, то можно к этому числу прибавить сначала первое слагаемое, а затем второе.

Слева от знака равно выражение со скобками, а справа — выражение без скобок. Значит, при переходе от левой части равенства к правой произошло раскрытие скобок.

Рассмотрим примеры.

Пример 1.

Раскрыв скобки, мы изменили порядок действий. Считать стало удобнее.

Пример 2.

Пример 3.

Заметим, что во всех трех примерах мы просто убирали скобки. Сформулируем правило:

Замечание.

Если первое слагаемое в скобках стоит без знака, то его надо записать со знаком «плюс».

Можно выполнить пример по действиям. Сначала к 889 прибавить 445. Это действие в уме выполнить можно, но это не очень просто. Раскроем скобки и увидим, что изменённый порядок действий значительно упростит вычисления.

Если следовать указанному порядку действий, то нужно сначала из 512 вычесть 345, а затем к результату прибавить 1345. Раскрыв скобки, мы изменим порядок действий и значительно упростим вычисления.

Иллюстрирующий пример и правило.

Рассмотрим пример: . Найти значение выражения можно, сложив 2 и 5, а затем взять полученное число с противоположным знаком. Получим -7.

С другой стороны, тот же самый результат можно получить, сложив числа, противоположные исходным.

Сформулируем правило:

Пример 1.

Пример 2.

Правило не изменяется, если в скобках не два, а три или более слагаемых.

Пример 3.

Замечание. Знаки меняются на противоположные только перед слагаемыми.

Для того чтобы раскрыть скобки, в данном случае нужно вспомнить распределительное свойство.

Сначала умножим первую скобку на 2, а вторую — на 3.

Перед первой скобкой стоит знак «+», значит, знаки нужно оставить без изменения. Перед второй стоит знак «-», следовательно, все знаки нужно поменять на противоположные

Список литературы

1. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М.: Мнемозина, 2012.
2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. — Гимназия, 2006.
3. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — Просвещение, 1989.
4. Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5-6 класс — ЗШ МИФИ, 2011.
5. Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Пособие для учащихся 6-х классов заочной школы МИФИ. — ЗШ МИФИ, 2011.
6. Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5-6 классов средней школы. Библиотека учителя математики. — Просвещение, 1989.

1. Онлайн тесты по математике ().
2. Можно скачать указанные в п. 1.2. книги ().

Домашнее задание

1. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М.: Мнемозина, 2012. (ссылка см. 1.2)
2. Домашнее задание: № 1254, № 1255, № 1256 (б,г)
3. Другие задания: № 1258(в), № 1248

«Раскрытие скобок» — Учебник по математике 6 класс (Виленкин)

Краткое описание:

В этом разделе Вы будете учиться раскрывать скобки в примерах. Для чего это нужно? Все для того же, что и раньше – чтобы Вам было легшее и проще считать, чтобы допускать меньше ошибок, а в идеале (мечта Вашего учителя математики) для того, чтобы вообще все решать без ошибок.
Вы уже знаете, что скобки в математической записи ставятся, если подряд идут два математических знака, если мы хотим показать объединение чисел, их перегруппировку. Раскрыть скобки означает избавиться от лишних знаков. Например: (-15)+3=-15+3=-12, 18+(-16)=18-16=2. А помните распределительное свойство умножения относительно сложения? Ведь в том примере мы также избавлялись от скобок для упрощения вычислений. Названное свойство умножения также можно применять для четырех, трех, пяти и более слагаемых. Для примера: 15*(3+8+9+6)=15*3+15*8+15*9+15*6=390. Вы заметили, что при раскрытии скобок числа, находящиеся в них не меняют знака, если стоящее перед скобками число положительное? Ведь пятнадцать – положительное число. А если решить такой пример: -15*(3+8+9+6)=-15*3+(-15)*8+(-15)*9+(-15)*6=-45+(-120)+(-135)+(-90)=-45-120-135-90=-390. У нас перед скобками стояло отрицательное число минус пятнадцать, когда мы раскрыли скобки все числа стали менять свой знак на другой — противоположный – с плюса на минус.
Исходя из вышеуказанных примеров, можно озвучить два основных правила раскрытия скобок:
1. Если у Вас перед скобками стоит положительное число, то после раскрытия скобок все знаки чисел, стоявших в скобках, не изменяются, а остаются точно такими же как и были.
2. Если у Вас перед скобками стоит отрицательное число, то после раскрытия скобок знак минуса больше не пишется, а знаки всех абсолютно чисел, стоявших в скобках, резко меняются на противоположные.
Для примера: (13+8)+(9-8)=13+8+9-8=22; (13+8)-(9-8)=13+8-9+8=20. Немного усложним наши примеры: (13+8)+2(9-8)=13+8+2*9-2*8=21+18-16=23. Вы заметили, что раскрывая вторые скобки, мы умножали на 2, но знаки оставались теми же как и были. А вот такой пример: (3+8)-2*(9-8)=3+8-2*9+2*8=11-18+16=9, в этом примере число два — отрицательное, оно перед скобками стоит со знаком минус, поэтому раскрывая их, мы меняли знаки чисел на противоположные (девять было с плюсом, стало с минусом, восемь было с минусом, стало с плюсом).

открытых учебников | Siyavula

Загрузите наши открытые учебники в различных форматах, чтобы использовать их так, как вам удобно. Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.

Математика

• • Читать онлайн

  • Учебники

    • Английский

      • • 7A PDF (CC-BY-ND)
        • 7B PDF (CC-BY-ND)

    • Африкаанс

      • • 7A PDF (CC-BY-ND)
        • 7B PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • 8A PDF (CC-BY-ND)
        • 8B PDF (CC-BY-ND)

    • Африкаанс

      • • 8A PDF (CC-BY-ND)
        • 8B PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • 9A PDF (CC-BY-ND)
        • 9B PDF (CC-BY-ND)

    • Африкаанс

      • • 9A PDF (CC-BY-ND)
        • 9B PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

  • Пособия для учителей

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

  • Пособия для учителей

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

  • Пособия для учителей

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

  • Пособия для учителей

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)

Наука

• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)

  • Пособия для учителей

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

  • Пособия для учителей

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

  • Пособия для учителей

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

  • Пособия для учителей

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

  • Пособия для учителей

    • Английский

      • Класс 7А

        • PDF (CC-BY-ND)

      • Класс 7Б

        • PDF (CC-BY-ND)

    • Африкаанс

      • Граад 7А

        • PDF (CC-BY-ND)

      • Граад 7Б

        • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

  • Пособия для учителей

    • Английский

      • Класс 8А

        • PDF (CC-BY-ND)

      • Класс 8Б

        • PDF (CC-BY-ND)

    • Африкаанс

      • Граад 8А

        • PDF (CC-BY-ND)

      • Граад 8Б

        • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

  • Пособия для учителей

    • Английский

      • Класс 9А

        • PDF (CC-BY-ND)

      • Класс 9Б

        • PDF (CC-BY-ND)

    • Африкаанс

      • Граад 9А

        • PDF (CC-BY-ND)

      • Граад 9Б

        • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

  • Пособия для учителей

    • Английский

      • Класс 4А

        • PDF (CC-BY-ND)

      • Класс 4Б

        • PDF (CC-BY-ND)

    • Африкаанс

      • Граад 4А

        • PDF (CC-BY-ND)

      • Граад 4Б

        • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

  • Пособия для учителей

    • Английский

      • Класс 5А

        • PDF (CC-BY-ND)

      • Класс 5Б

        • PDF (CC-BY-ND)

    • Африкаанс

      • Граад 5А

        • PDF (CC-BY-ND)

      • Граад 5Б

        • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

  • Пособия для учителей

    • Английский

      • Класс 6А

        • PDF (CC-BY-ND)

      • Класс 6Б

        • PDF (CC-BY-ND)

    • Африкаанс

      • Граад 6А

        • PDF (CC-BY-ND)

      • Граад 6Б

        • PDF (CC-BY-ND)

Лицензирование наших книг

Эти книги не только бесплатны, но и имеют открытую лицензию! Один и тот же контент, но разные версии (фирменные или нет) имеют разные лицензии, как объяснено:

CC-BY-ND (фирменные версии)

Вам разрешается и поощряется свободное копирование этих версий. Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported.

Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.

CC-BY (версии без торговой марки)

Эти версии одного и того же контента без торговой марки доступны для вас, чтобы вы могли делиться ими, адаптировать, преобразовывать, изменять или развивать их любым способом, при этом единственным требованием является предоставление соответствующей ссылки на Siyavula. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.

Расширение и упрощение — GCSE Math

Здесь мы научимся расширять и упрощать алгебраические выражения. Сначала раскрываем скобки, потом собираем однотипные члены для упрощения выражения.

В конце вы найдете рабочие листы с расширяющимися скобками, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.

Что означает «расширить и упростить»?

Чтобы расширить и упростить выражение, нам нужно умножить скобки, а затем упростить полученное выражение, собрав одинаковые члены.

Раскрытие скобок (или умножение) — это процесс удаления скобок.

Это обратный процесс факторизации. Чтобы раскрыть скобки, мы умножаем все, что за скобками, на все, что внутри скобок.

Раскрыв скобки, мы можем упростить выражение, собрав одинаковые члены.

Если мы расширим и упростим

\[2(x + 5) + 3(x − 2)\]

получим

\[2(x + 5) + 3(x − 2) = 2x + 10 + 3x − 6\]

Расширьте и упростите рабочие листы

Загрузите бесплатно расширьте и упростите рабочие листы с более чем 20 рассуждениями и прикладными вопросами, ответами и схемой оценок.

СКАЧАТЬ БЕСПЛАТНО

Икс

Расширение и упрощение рабочих листов

Загрузите бесплатно расширение и упрощение рабочих листов с более чем 20 рассуждениями и прикладными вопросами, ответами и схемой оценок.

СКАЧАТЬ БЕСПЛАТНО

Умножение скобок и упрощение Это означает ровно то же самое. «Раскрыть скобки» — это то же самое, что «умножить скобки», это просто дает дополнительную подсказку, что, когда мы раскрываем скобки, мы умножаем все, что находится за скобками, на все, что внутри скобок.

Как раскрыть и упростить скобки

Чтобы раскрыть и упростить скобки:

1. Раскрыть каждую скобку в выражении.
2. Соберите одинаковые термины.

Существует три способа расширения и упрощения скобок, как показано ниже:

• одиночные скобки
• две или более скобки
• кромки

1. Расширение и упрощение с помощью одиночных скобок .

Раскройте скобки, чтобы получить следующее выражение:

 Напр. 2 (х + 5) + 3 (х - 1)
= 2х + 10 + 3х - 3)
= 5x + 7 

Помните: выражения с двумя членами, такими как 5x + 7, называются биномами.

2 Расширьте и упростите с помощью двух или более кронштейнов .

Раскройте скобки, чтобы получить следующее выражение:

 Напр. (х + 5) (х - 1)
= х  2  + 5х - х - 5
= x  2  + 4x - 5 

Помните: выражения с тремя членами, такими как x ² + 4x — 5, известны как трехчлены.

Выражение, содержащее более двух членов и включающее переменные и коэффициенты, называется полиномом.

3 Расширьте и упростите с помощью сурдов .

 Напр. (3 + √5)(2 + √5)
= 6 + 3√5 + 2√5 + √5√5
= 11 + 5√5 

Чтобы раскрыть одну скобку, мы умножаем член вне скобки на все, что внутри скобки. Мы можем упростить выражение, собрав подобные члены.

Пример 1: константы вне скобок

Expand and simplify:

 2(x + 5) + 3(x − 2) 

1. Expand each bracket in the expression

Multiply the first bracket:

✕	x	+ 5
2	2x	+ 10

Multiply the second bracket – remember we are multiplying both x and − 2 by + 3:

✕	x	− 2
+ 3	+ 3x	− 6

Не забудьте включить знак – перед номером.

 2(х + 5) + 3(х - 2)
 = 2x + 10 + 3x − 6 

2 Соберите одинаковые члены

Выделите два члена x (2x и + 3x) и две константы (+ 10 и − 6).

Не забудьте также выделить знак перед номером!

 2x + 10 + 3x − 6 

 2x + 3x = 5x 

 10 − 6 = + 4 

 = 5x + 4 

Пример 2: константы и переменные вне скобок

Расширьте и упростите:

 2x(x + 6) - 3(x - 2) 

Раскройте каждую скобку в выражении.

Multiply the first bracket:

✕	x	+ 6
2x	2x 2	+ 12x

Multiply the second bracket – remember we are multiplying both х и — 2 на — 3:

✕	x	− 2
− 3	− 3x	+ 6

− ✕ − = + so − 3 ✕ − 2 gives a positive answer. Нам нужно написать + 6.

 2x(x + 6) − 3(x − 2)
= 2x  2  + 12x - 3x + 6 

Соберите подобные члены.

Единственные «подобные члены», которые у нас есть, — это два x-члена (+12x и -3x). Выделите их обоих.

 12x  2  + 12x - 3x + 6
12х - 3х = 9Икс
= 12x  2  + 9x + 6 

Пример 3: переменные в обоих членах в скобках

Развернуть и упростить:

 3(2x − 6y) − 5(x − 2y) 

Раскрыть каждую скобку в выражении .

Multiply the first bracket:

✕	2x	− 6y
3	6x	− 18y

+ ✕ − = − so 3 ✕ − 6y gives a отрицательный ответ. Нам нужно написать − 18y.

Multiply the second bracket, remember we are multiplying both x and − 2y by − 5:

✕	x	− 2y
− 5	− 5x	+ 10y

— ✕ — = + поэтому — 5 ✕ — 2y дает положительный ответ. Нам нужно написать + 10y.

 3(2х - 6у) - 5(х - 2у)
= 6x - 18y - 5x + 10y 

Соберите подобные члены.

Выделите два члена x (6x и − 5x) и два члена y (− 18y и + 10y).

Не забудьте также выделить знак перед номером!

 6x - 18 лет - 5x + 10 лет
6х - 5х = 1х = х
− 18 лет + 10 лет = − 8 лет
= х - 8 лет 

3(х+7)-2(х+3)

 

Раскройте каждую скобку

 

3х+21-2х-6

 

Собрать похожие термины

 

х+15

13 лет-30

13 лет-50

9{2}-22x

14x-20 лет

14x+20 лет

5(6х-2у)-2(8х-5у)

 

Раскройте каждую скобку

 

30х-10у-16х+10у

 

Собрать похожие термины

 

14x

2) Расширить и упростить с помощью двух или более скобок

Чтобы расширить две или более скобок, мы умножаем каждое слагаемое в первой скобке на каждое слагаемое в каждой из остальных скобок.

Раскрыть и упростить примеры (с двумя или более скобками)

Пример 1: переменные имеют коэффициент 1

Раскрыть и упростить:

 (x + 5)(x − 1) 

1. Раскрыть скобки в выражении.

✕	x	− 1
x	x 2	− x
+ 5	+ 5x	− 5

 х ✕ х = х  2 
х ✕ - 1 = - х 

+ ✕ — = — поэтому ответ отрицательный.

 х ✕ 5 = 5х
5 ✕ - 1 = - 5 

+ ✕ — = — поэтому ответ отрицательный.

 (x + 5)(x − 1) = x  2  − x + 5x − 5 

2 Соберите подобные члены.

Единственными похожими терминами, которые у нас есть, являются два термина x (− x и + 5x). Выделите их обоих.

 х  2  - х + 5х - 5
= x  2  + 4x − 5 

Пример 2: переменные имеют коэффициент больше 1

Расширить и упростить:

 (2x − 4)(x + 5) 

Раскрыть скобки в выражении.

✕	x	+ 5
2x	2x 2	+ 10x
− 4	− 4x	− 20

 2x ✕ x = 2x  2 
2x ✕ 5 = 10x
x ✕ - 4 = - 4x 

+ ✕ — = — поэтому ответ отрицательный.

 5 ✕ - 4 = - 20 

+ ✕ — = — поэтому ответ отрицательный.

 (2х - 4)(х + 5)
= 2x  2  + 10x - 4x - 20 

Соберите подобные члены.

Единственными подобными членами, которые у нас есть, являются два члена x (+ 10x и − 4x). Выделите их обоих.

 2x  2  + 10x - 4x - 20
= 2x  2  + 6x − 20 

Пример 3: с тройными скобками

Развернуть и упростить:

 (x + 3)  2  (x − 1) 

Развернуть и упростить первые две скобки в выражении .

 (x + 3)  2   = (x + 3)(x + 3) 

✕	x	+ 3
x	x 2	+ 3x
+ 3	+ 3x	+ 9

 х ✕ х = х  2 
х ✕ 3 = 3x
х ✕ 3 = 3x
3 ✕ 3 = 9
х  2  + 3х + 3х + 9
= x  2  + 6x + 9 

Умножьте это новое выражение на третью скобку, а затем упростите, собрав одинаковые члены.

✕	x 2	+ 6x	+ 9
x	x 3	+ 6x 2	+ 9x
− 1	− x 2	− 6x	− 9

 x ✕ x  2  = x  3 
х ✕ 6х = 6х  2 
х ✕ 9 = 9х
− 1 ✕ х  2  = − х  2 
− 1 ✕ 6x = − 6x
− 1 ✕ 9 = − 9
х  3 9{2}+6x-1
                                         

  
 3) Расширьте и упростите с помощью surds 
 
 Чтобы раскрыть скобки, нам нужно умножить каждый термин на каждый другой термин. 
 
 
 Расширить и упростить примеры (с сурдами) 
 
 
 Пример 1: с константами и сурдами 
  
 Раскрыть и упростить: 
 
 (3 + √5)(2 + √5) 
 Раскрыть скобки в выражении .
 ✕
 2
 + √5
 3
 6
 + 3√5
 + √5
 + 2√5
 + 5
 3 ✕ 2 = 6
3 ✕ √5 = 3√5
2 ✕ √5 = 2√5
√5 ✕ √5 = 5
= 6 + 3√5 + 2√5 + 5 
 2Соберите одинаковые члены.
 Выделите два постоянных члена (6 и 25) и выделите два поверхностных члена (3√5 и 2√5).
 6 + 3√5 + 2√5 + 25
= 11 + 5√5 
 Пример 2: со всеми терминами в виде сурдов 
 Расширьте и упростите:
 (√2 + √5)  2  − (3 + √5)  2  
 Раскройте скобки в выражении.
 Expand and simplify:
 (√2 + √5)  2   = (√2 + √5)(√2 + √5) 
 ✕
 √2
 + √5
 √2
 2
 + √10
 + √5
 + √10
 + 5
 2 + √10 + √10 + 5
= 7 + 2√10 
 Развернуть и упростить:
 (3 + √5)  2   = (3 + √5)(3 + √5) 
 ✕
 3
 + √5
 3
 9
 + 3 √5
 + √5
 + 3√5
 + 5
 9 + 3√5 + 3√5 + 5
= 14 + 6√5 
 Соберите подобные члены.
 Теперь мы вычтем два ответа.
 Помните, что поскольку мы убираем все (14 + 6√5), нам нужно использовать скобки.
 = 7 + 2√10 − (14 + 6√5) 
 = 7 + 2√10 − 14 − 6√5 
 = − 7 + 2√10 − 6√5
 Практика расширения и упрощения вопросов ( 
 32+5\sqrt{6}
 12+5\sqrt{6}
 12+6\sqrt{6}
 7\sqrt{6}
 (2+\sqrt{6) })(3+\sqrt{6})\\ 
 =6+2\sqrt{6}+3\sqrt{6}+6\\ 
 =12+5\sqrt{6}
 11- \sqrt {5}
 11-5\sqrt{5}
 1-5\sqrt{5}
 1-\sqrt{5}
 (3+\sqrt{5})(2-\sqrt{5) })\\ 9{2}\\ 
 =2-2\кв.{16}+8-2-2\кв.{16}-8\\ 
 =-16
 Распространенные заблуждения 
  Умножение всех слагаемых в скобках 
 Мы должны умножить значение вне скобок на каждое слагаемое внутри скобок (скобки).
 2(6x  2  - 3x) = 12x  2  - 3x ✖ 
 Здесь мы не умножали значение за скобками на второй член.
 Правильный ответ:
 2(6x  2  − 3x) = 12x  2  − 6x ✔ 
  Умножение с отрицательными числами 
 Чтобы два числа умножались на одинаковые, чтобы получить +.
 + ✕ + = + 
 − ✕ − = +
 напр. 2 ✕ 3 = 6 
 напр. − 2 ✕ − 3 = 6
 4 ✕ 5 = 20 
 − 4 ✕ − 5 = 20
 Чтобы при умножении двух чисел получилось a −, их знаки должны быть разными.
 + ✕ - = - 
 - ✕ + = -
 напр. 2 ✕ - 3 = - 6 
 напр. − 2 ✕ 3 = − 6
 4 ✕ − 5 = − 20 
 − 4 ✕ 5 = − 20
 - 4(3y - 5) = - 4y - 20 
 Здесь мы не использовали - ✕ - = +
 - 4 ✕ - 5 =  + 20  
 Таким образом, правильный ответ - 4(3y - 5) = − 4y + 20.
  Возведение члена в квадрат 
 Когда мы что-то возводим в квадрат, мы умножаем это само на себя.
 3  2  = 3 ✕ 3
х  2  = х ✕ х
(5 лет)  2 = 5y ✕ 5y 
 Когда мы возводим скобку в квадрат, мы умножаем ее на всю скобку.
 (х + 3)  2  = (х + 3)(х + 3)
= х  2  + 6х + 9
NOT x  2  + 9 
  Сбор похожих терминов 
 Когда мы собираем похожие термины, мы должны ставить знак перед числом.
No related posts.