Объем прямоугольника в м3, мм3, см3, л — стороны в мм
Введите а — длину прямоугольника в мм (миллиметрах):
Введите b — ширину прямоугольника в мм (миллиметрах):
Введите h — толщину прямоугольника в мм (миллиметрах):
Если прямоугольник имеет толщину, то фактически это параллелепипед. Объем параллелепипед в общем случае рассчитывается по формуле:
V = a x b х h
V — объем параллелепипеда . Объем прямоугольника имеющего толщину (высоту).
a — длина прямоугольника основания параллелепипеда
b — ширина прямоугольника основания параллелепипеда
h — высота параллелепипеда. Толщина прямоугольника.
Объем в миллиметрах кубических прямоугольника имеющего толщину (параллелепипед):
Vмм3 = aмм х bмм х hмм
Vмм3 — объем в миллиметрах кубических (мм3).
aмм — длина прямоугольника в миллиметрах (мм).
bмм— ширина прямоугольника в миллиметрах (мм).
hмм — толщина прямоугольника в миллиметрах (мм).
Объем в сантиметрах кубических прямоугольника имеющего толщину (параллелепипед):
Vсм3 = aмм х bмм х hмм / 1 000
Vсм3 — объем в сантиметрах кубических (см3).
aмм — длина прямоугольника в миллиметрах (мм).
bмм— ширина прямоугольника в миллиметрах (мм).
hмм — толщина прямоугольника в миллиметрах (мм).
Объем в метрах кубических прямоугольника имеющего толщину (параллелепипед):
Vм3 = aмм х bмм х hмм / 1 000 000 000
Vм3 — объем в метрах кубических (м3).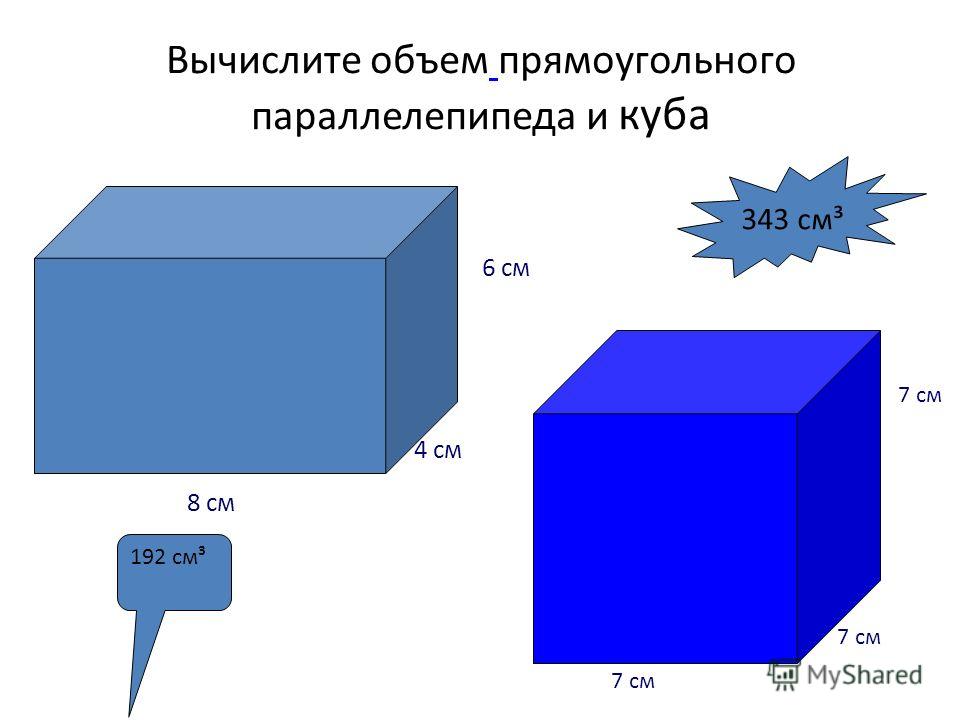
aмм — длина прямоугольника в миллиметрах (мм).
bмм— ширина прямоугольника в миллиметрах (мм).
hмм — толщина прямоугольника в миллиметрах (мм).
Объем в литрах прямоугольника имеющего толщину (параллелепипед):
Vл = aмм х bмм х hмм / 1 000 000
Vл — объем в литрах (л).
aмм — длина прямоугольника в миллиметрах (мм).
bмм— ширина прямоугольника в миллиметрах (мм).
hмм — толщина прямоугольника в миллиметрах (мм).
Объем прямоугольного параллелепипеда: онлайн калькулятор, формулы, примеры решений
Параллелепипед — это призматическая фигура, все грани которой являются параллелограммами.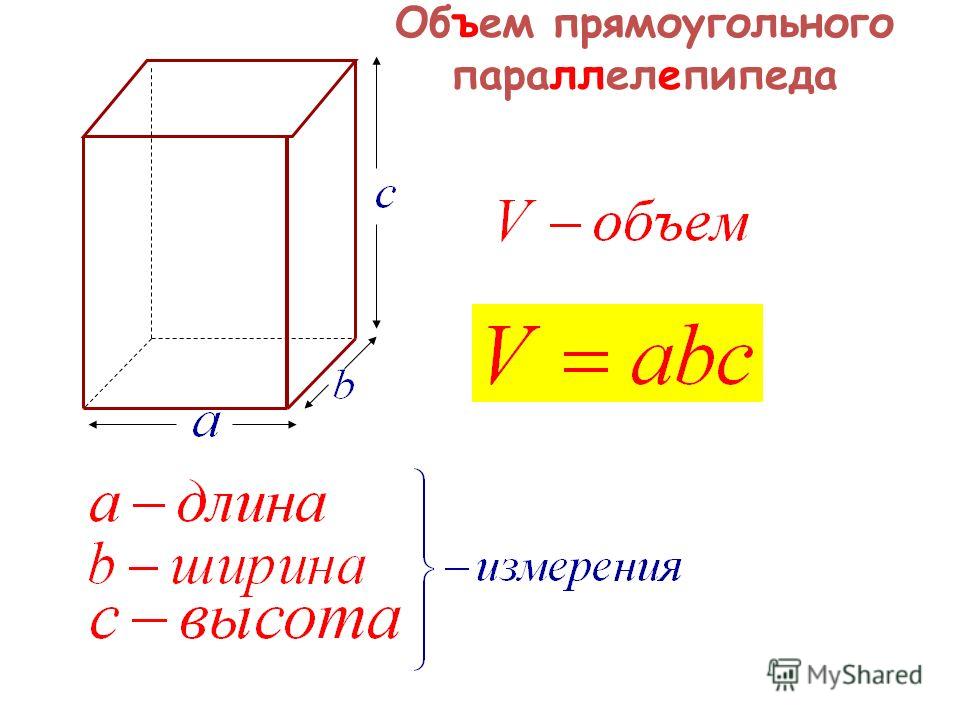 Если в роли граней выступают обычные прямоугольники, то параллелепипед является прямоугольным и именно форму данной фигуры имеют такие реальные объекты как панельные дома, аквариумы, книги, принтеры или кирпичи.
Если в роли граней выступают обычные прямоугольники, то параллелепипед является прямоугольным и именно форму данной фигуры имеют такие реальные объекты как панельные дома, аквариумы, книги, принтеры или кирпичи.
Геометрия параллелепипеда
Прямоугольный параллелепипед ограничен шестью гранями, при этом противоположные грани фигуры равны и параллельны друг другу. Данная геометрическая фигура представляет собой частный случай прямой четырехугольной призмы. Параллелепипед имеет 12 ребер и 8 вершин. В каждой из вершин сходятся по три ребра фигуры, которые являются длиной, шириной и высотой параллелепипеда или его измерениями. Если длина, ширина и высота фигуры равны, то параллелепипед превращается в куб.
Параллелепипеды в реальной жизни
Большое количество существующих в реальности объектов имеют форму параллелепипеда. Широкое распространение такая форма получила благодаря легкости производства, удобству хранения и транспортировки, идеальной сочетаемости одинаковых параллелепипедов, устойчивости и постоянству размеров. Параллелепипедную форму имеют такие объекты, как кирпичи, коробки, смартфоны, блоки питания, дома, комнаты и многое другое.
Параллелепипедную форму имеют такие объекты, как кирпичи, коробки, смартфоны, блоки питания, дома, комнаты и многое другое.
Объем параллелепипеда
Важным свойством любого геометрического тела является его вместимость, то есть объем фигуры. Объем — это характеристика объекта, которая показывает, сколько единичных кубов он способен вместить. В общем случае объем любой призматической фигуры рассчитывается по формуле:
V = So × h,
где So – площадь основания фигуры, а h – ее высота.
Данная формула легко иллюстрируется следующим примером. Представьте, что у вас есть один лист бумаги А4. Это обычный прямоугольник, который характеризуется строго определенной площадью. Грубо говоря, лист — это плоскость. Теперь представьте стандартную пачку бумаги из 500 листов формата А4. Это уже объемная фигура, имеющая форму параллелепипеда. Узнать ее объем легко, достаточно перемножить площадь листа, лежащего в основании, на их количество, то есть, на высоту призмы.
Параллелепипед — это частный случай призмы, в основании которой лежит прямоугольник.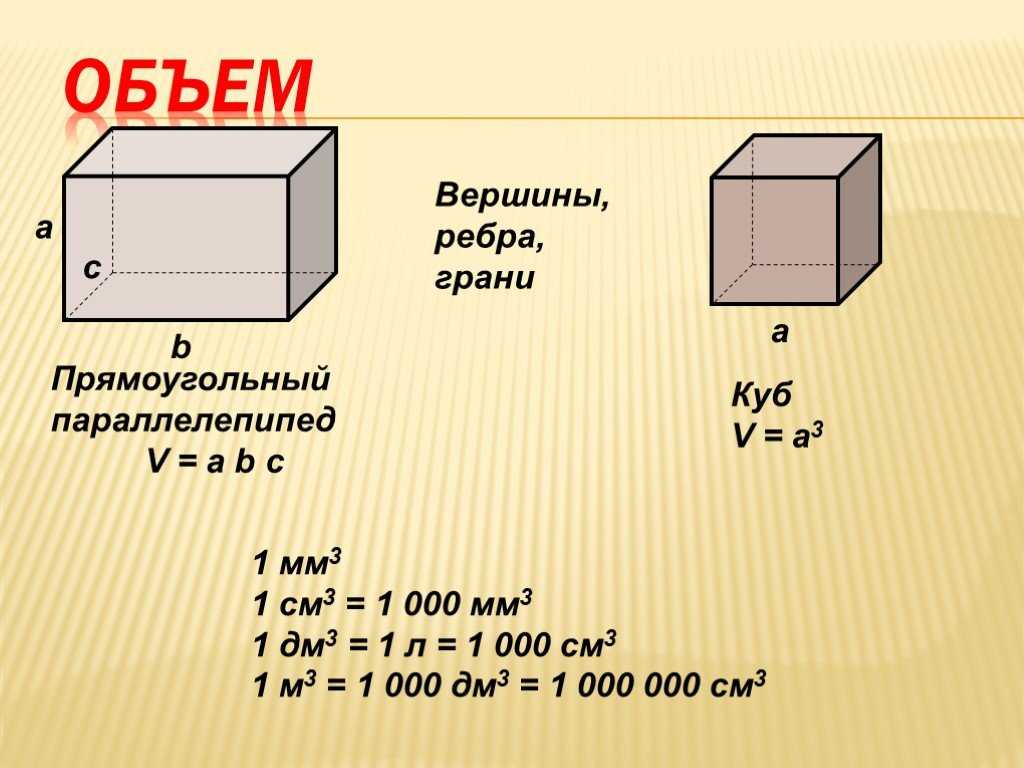 Площадь прямоугольника представляет собой простое произведение его сторон, следовательно, для параллелепипеда:
Площадь прямоугольника представляет собой простое произведение его сторон, следовательно, для параллелепипеда:
So = a × b
Для определения объема достаточно умножить So на высоту фигуры. Таким образом, объем прямоугольного параллелепипеда считается по простой формуле, представляющей перемножение трех сторон тела:
V = a × b × h,
где a – длина, b – ширина, h – высота геометрической фигуры.
Для определения объема прямоугольного параллелепипеда вам достаточно замерить три этих параметра и просто перемножить их. Если вы не хотите постоянно держать в голове формулы определения объемов и площадей геометрических фигур, то воспользуйтесь нашим каталогом онлайн-калькуляторов: каждый инструмент подскажет вам, какие параметры вы должны замерить и мгновенно вычислит результат. Рассмотрим пару примеров, когда вам может понадобиться определить объем параллелепипеда.
Примеры из жизни
Аквариум
К примеру, вы купили старый аквариум в форме параллелепипеда, но вам никто не сказал, какой объем имеет данная конструкция.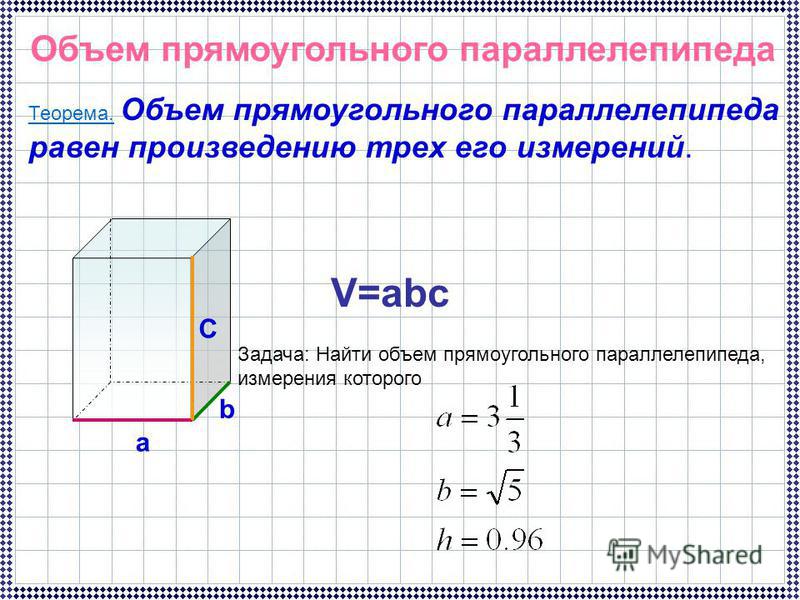 Объем аквариума — важный параметр, по которому определяется мощность системы обогрева для морских обитателей. Вычислить данную характеристику несложно — достаточно замерить длину, ширину и высоту аквариума и ввести эти данные в форму калькулятора. Допустим, длина аквариума составляет 1 м, ширина — 50 см, а высота — 70 см. Для правильного расчета важно выразить все стороны в одних единицах измерения, допустим, в метрах.
Объем аквариума — важный параметр, по которому определяется мощность системы обогрева для морских обитателей. Вычислить данную характеристику несложно — достаточно замерить длину, ширину и высоту аквариума и ввести эти данные в форму калькулятора. Допустим, длина аквариума составляет 1 м, ширина — 50 см, а высота — 70 см. Для правильного расчета важно выразить все стороны в одних единицах измерения, допустим, в метрах.
V = 1 × 0,5 × 0,7 = 0,35
Таким образом, объем аквариума составит 0,35 кубических метров или 350 литров. Зная объем, вы без проблем подберете мощность для системы обогрева.
Строительство
Допустим, вы заливаете плитный фундамент для своей дачи и вам необходимо узнать, сколько бетона понадобится для заливки основания. Плитный фундамент — это цельная монолитная плита, которая располагается под всей площадью здания. Для того чтобы узнать требуемый объем бетона, необходимо вычислить объем плиты. Плита, к счастью, имеет форму прямоугольного параллелепипеда, поэтому вы без проблем можете подсчитать нужное количество бетона. Допустим, ваша дача — это стандартный домик 6 на 6 метров. Вы уже знаете два из трех необходимых параметров. Согласно требованиям, толщина плитного фундамента должна быть не менее 10 см, и вы можете сами выбрать подходящий размер. К примеру, вы решили залить плиту толщиной 20 см. Для правильного расчета задайте все параметры в одних единицах измерения, то есть метрах, и получите результат:
Допустим, ваша дача — это стандартный домик 6 на 6 метров. Вы уже знаете два из трех необходимых параметров. Согласно требованиям, толщина плитного фундамента должна быть не менее 10 см, и вы можете сами выбрать подходящий размер. К примеру, вы решили залить плиту толщиной 20 см. Для правильного расчета задайте все параметры в одних единицах измерения, то есть метрах, и получите результат:
V = 6 × 6 × 0,2 = 7,2
Следовательно, для заливки фундамента вам понадобится 7,2 кубических метров бетона.
Заключение
Определение объема параллелепипедных фигур может пригодиться вам во многих случаях: от бытовых проблем до производственных вопросов, от школьных заданий до проектных задач. Наш онлайн-калькулятор поможет вам решить задания любой сложности.
Как рассчитать объем прямоугольной призмы?
В геометрии призма представляет собой объект трехмерной формы, который состоит из двух одинаковых многоугольников, обращенных друг к другу и соединенных по бокам прямоугольными или параллелограммными гранями.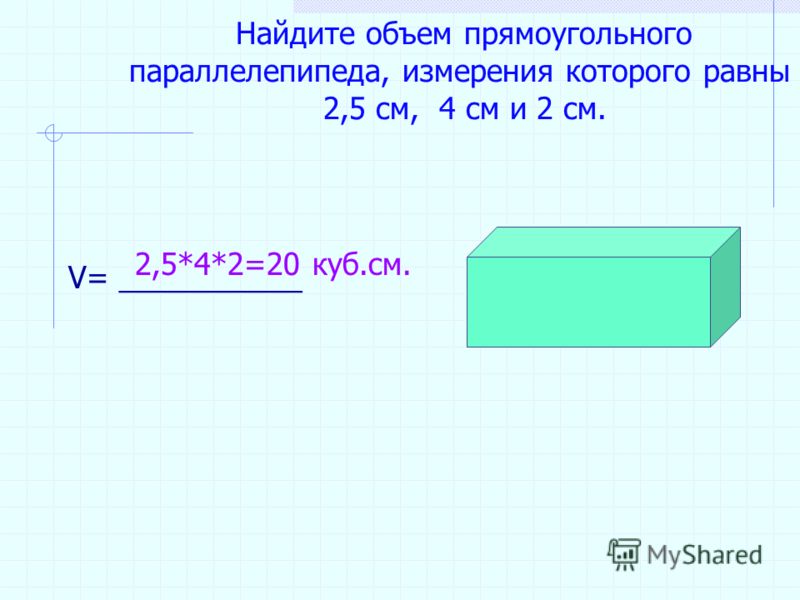 Эти одинаковые многоугольники называются основаниями призмы и могут иметь любую форму, например треугольники, квадраты, прямоугольники или любой n-сторонний многоугольник. Призма является важным членом семейства многогранников. В зависимости от типа многоугольного основания призмы делятся на два типа: правильные и неправильные призмы. И в зависимости от выравнивания оснований существует два типа призм: прямые призмы и наклонные призмы. Кроме того, в зависимости от формы многоугольного основания призмы подразделяются на различные типы: треугольные призмы, прямоугольные призмы, квадратные призмы, пятиугольные призмы, шестиугольные призмы и т. д.
Эти одинаковые многоугольники называются основаниями призмы и могут иметь любую форму, например треугольники, квадраты, прямоугольники или любой n-сторонний многоугольник. Призма является важным членом семейства многогранников. В зависимости от типа многоугольного основания призмы делятся на два типа: правильные и неправильные призмы. И в зависимости от выравнивания оснований существует два типа призм: прямые призмы и наклонные призмы. Кроме того, в зависимости от формы многоугольного основания призмы подразделяются на различные типы: треугольные призмы, прямоугольные призмы, квадратные призмы, пятиугольные призмы, шестиугольные призмы и т. д.
Прямоугольная призма
Прямоугольная призма представляет собой трехмерную фигуру, состоящую из шести прямоугольных плоских граней. Это призма с двумя прямоугольными основаниями и четырьмя боковыми прямоугольными гранями, двенадцатью сторонами и восемью вершинами. Согласно математическим исследованиям, прямоугольным параллелепипедом называется любой многогранник, напоминающий прямоугольную призму. В прямоугольной призме каждый угол прямой. Он также известен как прямоугольный шестигранник, правильная прямоугольная призма и прямоугольный параллелепипед.
В прямоугольной призме каждый угол прямой. Он также известен как прямоугольный шестигранник, правильная прямоугольная призма и прямоугольный параллелепипед.
Объем прямоугольной призмы
Объем прямоугольной призмы — это полное пространство, заключенное внутри прямоугольной призмы. Она обычно обозначается буквой «V» и измеряется в см 3 , м 3 , в 3 и т. д. Объем прямоугольной призмы определяется путем умножения площади ее основания на ее высоту.
Формула объема прямоугольной призмы дается следующим образом:
Объем прямоугольной призмы = площадь основания × высота призмы
Поскольку основание призмы представляет собой прямоугольник, его площадь равна произведению длины и ширины. Пусть «h» — высота призмы, «l» — длина основания, а «b» — ширина основания.
Теперь формула для объема прямоугольной призмы дается следующим образом:
Объем прямоугольной призмы = l × w × h кубических единиц
Решаемые примеры на основе
Объем прямоугольной призмы Задача 1. Найдите высоту прямоугольной призмы, если ее объем равен 90 кубических дюймов, а его базовая площадь равна 15 квадратных дюймов.
Найдите высоту прямоугольной призмы, если ее объем равен 90 кубических дюймов, а его базовая площадь равна 15 квадратных дюймов.
Решение:
Приведены данные,
Объем прямоугольной призмы = 90 куб. в
Площадь основания = 15 кв. в
Мы знаем, что,
Объем прямоугольной призмы формула = Площадь основания × Высота призмы
⇒ 90 = 15 × h
⇒ h = 90/15 = 6 дюймы.
Следовательно, высота данной призмы равна 6 дюймам.
Задача 2: Определить объем прямоугольной призмы, если длина ее основания 10 см, ширина основания 6 см, а высота призмы 15 см.
Раствор:
Приведены данные,
Высота прямоугольной призмы (h) = 15 см знать, что,
Объем прямоугольной призмы формула (V) = площадь основания × высота призмы
площадь основания = l × w
= 10 × 6 = 60 кв.см.
В = 60 × 15 = 900 куб.
см
Отсюда объем прямоугольной призмы 900 куб. см.
Задача 3. Какова ширина основания прямоугольной призмы, если ее объем 2100 куб. см, а его высота и длина основания равны 25 см и 12 см соответственно?
Решение:
Приведены данные,
Объем прямоугольной призмы = 2100 куб. см
Высота прямоугольной призмы (h) = 25 см
Длина основания (l) = 12 см
Мы знаем, что,
Объем прямоугольной призмы формула (V) = площадь основания × высота призмы
Площадь основания = l × w
⇒ V = l × w × h
⇒ 2100= 12 × w × 25
⇒ 300w = 2100
⇒ w = 2100/390 см ширина основания прямоугольной призмы 7 см.
Задача 4. Каков объем прямоугольной призмы высотой 20 единиц и площадью основания 120 квадратных единиц?
Решение:
Приведены данные,
Высота прямоугольной призмы (h) = 20 единиц
Площадь основания = 120 квадратных единиц
Мы знаем, что
Объем прямоугольной призмы по формуле (V) = Площадь основания × Высота призмы
V = 120 × 20 = 2400 кубических единиц.
Следовательно, объем прямоугольной призмы равен 2400 кубических единиц.
Задача 5. Какова длина основания прямоугольной призмы, если ее объем 150 куб. см, а его высота и ширина основания равны 10 см и 3 см соответственно?
Решение:
Приведенные данные,
Объем прямоугольной призмы = 150 куб. см
Высота прямоугольной призмы (h) = 10 см
Ширина основания (w) = 3 см
Мы знаем, что,
Формула объема прямоугольной призмы (V) = площадь основания × высота призмы
Площадь основания = l × w
⇒ V = l × w × h
⇒ 150 = l × 3 × 10
⇒ 30l = 150 длина основания прямоугольной призмы равна 5 см.
Задача 6. Каков объем прямоугольной призмы, высота которой равна 20 единицам, а длина и ширина основания равны 15 единицам и 12 единицам соответственно?
Решение:
Приведенные данные,
Высота прямоугольной призмы (h) = 20 ед.
Длина основания (l) = 15 ед. знать, что,
Объем прямоугольной призмы = l × w × h кубических единиц
V = 15 × 12 × 20 = 3600 кубических единиц.
Следовательно, объем прямоугольной призмы равен 3600 кубических единиц.
Задача 7. Определить объем прямоугольной призмы, если ее высота равна 10 см, а длина и ширина основания равны 8 см и 6 см соответственно.
Решение:
Приведенные данные,
Высота прямоугольной призмы (h) = 10 см0002 Мы знаем, что,
Объем прямоугольной призмы = l × w × h кубических единиц
V = 8 × 6 × 10 = 480 куб. см
Значит, объем прямоугольной призмы равен 480 куб. см.
Часто задаваемые вопросы на основе прямоугольной призмы
Вопрос 1: Каков объем прямоугольной призмы?
Ответ:
Объем прямоугольной призмы — это количество вещества, которое она может удержать, или это пространство, занимаемое ею в трехмерном пространстве.
Итак, объем прямоугольной призмы рассчитывается путем умножения площади ее основания на ее высоту. Формула для нахождения объема прямоугольной призмы:
Объем (V) = высота призмы × площадь основания.
Рассчитывается в кубических единицах, таких как см 3 , м 3 , 3 и т. д. ?
Ответ:
Объем прямоугольной призмы является произведением ее трех измерений, т. е.
объем = длина × ширина × высота.
Если высоту прямоугольной призмы увеличить вдвое, ее объем будет V 2 = l × w × (2h) = 2 × lwh = 2 × V 1 . Таким образом, можно с уверенностью сказать, что объем прямоугольной призмы удваивается, когда ее высота увеличивается вдвое.
Вопрос 3: Что произойдет с объемом прямоугольной призмы, если ее высоту уменьшить вдвое?
Ответ:
Объем прямоугольной призмы равен произведению ее трех измерений, т.
е.
объем = длина × ширина × высота.
Если высоту прямоугольной призмы уменьшить вдвое, ее объем будет V 2 = l × w × (h/2) = (lwh)/2 = V 1 /2. Таким образом, можно с уверенностью сказать, что объем прямоугольной призмы уменьшается вдвое, когда ее высота уменьшается вдвое.
Вопрос 4. Что произойдет с объемом прямоугольной призмы, если длину, ширину и высоту призмы удвоить?
Ответ:
Объем прямоугольной призмы является произведением ее трех измерений, то есть
объем = длина × ширина × высота.
Если длину, ширину и высоту прямоугольной призмы удвоить, ее объем будет V 2 = (2l) × (2w) × (2h) = 8 × lwh = 8 × V 1 . Следовательно, объем прямоугольной призмы увеличивается в восемь раз, когда все ее три измерения удваиваются.
Объем прямоугольной призмы – определение, формула, примеры
Объем — это общее количество трехмерного пространства, которое занимает объект.
Мы измеряем объем в кубических единицах. Итак, если объект имеет объем 1800 кубических единиц, это означает, что он состоит из 1800 единичных кубов. Призма – это многогранник с одинаковыми основаниями, плоскими прямоугольными боковыми гранями и одинаковым поперечным сечением. Есть несколько призм различной формы. В статье ниже мы узнаем о прямоугольной призме и формуле объема прямоугольной призмы . Читайте дальше, чтобы узнать, как найти объем прямоугольной призмы.
Вот что мы рассмотрим:
- Что такое прямоугольная призма?
- Каков объем прямоугольной призмы?
- Формула объема прямоугольной призмы
- Как найти объем прямоугольной призмы?
- Решенные примеры объема прямоугольной призмы
Что такое прямоугольная призма?
Прямоугольная призма представляет собой трехмерную фигуру с шестью гранями. Все грани призмы прямоугольники. Прямоугольная призма имеет кубическую форму. Этот многогранник имеет две пары конгруэнтных и параллельных оснований.
У него шесть граней, 12 сторон и восемь вершин. Некоторые распространенные названия прямоугольных призм: прямоугольный шестигранник, прямоугольный параллелепипед и прямоугольная призма.
Существует два основных типа прямоугольных призм – прямые прямоугольные призмы и наклонные призмы.
Прямоугольная призма имеет основания, перпендикулярные другим граням. Эта призма имеет форму геометрического тела. Он имеет многоугольник в качестве основания, а вертикальные стороны перпендикулярны основанию. Основание и вершина прямоугольной прямой призмы имеют одинаковую форму и размер. Ее называют «прямоугольной» призмой, потому что у нее прямые углы между основанием и сторонами.
Напротив, в наклонной прямоугольной призме основания призмы не перпендикулярны другим граням. В этом случае высота прямоугольной призмы проведена перпендикулярно из вершины одного основания к другому основанию прямоугольной призмы. Однако мы можем использовать ту же формулу для расчета объема прямоугольной призмы, независимо от типа призмы.
Свойства прямоугольной призмы
Прямоугольная призма имеет следующие свойства:
- Прямоугольная призма имеет прямоугольное поперечное сечение.
- Имеет две пары конгруэнтных и параллельных оснований.
- Прямоугольная призма имеет в общей сложности 6 граней, 12 сторон и восемь вершин.
- Как и прямоугольный параллелепипед, он имеет три измерения: ширину основания, высоту и длину.
- Вершина и основание прямоугольной призмы прямоугольные.
- Пары противоположных граней прямоугольной призмы равны или конгруэнтны.
- Прямоугольная призма имеет прямоугольные боковые грани.
- Наклонная прямоугольная призма имеет параллелограммы боковыми гранями.
Каков объем прямоугольной призмы?
Объем прямоугольной призмы определяется как общее пространство, занимаемое прямоугольной призмой. Мы можем получить объем прямоугольной призмы, умножив ее длину, ширину и высоту так же, как мы делаем это для прямоугольного параллелепипеда.
Следовательно, единица измерения объема прямоугольной призмы равна 3 см, 3 м и так далее.
Формула объема прямоугольной призмы
Формула для расчета объема прямоугольной призмы есть,
Объем = l b h
Где,
- «l» – ширина основания 94 призмы
- «b» — длина основания прямоугольной призмы
- «h» — высота прямоугольной призмы
Мы также можем записать эту формулу как
Объем прямоугольной призмы = площадь основания × высота призмы
Основание прямоугольной призмы — прямоугольник. Значит, площадь будет l × w. Когда мы умножаем эту площадь на высоту призмы, мы получаем объем прямоугольной призмы.
Как найти объем прямоугольной призмы?
Чтобы рассчитать объем прямоугольной призмы, мы должны сначала убедиться, что все размеры призмы имеют одинаковые единицы измерения. Следующие шаги помогут оценить объем прямоугольной призмы.
Шаг 1: Определите основание прямоугольной призмы и найдите ее площадь по формуле.
Шаг 2: Далее мы определим высоту призмы. Высота призмы перпендикулярна основанию призмы.
Шаг 3 : Теперь умножьте площадь основания и высоту прямоугольной призмы, чтобы получить объем.
Применение прямоугольной призмы в реальной жизни
Существует множество применений прямоугольных призм. Мы можем найти многих в нашем доме. Некоторые примеры прямоугольных призм вокруг нас:
- Аквариум
- Грузовик
- Ящики для хлопьев
- Комод
- Картонные коробки
- Прямоугольные коробки для салфеток
- Коробки для рубашек
- Стволы
- Цистерны
- Матрасы для сна
Решенный пример объема прямоугольной призмы
Пример 1: Длина основания прямоугольной призмы равна 10 см, ширина основания равна 5 см, а высота равна 15 см.
Найдите объем прямоугольной призмы?
Решение:
, дано,
B = 10 см
L = 5 см
H = 15 см
с использованием объема прямоугольной формулы Prism,
Объем прямоугольной Prism = =
. L B H= 10 × 5 × 15
= 750 см 3
Объем прямоугольной призмы составляет 750 см 3
Пример 2: объем прямоугольной пилоты 1920 см 3, и площадь основания прямоугольной призмы 240 см 2. Найдите высоту прямоугольной призмы?
Решение:
, дано,
Площадь = 240 см 2
Том = 1920 см 3
с использованием объема прямоугольной призму,
. Объем прямоугольной предпосылки = L = L = L = L = L = L = L = L = L = L = L = L = L = L.
б ч
1920 = 240 х h
h = 1920/240
Высота прямоугольной призмы 8 см.
Пример 3: Учитывая, что длина прямоугольной призмы 10 м, ширина 2 м, а объем 40 м 3. Найдите высоту призмы.
Решение:
Дано,
L = 10 м
B = 2 м
V = 40 м 3 По формуле объема, апризмы0003
Объем прямоугольной призмы= л b h
40 = 10 x 2 x h
h = 40/20
h = 2 м высота прямоугольника
Пример 4: Найдите объем прямоугольной призмы, если площадь основания прямоугольной призмы равна 160 см 2. Дана высота прямоугольной призмы 25 см.
Решение:
Дано,
Площадь = 160 см 2
Высота призмы = 25 см
с использованием объема прямоугольной формулы призмы,
Объем прямоугольной призмы = L B H
VOLUCT = 160 x 25Объем = 4000 см 3
Объем прямоугольной призмы равен 4000 см 3.

 см
см

 Итак, объем прямоугольной призмы рассчитывается путем умножения площади ее основания на ее высоту. Формула для нахождения объема прямоугольной призмы:
Итак, объем прямоугольной призмы рассчитывается путем умножения площади ее основания на ее высоту. Формула для нахождения объема прямоугольной призмы: е.
е.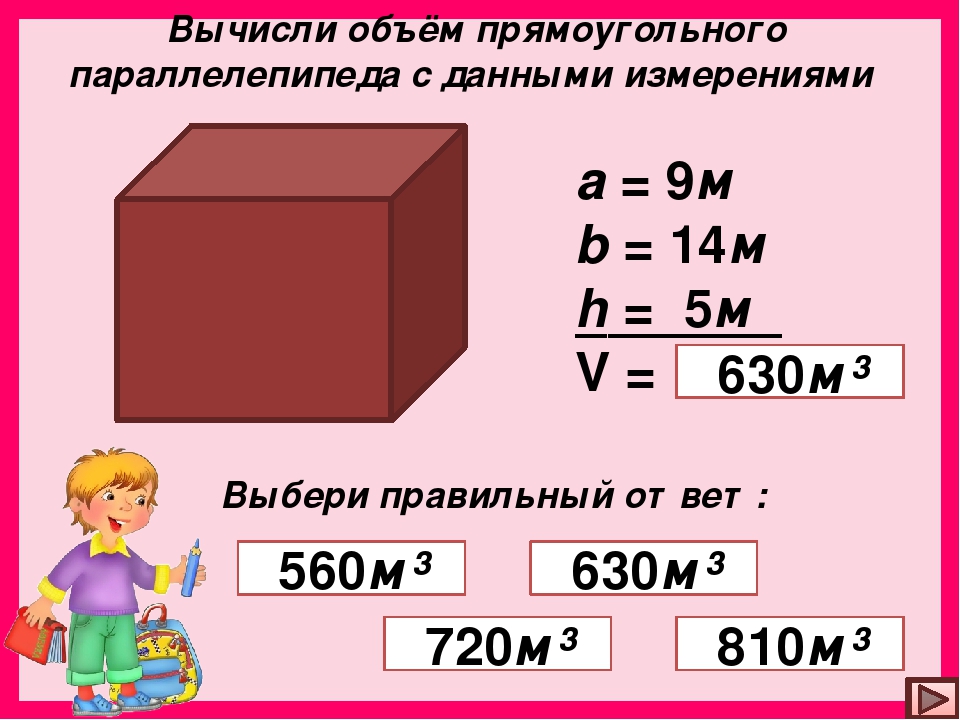 Мы измеряем объем в кубических единицах. Итак, если объект имеет объем 1800 кубических единиц, это означает, что он состоит из 1800 единичных кубов. Призма – это многогранник с одинаковыми основаниями, плоскими прямоугольными боковыми гранями и одинаковым поперечным сечением. Есть несколько призм различной формы. В статье ниже мы узнаем о прямоугольной призме и формуле объема прямоугольной призмы . Читайте дальше, чтобы узнать, как найти объем прямоугольной призмы.
Мы измеряем объем в кубических единицах. Итак, если объект имеет объем 1800 кубических единиц, это означает, что он состоит из 1800 единичных кубов. Призма – это многогранник с одинаковыми основаниями, плоскими прямоугольными боковыми гранями и одинаковым поперечным сечением. Есть несколько призм различной формы. В статье ниже мы узнаем о прямоугольной призме и формуле объема прямоугольной призмы . Читайте дальше, чтобы узнать, как найти объем прямоугольной призмы. У него шесть граней, 12 сторон и восемь вершин. Некоторые распространенные названия прямоугольных призм: прямоугольный шестигранник, прямоугольный параллелепипед и прямоугольная призма.
У него шесть граней, 12 сторон и восемь вершин. Некоторые распространенные названия прямоугольных призм: прямоугольный шестигранник, прямоугольный параллелепипед и прямоугольная призма.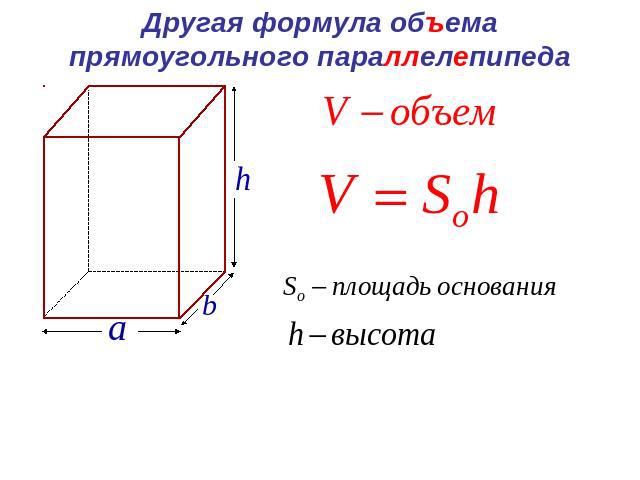
 Следовательно, единица измерения объема прямоугольной призмы равна 3 см, 3 м и так далее.
Следовательно, единица измерения объема прямоугольной призмы равна 3 см, 3 м и так далее.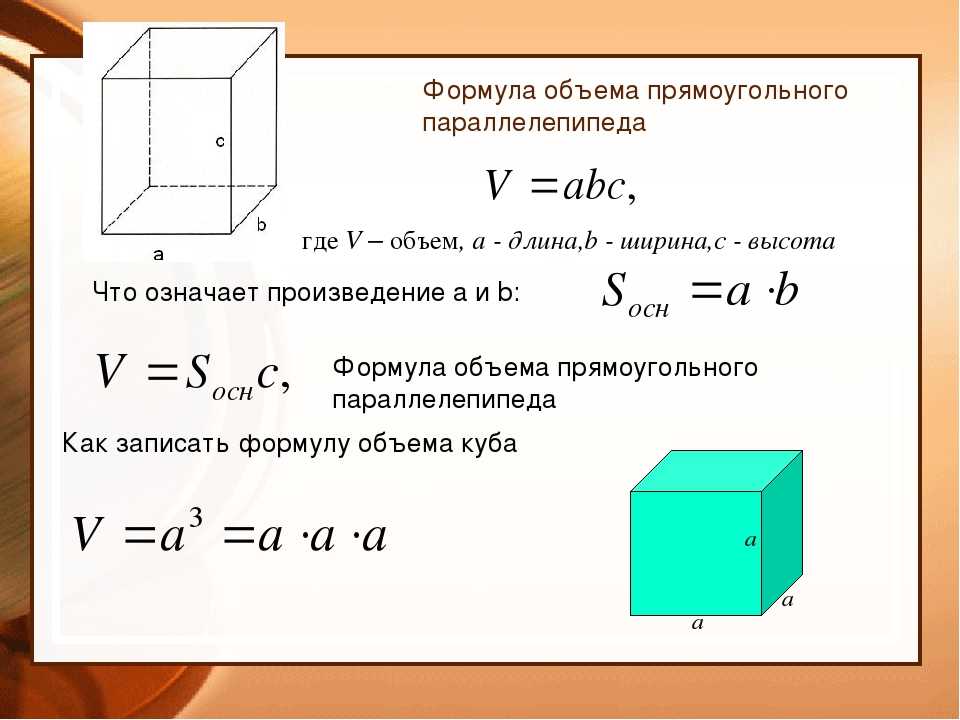
 Найдите объем прямоугольной призмы?
Найдите объем прямоугольной призмы?  б ч
б ч 