Как рассчитать окружность круга: Длина окружности круга | Онлайн калькулятор

Как рассчитать длину окружности, если не указан диаметр и радиус круга

Перед нами стоит вопрос: «Как рассчитать длину окружности?»

Одной линейкой здесь не обойтись, необходимо знать специальные формулы. Единственное, что от нас потребуется — это определить диаметр или радиус круга. В некоторых задачах эти величины обозначены. Но что делать, если у нас нет ничего, кроме рисунка? Не беда. Диаметр и радиус можно вычислить с помощью обычной линейки. Теперь приступим к самому основному.

Формулы, которые должен знать каждый

Еще в Древнем Вавилоне, почти 4 000 лет назад, учёные выявили удивительное соотношение: если длину окружности разделить на ее диаметр, то получается одно и то же число, которое равно примерно 3,14. Это значение назвали числом «Пи», именно с этой буквы в древнегреческом языке начиналось слово «периметр» и «окружность». На основании того открытия, которое совершили древние ученые, можно рассчитать длину любой окружности:

P = d П

Где P означает длину (периметр) окружности,

d – диаметр, П — число «Пи».

Длина окружности круга может также быть посчитана через ее радиус (r), который равен половине длины диаметра. Вот и вторая формула, которую нужно запомнить:

P = 2r П

Как узнать диаметр окружности?

Диаметр окружности представляет собой хорду, которая проходит через центр фигуры. При этом она соединяет две наиболее удалённые точки в круге. Исходя из этого, можно самостоятельно прочертить диаметр (радиус) и измерить его длину с помощью линейки.

Способ 1: вписываем прямоугольный треугольник в круг

Рассчитать длину окружности будет несложно, если мы найдем ее диаметр. Необходимо начертить в круге прямоугольный треугольник, где гипотенуза будет равна диаметру окружности. Для этого необходимо иметь под рукой линейку и угольник, иначе ничего не получится.

Способ 2: вписываем любой треугольник

На стороне круга отмечаем три любые точки, соединяем их – получаем треугольник. Важно, чтобы центр окружности лежал в области треугольника, это можно сделать на глаз.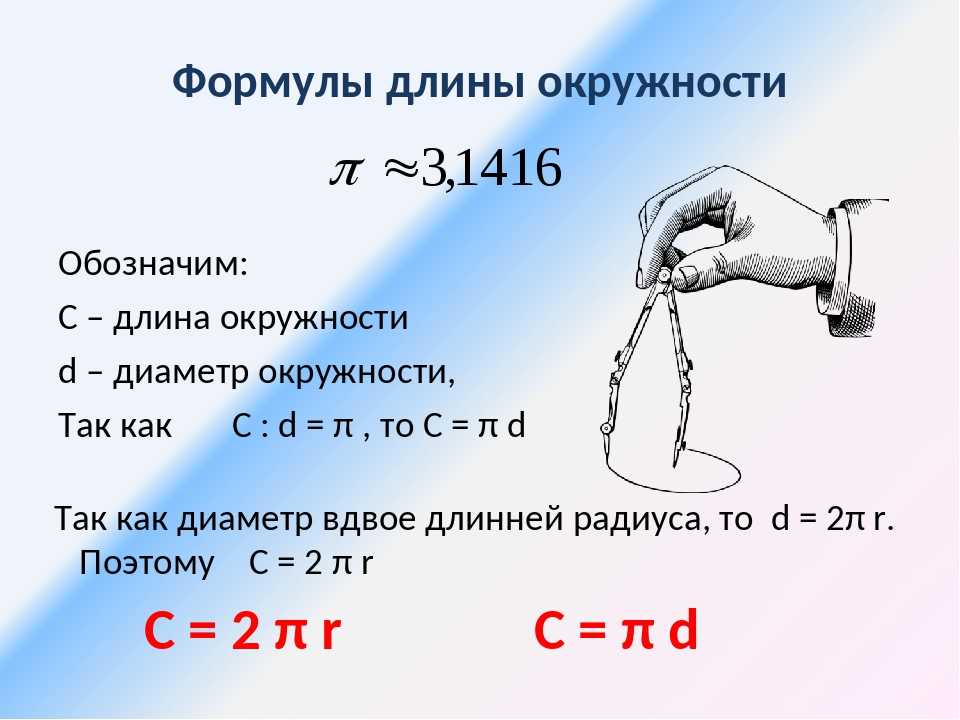 Проводим к каждой стороне треугольника медианы, точка их пересечения совпадёт с центром окружности. А когда нам известен центр, можно с помощью линейки легко провести диаметр.

Способ 3: как рассчитать длину окружности подручными средствами

Данный способ очень похож на первый, но может применяться при отсутствии угольника или в тех случаях, когда нет возможности чертить на фигуре, например на тарелке. Необходимо взять лист бумаги с прямыми углами. Прикладываем лист к кругу так, чтобы одна вершина его угла соприкасалась с краем круга. Далее отмечаем точками места, где стороны бумаги пересекаются с линией окружности. Соединяем эти точки с помощью карандаша и линейки. Если под рукой ничего нет, просто согните бумагу. Эта линия и будет равна длине диаметра.

Пример задачи

Перед нами задача: как рассчитать длину окружности, если не даны никакие цифровые значения, кроме самого круга. Запоминаем алгоритм:

1. Ищем диаметр с помощью угольника, линейки и карандаша по способу № 1. Предположим, получилось 5 см.
2. Зная диаметр, мы легко можем его вставить в нашу формулу: P = d П = 5*3,14 = 15,7  В нашем случае получилось около 15,7. Теперь вы без особых проблем сможете объяснить, как рассчитать длину окружности. 

Как рассчитать длину зная диаметр. Как рассчитать длину окружности, если не указан диаметр и радиус круга

Сначала разберемся в отличии между кругом и окружностью. Чтобы увидеть эту разницу, достаточно рассмотреть, чем являются обе фигуры. Это бесчисленное количество точек плоскости, располагающиеся на равном расстоянии от единственной центральной точки. Но, если круг состоит и из внутреннего пространства, то окружности оно не принадлежит. Получается, что круг это и окружность, ограничивающая его (о-кру(г)жность), и бесчисленное число точек, что внутри окружности.

Для любой точки L , лежащей на окружности, действует равенство OL=R . (Длина отрезка OL равняется радиусу окружности).

Отрезок, который соединяет две точки окружности, является ее хордой . {\circ}}

Используя радианную меру: CD = \alpha R

Диаметр, что перпендикулярен хорде, делит хорду и стянутые ею дуги пополам.

В случае, если хорды AB и CD окружности имеют пересечение в точке N , то произведения отрезков хорд, разделенные точкой N , равны между собой.

AN\cdot NB = CN \cdot ND

Касательная к окружности

Касательной к окружности принято называть прямую, у которой имеется одна общая точка с окружностью.

Если же у прямой есть две общие точки, ее называют секущей .

Если провести радиус в точку касания, он будет перпендикулярен касательной к окружности.

Проведем две касательные из этой точки к нашей окружности. Получится, что отрезки касательных сравняются один с другим, а центр окружности расположится на биссектрисе угла с вершиной в этой точке.

AC = CB

Теперь к окружности из нашей точки проведем касательную и секущую. Получим, что квадрат длины отрезка касательной будет равен произведению всего отрезка секущей на его внешнюю часть. {\circ}

\angle ADB = \angle AEB = \angle AFB

На одной окружности находятся вершины треугольников с тождественными углами и заданным основанием.

Угол с вершиной внутри окружности и расположенный между двумя хордами тождественен половине суммы угловых величин дуг окружности, которые заключаются внутри данного и вертикального углов.

\angle DMC = \angle ADM + \angle DAM = \frac{1}{2} \left (\cup DmC + \cup AlB \right)

Угол с вершиной вне окружности и расположенный между двумя секущими тождественен половине разности угловых величин дуг окружности, которые заключаются внутри угла.

\angle M = \angle CBD — \angle ACB = \frac{1}{2} \left (\cup DmC — \cup AlB \right)

Вписанная окружность

Вписанная окружность — это окружность, касающаяся сторон многоугольника.

В точке, где пересекаются биссектрисы углов многоугольника, располагается ее центр.

Окружность может быть вписанной не в каждый многоугольник.

Площадь многоугольника с вписанной окружностью находится по формуле:

S = pr ,

p — полупериметр многоугольника,

r — радиус вписанной окружности.

Отсюда следует, что радиус вписанной окружности равен:

r = \frac{S}{p}

Суммы длин противоположных сторон будут тождественны, если окружность вписана в выпуклый четырехугольник. И наоборот: в выпуклый четырехугольник вписывается окружность, если в нем суммы длин противоположных сторон тождественны.

AB + DC = AD + BC

В любой из треугольников возможно вписать окружность. Только одну единственную. В точке, где пересекаются биссектрисы внутренних углов фигуры, будет лежать центр этой вписанной окружности.

Радиус вписанной окружности вычисляется по формуле:

r = \frac{S}{p} ,

где p = \frac{a + b + c}{2}

Описанная окружность

Если окружность проходит через каждую вершину многоугольника, то такую окружность принято называть

описанной около многоугольника .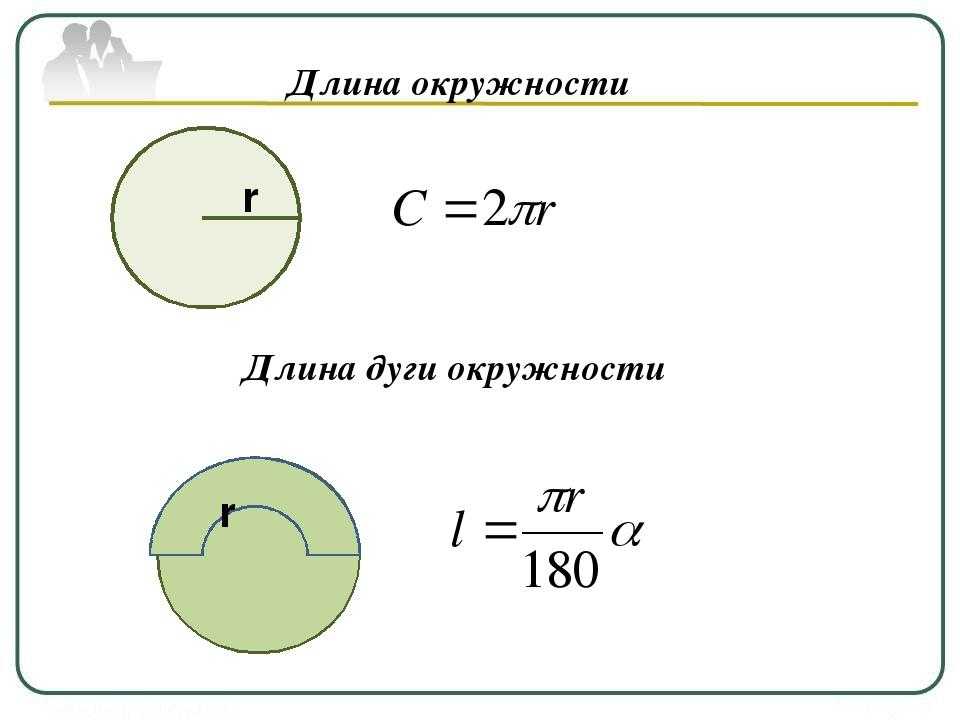 {\circ}

Около любого треугольника можно описать окружность, причем одну-единственную. Центр такой окружности будет расположен в точке, где пересекаются серединные перпендикуляры сторон треугольника.

Радиус описанной окружности можно вычислить по формулам:

R = \frac{a}{2 \sin A} = \frac{b}{2 \sin B} = \frac{c}{2 \sin C}

R = \frac{abc}{4 S}

a , b , c — длины сторон треугольника,

S — площадь треугольника.

Теорема Птолемея

Под конец, рассмотрим теорему Птолемея.

Теорема Птолемея гласит, что произведение диагоналей тождественно сумме произведений противоположных сторон вписанного четырехугольника.

AC \cdot BD = AB \cdot CD + BC \cdot AD

Окружностью называют кривую линию, которая ограничивает собой круг. В геометрии фигуры плоские, поэтому определение относится к двухмерному изображению. Предполагается, что все точки этой кривой удалены от центра круга на равное расстояние.

У окружности есть несколько характеристик, на основе которых производят расчеты, связанные с этой геометрической фигурой.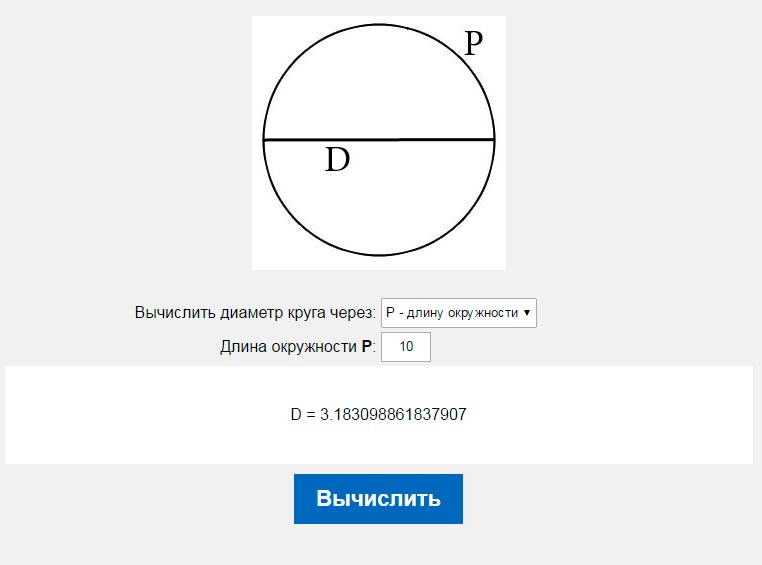 В их число входит: диаметр, радиус, площадь и длина окружности. Эти характеристики взаимосвязаны, то есть для их вычисления достаточно информации хотя бы об одной из составляющих. Например, зная только радиус геометрической фигуры по формуле можно найти длину окружности, диаметр, и ее площадь.

• Радиус окружности – это отрезок внутри окружности, соединённый с ее центром.
• Диаметр – это отрезок внутри окружности, соединяющий ее точки и проходящий через центр. По сути, диаметр – это два радиуса. Именно так выглядит формула для его вычисления: D=2r.
• Есть еще одна составляющая окружности – хорда. Эта прямая, которая соединяет две точки окружности, но не всегда проходит через центр. Так вот ту хорду, которая через него проходит, тоже называют диаметром.

Как узнать длину окружности? Сейчас выясним.

Длина окружности: формула

Для обозначения этой характеристики выбрана латинская буква p. Еще Архимед доказал, что отношение длины окружности к ее диаметру является одним и тем же числом для всех окружностей: это число π, которое приблизительно равно 3,14159. Формула для вычисления π выглядит так: π = p/d. Согласно этой формуле, величина p равна πd, то есть длина окружности: p= πd. Поскольку d (диаметр) равен двум радиусам, то эту же формулу длины окружности можно записать как p=2πr.Рассмотрим применение формулы на примере простых задач:

Задача 1

У основания царь-колокола диаметр равен 6,6 метров. Какова длина окружности основания колокола?

1. Итак, формула для вычисления окружности — p= πd
2. Подставляем имеющееся значение в формулу: p=3,14*6,6= 20,724

Ответ: длина окружности основания колокола 20,7 метра.

Задача 2

Искусственный спутник Земли вращается на расстоянии 320 км от планеты. Радиус Земли – 6370 км. Какова длина круговой орбиты спутника?

1. 1.Вычислим радиус круговой орбиты спутника Земли: 6370+320=6690 (км)
2. 2.Вычислим длину круговой орбиты спутника по формуле: P=2πr
3. 3.P=2*3,14*6690=42013,2

Ответ: длина круговой орбиты спутника Земли 42013,2 км.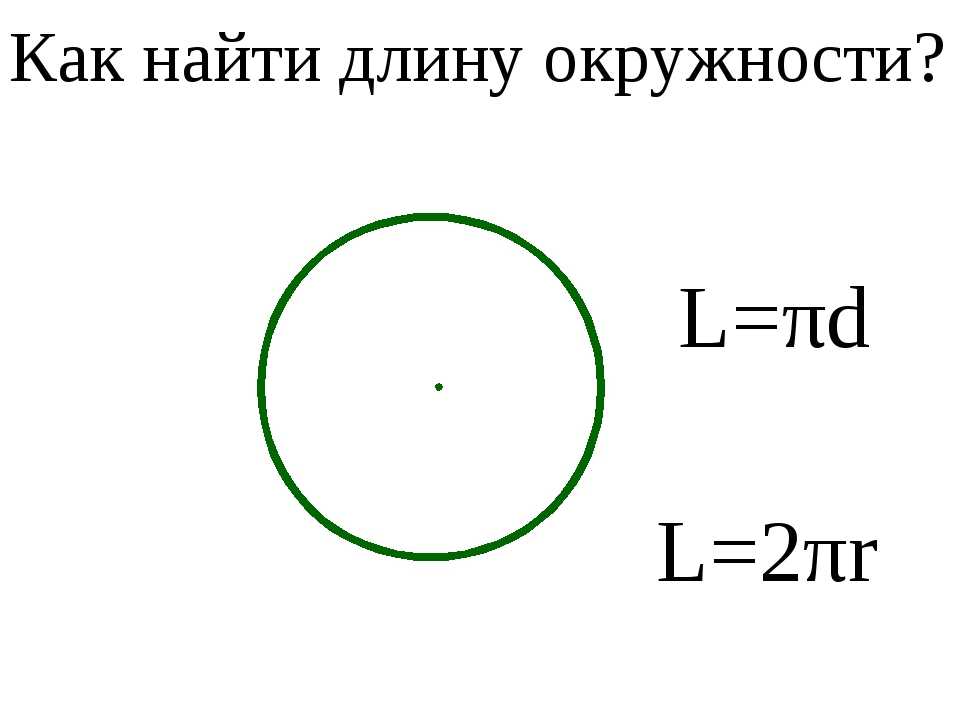

Способы измерения длины окружности

Вычисление длины окружности на практике используется не часто. Причиной тому приблизительное значение числа π. В быту для поиска длины круга используют специальный прибор – курвиметр. На окружности отмечают произвольную точку отсчета и ведут от нее прибор строго по линии, пока опять не дойдут до этой точки.

Как найти длину окружности? Нужно просто держать в голове незамысловатые формуля для вычислений.

Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.

Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π .

Определение длины окружности

Произвести расчёт окружности можно по следующей формуле:

L = π D = 2 π r

r — радиус окружности

D — диаметр окружности

L — длина окружности

π — 3. 14

Задача:

Вычислить длину окружности , имеющей радиус 10 сантиметров.

Решение:

Формула для вычисления дины окружности имеет вид:

L = π D = 2 π r

где L – длина окружности, π – 3,14 , r – радиус окружности, D – диаметр окружности.

Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:

L = 2 × 3,14 × 10 = 62,8 сантиметра

Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.

С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно.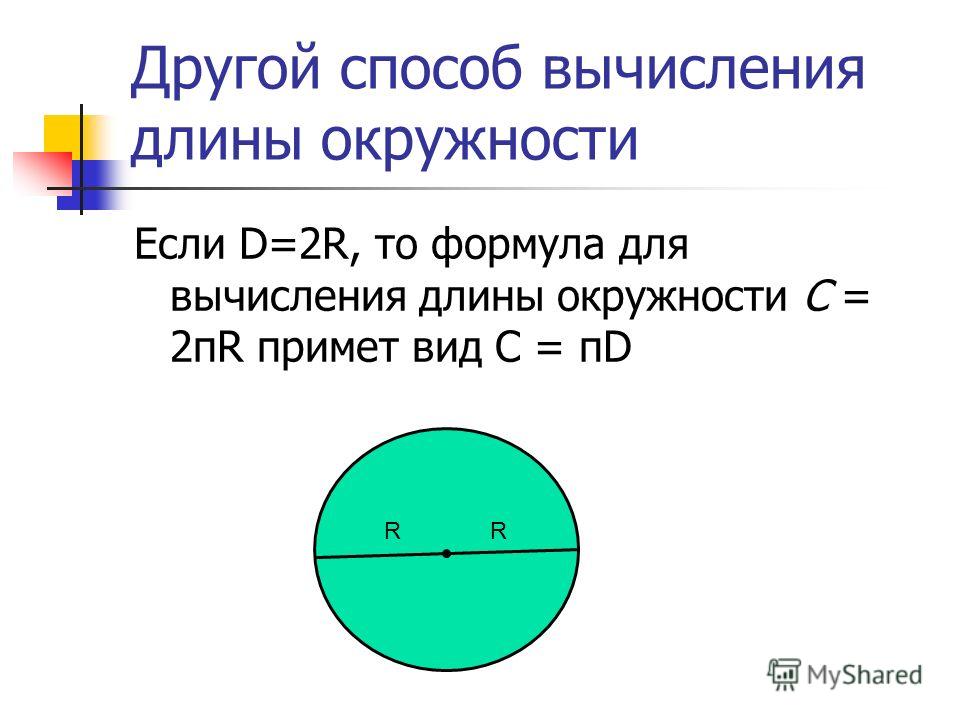 Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.

По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).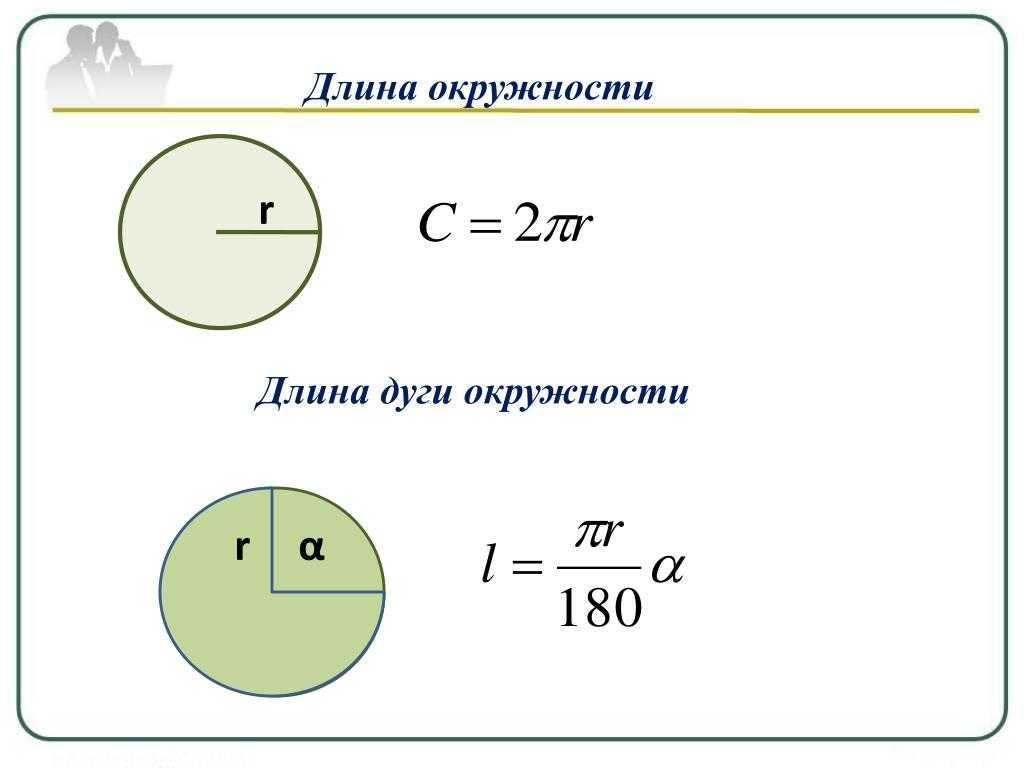

Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.

Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.

Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам.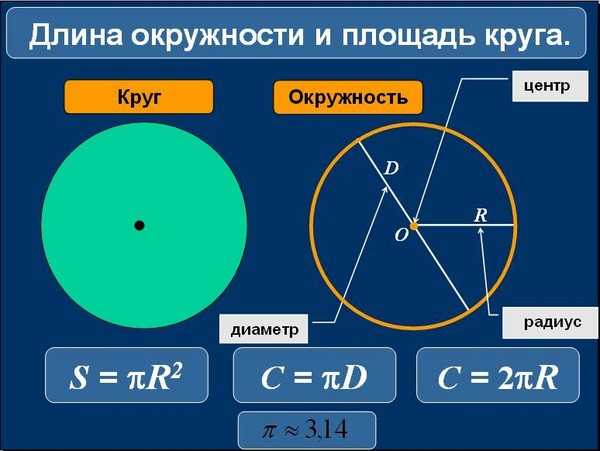 Поскольку число π , необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.

В какой бы сфере экономики человек ни трудился, вольно или невольно он пользуется математическими знаниями, накопленными за многие столетия. С устройствами и механизмами, содержащими окружности, мы сталкиваемся ежедневно. Круглую форму имеет колесо, пицца, многие овощи и фрукты в разрезе образуют круг, а также тарелки, чашки, да и многое другое. Однако, правильно рассчитывать длину окружности умеет не каждый.

Чтобы вычислить длину окружности, необходимо вначале вспомнить, что такое окружность. Это множество всех точек плоскости, равноудаленных от данной. А круг – это геометрическое место точек плоскости, находящееся внутри окружности. Из вышесказанного следует, что периметр круга и длина окружности – это одно и то же.

Способы нахождения длины окружности

Помимо математического способа нахождения периметра круга, есть и практические.

• Взять веревку или шнур и обернуть один раз вокруг.
• Затем веревку измерить, полученное число и будет длиной окружности.
• Прокатить круглый предмет один раз и посчитать длину пути. Если предмет очень небольшой, можно несколько раз обмотать его бечевкой, затем размотать нить, измерить и поделить на число витков.
• Найти требуемую величину по формуле:

L = 2πr = πD ,

где L – искомая длина;

π – константа, приблизительно равна 3,14 r – радиус окружности, расстояние от ее центра до любой точки;

D – диаметр, он равен двум радиусам.

Применение формулы, чтобы найти длину окружности

• Пример 1. Беговая дорожка проходит вокруг окружности радиусом 47,8 метров. Найти длину данной беговой дорожки, приняв π = 3,14.

L = 2πr =2*3,14*47,8 ≈ 300(м)

Ответ: 300 метров

• Пример 2. Колесо велосипеда, обернувшись 10 раз, проехало 18,85 метра. Найти радиус колеса.

18,85: 10 =1,885 (м) – это периметр колеса.

1,885: π = 1,885: 3,1416 ≈ 0,6(м) – искомый диаметр

Ответ: диаметр колеса 0,6 метра

Удивительное число π

Несмотря на кажущуюся простоту формулы, почему-то многим трудно ее запомнить. Видимо, это происходит из-за того, что в формуле есть иррациональное число π, которое не присутствует в формулах площади других фигур, например, квадрата, треугольника или ромба. Нужно просто запомнить, что это константа, то есть постоянная, означающая отношение длины окружности к диаметру. Около 4 тысяч лет назад люди заметили, что отношение периметра круга к его радиусу (или диаметру) одинаково для любых окружностей.

Древние греки приближали число π дробью 22/7. Долгое время π высчитывали как среднее между длинами вписанных и описанных многоугольников в окружность. В третьем столетии нашей эры китайский математик провёл вычисление для 3072-угольника и получил приближённое значение π = 3,1416. Необходимо помнить, что π всегда постоянно для любой окружности. Его обозначение греческой буквой π появилось в 18 веке. Это первая буква греческих слов περιφέρεια — окружность и περίμετρος — периметр. В восемнадцатом веке было доказано, что эта величина иррациональна, то есть ее нельзя представить в виде m/n, где m – целое, а n – натуральное число.

И в чем ее отличие от круга. Возьмите ручку или цвета и нарисуйте на листке бумаги обычный круг. Закрасьте всю середину полученной фигуры синим карандашом. Красный контур, обозначающий границы фигуры, — это окружность. А вот синее содержимое внутри нее — и есть круг.

Размеры круга и окружности определяются диаметром. На красной линии, обозначающей окружность, отметьте две точки таким образом, чтобы они оказались зеркальным отражением друг друга. Соедините их линией. Отрезок обязательно пройдет через точку в центре окружности. Этот отрезок, соединяющий противоположные части окружности, и называется в геометрии диаметром.

Отрезок, который тянется не через центр окружности, но смыкается с ней противоположными концами, называется хордой.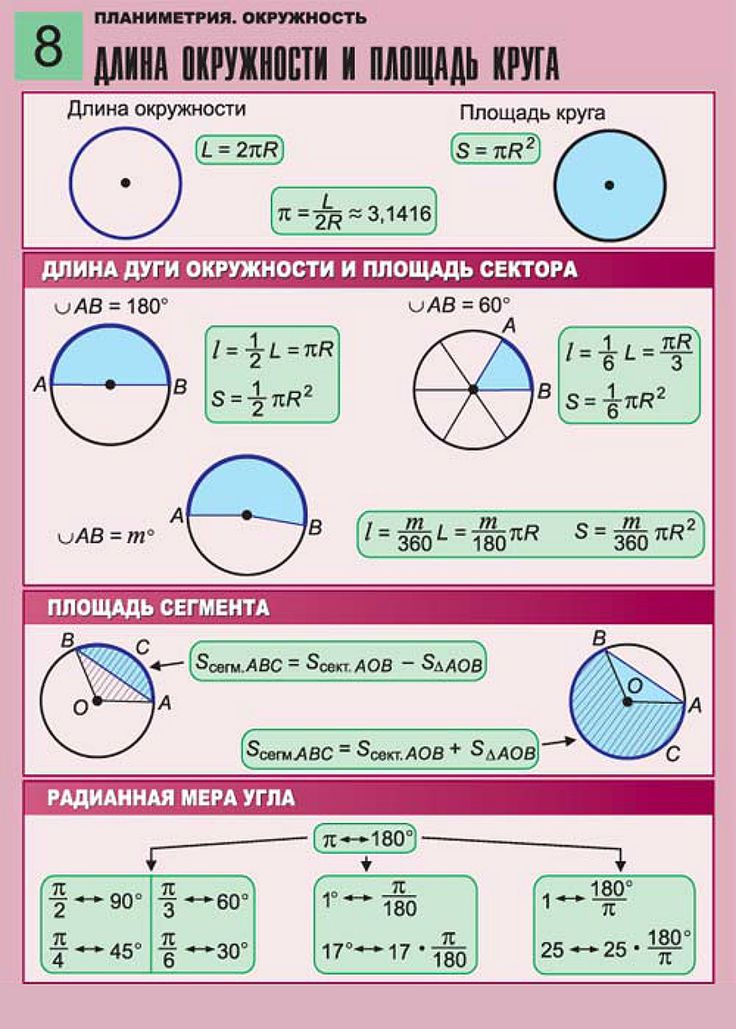 Следовательно, хорда, пролегающая через точку центра окружности, и является ее диаметром.

Обозначается диаметр латинской буквой D. Находить диаметр окружности можно по таким значениям, как площадь, длина и радиус круга.

Расстояние от центральной точки до точки, отложенной на окружности, называется радиусом и обозначается буквой R. Знание величины радиуса помогает вычислить диаметр окружности одним несложным действием:

К примеру, радиус — 7 см. Умножаем 7 см на 2 и получаем величину, равную 14 см. Ответ: D заданной фигуры равен 14 см.

Иногда приходится определять диаметр окружности лишь по ее длине. Здесь необходимо применить специальную формулу, помогающую определить Формула L = 2 Пи * R, где 2 — это неизменная величина (константа), а Пи = 3,14. А так как известно, что R = D * 2, то формулу можно представить и другим способом

Данное выражение применимо и как формула диаметра окружности. Подставив известные в задаче величины, решаем уравнение с одним неизвестным. Допустим, длина равна 7 м. Следовательно:

Ответ: диаметр равен 21,98 метрам.

Если известно значение площади, то также можно определить диаметр окружности. Формула, которая применяется в данном случае, выглядит так:

D = 2 * (S / Пи) * (1 / 2)

S — в данном случае Допустим, в задаче она равна 30 кв. м. Получаем:

D = 2 * (30 / 3, 14) * (1 / 2) D = 9, 55414

При обозначенной в задаче величине, равной объему (V) шара, применяется следующая формула нахождения диаметра: D = (6 V / Пи) * 1 / 3.

Иногда приходится находить диаметр окружности, вписанной в треугольник. Для этого по формуле находим радиус представленной окружности:

R = S / p (S — площадь заданного треугольника, а p — периметр, разделенный на 2).

Полученный результат увеличиваем вдвое, учитывая, что D = 2 * R.

Нередко находить диаметр окружности приходится и в быту. К примеру, при определении что равносильно его диаметру. Для этого необходимо обмотать палец потенциального обладателя кольца ниткой. Отметить точки соприкосновения двух концов. Измерить линейкой длину от точки до точки. Полученное значение умножаем на 3,14, следуя формуле определения диаметра при известной длине. Так что, утверждение о том, что познания в геометрии и алгебре в жизни не пригодятся, не всегда соответствует действительности. А это является серьезным поводом для того, чтобы более ответственно относиться к школьным предметам.

Длина окружности – определение, формулы, примеры

Что такое длина окружности

Длина окружности – это расстояние вокруг границы окружности. Это то же самое, что вычисление периметра любого многоугольника, такого как треугольник, квадрат и прямоугольник. Длина окружности измеряется в метрах, километрах, дюймах и т. д.

На приведенном ниже рисунке показана длина окружности.

Длина окружности

Формулы

Есть два способа получить длину окружности. Первый метод использует радиус окружности, а второй использует диаметр для расчета длины окружности. Но важно знать, что оба дают одинаковый результат.

Как найти длину окружности с радиусом

Когда известен радиус окружности, ниже приводится формула для определения длины окружности:

Длина окружности Формула

Давайте решим несколько примеров, чтобы лучше понять концепцию.

Решенные примеры

Найдите длину окружности радиусом 10 дюймов.

Решение:

Как мы знаем,
Окружность (C) = 2πr, здесь r = 10 дюймов, π = 3,141
= 2 × 3,141 × 10
= 62,82 дюйма

Рассчитайте Radius

Calcure Radius of Radius of Radius of Radius of Radius of Radius of Radius of Radius of Radius

. круг с окружностью 12 дюймов.

Решение:

Как мы знаем,
Окружность (C) = 2πr, здесь C = 12 дюймов, π = 3,141
12 = 2 × 3,141 × r
r = 12/2 × 3,141
= 1,91 дюйма

Как рассчитать длину окружности с диаметром

Когда диаметр окружности дан, формула для определения длины окружности приведена ниже:

Длина окружности с диаметром

Вывод

Приведенная выше формула может быть получена из стандартных формул A = 2 πr …. .(1)

Как мы знаем,

Диаметр

4 (

д ) = 2 × radius ( r )

r = d /2

Putting the value of r in equation (1) we get,

A = 2 × π × d /2

A = πd

Давайте решим несколько примеров, чтобы лучше понять концепцию.

Найдите точную длину окружности диаметром 6 дюймов через π ?

Решение:

Как известно,
A = πd, здесь d = 6 дюймов
= (π × 6) дюймов
= 18,84π дюймов

Какова примерная длина окружности данного круга?

Решение:

Как мы знаем,
A = πd, здесь π = 3,141, d = 8 дюймов
= (3,141 × 8) дюймов
= 25,12 дюймов

220 ярдов. Найдите диаметр и радиус окружности.

Решение:

Как мы знаем,
Длина окружности (C) = 2πr, здесь C = 220 дюймов, π = 3,141
Диаметр (d) = 2 × радиус (r)
d = (2 × 35,02) ярда
d = 70,04 ярда

Найдите площадь и длину окружности круга с радиусом 4 дюйма.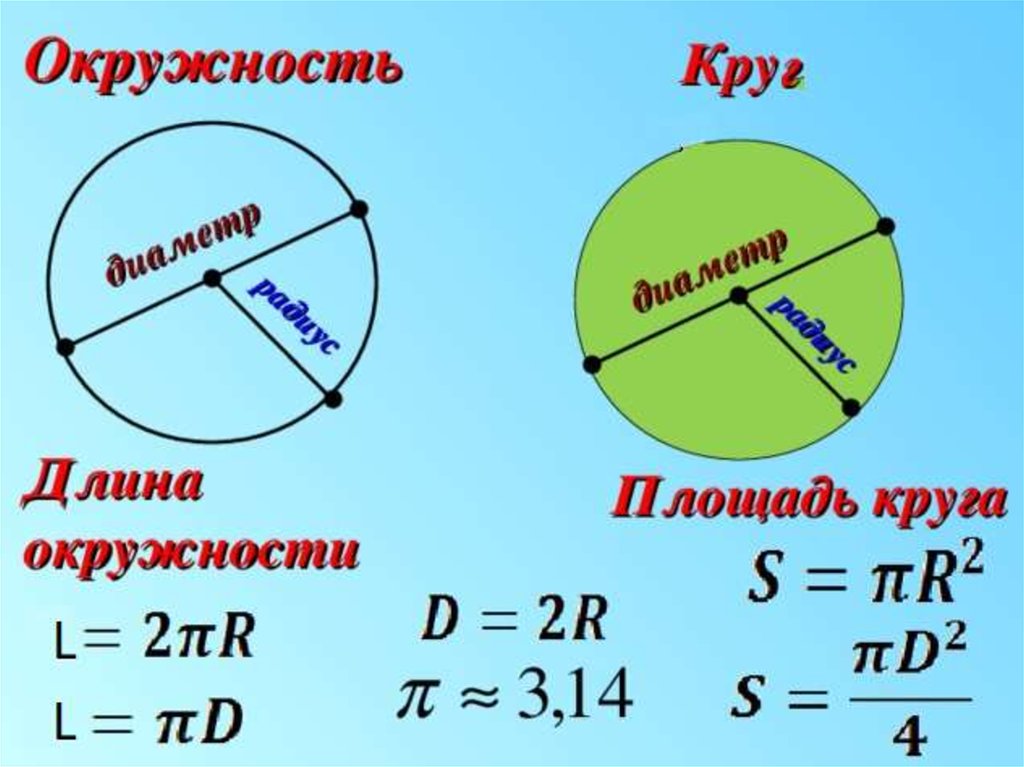

Решение:

Как мы знаем,
Окружность (C) = 2πr, здесь π = 3,141, r = 4 дюйма
= (2 × 3,141 × 4)
= 25,12 дюйма
Теперь
A = πr ² , здесь π = 3,141, r = 11 дюймов

Нахождение длины окружности с помощью эксперимента

Нахождение длины окружности во многих классах по всему миру сравнивает диаметр окружности с их окружностью:

Сравните длину окружности бочки с диаметром бочка.

Или на снегу:

Сравните длину окружности на снегу с ее диаметром или прокатом автомобильной шины.

Каждый ребенок в мире обнаружил, что

Примерно 3 диаметра = длина окружности
Неважно, какого размера круг

Чтобы быть более точным, математики обнаружили, что диаметр проходит по периметру 3,141592 …… и номер будет продолжаться вечно.

Окружность = 3,142…. диаметр

И чтобы еще больше запутать вещи, математики назвали это число 3,142….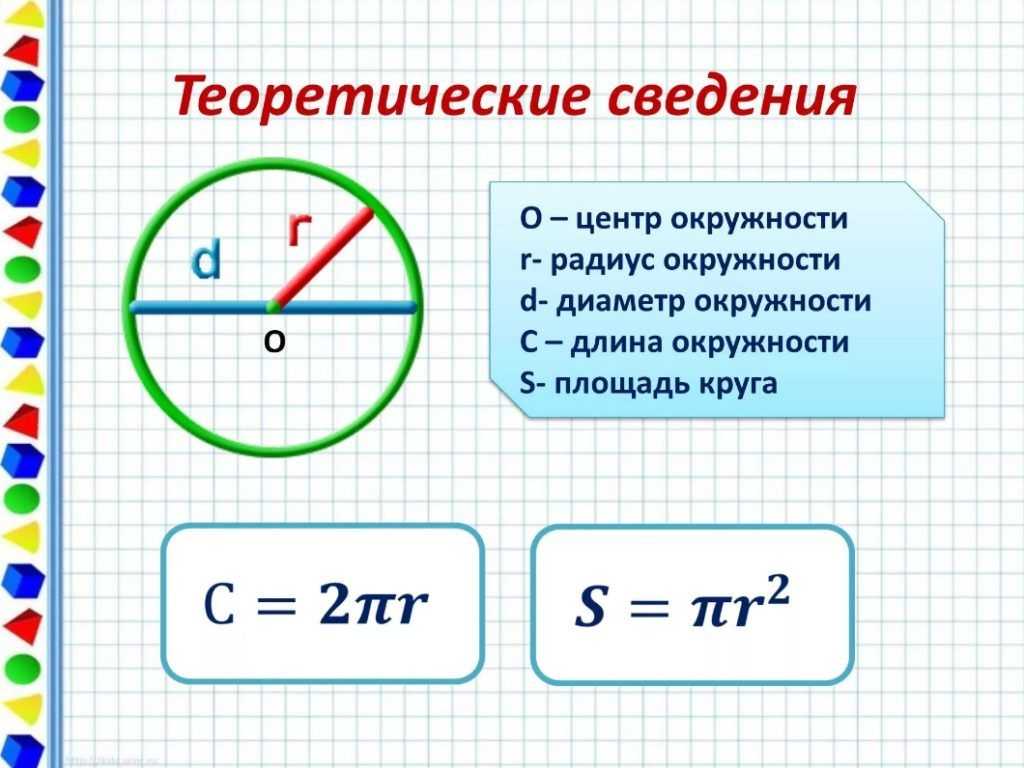 Пи (произносится как пирог).

3,142….= Pi

И, чтобы еще больше запутать, Пи обозначали символом π окружность = 3,142….умножить на диаметр

Или

Длина окружности = `pitimesD`

 

ПРИМЕЧАНИЕ 1: 92` 

 

Пример 1

Жестяная банка диаметром 8 см и высотой 15 см снабжена этикеткой. Этикетка склеивается с нахлестом 1 см. Зазор между этикеткой и верхом и дном банки составляет 1 см.

Какой длины и высоты должна быть этикетка?

Ответ:

Высота этикетки = высота банки – зазор сверху и снизу.

Следовательно, высота этикетки `=15–(1\times\2)=15–2=13 см`  

Длина этикетки = Окружность банки + нахлест

Следовательно, длина этикетки `=2\pir+ 1` 

`r = 1/2\ диаметр=1/2\times8=4` 

Длина этикетки `=2\times\pi\times4+1`

Длина этикетки `=25,13+1 =26,13 см`

Ответ:  

Этикетка должна быть 26,13 см в длину и 13 см в высоту

 

Пример 2

Фабрика производит новые гигантские скрепки. Диаграмма одного помещается рядом с сантиметровой линейкой, как показано ниже. Загнутые концы представляют собой полукруги.

 

Скрепки нарезаны из рулонов скрученной проволоки длиной 1000 м. Подсчитайте, сколько скрепок можно сделать из каждого рулона проволоки.

Ответ:

Сначала мы должны определить длину проволоки, необходимой для изготовления каждой скрепки.

Длина проволоки, необходимая для каждой скрепки, равна общей длине всех прямых участков (цветные участки показаны ниже) и дуговой длине трех полукругов (отмечены серым цветом ниже).

Длина красного прямого участка, показанного ниже:

`5см–0,9см=4,1см`

Длина желтого прямого участка, показанного ниже: –2,1 см=4,7 см`

Длина зеленого прямого участка, показанного ниже:

`5 см–2,1 см=2,9 см`

Длина показанного ниже фиолетового прямого участка:

«6,8–0,9 см = 5,9 см»

Следовательно, длина прямых участков = длина красного цвета + длина желтого цвета + длина зеленого цвета + длина фиолетового цвета

Длина прямых участков `=4,1+4,7+2,9+5,9=17,6 см` 

Длина дуги вокруг полукруга равна половине длины окружности всей окружности, поэтому если

Длина окружности `=2\pir`

Затем дуга полукруга `=\pir`

Радиус левого полукруга на скрепке, показанной ниже, равен:

`0,9см–0см=0,9см` semicircle `=\pir=\pi\times0.