Как разложить х в кубе минус 1: Как разложить х^3-y^3″х» в кубе минус «у» в кубе

правила применения формул сокращенного умножения

Формулы или правила сокращенного умножения используются в арифметике, а точнее — в алгебре, для более быстрого процесса вычисления больших алгебраических выражений. Сами же формулы получены из существующих в алгебре правил для умножения нескольких многочленов.

Использование данных формул обеспечивает достаточно оперативное решение различных математических задач, а также помогает осуществлять упрощение выражений. Правила алгебраических преобразований позволяют выполнять некоторые манипуляции с выражениями, следуя которым можно получить в левой части равенства выражение, стоящее в правой части, или преобразовать правую часть равенства (чтобы получить выражение, стоящее в левой части после знака равенства).

Удобно знать формулы, применяемые для сокращенного умножения, на память, так как они нередко используются при решении задач и уравнений. Ниже перечислены основные формулы, входящие в данный список, и их наименование.

Квадрат суммы

Чтобы вычислить квадрат суммы, необходимо найти сумму, состоящую из квадрата первого слагаемого, удвоенного произведения первого слагаемого на второе и квадрата второго. В виде выражения данное правило записывается следующим образом: (а + с)² = a² + 2ас + с².

Квадрат разности

Чтобы вычислить квадрат разности, необходимо вычислить сумму, состоящую из квадрата первого числа, удвоенного произведения первого числа на второе (взятое с противоположным знаком) и квадрата второго числа. В виде выражения данное правило выглядит следующим образом: (а — с)² = а² — 2ас + с².

Разность квадратов

Формула разности двух чисел, возведенных в квадрат, равна произведению суммы этих чисел на их разность. В виде выражения данное правило выглядит следующим образом: a² — с² = (a + с)·(a — с).

Куб суммы

Чтобы вычислить куб суммы двух слагаемых, необходимо вычислить сумму, состоящую из куба первого слагаемого, утроенного произведения квадрата первого слагаемого и второго, утроенного произведения первого слагаемого и второго в квадрате, а также куба второго слагаемого.

В виде выражения данное правило выглядит следующим образом: (а + с)³ = а³ + 3а²с + 3ас² + с³.

Сумма кубов

Согласно формуле, приравнивается к произведению суммы данных слагаемых на их неполный квадрат разности. В виде выражения данное правило выглядит следующим образом: а³ + с³ = (а + с)·(а² — ас + с²).

Пример. Необходимо вычислить объем фигуры, которая образована сложением двух кубов. Известны лишь величины их сторон.

Если значения сторон небольшие, то выполнить вычисления просто.

Если же длины сторон выражаются в громоздких числах, то в этом случае проще применить формулу «Сумма кубов», которая значительно упростит вычисления.

Куб разности

Выражение для кубической разности звучит так: как сумма третьей степени первого члена, утроенного отрицательного произведения квадрата первого члена на второй, утроенного произведения первого члена на квадрат второго и отрицательного куба второго члена. В виде математического выражения куб разности выглядит следующим образом: (а — с)³ = а³ — 3а²с + 3ас² — с³.

2\right)\]

Формулы сокращенного умножения.

Изучение формул сокращенного умножения: квадрата суммы и квадрата разности двух выражений; разности квадратов двух выражений; куба суммы и куба разности двух выражений; суммы и разности кубов двух выражений.

Применение формул сокращенного умножения при решении примеров.

Для упрощения выражений, разложения многочленов на множители, приведения многочленов к стандартному виду используются формулы сокращенного умножения. Формулы сокращенного умножения нужно знать наизусть

.

Пусть а, b R. Тогда:

1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

(a + b) 2 = a 2 + 2ab + b 2

2. Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

(a — b) 2 = a 2 — 2ab + b 2

3. Разность квадратов двух выражений равна произведению разности этих выражений и их суммы.

a 2 — b 2 = (a -b) (a+b)

4. Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

5. Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3

6. Сумма кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений.

a 3 + b 3 = (a + b) (a 2 — ab + b 2)

7. Разность кубов двух выражений равна произведению разности первого и второго выражения на неполный квадрат суммы этих выражений.

a 3 — b 3 = (a — b) (a 2 + ab + b 2)

Применение формул сокращенного умножения при решении примеров.

Пример 1.

Вычислить

а) Используя формулу квадрата суммы двух выражений, имеем

(40+1) 2 = 40 2 + 2 · 40 · 1 + 1 2 = 1600 + 80 + 1 = 1681

б) Используя формулу квадрата разности двух выражений, получим

98 2 = (100 – 2) 2 = 100 2 — 2 · 100 · 2 + 2 2 = 10000 – 400 + 4 = 9604

Пример 2.

Вычислить

Используя формулу разности квадратов двух выражений, получим

Пример 3.

Упростить выражение

(х — у) 2 + (х + у) 2

Воспользуемся формулами квадрата суммы и квадрата разности двух выражений

(х — у) 2 + (х + у) 2 = х 2 — 2ху + у 2 + х 2 + 2ху + у 2 = 2х 2 + 2у 2

Формулы сокращенного умножения в одной таблице:

(a + b) 2 = a 2 + 2ab + b 2
(a — b) 2 = a 2 — 2ab + b 2
a 2 — b 2 = (a — b) (a+b)
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3
a 3 + b 3 = (a + b) (a 2 — ab + b 2)
a 3 — b 3 = (a — b) (a 2 + ab + b 2)

В предыдущих уроках мы рассмотрели два способа разложения многочлена на множители: вынесение общего множителя за скобки и способ группировки .

В этом уроке мы рассмотрим еще один способ разложения многочлена на множители с применением формул сокращённого умножения .

Рекомендуем каждую формулу прописать не менее 12 раз. Для лучшего запоминания выпишите все формулы сокращённого умножения себе на небольшую шпаргалку .

Вспомним, как выглядит формула разности кубов.

a 3 − b 3 = (a − b)(a 2 + ab + b 2)

Формула разности кубов не очень проста для запоминания, поэтому рекомендуем использовать специальный способ для её запоминания.

Важно понимать, что любая формула сокращённого умножения действует и в обратную сторону .

(a − b)(a 2 + ab + b 2) = a 3 − b 3

Рассмотрим пример. Необходимо разложить на множители разность кубов.

Обратим внимание, что «27а 3 » — это «(3а) 3 », значит, для формулы разности кубов вместо «a » мы используем «3a ».

Используем формулу разности кубов. На месте «a 3 » у нас стоит «27a 3 », а на месте «b 3 », как и в формуле, стоит «b 3 ».

Применение разности кубов в обратную сторону

Рассмотрим другой пример. Требуется преобразовать произведение многочленов в разность кубов, используя формулу сокращенного умножения.

Обратите внимание, что произведение многочленов «(x − 1)(x 2 + x + 1) » напоминает правую часть формулы разности кубов «», только вместо «a » стоит «x », а на месте «b » стоит «1 ».

Используем для «(x − 1)(x 2 + x + 1) » формулу разности кубов в обратную сторону.

Рассмотрим пример сложнее. Требуется упростить произведение многочленов.

Если сравнить «(y 2 − 1)(y 4 + y 2 + 1) » с правой частью формулы разности кубов
«a 3 − b 3 = (a − b)(a 2 + ab + b 2) », то можно понять, что на месте «a » из первой скобки стоит «y 2 , а на месте «b » стоит «1 ».

Многочлены. Разложение многочлена на множители: способы, примеры :: SYL.ru

Понятия «многочлен» и «разложение многочлена на множители» по алгебре встречаются очень часто, ведь их необходимо знать, чтобы с легкостью производить вычисления c большими многозначными числами. В этой статье будет описано несколько способов разложения. Все они достаточно просты в применении, стоит лишь правильно подобрать нужный в каждом конкретном случае.

Понятие многочлена

Многочлен является суммой одночленов, то есть выражений, содержащих только операцию умножения.

Например, 2 * x * y – это одночлен, а вот 2 * x * y + 25 — многочлен, который состоит из 2 одночленов: 2 * x * y и 25. Такие многочлены называет двучленами.

Иногда для удобства решения примеров с многозначными значениями выражение необходимо преобразовать, например, разложить на некоторое количество множителей, то есть чисел или выражений, между которыми производится действие умножения. Есть ряд способов разложения многочлена на множители. Стоит рассмотреть их начиная с самого примитивного, который применяют еще в начальных классах.

Группировка (запись в общем виде)

Формула разложения многочлена на множители способом группировки в общем виде выглядит таким образом:

ac + bd + bc + ad = (ac + bc) + (ad + bd)

Необходимо сгруппировать одночлены так, чтобы в каждой группе появился общий множитель.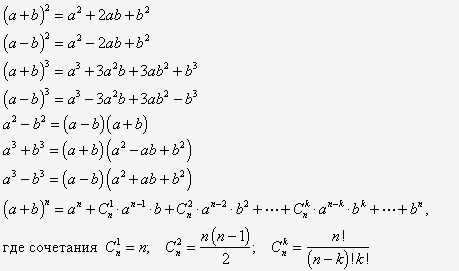 В первой скобке это множитель с, а во второй – d. Это нужно сделать для того, чтобы затем вынести его за скобку, тем самым упростив вычисления.

Алгоритм разложения на конкретном примере

Простейший пример разложения многочлена на множители способом группировки приведен ниже:

10ас + 14bc – 25a — 35b = (10ас – 25а) + (14bc — 35b)

В первую скобку нужно взять слагаемые с множителем а, который и будет общим, а во вторую – со множителем b. Обратите внимание на знаки + и – в готовом выражении. Мы ставим перед одночленом тот знак, который был в начальном выражении. То есть нужно работать не с выражением 25а, а с выражением -25. Знак минус как бы «приклеить» к стоящему за ним выражению и всегда учитывать его при вычислениях.

На следующем шаге нужно вынести множитель, который является общим, за скобку. Именно для этого и делается группировка. Вынести за скобку – значит выписать перед скобкой (опуская знак умножения) все те множители, которые с точностью повторяются во всех слагаемых, которые находятся в скобке. Если в скобке не 2, а 3 слагаемых и больше, общий множитель должен содержаться в каждом из них, иначе его нельзя вынести за скобку.

В нашем случае — только по 2 слагаемых в скобках. Общий множитель сразу виден. В первой скобке – это а, во второй – b. Здесь нужно обратить внимание на цифровые коэффициенты. В первой скобке оба коэффициента (10 и 25) кратны 5. Это значит, что можно вынести за скобку не только а, но и 5а. Перед скобкой выписать 5а, а затем каждое из слагаемых в скобках поделить на общий множитель, который был вынесен, и также записать частное в скобках, не забывая о знаках + и — Со второй скобкой поступить также, вынести 7b, так как и 14 и 35 кратно 7.

Итак:

10ас + 14bc – 25a — 35b = (10ас – 25а) + (14bc — 35b) = 5а(2c — 5) + 7b(2c – 5).

Получилось 2 слагаемых: 5а(2c — 5) и 7b(2c – 5). Каждое из них содержит общий множитель (все выражение в скобках здесь совпадает, значит, является общим множителем): 2с – 5. Его тоже нужно вынести за скобку, то есть во второй скобке остаются слагаемые 5а и 7b:

5а(2c — 5) + 7b(2c – 5) = (2c – 5)*(5а + 7b).

Итак, полное выражение:

10ас + 14bc – 25a — 35b = (10ас – 25а) + (14bc — 35b) = 5а(2c — 5) + 7b(2c – 5) = (2c – 5)*(5а + 7b).

Таким образом, многочлен 10ас + 14bc – 25a — 35b раскладываается на 2 множителя: (2c – 5) и (5а + 7b). Знак умножения между ними при записи можно опускать

Иногда встречаются выражения такого типа: 5а² + 50а³ , здесь можно вынести за скобку не только а или 5а, а даже 5а². Всегда нужно стараться вынести максимально большой общий множитель за скобку. В нашем случае, если разделить каждое слагаемое на общий множитель, то получается:

5а² / 5а² = 1; 50а³ / 5а² = 10а (при вычислении частного нескольких степеней с равными основаниями основание сохраняется, а показатель степени вычитается). Таким образом, в скобке остается единица (ни в коем случае не забывайте писать единицу, если выносите за скобку целиком одно из слагаемых) и частное от деления: 10а. Получается, что:

5а² + 50а³ = 5а² (1 + 10а)

Формулы квадратов

Для удобства вычислений были выведены несколько формул. Они называются формулами сокращенного умножения и используются довольно часто. Эти формулы помогают разложить на множители многочлены, содержащие степени. Это еще один действенный способ разложения на множители. Итак, вот они:

• a² + 2ab + b² = (a + b)² — формула, получившая название «квадрат суммы», так как в результате разложения в квадрат берется сумма чисел, заключенная в скобки, то есть значение этой суммы умножается само на себя 2 раза, а значит, является множителем.
• a² + 2ab — b² = (a — b)^{2 —} формула квадрата разности, она аналогична предыдущей. В результате получается разность, заключенная в скобки, содержащаяся в квадратной степени.
• a² — b² = (a + b)(а — b) — это формула разности квадратов, так как изначально многочлен состоит из 2 квадратов чисел или выражений, между которыми производится вычитание. Пожалуй, из трех названных она используется чаще всего.

Примеры на вычисления по формулам квадратов

Вычисления по ним производятся достаточно просто. Например:

1. 25x² + 20xy + 4y² — используем формулу «квадрат суммы».
2. 25x² являетсяквадратом выражения 5х. 20ху — удвоенное произведение 2*(5х*2у), а 4y² — это квадрат 2у.
3. Таким образом, 25x² + 20xy + 4y² = (5x+ 2у)² = (5x+ 2у)(5x+ 2у). Данный многочлен раскладывается на 2 множителя (множители одинаковые, поэтому записывается в виде выражения с квадратной степенью).

Действия по формуле квадрата разности производятся аналогично этим. Остается формула разность квадратов. Примеры на эту формулу очень легко определить и найти среди других выражений. Например:

• 25а² — 400 = (5а — 20)(5а + 20). Так как 25а² = (5а)², а 400 = 20²
• 36х² — 25у² = (6х — 5у) (6х + 5у). Так как 36х² = (6х)², а 25у² = (5у²)
• с² — 169b² = (с — 13b)(c + 13b). Так как 169b² = (13b)²

Важно, чтобы каждое из слагаемых являлось квадратом какого-либо выражения. Тогда этот многочлен подлежит разложению на множители по формуле разности квадратов. Для этого не обязательно, чтобы над числом стояла именно вторая степень. Встречаются многочлены, содежащие большие степени, но все равно подходящие к этим формулам.

a⁸+10a⁴+25 = (a⁴)² + 2*a⁴*5 + 5² = (a⁴+5)²

В данном примере а⁸можно представить как (a⁴)², то есть квадрат некого выражения. 25 — это 5², а 10а⁴ — это удвоенное произведение слагаемых 2*a⁴*5. То есть данное выражение, несмотря на наличие степеней с большими показателями, можно разложить на 2 множителя, чтобы в последствии работать с ними.

Формулы кубов

Такие же формулы существуют для разложения на множители многочленов, содержащих кубы. Они немного посложнее тех, что с квадратами:

• a³ + b³ = (а + b)(a² — ab + b²) — эту формулу называют суммой кубов, так как в начальном виде многочлен представляет собой сумму двух выражений или чисел, заключенных в куб.
• a³ — b³ = (а — b)(a² + ab + b²) — формула, идентичная предыдущей, обозначена как разность кубов.
• a³ + 3a²b + 3ab²+ b³ = (a + b)^{3 —} куб суммы, в результате вычислений получается сумма чисел или выражений, заключенная в скобки и умноженная сама на себя 3 раза, то есть находящаяся в кубе
• a³ — 3a²b + 3ab² — b³ = (a — b)³ — формула, составленная по аналогии предыдущей с изменением лишь некоторых знаков математических операций (плюс и минус), имеет название «куб разности».

Последние две формулы практически не испольуются с целью разложения многочлена на множители, так как они сложны, и достаточно редко встречаются многочлены, полностью соответствующие именно такому строению, чтобы их можно было разложить по этим формулам. Но их все равно нужно знать, так как они потребуются при действиях в обратном направлении — при раскрытии скобок.

Примеры на формулы кубов

Рассмотрим пример: 64a³ − 8b³ = (4a)³ − (2b)³ = (4a − 2b)((4a)² + 4a*2b + (2b)²) = (4a−2b)(16a² + 8ab + 4b²).

Здесь взяты достаточно простые числа, поэтому сразу можно увидеть, что 64а³ — это (4а)³, а 8b³ — это (2b)³. Таким образом, этот многочлен раскладывается по формуле разность кубов на 2 множителя. Действия по формуле суммы кубов производятся по аналогии.

Важно понимать, что далеко не все многочлены подлежат разложению хотя бы одним из способов. Но есть такие выражения, которые содержат большие степени, чем квадрат или куб, но их также можно разложить по формуам сокращенного умножения. Например: x¹² + 125y³=(x⁴)³+(5y)³=(x⁴+5y)*((x⁴)² − x⁴*5y+(5y)²)=(x⁴ + 5y)(x⁸ − 5x⁴y + 25y²).

В этом примере содержится аж 12 степень. Но даже его возможно разложить на множители по формуле суммы кубов. Для этого нужно представить х¹² как (x⁴)³ , то есть как куб какого-либо выражения. Теперь в формулу вместо а нужно подставлять именно его. Ну а выражение 125у³ — это куб 5у. Далее следует составить произведение по формуле и произвести вычисления.

На первых порах или в случае возникших сомнений, вы всегда можете произвести проверку обратным умножением. Вам нужно лишь раскрыть скобки в получившемся выражении и выполнить действия с подобными слагаемыми. Этот метод относится ко всем перечисленным способам сокращения: как к работе с общим множителем и группировке, так и к действиям по формулам кубов и квадратных степеней.

факторинговых полиномов | Колледж Алгебра

Результаты обучения

• Определите и факторизуйте наибольший общий делитель многочлена.
• Разложите трехчлен со старшим коэффициентом 1.
• Фактор по группировке.
• Разложите на множители совершенный квадратный трехчлен.
• Коэффициент разности квадратов.
• Фактор суммы и разности кубов.
• Фактор выражения с отрицательными или дробными показателями.

Представьте, что мы пытаемся найти площадь газона, чтобы определить, сколько семян травы нужно купить. Газон — это зеленая часть на рисунке ниже. 9{2}-40x[/латекс] единиц ² . Эта площадь также может быть выражена в факторизованной форме как [латекс]20x\влево(3x — 2\вправо)[/латекс] единиц ² . Мы можем подтвердить, что это эквивалентное выражение, путем умножения.

Многие полиномиальные выражения можно записать в более простой форме с помощью факторизации. В этом разделе мы рассмотрим различные методы, которые можно использовать для факторизации полиномиальных выражений.

Основы факторинга

Когда мы изучали дроби, мы узнали, что 9{2}[/латекс].

При разложении полиномиального выражения на множители первым шагом является проверка GCF. Ищите GCF коэффициентов, а затем ищите GCF переменных.

A Общее примечание: Наибольший общий делитель

Наибольший общий делитель (GCF) многочленов — это наибольший многочлен, который равномерно делится на многочлены.

Как: По полиномиальному выражению вынести наибольший общий делитель

9{2}\справа)[/латекс]

Ключевые понятия

• Наибольший общий множитель, или GCF, может быть вынесен из многочлена. Проверка GCF должна быть первым шагом в любой проблеме факторинга.
• Трехчлены со старшим коэффициентом 1 можно разложить на множители, найдя числа, у которых есть произведение третьего члена и суммы второго члена.
• Трехчлены можно разложить на множители, используя процесс, называемый разложением на множители путем группировки.
• Совершенные квадратные трехчлены и разность квадратов являются специальными произведениями и могут быть факторизованы с помощью уравнений. 9{2}+bx+c[/latex] путем деления терма 90 102 x 90 103 на сумму двух термов, факторизации каждой части выражения по отдельности, а затем вынесения на множитель GCF всего выражения 90 434.

  наибольший общий делитель

  наибольший полином, который делится нацело на каждый полином

  Как разложить полиномиальное выражение на множители

  В математике факторизация или разложение на множители — это разбиение многочлена на произведение других меньших многочленов. При желании вы можете затем перемножить эти множители вместе, и вы должны получить исходный многочлен (это отличный способ проверить свои навыки факторинга).

  Один набор множителей, например, 24 равен 6 и 4, потому что 6 умножить на 4 = 24. Когда у вас есть многочлен, один из способов его решения — разложить его на произведение двух двучленов.

  У вас есть несколько вариантов факторинга на выбор при решении полиномиальных уравнений:

  • Для полинома, независимо от того, сколько членов он имеет, всегда сначала проверяйте наибольший общий делитель (НОК). Буквально, наибольший общий делитель — это самое большое выражение, которое войдет во все термины. Использование GCF похоже на использование дистрибутивного свойства в обратном порядке.

  • Если уравнение представляет собой трехчлен — в нем три члена — вы можете использовать метод FOIL для обратного умножения двучленов.

  • Если это бином , ищите разность квадратов, разность кубов или сумму кубов.

  Наконец, после того, как полином полностью факторизован, вы можете использовать свойство нулевого произведения для решения уравнения.

  Если многочлен не имеет множителей, он называется простым числом , потому что его единственными делителями являются 1 и он сам. Когда вы испробовали все приемы факторизации, которые у вас есть (НОК, обратная ФОЛЬГА, разность квадратов и т. д.), и квадратное уравнение не будет факторизоваться, тогда вы можете либо дополнить квадрат, либо использовать квадратную формулу для решения уравнения . Выбор ваш.

  Потенциально вы даже можете всегда использовать формулу квадрата или квадрата (и пропустить разложение на множители) для решения уравнения. Факторинг иногда может быть быстрее, поэтому рекомендуется сначала попробовать его.

  Стандартная форма для квадратного выражения (просто квадратное уравнение без знака равенства) представляет собой член в квадрате x , за которым следует член x , за которым следует константа — другими словами,

  Если вам дано квадратное выражение не в стандартной форме, перепишите его в стандартной форме, расположив степени в порядке убывания. Это упрощает факторинг (а иногда даже необходим для факторинга).

  Всегда первый шаг: ищите GCF

  Независимо от того, сколько членов содержит многочлен, всегда важно сначала проверить наличие наибольшего общего делителя (НОД). Если есть GCF, это значительно упростит разложение полинома на множители, потому что количество множителей каждого члена будет меньше (потому что вы вынесете на множители один или несколько из них!). Это особенно важно, если GCF включает переменную.

  Если вы забудете учесть этот GCF, вы также можете забыть найти решение, и это может запутать вас во многих отношениях! Без этого решения вы можете пропустить корень, и тогда вы можете получить неправильный график для вашего многочлена.

  Например, чтобы разложить полином

  , выполните следующие действия:

  1. Разбейте каждый член на простые множители.

     Это расширяет выражение до

  2. Ищите факторы, которые появляются в каждом термине, чтобы определить GCF.

     В этом примере вы можете увидеть одну 2 и две x в каждом термине. Они подчеркнуты ниже:

  3. Вынесите GCF из каждого члена перед круглыми скобками и оставьте остатки внутри скобок.

     Теперь у вас есть

  4. Умножьте, чтобы упростить каждое слагаемое.

     Это дает вам

  5. Распространить, чтобы убедиться в правильности GCF.

  Подведение итогов: метод FOIL для трехчленов

  После того, как вы проверили полином на наличие GCF (независимо от того, есть он у него или нет), попробуйте еще раз провести факторинг. Вы можете обнаружить, что легче учитывать после того, как GCF был вынесен за скобки. Вышеприведенный многочлен имел два множителя:

  Тем не менее, второй множитель может снова разложиться на множители, потому что он трехчленный, и если это произойдет, у вас будет еще два множителя, оба из которых являются двучленными.

  Большинство учителей используют метод факторинга «угадай и проверь», когда вы записываете два набора скобок —

  — и буквально подставляете предположения для факторов, чтобы увидеть, работает ли что-нибудь. Возможно, вашим первым предположением для этого примера было бы (3 x – 2)( x – 1), но если вы СОЛОМАЕТЕ это, вы получите

  , и вам снова придется угадывать. Этот метод «угадай-и-проверь» в лучшем случае оооооочень утомительный. На самом деле, это конкретное квадратичное число равно простому числу , так что вы можете гадать и проверять его целый день, и оно не даст , а не множителей.

  Если вы занимаетесь предварительным исчислением, а ваш учитель использует метод факторинга «угадай-и-проверь», который вам не подходит, вы попали в нужный раздел. Следующая процедура, называемая методом факторинга FOIL (иногда называемая Британский метод ), всегда работает для разложения трехчленов на множители и является очень полезным инструментом, если вы не можете усвоить принцип догадок и проверок. Когда метод FOIL терпит неудачу, вы точно знаете, что данное квадратичное число является простым.

  Метод факторинга FOIL требует от вас выполнения шагов, необходимых для биномов FOIL, только в обратном порядке. Помните, что когда вы выполняете FOIL, вы умножаете первый, внешний, внутренний и последний члены вместе. Затем вы комбинируете любые подобные термины, которые обычно получаются в результате умножения Внешнего и Внутреннего терминов.

  Например, для коэффициента

  выполните следующие действия:

  1. Сначала проверьте GCF.

     Выражение

     не будет иметь GCF, когда вы разберете его и посмотрите на него в соответствии с шагами, описанными в последнем разделе. Разбивка выглядит так:

     Нет факторов, общих для каждого термина, поэтому GCF отсутствует. Это означает, что вы можете перейти к следующему шагу.

  2. Умножьте квадратичный член и постоянный член.

     При этом будьте осторожны со знаками. В этом примере квадратичный член равен

     .

  3. Запишите парами все факторы результата.

     • –1 x и 10 x

     • 1 x и –10 x

     • –2 x и 5 x

     • 2 x и –5 x

  4. Из этого списка найдите пару, которая складывается для получения коэффициента линейного члена.

     Вам нужна пара, сумма которых равна +3 x . Для этой задачи ответ равен –2 x и 5 x , потому что

  5. Разбейте линейный член на два члена, используя числа из шага 4 в качестве коэффициентов.

     Выписано, теперь у вас есть

     В долгосрочной перспективе жизнь станет проще, если вы всегда сначала упорядочиваете линейный член с наименьшим коэффициентом. Вот почему вы ставите -2 x перед +5 x .

  6. Сгруппируйте четыре термина в два набора по два.

     Всегда ставьте знак плюс между двумя наборами:

  7. Найдите GCF для каждого набора и разложите его.

     Посмотрите на первые два термина. Что у них общего? x. Если вычесть x , у вас будет x ( x — 2). Теперь посмотрим на вторые два термина. У них общая цифра 5. Если вычесть 5 из них, получится 5( х – 2). Полином теперь записывается как x ( x – 2) + 5 ( x – 2).

  8. Найдите GCF двух новых терминов.

     Вы видите ( x – 2) в обоих терминах? Здесь они подчеркнуты: x ( x – 2) + 5 ( x – 8 2) . Это GCF, потому что он появляется в обоих терминах (если вы используете этот метод, последний шаг всегда должен выглядеть так). Вынесите GCF из обоих терминов (это всегда выражение в скобках) на передний план; ты получишь ( x – 2)( ). Когда вы выносите это за скобки, члены, которые не являются GCF, остаются внутри новых круглых скобок. В этом случае вы получите ( x – 2)( x + 5). ( x + 5) — это остаток от удаления GCF.

  Иногда знак должен измениться на шаге 6, чтобы правильно выделить GCF. Но если вы не начнете со знака «плюс» между двумя наборами, вы можете потерять знак «минус», который необходимо учитывать на всем пути. Например, при факторинге

  , вы получите на шаге 5 следующий полином:

  Вынесите x из первого набора и 4 из второго набора, чтобы получить x ( x – 9) + 4 (– x ).

  No related posts.