Построить график функции онлайн с модулем: Построение графиков с модулем онлайн · Как пользоваться Контрольная Работа РУ

Содержание

График функции онлайн с модулем. График функции

К сожалению, не все студенты и школьники знают и любят алгебру, но готовить домашние задания, решать контрольные и сдавать экзамены приходится каждому. Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны. Но кому же хочется получать плохие оценки?

Не желаете пополнить когорту хвостистов и двоечников? Для этого у вас есть 2 пути: засесть за учебники и восполнить пробелы знаний либо воспользоваться виртуальным помощником — сервисом автоматического построения графиков функций по заданным условиям. С решением или без. Сегодня мы познакомим вас с несколькими из них.

Лучшее, что есть в Desmos.com, это гибко настраиваемый интерфейс, интерактивность, возможность разносить результаты по таблицам и бесплатно хранить свои работы в базе ресурса без ограничений по времени. А недостаток — в том, что сервис не полностью переведен на русский язык.

Grafikus. ru — еще один достойный внимания русскоязычный калькулятор для построения графиков. Причем он строит их не только в двухмерном, но и в трехмерном пространстве.

Вот неполный перечень заданий, с которыми этот сервис успешно справляется:

Черчение 2D-графиков простых функций: прямых, парабол, гипербол, тригонометрических, логарифмических и т. д.
Черчение 2D-графиков параметрических функций: окружностей, спиралей, фигур Лиссажу и прочих.
Черчение 2D-графиков в полярных координатах.
Построение 3D-поверхностей простых функций.
Построение 3D-поверхностей параметрических функций.

Готовый результат открывается в отдельном окне. Пользователю доступны опции скачивания, печати и копирования ссылки на него. Для последнего придется авторизоваться на сервисе через кнопки соцсетей.

Координатная плоскость Grafikus.ru поддерживает изменение границ осей, подписей к ним, шага сетки, а также — ширины и высоты самой плоскости и размера шрифта.

Самая сильная сторона Grafikus.ru — возможность построения 3D-графиков. В остальном он работает не хуже и не лучше, чем ресурсы-аналоги.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т. д.

Как мы используем вашу персональную информацию:

Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х , а на оси ординат — значения функции у = f (х) .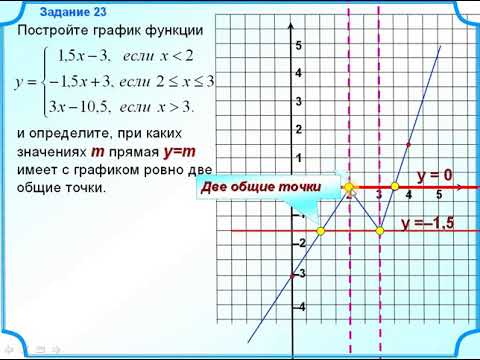

Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.

Другими словами, график функции y = f (х) — это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x) .

На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 — 2х .

Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости). В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».

С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x) , то для нахождения числа f(а) (т. е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).

Например, для функции f(х) = х 2 — 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.

График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция у = х 2 — 2х принимает положительные значения при х и при х > 2 , отрицательные — при 0 у = х 2 — 2х принимает при х = 1 .

Для построения графика функции f(x) нужно найти все точки плоскости, координаты х , у которых удовлетворяют уравнению y = f(x) . В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью.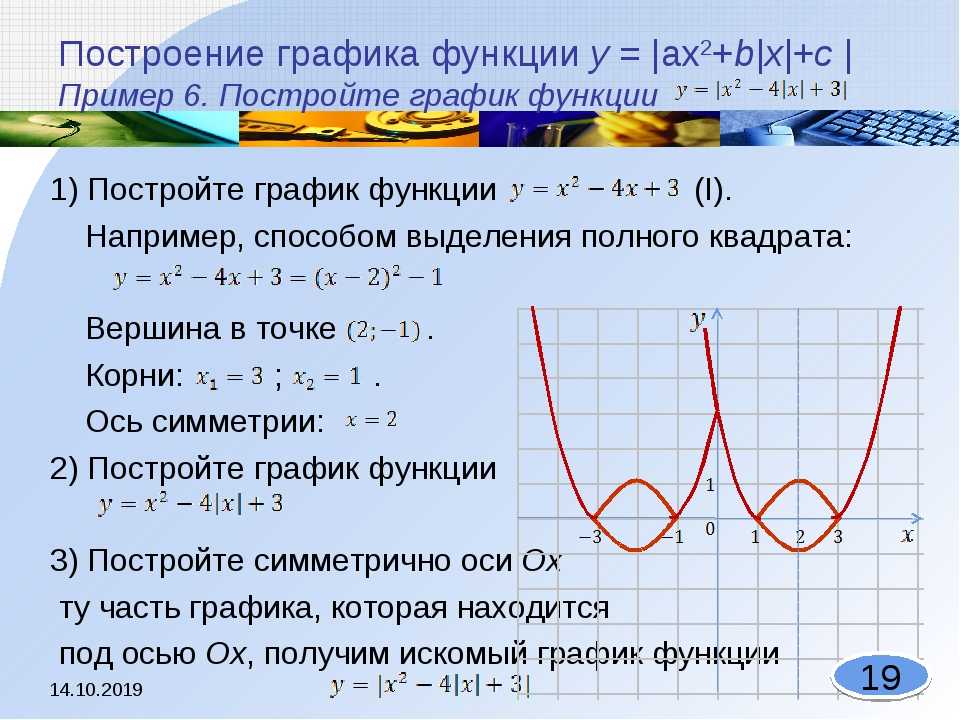 Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.

Таблица выглядит следующим образом:

Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x) . Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).

Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.

Пример 1 . Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:

Соответствующие пять точек показаны на рис. 48.

На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис.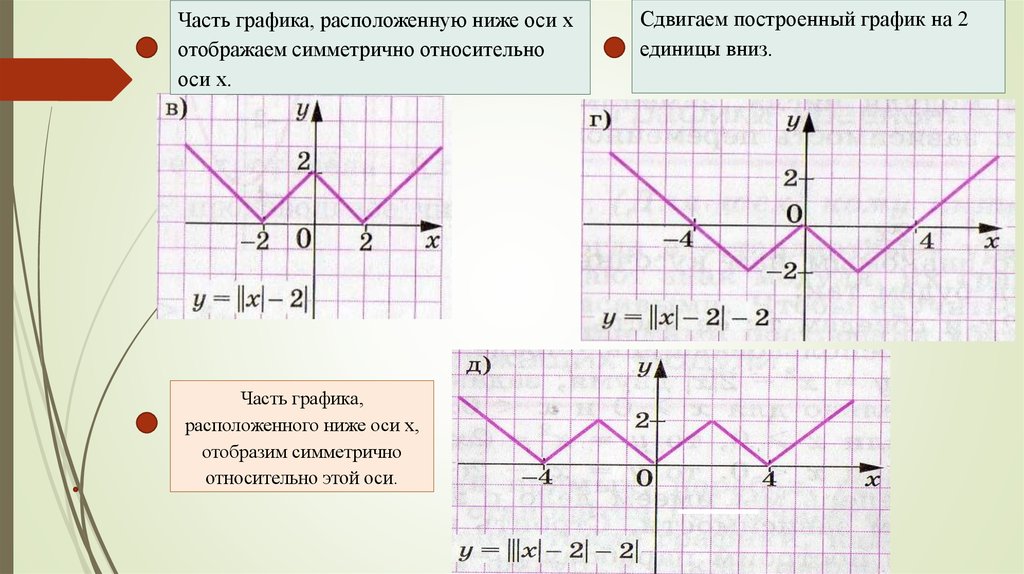 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.

Для обоснования своего утверждения рассмотрим функцию

Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.

Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции,как правило, поступают следующим образом. Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика.

И, наконец, через построенные точки проводят кривую, используя свойства данной функции.

Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.

График функции у = |f(x)|.

Нередко приходится строить график функции y = |f(x) |, где f(х) — заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать

Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х) , у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y = f(x) , имеющих отрицательные координаты, следует построить соответствующие точки графика функции

у = -f(x) (т. е. часть графика функции
y = f(x) , которая лежит ниже оси х, следует симметрично отразить относительно оси х ).

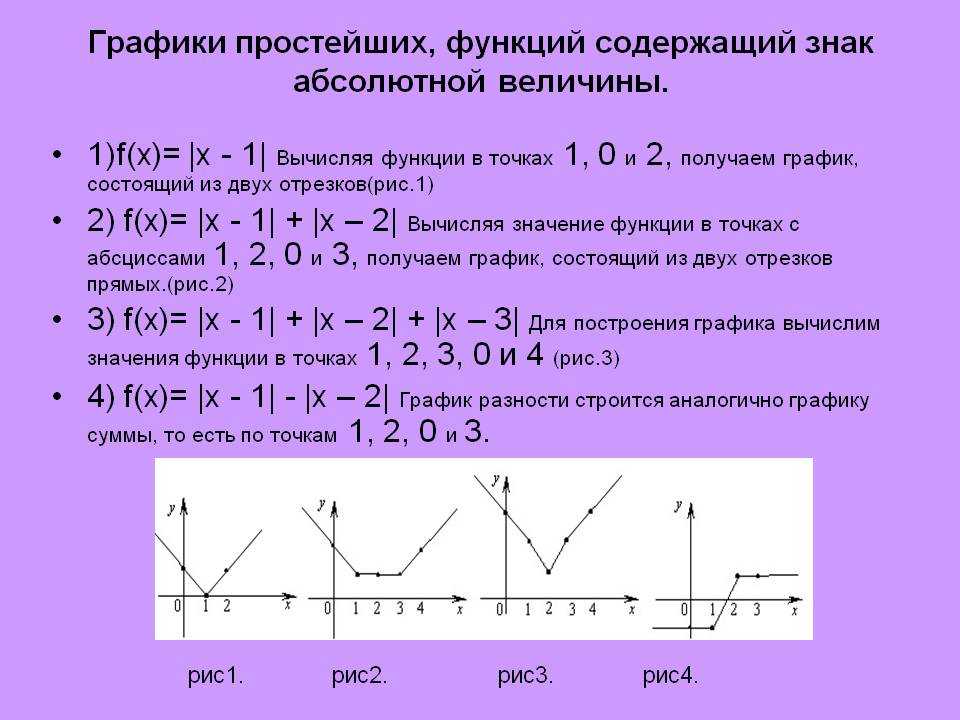
Пример 2. Построить график функции у = |х|.

Берем график функции у = х (рис. 50, а) и часть этого графика при х (лежащую под осью х ) симметрично отражаем относительно оси х . В результате мы и получаем график функции у = |х| (рис. 50, б).

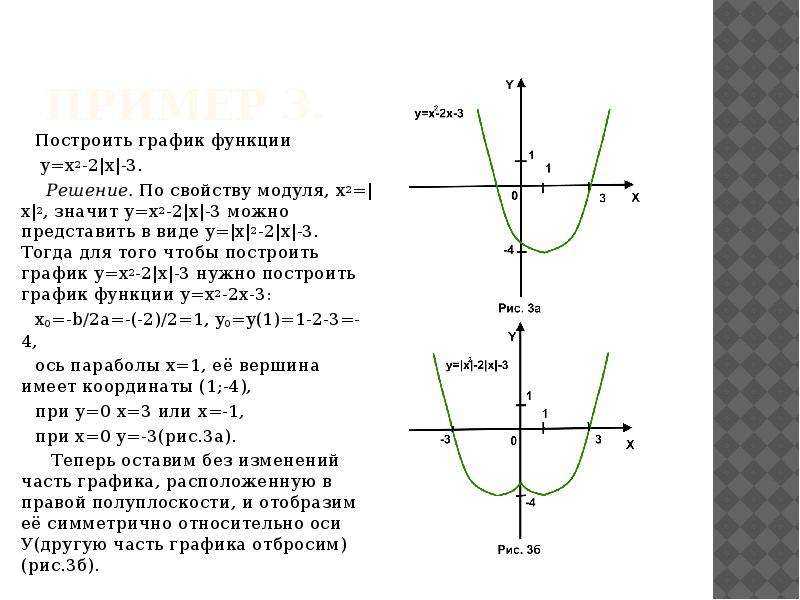
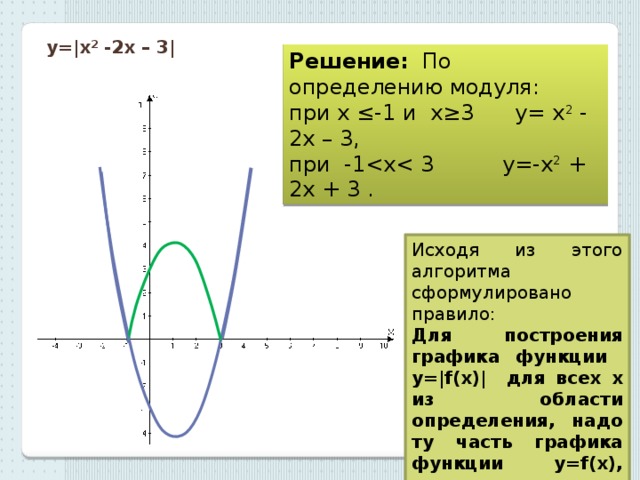
Пример 3 . Построить график функции y = |x 2 — 2x|.

Сначала построим график функции y = x 2 — 2x. График этой функции — парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции у = |х 2 -2х| , исходя из графика функции у = х 2 — 2x

График функции y = f(x) + g(x)

Рассмотрим задачу построения графика функции y = f(x) + g(x). если заданы графики функций y = f(x) и y = g(x) .

Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x).

Пусть точки (х 0 , y 1 ) и (х 0 , у 2 ) соответственно принадлежат графикам функций y = f{x) и y = g(х) , т. е. y 1 = f(x 0), y 2 = g(х 0). Тогда точка (x0;. y1 + y2) принадлежит графику функции у = f(х) + g(х) (ибо f(х 0) + g(x 0 ) = y1 +y2 ),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x) . и y = g(х) заменой каждой точки (х n , у 1) графика функции y = f(x) точкой (х n , y 1 + y 2), где у 2 = g(x n ), т. е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ).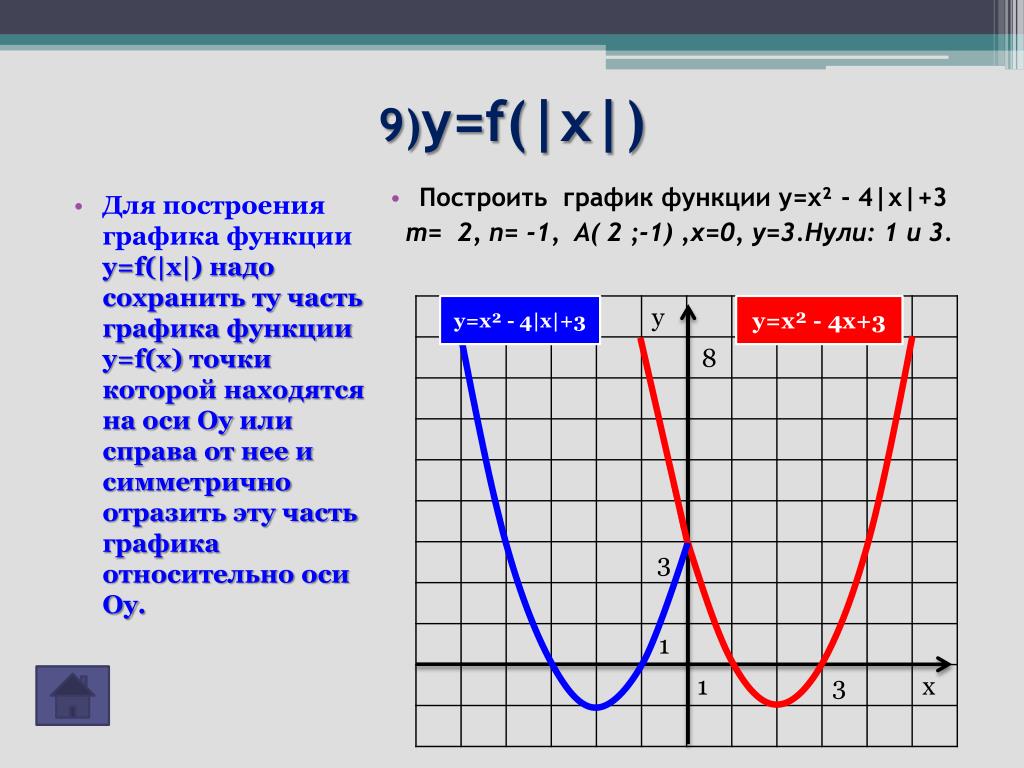 При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .

Такой метод построения графика функции y = f(x) + g(х ) называется сложением графиков функций y = f(x) и y = g(x)

Пример 4 . На рисунке методом сложения графиков построен график функции
y = x + sinx .

При построении графика функции y = x + sinx мы полагали, что f(x) = x, а g(x) = sinx. Для построения графика функции выберем точки с aбциссами -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Значения f(x) = x, g(x) = sinx, y = x + sinx вычислим в выбранных точках и результаты поместим в таблице.

«Натуральный логарифм» — 0,1. Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121.

«Степенная функция 9 класс» — У. Кубическая парабола. У = х3. 9 класс учитель Ладошкина И.А. У = х2. Гипербола. 0. У = хn, у = х-n где n – заданное натуральное число. Х. Показатель – четное натуральное число (2n).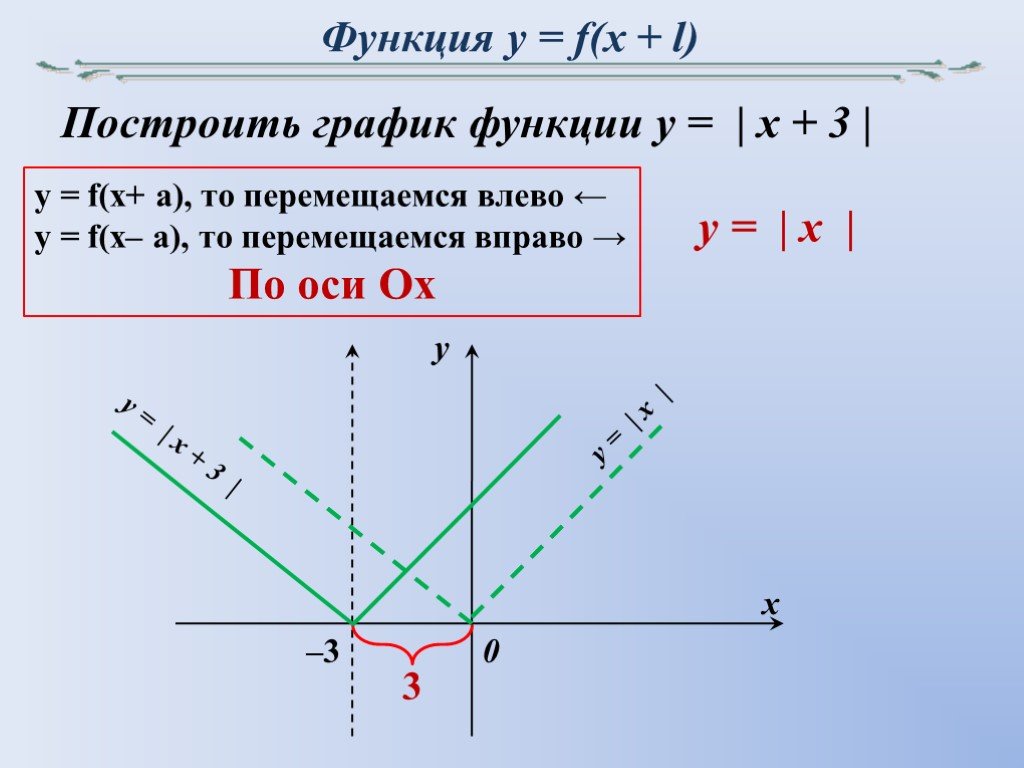

«Квадратичная функция» — 1 Определение квадратичной функции 2 Свойства функции 3 Графики функции 4 Квадратичные неравенства 5 Вывод. Свойства: Неравенства: Подготовил ученик 8А класса Герлиц Андрей. План: График: -Промежутки монотонности при а > 0 при а

«Квадратичная функция и её график» — Решение.у=4x А(0,5:1) 1=1 А-принадлежит. При а=1 формула у=аx принимает вид.

«8 класс квадратичная функция» — 1) Построить вершину параболы. Построение графика квадратичной функции. x. -7. Построить график функции. Алгебра 8 класс Учитель 496 школы Бовина Т. В. -1. План построения. 2) Построить ось симметрии x=-1. y.

§ Построить график функции онлайн

←Вернуться в «Калькуляторы онлайн»

	y =
	y =

Здесь будет анализ функции…

Инструкции

построить график функции онлайн

укажите функцию в поле выше в виде «y = x² — 3»;
нажмите кнопку «Построить график функции»;
ожидайте результат анализа функции (точки пересечения с осями координат) и график функции под полем задания функции.

При необходимости вы можете построить одновременно графики двух функций онлайн. Для этого нажмите кнопку «Добавить функцию».

В случае построения двух графиков функции будут показаны их точки пересечения.

Таблица обозначений для задания функций

Математическая операция	Символ	Пример использования
Десятичная дробь	Можно и через точку, и через запятую.	«2,789» или «2.879»
Сложение	«+»	x + 1
Вычитание	«-»	x — 2.5
Умножение	«*»(shift + 8)	2 * x Коэффициент при «x» можно записывать без знака умножения. (2)».
Корень	Кнопка	²√(x — 2) — квадратный корень ³√(2x — 1) — кубический корень
Синус	Кнопка	sin(x + 1)
Косинус	Кнопка	cos(x)
Тангенс	Кнопка	tg(2.5 — x)
Число π (пи)	Кнопка	sin(x + π) + 2
Логарифм	Кнопка	log₂(2x — 1,4)
Натуральный логарифм	Кнопка	ln(x) — 2
Десятичный логарифм	Кнопка	lg(2. 3 — x)
Основание натурального логарифма (число Эйлера)	Кнопка	e^x

Важно!

Научиться строить график функции самостоятельно можно в уроке «Функция в математике».

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи «ВКонтакте».

Оставить комментарий:


Отправить

20 апреля 2023 в 6:08

Илья Костромин Профиль Благодарили: 0
Сообщений: 1

y =
y= x +7

0 СпасибоОтветить

Python — NumWorks

Версия Python, доступная на вашем калькуляторе NumWorks, — MicroPython 1. 12, совместимая с Python 3.4.

Скрипты

Список скриптов

При входе в приложение вы можете увидеть список сохраненных скриптов. При первом использовании приложения в качестве примеров определяются четыре скрипта: squares.py , parabola.py , mandelbrot.py и polynomial.py .

Добавление и удаление скрипта из списка

В список можно добавить до 8 сценариев.

Выберите ячейку Добавить скрипт внизу списка.
Подтвердите, нажав ок .

В списке появится новый сценарий. Затем вы можете ввести имя для вашего нового скрипта.

Чтобы удалить скрипт, выберите значок настроек рядом с названием скрипта и нажмите ok . Выберите Удалить скрипт и нажмите ок .

Переименование сценария

Чтобы изменить имя сценария, выберите значок настроек рядом с именем сценария и нажмите ok .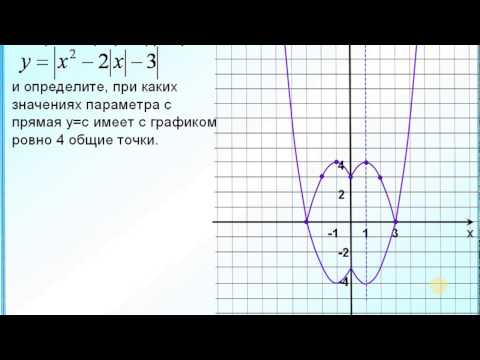 Выберите Переименовать сценарий и нажмите ok для подтверждения. Теперь вы можете изменить имя скрипта.

Редактирование сценария

Чтобы написать сценарий, просто выберите имя сценария и нажмите ok . Откроется редактор, и вы сможете написать свой код внутри.

Чтобы помочь вам написать, нажмите ящик для инструментов . Откроется меню с некоторыми ярлыками, чтобы упростить редактирование. Меню Loops and Tests предлагает предварительно заполненные блоки для и при этом циклов, if тестов и ряд условий . В меню Каталог перечислены функции, присутствующие в Python, и дано их краткое описание. Вы также можете использовать клавишу var для отображения списка функций, определенных в ваших сценариях, а также глобальных переменных.

Если вы хотите скопировать и вставить часть текста, выберите символы для копирования, удерживая нажатой клавишу shift и используя влево или вправо .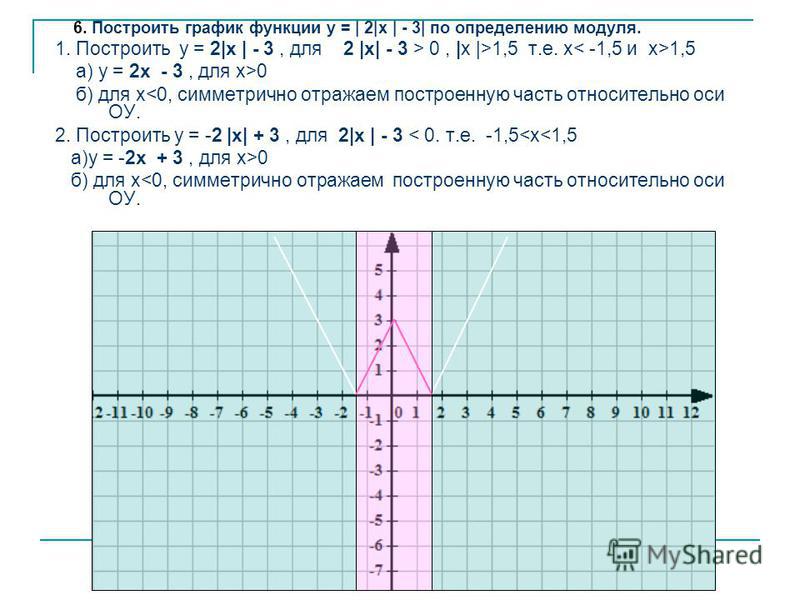 Затем нажмите shift , а затем var , чтобы скопировать выделение. Нажмите shift , а затем toolbox , чтобы вставить его.

Автодополнение

Редактор скриптов имеет функцию автодополнения. Когда вы начнете печатать, приложение предложит вариант, выделенный серым цветом.

Чтобы принять предложение, нажмите клавишу вправо или ok .
Чтобы отклонить предложение, нажмите назад или просто продолжайте печатать.
Чтобы получить новое предложение, нажмите клавишу вверх или вниз .
Все возможные предложения от введенного вами префикса перечислены в меню ключа var .

Отключение автоматического импорта в оболочку

Для ваших скриптов автоматически включается автоматический импорт. Это означает, что команда из script_name import * систематически вводится при открытии оболочки, чтобы вы могли использовать функции, определенные вами в сценариях внутри консоли.

Чтобы отключить автоматический импорт скрипта, выберите значок настроек рядом с названием скрипта и нажмите ok . Выберите Автоимпорт в оболочке и нажмите ok , чтобы переключить переключатель. Переключатель станет серым, и скрипт больше не будет активироваться автоматически.

Оболочка

Внизу списка скриптов находится кнопка Оболочка Python , которая открывает доступ к интерактивной оболочке Python.

Тройные стрелки >>> предлагают ввести команду.

Вы можете использовать ярлыки в меню панели инструментов , чтобы упростить ввод текста. Меню 9Клавиша 0024 var отображает список функций и глобальных переменных, содержащихся в импортированных скриптах.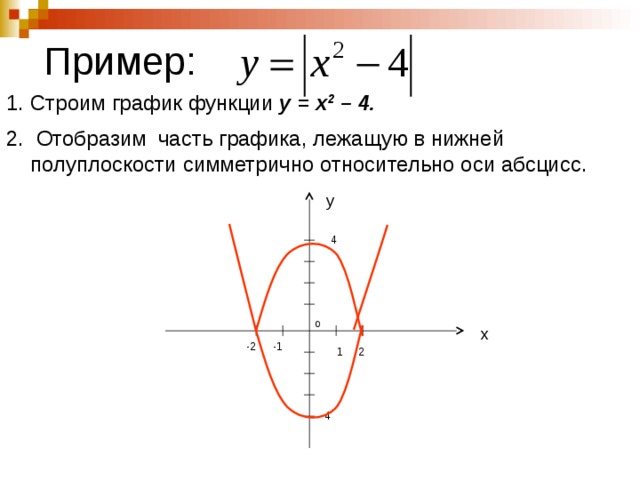

Чтобы прервать выполнение сценария, нажмите клавишу назад на клавиатуре. Если сценарий застрял в бесконечном цикле, нажмите и удерживайте обратно и повторяйте, пока сценарий не будет прерван.

Модули

Модули, присутствующие в этой версии Python: math , cmath , matplotlib.pyplot , random , черепаха , ion , time и kandinsky модули.

Математический модуль

Вот полное описание математического модуля . Вы можете получить этот список на своем калькуляторе, нажав toolbox и перейдя к Modules , затем math .

e

Константа e=2,718281828459045 .

9х-1ех-1.

log(x)

Натуральный логарифм: log(x) вычисляет ln(x)ln(x)ln(x).

log2(x)

Логарифм по основанию 2, тип log2(x) для ln(x)ln(2)\frac{ln(x)}{ln(2)}ln(2)ln (х).

log10(x)

Логарифм по основанию 10, тип log10(x) для ln(x)ln(10)=log(x)\frac{ln(x)}{ln(10)} =log(x)ln(10)ln(x)=log(x).

cosh(x)

Гиперболический косинус.

sinh(x)

Гиперболический синус.

tanh(x)

Гиперболический тангенс.

acosh(x)

Арктический гиперболический косинус.

asinh(x)

Обратный гиперболический синус.

atanh(x)

Арктический гиперболический тангенс.

cos(x)

Косинус в радианах.

sin(x)

Синус в радианах.

tan(x)

Тангенс в радианах.

acos(x)

Арккосинус.

asin(x)

Арксинус.

atan(x)

Арктангенс.

atan2(y,x)

Введите atan2(y,x) для вычисления atan(yx)atan(\frac{y}{x})atan(xy).

потолок(x)

Потолок.

copysign(x,y)

Возвращает x со знаком y , например copysign(3,-1)=-3 .

fabs(x)

Абсолютное значение, fabs(x) возвращает ∣x∣\mid x\mid∣x∣.

этаж(x)

Этаж, введите этаж(x) для вычисления ⌊x⌋\lfloor x \rfloor⌊x⌋.

fmod(a,b)

fmod(a,b) возвращает aaa по модулю bbb.

frexp(x)

Мантисса и показатель степени x : например, икс×2i.

 modf(x)  Дробные и целые части, например  modf(5.1)=(0.1,5.0)  .
 isfinite(x)  Проверяет, конечно ли  x .
 isinf(x)  Проверяет, является ли  x  бесконечным.
 isnan(x)  Проверяет, является ли  x   NaN  .
 trunc(x)  Возвращает  x , усеченное до целого числа, например 92} \, \mathrm dterf(x)=π2∫0xe−t2dt.
 erfc(x)  Дополнительная функция ошибки, erfc(x)=1-erf(x)erfc(x) = 1-erf(x)erfc(x)=1-erf(x).
 гамма(х)  Гамма-функция.
 lgamma(x)  Лог-гамма, lgamma(x)=ln(gamma(x))lgamma(x)=ln(gamma(x))lgamma(x)=ln(gamma(x)) .
 Модуль cmath 
 Это полное описание модуля  cmath . Вы можете получить этот список на своем калькуляторе, нажав   набор инструментов   и переход к  Модули  затем  cmath  .
 e  Константа  e=2,718281828459045  .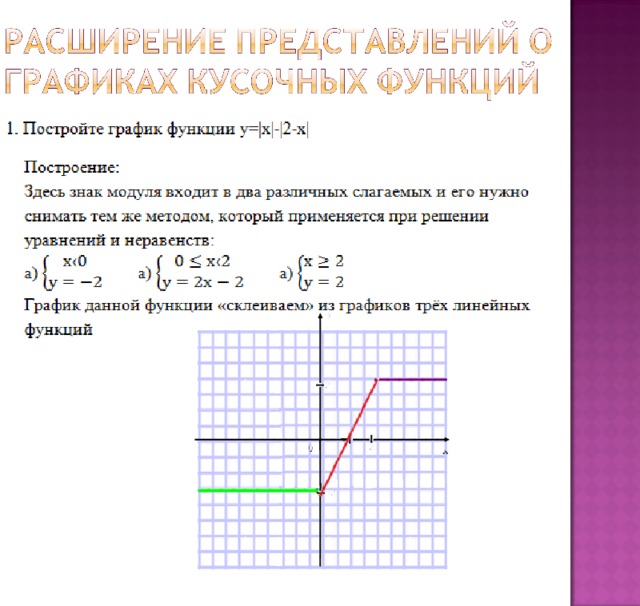
 пи  Константа  пи=3,141592653589793  .
 фаза(z)  Фаза  z  в радианах, например,  фаза(1j)=1,570796326794897  .
 полярный(z)  Представление  z  в полярных координатах:  полярный(1j)  возвращает  (1.0, 1.570796326794897)  .
 rect(z)  Представление  z  в декартовых координатах:  rect(1,pi/4)  возвращает  0.70710+0.70710j  .
 exp(x)  Экспоненциальная функция, например,  exp(i*pi/4)  возвращает  0,70710+0,70710j  .
 log(x)  Натуральный логарифм, например  log(1j)  возвращает  1.570796326794897j  .
 sqrt(x)  Квадратный корень.
 cos(x)  Косинус.
 sin(x)  Синус.
 Модуль matplotlib.pyplot 
 Это полное описание модуля  matplotlib.pyplot . Вы можете получить этот список на своем калькуляторе, нажав   toolbox   и перейдя к  Modules , затем  matplotlib.pyplot  .
 arrow(x,y,dx,dy)  Рисует стрелку из точки  (x,y)  в точку  (x+dx,y+dy)  . Можно использовать необязательный аргумент для настройки размера стрелки, написав:  head_width = 0,1  . Другой необязательный аргумент можно использовать для выбора цвета линии, написав:  color="red"  .
 axis((xmin,xmax,ymin,ymax))  Устанавливает окно отображения на  (xmin,xmax,ymin,ymax)  . Команда axis()  возвращает список значений границ осей. Кроме того, ось  ("выкл")  или ось  (ложь)  скрывает оси, а ось  ("вкл")  или ось  (правда)  отображает их. Чтобы сбросить оси с автоматической настройкой, вы можете использовать инструкцию  axis("auto") .
 bar(x,height,bin_width,bottom)  Рисует гистограмму, используя значения из списка  x  и подсчеты в  height 9список 0010. Последние два аргумента являются необязательными. Аргумент  bin_width  позволяет вам установить ширину столбцов, значение по умолчанию которых равно 0,8. Аргумент  bottom  — это список начальных ординат баров, по умолчанию равный 0. Можно разместить необязательный аргумент для выбора цвета линии, написав:  color="red"  .
 grid()  Отображает сетку, если она скрыта, или скрывает сетку, если она отображается. 9Инструкции 0009 grid(True)  и  grid(False)  позволяют показать или скрыть сетку.
 hist(x,bins)  Строит гистограмму, используя значения из списка  x . Второй аргумент является необязательным.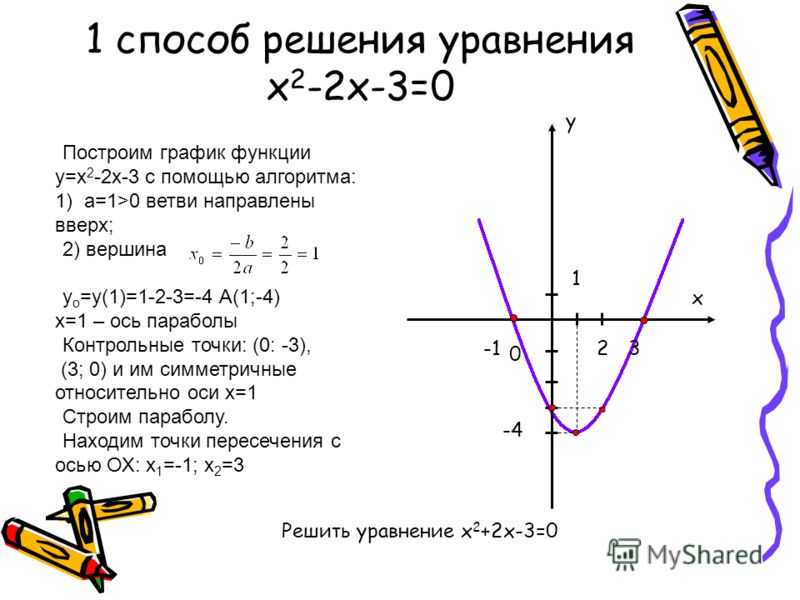 Если второй аргумент является целым числом, он устанавливает количество прямоугольников, составляющих гистограмму. По умолчанию это число равно 10. Если вторым аргументом является список, он позволяет вам выбирать интервалы гистограммы. Например, если  бин  равно  [0,1,3,5]  , бины будут:  [0,1[  ,  [1,3[  и  [3,5]  . Можно разместить необязательный аргумент для выбора цвета линии, написав:  color="red"  .
 plot(x,y)  Отображает список  y  в сравнении со списком  x .  (x,y)  точек соединены отрезками. Если задан только один список  y , предполагается, что  x  будет  [0,1,2,3...]  .  цвет  Аргумент необязателен. Позволяет выбрать цвет линии.
 scatter(x,y)  Строит диаграмму рассеяния на основе  (x,y)  значений. Аргументами функции могут быть числа или списки одинаковой длины. Можно разместить необязательный аргумент для выбора цвета линии, написав:  color="red"  .
 show()  Рисует фигуру.
 текст(x,y,"текст")  Отображает текст, установленный в качестве аргумента в координатах  (x,y) .
 Модуль черепахи 
 Это полное описание модуля  черепаха . Вы можете получить этот список на своем калькуляторе, нажав   toolbox   и перейдя к  Модули , затем  черепаха .
 вперед(x)  Переместиться вперед на  x  пикселей.
 назад(x)  Перейти назад на  х  пикселей.
 направо(а)  Поверните направо на  a  градусов.
 влево(а)  Поверните налево на  a  градусов.
 goto(x,y)  Перейти к координатам ( x ,  y ).
 setheading(a)  Установите ориентацию на  a  градусов.
 круг(r)  Круг радиусом  r  пикселей.
 скорость (x)  Скорость рисования ( x  от 0 до 10).
 position()  Возвращает текущее ( x ,  y ) местоположение.
 heading()  Возвращает текущий заголовок.
 pendown()  Потяните перо вниз.
 penup()  Потяните перо вверх.
 Pensize(x)  Установите толщину линии на  x  пикселей.
 write("текст")  Записывает текст, помещенный в качестве аргумента на позицию черепахи.
 isdown()  Вернуть  True , если перо опущено.
 reset()  Сбросить рисунок.
 showturtle()  Показать черепаху.
 hideturtle()  Спрячьте черепаху.
 цвет('c')  или  цвет(r,g,b)  Установите цвет пера.
 colormode(x)   colormode(1.0)  изменяет цветовой режим на 1.0, а цвета должны определяться кортежами типа  (0.5,1.0,0.5) , тогда как  colormode(0510) изменяет 90 цветовой режим на 255, а затем цвета определяются кортежами типа  (128 255 128)  . По умолчанию используется цветовой режим 255.
 синий  Синий цвет.
 красный  Красный цвет.
 зеленый  Зеленый цвет.
 желтый  Желтый цвет.
 коричневый  коричневый цвет.
 черный  Черный цвет.
 белый  Белый цвет.
 розовый  Розовый цвет.
 оранжевый  Оранжевый цвет.
 фиолетовый  Фиолетовый цвет.
 серый  Серый цвет.
 Случайный модуль 
 Это полное описание  случайного модуля . Вы можете получить этот список на своем калькуляторе, нажав   toolbox   и перейдя к  Modules , затем  random  .
 getrandbits(k)  Возвращает целое число из k  случайных битов.
 seed(x)  Инициализировать генератор случайных чисел.
 randrange(start,stop)  Возвращает случайное число в диапазоне (start,stop)  .
 randint(a,b)  Возвращает целое число в  [a,b]  .
 selection(list)  Возвращает случайное число в списке.
 random()  Возвращает случайное число с плавающей запятой в формате  [0,1)  .
 uniform(a,b)  Возвращает случайное число с плавающей запятой в  [а, б]  .
 Модуль Кандинского 
 Это полное описание модуля  Кандинского . Вы можете получить этот список на своем калькуляторе, нажав   toolbox   и перейдя к  Модули , затем  Кандинский .
 цвет(r,g,b)  Определяет цвет на основе значений  r  ,  g  ,  b  . Вы также можете просто использовать кортеж для определения цвета:  (r,g,b)  .
 get_pixel(x,y)  Возвращает цвет пикселя  x  ,  y  в виде кортежа  (r,g,b)  .
 set_pixel(x,y,color)  Цвет пикселя  x  ,  y  цвета   цветов.
 draw_string(text,x,y,[color1],[color2])  Отображает  текст  из пикселя  x  ,  y  . Аргументы  color1  (цвет текста) и color2  (цвет фона) являются необязательными.
 fill_rect(x,y,width,height,color)  Заполняет прямоугольник в пикселях  (x,y)  цветом  color  .
 Ионный модуль 
 Это описание ионного модуля  . Вы можете получить этот список на своем калькуляторе, нажав   toolbox   и перейдя к  Modules , затем  ion .
 keydown(k)  Возвращает  Истина , если нажата клавиша  k  в аргументе, и  Ложь  в противном случае.
 Другие пункты этого меню указывают синтаксис, используемый для идентификации клавиш на клавиатуре.
 Модуль времени 
 Вот описание модуля  time . Вы можете получить этот список на своем калькуляторе, нажав   toolbox   и перейдя к  Модули , затем  время .
 монотонный()  Возвращает значение часов на момент вызова функции.
 sleep(t)  Приостанавливает выполнение на  t  секунд.
 Панель инструментов и клавиши var 
 Клавиша var 
 В редакторе сценариев в меню клавиши   var   перечислены доступные варианты автодополнения.
 В консоли выполнения в меню клавиши   var   перечислены все функции, определенные в ваших импортированных сценариях (не содержащие ошибок), а также глобальные переменные.
 Клавиша панели инструментов 
 Меню клавиши   панели инструментов   содержит четыре раздела для более быстрого редактирования ваших сценариев.
 Циклы и тесты 
 Содержит инструкции для  для  и  для циклов , а также  для тестов .
 Модули 
 Содержит функции, доступные в  math  ,  cmath  ,  random  ,  matplotlib. pyplot  ,  ion  ,  time ,  черепаха  и  модули кандинского .
 Каталог 
 Содержит функции, которые можно использовать в Python, особенно модули, а также такие функции, как  print()  и  input()  . Возможен алфавитный поиск по буквам клавиатуры.
 Функции 
 Содержит инструкции по определению функции:  def function(argument):  и  return  .
 Matplotlib Графики 
 ❮ Предыдущий
 Далее ❯
 Нанесение точек x и y 
 Функция  plot()  используется для рисования точек (маркеров) на диаграмме. По умолчанию функция plot()  рисует линию от точки к точке.
 Функция принимает параметры для указания точек на диаграмме.
 Параметр 1 представляет собой массив, содержащий точки на  оси x  .
 Параметр 2 представляет собой массив, содержащий точки на  оси Y  .
 Если нам нужно построить линию от (1, 3) до (8, 10), мы должны передать в функцию plot два массива [1, 8] и [3, 10].
 Пример 
 Проведите линию на диаграмме от позиции (1, 3) к позиции (8, 10):
 импортировать matplotlib.pyplot как plt 
; .показывать()
 Результат: 
 Попробуйте сами »
  ось x  — это горизонтальная ось.
  Ось Y  — вертикальная ось.
 Построение без линии 
 Для построения только маркеров можно использовать  сокращенную строковую нотацию  параметр «o», что означает «кольца».
 Пример 
 Начертите две точки на диаграмме, одну в позиции (1, 3) и одну в позиции (8, 10):
 импортировать matplotlib.pyplot как plt 
 импортировать numpy как np
 xpoints = np.array([1, 8]) 
 ypoints = np.array([3, 10])
 plt. plot(xpoints, ypoints, 'o') 
 plt.show()
 Результат: 
 Попробуйте сами »
 Вы узнаете больше о маркерах в следующей главе.
 Несколько точек 
 Вы можете нанести столько точек, сколько захотите, просто убедитесь, что у вас одинаковое количество точек по обеим осям.
 Пример 
 Проведите линию на диаграмме от позиции (1, 3) к (2, 8), затем к (6, 1) и, наконец, к позиции (8, 10):
 импортировать matplotlib.pyplot как plt 
 импортировать numpy как np
 xpoints = np.array([1, 2, 6, 8]) 
 ypoints = np.array([3, 8, 1, 10])
 pt. график (xpoints, ypoints) 
 plt.show()
 Результат: 
 Попробуйте сами »
 Точки X по умолчанию 
 Если мы не укажем точки на оси X, они получат значения по умолчанию 0, 1, 2, 3 (и т. д., в зависимости от длины точки y.0003
 Пример 
 График без точек x:
 импортировать matplotlib. pyplot как plt 
 импортировать numpy как np
 ypoints = np.array([3, 8, 1, 10, 5, 7])
 plt.plot(ypoints) 
 plt.show()
 Результат: 
 Попробуйте сами »
  x-точки  в приведенном выше примере — это [0, 1, 2, 3, 4, 5].
 ❮ Предыдущий
 Следующий ❯
 
 ВЫБОР ЦВЕТА 
 Лучшие учебники 
 HTML Tutorial 
 CSS Tutorial 
 JavaScript Tutorial 
 How To Tutorial 
 SQL Tutorial 
 Python Tutorial 
 W3.CSS Tutorial 
 Bootstrap Tutorial 
 PHP Tutorial 
 Java Tutorial 
 C++ Tutorial 
 jQuery Tutorial 
 Top References 
 Справочник по HTML 
 Справочник по CSS 
 Справочник по JavaScript 
 Справочник по SQL 
 Справочник по Python 
 Справочник по W3.CSS 
 Справочник по Bootstrap 
 Справочник по PHP 
 Цвета HTML 
 Справочник по Java 
 Справочник по Angular 
 Справочник по jQuery 
 Основные примеры 
 Примеры HTML 
 Примеры CSS 
 Примеры JavaScript 
 Примеры How To Примеры 
 Примеры SQL 
 Примеры Python 
 Примеры W3.No related posts.