Разрежьте квадрат на 6 треугольников, среди которых есть… : Олимпиадные задачи (М)
| Ktina |
| ||
01/12/11 |
| ||
| |||
| gris |
| |||
13/08/08 |
| |||
| ||||
| Ktina |
| ||
01/12/11 8634 |
| ||
| |||
| gris |
| |||
13/08/08 |
| |||
| ||||
| Ktina |
| ||
01/12/11 |
| ||
| |||
| gris |
| |||
13/08/08 |
| |||
| ||||
| grizzly |
| |||
09/09/14 |
| |||
| ||||
| atlakatl |
| ||
21/09/12 |
| ||
| |||
| grizzly |
| |||
09/09/14 |
| |||
| ||||
| atlakatl |
| ||
21/09/12 |
| ||
| |||
| grizzly |
| |||
09/09/14 |
| |||
| ||||
| chh |
| ||
12/04/16 |
| ||
| |||
| grizzly |
| |||
09/09/14 |
| |||
| ||||
| gris |
| |||
13/08/08 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 14 ] |
Модераторы: Модераторы Математики, Супермодераторы
Разрезать фигуру на 10 равных частей.
 Задачи на разрезание все их сюжеты можно
Задачи на разрезание все их сюжеты можно
Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Опыт показывает, что при использовании
практических методов обучения удается
сформировать у учащихся ряд мыслительных
приемов, необходимых для правильного вычленения
существенных и несущественных признаков при
ознакомлении с геометрическими фигурами.
развивается математическая интуиция, логическое
и абстрактное мышление, формируется культура
математической речи, развиваются математические
и конструкторские способности, повышается
познавательная активность, формируется
познавательный интерес, развивается
интеллектуальный и творческий потенциал. В
статье приводится ряд практических задач на
разрезания геометрических фигур на части с целью
составить из этих частей новую фигуру. Ученики
работают над заданиями в группах. Затем каждая
группа защищает свой проект.
В
статье приводится ряд практических задач на
разрезания геометрических фигур на части с целью
составить из этих частей новую фигуру. Ученики
работают над заданиями в группах. Затем каждая
группа защищает свой проект.
Две фигуры называются равносоставленными, если, определённым образом разрезав одну из них на конечное число частей, можно (располагая эти части иначе) составить из них вторую фигуру. Итак, метод разбиения основан на том, что всякие два равносоставленных многоугольника равновелики. Естественно поставить обратный вопрос: всякие ли два многоугольника, имеющих одинаковую площадь, равносоставлены? Ответ на этот вопрос был дан (почти одновременно) венгерским математиком Фаркашем Бойяи (1832г.) и немецким офицером и любителем математики Гервином (1833г.): два многоугольника, имеющих равные площади, равносоставленны.
Теорема Бойяи-Гервина гласит: любой многоугольник можно так разрезать на части, что из этих частей удастся сложить квадрат.
Задание 1.
Разрежьте прямоугольник a х 2a на такие
части, чтобы из них можно было составить квадрат.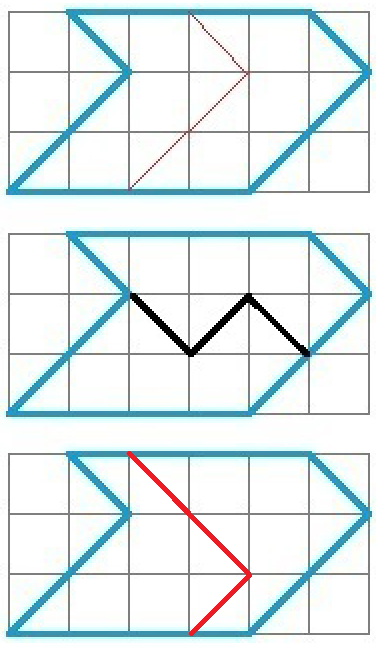
Прямоугольник ABCD разрежем на три части по линиям MD и MC (М – середина АВ)
Рисунок 1
Треугольник АMD переместим так, чтобы вершина М совместилась с вершиной С, катет АМ переместится на отрезок DС. Треугольник МВС переместим влево и вниз так, что катет МВ наложится на половину отрезка DС. (Рисунок 1)
Задание 2.
Разрезать равносторонний треугольник на части так, чтобы из них можно было сложить квадрат.
Обозначим данный правильный треугольник АВС. Необходимо разрезать треугольник АВС на многоугольники так, чтобы из них можно было сложить квадрат. Тогда эти многоугольники должны иметь по крайней мере по одному прямому углу.
Пусть К – середина СВ, Т – середина АВ, точки М и Е выберем на стороне АС так, что МЕ=АТ=ТВ=ВК=СК=а , АМ=ЕС=а /2.
Рисунок 2
Проведем отрезок МК и перпендикулярные к нему
отрезки ЕР и ТН. Разрежем треугольник на части
вдоль построенных линий. Четырехугольник КРЕС
повернем по часовой стрелке относительно
вершины К так, что СК совместится с отрезком КВ. Четырехугольник АМНТ повернем по часовой
стрелке относительно вершины Т так, что АТ
совместится с ТВ. Треугольник МЕР переместим так,
что в результате получится квадрат. (Рисунок 2)
Четырехугольник АМНТ повернем по часовой
стрелке относительно вершины Т так, что АТ
совместится с ТВ. Треугольник МЕР переместим так,
что в результате получится квадрат. (Рисунок 2)
Задание 3.
Разрезать квадрат на части так, чтобы из них можно было сложить два квадрата.
Обозначим исходный квадрат ABCD. Отметим середины сторон квадрата – точки M, N, K, H. Проведем отрезки МТ, НЕ, КF и NР – части отрезков МС, НВ, КА и ND соответственно.
Разрезав квадрат ABCD по проведенным линиям, получим квадрат PTEF и четыре четырехугольника MDHT, HCKE, KBNF и NAMP.
Рисунок 3
PTEF – уже готовый квадрат. Из оставшихся четырехугольников составим второй квадрат. Вершины A, B, C и D совместим в одну точку, отрезки АМ и ВК, MD и КС, BN и СН, DH и АN совместятся. Точки Р, Т, Е и F станут вершинами нового квадрата. (Рисунок 3)
Задание 4.
Из плотной бумаги вырезаны равносторонний
треугольник и квадрат. Разрезать эти фигуры
на многоугольники так, чтобы из них можно было
сложить один квадрат, при этом части должны
полностью его заполнять и не должны
пересекаться.
Треугольник разрежем на части и составим из них квадрат так, как показано в задании 2. Длина стороны треугольника – 2а . Теперь следует разделить на многоугольники квадрат так, чтобы из этих частей и того квадрата, который получился из треугольника, составить новый квадрат. Возьмем квадрат со стороной 2а , обозначим его LRSD. Проведем взаимно перпендикулярные отрезки UG и VF так, что DU=SF=RG=LV. Разрежем квадрат на четырехугольники.
Рисунок 4
Возьмем квадрат, составленный из частей треугольника. Выложим четырехугольники – части квадрата так, как показано на рисунке 4.
Задание 5.
Крест составлен из пяти квадратов: один квадрат в центре, а остальные четыре прилежат к его сторонам. Разрезать его на такие части, чтобы из них можно было составить квадрат.
Соединим вершины квадратов так, как показано на рисунке 5. Отрежем “внешние” треугольники и переместим их на свободные места внутри квадрата АВСК.
Рисунок 5
Задание 6.
Перекроить два произвольных квадрата в один.
На рисунке 6 показано, как нужно разрезать и переместить части квадратов.
Вступительное слово учителя:
Небольшая историческая справка: Задачами на разрезание увлекались многие ученые с древнейших времен. Решения многих простых задач на разрезание были найдены еще древними греками, китайцами, но первый систематический трактат на эту тему принадлежит перу Абуль-Вефа. Геометры всерьез занялись решением задач на разрезание фигур на наименьшее число частей и последующее построение другой фигуры в начале 20 века. Одним из основателей этого раздела был знаменитый основатель головоломок Генри Э.Дьюдени.
В наши дни любители головоломок увлекаются решением задач на разрезание прежде потому, что универсального метода решения таких задач не существует, и каждый, кто берется их решать, может в полной мере проявить свою смекалку, интуицию и способность к творческому мышлению. (На занятии мы будем указывать лишь один из возможных примеров разрезания. Можно допустить, что у учащихся может получиться какая-то другая верная комбинация — не надо этого бояться).
Можно допустить, что у учащихся может получиться какая-то другая верная комбинация — не надо этого бояться).
Данное занятие предполагается провести в виде практического занятия. Разбить участников кружка на группы по 2-3 человека. Каждой из групп предоставить заранее подготовленные учителем фигуры. Учащиеся располагают линейкой (с делениями), карандашом, ножницами. Разрешается производить с помощью ножниц лишь прямолинейные разрезы. Разрезав какую-нибудь фигуру на части, необходимо составить другую фигуру из тех же частей.
Задачи на разрезание:
1). Попробуйте разрезать изображенную на рисунке фигуру на 3 равные по форме части:
Подсказка: Маленькие фигуры очень похожи на букву Т.
2). Разрежьте теперь эту фигуру на 4 равные по форме части:
Подсказка: Легко догадаться, что маленькие фигурки будут состоять из 3 клеточек, а фигур из трех клеточек не так много. Их всего два вида: уголок и прямоугольник.
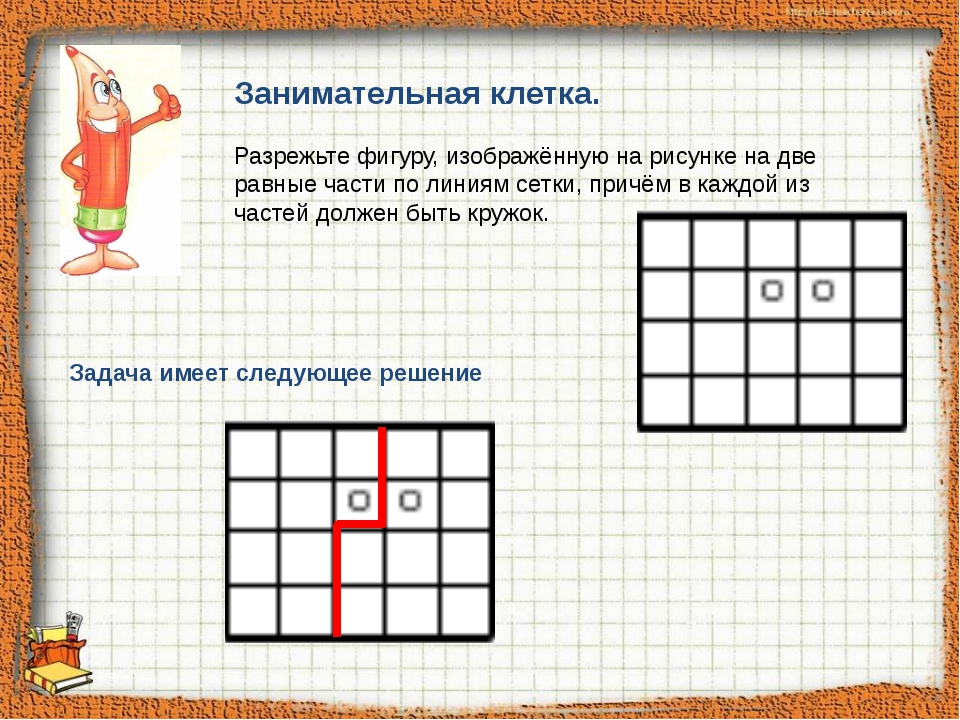
3). Разделите фигуру на две одинаковые части, и из полученных частей сложите шахматную доску.
Подсказка: Предложить начать выполнять задание со второй части, как бы получить шахматную доску. Вспомнить, какую форму имеет шахматная доска (квадрат). Посчитать имеющееся количество клеточек в длину, в ширину. (Напомнить, что клеток должно быть 8).
4). Попробуйте тремя движениями ножа разрезать сыр на восемь равных кусков.
Подсказка: попробовать разрезать сыр вдоль.
Задачи для самостоятельного решения:
1). Вырежьте квадрат из бумаги и выполните следующее:
· разрежьте на такие 4 части, из которых можно составить два равных меньших квадрата.
· разрежьте на пять частей — четыре равнобедренных треугольника и один квадрат — и сложите их так, чтобы получилось три квадрата.
Руководитель Варвара Алексеевна Косоротова
2009/2010 учебный год
Занятие 8. Разрезания на клетчатом листе бумаги
При решении задач такого типа полезно применять следующие соображения:
- Площадь. Если требуется разбить фигуру на несколько равных частей, стоит сначала найти площадь разрезаемой фигуры, а потом — каждой из частей.
 Сходным образом, если исходную фигуру нужно разбить на несколько фигур заданного вида, стоит предварительно посчитать, сколько их должно быть. Такие же соображения могут помочь и при решении других задач на разрезание. Для иллюстрации этой идеи автор этих строк добавил в список задачу 13, которой не было среди задач, предлагавшихся на занятии.
Сходным образом, если исходную фигуру нужно разбить на несколько фигур заданного вида, стоит предварительно посчитать, сколько их должно быть. Такие же соображения могут помочь и при решении других задач на разрезание. Для иллюстрации этой идеи автор этих строк добавил в список задачу 13, которой не было среди задач, предлагавшихся на занятии. - Симметрия. Свойствам симметрии следует уделять внимание, например, в случае, когда требуется разрезать одну фигуру на части и из них собрать другую фигуру.
К простым задачам приведены только ответы, к более сложным — еще и соображения, помогающие получить ответ.
Разрежьте квадрат 5×5 с дыркой (см. рисунок) на две равные части двумя способами. Способы разрезания квадрата на две части будем считать различными, если части квадрата, полученные при одном способе разрезания, отличаются по форме или размеру от частей, полученных при другом способе (то есть их нельзя совместить наложением).
Разделите квадрат 4×4 на две равные части четырьмя различными способами так, чтобы линия разреза шла по сторонам клеток. Флаг — 1. Разрежьте флаг с 6 полосами на две части так, что бы из них можно было сложить флаг с 8 полосами.
Флаг — 1. Разрежьте флаг с 6 полосами на две части так, что бы из них можно было сложить флаг с 8 полосами.
Флаг — 2. Разрежьте флаг А на четыре части так, чтобы из них можно было сложить флаг Б.
Разрежьте фигуру на 4 равные части.
Из двух — один. Разрежьте квадрат с дыркой двумя прямыми на 4 части так, чтобы из них и еще одного обычного квадрата 5×5 можно было сложить новый квадрат.
11*. Зубчатый квадрат. Превратите зубчатый квадрат в обыкновенный, разрезав его на 5 частей.
12*. Мальтийский крест — 2. Разрежьте «мальтийский крест» (см. задачу 8) на 5 частей так, чтобы из них можно было сложить квадрат.
13**.
Незнайка разрезал изображенную на рисунке фигуру на трехклеточные и четырехклеточные уголки (такие, как на рисунке). Сколько каких уголков могло получиться у Незнайки? Рассмотрите все возможные случаи!
Решение.
Площадь исходной фигуры равна 22 (за единицу площади принимаем одну клетку). Пусть при разрезании использовано n четырехклеточных и k трехклеточных уголков. Тогда выразим площадь большой фигуры как сумму площадей уголков: 22=3 k + 4 n . Перепишем это равенство в таком виде: 22 − 4 n =3 k . В левой части этого равенства стоит четное число, которое, однако, не делится на 4. Значит, 3 k — тоже четное число, не делящееся на 4, а следовательно, таковым является и само число k . Кроме того, в правой части равенства стоит число, кратное 3, поэтому 22 − 4 n тоже кратно 3. Таким образом, 22 − 4 n кратно 6. Перебирая значения n от 0 до 5 (при n ≥6 22 − 4 n
Заметим, что мы пока не доказали, что оба эти случая реализуются. Ведь равенство площадей есть лишь необходимое условие для существования способа разрезания, но никак не достаточное (например, прямоугольник размера 1×6, очевидно, нельзя разрезать на два трехклеточных уголка, хотя 3·2=6). Для завершения доказательства следует привести примеры разрезаний каждого типа. Это можно сделать многими разными способами. На рисунке приведен лишь один из них, а вы попробуйте придумать что-нибудь свое. Кстати, интересно было бы ответить на такой вопрос: а сколько всего разрезаний каждого типа существует? (Автор этих строк, к примеру, ответа на этот вопрос пока не знает).
Тогда выразим площадь большой фигуры как сумму площадей уголков: 22=3 k + 4 n . Перепишем это равенство в таком виде: 22 − 4 n =3 k . В левой части этого равенства стоит четное число, которое, однако, не делится на 4. Значит, 3 k — тоже четное число, не делящееся на 4, а следовательно, таковым является и само число k . Кроме того, в правой части равенства стоит число, кратное 3, поэтому 22 − 4 n тоже кратно 3. Таким образом, 22 − 4 n кратно 6. Перебирая значения n от 0 до 5 (при n ≥6 22 − 4 n
Заметим, что мы пока не доказали, что оба эти случая реализуются. Ведь равенство площадей есть лишь необходимое условие для существования способа разрезания, но никак не достаточное (например, прямоугольник размера 1×6, очевидно, нельзя разрезать на два трехклеточных уголка, хотя 3·2=6). Для завершения доказательства следует привести примеры разрезаний каждого типа. Это можно сделать многими разными способами. На рисунке приведен лишь один из них, а вы попробуйте придумать что-нибудь свое. Кстати, интересно было бы ответить на такой вопрос: а сколько всего разрезаний каждого типа существует? (Автор этих строк, к примеру, ответа на этот вопрос пока не знает).
В заключение еще раз подчеркнем, что полное решение этой задачи включает в себя два шага: нахождение возможных случаев и проверка того, что все они реализуются. Каждый из этих шагов по отдельности не является решением задачи!
С листом клетчатой бумаги при помощи ножниц можно решить множество самых разнообразных и интересных задач. Эти задачи не только интересны или забавны. В них заключается часто практическое разрешение и доказательство иногда очень сложных геометрических вопросов.
Начнем с главного правила разрезания и складывания: Два многоугольника называются равносоставленными, если один из них можно разбить (разрезать) на некоторые другие многоугольники, из которых затем можно составить второй многоугольник.
Равносоставленные многоугольники, конечно, имеют одинаковую площадь (равновелики), и поэтому свойство равносоставленности позволяет иногда получить формулы для вычисления площадей или сравнивать площади фигур (как говорят,
методом разбиения или разложения ). Примером является сравнение (вычисление) площадей параллелограмма и прямоугольника.
Примером является сравнение (вычисление) площадей параллелограмма и прямоугольника.Общий вопрос о равносоставленности двух многоугольников далеко не простой. Существует удивительная теорема, в которой утверждается, что из любого данного многоугольника, посредством разрезания его на части, может быть сконструирован любой другой многоугольник той же площади.
В этой теореме речь идет о так называемых простых многоугольниках. Простой многоугольник – это такой многоугольник, у которого граница состоит из одной замкнутой линии без самопересечений, и в каждой вершине этой ломаной сходится ровно два ее звена. Важным свойством простого многоугольника является тот факт, что он имеет, по крайней мере, одну внутреннюю диагональ.
Заметим, что для допустимого превращения прямоугольника в квадрат нам (рисунок 3) понадобилось разбить его на три части. Однако это разбиение не является единственным. Можно, например, привести пример разбиения прямоугольника на четыре части (рисунок 4).
https://pandia.ru/text/78/456/images/image005_116.gif»>
Вопрос о том, какое наименьшее число разрезов достаточно, чтобы сконструировать из одной фигуры другую, остается открытым и по сегодняшний день.
Задача 1.
У одной женщины был прямоугольный коврик размером 27 на 36 дюймов два противоположных его угла истрепались (рисунок 5) и их пришлось отрезать, но она хотела именно прямоугольный коврик. Она дала эту работу мастеру и он справился. Каким путем он это сделал?
Решение задачи видно из рисунка 6.
https://pandia.ru/text/78/456/images/image009_72.gif»>
Если зубчатую часть A вынуть из зубчатой части B и затем снова вдвинуть ее между зубьев части B, переместив на один зуб вправо, то получится желанный прямоугольник.
Задача 2.
Как из пяти одинаковых квадратов путем разрезания составить квадрат.
Как показано на рисунке 7, четыре квадрата нужно разрезать на треугольник и трапецию.
 Четыре трапеции приложить к сторонам пятого квадрата и, наконец, приложим треугольники катетами к основаниям трапеций.
Четыре трапеции приложить к сторонам пятого квадрата и, наконец, приложим треугольники катетами к основаниям трапеций.https://pandia.ru/text/78/456/images/image011_68.gif»>
Задача 3.
Разрезать квадрат на семь таких частей, чтобы, сложив их, получить три равных квадрата. (Рисунки 8, 9)
https://pandia.ru/text/78/456/images/image013_60.gif»>
Задача 4.
Разрезать квадрат на восемь частей так, чтобы сложив их, получить два квадрата, один из которых вдвое меньше другого.
Из рисунка 10 видно, как нужно разрезать квадрат. Решение схоже с решением предыдущей задачи. На рисунке 11 показано, как нужно сложить части, чтобы получить два искомых квадрата.
Обучающий тур
Задачи для самостоятельного решения командами «младшей» возрастной группы
Задача 1
Улитка ползёт вверх по столбу высотой 10 м. За день она поднимается на 5 м, а за ночь — опускается на 4 м. За какое время улитка доберётся от подножья до вершины столба?
За какое время улитка доберётся от подножья до вершины столба?
Задача 2
Можно ли в тетрадном листке вырезать такую дырку, через которую пролез бы человек?
Задача 3
Зайцы пилят бревно. Они сделали 10 распилов. Сколько получилось чурбачков?
Задача 4
Бублик режут на сектора. Сделали 10 разрезов. Сколько получилось кусков?
Задача 5
На большом круглом торте сделали 10 разрезов так, что каждый разрез идёт от края до края и проходит через центр торта. Сколько получилось кусков?
Задача 6
У двух человек было два квадратных торта. Каждый сделал на своём торте по 2 прямолинейных разреза от края до края. При этом у одного получилось три куска, а у другого — четыре. Как это могло быть?
Задача 7
Зайцы снова пилят бревно, но теперь уже оба конца бревна закреплены. Десять средних чурбачков упали, а два крайних так и остались закреплёнными. Сколько распилов сделали зайцы?
Сколько распилов сделали зайцы?
Задача 8
Как разделить блинчик тремя прямолинейными разрезами на 4,5, 6, 7 частей?
Задача 9
На прямоугольном торте лежит круглая шоколадка. Как разрезать торт на две равные части так, чтобы и шоколадка тоже разделилась ровно пополам?
Задача 10
Можно ли испечь такой торт, который может быть разделён одним прямолинейным разрезом на 4 части?
Задача 11
На какое максимальное число кусков можно разделить круглый блинчик при помощи трех прямолинейных разрезов?
Задача 12
Во сколько раз лестница на четвёртый этаж дома длиннее, чем лестница на второй этаж этого же дома?
Задача 13
У Джузеппе есть лист фанеры, размером 22× 15. Джузеппе хочет из него вырезать как можно больше прямоугольных заготовок размером 3× 5. Как это сделать?
Задача 14
В Волшебной Стране свои волшебные законы природы, один из которых гласит: «Ковёр-самолёт будет летать только тогда, когда он имеет прямоугольную форму».
У Ивана-царевича был ковёр-самолёт размером 9 × 12. Как-то раз Змей Горыныч подкрался и отрезал от этого ковра маленький коврик размером 1 × 8. Иван-царевич очень расстроился, и хотел было отрезать ещё кусочек 1 × 4, чтобы получился прямоугольник 8 × 12, но Василиса Премудрая предложила поступить по-другому. Она разрезала ковёр на три части, из которых волшебными нитками сшила квадратный ковёр-самолёт размером 10× 10.
Сможете ли вы догадаться, как Василиса Премудрая переделала испорченный ковёр?
Задача 15
Когда Гулливер попал в Лилипутию, он обнаружил, что там все вещи ровно в 12 раз короче, чем на его родине. Сможете ли вы сказать, сколько лилипутских спичечных коробков поместится в спичечный коробок Гулливера?
Задача 16
На мачте пиратского корабля развевается двухцветный прямоугольный флаг, состоящий из чередующихся чёрных и белых вертикальных полос одинаковой ширины. Общее число полос равно числу пленных, находящихся в данный момент на корабле. Сначала на корабле было 12 пленных, а на флаге — 12 полос; затем два пленных сбежали. Как разрезать флаг на две части, а затем сшить их, чтобы площадь флага и ширина полос не изменились, а число полос стало равным 10?
Сначала на корабле было 12 пленных, а на флаге — 12 полос; затем два пленных сбежали. Как разрезать флаг на две части, а затем сшить их, чтобы площадь флага и ширина полос не изменились, а число полос стало равным 10?
Задача 17
В круге отметили точку. Можно ли так разрезать этот круг на три части, чтобы из них можно было бы сложить новый круг, у которого отмеченная точка стояла бы в центре?
Задача 18
Можно ли разрезать квадрат на четыре части так, чтобы каждая часть соприкасалась (т. е. имела общие участки границы) с тремя другими?
DIV_ADBLOCK245″>
Задача 24
На линейке длиной 9 см нет делений. Нанесите на неё три промежуточных деления так, чтобы ею можно было измерять расстояние от 1 до 9 см с точностью до 1 см.
Задача 25
Около каждой вершины треугольника напишите какие-нибудь числа, возле каждой стороны треугольника напишите сумму чисел, стоящих на концах этой стороны. Теперь каждое число, стоящее около вершины, сложите с числом, стоящим около противоположной стороны. Как вы думаете, почему получились одинаковые суммы?
Теперь каждое число, стоящее около вершины, сложите с числом, стоящим около противоположной стороны. Как вы думаете, почему получились одинаковые суммы?
Задача 26
Чему равна площадь треугольника со сторонами 18, 17, 35?
Задача 27
Разрежьте квадрат на пять треугольников так, чтобы площадь одного из этих треугольников равнялась сумме площадей оставшихся.
Задача 28
Квадратный лист бумаги разрезали на шесть кусков в форме выпуклых многоугольников; пять кусков затерялись, остался один кусок в форме правильного восьмиугольника (см. рисунок). Можно ли по одному этому восьмиугольнику восстановить исходный квадрат?
Задача 29
Легко можно разрезать квадрат на два равных треугольника или два равных четырехугольника. А как разрезать квадрат на два равных пятиугольника или два равных шестиугольника?
Задача 30
Пошёл Иван-царевич искать похищенную Кощеем Василису Прекрасную. Навстречу ему Леший.
Навстречу ему Леший.
Знаю, — говорит, — я дорогу в Кощеево Царство, случалось, ходил туда. Шёл я четыре дня и четыре ночи. За первые сутки я прошёл треть пути-прямой дорогой на север. Потом повернул на запад, сутки продирался лесом и прошёл вдвое меньше. Третьи сутки я шёл лесом, уже на юг, и вышел на прямую дорогу, ведущую на восток. Прошагал я по ней за сутки 100 вёрст и попал в Кощеево царство. Ты ходок такой же резвый, как и я. Иди, Иван-царевич, глядишь, на пятый день будешь в гостях у Кощея.
Нет,- отвечал Иван-царевич, — если всё так, как ты говоришь, то уже завтра я увижу мою Василису Прекрасную.
Прав ли он? Сколько вёрст прошёл Леший и сколько думает пройти Иван-царевич?
Задача 31
Придумайте раскраску граней кубика, чтобы в трёх различных положениях он выглядел, как показано на рисунке. (Укажите, как раскрасить невидимые грани, или нарисуйте развёртку.)
https://pandia.ru/text/78/456/images/image023_44.gif» align=»left»>Задача 32
У нумизмата Феди все монеты имеют диаметр не больше 10 см. Он хранит их в плоской коробке размером 30 см * 70 см (в один слой). Ему подарили монету диаметром 25 см. Докажите, что все монеты можно уложить в одну плоскую коробку размером 55 см *55 см.
Он хранит их в плоской коробке размером 30 см * 70 см (в один слой). Ему подарили монету диаметром 25 см. Докажите, что все монеты можно уложить в одну плоскую коробку размером 55 см *55 см.
Задача 33
Из квадрата 5×5 вырезали центральную клетку. Разрежьте получившуюся фигуру на две части, в которые можно завернуть куб 2×2×2.
Задача 34
Разрежьте данный квадрат по сторонам клеток на четыре части так, чтобы все части были одинакового размера и одинаковой формы и чтобы каждая часть содержала по одному кружку и по одной звёздочке.
Задача 35
Автостоянка в Цветочном городе представляет собой квадрат 7x 7 клеточек, в каждой из которых можно поставить машину. Стоянка обнесена забором, одна из сторон угловой клетки удалена (это ворота). Машина ездит по дорожке шириной в клетку. Незнайку попросили разместить как можно больше машин на стоянке таким образом, чтобы любая могла выехать, когда прочие стоят. Незнайка расставил 24 машины так, как показано на рис. Попытайтесь расставить машины по-другому, чтобы их поместилось больше.
Попытайтесь расставить машины по-другому, чтобы их поместилось больше.
Задача 36
Петя и Вася живут в соседних домах (см. план на рисунке). Вася живет в четвертом подъезде. Известно, что Пете, чтобы добежать до Васи кратчайшим путем (не обязательно идущим по сторонам клеток), безразлично, с какой стороны обегать свой дом. Определите, в каком подъезде живет Петя.
Задача 37
Предложите способ измерения диагонали обычного кирпича, который легко реализуется на практике (без теоремы Пифагора).
Задача 38
Разрежьте крест, составленный из пяти одинаковых квадратов, на три многоугольника, равных по площади и периметру.
Задача 39
https://pandia.ru/text/78/456/images/image033_35.gif»>
Задача 46
а) Тетраэдр б) куб разрезали по ребрам, выделенным жирными линиями (см. рисунки) и развернули. Нарисуйте получившиеся развертки.
Задача 47
Развертки каких тел изображены на рисунках? Выполните чертежи по рисункам, склейте их так, чтобы получилось геометрическое тело.
1)2) 3) 4)https://pandia.ru/text/78/456/images/image039_30.gif»>.gif»>8)
Задания 2-го модуля (3 курс)
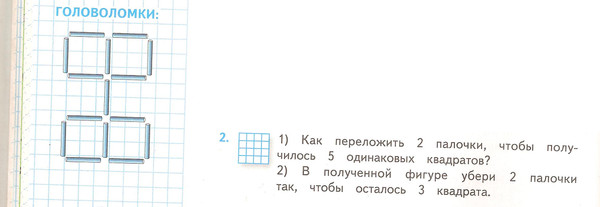
Галкина Алена Тема: Площадь фигуры Задание: разделить приведенную фигуру на 8 одинаковых частей Пример выполнения: Демитриев Евгений Тема: Построение рисунков на графике. Задание: Добавьте к правильному пятиугольнику 5 одинаковых треугольников так, что бы получилась звезда. Пример выполнения: Ивлев Алексей Задание.Подобрать ключ. В этой задаче из 10 спичек сложена форма ключа. Передвиньте 4 спички так, чтобы получилось три квадрата.
Пример выполнения. Задача решается достаточно просто. Четыре спички, образующие ту часть ручку ключа, нужно переместить на стержень ключа, так чтобы 3 квадрата были выложены в ряд. Павлущенко Ирина Тема: Графики линейной функции и их свойства. Задание. Загрузите предложенную картинку в Desmos. И по данному шаблону, используя графики линейной функции, постройте корову. Переставьте ровно 2 линии так, чтобы корова смотрела вправо. Пример выполнения:
Поплавская Мария Тема: Координатная плоскость Задание: В координатной плоскости построить следующие точки:
Соедините данные точки отрезками.
Саяпина Наталья Тема: Площадь фигур Задание: Пример выполнения:
Трушкин Антон Тема: Графики линейной функции и окружности. Свойства. Задание: Дана часть домика. Воспользуйтесь свойствами графика линейной функции , окружности и постройте недостающую часть дома, симметричную относительно оси Y. Пример выполнения:
| Девятова Анастасия Тема: Построение точек по их координатам. Задание. «Какие суда сейчас находятся в зоне особого внимания (голубой сектор на экране радара)?» В левой части экрана расположены координаты, записанные в виде выражений на действия с положительными и отрицательными числами. Задание: Пример выполнения:
Карапетян Анжелика Тема: График и свойства линейной функции и окружности Задание: Загрузите в Desmos данную картинку; постройте «бокал» и «вишенку» по картинке, как по шаблону. Как нужно переместить «бокал», переложив две палочки, чтобы «вишенка» оказалась снаружи? Пример выполнения:
Назарова Екатерина Тема: Решение неравенств графическим способом Задание: Разрежьте квадрат на 5 прямоугольников, так чтобы у соседних прямоугольников стороны не совпадали. (Учебно-методическое пособие «Готовимся к олимпиадам по математике» А. Задание: Пример выполнения:
Стифорова Анна Тема: Координатная плоскость. Построение точек по их координатам. График и свойства линейной функции. Задание: На звездном небе (координатной плоскости) точками обозначены некоторые звезды одного из созвездий. Но самые яркие звезды Вам предстоит отыскать и отметить самим. Для этого: а) вычислите вторую координату точки-звезды, затем постройте их на звездном небе. Лучше выделить звезды ярким цветом; б) последовательно соедините полученные точки; в) соедините также точку-звезду A c точкой (-1;-5), Е с (7;-2), а G с началом координат. Узнали? Как называется это созвездие? Задание: Пример выполнения:
Шавелько Татьяна Тема: Графики линейной функции и их свойства. Задача: Проведите непрерывную ломаную линию с минимальным числом отрезков, проходящих через центры всех точек. Пример выполнения: Тумандеева Алевтина Тема: Площадь фигуры Задача: Разрежьте фигуру на четыре одинаковых многоугольника отличающихся по своей форме от исходной фигуры. Пример выполнения:
Тиморевская Влада Тема: Площадь фигуры Задание: Сколько кругов радиуса 1 надо взять, чтобы покрыть ими квадрат со стороной 2? Пример выполнения: Черныш Кристина Тема: Деление отрезка на 2 равные части Задание: Найдите середину отрезка, используя графики окружности. Задание: Пример выполнения: Трушкина Марина Тема: Координатная плоскость и свойства линейной функции Задание: Дана начальная часть рисунка.
|
Разрезание Дьюдени — Mnogogranniki.ru
Разрезание Дьюдени — Mnogogranniki.ru- Вы здесь:
- Главная
- Разрезание Дьюдени — неразрывная цепочка разрезания
Можно ли разрезать треугольник на такое количество частей, чтобы из них можно было сложить квадрат?
Утвердительный ответ на этот вопрос был дан еще в 1807 году. В более общем виде это звучало так: «Любые два многоугольника общей площади должны иметь общее разрезание». Это теорема Бойля –Гервина, доказанная в 1807. Если у нас есть треугольник и квадрат и мы знаем, что их площади одинаковы, разрезав треугольник на несколько многоугольников, мы можем как из мозаики сложить квадрат.
Но вот более сложный вопрос. А можно ли разрезать так, чтобы все части оставались соединенными в неразрывную цепочку?
А можно ли разрезать так, чтобы все части оставались соединенными в неразрывную цепочку?
Шарнирное разрезание или разрезания Дью-дени (по имени автора), выполненное в виде анимации, демонстрирует нам как треугольник преобразуется в квадрат, а затем в шестиугольник и обратно в треугольник (использован анимационный ролик из Wikipedia).
В переведенном издании (Дьюдени Г. Э. Кентерберийские головоломки / Перевод с английского Ю. Н. Сударева. — М.: Мир, 1979. — С. 46—47.) исходный текст звучит следующим образом:
«Много попыток было предпринято, чтобы побудить Галантерейщика предложить компании какую-нибудь головоломку, но они долго оставались безуспешными. Наконец, на одной из стоянок Галантерейщик сказал, что покажет всем нечто, отчего «их мозги перекрутятся, как веревка от колокола». Кстати, он сыграл с компанией шутку, ибо сам не знал ответа на головоломку, которую предложил. Достав кусок материи в форме правильного равностороннего треугольника, он сказал:
— Есть ли среди вас кто-нибудь, кому приходилось бы раскраивать материю? Побожусь, что нет. Каждый умеет что-то свое, и школяр может чему-нибудь поучиться у простолюдина, а мудрец у дурака. Покажите мне, если умеете, каким образом этот кусок материи можно разрезать на четыре части так, чтобы потом из них удалось составить правильный квадрат.
Каждый умеет что-то свое, и школяр может чему-нибудь поучиться у простолюдина, а мудрец у дурака. Покажите мне, если умеете, каким образом этот кусок материи можно разрезать на четыре части так, чтобы потом из них удалось составить правильный квадрат.
Некоторые из наиболее образованных паломников сумели сделать это с пятью частями, но не с четырьмя. Но когда они насели на Галантерейщика, требуя от него правильного ответа, он после долгих увиливаний признался, что не умеет решать эту задачу ни для какого числа частей.
— Клянусь святым Франциском, — сказал он, — каждый мошенник, думается мне, может придумать головоломку, но она хороша для тех, кто умеет ее решать.
После этих слов он едва унес ноги».
Решение задачи.
На рисунках показано, каким образом треугольный кусок материи можно разрезать на 4 части, из которых затем удается сложить правильный квадрат.
1. Разделим AB пополам в точке D
Разделим AB пополам в точке D
2. ВС разделим пополам в точке Е.
4. Строим дугу из точки E, радиусом EB. На пересечении с прямой АЕ получаем точку F.
5. Разделим пополам AF в точке G.
6. Проведем дугу AF с центром в точке G.
7. Продолжим ЕВ до пересечения с дугой в точке Н.
8. Из Е как из центра радиусом ЕН опишем дугу HJ.
После этой операции нам удалось получить первый разрез треугольника — отрезок EJ.
9. Отложим отрезок JK, равный BE.
10. Из точки D опустим перпендикуляр на EJ с основанием в точке L.
11. Из точки К опустим перпендикуляр на EJ с основанием в точке М.
Получаем отрезки, вдоль которых следует провести разрезы.
Автор задачи – английский математик Генри Эрнест Дью-дени (1857 — 1930 гг.) известен как один из выдающихся создателей математических головоломок.
Выступая с этой задачей, поставленной в более общей форме, перед Королевским обществом в Берлингтон-Хауз, а также в Королевском институте, добавил еще один рисунок, на котором решение задачи показано в более любопытной и удобной для практики форме. Все части модели можно сделать из красного дерева, скрепив их бронзовыми шарнирами, дабы ее удобно было показывать в аудитории. Легко заметить, что все четыре части образуют нечто вроде цепочки. Если закрутить эту цепочку в одном направлении, то получится треугольник, а если ее закрутить в противоположную сторону, то получится квадрат.
Сейчас такое разбиение треугольника так и называется — «Разрезание Дьюдени» в честь автора или «шарнирное разрезание», так как в узлах соединения многоугольников должны находиться шарниры, позволяющие легко крутиться конструкции и переходить из треугольника в квадрат и обратно.
Изготовить такую занимательную головоломку, позволяющую преобразовать правильный треугольник в квадрат неразрывной цепочкой многоугольников, можно самостоятельно из бумаги.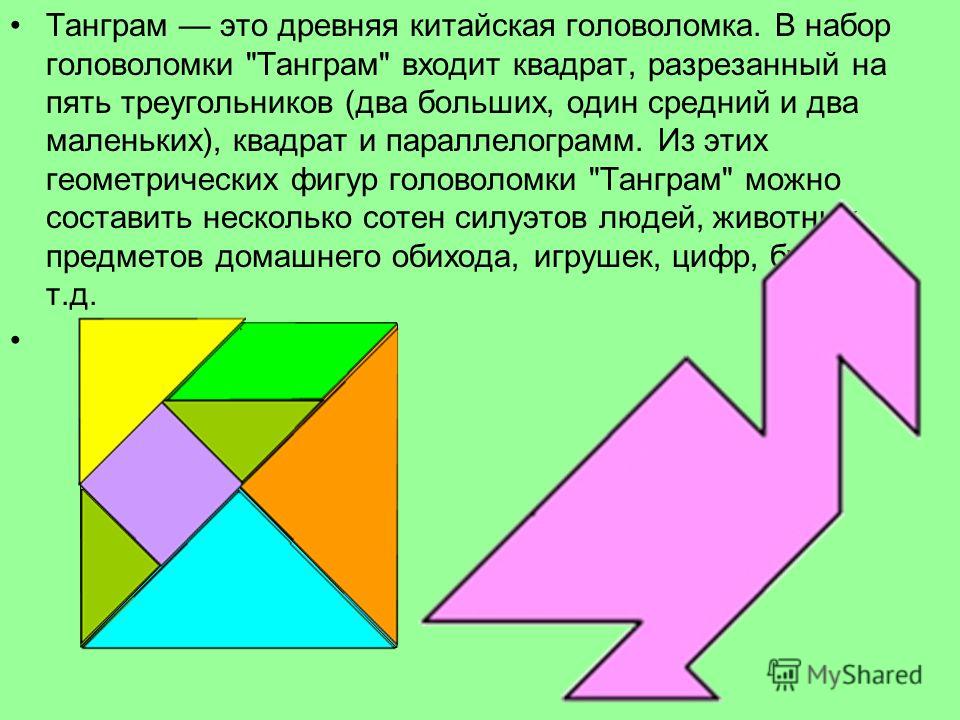 Но, чтобы сделать её подвижной, необходимо, чтобы это была не плоская, а объемная конструкция. Поэтому каждый из многоугольников получает высоту и преобразуется в призму.
Но, чтобы сделать её подвижной, необходимо, чтобы это была не плоская, а объемная конструкция. Поэтому каждый из многоугольников получает высоту и преобразуется в призму.
Мы предлагаем Вам скачать развертки деталей в виде 4-й призм.
Для каждого «кусочка» головоломки мы склеиваем отдельную призму, а затем соединяем отдельные призмы между собой в виде шарниров.
Развертка часть 1
Развертка часть 2
Развертка часть 3
Схема сборки:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
Кроме «классического» разрезания треугольника, можно также изготовить другие, весьма привлекательные шарнирные разрезания геометрических фигур.
1. Шарнирное разрезание квадрата, позволяющее преобразовать его в правильный шестиугольник.
Задача звучит следующим образом: как разрезать квадрат, чтобы из его частей можно было собрать правильный шестиугольник?
Скачать 1 развертку разрезания квадрата
Скачать 2 развертку разрезания квадрата
Скачать 3 развертку разрезания квадрата
Скачать 4 развертку разрезания квадрата
Скачать 5 развертку разрезания квадрата
Скачать 6 развертку разрезания квадрата
2. Шарнирное разрезание правильного шестиугольника, позволяющее преобразовать его в треугольник.
Задача звучит следующим образом: как правильный шестиугольник, чтобы из его частей можно было собрать треугольник?
Скачать 1 развертку разрезания правильного шестиугольника
Скачать 2 развертку разрезания правильного шестиугольника
Скачать 3 развертку разрезания правильного шестиугольника
Скачать 4 развертку разрезания правильного шестиугольника
Скачать 5 развертку разрезания правильного шестиугольника
3. Шарнирное разрезание креста, образованного пятью квадратами, и позволяющее преобразовать его в единый квадрат.
Шарнирное разрезание креста, образованного пятью квадратами, и позволяющее преобразовать его в единый квадрат.
Задача звучит следующим образом: как разрезать крест, образованный пятью квадратами, чтобы из его частей можно было собрать единый квадрат?
Скачать 1 развертку разрезания креста
Скачать 2 развертку разрезания креста
Скачать 3 развертку разрезания креста
Скачать 4 развертку разрезания креста
Канадский дизайнер Эммануэль Пелючон (Emmanuel Peluchon), повторил головоломку Дьюдени изготовив её из дерева и поместив внутри часы:
Конструкция выполнена из деревянных призм, аккуратно скрепленных обычными петлями.
Стоимость такой дизайнерской головоломки 380 канадских долларов. Канада – дорогая страна 🙂
На картинке представлены все головоломки, иллюстрирующие шарнирное разрезание, собранные из предложенных разверток.
Популярное
Выбрать один продукт
В настоящее время покупатель столкнулся с настолько широким ассортиментом товаров, что сил на то чтобы сделать рациональный выбор уже не хватает. И реклама иногда только усиливает…
И реклама иногда только усиливает…
Многогранники для Хэллоуина
Если ты не любишь математику, опасайся хэллоуина! Злые силы придут за тобой в хэллоуин! Создай двух стражей, которые будут оберегать тебя от злых сил! Ну, или,…
Самая прочная конструкция
Какое из известных нам геометрических тел обладает наибольшей прочностью? Наиболее устойчиво к внешним деформациям?
Разделить икосаэдр!
Можно ли представить икосаэдр в виде более простых многогранников?…
Развертки просто необходимы в Mcdonalds
Знакомые каждому с детства коробочки для Биг-Мака и картошки, стаканчик для Кока-Колы так же делают из бумажных разверток.
Шесть коробочек и золотое сечение
Эта модель многогранника представляет из себя пересечение трёх параллелепипедов. В её основе пересечение трёх прямоугольников, где…
В её основе пересечение трёх прямоугольников, где…
3D – календарь ромбододекаэдр на 2021 год
Изобретение календаря замечательное событие для человечества. То, что год состоит из 12ти месяцев ни для кого не секрет. С тех пор люди самыми различными способами группируют…
Ответы на вопросы в конкурсе “Смарт КЕНГУРУ” 25 января 2022
В 1991 году два французских математика решили провести эту игру во Франции, назвав ее “Кенгуру” в честь собственных австралийских друзей. Французские организаторы решили назвать новый вид соревнований конкурсом-игрой, подчеркивая тем самым занимательный характер многих заданий.
Первая игра собрала 120 тысяч учеников колледжей, позднее конкурс охватил также школьников и лицеистов. В июне 1993 года французские организаторы “Кенгуру” устроили встречу в Париже для управляющих математических соревнований европейских государств. На приглашенных математиков огромное впечатление произвел успех конкурса “Кенгуру – математика для всех” во Франции: 1991 год – 120 тысяч участников, 1992 год – 300 тысяч, 1993 год – 500 тысяч.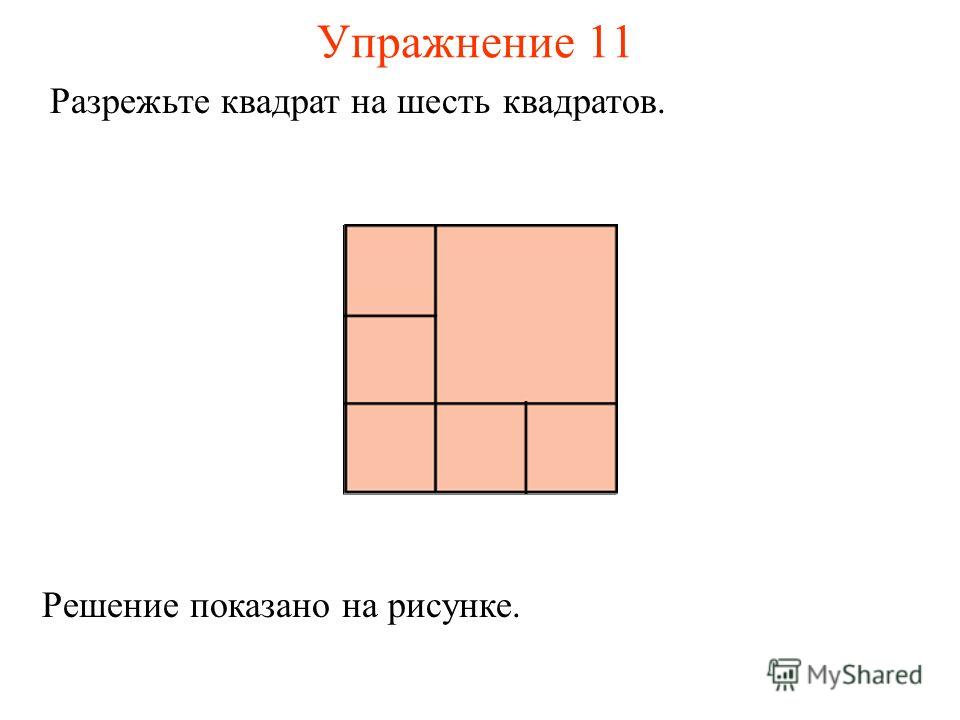 В мае 1994 года Белоруссия, Венгрия, Испания, Нидерланды, Польша, Россия и Румыния решили тоже участвовать в конкурсе.
В мае 1994 года Белоруссия, Венгрия, Испания, Нидерланды, Польша, Россия и Румыния решили тоже участвовать в конкурсе.
В июле 1994 года, в Страсбурге, на Совете Европы, Генеральная ассамблея образовала из 10 европейских государств Ассоциацию “Кенгуру без границ” (Le Kangourou sans frontieres) с бюро из 6 выборных членов в Париже. Сейчас эта Ассоциация объединяет участников из почти всех государств. Целью Ассоциации является обширное распространение общей математической культуры и в частности организация конкурса-игры “Кенгуру”, проводимой в один и тот же день во всех странах-участницах. Сохранилась форма конкурса – вопросник с выбором предложенных ответов, день и час проведения и основной принцип – “приз для всех“, для каждого участника. При этом любая страна имеет собственный оргкомитет, свои призы, результаты различных государств не сравниваются меж собой.
1. Смартик сложил из спичек свое имя. В какой букве больше всего спичек?
Ответ: Б — М
2. Катя расположила числа 10, 7, 9, 3, 13, 5, 15 в порядке возрастания. Какое число она поставила предпоследним?
Катя расположила числа 10, 7, 9, 3, 13, 5, 15 в порядке возрастания. Какое число она поставила предпоследним?
Ответ: А — 13
3. Что может получиться, если полоску, показанную на рисунке, склеить в кольцо, а потом разрезать в другом месте?
Ответ: В
4. Робот может за один ход пройти или на три клетки вправо, или на две клетки вниз. Если следующий ход сделать нельзя, он останавливается. Робот начинает с клетки, отмеченной кружком. В какой клетке он остановится?
Ответ: Б — Б
5. Винни-Пух собирался сделать одно важное дело. Если бы он начал в понедельник, то закончил бы в четверг. На самом деле он закончил в субботу. В какой день недели он начал?
Ответ: Б — в среду
6. На сколько разных цифр можно заменить звездочку, чтобы получилось двузначное число, большее 43?
Ответ: Г — 6
7. В
8. Б
9. Б
10. Б
Б
11. В
12. Г
13. В коробке лежат шарики. Среди фраз А-Д об этих шариках ровно одна неверная. Какая?
Ответ: Г — шариков 4 или меньше
14. Квадратный лист в клеточку 4х4 несколько раз согнули по линиям сетки. Сложенный лист проткнули один раз и разогнули обратно. Какая картинка могла получится?
Ответ: В
15. В ребусе разные буквы заменяют разные цифры, а одинаковые буквы — одинаковые цифры. Смартик нашёл решение ребуса, в котором есть цифра 6. Какую цифру в этом решении заменяет буква И?
Ответ: Д — 9
- Смартик выписал первые буквы названий всех цифр. Сколько из этих букв встречаются в слове СМАРТИК?
Ответ: Б — 2
- Смартик построил домики из деталей трех видов. В каком из домиков меньше деталей, чем в остальных?
Ответ: Д
- Как называется одно из арифметических действий?
Ответ: Г — вычитание
4. Какое число получится, если выписать цифры, двигаясь по стрелочкам на рисунке?
Какое число получится, если выписать цифры, двигаясь по стрелочкам на рисунке?
Ответ: Г — 35124
- Электронные часы сейчас показывают 10 :10. Через сколько минут на часах будет тот же набор цифр?
Ответ: Б — 50
- Прямоугольный коврик размером 2 × 3 сшит из шести квадратиков. Три таких коврика положили на пол, как показано на рисунке. В середину какого квадратика надо вбить гвоздик, чтобы приколотить к полу все три коврика?
Ответ: В — В
- В альбоме с раскрасками Маша раскрашивает каждый день по одной картинке. Первую картинку она раскрасила в пятницу. В какой день Маша раскрасит пятую картинку?
Ответ: Г — во вторник
- У Насти на новогодней елке было 19 игрушек: шарики, звездочки и фонарики. Из них 10 игрушек — не шарики, а звездочек на 2 меньше, чем шариков. Сколько фонариков было на елке?
Ответ: В — 3
Задачи, оцениваемые в 4 балла
- Из лагеря выехала группа велосипедистов, всего 16 человек.
 Их маршрут обозначен стрелочками на рисунке. На каждой развилке велосипедисты делились на две равные группы. Сколько велосипедистов приехало в Комарово?
Их маршрут обозначен стрелочками на рисунке. На каждой развилке велосипедисты делились на две равные группы. Сколько велосипедистов приехало в Комарово?
Ответ: Г — 10
- Название какой цифры можно составить из букв слова СМАРТИК?
Ответ: В — 3
- Смартик склеил круг, квадрат и треугольник так, как показано на рисунке. Как выглядит его конструкция с другой стороны?
Ответ: Б
- Предпоследнее число четвертого десятка — это
Ответ: Б — 38
- Смартик правильно заполнил схему на рисунке. В каких двух клетках оказались равные числа?
Ответ: Д — A и D
- Сначала Смартик выписал в ряд четные числа из набора 1, 2, 3, 4, 5, 6, 7, 8, 9 в порядке убывания, а потом справа приписал нечетные числа в порядке возрастания. Какой фрагмент есть в его ряду?
Ответ: А — 4213
- В Цветочном городе коротышки учатся с понедельника по пятницу.
 Незнайка прогулял уроки в среду 1 сентября, после чего стал прогуливать каждый четвертый учебный день. Какой из следующих дней он прогулял?
Незнайка прогулял уроки в среду 1 сентября, после чего стал прогуливать каждый четвертый учебный день. Какой из следующих дней он прогулял?
Ответ: А — 9 сентября
- Три картонных прямоугольника 3 × 4 положили на клетчатый лист так, как показано на рисунке. Сколько клеток листа покрыто ровно двумя прямоугольниками?
Ответ: В — 7
- Электронные часы показывают 22 : 20. Через какое время они покажут тот же набор цифр?
Ответ: В — через 4 часа 2 минуты
Задачи, оцениваемые в 4 балла
- В турнире по теннису было 8 участников. Они разбились на пары и сыграли четыре матча, победители вновь разбились на пары и сыграли еще два матча. Наконец, победители этих матчей сыграли между собой финал. В этих семи матчах победили Вася, Аня, Миша, Аня, Толя, Аня, Миша (может быть, в другом порядке). Кто выиграл турнир?
Ответ: А — Аня
Задачи, оцениваемые в 3 балла
- В клетки квадрата на рисунке Смартик вписал последовательно буквы своего имени.
 Он начал с центральной клетки и двигался по стрелкам. Какие две буквы оказались в соседних клетках?
Он начал с центральной клетки и двигался по стрелкам. Какие две буквы оказались в соседних клетках?
Ответ: Д — С и И
- Смартик решал уравнение. Он понял: чтобы найти х, нужно сначала вычесть из числа 12 число 4, а потом результат поделить на 2. Что это было за уравнение?
Ответ: А — 2х+4=12
- Смартик измерил два угла треугольника. Оказалось, что они равны 20° и 22°. Тогда этот треугольник
Ответ: Д — тупоугольный
- Смартик склеил круг, квадрат и треугольник так, как показано на рисунке. Как выглядит его конструкция с другой стороны?
Ответ: Д
- Винни-Пух два дня подряд ходит в гости к Кролику, потом два дня подряд ходит в гости к Пятачку, потом снова два дня к Кролику и так далее. В воскресенье он был в гостях у Пятачка. В какой из дней на следующей неделе он наверняка ходил к Кролику?
Ответ: Б — вторник
- На рисунке изображено несколько замкнутых линий.
 Смартик хочет соединить точку А с точкой В. Какое наименьшее число линий ему придется пересечь?
Смартик хочет соединить точку А с точкой В. Какое наименьшее число линий ему придется пересечь?
Ответ: Б — 4
- Между какими двумя числами расположена дробь 2023/2022?
Ответ: В — 1,0001 и 1,001
- Из цифр года 2022 можно составить ровно одну дату: 22.02, то есть 22 февраля. Через сколько лет будет год, из цифр которого тоже можно составить ровно одну дату?
Ответ: Г — 11
Задачи, оцениваемые в 4 балла
- У Маши есть 10 проволочных уголков (см. рисунок 1). Какое наименьшее число уголков нужно разогнуть, чтобы сложить контур, изображенный на рисунке 2?
Ответ: Б — 3
На рисунке изображены три одинаковых квадрата. Чему равен отмеченный угол?
Ответ: В — 120°
Чему равно наименьшее двузначное число, большее наибольшего двузначного числа, делящегося на 13?
Ответ: В — 91
Из города в Простоквашино в 14:00 выехал дядя Федор на велосипеде, и одновременно из Простоквашино выехал почтальон Печкин на тракторе. В 16:00 они встретились, а в 17:30 дядя Федор приехал в Простоквашино. Когда Печкин приехал в город?
В 16:00 они встретились, а в 17:30 дядя Федор приехал в Простоквашино. Когда Печкин приехал в город?
Ответ: А — 18:00
На прямой отмечены точки А, В, С и D. Известно, что расстояние между А и В равно 2, между B и C — 3, а между С и D — 4 . Чему не может быть равно расстояние между А и D?
Ответ: Г — 7
На какое наименьшее число нужно умножить 20²², чтобы получился куб натурального числа?
Ответ: Г — 2²•5²
На сторонах равнобедренного треугольника ABC с основанием АС отмечены точки Е и D так, что BE=ED и AD=AC. Угол при вершине В равен 30°. Найдите угол EDA.
Ответ: Г — 75°
Задачи, оцениваемые в 3 балла
- В день конкурса Смартик склеил бумажные буквы С и М (см. рисунок). Как может выглядеть его конструкция с другой стороны?
Ответ: Г
- Карта страны Квадра поделена на 16 одинаковых квадратиков (см. рисунок). Какой из них является северо-западной частью юго-востока этой страны?
Ответ: В — 3
- Семь чисел отмечены точками на числовой прямой.
 Произведение чисел P и Q равно одному из этих чисел. Какому?
Произведение чисел P и Q равно одному из этих чисел. Какому?
Ответ: Б — В
- Сколько дней в килосантинеделе?
Ответ: Б — 70
- Площади треугольников на рисунке равны 5 и 10, а прямые a, b и с параллельны. Расстояние между прямыми a и b равно 6. Чему равно расстояние между прямыми b и с?
Ответ: Д — 3
- Чему равна разность суммы чисел a и b и разности их суммы и разности?
Ответ: Д — a+b
- Каждый день Вася ходит или на футбольную секцию, или на занятие математического кружка: 3 дня подряд — на футбол, потом 2 дня — на кружок, потом опять 3 дня — на футбол и так далее. В воскресенье он был на футболе. В какой из дней на следующей неделе он наверняка ходил на футбол?
Ответ: Д — пятница
- Если 4a ∙ 8b = 16 c, то
Ответ: А — 2a+3b= 4 c
Задачи, оцениваемые в 4 балла
- Диагональ квадрата равна квадрату стороны этого квадрата.
 Чему равна эта диагональ?
Чему равна эта диагональ?
Ответ: А — √2
Вырезание треугольников в половину и четверть квадрата
Пропуск слайдов галереи
Вырезание треугольников в половину и четверть квадрата
Используйте эти советы для вырезания треугольников в половину и четверть квадрата. Приведены инструкции для правой и левой резки.
Начать слайд-шоу
1 из 21
Вырезание полуквадратных треугольников (правая сторона)
Вырезание полуквадратных и четвертьквадратных треугольников
1. Расправьте ткань.
2. Нарежьте ткань полосами шириной, равной желаемой ширине треугольных квадратов в готовом виде, плюс 7/8 дюйма на припуски на швы. Полоса ткани шириной 8 дюймов.
Реклама
Реклама
2 из 21
Вырезание полуквадратных треугольников (правосторонние)
Вырезание полуквадратных треугольников (правосторонние)
3. Подровняйте один конец каждой полосы.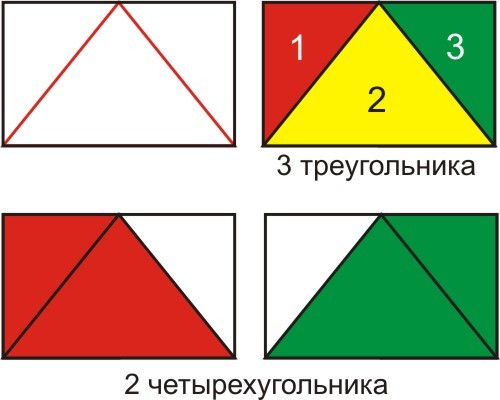
3 из 21
Нарезка полуквадратных треугольников (правосторонняя)
Нарезка полуквадратных треугольников (правосторонняя)
4. С помощью линейки нарежьте полосу на куски, равные ширине полоски. В этом примере полоса будет разрезана на куски длиной 3-7/8 дюйма.
Реклама
4 из 21
Вырезание полуквадратных треугольников (правосторонний)
Вырезание полуквадратных треугольников (правосторонний)
5. Расположите линейку по диагонали над квадратом и разрежьте квадрат пополам, чтобы составить два равновеликих прямоугольных треугольника.
5 из 21
Вырезание полуквадратных треугольников (для левой руки)
Вырезание полуквадратных треугольников (для левой руки)
1. Расправьте ткань.
2. Нарежьте ткань полосами шириной, равной желаемой ширине треугольных квадратов в готовом виде, плюс 7/8 дюйма на припуски на швы. Полоса ткани шириной 8 дюймов.
6 из 21
Вырезание полуквадратных треугольников (для левой руки)
Вырезание полуквадратных треугольников (для левой руки)
3. Подровняйте один конец каждой полосы. 7 из 21 длины, равные ширине полосы. В этом примере полоса будет разрезана на куски длиной 3-7/8 дюйма.
Подровняйте один конец каждой полосы. 7 из 21 длины, равные ширине полосы. В этом примере полоса будет разрезана на куски длиной 3-7/8 дюйма.
8 из 21
Вырезание полуквадратных треугольников (для левой руки)
Вырезание полуквадратных треугольников (для левой руки)
5. Расположите линейку по диагонали над квадратом и разрежьте квадрат пополам, чтобы получить два равных -размер прямоугольных треугольников.
9 из 21
Вырезание треугольников в четверть квадрата (правая сторона)
Вырезание треугольников в четверть квадрата (правая сторона)
1. Расправьте ткань.
2. Разрежьте ткань на полоски шириной, равной желаемой ширине треугольника в четверть квадрата, плюс 1-1/4 дюйма на припуски на швы. Полоса ткани шириной 1/4″.
Объявление
Объявление
Объявление
10 из 21
Резка треугольников в четверть квадрата (правосторонняя)
Резка треугольников в четверть квадрата (правосторонняя) 900
11 из 21
Вырезание треугольников в четверть квадрата (правосторонние)
Вырезание треугольников в четверть квадрата (правосторонние)
4. С помощью линейки нарежьте полосу на куски, равные ширине полоски. В этом примере полоса будет разрезана на куски длиной 4-1/4 дюйма.
С помощью линейки нарежьте полосу на куски, равные ширине полоски. В этом примере полоса будет разрезана на куски длиной 4-1/4 дюйма.
12 из 21
Вырезание треугольников в четверть квадрата (правосторонних)
Вырезание треугольников в четверть квадрата (правосторонних)
5. Расположите линейку по диагонали над квадратом и разрежьте квадрат пополам, чтобы получить два равных размеры прямоугольных треугольников. Не двигайте и не поднимайте треугольники.
Реклама
Реклама
Реклама
13 из 210003
6. Расположите линейку по диагонали над разрезанным квадратом в противоположном направлении и снова разрежьте квадрат пополам, чтобы получилось четыре треугольника одинакового размера.
14 из 21
Вырезание треугольников в четверть квадрата (для левой руки)
Вырезание треугольников в четверть квадрата (для левой руки)
1. Расправьте ткань.
2. Разрежьте ткань на полоски шириной, равной желаемой ширине треугольника в четверть квадрата, плюс 1-1/4 дюйма на припуски на швы. Полоса ткани шириной 1/4″.
Полоса ткани шириной 1/4″.
15 из 21
Вырезание треугольников в четверть квадрата (для левой руки)
Вырезание треугольников в четверть квадрата (для левой стороны)
3. Подровняйте один конец каждой полосы. 16 из 21 длины, равные ширине полосы. В этом примере полоса будет разрезана на куски длиной 4-1/4 дюйма.
17 из 21
Вырезание треугольников в четверть квадрата (для левой руки)
Вырезание треугольников в четверть квадрата (для левой стороны)
5. Расположите линейку по диагонали от угла к углу и разрежьте квадрат пополам, чтобы составить два равновеликих прямоугольных треугольника. Не двигайте и не поднимайте треугольники.
18 из 21
Вырезание треугольников в четверть квадрата (для левой руки)
Вырезание треугольников в четверть квадрата (для левой стороны)
6. Расположите линейку по диагонали от угла к углу в противоположном направлении и вырежьте квадрат еще раз пополам, чтобы в общей сложности получилось четыре треугольника одинакового размера.
Реклама
Реклама
Реклама
19 из 21
Резка треугольников в четверть квадрата (левая)
Резка треугольников в четверть квадрата (левая сторона) 900
20 из 21
Вырезание треугольников в четверть квадрата (для левой руки)
Вырезание треугольников в четверть квадрата (для левой стороны)
4. С помощью линейки нарежьте полосу на куски, равные ширине полосы. В этом примере полоса будет разрезана на куски длиной 4-1/4 дюйма.
21 из 21
Вырезание треугольников в четверть квадрата (для левой руки)
Вырезание треугольников в четверть квадрата (для левой стороны)
6. Расположите линейку по диагонали от угла к углу в противоположном направлении и вырежьте квадрат еще раз пополам, чтобы в общей сложности получилось четыре треугольника одинакового размера.
Реклама
Реклама
Реклама
Галерея повторовПоделиться галереей
Впереди
Общий доступ к галерее
Пропустить сводку слайдов
Все в этом слайд-шоу
Реклама
Эта ссылка ведет на внешний сайт, который может соответствовать или не соответствовать правилам доступности.
Шесть кругов | NZ Maths
Последовательность уроков
Сессия 1
Найдите все четыре ответа на задачу шести кругов и убедитесь, что других нет. Попытка показать, что это так. Что вы можете сказать по поводу ответов, которые вы нашли?
Предыстория
Сначала мы начнем с проблемы, на которой основан весь этот раздел.
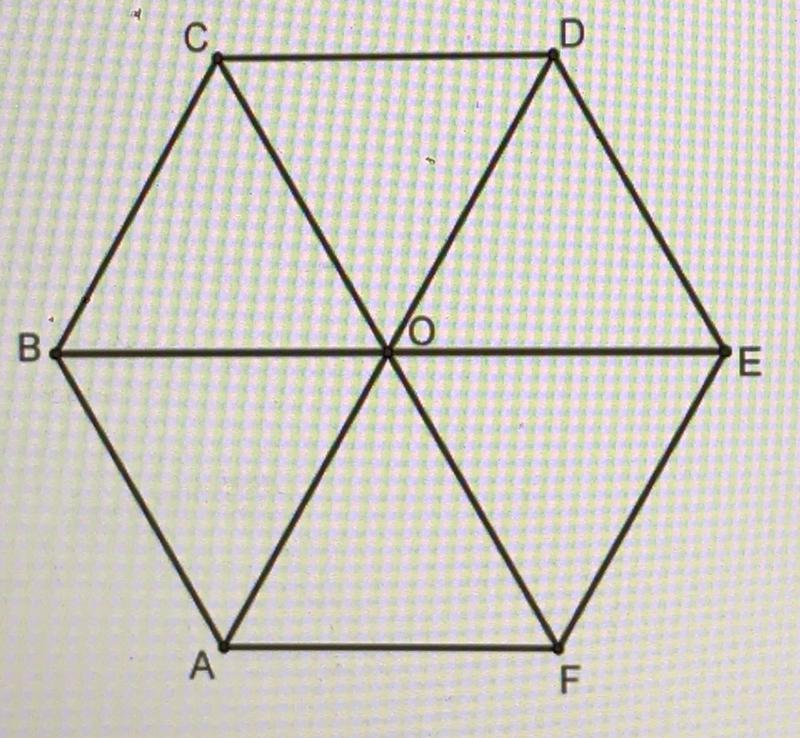
Основная задача (задача шести кругов): можно ли разместить числа 1, 2, 3, 4, 5, 6 в кругах так, чтобы суммы трех чисел по обе стороны треугольника были одинаковыми ?
Прежде чем представить задачу классу, стоит немного подумать над ней. Есть несколько вещей, которые необходимо учитывать.
- Не беспокойтесь слишком сильно о том, чтобы заставить учащихся найти формулу или метод для решения этой задачи. Важная вещь, которую они должны сделать в начале, — это использовать свою интуицию. На самом деле это означает поощрять их пробовать все, что приходит им в голову.
 Так что поощряйте их угадывать, экспериментировать и не беспокоиться о том, какой метод они используют, даже если он кажется совершенно нематематическим!
Так что поощряйте их угадывать, экспериментировать и не беспокоиться о том, какой метод они используют, даже если он кажется совершенно нематематическим! - Затем, когда они начнут получать ответы, вам нужно будет заставить их подумать, какие ответы отличаются друг от друга. Дело в том, что, получив один ответ, они могут получить еще пять, просто используя повороты равностороннего треугольника. Поскольку мы можем получить любой из шести из других здесь, мы могли бы также сказать, что они все одинаковы. Итак, мы скажем, что два ответа ниже одинаковы.
- Какие ответы существуют и сколько их? Методом проб и ошибок будет как минимум четыре. Мы показываем их ниже. Но есть ли еще что-то, что мы еще не показали?
- Важно отметить суммы сторон по двум причинам. Во-первых, нам нужно проверить, что сумма на всех трех сторонах одинакова, чтобы убедиться, что у нас есть правильный ответ. Во-вторых, эта сумма окажется фундаментальной в дальнейшем.

Что теперь можно сказать об ответах? Есть ли между ними какая-то связь? Есть ли какие-то закономерности, которые мы должны увидеть? Вот список того, что могут найти ваши ученики.
- Угловые круги содержат 1, 2, 3; 4, 5, 6; 1, 3, 5; и 2, 4, 6. Это самые маленькие и самые большие последовательные числа, нечетные числа и четные числа.
- Если вы переместите цифры одного ответа по одному кругу, вы получите другой ответ. Неважно, как вы их двигаете: по часовой или против часовой стрелки. Используя этот ход, A становится D становится A, а B становится C становится B.
- Замена угловых номеров на средние и наоборот меняет один ответ на другой. Это вызывает те же переключатели, что и последний элемент в списке.
- Разница между противоположными угловыми и средними числами одинакова. Посмотрите на А. 4 напротив 1 и 4 – 1 = 3. 5 напротив 2 и 5 – 2 = 3. 6 напротив 3 и 6 – 3 = 3.
- Если вы замените каждое число m на 7 – m, вы получите другой ответ.
 Таким образом, в B, если вы замените 1 на 6, 2 на 5 и т. д., B превратится в C.
Таким образом, в B, если вы замените 1 на 6, 2 на 5 и т. д., B превратится в C.
Мы не утверждаем, что это исчерпывающий список. Если ваши ученики найдут какие-то другие свойства четырех ответов, мы будем рады услышать о них и добавить в список.
Последовательность обучения
- Относитесь к этому уроку как к любому из уроков-задач, которые можно найти в другом месте на этом сайте. Представьте проблему и обсудите ее, чтобы убедиться, что все учащиеся понимают, о чем идет речь в вопросе и как его можно решить. Затем в группах от 2 до 4 дайте учащимся возможность решить задачу.
- По мере того, как группы придумывают ответы, предложите им найти больше ответов, спросив: «Вы можете найти еще?». Сделайте это, даже если они получили все четыре ответа. Также предложите им подумать о том, когда два ответа одинаковы или различны. («Этот ответ такой же, как и все остальные, которые вы нашли?» «Можете ли вы получить этот ответ из этого ответа?») Дайте каждому возможность добиться некоторого прогресса в решении проблемы.
 Это может означать, что вам нужно будет предложить несколько угловых номеров или, если у них есть некоторые номера в правильных позициях, вам может потребоваться сказать им, что это нормально, но они могут подумать о перемещении других в другое место.
Это может означать, что вам нужно будет предложить несколько угловых номеров или, если у них есть некоторые номера в правильных позициях, вам может потребоваться сказать им, что это нормально, но они могут подумать о перемещении других в другое место. - Когда они решат, что нашли все возможные ответы, предложите им доказать, что ответы, которые они нашли, являются единственными существующими. («Как вы думаете, почему ответов больше нет?») В рамках этого процесса попросите их подумать, как ответы связаны друг с другом, как мы сделали в списке из пяти пунктов выше. Этот список пригодится позже и является хорошим математическим инструментом — посмотрите на то, что у вас есть, чтобы увидеть, есть ли какой-то способ понять это лучше.
- Обсудите в классе результаты исследования. Попросите разных учащихся написать один ответ на доске, пока они не увидят, когда два ответа совпадают (из-за симметрии треугольника) и что ответов всего четыре. Сделайте предположение о количестве ответов.

- Наконец-то проведите сеанс мозгового центра, чтобы сгенерировать идеи для следующего урока. Как мы можем доказать/обосновать, что ответов всего четыре? Каковы ключевые идеи? Как мы можем ограничить проблему?
Обратите внимание, что вы вполне можете подумать об идеях, которые мы здесь не рассмотрели. Важно, чтобы вы следили за ними, чтобы увидеть, куда они ведут. Если вы получите хорошие результаты, пожалуйста, сообщите нам, чтобы мы могли рассказать другим. Мы обязательно признаем все, что вы размещаете в сети.
Сессия 2
Покажите, что есть только четыре ответа на задачу о шести кругах.
Предыстория
Так как же и почему на исходный вопрос есть только 4 ответа? И как мы можем установить это вне всяких разумных сомнений? На самом деле есть несколько способов сделать это. Мы перечислим их здесь для использования в следующих двух сессиях. Частично это делается для того, чтобы показать, что есть много способов доказать или оправдать что-либо. В некотором смысле каждый из них одинаково действителен. Однако есть некоторые доказательства, которые «лучше», «эффективнее» или «сложнее», чем другие. Ниже мы приведем некоторые доказательства и прокомментируем их качество.
В некотором смысле каждый из них одинаково действителен. Однако есть некоторые доказательства, которые «лучше», «эффективнее» или «сложнее», чем другие. Ниже мы приведем некоторые доказательства и прокомментируем их качество.
- «Я работаю над этим уже 15 минут и больше не могу найти. Значит, их должно быть только четыре».
Это не доказательство. Мы не можем быть уверены, что не смогли найти другого ответа, уделив проблеме больше времени. Или, может быть, кто-то умнее нас мог бы найти другой ответ. Или, может быть, кто-то в другой стране мог. Здесь слишком много места для сомнений. Это не основание для математического доказательства.
Однако, возможно, это лучшее, что мы можем сделать. Например, на одном этапе мы думали, что планет всего 7. Мы смотрели на небо тысячи лет, а видели только семь. Но потом появился Джон Адамс и сказал, что если уравнения движения Ньютона верны, то там происходит что-то странное. Было некоторое «колебание» планет, которое навело его на мысль, что есть еще одна планета, которую мы не обнаружили к 1845 году.
Он рассчитал, где должна быть планета, а затем кто-то пошел искать и в конце концов нашел ее в сентябре 1846 года.
Если у нас нет инструментов для урегулирования чего-либо, нам, возможно, придется полагаться на подход «Я больше не могу найти». Хотя в какой-то момент это может представлять собой наилучшее состояние наших знаний, в математике это в лучшем случае предположение — догадка о том, каков ответ на самом деле. Математика требует доказательства, обоснования, к которому нельзя придраться. Проблема в том, что если вы поработаете еще 10 минут, вы можете просто найти другой ответ.
- «Я рассмотрел все варианты, и ответов всего четыре».
Это достаточно хорошее доказательство, если можно показать, что были рассмотрены все возможные случаи. Что здесь нужно сделать, так это перечислить все возможные способы размещения чисел от 1 до 6 в 6 кругах, а затем выбрать из этого списка те, которые дают равные суммы по всем трем сторонам.
Одним из способов сделать это было бы написать компьютерную программу. На первый взгляд, есть 6 способов вставить первое число, 5 — следующее и так далее. Следовательно, существует 6 х 5 х 4 х 3 х 2 х 1 = 720 способов сложить 6 чисел. Это не займет у компьютера много времени. Вы даже можете заставить класс сделать это за разумное время, разделив дела между ними. Ниже мы даем способ сделать это, что означает, что нам не нужно рассматривать все 720 возможностей.
Подумайте, где поставить цифру 1. Из-за симметрии треугольной формы есть только два места, где можно поставить 1: в угловом круге или в круге посередине стороны. Мы показываем эти две ситуации ниже.
На следующем этапе мы хотим поставить 2 во всех возможных местах. Это можно сделать тремя способами для каждого из способов поставить 1. Поскольку это утомительно, мы сделаем это только для одного случая. Если вы хотите, вы можете заставить свой класс завершить аргумент.
Теперь в первой из этих трех ситуаций мы можем поставить 3 в четырех местах.
Симметрия треугольника нам сейчас совсем не поможет. Если мы поместим 3 в кружок «а», то сумма стороны, которую мы произвели, будет равна 6. Нет другого способа составить 6, поэтому здесь нет возможного ответа.
Если мы поместим 3 в круг «b», то мы получим сумму a + 3 в левой части и a + 3 + c в нижней части. Они никогда не могут быть равны.
Если мы поместим 3 в круг «с», то аналогичное рассуждение показывает, что левая сторона имеет сумму а + 3, а нижняя — сумму а + b + 3. Они тоже никогда не могут быть равны.
Если мы поместим 3 в круг «d», мы должны поставить 4, 5, 6 внизу в некотором порядке. Это дает сумму, которая больше, чем можно получить на двух других сторонах.
Мы оставляем вас и ваш класс на рассмотрение всех остальных дел. Вы можете разделить вещи так, чтобы разные группы студентов выполняли разные кейсы. Это бы ускорило дело. Возможно, единственное утешение в том, что делать это таким образом, это то, что это намного проще, чем делать 720 разных случаев.
Но это некрасиво. Мы надеемся, что есть лучший способ.
Во всяком случае, вышеизложенное является упражнением в систематичности. Важно делать все осторожно и в определенном порядке, чтобы были учтены все возможности.
- Паритет – нечетные и нечетные. «Где я могу поставить четные числа и где я могу поставить нечетные числа?»
Аргумент здесь основан на том факте, что сумма двух четных чисел четна; сумма двух нечетных чисел четна, а сумма четного и нечетного числа нечетна.
Теперь есть только три нечетных числа, и у нас может быть либо нечетное количество нечетных чисел на одной стороне треугольника, либо четное число. При внимательном рассмотрении мы видим, что существует всего четыре возможных расположения шансов и четов. Мы показываем их ниже. Четные числа указаны в пустых кружках, а нечетные — в кружках, отмеченных буквой «о».
Теперь мы знаем, куда идут 1, 3, 5. Из-за симметрии равностороннего треугольника числа 1, 3, 5 можно вставить в первую и четвертую указанные выше возможности только одним способом.
Оттуда достаточно быстро увидеть, куда должны идти четные числа. Есть три возможных расположения 1, 3, 5 в двух других случаях. Систематическая работа выявит, какие схемы работают, а какие нет. Когда все это будет сделано, мы получим четыре ответа, которые мы нашли ранее.
- Сократите суммы и произведите суммы.
В этом методе доказательства мы прежде всего показываем, что суммы, которые мы можем получить на каждой стороне треугольника в ответе, довольно ограничены. В конце концов, у вас может быть боковая сумма 24, 18, 13, 12?
Для этого подумайте сначала о 1. В какой наибольшей сумме может быть 1? Самая большая сумма будет с 5 и 6, чтобы дать сумму 12. Таким образом, это самая большая сумма, которую мы можем получить. Теперь переверни это. В какой наименьшей сумме может быть 6? Конечно, это с 1 и 2, чтобы получить наименьшую сумму 9. Таким образом, суммы могут лежать только между 9 и 12 включительно.
Итак, как мы можем получить 9? Делайте это систематически.
Если бы мы использовали 6, нам пришлось бы составить 3, используя два числа. Это можно сделать только с 1 и 2. Если бы мы использовали 5, нам пришлось бы составить 4, используя два числа. Это можно сделать только с 1 и 3. (2 и 2 не допускаются.) Если бы мы использовали 4, нам пришлось бы составить 5, используя два числа. Это можно сделать только с 2 и 3. (1 и 4 не допускаются.) Таким образом, есть только три возможности:
6 + 2 + 1; 5 + 3 + 1; 4 + 3 + 2.
У треугольника всего три стороны, поэтому они у нас есть. Вопрос только в том, какие цифры стоят в углах? Но это легко. Это числа, которые встречаются дважды в трех суммах. Так мы быстро получаем четыре ответа, которые получили методом проб и ошибок в первой сессии.
Этот метод доказательства того, что существует ровно четыре ответа, возможно, самый приятный из всех. У него определенно есть хороший аргумент, который показывает, что суммы ограничены от 9 до 12 включительно.
- Немного алгебры.

Здесь мы пытаемся использовать алгебру, чтобы увидеть, какой прогресс может быть достигнут. Начнем с расстановки букв a, b, c, d, e, f в кружках. Как показано на диаграмме ниже.
Предположим, что сумма по каждой стороне равна s. Тогда у нас есть следующее уравнение:
3s = (a + b + c) + (c + d + e) + (e + f + a)
= (a + b + c + d + e + f) + (a + c + e) Но сумма в первой скобке равна 1 + 2 + 3 + 4 + 5 + 6 в некотором порядке, так что сумма равна 21. Сумма во второй скобке — это просто сумма трех углов. Итак, у нас теперь
3s = 21 + углы.
Но наименьшее значение углов равно 1 + 2 + 3 = 6, а наибольшее значение углов равно 4 + 5 + 6 = 15. Итак, у нас есть
27 = 21 + 6 < 3 с < 21 + 15 = 36.
Таким образом, сумма должна лежать между 9 и 12, как мы обнаружили в Методе 4 выше. Но теперь у нас есть бонус, потому что уравнение здесь говорит нам, чему равна сумма углов. Если s = 9, сумма углов равна 6 и, следовательно, 1, 2, 3.
Если s = 10, сумма углов равна 9 и, следовательно, 1, 2, 6; 1, 3, 5; или 2, 3, 4. Если s = 11, сумма углов равна 12 и, следовательно, 1, 5, 6; 2, 4, 6; 3, 4, 5. Если s = 12, сумма углов равна 15 и, следовательно, 4, 5, 6.
Для s = 9 и 12 ответы теперь просто выпадают. Для s = 10 и 11 необходимо проделать некоторую работу, но ясно, что, например, если 1, 5 и 6 находятся в углах, невозможно получить сумму 11. Таким образом, работа Это слишком сложно и, возможно, проще, чем найти все способы получить 10. Как бы то ни было, мы все равно получаем четыре ответа, которые продолжаем получать.
Итак, каковы же ставки этого метода на «привлекательность»? Он действительно полагается на знание алгебры, но как только преодолев это препятствие, он довольно быстро дает числа углового круга, а остальные числа встают на свои места. Единственная небольшая задержка заключается в том, что мы должны учитывать некоторые угловые числа, которые не работают; но, возможно, это небольшая цена. Конечно, это намного лучше, чем метод 1.
Последовательность обучения
- Вспомните задачу и обсудите предположение, сделанное на прошлом уроке. Как мы можем доказать эту гипотезу? Обратите внимание, что было бы хорошо ограничить возможные побочные суммы. «Как мы можем это сделать?» В ходе обсуждения подведите их к некоторым идеям, лежащим в основе различных доказательств.
- В группах по 2 или 4 человека пусть они поработают над придуманными ими идеями. Наш опыт показывает, что с минимальными подмостками учащиеся могут прийти к идее метода 4. Возможно, вам придется помочь им, спросив: «Какова наибольшая сумма, в которую может быть вовлечено 1?», «Какова наименьшая сумма, в которую может быть вовлечено 6». может участвовать?
Любую из более быстрых групп следует поощрять к поиску другого решения. - Когда несколько групп придут к доказательству (возможно, с вашей помощью), проведите отчетную сессию. Пусть один из учащихся скажет, что придумала их группа. Попросите остальную часть класса проверить, что утверждает этот ученик.
 ‘Есть ли что-то непонятное?’ ‘Есть ли какая-то часть, которой вы не следуете?’ ‘Есть ли какая-то часть, которая неверна?’
‘Есть ли что-то непонятное?’ ‘Есть ли какая-то часть, которой вы не следуете?’ ‘Есть ли какая-то часть, которая неверна?’ - Дайте всему классу возможность написать доказательство своими словами.
- Покажите классу другой способ доказать, что ответов всего четыре. «Какое доказательство лучше?» «Какое доказательство «наилучшее»?»
- В качестве введения к следующему уроку попросите их подумать о том, как можно обобщить или расширить задачу. «Какие еще проблемы мы можем сделать из этой?» Именно на этом этапе опыт отдела решения проблем V-sets будет ценным.
Занятие 3
Рассмотрим расширение задачи шести кругов – задачу восьми кругов. Найдите все его ответы и покажите, что других нет.
Предыстория
Здесь мы рассмотрим задачу, похожую на задачу шести кругов. Учитывая опыт, который мы получили с Задачей шести кругов, мы должны быть в состоянии добиться некоторого прогресса в этой новой задаче. Эта задача является расширением задачи шести кругов.
Задача о восьми кругах: можно ли расположить числа 1, 2, 3, 4, 5, 6, 7, 8 в кругах так, чтобы суммы трех чисел по обе стороны квадрата были одинаковыми ?
Технику, которую мы использовали в задаче шести кругов, можно использовать и здесь. Здесь сработает любой из методов, отмеченных нами при доказательстве гипотезы о четырех ответах (см. Предысторию занятия 2). Однако очевидно, что некоторые из них более эффективны. Например, если у ваших учеников есть достаточные способности к алгебре, мы предлагаем им попробовать метод 5, чтобы получить боковые суммы. Этот метод сокращает количество вариантов более эффективно, чем поиск наибольшей суммы, в которой может быть 1. Таким образом, ваш класс должен обнаружить, что единственными возможными суммами являются 12, 13, 14 и 15.
Эта задача требует немного больше усилий, чем задача шести кругов, но в конце, благодаря систематическому подходу к ней, ваши ученики узнают, что нашли все возможные ответы. Из-за дополнительной работы мы предлагаем вашему классу работать в группах не менее 4 человек и распределять работу между ними.
В итоге они должны найти шесть ответов. Мы перечисляем их ниже.
Последовательность обучения
- Предложите учащимся подумать о расширениях или обобщениях задачи шести кругов. Постарайтесь получить от класса несколько идей (некоторые возможности можно найти в этом разделе). Подведите их к задаче о восьми кругах.
- Следуйте шагам Сессии 1, чтобы позволить им решить Задачу Восьми Кругов. Это сложнее, чем задача шести кругов, поэтому может быть полезно, если они разделят определенные части задачи между собой. Соберите их вместе, когда они решат, что у них есть ответы на большинство вопросов. Обсудите, как они могут получить остальные. Обсудите, как они могут доказать, что существует только шесть ответов.
Занятие 4
Обобщите задачу шести кругов, найдя, какие наборы из шести чисел могут заменить 1, 2, 3, 4, 5, 6, и уравновесив суммы по обе стороны треугольника.
Предыстория
Пришло время обобщить.
Задача: Какие другие наборы из 6 чисел можно разместить в шести кругах ниже, чтобы суммы чисел на каждой из сторон были одинаковыми?
Это обобщение исходной задачи шести кругов, поскольку, когда мы находим ответ, он также дает нам ответ на исходную задачу. В этом смысле проблема восьми кругов не является обобщением, потому что ее решение не дает нам немедленно решения проблемы шести кругов.
Еще раз поэкспериментировать. Что вы можете придумать? Вероятно, тот факт, что любые шесть последовательных чисел сработают, не так уж трудно понять. Тогда, возможно, подойдут любые шесть чисел, находящихся на одинаковом расстоянии друг от друга, например 5, 8, 11, 14, 17 и 20. Их можно рассматривать как любую линейную комбинацию 1, 2, 3, 4, 5, 6. Это потому, что их можно записать в форме {m + in: где i = 1, 2, 3, 4, 5, 6, а m и n — любые целые числа}.
Но разве это единственные возможности? Как насчет {1, 2, 3, 4, 5, 100} или {1, 2, 3, 4, 5, 6, 50} или {1, 2, 3, 4, 5, 7}? Удивительно, но последняя из этих работ дает два ответа. Итак, если бы у нас был набор вроде {a, b, c, d, e, f}, как бы мы узнали, даст он нам ответ или нет? Хитрость здесь заключается в том, чтобы поэкспериментировать и посмотреть, какие предположения вы можете придумать.
Итак, если бы у нас был набор вроде {a, b, c, d, e, f}, как бы мы узнали, даст он нам ответ или нет? Хитрость здесь заключается в том, чтобы поэкспериментировать и посмотреть, какие предположения вы можете придумать.
И когда вы это сделаете, вы начнете видеть, сколько ответов вы получаете для каждого набора. Тогда вы можете задать еще несколько вопросов.
Можете ли вы найти наборы чисел, для которых существует только один способ сделать все суммы равными? Что можно сказать о таких наборах?
Можете ли вы найти наборы чисел, для которых есть ровно два способа сделать все суммы равными? Что можно сказать о таких наборах?
Сможете ли вы найти наборы чисел, для которых существует ровно три способа сделать все суммы равными? Что можно сказать о таких наборах?
Сможете ли вы найти наборы чисел, для которых существует ровно четыре способа сделать все суммы равными? Что можно сказать о таких наборах?
Но давайте сначала рассмотрим общую проблему. Мы уже знаем по четырем ответам, которые мы получили в Сессии 1, что
Мы уже знаем по четырем ответам, которые мы получили в Сессии 1, что
- Разница между противоположными угловыми и средними числами одинакова. Посмотрите на А. 4 напротив 1 и 4 – 1 = 3. 5 напротив 2 и 5 – 2 = 3. 6 напротив 3 и 6 – 3 = 3.
Вы должны убедиться, что это верно для всех возможных правильных способов заполнить шесть кругов. Разница между противоположными угловыми и средними числами одинакова. Так что возьмите это и немного поработайте с этим, превратив его в гипотезу.
Гипотеза: набор из шести чисел правильно заполнит шесть кругов тогда и только тогда, когда набор состоит из трех различных пар, имеющих общую разность.
Просто чтобы проверить, что это значит, набор из шести чисел должен иметь форму a, a + d; б, б + г; в, в + г.
Но как это доказать? Итак, если мы поместим a, b и c в углы и их пары в противоположный средний круг, мы получим конфигурацию, показанную ниже.
Тогда сумма трех чисел с каждой стороны равна a + b + c + d. Таким образом, мы получаем законный набор.
Таким образом, мы получаем законный набор.
Но что, если у нас есть законный набор? Можем ли мы показать, что их можно расположить в три пары с общим различием?
Итак, давайте предположим, что у нас есть ответ, подобный тому, что на диаграмме выше, где шесть чисел — это j, k, m, n, p, r. Поскольку у нас есть три равные суммы, то
j + k + m = m + n + p = p + r + j.
Теперь j + k + m = m + n + p подразумевает, что j + k = n + p или что j – n = p – k.
И m + n + p = p + r + j означает, что m + n = r + j или что j – n = m – r.
Это дает j – n = m – r = p – k. Таким образом, набор состоит из трех различных пар, имеющих общую разность.
Итак, теперь, когда мы видим шесть чисел, мы можем сказать, сможем ли мы поместить их в шесть кругов так, чтобы суммы на каждой стороне треугольника были одинаковыми.
Последовательность обучения
- Рассмотрев расширение задачи шести кругов, пора перейти к ее обобщению. В ходе обсуждения предложите им подумать о том, какие наборы из шести чисел могут работать в шести кругах.

- Пусть они разделятся на группы и найдут другие наборы из шести чисел, которые «работают». Предложите им увидеть, что общего у этих наборов.
- Возможно, вам придется снова собрать класс, чтобы подумать о найденных наборах. Нашли ли они какие-либо наборы, кроме линейных комбинаций исходных чисел? Если нет, попросите их попробовать {1, 2, 3, 4, 5, 100} или {1, 2, 3, 4, 5, 6, 50} или {1, 2, 3, 4, 5, 7}. «Вы можете придумать что-нибудь еще?»
- Пусть они поработают над этим некоторое время, пока не придут к выводу. Предложите им доказать гипотезу.
- Дайте им возможность обсудить свои доказательства перед всем классом. Пусть пишут доказательство.
Сессия 5
Найдите и докажите, что в задаче о шести кругах есть только ноль, два или четыре ответа для любого набора из шести чисел.
Фон
Здесь мы рассмотрим вопросы о том, какие наборы дают 1, 2, 3 или 4 ответа. Опять же, для начала нужно провести эксперимент, но ключ к проблеме можно найти в списке свойств ответов из Сессии 1. Помните, номер 3 в списке говорит:
Помните, номер 3 в списке говорит:
Изменение угловых номеров на средние и наоборот меняет один ответ на другой. В результате нетрудно увидеть, что ответы приходят парами. Немного сложнее понять, какие наборы дают четыре ответа, но оказывается, что четыре ответа можно получить, только если набор представляет собой линейную комбинацию чисел 1, 2, 3, 4, 5, 6.
Теорема 1. ответы из набора из шести разных чисел идут парами.
Доказательство. Предположим, что шесть чисел — это a, a + d, b, b + d, c c + d, и они расположены, как мы делали выше, с a, b, c в углах. Тогда нетрудно заметить, что мы можем составить другой ответ с a, b, c в средних кругах и a + d, b + d, c + d соответственно напротив них в углах.
Теорема 2. Набор из шести чисел дает четыре ответа тогда и только тогда, когда набор представляет собой линейную комбинацию чисел 1, 2, 3, 4, 5, 6.
Конечно, если у нас есть такая линейная комбинация, мы можно получить четыре ответа, заменив i в исходных четырех ответах на m + in.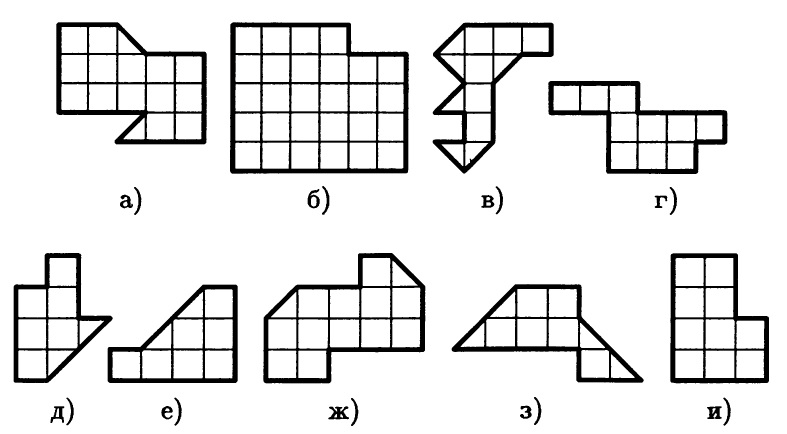 Вы можете проверить, что боковые суммы по-прежнему равны. (Обратите внимание, что здесь мы не можем сформировать более четырех ответов, потому что в противном случае замена m + на i даст нам больше ответов на исходную задачу.)
Вы можете проверить, что боковые суммы по-прежнему равны. (Обратите внимание, что здесь мы не можем сформировать более четырех ответов, потому что в противном случае замена m + на i даст нам больше ответов на исходную задачу.)
Предположим, что шесть чисел равны a, a + d, b, b + d, c, c + d и что a < b < c. Затем, поскольку у нас есть другой возможный ответ (кроме очевидного), a + e для некоторого, возможно, нового значения e должно равняться одному из пяти других чисел. Посмотрите на возможные 5 случаев.
a + e = c + d: Но поскольку a — наименьшее число, любое другое число в наборе плюс e будет больше, чем c + d. Это невозможно.
a + e = b + d: Очевидно, что d не равно e, иначе a равнялось бы b. Теперь есть три возможности: c + d = c + e; с + д = б + е; и c + d = a + d + e. Единственное, что ведет куда-либо, это c + d = b + e, когда e = 3d, и мы получаем линейную комбинацию a, a + d, a + 2d = b, a + 3d = b + d, a + 4d = c и а + 5d = с + d.
а + е = а + d: Здесь е = d и, следовательно, с + d = с + е; с + д = б + е; и c + d = b + d + e. Все это приводит к противоречиям или отсутствию прогресса.
Все это приводит к противоречиям или отсутствию прогресса.
а + е = с: Следовательно, с + d = b + е; с + д = б + д + е; и c + d = a + d + e. Все это приводит к противоречиям.
а + е = b: Следовательно, с + d = с + е; с + d = b + d + e; и c + d = a + d + e. Единственное, что ведет куда-либо, это c + d = b + d + e, что дает d = 3e и линейную прогрессию a, a + e = b, a + 2e = c, a + 3e = a + d, a + 4e. = b + d и a + 5e = c + d.
Таким образом, единственная возможность для четырех ответов — это когда у нас есть линейная прогрессия.
Последовательность обучения
В первую очередь стоит отметить, что работы в этом блоке очень много и некоторые вещи можно выкинуть. Мы предполагаем, что доказательство случая с четырьмя ответами может быть единственно возможным, поскольку оно концептуально сложно. Однако они могут дойти хотя бы до предположения, что для любого набора из шести чисел существует не более четырех ответов.
Начните урок с того, что предложите им подумать о том, сколько ответов может дать любой набор.
 Это может быть сделано в обстановке всего класса или в их группах. Как обычно, они должны сначала выдвинуть гипотезу, а затем попытаться найти доказательство этой гипотезы.
Это может быть сделано в обстановке всего класса или в их группах. Как обычно, они должны сначала выдвинуть гипотезу, а затем попытаться найти доказательство этой гипотезы.Обсудите их предположения всем классом и поговорите о том, какие методы доказательства можно использовать.
Когда доказательство найдено, попросите ученика представить его всему классу. Пусть критикуют. Если никто не может найти доказательства, даже с вашей помощью, дайте доказательство сами. Пусть критикуют. (Это может быть полезно, если вы делаете это, чтобы обнаружить странную ошибку, чтобы держать их в напряжении.) Пусть все они напишут доказательство.
Просмотрите и обсудите результаты подразделения в целом. Что им понравилось? Что было тяжело?
Схемы и формулы полуквадратных треугольников
Спланируйте свой следующий проект по выстегиванию полуквадратных треугольников с помощью этих измерительных таблиц HST и шпаргалок. Если вы хотите сделать полуквадратные треугольники по 2 за раз, по 4 за раз, по 8 за раз или методом полос, я покажу вам, какой именно размер ткани вам нужно вырезать.
Если вы хотите сделать полуквадратные треугольники по 2 за раз, по 4 за раз, по 8 за раз или методом полос, я покажу вам, какой именно размер ткани вам нужно вырезать.
Кроме того, я дам вам свои лучшие советы и рекомендации, которые сделают сборку полуквадратных треугольников проще, чем когда-либо!
Полуквадратные треугольники — одни из самых распространенных блоков для квилтинга, и не зря! Их просто сделать, и вы можете расположить их почти бесконечным образом.
Половина квадратного треугольника представляет собой блок квадратного квилта, состоящий из двух прямоугольных треугольников. Треугольники сшиваются вместе по их длинной (диагональной) стороне. Каждый треугольник образует одну «половину» квадрата.
4 Методы получения полуквадратных треугольников
Существует множество способов изготовления полуквадратных треугольников. Метод, который вы выберете, будет зависеть от того, сколько квадратов вам нужно, и какого размера ткань вы должны начать.
Основной метод
Вы можете сделать один полуквадрат из двух квадратов ткани одинакового начального размера. Например, если вы начинаете с двух 3-дюймовых квадратов, вы можете сделать 1 3-дюймовый HST.
Чтобы сделать по 1 полуквадратному треугольнику: Сложите два тканевых квадрата лицевыми сторонами друг к другу. Проведите диагональную линию из угла в угол на обратной стороне одного квадрата. Сшейте по линии и обрежьте припуск на шов 1/4″. (Ткани будет отрезано довольно много.)
Этот базовый метод даст вам один HST того же размера, что и два квадрата, с которых вы начали. Это быстро и просто, но за один раз получается только один HST (плюс много обрезков).
Улучшенные методы
Если вам нужно более одного полуквадратного треугольника, есть множество других, более совершенных методов на выбор. На самом деле проще и быстрее сделать полуквадратные треугольники одним из следующих способов быстрой сборки.
Вот 4 простых способа собрать полуквадратные треугольники.
- 2 за один раз
- 4 за один раз
- 8 за один раз
- прошивание полос
Какой метод HST выбрать?
У каждого метода резки полуквадратного треугольника есть свои плюсы и минусы. Метод, который вы должны выбрать, зависит от того, сколько HST вам нужно, как вы любите шить и с какого размера ткани вам нужно начать. Кроме того, нужно учитывать эти надоедливые края смещения!
Размер : Если вам нужны HST большего размера, вы, вероятно, выберете метод резки 1 или 2 за раз. Принимая во внимание, что если вам нужны маленькие HST, более эффективно использовать 4 за один раз или «магическую восьмерку».
Количество : Резка 4 или 8 HST за один раз определенно сэкономит вам время!
Суетливая резка : У вас будет больше контроля над ориентацией ваших отпечатков с помощью метода «1 за раз».
Смещенные кромки : Метод «4 за раз» и полосовой метод дадут вам HST со смещенными кромками.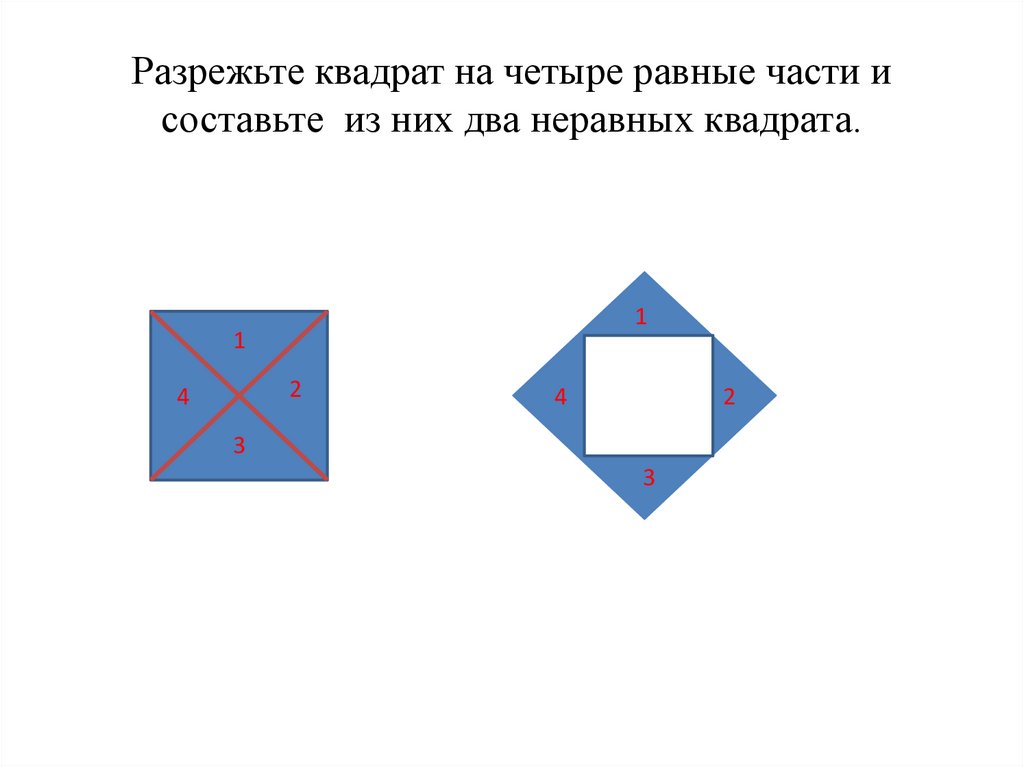 Если вы позаботитесь о том, чтобы не растягивать косые края во время глажки и шитья, они действительно не должны доставить вам никаких проблем. Но, они то, что нужно знать!
Если вы позаботитесь о том, чтобы не растягивать косые края во время глажки и шитья, они действительно не должны доставить вам никаких проблем. Но, они то, что нужно знать!
Точная раскройка и сшивание
Прежде чем мы перейдем к 4 методам и их соответствующим таблицам, я хочу сделать небольшую заметку о «точной» раскройке и сшивании.
Размеры в этих таблицах основаны на точном кройке и шитье. Если вы один из тех счастливчиков, которые умеют шить со 100% точностью, я должен вас поздравить! Вы можете продолжить измерения диаграммы, как написано.
Если вы, как и я, не умеете делать идеальные припуски на швы, вам может понадобиться добавьте 1/4″ или около того к размерам резки, указанным в таблицах. Я предпочитаю сшивать блоки немного большего размера, которые затем можно обрезать до их точного незавершенного размера.
Если добавить немного ткани к начальному размеру ткани, у вас будет достаточно места для обрезки полуквадратных треугольников по размеру.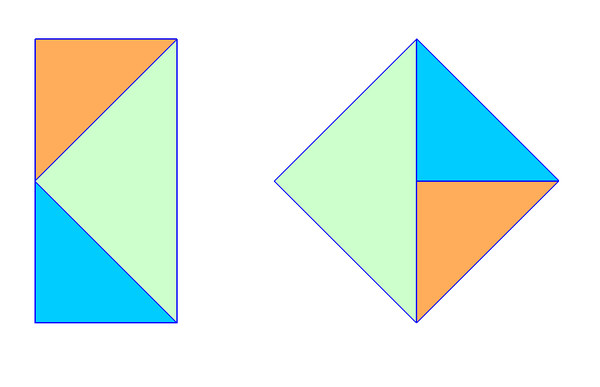 Вы можете думать об этом как о страховке от ошибок при раскрое или шитье.
Вы можете думать об этом как о страховке от ошибок при раскрое или шитье.
Я знаю, что обрезка всех этих треугольников может показаться утомительной! Но, имея стопку точных блоков HST, готовых к работе, вы сделаете сшивание вашего лоскутного одеяла намного веселее! Ваше будущее «я» скажет вам спасибо.
Вы можете обнаружить, что вращающийся коврик для резки и линейка для квилтинга значительно ускоряют процесс обрезки. Мне нравится использовать квадратные линейки для квилтинга, чтобы обрезать HST. И недавно я использовал треугольную линейку HST, которая экономит еще больше времени.
Как читать таблицы
Готовый размер соответствует размеру блока HST после того, как вы прострочите все 4 стороны с припуском на шов 1/4.
Незавершенный размер . Размер — это размер блока HST до того, как вы сшьете какой-либо из внешних краев. Это также размер, до которого вы обрезаете готовую HST, когда работаете с выкройкой.
Начальные квадраты — это два больших куска ткани, которые будут сшиты и вырезаны в HST.
Традиционный метод: 2 за раз
Вот как можно сделать блоки HST по 2 за раз.
Сначала сложите два тканевых квадрата лицевыми сторонами друг к другу. Нарисуйте диагональную линию из угла в угол на обратной стороне светлого квадрата.
Затем прошейте 2 линии шва по обе стороны от этой диагональной линии, каждая на расстоянии 1/4″ от линии. Разрежьте две части по диагонали.
Затем разутюжьте припуски на швы по направлению к темной стороне (или как вам больше нравится). Обрежьте «собачьи уши» или те маленькие уголки, которые выступают за края квадрата.
С помощью линейки обрежьте HST до исходного размера. Вы можете обнаружить, что вращающийся коврик для резки и линейка значительно ускоряют процесс обрезки.
Диаграмма HST «2 за раз»
| Готовая HST | Незавершенная HST | Начальные квадраты | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x | x + 1/2 | x + 7/8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 1 1/2 | 1 7/8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 1/2 | 2 | 2 3/8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | 2 1/2 | 2 7/8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 1/2 | 3 | 3 3/8 | . | 3 7/8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 1/2 | 4 | 4 3/8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | 4 1/2 | 4 7/8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 1/2 | 5 | 5 3/8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | 5 1/2 | 5 7/8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 1/2 | 6 | 6 3/8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
. Припуски на швы 1/4″ со всех сторон.Быстрый метод: 4 за разВот как сделать блоки HST по 4 за раз: Сначала сложите два тканевых квадрата лицевыми сторонами друг к другу. С припуском на шов 1/4″ прошейте по всему периметру сложенных квадратов. Затем проведите две диагональные линии из угла в угол. Линии пересекутся в центральной точке, образуя букву X. Разрежьте по этим диагональным линиям, чтобы получилось 4 полуквадратных треугольника. Приутюжьте припуски к темной стороне (или как вам больше нравится). Используя линейку, обрежьте HST до их незавершенного размера. Работа со смещенными краями Существует один потенциальный недостаток метода «4 одновременно»: края результирующих HST будут со смещением. Однако, если вы помните об этой проблеме и следите за тем, чтобы края смещения не растягивались во время глажки и шитья, у вас не должно возникнуть проблем. Таблица размеров HST «4 за раз»Математика для этих HST «4 за раз» немного сложнее, а дроби не такие аккуратные. Итак, на этой диаграмме я округлил до ближайшей 1/8 дюйма. Поскольку вы все равно будете обрезать, я рекомендую вам добавить еще 1/4″ к начальному размеру квадрата. Это даст вам дополнительное пространство для маневра, когда придет время выравнивать блоки.
Еще более быстрый метод: 8 за разВот как можно сделать блоки HST по 8 за раз. Сначала сложите два тканевых квадрата лицевыми сторонами друг к другу. Нарисуйте две диагональные линии из угла в угол на обратной стороне светлого квадрата. Линии пересекутся в центральной точке, образуя букву X. Затем прошейте по 2 шва по обе стороны от каждой диагональной линии (всего 4 шва). Каждая линия шва должна быть на расстоянии 1/4 дюйма от нарисованных линий. Разрежьте по каждой из диагональных линий, а затем еще раз по вертикальной средней и горизонтальной средней линиям. Приутюжьте припуски к темной стороне (или как вам больше нравится). Используя линейку, обрежьте HST до их незавершенного размера. Вы сделаете 8 HST. Смотри, ты идешь! Таблица размеров HST «8 за раз»
 Метод пришивания полосокЭтот метод действительно полезен, если вы работаете с рулетиками из желе или другими предварительно нарезанными полосками ткани. Этот метод идеально подходит для использования обрезков ткани из вашего тайника. Я думаю, вы будете удивлены тем, какие размеры HST можно сделать из предварительно нарезанных струн. Например, знаете ли вы, что можете сделать 2-дюймовые готовые HST со стандартной 2 1/2-дюймовой полоской желейного рулета? Вот как сделать HST из рулона желе или другой полоски ткани. Сначала сложите две полоски ткани лицевыми сторонами друг к другу. Затем прострочите оба длинных края с припуском на шов 1/4. Затем с помощью линейки для квилтинга вырежьте треугольники. Совместите шов с измерениями для желаемого незавершенного измерения. (На фотографии ниже я вырезаю 3 1/2 дюйма незавершенные HST, поэтому я расположил линейку так, чтобы линия шва касалась обеих отметок 3 1/2 дюйма.) Вырежьте первый треугольник. Смещенные кромки : Как и в случае с методом «4 за один раз», края HST, изготовленные полосовым методом, будут смещены. Strip Method HST Size Chart
 Советы по обрезке HSTЕсли вы делаете много полуквадратных треугольников, вам может понадобиться несколько инструментов, чтобы сделать их проще, быстрее и точнее.
Узнайте больше о квилтинговых идеях Если вы любите квилтинг так же сильно, как и я, мне нравится, что вам понравятся эти другие проекты.
Что дальше?Закрепите это сообщение: Сохраните этот урок на своих досках Pinterest, чтобы вернуться к нему позже. Оставить комментарий: Мне приятно слышать ваши отзывы. Расскажите мне в комментариях ниже! Поделиться в Instagram или Facebook: Когда вы сделаете этот проект, поделитесь им в социальных сетях и отметьте меня @sarahmaker. Я люблю смотреть, что ты делаешь! Есть вопросы? Присоединяйтесь к группе в Facebook!Надеюсь, эта статья была для вас полезной! Если у вас есть дополнительные вопросы, не стесняйтесь присоединиться к моей группе Facebook. Я создал эту группу, чтобы вы могли обмениваться фотографиями, задавать вопросы и помогать друг другу. Sarah Stearns Sarah Stearns помогла тысячам рукодельниц найти свой следующий поделочный проект с помощью бесплатных выкроек и пошаговых руководств в своем блоге sarahmaker. О ее работе писали в The New York Times, Scientific American, Good Housekeeping, Vox, Apartment Therapy, Lifehacker и других изданиях. 3.1: От параллелограммов к треугольникам
УрокСравним параллелограммы и треугольники. Упражнение \(\PageIndex{1}\): одинаковые параллелограммы, разные основания Вот две копии параллелограмма. Каждая копия имеет одну сторону, помеченную как основание \(b\), и сегмент, нарисованный для соответствующей высоты и помеченный \(h\).
Упражнение \(\PageIndex{2}\): История двух треугольников (часть 1) Два многоугольника идентичны, если они точно совпадают при размещении один поверх другого.
Готовы ли вы к большему? Нарисуйте некоторые другие типы четырехугольников, которые еще не показаны. Попробуйте разложить их на два одинаковых треугольника. Ты можешь сделать это? Придумайте общее правило о том, что должно быть правдой, если четырехугольник можно разложить на два одинаковых треугольника. Апплет GeoGebra XpEZQfqp Упражнение \(\PageIndex{3}\): История двух треугольников (часть 2) Этот апплет имеет восемь пар треугольников. Каждый член группы должен выбрать 1–2 пары треугольников. Используйте их, чтобы ответить на следующие вопросы.
ИтогПараллелограмм всегда можно разложить на два одинаковых треугольника отрезком, соединяющим противоположные вершины. Рисунок \(\PageIndex{2}\)И наоборот, две идентичные копии треугольника всегда можно расположить так, чтобы получился параллелограмм, независимо от используемого типа треугольника. Чтобы получить параллелограмм, мы можем соединить треугольник и его копию по любой из трех сторон, так что из одной и той же пары треугольников могут получиться разные параллелограммы. Вот примеры того, как две копии треугольника A и треугольника F могут быть составлены в три разных параллелограмма. Рисунок \(\PageIndex{3}\) Эта особая связь между треугольниками и параллелограммами может помочь нам определить площадь любого треугольника. ПрактикаУпражнение \(\PageIndex{4}\) Чтобы разложить четырехугольник на две одинаковые фигуры, Клэр провела пунктирную линию, как показано на рисунке. Рисунок \(\PageIndex{4}\)
Упражнение \(\PageIndex{5}\) Треугольник R прямоугольный. Можем ли мы использовать две копии треугольника R, чтобы составить параллелограмм, который не является квадратом? Рисунок \(\PageIndex{5}\)Если да, объясните, как это сделать, или набросайте решение. Если нет, объясните почему. Упражнение \(\PageIndex{6}\) Две копии этого треугольника составляют параллелограмм. Какой параллелограмм не может быть результатом композиции ? Если вы застряли, рассмотрите возможность использования кальки. Рисунок \(\PageIndex{6}\)Рисунок \(\PageIndex{7}\)
Упражнение \(\PageIndex{7}\)
Упражнение \(\PageIndex{8}\)
(из блока 1.2.3) Упражнение \(\PageIndex{9}\) Выберите все сегменты, которые могут представлять высоту, если сторона \(n\) является основанием. Рисунок \(\PageIndex{9}\)
(из модуля 1. Эта страница под названием 3.1: From Parallelograms to Triangles распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Illustrative Mathematics посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
Как найти длину диагонали квадратаВсе ресурсы по базовой геометрии9 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept ← Предыдущая 1 2 3 Следующая → Справка по базовой геометрии » Плоская геометрия » Четырехугольники » Площади » Как найти длину диагонали квадрата Сторона квадрата ниже имеет длину 12. Какова длина диагонали? Возможные ответы: Невозможно определить из предоставленной информации. Правильный ответ: Объяснение: Диагональ образует треугольник со смежными сторонами . (Примечание: четыре основания являются вершинами идеального квадрата, причем основания называются исходной пластиной, первое основание, второе основание, третье основание, в указанном порядке). Возможные ответы: Правильный ответ: Объяснение: Путь от домашней пластины до первой базы является стороной правильного квадрата; путь от домашней пластины до второй базы является диагональю. Расстояние до второй базы от дома умножено на расстояние до первой базы: Сообщить об ошибке Квадратный участок площадью 1200 квадратных метров. С точностью до метра, какое расстояние от одного угла до противоположного? Возможные ответы: Правильный ответ: Объяснение: Квадрат также является ромбом, поэтому его площадь может быть рассчитана как половина продукта его диагонали: , , где является общая диагональная длина. С , . Расстояние между противоположными углами около 49 метров. Сообщить об ошибке Найдите длину диагонали квадрата. Возможные ответы: Ни один из других ответов не является правильным. Правильный ответ: Пояснение: Диагональная линия делит квадрат на два равных треугольника. Их гипотенуза является диагональю квадрата, поэтому мы можем найти гипотенузу. Нам нужно использовать теорему Пифагора: , где a и b — катеты, а c — гипотенуза. Длина двух катетов равна 8. Подставьте это значение и решите для c: Сообщить об ошибке Найдите длину диагонали квадрата, длина стороны которого равна см. Возможные ответы: Правильный ответ:
Объяснение: Вы можете решить эту задачу двумя разными способами, которые приведут к окончательному ответу: 1. Теорема Пифагора 2. Специальные треугольники (45-45-90) 1.
2. Если вы знаете, что ВСЕ квадраты можно превратить в два особых прямоугольных треугольника с углами 45-45-90, то можно использовать следующую формулу: скажем, что длина стороны квадрата равна «а». Тогда диагональ квадрата (или гипотенуза прямоугольного треугольника) будет равна .Итак, используя это с a=4: Сообщить об ошибке Периметр квадрата равен 48. Какова длина его диагонали? Возможные ответы: Правильный ответ: Объяснение: Периметр = сторона * 4 48 = сторона * 4 Сторона = 12 Квадрат можно разбить на два равных прямоугольных треугольника. Тогда диагональ квадрата является гипотенузой этих двух треугольников. Следовательно, мы можем использовать теорему Пифагора для вычисления диагонали:
Сообщить об ошибке площади 3 . Сколько единиц длины диагонали квадрата? Возможные ответы: Правильный ответ: Пояснение: Из периметра мы можем найти длину каждой стороны квадрата. Длины сторон квадрата равны по определению, поэтому периметр можно переписать как Затем мы используем теорему Пифагора, чтобы найти диагональ, которая является гипотенузой прямоугольного треугольника, каждый катет которого является стороной квадрата.
Сообщить об ошибке Найдите длину диагонали квадрата со стороной . Возможные ответы: Правильный ответ: Объяснение: Диагональ квадрата также является гипотенузой прямоугольного треугольника с длинами сторон как катетами треугольника. Используйте теорему Пифагора, чтобы найти длину диагонали. Для квадрата, указанного в вопросе, Сообщить об ошибке Найдите длину диагонали квадрата со сторонами . Возможные ответы: Правильный ответ: Объяснение: Диагональ квадрата также является гипотенузой прямоугольного треугольника с длинами сторон как катетами треугольника. Используйте теорему Пифагора, чтобы найти длину диагонали. Для квадрата, указанного в вопросе, Сообщить об ошибке Найдите длину диагонали квадрата со сторонами . Возможные ответы: Правильный ответ: Объяснение: Диагональ квадрата также является гипотенузой прямоугольного треугольника с длинами сторон как катетами треугольника. Используйте теорему Пифагора, чтобы найти длину диагонали. Для квадрата, указанного в вопросе, Сообщить об ошибке ← Предыдущий 1 2 3 Далее → Уведомление об авторских правах Все ресурсы по базовой геометрии9 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept Формула многогранника Эйлера | plus.maths.orgИюнь 2007 Леонард Эйлер, 1707 — 1783 Начнем с главного героя этой истории — формулы Эйлера: Хотя это может показаться простым, эта маленькая формула заключает в себе фундаментальное свойство тех трехмерных тел, которые мы называем многогранниками , которые очаровывали математиков на протяжении более 4000 лет. На самом деле я могу пойти дальше и сказать, что формула Эйлера говорит нам нечто очень глубокое о форме и пространстве. Что такое многогранник?Прежде чем мы рассмотрим, что говорит нам формула Эйлера, давайте рассмотрим многогранники более подробно. Многогранник — это твердый объект, поверхность которого состоит из множества плоских граней , которые сами ограничены прямыми линиями. Каждая грань на самом деле представляет собой многоугольник , замкнутую фигуру на плоской двумерной плоскости, состоящую из точек, соединенных прямыми линиями. Рис. 1. Знакомые треугольник и квадрат — это многоугольники, но многоугольники также могут иметь более неправильную форму, как показано справа. Многоугольники не должны иметь отверстий, как показано на рисунке ниже: левая фигура здесь является многоугольником, а правая — нет. Рис. 2. Фигура слева представляет собой многоугольник, а фигура справа — нет, так как в нем есть «отверстие». Многоугольник называется правильным , если все его стороны имеют одинаковую длину и все углы между ними одинаковы; треугольник и квадрат на рисунке 1 и пятиугольник на рисунке 2 правильные. Многогранник — это то, что получается при перемещении на одно измерение вверх. Это замкнутый твердый объект, поверхность которого состоит из множества многоугольных граней. Мы называем стороны этих граней ребрами — две грани встречаются вдоль каждого из этих ребер. Назовем углы граней вершинами , так что любая вершина лежит не менее чем на трех разных гранях. Чтобы проиллюстрировать это, приведем два примера известные многогранники. Рисунок 3: Знакомый куб слева и икосаэдр справа. Многогранник состоит из многоугольников граней , их стороны известны как ребер , а углы как вершин . Многогранник состоит всего из одной части. Он не может, например, состоять из двух (или более) в основном отдельных частей, соединенных только ребром или вершиной. Рис. 4. Эти объекты не являются многогранниками, поскольку состоят из двух отдельных частей, сходящихся только ребром (слева) или вершиной (справа). Что говорит нам формула?Теперь мы готовы посмотреть, что говорит нам формула Эйлера о многогранниках. Посмотрите на многогранник, например на куб или икосаэдр выше, посчитайте количество его вершин и назовите это число V . Куб, например, имеет 8 вершин, поэтому 90 250 V = 8 90 251 . Затем подсчитайте количество ребер многогранника и назовите это число E . У куба 12 ребер, поэтому в случае куб E = 12 . Наконец, посчитайте количество граней и назовите его 9.0250 Ф . В случае куба F = 6 . Теперь формула Эйлера говорит нам, что или, говоря словами: количество вершин минус количество ребер плюс количество граней равно двум. В случае с кубом мы уже видели, что V = 8, E = 12 и F = 6 . , что и должно быть по формуле Эйлера. Если мы теперь посмотрим на икосаэдр, то обнаружим, что В = 12, E = 30 и F = 20 . Теперь как мы и ожидали. Формула Эйлера верна для куба и икосаэдра. Оказывается, довольно красиво, что это верно для практически для каждого многогранника . Единственные многогранники, для которых это не работает, это те, в которых есть сквозные отверстия, как показано на рисунке ниже. Рисунок 5: В этом многограннике есть сквозное отверстие. Формула Эйлера в этом случае не выполняется. Эти многогранники называются непростыми , в отличие от тех, у которых нет отверстий, которые называются простыми . Непростые многогранники, возможно, не первые, что приходят на ум, но их много, и мы не можем уйти от того факта, что формула Эйлера не работает ни для одного из них. Сила формулы ЭйлераВсякий раз, когда математики натыкаются на инвариантное свойство, которое верно для целого класса объектов, они знают, что наткнулись на что-то хорошее. Они используют его для исследования того, какими свойствами может обладать отдельный объект, и для определения свойств, которыми должны обладать все они. Формула Эйлера может сказать нам, например, что не существует простого многогранника с ровно семь ребер. Вам не нужно садиться с картоном, ножницами и клеем, чтобы выяснить это — формула — это все, что вам нужно. Аргумент, показывающий, что семигранного многогранника не существует, довольно прост, так что взгляните на него, если вам интересно. Используя формулу Эйлера аналогичным образом, мы можем обнаружить, что не существует простого многогранника с десятью гранями и семнадцатью вершинами. Показанная ниже призма, в основе которой лежит восьмиугольник, действительно имеет десять граней, но количество вершин здесь равно шестнадцати. Рис. 6: Оба этих многогранника имеют десять граней, но ни один из них не имеет семнадцати вершин. Подобные размышления привели нас к, пожалуй, самому прекрасному открытию. В нем задействованы Платоновых тел , хорошо известный класс многогранников, названный в честь древнегреческого философа Платона, в чьих трудах они впервые появились. Рисунок 7: Платоновы тела. Слева направо у нас есть тетраэдр с четырьмя гранями, куб с шестью гранями, октаэдр с восемью гранями, додекаэдр с двенадцатью гранями и икосаэдр с двадцатью гранями. Хотя их симметричная элегантность сразу становится очевидной, когда вы смотрите на приведенные выше примеры, на самом деле это не так просто выразить словами. Оказывается, он описывается двумя признаками. Во-первых, в платоновых телах нет пиков или провалов, поэтому их форма приятная и округлая. Куб правильный, так как все его грани квадраты и из каждой вершины выходит ровно три ребра. Вы можете убедиться сами, что тетраэдр, октаэдр, икосаэдр и додекаэдр тоже правильные. Вам может быть интересно, сколько существует различных Платоновых тел. С момента открытия куба и тетраэдра математиков так привлекала элегантность и симметрия Платоновых тел, что они искали больше и пытались перечислить их все. Здесь на помощь приходит формула Эйлера. Вы можете использовать ее, чтобы найти все возможные числа граней, ребер и
вершин правильного многогранника. Доказательство Рене Декарт, Игра с различными простыми многогранниками покажет вам, что формула Эйлера всегда верна. Но если вы математик, этого недостаточно. Вам понадобится доказательство, неопровержимый логический аргумент, показывающий, что это действительно работает для всех многогранников , включая те, которые у вас никогда не будет времени проверить. Адриан-Мари Лежандр, (1752 — 1833) Несмотря на название формулы, на самом деле не Эйлер придумал первое полное доказательство. Его история сложна, охватывает 200 лет и включает в себя некоторые из величайших имен в области математики, включая Рене Декарта (159 г. Огюстен-Луи Коши, (1789 — 1857) Интересно отметить, что все эти математики использовали очень разные подходы к доказательству формулы, каждый из которых поражал своей изобретательностью и проницательностью. Однако это доказательство Коши, и я хотел бы дать вам представление об этом. Его метод состоит из нескольких стадий и шагов. Первый этап включает построение так называемой сети 9.0251 . Формирование сети Представьте, что вы держите многогранник одной гранью вверх. Теперь представьте, что вы «удаляете» только эту грань, оставляя края и вершины вокруг нее позади, так что у вас есть открытая «коробка». Затем представьте, что вы можете держаться за коробку и оттягивать края отсутствующей грани друг от друга. Если вы потянете их достаточно далеко, коробка расплющится и превратится в сеть точек и линий.
в плоской плоскости. Серия диаграмм ниже иллюстрирует этот процесс применительно к кубу. Рисунок 8: Превращение куба в сеть. Как видно из диаграммы выше, каждая грань многогранника становится областью сети, окруженной ребрами, и это то, что мы будем называть гранью сети. Это внутренних граней сети. Существует также внешняя сторона , состоящая из области вне сети; это соответствует грани, которую мы удалили из многогранника. Итак, сеть имеет вершины, прямые ребра и многоугольные грани. Рисунок 9: Сеть имеет грани, ребра и вершины. При построении сети вы не добавили и не удалили ни одной вершины, поэтому в сети столько же вершин, сколько и в многограннике — V . Сеть также имеет то же количество ребер — E — что и многогранник. Теперь о лицах; все грани многогранника, кроме «недостающей», оказываются «внутри» сети. Отсутствующее лицо стало внешним лицом, которое растягивается.
далеко по всей сети. Итак, включая внешнюю грань, сеть имеет F лиц. Таким образом, вы можете использовать сеть , а не сам многогранник, чтобы найти значение V — E + F . Преобразование сетиЕсть три типа операций, которые мы можем выполнять в нашей сети. Мы представим три шага, связанные с ними. Шаг 1 Начнем с рассмотрения многоугольных граней сети и спросим: существует ли грань с более чем тремя сторонами? Если есть, мы проводим диагональ, как показано на диаграмме ниже, разделяя грань на две меньшие грани. Рисунок 10: Разделительные грани. Повторяем это с выбранной нами гранью, пока грань не будет разбита на треугольники. Рисунок 11: В итоге у нас остались треугольные грани. Если есть еще одна грань с более чем тремя сторонами, мы используем Шаг 1 для этой грани, пока она тоже не будет разбита на треугольные грани. Таким образом, мы можем разбить каждую грань на треугольные грани, и мы получим новую сеть, все грани которой треугольные. Мы проиллюстрируем этот процесс, показав, как мы преобразовали бы сеть, которую мы сделали из куба. Рисунок 12: Вот что происходит с сетью куба, когда мы многократно выполняем Шаг 1. Мы возвращаемся к Шагу 1 и смотрим на сеть, которую мы получаем после выполнения Шага 1 всего один раз. Теперь, проведя диагональ, мы добавили одно ребро. Наше исходное лицо стало двумя лицами, поэтому мы добавили одно к числу лиц. Мы не изменили количество вершин. Теперь в сети V вершин, E + 1 ребро и F + 1 грань. Так как же В — E + F изменился после того, как мы один раз выполнили шаг 1? Используя то, что мы знаем об изменениях в V , E и F , мы можем видеть, что V — E + F стало V — (E + 1) + (F + 1) . Теперь у нас есть 
Теперь мы представляем шаги 2 и 3. Шаг 2 Проверяем, есть ли в сети грань, которая имеет только одно общее ребро с внешней гранью. Если это так, мы удаляем эту грань, удаляя одно общее ребро. Область, которая была покрыта выбранной нами гранью, становится частью внешней грани, и у сети появляется новая граница. Это показано на диаграмме ниже для сети, состоящей из куба. Рис. 13. Удаление граней с одним внешним ребром. Теперь возьмем V , E и F должны быть числами вершин, ребер и граней, которые сеть, состоящая из треугольных граней, имела до того, как мы выполнили шаг 2. Теперь мы посмотрим, как число V — E + F изменилось после того, как мы выполнили Шаг 2 один раз. Мы удалили одно ребро, поэтому наша новая сеть имеет 90 250 E – 1 90 251 ребро. Мы не коснулись вершин в
все, значит у нас еще V вершин. Итак, еще раз V — E + F не изменилось. Шаг 3 Мы проверяем, есть ли в нашей сети грань, которая имеет два общих ребра с внешней гранью. Если это так, мы удаляем эту грань, удаляя оба этих общих ребра и их общую вершину, так что снова область, принадлежащая выбранной нами грани, становится частью внешней грани. Это показано ниже в случае сети, состоящей из куба, после выполнения шага 2. дважды. Рис. 14. Удаление граней с двумя внешними ребрами. Как и прежде, теперь мы принимаем V , E и F как количество вершин, ребер и граней сети, с которой мы начинаем. Теперь, как шаг 3 повлиял на число V — E + F ? Мы удалили одну вершину — ту, что находится между двумя ребрами, — так что теперь у нас 90 250 V — 1 90 251 вершина. Итак, еще раз V — E + F не изменилось. Секрет доказательства заключается в выполнении последовательности шагов 2 и 3 для получения очень простой сети. Вспомните, что мы неоднократно использовали шаг 1 для создания сети только с треугольными гранями. Эта сеть обязательно будет иметь грань, которая имеет ровно одно общее ребро с внешней гранью, поэтому мы берем эту грань и выполняем шаг 2. Мы можем выполнять шаг 2 на нескольких гранях, по одной за раз, пока не появится
появляется грань, имеющая два ребра с внешней гранью. Затем мы можем выполнить шаг 3, используя это лицо. Мы продолжаем выполнять шаги 2 и 3 и продолжаем удалять лица таким же образом. При этом необходимо соблюдать два важных правила. Во-первых, мы всегда должны выполнять шаг 3, когда это возможно; если есть выбор между Шагом 2 и Шагом 3, мы всегда должны выбирать Шаг 3. Если мы этого не сделаем, сеть может разбиться на отдельные части. Во-вторых, мы должны удалять лица только по одному. Если мы этого не сделаем, мы можем получить края, которые сами по себе будут торчать наружу. лицо, и у нас больше не будет нормальной сети. Чтобы проиллюстрировать процесс, мы выполним несколько шагов в сети кубов, продолжая с того места, где мы остановились на последней диаграмме. Рисунок 15: Применение нашего алгоритма к сети куба. Теперь мы можем задать себе один или два вопроса. Остановится ли когда-нибудь этот процесс удаления лиц, и если остановится, то с чем мы останемся? Небольшое размышление покажет вам, что он должен остановиться — существует только конечное число граней и ребер, которые мы можем удалить, — и что когда это произойдет, у нас останется один треугольник. Теперь посмотрите на количество вершин, ребер и граней в нашей конечной сети — единственном треугольнике. У нас есть V=3 , E=3 и F=2 — мы все равно должны включить внешнюю грань. Теперь На протяжении всего процесса, начиная с полного многогранника и заканчивая треугольником, значение V — E + F не изменилось. . Таким образом, если 90 250 В — E + F = 2 90 251 для конечной сети, мы также должны иметь В — E + F = 2 для самого многогранника! Доказательство завершено! За пределами многогранников В заключение упомяну некоторые следствия формулы Эйлера за пределами мира многогранников. Я начну с чего-то очень малого: компьютерных чипов. Компьютерные чипы — это интегральные схемы, состоящие из миллионов мельчайших компонентов, соединенных миллионами проводящих дорожек. Теперь давайте перейдем к самому большому: к нашей вселенной. До сих пор космологи не пришли к единому мнению о его точной форме. Центральное место в их рассмотрении занимает топология , математическое исследование формы и пространства. В 19 веке математики обнаружили, что все поверхности в трехмерном пространстве в основном характеризуются количеством отверстий, которые они имеют: наши простые многогранники не имеют отверстий, а
пончик имеет одну дырку и т. д. Формула Эйлера не работает для многогранников с дырками, но математики обнаружили интересное обобщение. Для любого многогранника В — E + F это ровно 2 минус 2 раза количество отверстий! Оказывается, это число, называемое эйлеровой характеристикой , имеет решающее значение для изучения всех трехмерных поверхностей, а не только многогранников. |

 Хотя… чем Р-36М не шутит…
Хотя… чем Р-36М не шутит… Сначала на три полоски, а потом каждую пополам.
Сначала на три полоски, а потом каждую пополам. ..
..
 ..
.. ..
.. ..
..
 Она будет совпадать со второй диагональю квадрата.
Она будет совпадать со второй диагональю квадрата. Выходит и это не намного сложнее 🙂 Может, оно так и было задумано в оригинальном первоисточнике? (всё зависит от уровня серьёзности оного)
Выходит и это не намного сложнее 🙂 Может, оно так и было задумано в оригинальном первоисточнике? (всё зависит от уровня серьёзности оного) Сходным образом, если исходную фигуру нужно разбить на несколько фигур заданного вида, стоит предварительно посчитать, сколько их должно быть. Такие же соображения могут помочь и при решении других задач на разрезание. Для иллюстрации этой идеи автор этих строк добавил в список задачу 13, которой не было среди задач, предлагавшихся на занятии.
Сходным образом, если исходную фигуру нужно разбить на несколько фигур заданного вида, стоит предварительно посчитать, сколько их должно быть. Такие же соображения могут помочь и при решении других задач на разрезание. Для иллюстрации этой идеи автор этих строк добавил в список задачу 13, которой не было среди задач, предлагавшихся на занятии.
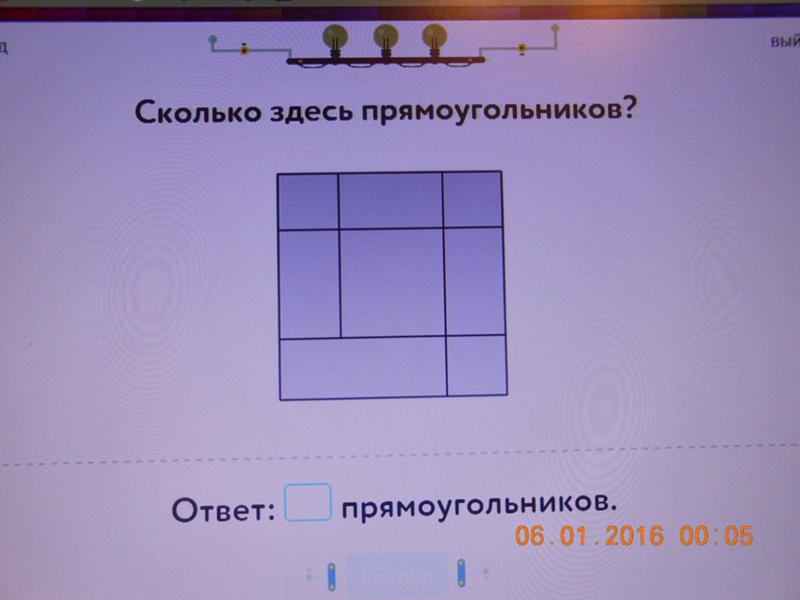
 Изображение какой фигуры вы получите?Задание: Пример выполнения:
Изображение какой фигуры вы получите?Задание: Пример выполнения: Найдите координаты точек, а затем постройте эти точки на координатной плоскости и определите, лежат они внутри выделенного сектора или нет.
Найдите координаты точек, а затем постройте эти точки на координатной плоскости и определите, лежат они внутри выделенного сектора или нет. В. Фарков)
В. Фарков)  Логические задачи.
Логические задачи.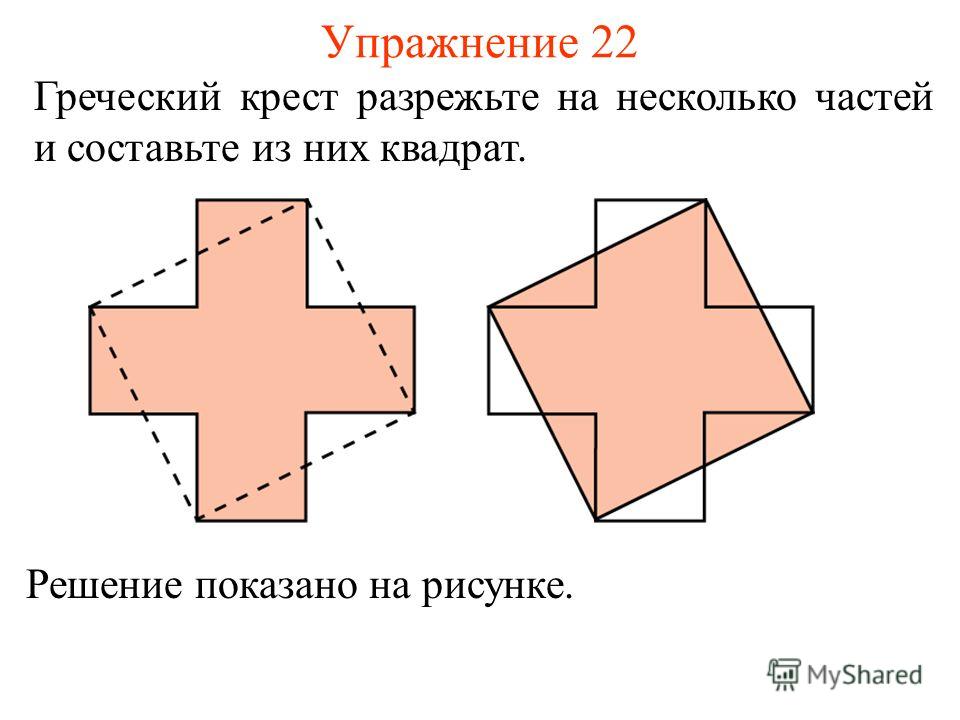 Задайте значения коэффициентов линейной функции так, чтобы получилась готовая картинка. Какое изображение Вы получите? Пример выполнения:
Задайте значения коэффициентов линейной функции так, чтобы получилась готовая картинка. Какое изображение Вы получите? Пример выполнения:  Их маршрут обозначен стрелочками на рисунке. На каждой развилке велосипедисты делились на две равные группы. Сколько велосипедистов приехало в Комарово?
Их маршрут обозначен стрелочками на рисунке. На каждой развилке велосипедисты делились на две равные группы. Сколько велосипедистов приехало в Комарово? Незнайка прогулял уроки в среду 1 сентября, после чего стал прогуливать каждый четвертый учебный день. Какой из следующих дней он прогулял?
Незнайка прогулял уроки в среду 1 сентября, после чего стал прогуливать каждый четвертый учебный день. Какой из следующих дней он прогулял? Он начал с центральной клетки и двигался по стрелкам. Какие две буквы оказались в соседних клетках?
Он начал с центральной клетки и двигался по стрелкам. Какие две буквы оказались в соседних клетках?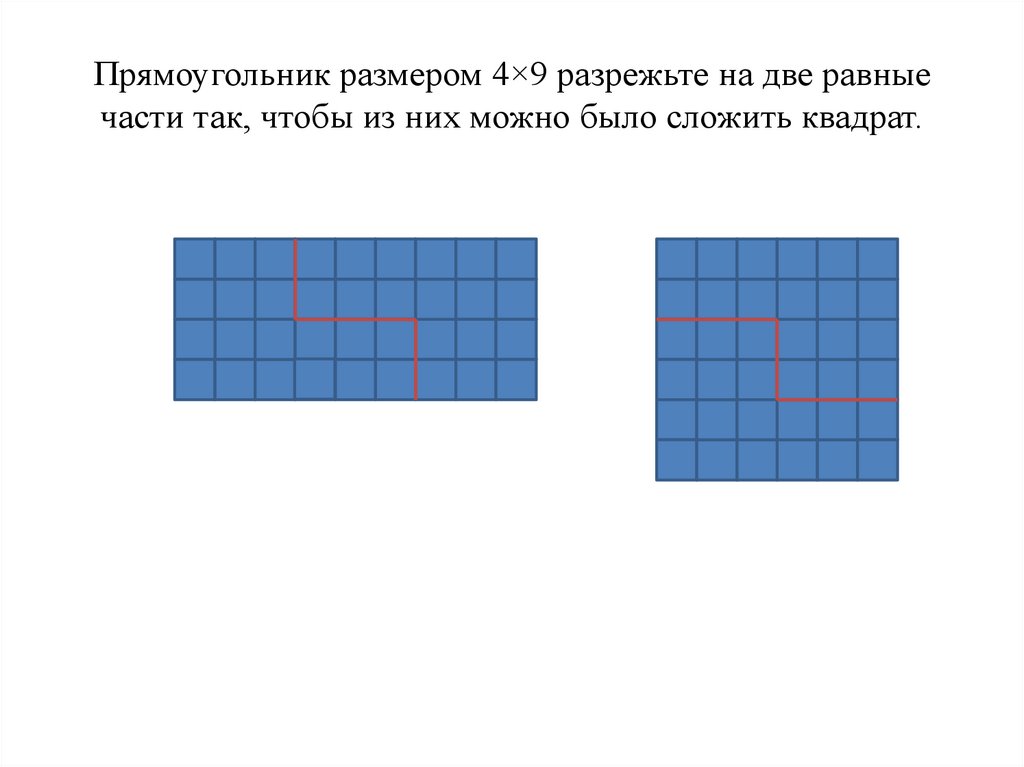 Смартик хочет соединить точку А с точкой В. Какое наименьшее число линий ему придется пересечь?
Смартик хочет соединить точку А с точкой В. Какое наименьшее число линий ему придется пересечь? Произведение чисел P и Q равно одному из этих чисел. Какому?
Произведение чисел P и Q равно одному из этих чисел. Какому? Чему равна эта диагональ?
Чему равна эта диагональ? Так что поощряйте их угадывать, экспериментировать и не беспокоиться о том, какой метод они используют, даже если он кажется совершенно нематематическим!
Так что поощряйте их угадывать, экспериментировать и не беспокоиться о том, какой метод они используют, даже если он кажется совершенно нематематическим!
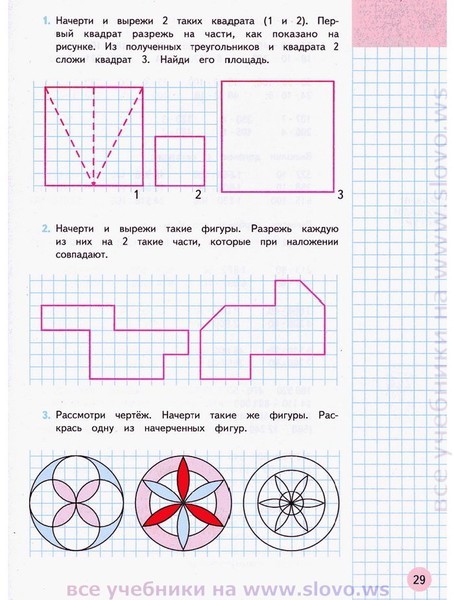 Таким образом, в B, если вы замените 1 на 6, 2 на 5 и т. д., B превратится в C.
Таким образом, в B, если вы замените 1 на 6, 2 на 5 и т. д., B превратится в C.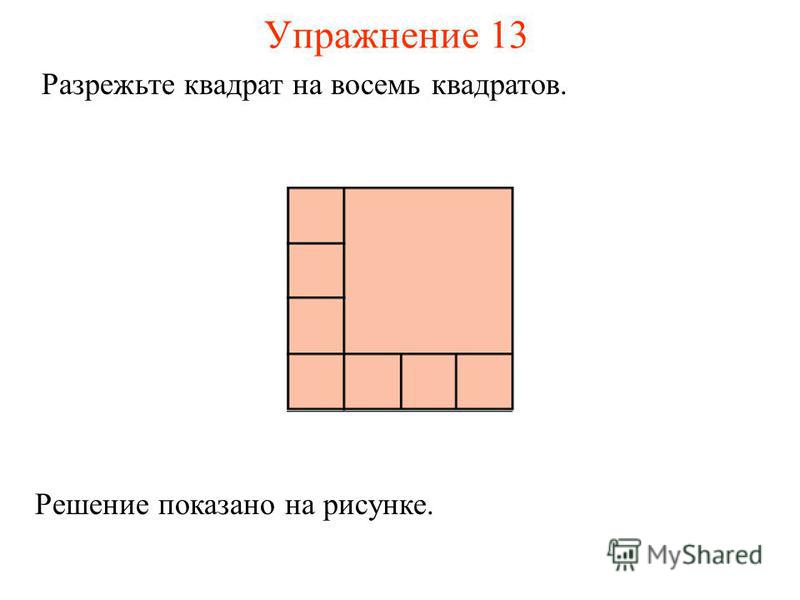 Это может означать, что вам нужно будет предложить несколько угловых номеров или, если у них есть некоторые номера в правильных позициях, вам может потребоваться сказать им, что это нормально, но они могут подумать о перемещении других в другое место.
Это может означать, что вам нужно будет предложить несколько угловых номеров или, если у них есть некоторые номера в правильных позициях, вам может потребоваться сказать им, что это нормально, но они могут подумать о перемещении других в другое место.
 Он рассчитал, где должна быть планета, а затем кто-то пошел искать и в конце концов нашел ее в сентябре 1846 года.
Он рассчитал, где должна быть планета, а затем кто-то пошел искать и в конце концов нашел ее в сентябре 1846 года.
 Симметрия треугольника нам сейчас совсем не поможет. Если мы поместим 3 в кружок «а», то сумма стороны, которую мы произвели, будет равна 6. Нет другого способа составить 6, поэтому здесь нет возможного ответа.
Симметрия треугольника нам сейчас совсем не поможет. Если мы поместим 3 в кружок «а», то сумма стороны, которую мы произвели, будет равна 6. Нет другого способа составить 6, поэтому здесь нет возможного ответа. Но это некрасиво. Мы надеемся, что есть лучший способ.
Но это некрасиво. Мы надеемся, что есть лучший способ. Оттуда достаточно быстро увидеть, куда должны идти четные числа. Есть три возможных расположения 1, 3, 5 в двух других случаях. Систематическая работа выявит, какие схемы работают, а какие нет. Когда все это будет сделано, мы получим четыре ответа, которые мы нашли ранее.
Оттуда достаточно быстро увидеть, куда должны идти четные числа. Есть три возможных расположения 1, 3, 5 в двух других случаях. Систематическая работа выявит, какие схемы работают, а какие нет. Когда все это будет сделано, мы получим четыре ответа, которые мы нашли ранее. Если бы мы использовали 6, нам пришлось бы составить 3, используя два числа. Это можно сделать только с 1 и 2. Если бы мы использовали 5, нам пришлось бы составить 4, используя два числа. Это можно сделать только с 1 и 3. (2 и 2 не допускаются.) Если бы мы использовали 4, нам пришлось бы составить 5, используя два числа. Это можно сделать только с 2 и 3. (1 и 4 не допускаются.) Таким образом, есть только три возможности:
Если бы мы использовали 6, нам пришлось бы составить 3, используя два числа. Это можно сделать только с 1 и 2. Если бы мы использовали 5, нам пришлось бы составить 4, используя два числа. Это можно сделать только с 1 и 3. (2 и 2 не допускаются.) Если бы мы использовали 4, нам пришлось бы составить 5, используя два числа. Это можно сделать только с 2 и 3. (1 и 4 не допускаются.) Таким образом, есть только три возможности:
 Если s = 10, сумма углов равна 9 и, следовательно, 1, 2, 6; 1, 3, 5; или 2, 3, 4. Если s = 11, сумма углов равна 12 и, следовательно, 1, 5, 6; 2, 4, 6; 3, 4, 5. Если s = 12, сумма углов равна 15 и, следовательно, 4, 5, 6.
Если s = 10, сумма углов равна 9 и, следовательно, 1, 2, 6; 1, 3, 5; или 2, 3, 4. Если s = 11, сумма углов равна 12 и, следовательно, 1, 5, 6; 2, 4, 6; 3, 4, 5. Если s = 12, сумма углов равна 15 и, следовательно, 4, 5, 6.
 ‘Есть ли что-то непонятное?’ ‘Есть ли какая-то часть, которой вы не следуете?’ ‘Есть ли какая-то часть, которая неверна?’
‘Есть ли что-то непонятное?’ ‘Есть ли какая-то часть, которой вы не следуете?’ ‘Есть ли какая-то часть, которая неверна?’
 Это может быть сделано в обстановке всего класса или в их группах. Как обычно, они должны сначала выдвинуть гипотезу, а затем попытаться найти доказательство этой гипотезы.
Это может быть сделано в обстановке всего класса или в их группах. Как обычно, они должны сначала выдвинуть гипотезу, а затем попытаться найти доказательство этой гипотезы. Края смещения могут быть проблематичными, потому что они растягиваются. Если вы не будете осторожны, вы можете получить шаткие HST.
Края смещения могут быть проблематичными, потому что они растягиваются. Если вы не будете осторожны, вы можете получить шаткие HST.

 Переверните линейку и совместите ее со швом на другой стороне. Вырежьте второй треугольник. Повторите на остальной части полосы.
Переверните линейку и совместите ее со швом на другой стороне. Вырежьте второй треугольник. Повторите на остальной части полосы.
 com. Читать далее.
com. Читать далее.


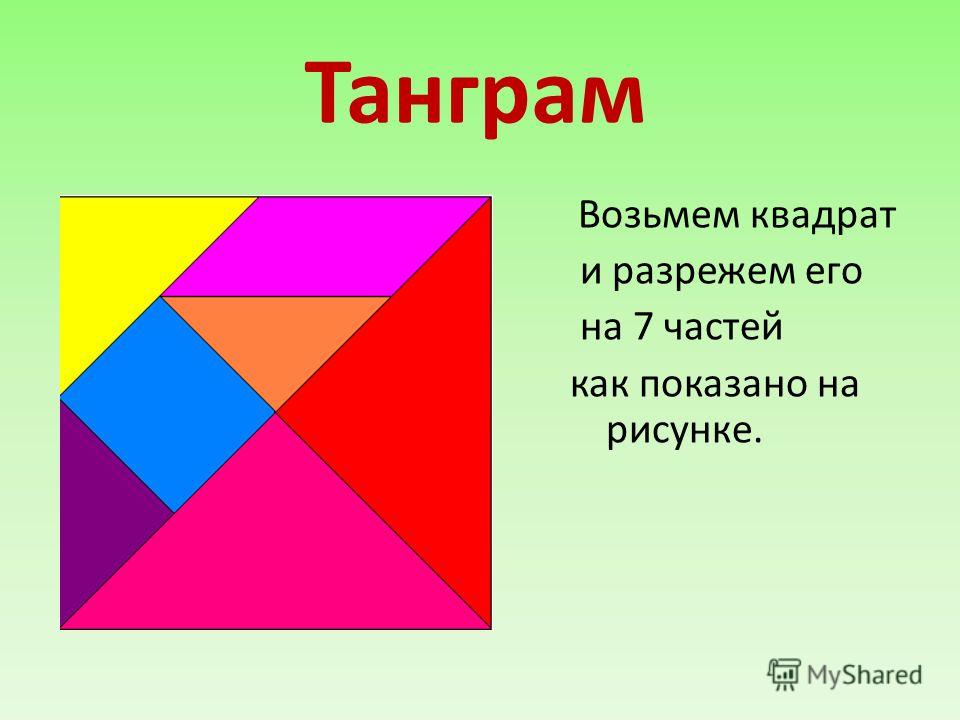 Один или несколько четырехугольников должны иметь непрямые углы.
Один или несколько четырехугольников должны иметь непрямые углы.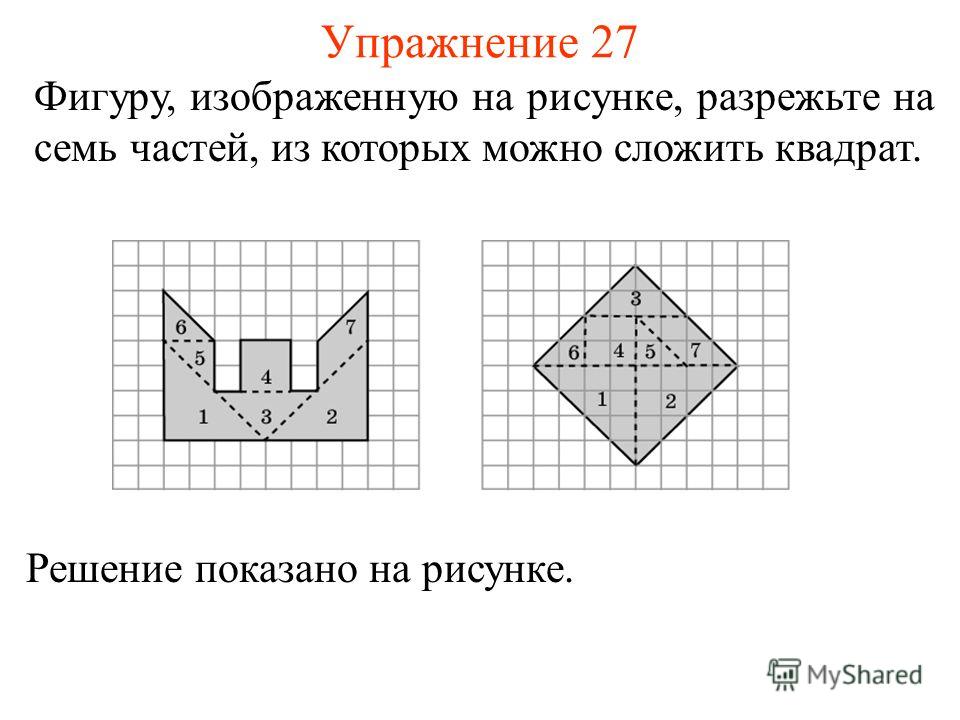 2.2)
2.2) openupresources.org/curricula/our6-8math/en/grade-6/index.html
openupresources.org/curricula/our6-8math/en/grade-6/index.html Поскольку это квадрат, мы знаем, что это прямоугольный треугольник, и мы можем использовать теорему Пифагора, чтобы определить длину . Стороны длины формируют каждый из катетов и являются гипотенузой. Таким образом, уравнение выглядит так: 9Мы можем упростить это до достаточно места, чтобы сделать расстояние между домашней площадкой и первой базой 44 фута. Какое расстояние (ближайший фут) будет от домашней площадки до второй базы, если предположить, что он построил ее в соответствии с этой спецификацией?
Поскольку это квадрат, мы знаем, что это прямоугольный треугольник, и мы можем использовать теорему Пифагора, чтобы определить длину . Стороны длины формируют каждый из катетов и являются гипотенузой. Таким образом, уравнение выглядит так: 9Мы можем упростить это до достаточно места, чтобы сделать расстояние между домашней площадкой и первой базой 44 фута. Какое расстояние (ближайший фут) будет от домашней площадки до второй базы, если предположить, что он построил ее в соответствии с этой спецификацией? Поскольку две стороны и диагональ образуют треугольник, длина диагонали равна длине стороны.
Поскольку две стороны и диагональ образуют треугольник, длина диагонали равна длине стороны.