Как решать дробные квадратные неравенства: Дробные рациональные неравенства

alexxlab / / Разное

Математика: Справ. материалы

Математика: Справ. материалы
  

Гусев В. А., Мордкович А. Г. Математика: Справ. материалы: Кн. для учащихся.— М.: Просвещение, 1988.— 416 с.

В книге дано краткое изложение основных разделов школьных курсов алгебры и начал анализа, геометрии. Книга окажет помощь в систематизации и обобщении знаний по математике.



Оглавление

СЛОВО К УЧАЩИМСЯ
ГЛАВА I. ЧИСЛА
§ 1. Натуральные числа
2. Арифметические действия над натуральными числами.
3. Деление с остатком.
4. Признаки делимости.
5. Разложение натурального числа на простые множители.
6. Наибольший общий делитель нескольких натуральных чисел.
7. Наименьшее общее кратное нескольких натуральных чисел.

8. Употребление букв в алгебре. Переменные.
§ 2. Рациональные числа
10. Равенство дробей. Основное свойство дроби. Сокращение дробей.
11. Приведение дробей к общему знаменателю.
12. Арифметические действия над обыкновенными дробями.
13. Десятичные дроби.
14. Арифметические действия над десятичными дробями.
15. Проценты.
16. Обращение обыкновенной дроби в бесконечную десятичную периодическую дробь.
17. Обращение бесконечной десятичной периодической дроби в обыкновенную дробь.
18. Координатная прямая.
19. Множество рациональных чисел.
§ 3. Действительные числа
21. Действительные числа. Числовая прямая.
22 Обозначения некоторых числовых множеств.
23. Сравнение действительных чисел.
25. Числовые промежутки.
26. Модуль действительного числа.
27. Формула расстояния между двумя точками координатной прямой.
28. Правила действий над действительными числами.
29. Свойства арифметических действий над действительными числами.

30. Пропорции.
31. Целая часть числа. Дробная часть числа.
32. Степень с натуральным показателем.
33. Степень с нулевым показателем. Степень с отрицательным целым показателем.
34. Стандартный вид положительного действительного числа.
35. Определение арифметического корня.
36. Корень нечетной степени из отрицательного числа.
37. Степень с дробным показателем.
38. Свойства степеней с рациональными показателями.
39. Приближенные значения чисел. Абсолютная и относительная погрешности.
40. Десятичные приближения действительного числа по недостатку и по избытку.
41. Правило извлечения квадратного корня из натурального числа.
42. Понятие о степени с иррациональным показателем.
43. Свойства степеней с действительными показателями.
§ 4. Комплексные числа
45. Арифметические операции над комплексными числами.
46. Алгебраическая форма комплексного числа.
47. Отыскание комплексных корней уравнений.
ГЛАВА II. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ
49. 3.
112. Построение графика функции y = f(x-m)+n
113. График квадратичной функции.
114. Способы построения графика квадратичной функции
115. Построение графика функции y = f(kx).
116. Сжатие и растяжение графиков тригонометрических функций.
117. График гармонического колебания
ГЛАВА IV. ТРАНСЦЕНДЕНТНЫЕ ВЫРАЖЕНИЯ
§ 12. Преобразование выражений, содержащих переменную под знаком логарифма
119. Определение логарифма положительного числа по данному основанию.
120. Свойства логарифмов.
121. Переход к новому основанию логарифма.
122. Логарифмирование и потенцирование.
123. Десятичный логарифм. Характеристика и мантисса десятичного логарифма.
§ 13. Формулы тригонометрии и их использование для преобразования тригонометрических выражений
125. Формулы сложения и вычитания аргументов.
126. Формулы приведения.
127. Соотношения между тригонометрическими функциями одного и того же аргумента.
128. Формулы двойного угла.
129. Формулы понижения степени.
130. Преобразование суммы тригонометрических функций в произведение.
131. Преобразование произведения тригонометрических функций в сумму.
132. Преобразование выражения a cos t + b sin t к виду A sin (t + a).
133. Примеры преобразований выражений, содержащих обратные тригонометрические функции.
ГЛАВА V. УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ
§ 14. Уравнения с одной переменной
135. Равносильность уравнений.
136. Линейные уравнения.
137. Квадратные уравнения.
138. Неполные квадратные уравнения.
139. Теорема Виета.
140. Системы и совокупности уравнений.
141. Уравнения, содержащие переменную под знаком модуля.
142. Понятие следствия уравнения. Посторонние корни.
143. Уравнения с переменной в знаменателе.
144. Область определения уравнения.
145. Рациональные уравнения.
146. Решение уравнения p(x) = 0 методом разложения его левой части на множители.
147. Решение уравнений методом введения новой переменной.
148. Биквадратные уравнения.
149. Решение задач с помощью составления уравнений.
150. Иррациональные уравнения.
151. Показательные уравнения.
152. Логарифмические уравнения.
153. Примеры решения показательно-логарифмических уравнений.
154. Простейшие тригонометрические уравнения.
155. Методы решения тригонометрических уравнений.
156. Универсальная подстановка (для тригонометрических уравнений).
157. Метод введения вспомогательного аргумента (для тригонометрических уравнений).
158. Графическое решение уравнений.
159. Уравнения с параметром.
§ 15. Уравнения с двумя переменными
161. График уравнения с двумя переменными.
162. Линейное уравнение с двумя переменными и его график.
§ 16. Системы уравнений
164. Решение систем двух уравнений с двумя переменными методом подстановки.
165. Решение систем двух уравнений с двумя переменными методом сложения.
167. Графическое решение систем двух уравнений с двумя переменными.
168. Исследование системы двух линейных уравнений с двумя переменными.
169. Решение систем двух уравнений с двумя переменными методами умножения и деления.
170. Системы показательных и логарифмических уравнений.
171. Системы тригонометрических уравнений с двумя переменными.
172. Системы трех уравнений с тремя переменными.
173. Решение задач с помощью составления систем уравнений.
Глава VI. НЕРАВЕНСТВА
§ 17. Решение неравенств с переменной
175. Графическое решение неравенств с одной переменной.
176. Линейные неравенства с одной переменной.
177. Системы неравенств с одной переменной.
178. Совокупность неравенств с одной переменной.
179. Дробно-линейные неравенства.
180. Неравенства второй степени.
181. Графическое решение неравенств второй степени.
182. Неравенства с модулями.
183. Решение рациональных неравенств методом промежутков.
184. Показательные неравенства.
185. Логарифмические неравенства.
186. Иррациональные неравенства.
187. Решение тригонометрических неравенств.
188. Неравенства и системы неравенств с двумя переменными.
§ 18. Доказательство неравенств
190. Синтетический метод доказательства неравенств.
191. Доказательство неравенств методом от противного.
192. Использование неравенств при решении уравнений.
ГЛАВА VII. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА
§ 19. Числовые последовательности
194. Способы задания последовательности.
195. Возрастание и убывание последовательности.
196. Определение арифметической прогрессии.
197. Свойства арифметической прогрессии
198. Определение геометрической прогрессии.
199. Свойства геометрической прогрессии.
200. Понятие о пределе последовательности.
201. Вычисление пределов последовательностей.
202. Сумма бесконечной геометрической прогрессии при |q| § 20. Предел функции
204. Вычисление пределов функции при х->оо.
205. Предел функции в точке. Непрерывные функции.
206. Вертикальная асимптота.
207. Вычисление пределов функций в точке.
§ 21. Производная и ее применения
209. Определение производной.
210. Формулы дифференцирования. Таблица производных.
211. Дифференцирование суммы, произведения, частного.
212. Сложная функция и ее дифференцирование.
213. Физический смысл производной.
214. Вторая производная и ее физический смысл.
215. Касательная к графику функции.
216. Применение производной к исследованию функций на монотонность.
217. Применение производной к исследованию функций на экстремум.
218. Отыскание наибольшего и наименьшего значений непрерывной функции на отрезке.
219. Отыскание наибольшего или наименьшего значения непрерывной функции на незамкнутом промежутке.
220. Задачи на отыскание наибольших или наименьших значений величин.
221. Применение производной для доказательства тождеств.
222. Применение производной для доказательства неравенств.
223. Общая схема построения графика функции.
§ 22. Первообразная и интеграл
225. Таблица первообразных.
226. Правила вычисления первообразных.
227. Интеграл.
228. Связь между интегралов и первообразной (формула Ньютона—Лейбница).
229. Правила вычисления интегралов.
230. Использование интеграла для вычисления площадей плоских фигур.
ГЕОМЕТРИЯ. ГЛАВА I. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ НА ПЛОСКОСТИ
2. Точка. Прямая.
3. Определения. Аксиомы. Теоремы.
§ 2. Основные свойства простейших геометрических фигур
5. Луч.
6. Окружность. Круг.
7. Полуплоскость.
8. Угол. Градусная мера угла.
9. Смежные и вертикальные углы.
10. Центральные и вписанные углы.
11. Параллельные прямые.
12. Признаки параллельности прямых.
13. Перпендикулярные прямые.
14. Касательная к окружности.
15. Треугольники.
16. Равенство треугольников.
17. Равнобедренный треугольник.
18. Сумма углов треугольника.
19. Прямоугольный треугольник. Теорема Пифагора.
20. Окружности, вписанные в треугольник и описанные около треугольника.
§ 3. Геометрические построения на плоскости
22. Простейшие задачи на построение.
23. Геометрическое место точек на плоскости.
§ 4. Четырехугольники
25. Параллелограмм.
26. Прямоугольник. Ромб. Квадрат.
27. Трапеция.
§ 5. Многоугольники
29. Выпуклые многоугольники.
30. Правильные многоугольники.
31. Длина окружности.
§ 6. Решение треугольников
33. Соотношения между сторонами и углами в прямоугольном треугольнике.
34. Теорема косинусов. Теорема синусов.
35. Решение треугольников.
§ 7. Площади плоских фигур
37. Площади многоугольников.
38. Площади подобных фигур.
39. Площадь круга.
ГЛАВА II. Прямые и плоскости в пространстве
§ 9. Параллельность прямых и плоскостей
42. Параллельность прямой и плоскости.
43. Параллельные плоскости.
§ 10. Перпендикулярность прямых и плоскостей
45. Перпендикуляр и наклонная к плоскости.
46. Перпендикулярность плоскостей.
ГЛАВА III. ТЕЛА В ПРОСТРАНСТВЕ
§ 11. Многогранники
48. Многогранные углы. Многогранники.
49. Призма. Параллелепипед. Куб.
50. Пираприда.
51. Правильные многогранники.
§ 12. Тела вращения
53. Конус.
54. Шар.
§ 13. Изображение пространственных фигур на плоскости
56. Ортогональное проектирование.
57. Геометрическое место точек в пространстве.
§ 14. Объемы тел
59. Объем параллелепипеда, призмы и пирамиды.
60. Объем цилиндра и конуса.
61. Общая формула объемов тел вращения.
§ 15. Площади поверхностей тел
63. Понятие площади поверхности.
64. Площади поверхностей тел вращения.
ГЛАВА IV. ДЕКАРТОВЫ КООРДИНАТЫ
§ 16. Координаты на плоскости и в пространстве
66. Координаты середины отрезка.
§ 17. Уравнения фигур на плоскости
68. Пересечение двух окружностей.
69. Уравнение прямой.
70. Пересечение прямой и окружности.
§ 18. Уравнения фигур в пространстве
72. Уравнение сферы.
73. Взаимное расположение сферы и плоскости.
74. Пересечение двух сфер.
ГЛАВА V. РЕОБРАЗОВАНИЯ ФИГУР
76. Понятие движения.
§ 20. Подобие фигур
78. Подобные фигуры.
ГЛАВА VI. ВЕКТОРЫ
80. Понятие вектора.
81. Координаты вектора.
§ 22. Операции над векторами
83. Умножение вектора на число. Коллинеарные векторы.
84. Скалярное произведение векторов.
ПРИЛОЖЕНИЯ
ГЕОМЕТРИЯ

Методика решения дробно — рациональных уравнений. Подготовка учащихся к ОГЭ. | Методическая разработка по алгебре (9 класс):

 Методика решения дробно — рациональных уравнений.

 Подготовка учащихся к ОГЭ.

( из опыта работы учителя математики МБОУ Погребская средняя общеобразовательная школа Стратий Татьяны Николаевны)

Кодификатор требований к уровню подготовки обучающихся для проведения основного государственного экзамена по математике является одним из документов, определяющих структуру и содержание КИМов. В нем сформулированы требования к уровню подготовки выпускников основной школы. В разделе III прописано требование «Уметь решать уравнения, неравенства и их системы»

Код раздела

Код контролируемого умения

Уметь решать уравнения, неравенства и их системы

3

3. 1

Решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы

3.2

Решать линейные и квадратные неравенства  с одной переменной и их системы

3.3

Применять графические представления  при решении уравнений, систем, неравенств

3.4

Решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений исходя из формулировки задачи

С темой «Дробные рациональные уравнения » учащиеся впервые знакомятся на уроках алгебры в 8 классе. Вводится понятие дробно-рационального уравнения, указывается чёткий алгоритм его решения, разбираются базовые примеры. В 9 классе при изучении главы II «Уравнения и неравенства с одной переменной»  расширяем знания учащихся по теме «Дробные рациональные уравнения», решаем более сложные задания. Результаты обучения в значительной степени зависят от конкретной методики обучения, которую применяет учитель на уроках. Учитель, при активном сотрудничестве с обучающимися, должен помочь им выделить систему общих указаний, которые будут служить  ориентирами при решении уравнений.

Целесообразно четко сформулировать  алгоритм решения дробно-рационального уравнения:

1) найти общий знаменатель дробей, входящих в уравнение;

2) умножить обе части уравнения на общий знаменатель;

3) решить получившееся целое уравнение;

4) исключить из его корней те, которые обращают в нуль общий знаменатель.

В ходе решения дробно-рациональных уравнений необходимо установить, являются ли найденные корни целого уравнения допустимыми значениями переменной. Учащиеся нередко ошибаются, пропуская этот момент, поэтому надо настойчиво добиваться, чтобы в каждом случае алгоритм был выполнен до конца.

       Важно  научить обучающихся  пользоваться «методом пристального взгляда» чтобы они зрительно видели разложение знаменателей на простые множители и безошибочно находили наименьший общий знаменатель. Такая методика решения уравнений позволяет школьникам не допускать ошибок при решении дробных рациональных уравнений,  успешно решать задачи с помощью дробных рациональных уравнений.

     Следует также предварительно отработать умения и навыки учащихся при выполнении тождественных преобразований, решения квадратных и линейных уравнений, раскладывания квадратного трёхчлена на множители, нахождения ОДЗ, основного свойства пропорции, формул сокращённого умножения

Приемы решения дробных рациональных уравнений  находят естественное и важное применение при решении текстовых задач. При решении текстовой задачи учащиеся выполняют три этапа, входящие в процесс решения:

— переводят задачу на язык алгебры (составляют математическую модель),

— решают полученное уравнение,

— выполняют содержательный анализ полученного ответа.

    В практической деятельности при проведении уроков по этой теме я  применяю   организацию учебной деятельности следующим образом: обучающиеся работают по группам. Одна группа   решает текстовые задачи – им требуется  в процессе решения  получить дробное рациональное уравнение. Другая группа  работает над решением этих же уравнений. Последующая проверка у доски работы двух групп представляет полное решение текстовой задачи с обоснованной записью ответа. В зависимости от наполняемости класса можно организовать подобным образом работу четырех или шести групп. Такая организация урока позволяет активизировать мыслительную деятельность учащихся, развивает коммуникативные навыки, умение работать в сотрудничестве позволяет закрепить умение решать текстовые задачи и одновременно умение решать дробные рациональные уравнения.

        Все выпускники 9 класса должны уметь решать дробные рациональные уравнения.

     Чтобы достичь поставленной задачи учителю следует руководствоваться методическими требованиями к системе упражнений, направленной на организацию усвоения приемов решения дробных рациональных уравнений.

  1. система упражнений должна обеспечивать возможность активного участия обучаемых в конструировании приема решения рассматриваемого класса задач (в нашем случае решения дробных рациональных уравнений)
  2.   система упражнений должна обеспечить усвоение и необходимое повторение каждого из приемов, входящих в качестве составной части в формируемый прием ( решения дробных рациональных уравнений)
  3. система упражнений должна строиться по принципу систематичности, постепенного нарастания сложности, содержать задания комплексного характера, выполнение которых  требует распознания типа уравнения и осознанного выбора способа его решения.

Дробно-рациональные уравнения

Стандартный вид дробно-рационального уравнения:

Где – многочлены.

Область допустимых значений (ОДЗ) данного уравнения: Решение уравнений  сводится к решению системы

Дробно-рациональные уравнения вида

Где – многочлены, можно решать, используя основное свойство пропорции:

               Основные методы решения рациональных уравнений.

         1. Простейшие: решаются путём обычных упрощений — приведение к общему знаменателю, приведение подобных членов и так далее.

Квадратные уравнения ax2 + bx + c = 0 решаются по  формуле  или используется теорема Виета: x1 + x2 = – b / a; x1x2 = c / a.

         2.Способ группировки: путём группировки слагаемых, применения формул сокращённого умножения привести (если удастся) уравнение к виду, когда слева записано произведение нескольких сомножителей, а справа — ноль. Затем приравниваем к нулю каждый из сомножителей.

        3. Способ подстановки: ищем в уравнении некоторое повторяющееся выражение, которое обозначим новой переменной, тем самым упрощая вид уравнения. В некоторых случаях очевидно какую следует сделать подстановку.

Например, уравнение

      (x2 + x – 5) / x  +  3x / (x2 + x – 5) + 4 = 0,

легко решается с помощью подстановки (x2 + x – 5) / x = t,

 получаем t + (3 / t) + 4 = 0.

     Или: 21 / (x2 – 4x + 10) – x2 + 4x = 6.

Здесь можно сделать подстановку x2 – 4 = t. Тогда 21 / (t + 10) — t = 6 и т.д.

        В более сложных случаях подстановка видна лишь после нескольких преобразований.               Например, дано уравнение

(x2 + 2x)2 – (x +1)2 = 55.

Переписав его иначе, а именно (x2 + 2x)2 – (x2 + 2x + 1) = 55, сразу увидим подстановку x2 + 2x=t.

Имеем t2 – t – 56 = 0, t1 = – 7, t2 = 8. Осталось решить x2 + 2x = – 7 и x2 + 2x = 8.

            В ряде других случаев удобную подстановку желательно знать “заранее”. Например

Уравнение (x + a)4 + (x + b)4 = c сводится к биквадратному, если сделать подстановку

x = t – (a + b) / 2.

     Симметрическое уравнение (возвратное) a0xn + a1xn – 1 + … + a1x + a0 = 0 (коэффициенты членов, равностоящих от концов, равны) решается с помощью подстановки x + 1 / x = t, если n —чётное; если n — нечётное, то уравнение имеет корень x = – 1.

     Уравнение вида (x + a)(x + b)(x + c)(x + d) = l сводится к квадратному, если

    a + b = c + d и т.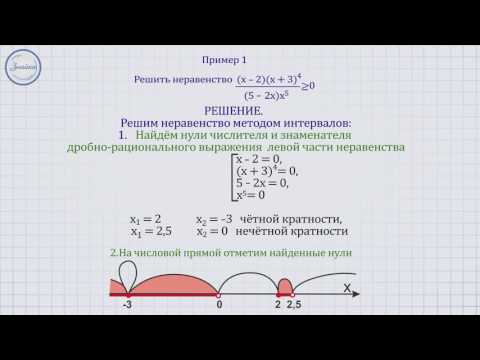 д.

    К основному методу решения дробно-рациональных уравнений относится также метод замены переменной.

  1. Подбор:  при решении уравнений высших степеней рациональные корни уравнения anxn + an – 1xn – 1 + … + a1x + a0 = 0 ищем в виде p / q,

 где p — делитель a0, q — делитель an, p и q взаимно просты, pÎ Z, qÎ N.

5. “Искусство”, т.е. решать пример нестандартно, придумать “свой метод”, догадаться что-то прибавить и отнять, выделить полный квадрат, на что-то разделить и умножить и т.д.

Некоторые  приемы решения дробно- рациональных уравнений рассмотрим на  примерах.

Пример 1. Решить уравнение

Решение. Сводим заданное уравнение к стандартному виду :

т. е.

Его решением будет решение системы

т. е.

Значит, решением заданного уравнения является

Ответ:

Пример 2. Решить уравнение

Решение. Применим основное свойство пропорции с учетом ОДЗ уравнения:

Получаем:

Откуда

Оба корня являются решениями, так как подходят по ОДЗ. В ответе имеем:

Ответ:

Пример 3. Решить уравнение

Решение. Группируем слагаемые

Заменяем

откуда

т. е. и

Получаем уравнение или, то же самое,

Полученное уравнение имеет корни:

Возвращаемся к переменной Х:

В результате приходим к совокупности 2-х квадратных уравнений

Которые решаем на ОДЗ: Приходим к ответу

Ответ:

Пример 4. Решить уравнение

Решение. Выделим в левой части уравнения полный квадрат суммы:

Получаем уравнение, которое приобретает вид

Заменяем и приходим к уравнению

Решая его, найдем корни:

Возвращаемся к старой переменной:

Решаем полученные уравнения по свойству пропорции (с учетом ОДЗ):

Ответ: 

Пример 5. Решить уравнение

Решение. Введем замену:

Тогда и получим уравнение

Решаем его:

т. е.

Решая квадратное уравнение, находим корни:

Вернемся к переменной Х:

Решаем первое уравнение:

Второе уравнение не имеет решения, так как

 Ответ: 

Заключение:  Чтобы сформировать умение  решать дробные рациональные уравнения всеми обучающимися 9 класса, учителю математики необходимо разработать систему упражнений, направленную на отработку приемов и методов решения этих уравнений.

          На этапе подготовки  — создать условия для активного восприятия, через упражнения  на повторение, упражнения пропедевтического характера.

          На этапе  усвоения —  через систему упражнений необходимо создать условия, которые позволяют обучающимся осознать и  прочно запомнить новые сведения ( последовательность действий, алгоритм).

         На этапе закрепления – создать условия для усвоения знаний в ходе их применения в различных ситуациях.

                                     Используемая литература и электронные ресурсы

1.  Д.Т. Письменный «Готовимся к экзамену по математике»- М.; Рольф, Айрис-пресс,1998г.

2.   «Математика. Подготовка к ГИА- 2015»- под редакцией Ф.Ф. Лысенко, Ростов- на-Дону, Легион. 2014г.

3.   «Алгебра -9 класс»- Ю.Н. Макарычев, Н.Г.Миндюк и др. под редакцией

С.А. Теляковского, М.: Просвещение,2010г.

4.   Л.И. Заввич «Итоговая аттестация. Задания по математике»М,:Просвещение,2011г.

5.   С.С.Минаева,Л.О.Рослова   «Алгебра. Сборник заданий для подготовки к итоговой аттестации».М.,Экзамен.2014г.

6.  М.Р.Леонтьева, С.Б. Суворова «Упражнения в обучении алгебре»,М.,Просвещение,2005г.

7.   Ресурсы, представленные на портале ФЦИОР (Федеральный центр информационных образовательных ресурсов) – http://fcior.edu.ru , http://eor.edu.ru 

 8.  Каталог образовательных ресурсов сети Интернет для школы —     http://katalog.iot.ru/

9.  Справочная информация по математическим дисциплинам      

        http:/www. mathem.h2.ru/

10.     Образовательный математический сайт          http://www.exponenta/ru

 11.     Публикации по алгебре, геометрии, тригонометрии  

                     http://www.ega-math.narod.ru/

 12. Сеть творческих учителей           http://www.it-n.ru

 13. Материалы газеты «Математика»       http://mat.1september. ru

14.Интернет-проект «Задачи» . Помощь при подготовке уроков, кружков             http://www.problems.ru/

линейная алгебра — Решение неравенств с дробями с неразложимыми полиномами

Задать вопрос

спросил

Изменено 8 лет, 10 месяцев назад

Просмотрено 1к раз

$\begingroup$

Итак, я сломал себе голову, пытаясь решить это неравенство:

$$\frac {x+1}{2-x} \le \frac {x}{3+x}$$

I вас учили, что вы должны поместить все множители в одну сторону неравенства (оставив ноль в другой части), а затем разложить полиномы на множители. Итак, я сделал следующее:

$$\frac {x+1}{2-x}-\frac {x}{3+x} \le 0$$

Затем:

$$\frac {( x+1)(3+x)- x(2-x)}{(2-x)(3+x)}\le 0$$

Что равно: 92+2x+3$ как произведение двух биномов, и (насколько мне известно) мне нужно сделать это, чтобы решить его, выполнив следующие шаги: http://www. purplemath.com/modules/ineqrtnl.htm Кто-нибудь может пожалуйста, помогите мне? Есть ли способ факторизовать полином или другой способ решить это неравенство?

Кстати, это мой первый пост, так что извините, если я допустил какие-то ошибки. Английский также не мой родной язык, извините за это. Заранее большое спасибо.

  • линейная алгебра
  • неравенство
    • 92 — 4\cdot 2 \cdot 3 = -20 < 0$. Так что числитель всегда строго положителен.

    Итак, знак вашей дроби определяется знаком вашего знаменателя. При $x>2$ знаменатель отрицателен (поскольку первое слагаемое $2-x$ отрицательно, второе положительно). Таким образом, вся дробь отрицательна (положительное число, деленное на отрицательное, равно отрицательному).

    Для $x \in (-3,2)$ оба члена в знаменателе положительны; поэтому вся дробь также положительна (рассуждая, как указано выше). 92 +bx +c = 0$ не имеет решений. Предположим далее, что $a>0$, как в нашем случае. Тогда форма квадратичного числа является U-образной (в отличие от n-образной) и не пересекает ось $x$. Поэтому он всегда положительный.

    $\endgroup$

    3

    $\begingroup$

    Пока ваши расчеты верны. Теперь определите знак каждого из двух полиномов, стоящих в числителе и знаменателе й дроби 9.2-4(2)(3)=4-24=-20<0$$, так что многочлен в числителе всегда положителен. Таким образом, его можно не учитывать при последующем анализе, так как он не влияет на знак LHS.

  • $d(x)=(2-x)(3+x)$. Непосредственно (из формы многочлена) $$\begin{cases}d(x) > 0, & \text{for } x \in (-3,2) \\ d(x)\le 0 , & \text{else}\end{cases}$$

    • Таким образом, неравенство выполняется всякий раз, когда $d(x)\le 0$, т. е. при $x \notin (-3,2)$, то есть при $$x\in(-\infty, -3) \cup( 2,+\infty)$$ Значения $x=-3$ и $x=2$ исключаются, поскольку они обнуляют знаменатель.

    $\endgroup$

    1

    Нелинейные неравенства

    Нелинейные неравенства и теорема Пифагора

    Квадратные неравенства

    Мы решим, используя следующие шаги

    1. Положите все на левая сторона, так что мы имеем, например, Квадрат > 0,

    2. Фактор и установить равным к нуль.

    3. Решите и поместите ответы на число линия. Это сократит числовая линия на две или три области.

    4. Выберите тестовое значение для каждого региона и вставьте это тестовое значение в каждый из факторов. Ставьте плюсы или минусы над регионом в зависимости от того, являются ли тестовые значения положительными или отрицательными.

    5. Если регион имеет два плюса или два минуса, то регион положительный. Если в регионе есть по одному из каждого, то регион отрицательный.

    6. Если неравенство «<", то включить отрицательные регионы.

      Если неравенство «>», то включите положительные регионы.

    7. Если неравенство меньше (больше) или равно затем включите конечные точки со сплошной точкой и интервалом []

      Если неравенство меньше (больше), то не включайте конечные точки показывая открытую точку и интервал ()

    Пример

    Решить

    х 2 + 3 шт. > -2

    1. х 2 + 3х + 2  >  0

    2. (х + 2)(х + 1) = 0

    3. х = -2     или x = -1      Это разрезает числовую прямую на три региона.

    4. Для левой области мы выбираем -5 и имеем это

      -5 + 2 < 0, -5 + 1 < 0 (два минуса)

    5. Для средней области мы выбираем -1,5 и получаем, что

      -1,5 + 2 > 0, -1,5 + 1 < 0     (по одному каждому)

      Для левой области мы выбираем 0 и имеем это

      0 + 2 >0,         0+ 1 >0 (два плюса)

      х+2 х+1 Итого
      Левый (-5)

      —

      —

      +

      Средний (-1,5)

      —

      +

      —

      Справа(0)

      +

      +

      +

    6. Мы видим, что левая и правая области положительны, а средняя регион отрицательный.

    7. Так как неравенство больше, то имеем решение:

      (- ,-2) У (-1,)

    Упражнение

    Решить

    х 2 — 3 <   2x

    Рациональные неравенства

    Для решения рациональных неравенств мы можем использовать ту же технику, что и для квадратных неравенств со следующими корректировками:

    1. Положив все на левую сторону, мы кладем левую руку стороны над общим знаменателем.

    2. Вместо факторизации и решения, чтобы найти точки разреза, мы просто приравнять числитель и знаменатель к нуль.

    3. Точка отсечки, которая определяется из этого знаменатель будет никогда будет включен, поэтому будет окаймлен «(» и показан в виде открытой точки.

    Пример

    2x + 3   
    <    2    
    х -1

    1. 2x + 3   
      —   2    < 0   
      х -1

                2x + 3           2(x — 1)
      — <    0   
      Икс -1 х — 1

                2x + 3 — 2x + 2   
      <    0   Уведомление что — 2(x — 1)  =  -(2x — 2) = -2x + 2
      х -1

      5   
      <    0   
                x -1

    2. Обратите внимание, что числитель никогда не равен нулю, а знаменатель равен нулю только при х = 1.

    3. x = 1 делит числовую прямую на две области.

    4. Для левой области мы выбираем 0 и видим, что

      5  >  0         и 0–1 < 0     (по одному каждому)

      Для правильного региона выбираем 2 и видим, что

      5 > 0 и 2–1 > 0 (два положительных результата)

      х-1 Итого
      Левый (0)

      —

      —

      Правый(2)

      +

      +

    5. Мы видим, что левая область отрицательна, а правая область положительный.

    6. Поскольку неравенство « < », мы включаем эту левую область.

    7. Хотя неравенство как равенство под ним, точка отсечения исходит из знаменатель, поэтому мы не включаем эту точку отсечения. Следовательно решение

      (-,1)

    Теорема Пифагора

    Наиболее важной формулой в математике является пифагорейская формула . теорема , которая утверждает, что для прямоугольного треугольника, если a и b — длины катетов (короткие стороны) и с — длина гипотенузы (длинная сторона), затем

    2 + б 2 = в 2

    Пример

    Предположим, что длина гипотенузы прямоугольного треугольника равна 12, а Длина ноги равна 9. Найдите длину другой ноги.

    No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *