Как решать дробные системы уравнений: Решение систем уравнений — метод как решить систему линейных уравнений

alexxlab / / Разное

Вестник КРАУНЦ. Физ.-мат. науки. 2018. № 3(23). C. 76-82. ISSN 2079-6641 — Вестник КРАУНЦ. Физико-математические науки

Содержание

DOI: 10.18454/2079-6641-2018-23-3-76-82

УДК 517.95

ЗАДАЧА КОШИ ДЛЯ СИСТЕМЫ УРАВНЕНИЙ СЧАСТНЫМИ ПРОИЗВОДНЫМИ ДРОБНОГО ПОРЯДКА

М. О. Мамчуев

Институт прикладной математики и автоматизации КБНЦ РАН, 360000, г. Нальчик, ул. Шортанова, 89 А

E-mail: [email protected]

Для системы уравнений первого порядка с частными производными дробного порядка в смысле Римана-Лиувилля дана корректная постановка задачи Коши в случае, когда матричный коэффициент в главной части имеет только положительные собственные значения.

Ключевые слова: система уравнений в частных производных, дробные производные, задача Коши, корректность, фундаментальное решение, функция
Райта матричного аргумента

© Мамчуев М. О., 2018

MSC 35N05

CAUCHY PROBLEM FOR THE SYSTEM OF EQUATIONS WITH PARTIAL DERIVATIVES OF FRACTIONAL ORDER

M. O. Mamchuev

Institute of Applied Mathematics and Automation of KBSC RAS, 360000, Nal’chik, Shortanov., 89 A, Russia

E-mail: [email protected]

For a system of first-order equations with partial derivatives of fractional order in the Riemann-Liouville sense, we give a correct statement of the Cauchy problem in the case when the matrix coefficient in the main part has only positive eigenvalues.

Key words: system of partial differential equations, fractional derivatives, Cauchy problem, well-posedness, fundamental solution, Wright’s function of the matrix argument.

© Mamchuev M. O., 2018

Список литературы

  1. Нахушев А.М., Дробное исчисление и его применение, Физматлит, М., 2003, 272 с. [Nahushev A.M., Drobnoe ischislenie i ego primenenie, Fizmatlit, M., 2003].
  2. Мамчуев М.О., “Фундаментальное решение системы уравнений с частными производными дробного порядка”, Дифференциальные уравнения, 46:8 (2010), 1113-1124.
    [Mamchuev M.O., “Fundamental’noe reshenie sistemy uravnenij s chastnymi proizvodnymi drobnogo poryadka”, Differencial’nye uravneniya, 46:8 (2010), 1113-1124].
  3. Мамчуев М.О., “Задача Коши в нелокальной постановке для системы уравнений с частными производными дробного порядка”, Дифференциальные уравнения, 48:3 (2012), 351-358. [Mamchuev M.O., “Zadacha Koshi v nelokal’noj postanovke dlya sistemy uravnenij s chastnymi proizvodnymi drobnogo poryadka”, Differencial’nye uravneniya, 48:3 (2012), 351-358].
  4. Мамчуев М.О., “Смешанная задача для нагруженной системы уравнений с производными Римана-Лиувилля”, Математические заметки, 97:3 (2015), 428-439. [Mamchuev M.O., “Smeshannaya zadacha dlya nagruzhennoj sistemy uravnenij s proizvodnymiRimana-Liuvillya”, Matematicheskie zametki, 97:3 (2015), 428-439].
  5. Мамчуев М.О., “Смешанная задача для системы уравнений с частными производными дробного порядка”, Дифференциальные уравнения, 52:1 (2016), 132-137. [Mamchuev M.O., “Smeshannaya zadacha dlya sistemy uravnenij s chastnymi proizvodnymi drobnogo poryadka”, Differencial’nye uravneniya, 52:1 (2016), 132-137].
  6. Мамчуев М.О., “Краевая задача для системы уравнений с частными производными дробного порядка”, Дифференциальные уравнения, 44:12 (2008), 1674-1686. [Mamchuev M.O., “Kraevaya zadacha dlya sistemy uravnenij s chastnymi proizvodnymi drobnogo poryadka”, Differencial’nye uravneniya, 44:12 (2008), 1674-1686].
  7. Мамчуев М.О., “Краевая задача для системы многомерных дифференциальных уравнений дробного порядка”, Вестник СамГУ. Естественнонаучная серия., 8/2:67 (2008), 164-175. [Mamchuev M.O., “Kraevaya zadacha dlya sistemy mnogomernyh differencial’nyh uravnenij drobnogo poryadka”, Vestnik SamGU. Estestvennonauchnaya seriya., 8/2:67 (2008), 164-175].
  8. Мамчуев М.О., “Краевая задача для линейной системы уравнений с частными производными дробного порядка”, Челябинский физико-математический журнал, 2:3 (2017), 295-311. [Mamchuev M.O., “Kraevaya zadacha dlya linejnoj sistemy uravnenij s chastnymi proizvodnymi drobnogo poryadka”, CHelyabinskij fiziko-matematicheskij zhurnal, 2:3 (2017), 295-311].
  9. Kochubei A.N., “Fractional-hiperbolic systems”, Fractional Calculus and Applied Analysis, 16:4 (2013), 860-873.

Список литературы (ГОСТ)

  1. Нахушев А.М. Дробное исчисление и его применение. М.: Физматлит. 2003. 272 c.
  2. Мамчуев М.О. Фундаментальное решение системы уравнений с частными производными дробного порядка // Дифференциальные уравнение. 2010. Т. 46. №8. С. 1113-1124.
  3. Мамчуев М.О. Задача Коши в нелокальной постановке для системы уравнений с частными производными дробного порядка //Дифференциальные уравнения. 2012. Т. 48. № 3. С. 351-358.
  4. Мамчуев М.О. Смешанная задача для нагруженной системы уравнений с производными Римана-Лиувилля // Математические заметки. 2015. Т. 97. №3. С. 428-439.
  5. Мамчуев М.О. Смешанная задача для системы уравнений с частными производными дробного порядка // Дифференциальные уравнения. 2016. Т. 52. №1. C. 132-137.
  6. Мамчуев М.О. Краевая задача для системы уравнений с частными производными дробного порядка // Дифференциальные уравнения. 2008. Т. 44. № 12. С. 1674-1686.
  7. Мамчуев М.О. Краевая задача для системы многомерных дифференциальных уравнений дробного порядка // Вестник СамГУ. Естественнонаучная серия. 2008. Т. 67. №8/2. С. 164-175.
  8. Мамчуев М.О. Краевая задача для линейной системы уравнений с частными производными дробного порядка // Челябинский физико-математический журнал. 2017. T. 2. №3. С. 295-311.
  9. Kochubei A.N. Fractional-hiperbolic systems // Fractional Calculus and Applied Analysis. 2013. vol. 16. №4. pp. 860-873.

Для цитирования: Мамчуев М. О. Задача Коши для системы уравнний с частными производными дробного поррядка // Вестник КРАУНЦ. Физ.-мат. науки. 2018. № 3(23). C. 76-82. DOI: 10.18454/2079-6641-2018-23-3-76-82
For citation: Mamchuev M. O. Cauchy problem for the system of equations with partial derivatives of fractional order, Vestnik KRAUNC. Fiz.-mat. nauki. 2018, 23: 3, 76-82. DOI: 10.18454/2079-6641-2018-23-3-76-82

Поступила в редакцию / Original article submitted: 08. 06.2018

  Мамчуев Мурат Османович – кандидат физико-математических наук, старший научный сотрудник, отдел дробного исчисления, Институт прикладной математики и автоматизации, Кабардино-Балкарская Республика, г. Нальчик, Россия.

   Mamchuev Murat Osmanovich – Ph.D. (Phys. & Math.), Senior Researcher, Department of Fractional Calculus, Institute of Applied Mathematics and Automation, Kabardino-Balkar Republic, Nalchik, Russia.

Скачать статью  Мамчуева М.О.

Урок 2. Линейные уравнения с одной переменной и дробными свободными членами

Урок 2. Линейные уравнения с одной переменной и дробными свободными членами

Уравнение, у которого коэффициенты всех или некоторых членов – дробные числа, можно заменить равносильным уравнением с целыми коэффициентами (для этого обе две части уравнения надо умножить на наименьшее общее кратное знаменателей дробных коэффициентов).

ПРИМЕР:


Уравнение

После умножения обоих его частей на  14  получим

(5х – 4) × 7 

= (16х + 1) × 2;

35х – 28 

= 32х + 2.

Легко убедиться в том, что первое и последнее уравнения имеют один корень  х = 10.


Общая схема решения уравнений первой степени.

ПРИМЕР:


Пусть необходимо решить уравнение:

Умножим все члены на наименьшее общее кратное знаменателей, которое равно  12. После сокращения получим:

4(х – 4) + 6(х + 1) – 12 

= 30(х – 3) + 24х

– 2(11х + 43).

Чтобы выделить члены, в которых находятся неизвестные и свободные члены, раскроем скобки:

4х – 16 + 6х + 6 –12 

= 30х – 90 + 24х – 22х – 86.

Сгруппируем в одной части члены, которые содержат неизвестные, а в другой – свободные члены:

4х + 6х – 30х – 24х + 22х 

= –90 – 86 + 16 – 6 + 12.

Приведём подобные члены:

–22х = –154.

Поделим обе части на  –22. Получим:

х = 7.

Как видим, корень можно найти по такой схеме:

 – привести уравнение к целому виду;

 – раскрыть скобки;

 – сгруппировать члены, которые содержат неизвестные, в одной части  уравнения, а свободные члены – в другой;

 – свести подобные члены;

 – решить уравнение вида  ах = b, которое получили после приведения подобных членов.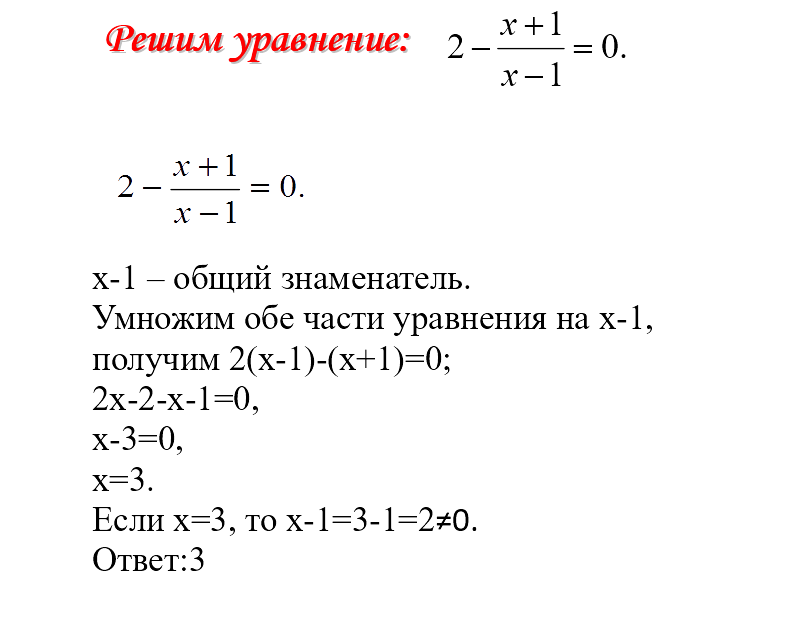

Однако эта схема не обязательна для любого уравнения. Во-первых, при решении многих простых уравнений приходится начинать не с первого, а со второго, третьего и может пятого этапу. Во-вторых, некоторые промежуточные этапы могут оказаться ненужными. В-третьих, иногда бывает выгодно для простоты решения нарушить порядок, указанной схемы.


Задания к уроку 2

  • Задание 1
  • Задание 2
  • Задание 3

Другие уроки:

Следующее Предыдущее Главная страница

Подписаться на: Комментарии к сообщению (Atom)

Как решить методом исключения дробью?

Ответить

Проверено

206,4 тыс.+ просмотров

Подсказка : Мы собираемся объяснить это на примере. Возьмем некоторое линейное уравнение с двумя переменными, которое содержит дроби. При исключении дробей мы исключаем дроби, умножая каждую часть уравнения на общий знаменатель. Теперь мы можем решить полученную систему, используя метод сложения, метод исключения или метод подстановки.

Полный пошаговый ответ :
Теперь рассмотрим систему уравнений с двумя переменными,
 \[\dfrac{1}{4}x + \dfrac{1}{2}y = 8{\ text{ — — — — — (1)}}\]
и \[\dfrac{1}{8}x + \dfrac{1}{6}y = 4{\text{ — — — — — (2 )}}\] .
Нам нужно исключить дроби из обоих уравнений.
Теперь рассмотрим уравнение (1):
 \[\dfrac{1}{4}x + \dfrac{1}{2}y = 8\] умножьте это уравнение на «4» в обеих частях уравнения,
 \ [ \Rightarrow 4 \times \dfrac{1}{4}x + 4 \times \dfrac{1}{2}y = 8 \times 4\]
 \[x + 2y = 32{\text{ — — — — — — — (3)}}\]
Теперь рассмотрим уравнение (2),
 \[\dfrac{1}{8}x + \dfrac{ 1}{6}y = 4\] умножьте это уравнение на «8» в обеих частях уравнения,
 \[ \Rightarrow 8 \times \dfrac{1}{8}x + 8 \times \dfrac{1} {6}y = 1 \times 8\]
 \[ \Rightarrow x + \dfrac{4}{3}y = 8\] .
Но у нас все еще есть дробь в этом уравнении. Итак, мы умножаем «3» на обе части уравнения:
 \[3x + 3 \times \dfrac{4}{3}y = 3 \times 8\]
 \[3x + 4y = 24{\text{ — — — — — — (4)}}\]
Таким образом, мы имеем систему уравнений \[x + 2y = 32\] и \[3x + 4y = 24{\text{ }}\] .
Мы можем решить это, сделав один из коэффициентов переменной одинаковым и вычитая, мы получим требуемый результат,
Имеем, \[3x + 4y = 24{\text{ — — — — — — (4)}}\ ]
Умножаем 3 на уравнение (3) с обеих сторон имеем
 \[3 \times x + 2 \times 3y = 32 \times 3\]
 \[3x + 6y = 96{\text{ — — — — — — — (5)}}\]
Теперь, вычитая уравнение (5) из уравнения (4), мы имеем,
 \[ \Стрелка вправо 3x + 6y — (3x + 4y) = 96 — 24\]
 \[ \Стрелка вправо 3x + 6y — 3x — 4y = 72\]
Отменив переменный член ‘x’, мы получим
 \[ \Стрелка вправо 6y — 4y = 72\]
 \[ \Стрелка вправо 2y = 72\]
Разделить на 2 с обеих сторон,
 \[ \Стрелка вправо y = \dfrac{{72}}{2}\]
 \[ \ Rightarrow y = 36\]
Мы можем получить значение ‘x’, подставив любое из приведенных выше уравнений.
Теперь подставим \[y = 36\] в уравнение (3) и получим
 \[ \Rightarrow x + 2 \times 36 = 32\]
 \[ \Стрелка вправо x + 72 = 32\]
 \[ \Стрелка вправо x = 32 — 72\]
 \[ \Стрелка вправо x = — 40\]
Таким образом, мы имеем значения переменных, \[x = — 40\ ] и \[y = 36\]
Таким образом, правильный ответ «\[x = — 40\] и \[y = 36\]».

Примечание : Все, что мы сделали выше, это преобразовали данную систему уравнений, содержащую дробь, в простую линейную систему уравнений, и мы решили ее. Выполните ту же процедуру для любой заданной пары линейных уравнений с двумя переменными. У нас есть много методов для решения этих уравнений; это метод исключения, метод перекрестного умножения и метод замены. Во всех случаях мы получим один и тот же ответ.

Недавно обновленные страницы

Если ab и c единичные векторы, то left ab2 right+bc2+ca2 математика класса 12 JEE_Main

Стержень AB длиной 4 единицы перемещается горизонтально, когда математика класса 11 JEE_Main

Вычислить значение intlimits0 cos 3xdx A 0 B 1 class 12 maths JEE_Main

Что из следующего верно0002 Координаты точек A и B равны a0 и a0 математическому классу 11 JEE_Main

Если ab и c единичные векторы, то влево ab2 right+bc2+ca2 математическому классу 12 JEE_Main

Стержень AB длиной 4 единицы движется горизонтально, когда class 11 maths JEE_Main

Оценить значение intlimits0pi cos 3xdx A 0 B 1 class 12 maths JEE_Main

Что из следующего верно 1 nleft S cup T right class 10 maths JEE_Main

Какова площадь треугольника с вершинами Левый класс 11 математика JEE_Main

Координаты точек A и B равны a0 и a0 класс 11 математики JEE_Main

Сомнения в тренде проще говоря? Нет? Мы так не думали, но бывают ситуации, когда вам нужно упростить алгебраическую дробь, когда вы начинаете изучать исчисление.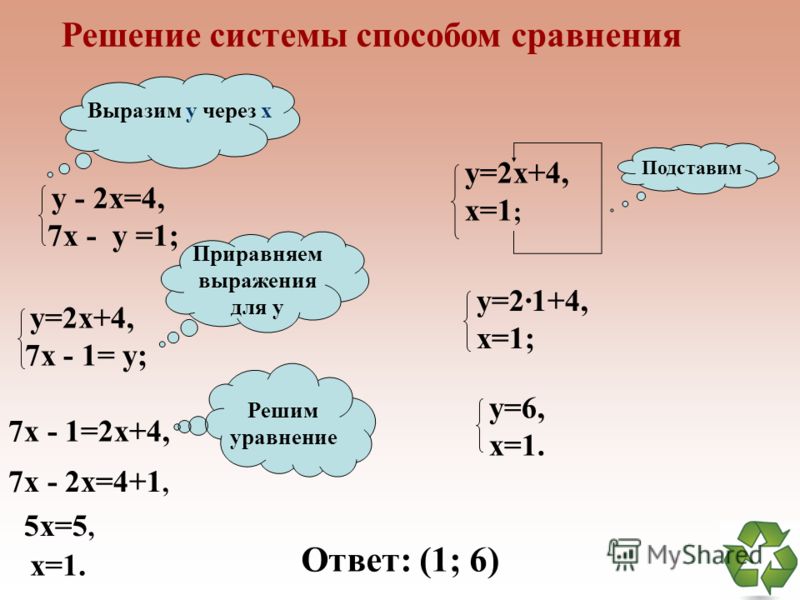 В этом разделе мы научим вас основам упрощения или разложите алгебраическую дробь на более простые суммы.

Здесь вы готовите свой мозг к тому, что грядет. Точно так же, как когда вам нужно было научиться складывать и вычитать, прежде чем вы могли решить алгебраическое уравнение. Начинается подготовка мозга.

Давайте пройдемся по правилам разложения алгебраической дроби. Алгебраическая дробь имеет алгебраическое выражение в числителе и знаменателе, подобное этому:

Разложение неполных дробей: правила

  1. Полностью разложите г ( x ) на множители, если сможете. Храните несколько факторов в экспоненциальной форме.
  2. , если есть факторы, которые выглядят как ( MX + B ) U , Настройка частичных фракций, таких как это:


  3. Если есть факторы, которые выглядят как ( AX 999
  4. , если есть факторы, которые выглядят как ( AX 999999012
  5. . + bx + c ) u , настройте частичные дроби следующим образом:
     

     
  6. Очистите дроби, умножив каждую часть уравнения на знаменатель левой части.
     
  7. Выберите значения x , которые аннулируют члены для решения ваших констант A, B, C и т. д. Подставьте и решите константы в you can. При необходимости повторите этот шаг.
     
  8. Если вы не можете найти константу, выберите другое значение x и задайте систему уравнений.
     
  9. Если вам нужно настроить систему уравнений для решения констант A, B, C и т. д., попробуйте решить с помощью операций с обратной матрицей.
     
  10. Ваш мозг уже разлагается? Надеюсь, нет, только ваши дроби.

Пример задачи

Преобразуйте следующую дробь в термины с константами, используя правила разложения.

Давайте разберем это по частям. Начиная с множителя x 3 внизу, нам понадобится:0098 х + 4).

Наконец, ( x 2 + 1) будут разложены следующим образом: умножение? Мы еще не знаем значения констант ( A или B и т. д.), но следующие несколько примеров задач покажут вам, как найти значения констант.

Пример задачи

Установите термины для частичных дробей, но не находите константы.

Поскольку мы можем немного разложить знаменатель, давайте перепишем нашу дробь.

А теперь (барабанная дробь), уравнение для нашей частичной дроби будет выглядеть так:

Пример задачи

наши настоящие частичные дроби. Мы закончили на этом шаге:

Возвращаясь к нашим инструкциям, нам нужно очистить дроби, умножив каждую сторону на x ( x + 4)( x – 4). Так все будет выглядеть немного проще. (И на этом этапе проще — это хорошо. Возьмем то, что есть.)

x 2 – 8 = A ( x – 4)( x + 4) + В ( х )( х + 4) + С ( х )( x – 4)

Наша цель – выяснить, что такое A, B и C , чтобы записать нашу официальную частичную дробь этой задачи. Нам нравится метод попытки отменить условия. Если x = 4, обратите внимание, что член A и C будет равен 0, так что давайте сначала попробуем это.

Попробуйте x = -4:

Попробуйте x = 0:

Наконец, мы можем записать состав нашей частичной дроби, потому что теперь мы знаем значение констант.

Мы знаем, что это был не простой процесс, но взгляните на правую часть уравнения. Выглядит намного проще, чем левая сторона. В исчислении вы будете находить области функций (интегрирование), а три дроби справа интегрировать гораздо проще, чем сложную алгебраическую дробь слева.

Пример задачи

Используйте частичные дроби, чтобы упростить эту дробь:

Сначала мы запишем наши термины с константами.

Очистка фракции слева, умножив каждую сторону на ( x 2 + 1) 2 , мы получаем:

2 x 2 — 7 = A (9 .

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *