Как решать круги эйлера 7 класс: Решение задач с помощью кругов Эйлера

Множества. Решение задач с помощью кругов Эйлера. 5, 6, 7 класс

Братунова Вера Дмитриевкна,

преподаватель математики и информатики,

Гимназия-детсад им. С. Демиреля, мун. Комрат, АТО Гагауз Ери, Республика Молдова

 

Множества. Решение задач с помощью кругов Эйлера

 

Классы: 5, 6, 7

Ключевые слова: круги Эйлера

 

Пояснительная записка

 

Очень часто решение задачи помогает найти рисунок. Использование рисунка делает решение простым и наглядным.

В данной разработке приведены примеры решения задач с помощью кругов Эйлера. Это не просто занимательная и интересная штука, но и весьма полезный метод решения задач. Они помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.

С данным способом решения задач учащихся можно познакомить как на уроках, так и на кружковых занятиях.

Главной целью этой работы является помощь учителям математики для подготовки учащихся к олимпиадам, а также к экзаменам.

 

Основные понятия

Понятие множества − одно из первичных в математике. Поэтому очень трудно дать ему какое-либо определение, которое бы не заменяло слово «множество» каким-нибудь равнозначным выражением, например, совокупность, собрание элементов и т.д. Элементы множества − это то, из чего это множество состоит, например, каждый ученик вашего класса есть элемент множества школьников.

 

Пересечение множеств в теории множеств — это множество, которому принадлежат те и только те элементы, которые одновременно принадлежат всем данным множествам.

Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Леонардом Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях.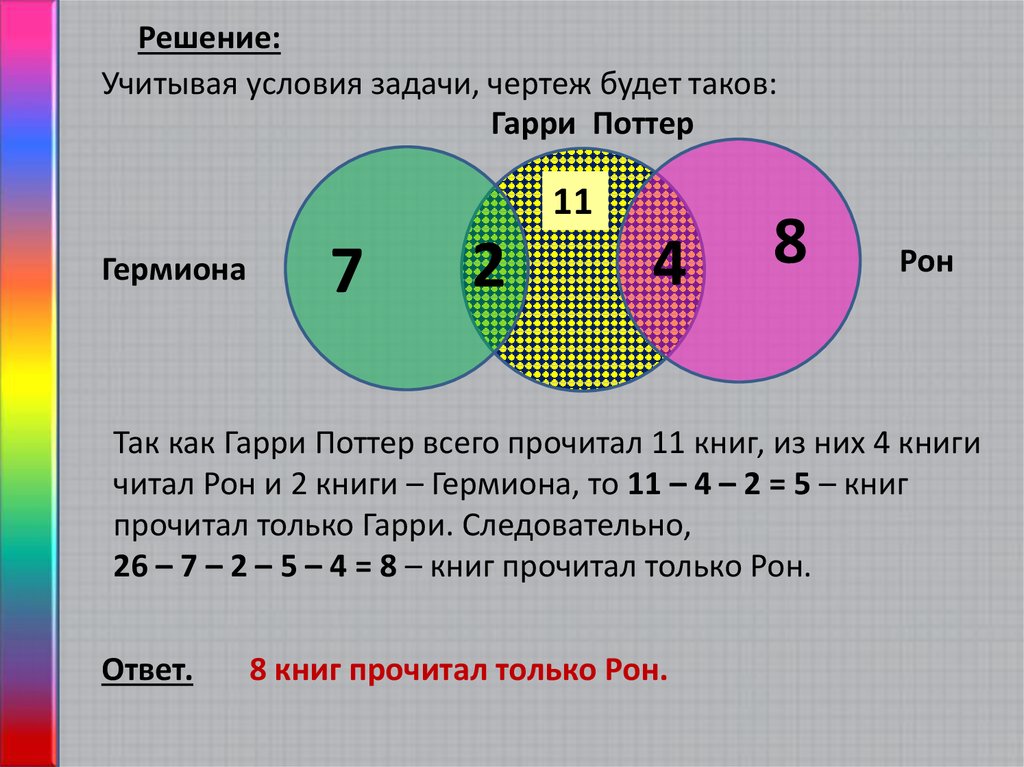

 

2. Решение задач с помощью кругов Эйлера

 

2.1. «Обитаемый остров» и «Стиляги»

Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек — фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?

 

Решение:

Чертим два множества таким образом:

6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств.

1. 15 — 6 = 9 — человек, которые смотрели только «Обитаемый остров»,

2. 11- 6 = 5 — человек, которые смотрели только «Стиляги».

Получаем:

Ответ: 5 человек.

 

2.2. Задача про библиотеки

Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги в школьной библиотеке, 20 — в районной.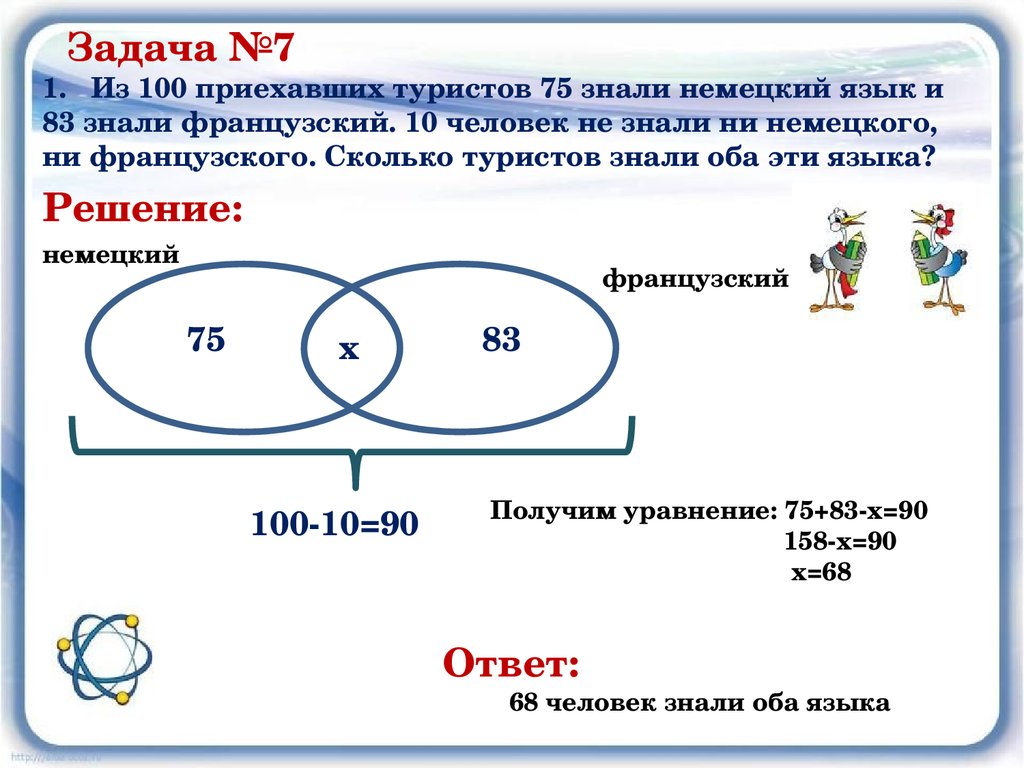

Сколько шестиклассников:

1.     Являются читателями обеих библиотек;

2.     Не являются читателями районной библиотеки;

3.     Не являются читателями школьной библиотеки;

4.     Являются читателями только районной библиотеки;

5.     Являются читателями только школьной библиотеки?

 

Решение:

Чертим два множества таким образом:

1) 20+ 25 — 35 = 10 (человек) — являются читателями обеих библиотек. На схеме это общая часть кругов. Мы определили единственную неизвестную нам величину. Теперь, глядя на схему, легко даем ответы на поставленные вопросы.

2) 35 — 20 = 15 (человек) — не являются читателями районной библиотеки,

3) 35 — 25 = 10 (человек) — не являются читателями школьной библиотеки,

4) 35- 20 = 10 (человек) — являются читателями только районной библиотеки,

5) 35- 20 = 15 (человек) — являются читателями только школьной библиотеки.

Очевидно, что вопросы 2 и 5, а также 3 и 4 — равнозначны и ответы на них совпадают.

Ответ: 10 человек; 15 человек; 10 человек; 10 человек; 15 человек.

 

2.3. Гарри Поттер, Рон и Гермиона

На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал только Рон?

 

Решение:

Учитывая условия задачи, сделаем чертеж:

Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги — Гермиона, то 11 — 4 — 2 = 5 — книг прочитал только Гарри.

Следовательно, 26 — 7 — 2 — 5 — 4 = 8 — книг прочитал только Рон.

Ответ: 8 книг.

 

2.4. Задача про любимые мультфильмы

Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах.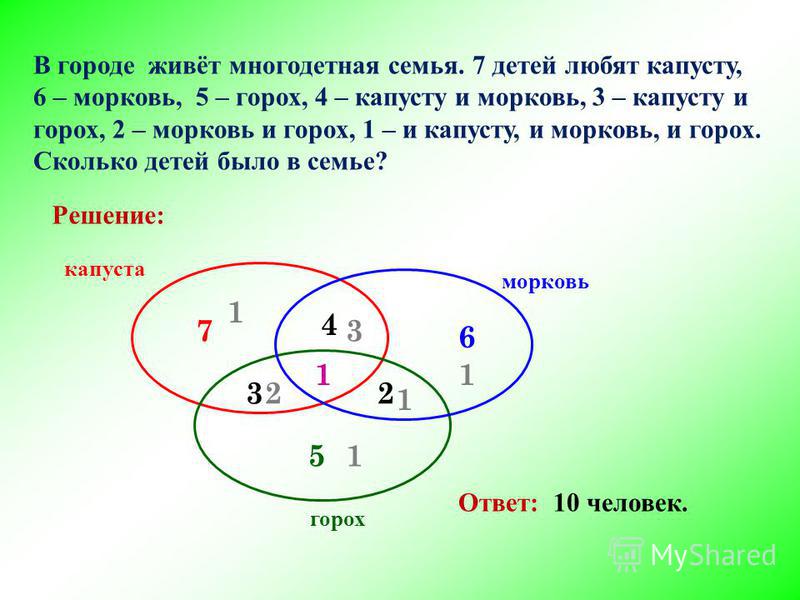 Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок», шестерым — «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма. У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка Боб Квадратные Штаны».

 

Решение:

Чертим три круга, таким образом:

Из условия знаем, что трем ученикам нравиться и «Белоснежка и семь гномов», и «Волк и теленок», шестерым — «Белоснежка и семь гномов» и «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма.

Мы помним, что по условиям задачи среди фанатов мультфильма «Волк и теленок» пятеро ребят выбрали два мультфильма сразу, т.е. 5 — 3 = 2 — ученика выбрали «Волк и теленок» и «Губка Боб Квадратные Штаны».

1) 21 — 3 — 1 — 6 = 11 — учеников выбрали только «Белоснежка и семь гномов»,

2) 13 — 3 — 1 — 2 = 7 — учеников выбрали — «Волк и теленок»,

3) 38 — (11 + 3 + 1 + 2 + 6 + 7) = 8 — ребят выбрали «Губка Боб Квадратные Штаны».

 

 

4) 8 + 2 + 1 + 6 = 17 — человек выбрали мультик «Губка Боб Квадратные Штаны».

Ответ: 17 учеников.

 

2.5. Задача про Крейсер и Линкор

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.

Запрос	Найдено страниц, тыс.
Крейсер и Линкор	7000
Крейсер	4800
Линкор	4500

Какое количество страниц (в тысячах) будет найдено по запросу Крейсер и Линкор? (Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.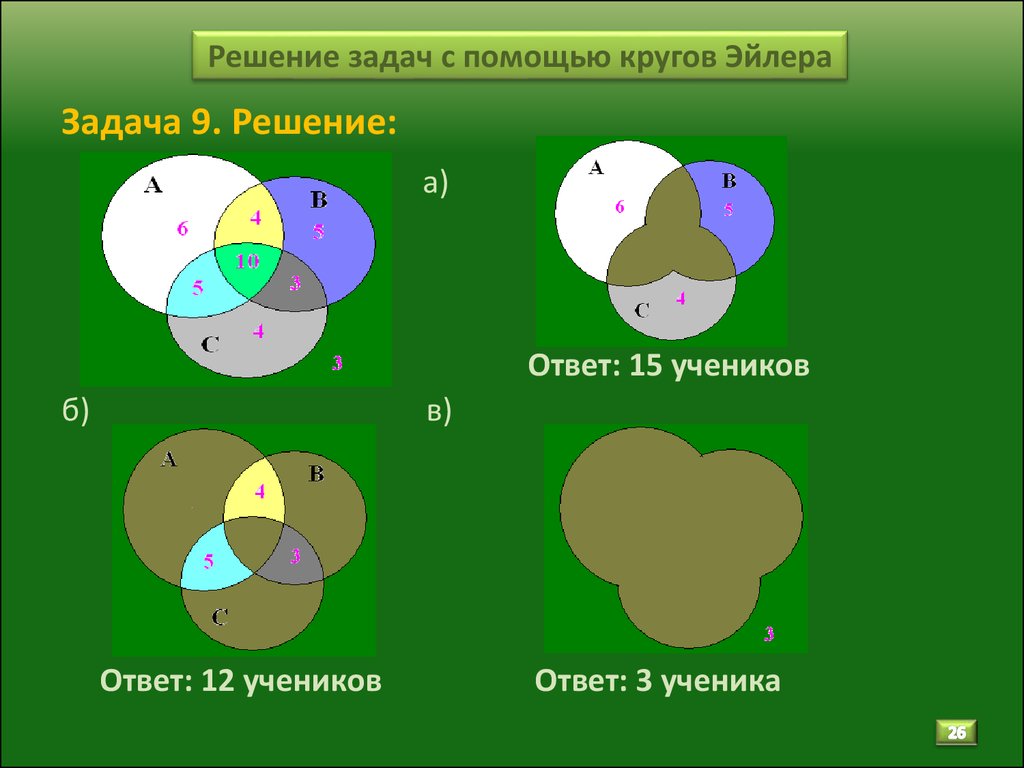

)

 

Решение:

При помощи кругов Эйлера изобразим условия задачи.

1) 4800 + 4500 — 7000 = 2300 (тыс. страниц) — найдено по запросу Крейсер и Линкор,

2) 4800 — 2300 = 2500 (тыс. страниц) — найдено по запросу Крейсер,

3) 4500 — 2300 = 2200 (тыс. страниц) — найдено по запросу Линкор.

Ответ: 2300 тыс. страниц.

 

2.6. Задача про блондинок

Каждый ученик класса — либо девочка, либо блондин, либо любит математику. В классе 20 девочек, из них 12 блондинок, но одна блондинка любит математику. Всего в классе 24 ученика — блондина, математику из них любят 12, а всего учеников (мальчиков и девочек), которые любят математику, 17, из них 6 девочек. Сколько учеников в данном классе?

 

Решение:

Изобразим с помощью кругов Эйлера данные из задачи:

1) 12 — 1 = 11 (учеников) — девочек блондинок,

2) 12 — 1 = 11 (учеников) — блондины и любят математику,

3) 6 — 1 = 5 (учеников) — девочек, которые любят математику,

 

4) 20 — 11 — 1 — 5 = 3 (ученика) — девочки,

5) 24 — 11 — 1 — 11 = 1 (ученик) — блондин,

6) 17- 5 — 1 — 11 = 0 (учеников) — любят математику,

7) 3 + 1 + 0 + 5 + 11 + 11 + 1 = 32 (ученика) — всего в классе.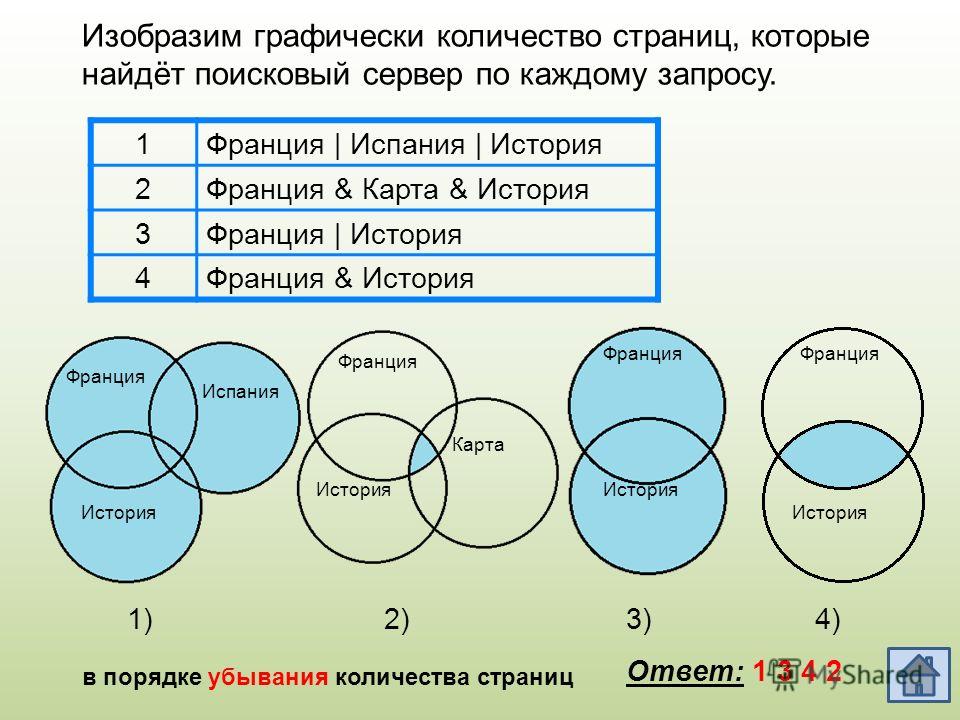

Ответ: 32 ученика.

 

2.7. Задача про кружки

В трёх седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?

 

Решение:

Учитывая условия задачи, сделаем чертеж:

 

1) 10 — 3 = 7 (ребят) — посещают драмкружок и хор,

2) 6 — 3 = 3 (ребят) — поют в хоре и занимаются спортом,

3) 8 — 3 = 5 (ребят) — занимаются спортом и посещают драмкружок,

4) 27 — 7 — 3 — 5 = 12 (ребят) — посещают драмкружок,

5) 32 — 7 3 — 3 = 19 (ребят) — поют в хоре,

6) 22 — 5 — 3 — 3 = 11 (ребят) — увлекаются спортом,

 

7) 70 — (12 + 19 + 11 + 5+ 7 + 3 + 3) = 10 (ребят) — не поют в хоре, не увлекаются спортом и не занимаются в драмкружке.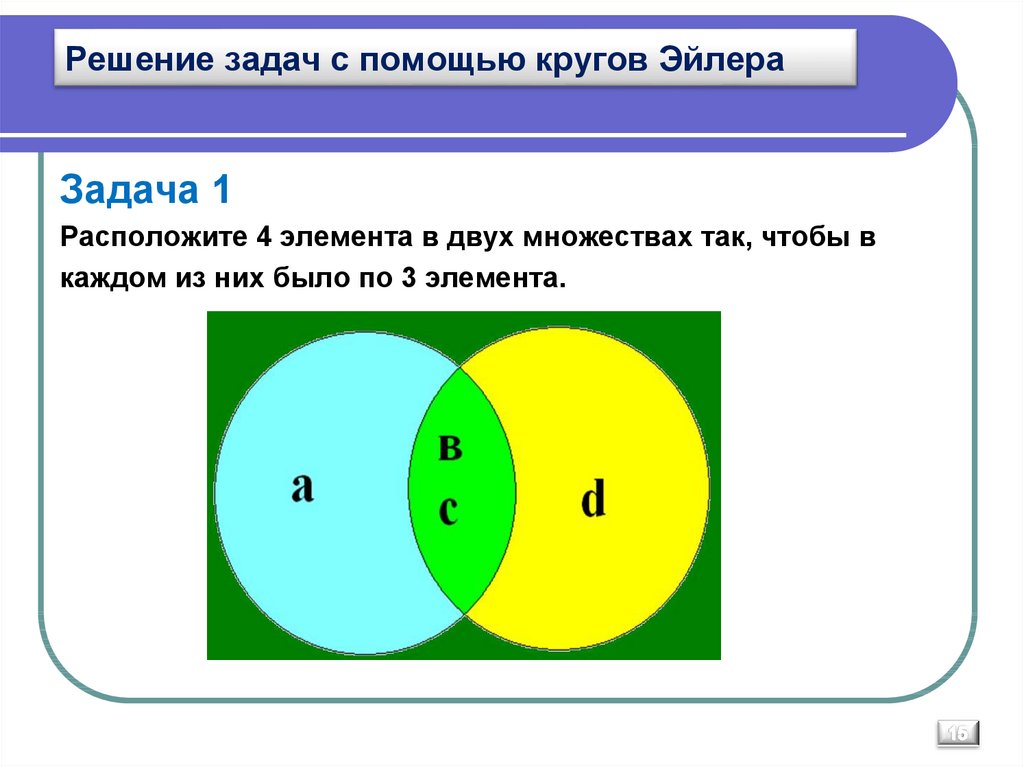

 

Ответ: 10 человек и 11 человек.

 

 

 

 

 

 

 

 

 

Задачи для самостоятельного решения

 

1.     На фирме работают 67 человек. Из них 47 знают английский язык, 35 — немецкий язык, а 23 — оба языка. Сколько человек фирмы не знают ни английского, ни немецкого языков?

2.     Из 40 учащихся нашего класса 32 любят молоко, 21 — лимонад, а 15 — и молоко, и лимонад. Сколько ребят в нашем классе не любят ни молоко, ни лимонад?

3.     12 моих одноклассников любят читать детективы, 18 — фантастику, трое с удовольствием читают и то, и другое, а один вообще ничего не читает. Сколько учеников в нашем классе?

4.     Из тех 18 моих одноклассников, которые любят смотреть триллеры, только 12 не прочь посмотреть и мультфильмы. Сколько моих одноклассников смотрят одни «мультики», если всего в нашем классе 25 учеников, каждый из которых любит смотреть или триллеры, или мультфильмы, или и то и другое?

5.      Из 29 мальчишек нашего двора только двое не занимаются спортом, а остальные посещают футбольную или теннисную секции, а то и обе. Футболом занимается 17 мальчишек, а теннисом — 19. Сколько футболистов играет в теннис? Сколько теннисистов играет в футбол?

6.     В одном классе 25 учеников. Из них 7 любят груши, 11 — черешню. Двое любят груши и черешню; 6 — груши и яблоки; 5 — яблоки и черешню. Но есть в классе два ученика, которые любят все и четверо таких, что не любят фруктов вообще. Сколько учеников этого класса любят яблоки?

7.     В конкурсе красоты участвовали 22 девушки. Из них 10 было красивых, 12 — умных и 9 — добрых. Только 2 девушки были и красивыми, и умными; 6 девушек были умными и одновременно добрыми. Определите, сколько было красивых и в то же время добрых девушек, если я скажу вам, что среди участниц не оказалось ни одной умной, доброй и вместе с тем красивой девушки?

8.     В нашем классе 35 учеников. За первую четверть пятерки по русскому языку имели 14 учеников; по математике — 12; по истории — 23.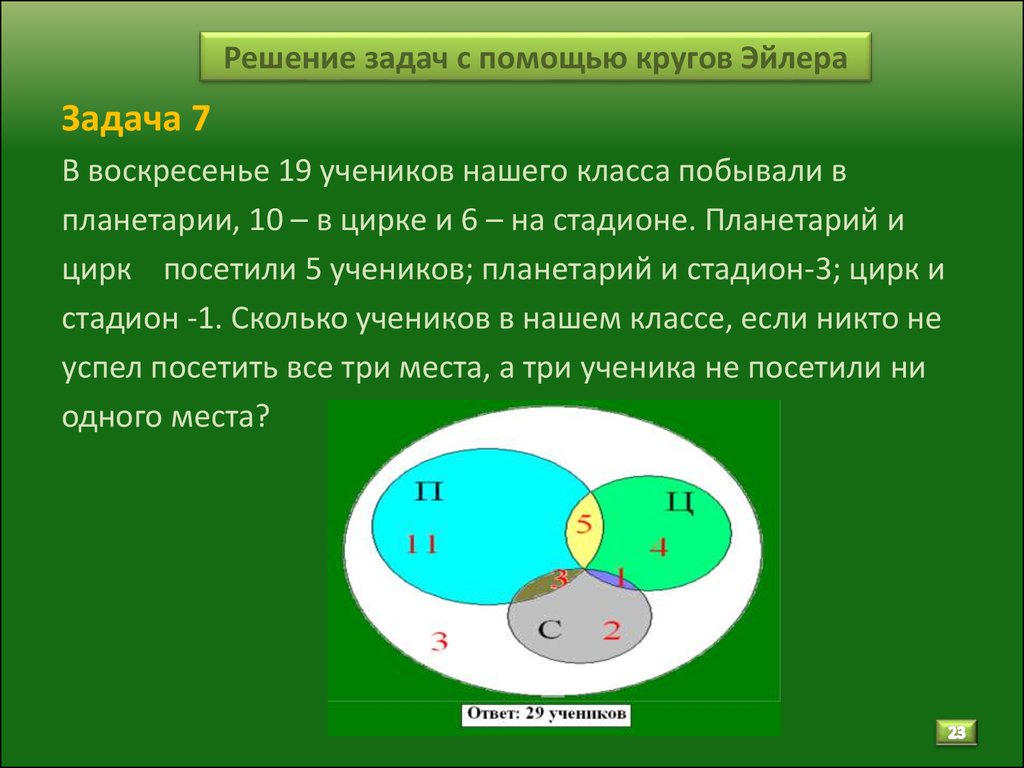 По русскому и математике — 4; по математике и истории — 9; по русскому языку и истории — 5. Сколько учеников имеют пятерки по всем трем предметам, если в классе нет ни одного ученика, не имеющего пятерки хотя бы по одному из этих предметов?

9.     Из 100 человек 85 знают английский язык, 80 — испанский, 75 — немецкий. Все владеют, по крайней мере, одним иностранным языком. Среди них нет таких, которые знают два иностранных языка, но есть владеющие тремя языками. Сколько человек из этих 100 знают три языка?

10. Из сотрудников фирмы 16 побывали во Франции, 10 — в Италии, 6 — в Англии; в Англии и Италии — 5; в Англии и Франции — 6; во всех трех странах — 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них побывал хотя бы в одной из названных стран?

 

Список использованных источников

 

1. Баженов И.И, Порошкин А.Г., Тимофеев А.Ю., Яковлев В.Д. Задачи для школьных математических кружков: учеб. пособие / Сыктывкар: Сыктывкарский университет, 2006.

2. Марков И.С. Новые олимпиады по математике — Ростов н/Д: Феникс, 2005.

3. https://ru.wikipedia.org/wiki/

4. http://logika.vobrazovanie.ru

5. http://www.otvet-prost.ru/load/diskretnaja_matematika/na_krugi_ehjlera/zadacha_na_krugi_ehjlera/18-1-0-22

6. http://urok.1sept.ru/articles/550092/

7. http://www.tutoronline.ru/blog/reshit-zadachu-pomogut-krugi-jejlera

 

6 класс Математика. Решение задач с помощью кругов Эйлера | Презентация к уроку по математике (6 класс):

Конспект урока

6 класс

Предмет: Математика

Тема: Решение задач с помощью кругов Эйлера

Здравствуйте, ребята! Сегодня на занятии мы с вами познакомимся с новым для вас методом решения логических задач — кругами Эйлера. Мы научимся решать некоторые из тех задач, которые входят в группу конкурсных и олимпиадных. Целью нашего урока: является познакомиться с решением простейших логических задач методом кругов.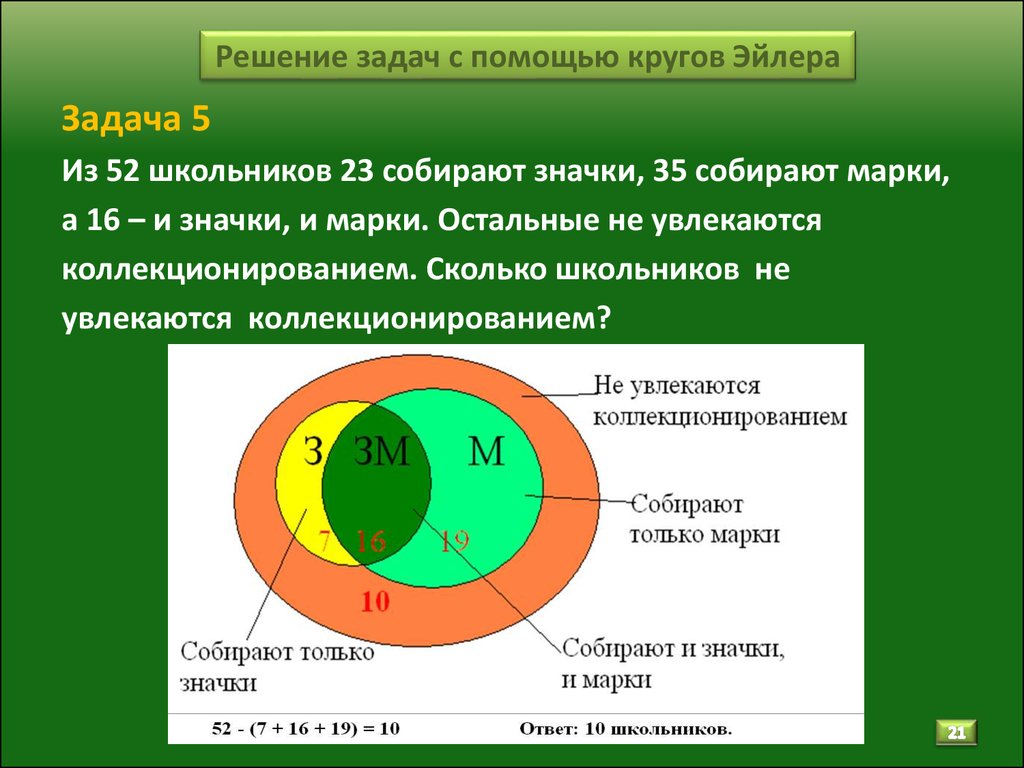

Разминка

 Устно:

1. Кирпич весит 3кги ещё полкирпича. Сколько весит кирпич?
2. Два спортсмена на соревновании пробежали по стадиону 8 кругов. Сколько кругов пробежал каждый?
3. Назовите два числа, разность которых равна их сумме.
4. Сколько будет: два плюс пять умножить на три?

Изучение нового материала

В математике рисунки в виде кругов, изображающих множества, используются очень давно. Одним из первых, кто пользовался этим методом, был выдающийся немецкий математик и философ Готфрид Вильгельм Лейбниц (1646-1716). В его черновых набросках были обнаружены рисунки с такими кругами. Затем этот метод довольно основательно развил и Леонард Эйлер. Он долгие годы работал в Петербургской Академии наук.

Для наглядной геометрической иллюстрации понятий и соотношений между ними используется диаграммы Эйлера-Венна (круги Эйлера). Если имеются какие-либо понятия А, В, С и т.д., то объем каждого понятия (множество) можно представить в виде круга, а отношения между этими объектами (множествами) — в виде пересекающихся кругов.

Перед решением задачи ответьте сначала на следующие вопросы:

1. О скольких множествах идет речь в данной задаче?
2. Какие из перечисленных в задаче данных относятся к разным множествам одновременно?

Задачи разобрать и записать в тетрадь с правильным оформлением: дано, рисунок (круги Эйлера), решение, ответ.

Задача 1. Домашние любимцы. У всех моих подруг есть домашние питомцы. Шестеро из них любят и держат кошек, а пятеро — собак. И только у двоих есть и те и другие. Угадайте, сколько у меня подруг?

Решение: Изобразим два круга, так как у нас два вида питомцев. В одном будем фиксировать владелиц кошек, в другом — собак. Поскольку у некоторых подруг есть и те, и другие животные, то круги нарисуем так, чтобы у них была общая часть. В этой общей части ставим цифру 2 так как кошки и собаки есть у двоих. В оставшейся части «кошачьего» круга ставим цифру 4 (6 — 2 = 4). В свободной части «собачьего» круга ставим цифру 3 (5 — 2 = 3). А теперь рисунок сам подсказывает, что всего у меня 4 + 2 + 3 = 9 подруг.

Ответ. 9 подруг.

Задача 2. Библиотеки. В классе 30 учеников. Все они являются читателями школьной и районной библиотек. Из них 20 ребят берут книги в школьной библиотеке, 15 — в районной. Сколько учеников не являются читателями школьной библиотеки?

Решение: Пусть круг Ш изображает читателей только школьной библиотеки, круг Р — только районной. Тогда ШР — изображение читателей и районной, и школьной библиотек одновременно. Из рисунка следует, что число учеников, не являющихся читателями школьной библиотеки, равно:

(не Шк.биб) = Р — ШР.

Всего 30 учеников,

Ш = 20 человек,

Р = 15 человек.

Тогда значение ШР может быть найдено так (см. рисунок): ШР = (Ш + Р) — 30 = (20 + 15) — 30 =  5, т.е. 5 учеников являются читателями школьной и районной библиотек одновременно.

Тогда (не Шк.биб) = Р — ШР= 15 — 5= 10.

Ответ: 10 учеников не являются читателями школьной библиотеки.

Задача 3. Любимые мультфильмы. Среди школьников пятого класса проводилось анкетирование по любимым мультфильмам. Самыми популярными оказались три мультфильма: «Белоснежка и семь гномов», «Винни Пух», «Микки Маус». Всего в классе 28 человек. «Белоснежку и семь гномов» выбрали 16 учеников, среди которых трое назвали еще «Микки Маус», шестеро — «Винни Пух», а один написал все три мультфильма. Мультфильм «Микки Маус» назвали 9 ребят, среди которых пятеро выбрали по два мультфильма. Сколько человек выбрали мультфильм «Винни Пух»?

Решение: В этой задаче 3 множества, из условий задачи видно, что все они пересекаются между собой. Только «Белоснежку» выбрали 16-6-3-1=6 человек. Только «Микки-Маус» выбрали 9-3-2-1=3 человека.

Только «Винни-Пух» выбрали 28-(6+3+3+2+6+1)=7 человек. Тогда, учитывая, что некоторые выбрали по несколько мультфильмов, получаем, что «Винни-Пух» выбрали 7+6+1+2=16 человек.

Задачи на оценку:

Задача 1. Спортивный класс. В классе 35 учеников. 24 из них играют в футбол, 18 — в волейбол, 12 — в баскетбол. 10 учеников одновременно играют в футбол и волейбол, 8 — в футбол и баскетбол, а 5 — в волейбол и баскетбол. Сколько учеников играют и в футбол, и в волейбол, и в баскетбол одновременно?

Задача 2. Из 40 учащихся нашего класса 32 любят молоко, 21 – лимонад, а 15 – и молоко, и лимонад. Сколько ребят в нашем классе не любят ни молоко, ни лимонад?

Задача 3. 12 моих одноклассников любят читать детективы , 18 – фантастику, трое с удовольствием читают и то, и другое, а один вообще ничего не читает. Сколько учеников в нашем классе?

Домашнее задание:

Задача 1. Хобби. Из 24 учеников 5 класса музыкальную школу посещают 10 человек, художественную школу — 8 человек, спортивную школу — 12 человек, музыкальную и художественную школу- 3, художественную и спортивную школу — 2, музыкальную и спортивную школу — 2, все три школы посещает 1 человек. Сколько учеников посещают только одну школу? Сколько учащихся ни в чем себя не развивают?

 

Математика — это больше, чем соревнования.

Вы старшеклассник, который любит математику? Вы находите традиционную учебную программу по математике слишком простой? Вы хотите изучать увлекательную и сложную математику? Вы хотите работать над задачами и подружиться с математически мыслящими сверстниками? Если это так, вы пришли в нужное место!

What

Euler Circle — математический институт для продвинутых студентов, любящих математику. Мы предлагаем ряд занятий по математике на уровне колледжа, специально адаптированных к потребностям старшеклассников, многие из которых исчерпали учебную программу по математике в своих школах и хотят узнать больше. Каждый предлагаемый нами курс эквивалентен уроку математики в колледже. На каждом занятии учащиеся решают множество задач, чтобы ознакомиться с новым материалом, а на продвинутых занятиях каждый учащийся пишет пояснительную работу по теме, связанной с материалом занятия.

Классы устроены таким образом, чтобы обеспечить путь к независимым исследованиям. Многие из наших наборов задач в продвинутых классах включают нерешенные проблемы, которые учащиеся могут исследовать после того, как освоят материал, представленный в классе. Мы предлагаем встречи в небольших группах для студентов, заинтересованных в работе над исследовательскими проблемами, после того, как они продемонстрировали способность усердно работать над сложными задачами. Подробнее об исследованиях см. в круге Эйлера.

Почему

Математика — это больше, чем соревнования. Тем не менее, у старшеклассников мало ресурсов, чтобы узнать об остальном чудесном мире математики. Мы считаем, что многие студенты хотели бы увидеть, что еще есть, и мы хотим поделиться тем, что знаем.

Когда/где

Прием заявок на летние и осенние курсы. Осенние занятия можно будет посещать онлайн или лично в Пало-Альто. Все летние занятия пройдут онлайн. Таким образом, студенты со всего мира могут подать заявку.

Летом у нас будет два продвинутых класса. На первой летней сессии у нас будет независимый класс по исследованию и написанию статей, а на второй летней сессии у нас будет класс по математике Эйлера. Летние занятия будут проходить полностью онлайн.

Осенью у нас будет промежуточный класс по переходу к доказательствам в теории чисел, класс между средним и продвинутым уровнем по основам высшей математики с упором на линейную и абстрактную алгебру и продвинутый класс по теории чисел. Занятия будут проходить в гибридном очном и онлайн-формате, поэтому подавать заявки могут студенты со всего мира.

Вот даты и время летних занятий:

Класс	Дата начала	Дата окончания	раза
Независимые исследования и написание статей	12 июня	14 июля	Понедельник, вторник, четверг и пятница с 17:00 до 19:00
Математика Эйлера	17 июля	18 августа	Понедельник, вторник, четверг и пятница с 17:00 до 19:00

Заявки на летние курсы принимаются 9 апреля . После этого мы продолжим принимать заявки, пока места остаются на постоянной основе. Нажмите здесь, чтобы подать заявку!

Вот даты и время осенних занятий:

Класс	Дата начала	Дата окончания	Все	Онлайн	Лично
Переход к доказательствам	25 сентября	6 декабря	Понедельник 17:00–18:00	Вторник 17:00–19:00	Среда 18:30–20:30
Основы высшей математики	25 сентября	6 декабря	Понедельник 17:00–18:30 (ориентировочно)	Среда 17:00–19:00 (ориентировочно)	Среда 18:30–20:30
Углубленная теория чисел	25 сентября	6 декабря	Понедельник 18:30–20:30	Вторник 17:00–19:00	Среда 18:30–20:30

Заявки на осенние занятия принимаются 30 июля . После этого мы продолжим принимать заявки, пока места остаются на постоянной основе. Нажмите здесь, чтобы подать заявку!

Нажмите здесь, чтобы подписаться на рассылку!

2.3: диаграммы Венна и диаграммы Эйлера

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

4871

• Памини Тангараджа
• Университет Маунт-Ройял

При работе с множествами и их операциями часто полезно использовать диаграммы Венна:

Пример \(\PageIndex{1}\): \((A \cap B) \cap C\)

Рассмотрим \((A \cap B) \cap C\):

Пример \(\PageIndex{2}\): \((A \cap B) \cup C\)

Рассмотрим \( (A \cap B) \cup C\):

Теперь рассмотрим \((A \cup C) \cap (B \cup C)\):

Пример \(\PageIndex{3}\ ):

Рассмотрим \(A\) ^c \(\cup B\):

Пример \(\PageIndex{4}\):

Рассмотрим \(A\) ^c \(\ крышка (B \чашка C)\):

Другое использование диаграмм Венна иллюстрирует следующий результат:

Определение: Термин

Пусть \( n(A)=\) число элементов множества \(A. \). Тогда для любых двух конечных множеств \(A\) и \(B,\) \(n(A \cup B)= n(A)+n(B)-n(A \cap B).\)

 

Пример \(\PageIndex{5}\):

Был проведен опрос 150 студентов первого курса университета. 40 из них специализировались на математике, 30 из них специализировались на английском языке, 20 специализировались на естественных науках, 7 имели двойную специализацию по математике и английскому языку, и ни у кого не было двойной (тройной) специальности по естествознанию. У скольких студентов были специальности, отличные от математики, английского языка или естественных наук?

Давайте для начала воспользуемся диаграммой Венна, хорошо?

Итак, мы знаем, что \(n = 150\), и мы можем подсчитать, сколько студентов мы учитываем в настоящее время:

\[s = \Sigma \{23 + 33 + 20 + 7\} = 83\]

Используя это, мы можем вычислить, сколько студентов мы еще не подсчитали:

\[150 — 83 = 67.\]

Итак, 67 студентов имели специальности, не входящие в наши три категории.

Пример \(\PageIndex{6}\):

Предположим, группу студентов в кампусе колледжа попросили сравнить несколько анимационных фильмов будущего, и они получили следующую информацию.

• 37 нравится «Красавица и Чудовище»
• 26 Нравится «Босс-молокосос»
• 25 Нравится «Король Лев»
• 16 лайков «Красавица и чудовище» и «Босс-молокосос»
• 12 лайков «Красавица и чудовище» и «Король Лев»
• 10 лайков «Босс Бэби» и «Король Лев»
• 4 нравятся все три фильма
• 5 не нравится ни один из этих фильмов.

1. Скольким студентам понравился только «Король Лев»?
2. Скольким студентам понравились только два фильма?
3. Сколько студентов было опрошено?

Давайте воспользуемся диаграммой Венна, чтобы разобраться:

Здесь мы знаем общее количество голосов, полученных за каждый фильм, но некоторые люди могли проголосовать дважды! Итак, используя данные, сначала заполним пересекающиеся участки:

Теперь мы можем использовать данные, чтобы заполнить остальные, прежде чем отвечать на вопросы. Не забудьте включить в \(U\) тех, кто не попадает ни в одну другую категорию:

Теперь, когда у нас есть четкая картина, мы можем начать отвечать на вопросы:

1. Сколько студентов понравился только «Король Лев»?

Итак, наш ответ: «Семи студентам понравился только «Король Лев».

2. Скольким студентам понравились только два фильма?

Наш ответ: \(8 + 6 + 12 = 26\) (сумма трех выделенных разделов), поэтому «26 студентам понравились только два фильма».

3. Каково было общее количество опрошенных студентов?

Начнем со сложения значений каждой секции:

\(n = \Sigma \{7, 4, 13, 6, 12, 8, 4, 5\} = 59\)

Итак, наш ответ: «Было опрошено 59 студентов».

Резюме

Пусть \( n(A)=|A|=\) количество элементов в множестве \(A.\) Тогда для любых двух множеств \(A\) и \(B,\) \( n(A \чашка B)=n(A)+n(B)-n(A \cap B).\)

Диаграмма Эйлера

Диаграмма Эйлера показывает соответствующие отношения между наборами, а диаграмма Венна показывает все возможности.