Площадь поверхности цилиндра
Не откладывайте! ЗАГОВОРИТЕ на Английском!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2015-01-15
Площадь поверхности цилиндра. В этой статье мы рассмотрим задания связанные с площадью поверхности цилиндра. На блоге уже рассмотрены задания с таким телом вращения как конус. Цилиндр тоже относится к телам вращения. Что требуется и нужно знать о площади поверхности цилиндра? Давайте посмотрим на развёртку цилиндра:
Верхнее и нижнее основание это два равных круга:
Боковая поверхность это прямоугольник. При чём одна сторона этого прямоугольника равна высоте цилиндра, а другая длине окружности основания. Напомню, что длина окружности равна:
Итак, формула поверхности цилиндра:
*Учить эту формулу не нужно! Достаточно знать формулы площади круга и длины его окружности, тогда вы всегда сможете записать указанную формулу. Важно её понимание! Рассмотрим задачи:
Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту и площадь поверхности цилиндра (считайте, что число Пи равно 3,14 и результат округлите до десятых).
Площадь боковой поверхности равна 6. Найдите высоту и площадь поверхности цилиндра (считайте, что число Пи равно 3,14 и результат округлите до десятых).
Площадь полной поверхности цилиндра:
Даны длина окружности основания и площадь боковой поверхности цилиндра. То есть, нам дана площадь прямоугольника и одна его сторона, требуется найти другую сторону (это есть высота цилиндра):
Требуется радиус и тогда мы сможем найти указанную площадь.
Длина окружности основания равна трём, тогда запишем:
Таким образом
Округляем до десятых, получаем 7,4.
Ответ: h = 2; S = 7,4
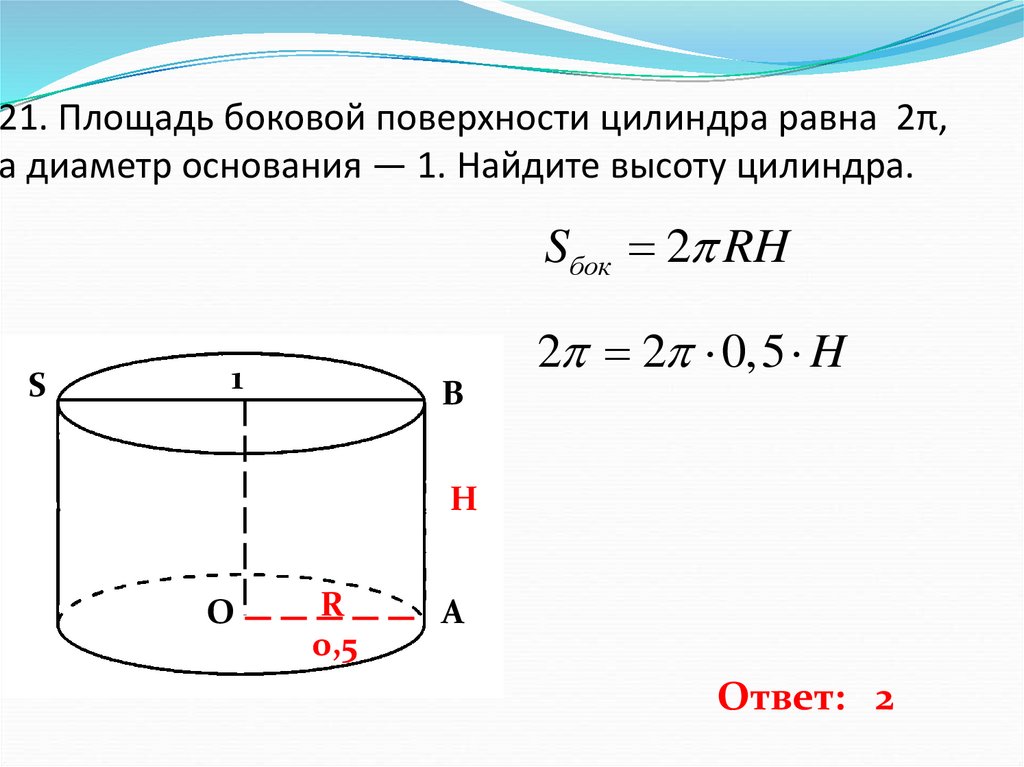
Площадь боковой поверхности цилиндра равна 72Пи, а диаметр основания — 9. Найдите высоту цилиндра.
Площадь боковой поверхности цилиндра находится по формуле:
Значит
Ответ: 8
Площадь боковой поверхности цилиндра равна 64Пи, а высота — 8 . Найдите диаметр основания.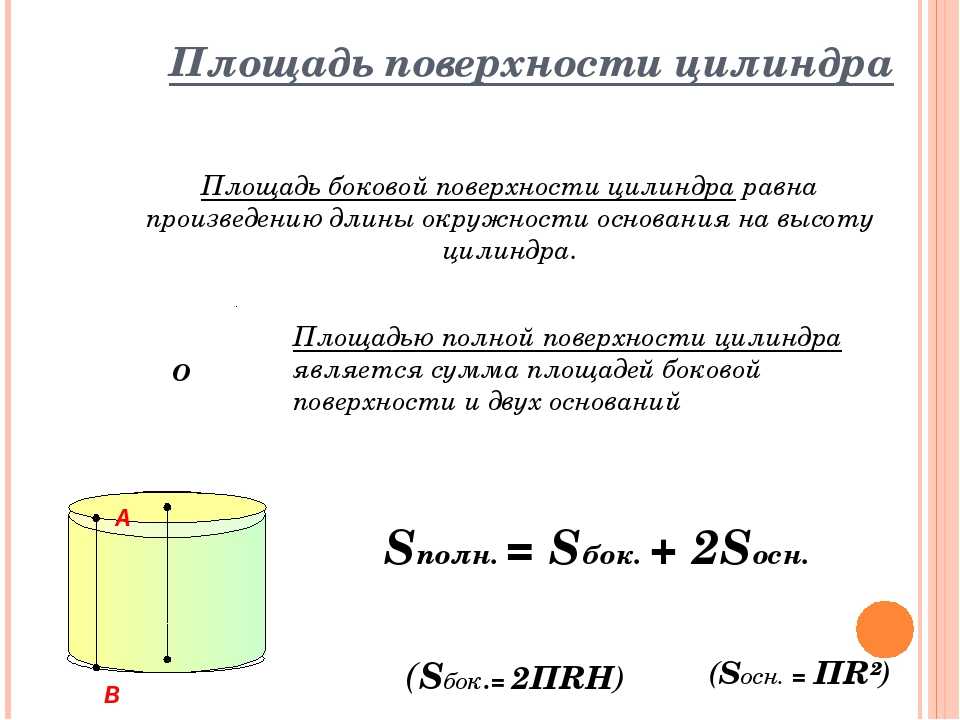
Площадь боковой поверхности цилиндра находится по формуле:
Найдём радиус основания и далее определим диаметр:
Диаметр равен двум радиусам, значит:
Ответ: 8
27058. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на Пи.
Посмотреть решение
27133. Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.
Посмотреть решение
27173. Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндра, деленную на Пи.
Посмотреть решение
284361. Площадь боковой поверхности цилиндра равна 2Пи, а диаметр основания — 1. Найдите высоту цилиндра.
Посмотреть решение
284362. Площадь боковой поверхности цилиндра равна 2Пи, а высота — 1. Найдите диаметр основания.
Посмотреть решение
Будет ещё пару статей с цилиндрами, не пропустите!
На этом всё. Успеха Вам!
Успеха Вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Категория: Стереометрия КОНУС ЦИЛИНДР | ЕГЭ-№2Площадь
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Как найти площадь поверхности цилиндра? – Обзоры Вики
Формула для расчета общей площади поверхности цилиндра представляет собой общую площадь поверхности цилиндра. = 2u03c0r(ч + г), а формула площади криволинейной поверхности цилиндра: площадь криволинейной/боковой поверхности цилиндра = 2u03c0rh, где «r» — радиус основания, а «h» — высота цилиндра.
Отсюда, какова формула площади поверхности? переменные:
| Формула площади поверхности | Значение площади поверхности |
|---|---|
| SA = 2B + Ph | Найдите площадь каждого лица. Сложите все области. Сложите все области. |
| SA = B + 12sP | Найдите площадь каждого лица. Сложите все области. |
| СА=2B+2u03c0rh | Найдите площадь основания, умноженную на 2, затем добавьте площади к площадям прямоугольника, равным длине окружности, умноженной на высоту. |
• 17 сентября 2020 г.
Какая формула цилиндра? Формула объема цилиндра: V = Bh или V=u03c0r2h . Радиус цилиндра 8 см, высота 15 см. Подставьте 8 вместо r и 15 вместо h в формуле V=u03c0r2h . V=u03c0(8)2(15) Упростить.
Дополнительно Как найти площадь поверхности и объем цилиндра? То, что нужно запомнить
- Площадь цилиндра = 2πr 2 + 2πрч.
- Объем цилиндра = πr 2 h.
- Вам нужно знать радиус и высоту, чтобы определить как объем, так и площадь цилиндра.
- Ответы на проблемы с объемом всегда должны быть в кубических единицах.
- Ответы на проблемы с площадью поверхности всегда должны быть в квадратных единицах.
 2) + (2*пи*г*л).
2) + (2*пи*г*л).Что такое Пи в цилиндре? Если у нас есть цилиндр с радиусом r и высотой h, объем V цилиндра равен: V = πr2h. где π — число, приблизительно равное 3.14.
Чему равна полная площадь правого цилиндра? Формула площади поверхности правильного кругового цилиндра
⇒ Общая площадь поверхности (TSA) = 2πр + 2πr2 = 2πr (h + r) квадратных единиц.
Какова площадь криволинейной поверхности цилиндра?
Радиус r цилиндра — это радиус его основания. Теперь площадь прямоугольника = длина × ширина. 2πr — длина окружности, а h — высота. Площадь криволинейной поверхности будет = 2πr × ч = 2πrh.
Также по какой формуле находится объем полого цилиндра? В случае полого цилиндра мы измеряем два радиуса, один для внутренней окружности и один для внешней окружности, образованной основанием полого цилиндра. Предположим, г1 и R2 — два радиуса данного полого цилиндра с высотой h, тогда объем этого цилиндра можно записать как; V = πh (r12 — р22)
Как найти площадь поверхности числа пи?
Площадь круга равна пи умножить на квадрат радиуса (А = π r²).

Сколько поверхностей у цилиндра?
Теперь у нас есть три поверхности, круглая плоская поверхность вверху, круглая плоская поверхность внизу и изогнутая поверхность спереди. Следовательно, общее количество поверхностей в цилиндре равно 3.
Сколько плоских поверхностей у цилиндра?
Цилиндр имеет два ровные или плоские поверхности, равные по площади, соединяются с изогнутой трубчатой (неплоской) поверхностью по ее высоте.
Что такое плоская часть цилиндра? Цилиндр имеет два плоских конца в форме кругов. Эти две грани соединены изогнутой гранью, похожей на трубку. Если вы сделаете плоскую сетку для цилиндра, она будет выглядеть как прямоугольник с кружками на каждом конце.
Что такое плоская поверхность? Поверхность, которая не изогнута.
Сколько плоских и изогнутых поверхностей у цилиндра?
Цилиндр имеет 2 плоские поверхности и одна изогнутая поверхность.

Сколько углов в цилиндре? Цилиндр можно рассматривать как фигуру с тремя гранями, двумя изогнутыми краями и ноль углов.
Является ли сфера плоской поверхностью?
Форма сферы
Сфера представляет собой геометрическое трехмерное тело, имеющее криволинейную поверхность. Как и другие твердые тела, такие как куб, прямоугольный параллелепипед, конус и цилиндр, сфера не имеет ни плоской поверхности, ни вершины, ни край.
Является ли круг плоской поверхностью? Все эти геометрические фигуры имеют грани. Мы узнали о лицах, таких как треугольное лицо, прямоугольное лицо, квадратное лицо и круглое лицо. Все эти лица плоский но некоторые кривые. Цилиндр, шар, конус и т.д. имеют изогнутые лица.
Сколько плоских поверхностей у шара?
Лицо — это плоская или изогнутая поверхность трехмерной фигуры. Например, у куба шесть граней, у цилиндра — три, а у сферы — только один.
Сколько поверхностей у конуса? У шара нет граней, у конуса есть одно круглое лицо, а цилиндр имеет две круговые грани.

Сколько ребер в цилиндре?
Цилиндр имеет 2 ребра. Цилиндр имеет 2 грани и 1 криволинейную поверхность.
Нахождение объема и площади поверхности цилиндра
В геометрии цилиндр представляет собой трехмерную объемную фигуру, состоящую из двух параллельных круглых оснований, соединенных криволинейной поверхностью, расположенной на определенном расстоянии от центра цилиндра. Например, рулоны туалетной бумаги, пластиковые банки для холодных напитков являются примерами цилиндров. Цилиндр характеризуется двумя основными свойствами: площадью поверхности и объемом. Слово «цилиндр» происходит от латинского (Cylindrus) слова, означающего «рулон», «ролик» и «тумблер».
Определение цилиндра
Цилиндр представляет собой трехмерное твердое тело, содержащее два параллельных основания, удерживаемых вместе изогнутой поверхностью на фиксированном расстоянии. Основания цилиндра обычно имеют круглую форму, похожую на круг. Основания удерживаются вместе отрезком линии, который называется осью.
 Расстояние от этого отрезка до внешней поверхности цилиндра называется радиусом. Это можно обозначить буквой «р». Перпендикулярное расстояние между основаниями цилиндра называется высотой цилиндра, обозначаемой буквой «h».
Расстояние от этого отрезка до внешней поверхности цилиндра называется радиусом. Это можно обозначить буквой «р». Перпендикулярное расстояние между основаниями цилиндра называется высотой цилиндра, обозначаемой буквой «h».Части цилиндра
Считается, что цилиндр состоит из 2 кругов + 1 прямоугольник. На следующем рисунке показано образование цилиндра:
Типы цилиндров
Геометрия состоит из четырех типов цилиндров, а именно:
- Эллиптический цилиндр: Цилиндр, образующий эллипс, называется эллипсом.
- Правый круговой цилиндр: Правый круговой цилиндр содержит оси двух параллельных прямых, перпендикулярных центру основания.
- Наклонный цилиндр: Наклонный цилиндр — это цилиндр, стороны которого опираются на основание. В косом цилиндре стороны не перпендикулярны центру основания. Пизанская башня — реальный пример наклонного цилиндра.

- Прямой круглый полый цилиндр или цилиндрическая оболочка: Также называется цилиндрической оболочкой, содержит два правильных круглых цилиндра, ограниченных одной стороной с другой. Точка оси является общей для пересечения и перпендикулярна центральному основанию. Поскольку внутри цилиндра имеется некоторое пространство, он полый изнутри.
Формулы цилиндра
Цилиндр связан с тремя формулами, находящими применение к площади и объему:
- Площадь боковой поверхности или площадь криволинейной поверхности
- Общая площадь поверхности
- 90 Объем цилиндра 90 Площадь боковой поверхности или площадь изогнутой поверхности цилиндра
Площадь изогнутой поверхности также называется площадью боковой поверхности. Площадь, образованная изогнутой поверхностью цилиндра, т. е. пространство, занимаемое между двумя параллельными круглыми основаниями, известна как CSA. Формула для CSA дается как:
Площадь криволинейной поверхности (CSA) = 2πrh квадратных единиц
Здесь h — высота, а r — радиус
Общая площадь поверхности цилиндра
Из общей площади поверхности цилиндра мы вычисляем площадь криволинейной поверхности и площадь двух кругов.

Общая площадь поверхности цилиндра определяется как общая площадь, занимаемая им. Цилиндр состоит из двух окружностей и изогнутого листа. Общая площадь поверхности цилиндра может быть рассчитана путем комбинации площади криволинейной поверхности и площади двух кругов.
Площадь криволинейной поверхности (CSA) = окружность круга × высота
C.S.A = 2r × h
Площадь круга = πr круг)
Мы знаем,
Площадь криволинейной поверхности = 2πrh
Площадь круга = πr 2
Полная площадь поверхности (TSA) = 2πrh + 2πr2(r)4(
3 r)4 единицы измерения.
Так как кругов два, расчет производится путем умножения на 2.
где h — высота, r — радиус цилиндра.
Объем цилиндра
Объем цилиндра определяется плотностью или объемом занимаемого им пространства.
Имеем,
Объем цилиндра = Площадь круга × высота
Так как площадь круга = πr 2
Объем = πr 2 × h , V = πr 2 ч кубических единиц
, где h — высота, а r — радиус цилиндра.

Примеры задач
Вопрос 1: Вычислите общую площадь поверхности цилиндра с радиусом 5 см и высотой 10 см?
Решение:
Поскольку мы знаем, что
Полная площадь поверхности цилиндра, A = 2πr(r+h) квадратных единиц
Следовательно, A = 2π × 5(5 + 10) = 2π × 5(15)
= 2π × 75 = 150 × 3,14
= 471 см 2
Вопрос 2: Каков объем емкости для воды цилиндрической формы высотой 7 см и диаметром 10 см?
Решение:
Дано,
Диаметр сосуда = 10 см
Таким образом, радиус сосуда = 10/2 = 5 см формула,
Объем цилиндра = πr 2 ч кубических единиц.
Следовательно, объем данного контейнера, V = π × 52 × 7
V = π × 25 × 7 = (22/7) × 25 × 7 = 22 × 25
V = 550 см 3
радиус эквивалентен 5 дюймам.
 Банка содержит 1 галлон масла. Найдите высоту цилиндра .
Банка содержит 1 галлон масла. Найдите высоту цилиндра . Решение:
Объем V определяется как 1 галлон
1 галлон = 231 кубический дюйм
Радиус r = 5 дюймов
Объем f цилиндра определяется как0003
V = πr 2 ч
231 = 22/7 × (5) 2 × ч
(231 × 7)/(22 × 25) = ч
ч = 2,94 дюйма.
Таким образом, высота эквивалентна 2,94 дюйма.
Вопрос 4. Резервуар для воды имеет радиус 40 дюймов и высоту 150 дюймов. Найдите площадь.
Решение:
Резервуар для воды имеет цилиндрическую форму.
Общая площадь поверхности цилиндра определяется как 2πr(h+r)
TSA = 2 × 22/7 × 40(150 + 40)
TSA = 2 × 22/7 × 7600
TSA = 47 771,42 кв. дюйма
Площадь = 47 771,42 кв. дюйма.
Вопрос 5. Найдите объем цилиндра, имеющего радиус 5 единиц и высоту 8 единиц?
Решение:
Имеем,
Радиус,r = 5 ед.

Высота,h = 8 ед.
В = (22/7) × 5 2 × 8
В = 22/7 × 25 × 8
В = 628,57 кубических единиц.
Отсюда объем цилиндра равен 628,57 кубических единиц.
Площадь поверхности цилиндра: формула и примеры
Давайте узнаем, как определить площадь поверхности цилиндра .
Что такое цилиндр?
Цилиндр представляет собой трубчатый объект с двумя круглыми основаниями одинакового размера, параллельными прямыми сторонами и круглым или овальным поперечным сечением. высота — это расстояние между двумя основаниями, а радиус — это расстояние от центра основания до любой точки на том же основании. Примерами объектов цилиндрической формы являются банки из-под газировки и трубы.
Связанные материалы: Объем цилиндра – формула и примеры
Как найти площадь поверхности цилиндра :основания и площадь прямоугольной поверхности, выраженные в этой формуле.

SA=2πr 2 +2πrh, где h=рост и π = 3,14
Площадь поверхности (SA или S) измеряется в квадратных единицах, таких как квадратные метры (м 2 ), квадратные сантиметры (см 2 ) и квадратных дюймов (в 2 ).
Чтобы лучше понять площадь поверхности цилиндра, представьте банку газировки с развернутой этикеткой или оберткой. Распространение метки дает нам прямоугольник (см. иллюстрацию ниже). Как вы помните, длина окружности
(C = 2πr) относится к изогнутой длине окружности, поэтому «разгибание» оснований (метки) даст вам длину прямоугольника. Ширина прямоугольника равна высоте цилиндра.Теперь, когда у вас есть длина прямоугольника (2πr) и ширина (h), , вы можете вычислить его площадь, умножив их на (2πr x h) , но это не даст вам общую площадь поверхности прямоугольника. цилиндр.
Чтобы найти общую площадь поверхности цилиндра, сложите площади двух кругов и площади прямоугольника, как показано на рисунке выше.
 Вот как была выведена формула:
Вот как была выведена формула:S=Площадь основания 1+Площадь основания 2+Площадь прямоугольника 2πr) (h)
S=2r 2 +2πrh где: r2=площадь круга или основания; 2πr=длина поверхности, полученной из окружности окружности; h=высота цилиндра или ширина поверхности
Вот краткое руководство по нахождению площади поверхности цилиндра :
Шаг 1. Запишите указанные числа. Вам понадобится радиус и высота цилиндра. Убедитесь, что все единицы измерения одинаковы. Если нет, преобразуйте любой из них, чтобы он соответствовал другому.
Шаг 2. Подставьте цифры в формулу.
Шаг 3. Выполните операции. Не забудьте указать единицу локтя вместе с ответом.
Пример 1: Найдите площадь поверхности цилиндра, зная высоту и радиус
Найдите площадь поверхности цилиндра ниже.
Решение для примера 1:
Сначала запишите данные числа: радиус (r = 2 м) и высота (h = 3 м) .

Затем подставьте в уравнение 2 м вместо r и 3 м вместо ч .
S = 2πr 2 + 2πrh
S = 2π(2m) 2 +2π(2m)(3m)
Наконец, упростим.
S = 2π (4M 2 ) + 2π (6M 2 )
S = 62,83… M 2
Следовательно, площадь — около 62,83 м 2 6.
Пример 2. Найдите площадь поверхности цилиндра, зная высоту и радиус
Найдите площадь поверхности цилиндра ниже.
Решение для примера 2:
Во-первых, запишите данные числа: диаметр (d = 3 м) и высота (h = 125 см) . Напомним, что формула требует радиуса, а не диаметра. Итак, разделите диаметр (3 м) на 2, чтобы найти радиус.
r = d/2 = 3 м/2 = 1,5 м
Затем преобразуем высоту (125 см) в , чтобы она соответствовала единице измерения радиуса (м).


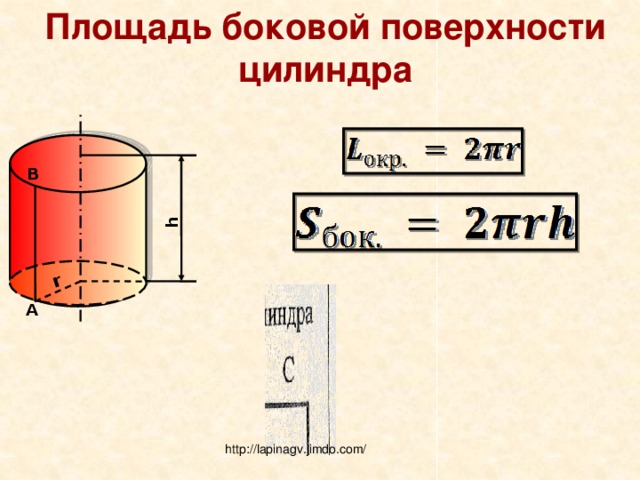 2) + (2*пи*г*л).
2) + (2*пи*г*л).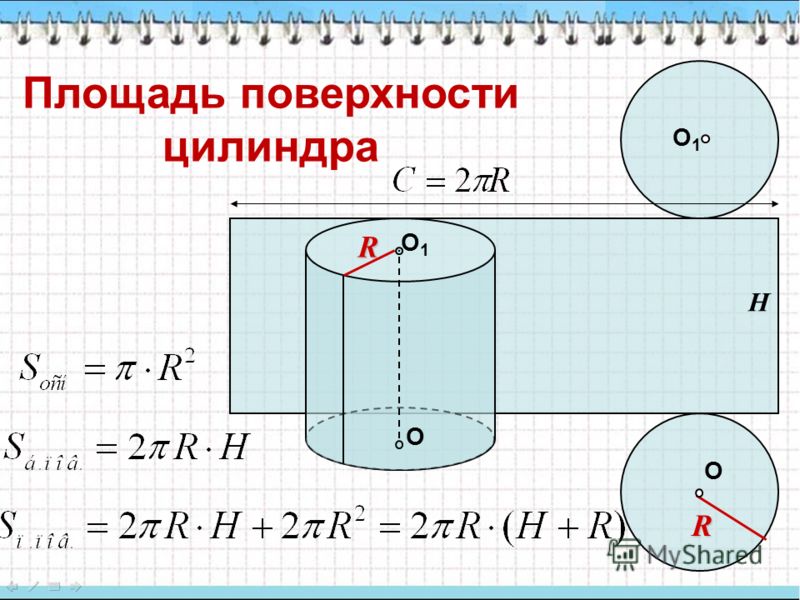


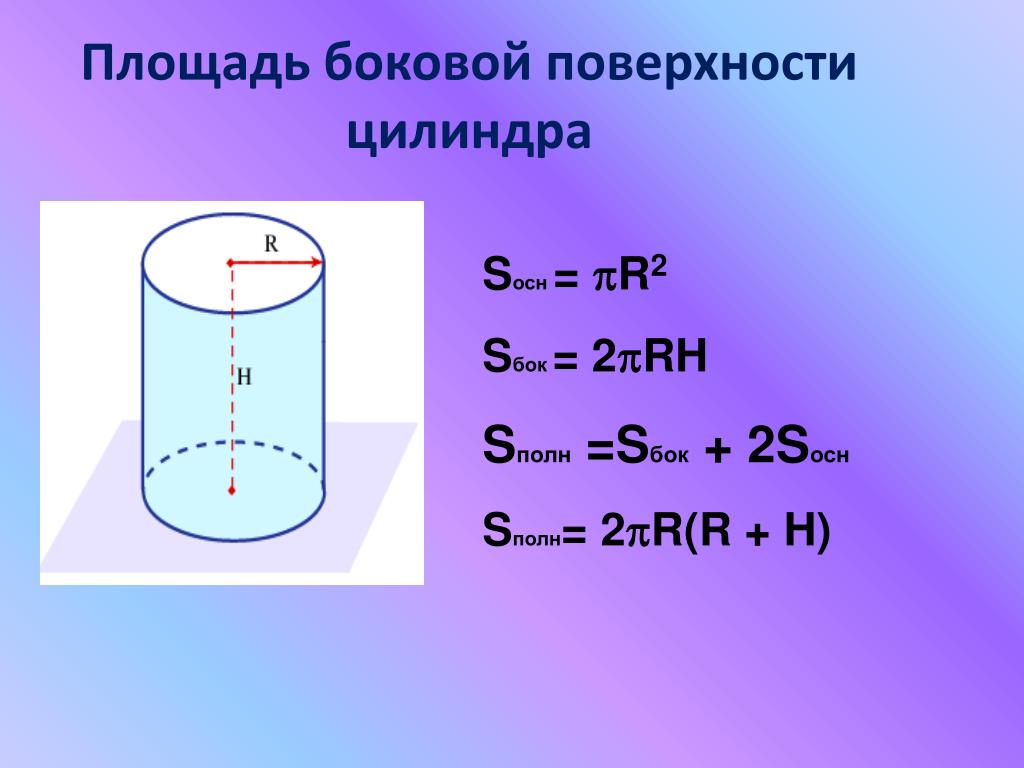 Расстояние от этого отрезка до внешней поверхности цилиндра называется радиусом. Это можно обозначить буквой «р». Перпендикулярное расстояние между основаниями цилиндра называется высотой цилиндра, обозначаемой буквой «h».
Расстояние от этого отрезка до внешней поверхности цилиндра называется радиусом. Это можно обозначить буквой «р». Перпендикулярное расстояние между основаниями цилиндра называется высотой цилиндра, обозначаемой буквой «h».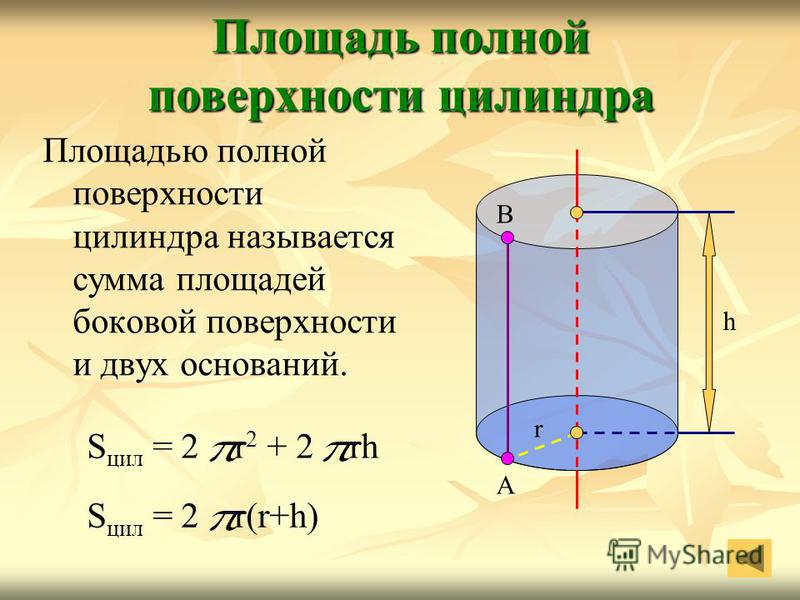

 Банка содержит 1 галлон масла. Найдите высоту цилиндра .
Банка содержит 1 галлон масла. Найдите высоту цилиндра . 

 Вот как была выведена формула:
Вот как была выведена формула:
