Как решать логические задачи на собеседованиях — Work.ua
Если вы еще не сталкивались с головоломками на собеседованиях, то вполне возможно, что все впереди. Какие же головоломки используют современные компании при найме сотрудников, и как научиться их решать?
В предыдущей статье Work.ua, посвященной задачам на логику, «Вопросы-головоломки на собеседованиях с ответами» (часть 1, часть 2) мы собрал самые популярные вопросы-головоломки и подготовили ответы и рекомендации к ним. Теперь давайте углубимся в эту тему. Писатель, колумнист The Economist и New York Times Уильям Паундстоун в своей книге «Найти умного» описал, как при помощи эффективного творческого и аналитического мышления можно отыскать ответы на самые нестандартные вопросы.
Если говорить о решении головоломок как особом жанре, то нельзя не признать, что он условен и стилизован в не меньшей степени, чем японский театр кабуки. Если вы не понимаете характерных для жанра кабуки идиом, вам будет трудно понять происходящее. То же относится и к «задачам без ответа», предложениям спроектировать что-либо и т. д. Как и другие интересующие нас способности, способность решать головоломки — это сочетание врождённых задатков и приобретённых навыков. На первый взгляд вопросы кажутся бесконечно разнообразными, но если вы присмотритесь внимательнее, то поймёте, что в большинстве головоломок используется небольшой набор одних и тех же когнитивных трюков, особенно часто — эффект дизъюнкции и сбивающая вас с толку формулировка проблемы. Знания об этом могут вам помочь.
То же относится и к «задачам без ответа», предложениям спроектировать что-либо и т. д. Как и другие интересующие нас способности, способность решать головоломки — это сочетание врождённых задатков и приобретённых навыков. На первый взгляд вопросы кажутся бесконечно разнообразными, но если вы присмотритесь внимательнее, то поймёте, что в большинстве головоломок используется небольшой набор одних и тех же когнитивных трюков, особенно часто — эффект дизъюнкции и сбивающая вас с толку формулировка проблемы. Знания об этом могут вам помочь.
Монолог или диалог
Самые трудные вопросы, применяющиеся в интервью, требуют, чтобы вы объяснили ваш подход к решению проблемы и потом дали правильный или подходящий ответ. Нужно решить, требует данный вопрос монолога или диалога. Логические головоломки обычно подразумевают монолог. Вам намеренно дают ограниченное количество информации и ожидают, что вы сами найдёте ответ. Вам трудно в этом случае получить от интервьюера дополнительную информацию, поскольку её намеренно вам не сообщили.
Во многих случаях, когда задаются вопросы о разработке дизайна и анализе кейсов (конкретных ситуациях), интервьюеры ожидают, что вы попросите дополнительную информацию. Вам понизят оценку, если вы этого не сделаете. Для вопросов о дизайне («разработайте дизайн полки для специй») нет единственно правильного ответа. Умные кандидаты понимают, что дизайн — это трудная последовательность компромиссов.
Интервьюер обращает внимание, задумываетесь ли вы о том, кто будет пользоваться этой полочкой и где именно она будет находиться. Он готов отвечать, и вы в результате получите массу важной дополнительной информации. Такая беседа может продолжаться долго.
Некоторые «открытые вопросы» («Какой из пятидесяти штатов США вы бы упразднили?») похожи на пятна Роршаха, которые используют в психологических проективных тестах, — люди смотрят на эти пятна, и каждый видит в них что-то своё. Открытые вопросы намеренно неструктурированны. Для всех типов вопросов, но особенно для этих, цель вопроса — завязать получасовую беседу. Заключение о том, насколько умён данный человек, делается на основе этой беседы. Хорошим планом будет предположить, что нужен диалог с интервьюером, если только для вас неочевидно, что данный вопрос — это обычная логическая головоломка. Под диалогом я подразумеваю, что, вероятно, говорить в основном будете вы, но при этом вы можете также и задавать интервьюеру умные вопросы.
Заключение о том, насколько умён данный человек, делается на основе этой беседы. Хорошим планом будет предположить, что нужен диалог с интервьюером, если только для вас неочевидно, что данный вопрос — это обычная логическая головоломка. Под диалогом я подразумеваю, что, вероятно, говорить в основном будете вы, но при этом вы можете также и задавать интервьюеру умные вопросы.
Первая мысль ошибочна
Когда речь идёт о головоломках и загадках, первый потенциальный ответ, который приходит в голову разумному человеку, — это обычно неправильный ответ. Если бы это было не так, данный вопрос не стоило бы называть головоломкой. Подобно оптическим иллюзиям, или трюкам фокусников, или уловкам мошенников, головоломки рассчитаны на то, что вас собьёт с толку ваш собственный привычный повседневный опыт. Дети — это наиболее скептическая и трудная аудитория для фокусников, люди с некоторыми повреждениями мозга не подвержены оптическим иллюзиям, и мошенникам не удается обжулить абсолютно честного человека. То, что вы не можете «с ходу» решить головоломку, просто означает, что ваш мозг работает нормально, так и должно быть, когда вы их решаете. Многие люди начинают нервничать, если ответ не приходит им в голову немедленно. Лучший способ начать диалог, который ожидается от вас, — это объяснить, почему «очевидное» решение неверно. Это не только позволит прервать молчание, но и послужит отличным средством для того, чтобы понять, в чём проблема.
То, что вы не можете «с ходу» решить головоломку, просто означает, что ваш мозг работает нормально, так и должно быть, когда вы их решаете. Многие люди начинают нервничать, если ответ не приходит им в голову немедленно. Лучший способ начать диалог, который ожидается от вас, — это объяснить, почему «очевидное» решение неверно. Это не только позволит прервать молчание, но и послужит отличным средством для того, чтобы понять, в чём проблема.
Забудьте об интегралах
Это относится, конечно, только к логическим головоломкам. Ни одна из распространённых в корпоративных интервью задач не потребует от вас знания интегралов. Если вы думаете, что для решения головоломки нужны более обширные знания, чем те, которыми обладают участники телешоу, подобных «Счастливому случаю» и иже с ним, в каких-то сферах, которые прямо не относятся к той области, где вы хотели бы работать, — скорее всего, вы ошибаетесь. Есть такой тип задач, которые, на первый взгляд, требуют знания интегрального счисления, но на самом деле у них есть простое решение. Всегда старайтесь дать простой ответ. Даже если вы нашли решение при помощи высшей математики, вы можете получить невысокую оценку, так как «за деревьями не видите леса».
Всегда старайтесь дать простой ответ. Даже если вы нашли решение при помощи высшей математики, вы можете получить невысокую оценку, так как «за деревьями не видите леса».
Ищите сложные ответы
Для вопросов с простой, всего в одно предложение, формулировкой — например, «Почему в зеркальном отражении правое и левое меняется местами?» или «Почему пивные банки сужаются вверху и внизу?» — часто требуются длинные и сложные ответы. Позаботьтесь о том, чтобы хорошо продумать эти вопросы. Вы можете получить низкую оценку, если интервьюер решит, что вы упустили что-то важное в вашем ответе. Если короткий вопрос задаётся о дизайне или тестировании («Разработайте дизайн туалетной комнаты для Билла Гейтса»; «Как вы стали бы тестировать лифт?»), то это часто означает, что вы должны попросить дополнительную информацию от интервьюера.
«Безупречно логичные существа» не похожи на людей
Во многих логических головоломках речь идёт о «безупречно логичных существах» (БЛС). Примером могут служить задачи о супружеских изменах в деревне или о пиратах, которым нужно поделить золотые монеты. «Безупречно логичный» — это кодовое слово, которое понятно любителям головоломок, но непонятно тем, кто не входит в их круг. Если вы слышите такую кодовую фразу, это значит, что при решении этой задачи вам нужно забыть практически обо всём, что вы знаете о людской психологии. Вам нужно придерживаться следующих предположений: у БЛС очень простая одномерная мотивация, они озабочены только тем, чтобы получить как можно больше денег, убежать от демона, жёстко следовать какому-либо глупому закону и т. д.
Примером могут служить задачи о супружеских изменах в деревне или о пиратах, которым нужно поделить золотые монеты. «Безупречно логичный» — это кодовое слово, которое понятно любителям головоломок, но непонятно тем, кто не входит в их круг. Если вы слышите такую кодовую фразу, это значит, что при решении этой задачи вам нужно забыть практически обо всём, что вы знаете о людской психологии. Вам нужно придерживаться следующих предположений: у БЛС очень простая одномерная мотивация, они озабочены только тем, чтобы получить как можно больше денег, убежать от демона, жёстко следовать какому-либо глупому закону и т. д.
Всё остальное для них неважно. Следовательно, БЛС никогда не оказывают дружеских услуг — каждый из них сам за себя. БЛС никогда не отвлекается, никогда не делает ошибок, никогда ничего не забывает.
Для поступков обычных людей всегда характерна неопределённость. Это значит, что подразумеваемое решение головоломок, в которых действуют БЛС, абсолютно нереалистично. Они обычно формулируются так: A приходит к выводу, что B придёт к выводу, что C придёт к выводу, что D… и т. д. Такое никогда не случится в реальном мире. Вы можете использовать это как подсказку. Когда вы слышите о безупречно логичных существах, то решение почти всегда подразумевает рассуждения БЛС о других БЛС (или вы должны рассуждать так о самих себе, когда решаете задачи, в которых задаётся вопрос: «Что вы станете делать в такой ситуации?»).
Они обычно формулируются так: A приходит к выводу, что B придёт к выводу, что C придёт к выводу, что D… и т. д. Такое никогда не случится в реальном мире. Вы можете использовать это как подсказку. Когда вы слышите о безупречно логичных существах, то решение почти всегда подразумевает рассуждения БЛС о других БЛС (или вы должны рассуждать так о самих себе, когда решаете задачи, в которых задаётся вопрос: «Что вы станете делать в такой ситуации?»).
Перечисляйте гипотезы
Подумайте о том, что произойдёт, если вы будете последовательно одно за другим отвергать эти предположения. В самых хитрых и сложных головоломках неверные предпосылки и предположения могут выглядеть так естественно, что вы даже вряд ли задумаетесь о них как о предположениях. И всё же стоит попробовать. Просмотрите список и предположите для каждого из них, что верно обратное. Помогает ли это решать задачу? Если вам повезёт, то вы увидите, что есть такое предположение, что, если от него отказаться, задача окажется решаемой. Даже если это вам не поможет и вы не решите задачу, мнение интервьюера о вас улучшится. Он увидит, что вы понимаете роль изменений формулировки проблемы для решения задач.
Даже если это вам не поможет и вы не решите задачу, мнение интервьюера о вас улучшится. Он увидит, что вы понимаете роль изменений формулировки проблемы для решения задач.
Подробности не нужны
Почти всегда то, что мы называем логическими головоломками, использует один и тот же трюк, а именно: большинство людей не может найти решение, потому что считает, что им не хватает для этого информации. Если головоломка — это дизъюнкция, вам неизвестно, что выбрать, одно или другое, и вы не знаете, как найти решение, вам нужно быть готовым методично продумать все возможные варианты и следствия. Предположим, что верен вариант Х — какие вы сможете сделать выводы? Допустим, что это Y — к каким заключениям можно прийти в этом случае? Вы почти всегда обнаружите, что этот способ рассуждения поможет выйти из тупика, и окажется, что вам не нужна для того, чтобы решить задачу, та самая «недостающая информация». Подумайте об этом так: если мост взорван, вам придётся переплыть реку. К счастью, вам никогда не нужно будет плыть очень долго (ведь мосты обычно строятся в самых узких местах рек).
К счастью, вам никогда не нужно будет плыть очень долго (ведь мосты обычно строятся в самых узких местах рек).
Найдите нетривиальный ответ
Это в особенной степени важно при ответах на открытые вопросы, для которых не существует «правильных ответов». Интервьюеры много раз выслушивали обычные ответы на эти вопросы. Когда Сполски попросил одного из кандидатов на работу в Microsoft разработать дизайн полочки для специй для слепого человека, этот кандидат решил, что для слепого будет удобнее не полочка для специй, расположенная на уровне груди или лица, а выдвижной ящик для специй на уровне пояса. Он считал, что вместо того, чтобы искать полку со специями на ощупь, а потом, подняв руку, пытаться прочесть текст, написанный шрифтом Брайля, гораздо удобнее подойти к кухонному столу, найти нужный ящик, выдвинуть его и спокойно прочесть надписи на крышках баночек со специями, скользнув по ним пальцами. Такое эргономичное решение раньше никто из кандидатов не предлагал.
Также впечатляющим было и то, что кандидат эффективно переформулировал проблему. «Полочка для специй» не обязательно должна быть именно полочкой, если есть основание использовать другой дизайн». Сполски рассказывает: «На основании этого единственного ответа я принял на работу кандидата, который стал одним из лучших менеджеров программ в команде, разрабатывавшей Excel». Есть много примеров, которые убеждают меня в том, что интервьюеры не просто ценят, а, пожалуй, даже чрезмерно ценят оригинальные ответы. Может быть, это связано со скукой. Вы знаете, что некоторые простаки пытаются привлечь внимание работодателей, рассылая очень яркие резюме? Такой приём обычно не работает, но во время интервью творческий и хороший ответ поможет вам выделиться среди других кандидатов. Только позаботьтесь о том, чтобы это был действительно хороший ответ.
Читайте нас в Telegram
Чтобы оставить комментарий, нужно войти.
Как научить ребёнка решать логические задачки
Развитая логика — важное качество, которое пригодится в жизни в любом возрасте и позволит не попадать под чужое влияние, грамотно вести спор, видеть перспективные варианты развития событий. Вот почему необходимо изучать логику.
Вот почему необходимо изучать логику.
Лучший способ начать развивать логическое мышление — это играть с ребёнком в интеллектуальные игры: головоломки, ребусы, решать задачи по логике. Чем больше ребёнок выполнит таких заданий, тем лучше. Миссия родителя — вовремя «подкидывать» интересные задания и на первых порах направлять рассуждения ребёнка в правильное русло. Какими способами можно решать логические задачи?
Вам в помощь — список занятий, способствующих развитию логики у детей.
Круги Эйлера
Это задачи про два круга. У этих кругов есть какие-либо характеристики, например, красный и круглый. Даётся несколько вариантов ответа, из которых ребёнок должен выбрать подходящий под описание. Решение этих задач формирует у ребёнка операции сравнения и анализа, а также учит вычленять существенные признаки предметов.
Судоку
Известная японская головоломка, в которой ребёнку нужно умудриться не запутаться, а потому ему понадобится не только логика, но и внимательность. Начинать лучше с простых судоку 3*3, а после переходить к более сложным. Судоку прекрасно подходит для улучшения памяти.
Начинать лучше с простых судоку 3*3, а после переходить к более сложным. Судоку прекрасно подходит для улучшения памяти.
Найди отличия
Одна из любимых игр детей как дошкольного возраста, так и младшеклассников. Это задачи, в которых ребёнку нужно сравнить две картинки и найти, чем они отличаются друг от друга. Игра развивает внимательность, умение сравнивать предметы, устанавливать их сходство и различие.
Ребусы
Это увлекательное задание, в котором зашифрованы слова, фразы или целые предложения при помощи рисунков в сочетании с буквами, фигурами и знаками. Ребусы развивают внимание, память.
Текстовые гибриды
Это загадки. Ответом на них будет слово, состоящее из двух, которые при объединении пересекаются не менее, чем в трёх буквах. Например, спрятал драгоценный камень под одеждой. Ответ: топазуха. Игра развивает способность строить логические цепочки и ассоциации к ним.
Магические квадраты
Это квадратные таблицы, построенные из чисел так, что суммы чисел в каждой строке, в каждом столбце и в каждой диагонали равны одному и тому же числу. Задачи с нестандартной записью всегда увлекают детей. Так ребёнок не просто находит решение, но и развивает внимательность, зрительную память и пространственное мышление.
Задачи с нестандартной записью всегда увлекают детей. Так ребёнок не просто находит решение, но и развивает внимательность, зрительную память и пространственное мышление.
Логогрифы
Загадки, в которых новые слова образуются в результате прибавления или убавления одной буквы или слова, например: пара — парта, кран — экран. Тренируют сообразительность, логическое мышление.
Логические задачи
Как положить спички нужным образом, переправить животных на другой берег или узнать, что лежит в коробке? Решая задачи на логику, ребёнок становится настоящим детективом, учится нестандартно мыслить.
Футошики
Японская игра, цель которой заполнить сетку 5 x 5 числами от 1 до 5, используя их однократно в строке и столбце и следуя указанным символам больше / меньше. Есть только одно верное решение, достигаемое исключительно с помощью логики и ясного мышления. Игра заставит думать, просчитывать ходы, тренировать логику.
Кроссворд
Это словесная головоломка, которая чрезвычайно полезна для улучшения словарного запаса. Она развивает и логику. Ребёнок должен заполнить пронумерованную сетку с подсказками: от названий фигур, названий продуктов до названий мультфильмов.
Она развивает и логику. Ребёнок должен заполнить пронумерованную сетку с подсказками: от названий фигур, названий продуктов до названий мультфильмов.
Кубик Рубика
Доступный способ попрактиковаться в логике и решении задач. Есть множество онлайн-уроков на тему, как научить вашего ребёнка собирать кубик Рубика. Постоянно переставляя его в соответствии с правильным цветовым узором, школьник учится визуализации, оттачивает свою память и ловкость рук.
Крестики-нолики
Это простая игра, требующая применения простой логики, и в неё могут играть дети любого возраста. Игра ведётся по сетке, есть два игрока X и O, цель — поставить 3 своих знака рядом на одной линии. Это просто и увлекательно!
Обратный поиск слов
Это головоломка с поиском слова, которая решается в обратном порядке. Ребёнку предоставляется в основном пустая сетка и список слов, в котором только первая буква слова помещается в случайном порядке.
Поиск в обратном направлении способствует развитию критического мышления и оттачивает у детей навыки поиска решения.
Считаем преимущества решения головоломок для развития логики у детей.
Укрепляет навыки критического мышления.
Способствует решению проблем и развитию устойчивости.
Помогает детям отвлечься от напряженного графика.
Делает сложные конструкции лёгкими и интересными.
Учит детей разбирать сложные математические концепции.
Способствует нестандартному мышлению, логическому анализу.
Вопрос, как ребёнка научить решать задачи, требует погружения в тему. После того как ребёнок освоил различные игры, можно переходить к решению логических задач посложнее. Например, к задачам на истинность утверждений, на сопоставление «кто есть кто», на работу с множествами и т. д. Способ решения задачи зависит от её типа. Достаточно объяснить простые алгоритмы решения разных типов задач, чтобы ребёнок стал их «щёлкать» как орешки. Как решать задачи на логику? Общий алгоритм действий таков:
1. Читаем условие задачи внимательно. Разбираем всё, что ребёнку непонятно.
Читаем условие задачи внимательно. Разбираем всё, что ребёнку непонятно.
2. Ещё более внимательно читаем вопрос. Что нужно в конце концов определить?
3. Делаем запись условия задачи. Выписываем всё: что дано и что нужно найти. Прям как на уроке математики.
4. Визуализируем условие в виде чертежа, схемы или таблицы. Это действительно облегчает понимание смысла задачи и подсказывает, как её решить. Например, для понимания задачи на определение множества — чертим круги Эйлера (уже знакомые по играм предыдущего этапа) и область их пересечения.
5. Выбираем способ решения. Как только разобрались с условием, становится легче определиться со способом ее решения. В примере с кругами Эйлера, ответ вообще лежит на поверхности, а точнее на её рисунке, каким бы запутанным не было условие. Чтобы легко и быстро определять тип задачи и подбирать подходящий способ решения, нужно регулярно практиковаться и развивать способности.
6. Записываем подробное решение. Оно должно отражать всю последовательность действий, то есть должна быть понятна логика решения. Так ребёнок сможет запомнить алгоритм и пользоваться им в дальнейшем.
Так ребёнок сможет запомнить алгоритм и пользоваться им в дальнейшем.
7. Формулируем ответ. Это должен быть полный и точный ответ на вопрос, заданный в условиях задачи на логику.
Как ребёнка научить решать задачи? Ещё одним эффективным способом развития логического мышлений является образовательная онлайн-платформе iSmart, на которой представлены логические задачи всех видов. Они дают возможность развивать детскую логику с разных сторон. Они геймифицированы, а потому вдвойне нравятся детям. Даже 10-15 минут в день, посвящённые таким задачкам, сыграют огромную роль в развитии вашего ребёнка. Регистрируйтесь на платформе и начинайте заниматься уже сегодня!
Методы решения логических задач — Математическая логика для любознательных школьников
| Из анализа специальной литературы мы выделяем несколько различных способов решения логических задач:
Остановимся отдельно на каждом из выделенных методов, иллюстрируя их примерами решения конкретных задач. Метод первый: Метод рассужденийИдея метода состоит в том, что мы проводим рассуждения, используя последовательно все условия задачи, и приходим к выводу, который и будет являться ответом задачи. Этим способом обычно решают несложные логические задачи.Например. Возраст мамы и дочки в сумме составляет 98 лет. Дочь родилась, когда маме было 22 года. Сколько лет маме и дочке? Решение: так как разница в их возрасте 22 года (именно в этом возрасте у мамы родилась дочь), то 98 – 22 =76 (лет). Это удвоенный возраст дочери, тогда 76 : 2 = 38(лет). Значит, матери 98 – 38 = 60 (лет). Задача 1. Вадим, Сергей и Михаил изучают различные
иностранные языки: китайский, японский и арабский. На вопрос, какой язык
изучает каждый из них, один ответил: «Вадим изучает китайский, Сергей не
изучает китайский, а Михаил не изучает арабский». Впоследствии выяснилось,
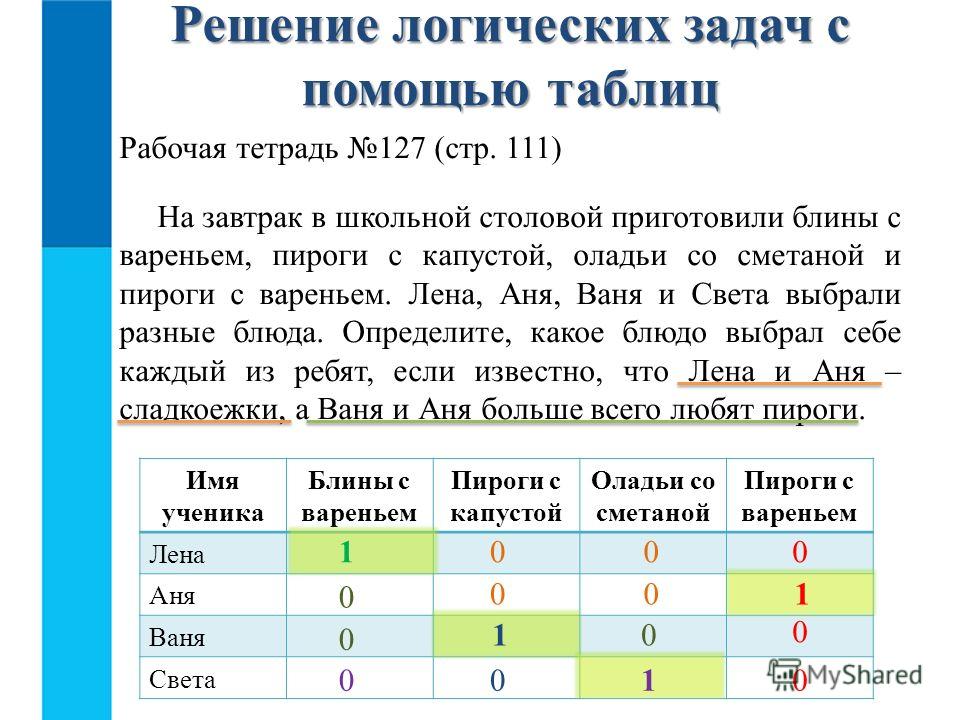
что в этом ответе только одно утверждение верно, а два других ложны. Решение: Имеется три утверждения. Если верно первое утверждение, то верно и второе, так как юноши изучают разные языки. Это противоречит условию задачи, поэтому первое утверждение ложно. Если верно второе утверждение, то первое и третье должны быть ложны. При этом получается, что никто не изучает китайский. Это противоречит условию, поэтому второе утверждение тоже ложно. Остается считать верным третье утверждение, а первое и второе — ложными. Следовательно, Вадим не изучает китайский, китайский изучает Сергей. Ответ: Сергей изучает китайский язык, Михаил — японский, Вадим — арабский.Метод второй: Метод таблиц
Метод третий: Метод блок-схем
Более систематический
подход к решению задач «на переливание» заключается в использовании
блок-схем. Суть этого метода состоит в следующем. Сначала выделяются операции,
которые позволяют нам точно отмерять жидкость. Эти операции называются командами.
Затем устанавливается последовательность выполнения выделенных команд. Эта
последовательность оформляется в виде схемы. Подобные схемы называются
блок-схемами и широко используются в программировании. Составленная блок-схема
является программой, выполнение которой может привести нас к решению
поставленной задачи. Для этого достаточно отмечать, какие количества жидкости
удается получить при работе составленной программы. При этом обычно заполняют
отдельную таблицу, в которую заносят количество жидкости в каждом из имеющихся
сосудов. Идея метода: описать последовательность выполнения операций, определить порядок их выполнения и фиксировать состояния. Задача 3. Имеются два сосуда — трехлитровый и пятилитровый. Нужно, пользуясь этими сосудами, получить 1, 2, 3, 4, 5, 6, 7 и 8 литров воды. В нашем распоряжении водопроводный кран и раковина, куда можно выливать воду. Решение. Перечислим все возможные операции, которые могут быть использованы нами, и
введем для них следующие сокращенные обозначения: НБ — наполнить больший сосуд
водой из-под крана; НМ — наполнить меньший сосуд водой из-под крана; ОБ —
опорожнить больший сосуд, вылив воду в раковину; ОМ — опорожнить меньший сосуд,
вылив воду в раковину; Б→М — перелить из большего в меньший, пока больший сосуд
не опустеет или меньший сосуд не наполнится; М→Б — перелить из меньшего в
больший, пока меньший сосуд не опустеет или больший сосуд не наполнится.
Выделим среди перечисленных команд только три: НБ, Б→М, ОМ. Кроме этих трех
команд рассмотрим еще две вспомогательные команды: Б = 0 ? — посмотреть,
пуст ли больший сосуд; М = З ? — посмотреть, наполнен ли малый сосуд. В зависимости от результатов этого осмотра мы переходим к выполнению следующей команды по одному из двух ключей — «да» или «нет». Такие команды в программировании принято называть командами «условного перехода» и изображать в блок-схемах в виде ромбика с двумя ключами-выходами. Договоримся теперь о последовательности выполнения выделенных команд. После Б→М будем выполнять ОМ всякий раз, как меньший сосуд оказывается наполненным, и НБ всякий раз, как больший сосуд будет опорожнен. Последовательность команд изобразим в виде блок-схемы. Начнем выполнение программы. Будем фиксировать, как меняется количество воды в сосудах, если действовать по приведенной схеме. Результаты оформим в виде таблицы. Дальше эта последовательность будет полностью повторяться. Из
таблицы видим, что количество воды в обоих сосудах вместе образует следующую
последовательность: 0, 5, 2, 7, 4, 1, 6, 3, 0 и т.д. Таким образом, действуя по
приведенной схеме, можно отмерить любое количество литров от 1 до 7. Метод четвертый: метод графов. Граф — множество точек, изображенных на плоскости (листе бумаги, доске), некоторые пары из которых соединены отрезками. Точки называют вершинами графов, а отрезки — ребрами графов. Выделяя из словесных рассуждений главное — объекты и отношения между ними, графы представляют изучаемые факты в наглядной форме. Примеры
решения логических задач с использованием графов подкупают своей наглядностью и
простотой, избавляют от лишних рассуждений, во многих случаях сокращают
нагрузку на память. С одной стороны, графы позволяют проследить все логические
возможности изучаемой ситуации, с другой, благодаря своей обозримости, помогают
в ходе решения задачи классифицировать логические возможности, отбрасывать
неподходящие случаи, не доводя до полного перебора всех случаев. Задача 4. Три ученицы — Аня, Варя и Клава — на первомайской демонстрации были: одна в красном, другая в белом, третья в синем платье. В высказывании: Аня была в красном платье, Варя не в красном, Клава не в синем — одна часть верна, а две неверны. В каком платье была каждая из учениц? Решение: Будем исходить из двух возможностей: Аня была в красном платье (Ак) и Аня была не в красном (то есть в белом или синем) и изобразим эти возможности: первую ребром Ак, а вторую двумя ребрами Ас и Аб, исходящими из одной точки. Если Аня была в красном платье, то в синем могла быть или Варя, или Клава. Поэтому к ребру Ак присоединим 2 ребра Вс и Кс. Путь АкВс закончим Кб, а путь АкКс закончим Вб. Но из двух получившихся путей условию задачи ни один не удовлетворяет. Обратимся ко
второй возможности. К ребру Ас присоединим два ребра Вк и Кк, так как в красном
платье в этом случае могла быть Варя или Клава. Такие же два ребра присоединим
к Аб. Закончить каждый из получившихся путей очень просто: нужно присоединить
последовательно ребра Кб, Вб, Кс и Вс. Метод пятый: метод кругов Эйлера. Упростить решение многих логических задач помогают так называемые круги Эйлера, с помощью которых можно изобразить множество элементов, обладающих определенным свойством. Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Тип задач: Метод кругов Эйлера позволяет графически решать математические задачи, основанные на применении теории множеств. Формальный способ решения подобных задач: 1. Выделить в тексте задачи рассматриваемые свойства объектов. 2. Заполнить круги Эйлера-Венна, проанализировав соответствие объектов и присущих им свойств. 3. Выбрать решение –
набор значений простых высказываний, при котором соответствие объектов и
свойств является истинным. 4. Проверить, удовлетворяет ли полученное решение условию задачи. Преимущества и недостатки данного способа:
Задача 5. Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги в школьной библиотеке, 20 – в районной. Сколько шестиклассников: 1. Решение: Заметим, что первый вопрос является ключевым для понимания и решения данной задачи. Ведь не сразу сообразишь, как получается 20 + 25 = 45 из 35. В первом вопросе звучит подсказка к пониманию условия: есть ученики, которые посещают обе библиотеки. А если условие задачи изобразить на схеме, то ответ на первый вопрос становится очевидным. 1. 20 + 25 – 35 = 10 (человек) – являются читателями обеих библиотек. На схеме это общая часть кругов. Мы определили единственную неизвестную нам величину. Теперь, глядя на схему, легко даем ответы на поставленные вопросы. 2. 35 – 20 = 15 (человек) – не являются читателями районной библиотеки. (На схеме левая часть левого круга) 3. 35 – 25 = 10 (человек) – не являются читателями школьной
библиотеки. 4. 35 – 25 = 10 (человек) – являются читателями только районной библиотеки. (На схеме правая часть правого круга) 5. 35 – 20 = 15 (человек) – являются читателями только школьной библиотеки. (На схеме левая часть левого круга). Очевидно, что 2 и 5, а также 3 и 4 – равнозначны и ответы на них совпадают. |
игровых советов |
Charlie21 декабря 2017 г. Советы по игре Комментариев нет
Многие головоломки Daily Challenge и наборы головоломок сложного уровня содержат игры, требующие более глубоких знаний подсказок «или-или».
Если вы посмотрите на пример головоломки здесь, вторая часть подсказки 3 сообщает нам некоторую информацию, которая может быть скрыта от логического головоломка новичка. Из этой подсказки мы знаем, что Глазго и автобусы — это разные события, но это также говорит нам больше. Если вы посмотрите вниз на столбец сетки, вы увидите, что игрок уже пометил Глазго и автобусы как False. . . НО . . если вы продолжите эту же колонку, вы увидите, что Глазго также не равен Instagram или сотовым телефонам.
. . НО . . если вы продолжите эту же колонку, вы увидите, что Глазго также не равен Instagram или сотовым телефонам.
Итак, глядя на первую часть подсказки, мы знаем, что 14 мая должно быть равно Глазго или Автобусам; и теперь мы знаем, что Глазго не равен Instagram или сотовым телефонам, а автобусы не равны Instagram или мобильным телефонам, поскольку они находятся в одном и том же разделе. . из этого следует, что 14 мая НЕ МОЖЕТ быть приравнено к Instagram или сотовым телефонам. Из предыдущей подсказки 14 мая и Instagram уже заполнены как ложные, но теперь мы можем заполнить 14 мая и сотовые телефоны как ложные.
Тот же процесс теперь применяется к 6000 (другой элемент в первой части подсказки 3), который также НЕ МОЖЕТ равняться Instagram или сотовым телефонам, поэтому теперь вы можете заполнить эти два поля как ложные.
Тот же процесс можно использовать как для строк, так и для нижних столбцов. Так что там, где мы видим, что Автобусы и Глазго уже неверны, мы также можем видеть, что Автобусы также не равны Бирмингему. Таким образом, это говорит нам о том, что 14 мая и 6000 также НЕ МОГУТ равняться Бирмингему.
Таким образом, это говорит нам о том, что 14 мая и 6000 также НЕ МОГУТ равняться Бирмингему.
Используйте эту технику каждый раз, когда видите подсказку, начинающуюся с «Из . . . ». и вы сможете решить некоторые из более сложных головоломок.
Подробнее
Charlie14 декабря 2017 г. Советы по игре Комментариев нет
Продолжая наш последний пост с советами по игре о подсказках «Или-ИЛИ», здесь мы рассмотрим еще один аспект информации, которую можно получить из подсказок такого типа.
В этом примере головоломки подсказка 3 гласит: «О шоу, состоявшемся 14 мая, и шоу, которое он провел перед 6000 человек. . .”.
Теперь, если вы посмотрите на сетку, вы увидите, что на шоу 14 мая уже было подтверждено присутствие 7000 человек. Если вы добавите эту информацию в подсказку 3, она теперь может выглядеть так: «Из представлений, которые он давал перед 6000 и 7000 человек. . ».
Это говорит вам о том, что информация во второй части подсказки (в данном случае Глазго и автобусы) может быть равна только 6000 или 7000.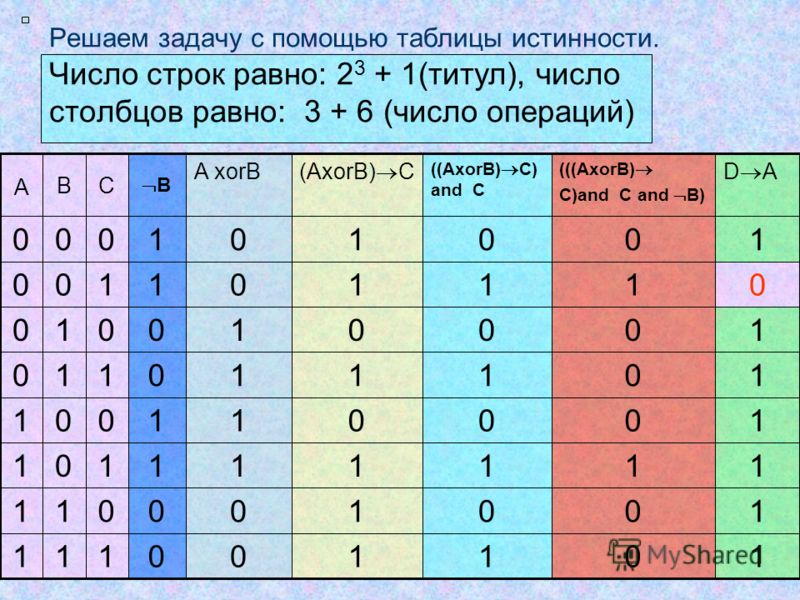 В результате мы можем заполнить следующее с помощью X как ложное: Глазго и 5000 , Глазго и 9000, автобусы и 5000, автобусы и 8000, автобусы и 9000.
В результате мы можем заполнить следующее с помощью X как ложное: Глазго и 5000 , Глазго и 9000, автобусы и 5000, автобусы и 8000, автобусы и 9000.
Во второй части этого поста мы объясним еще один более сложный способ получения информации из подсказок «Или-Или».
Подробнее
Charlie15 февраля 2016 г. Советы по игре Комментариев нет
Многие логические головоломки содержат либо / или подсказки, в которых один набор фактов зависит от другого. Например, если вы посмотрите на шестую подсказку в головоломке «Игра в риск», изображенную ниже, вы увидите, что в ней говорится «о зеленом игроке и человеке с наибольшим количеством армий, одна — Мария, а другая доминировала в Северной Америке».
Так вот, в подобных подсказках хранится некоторое количество битов информации. Начнем с того, что подсказки «или-или» — это ОТДЕЛЬНЫЕ события. Таким образом, мы сразу понимаем, что у зеленого игрока НЕ было больше всего армий, а Мария НЕ доминировала над Северной Америкой на доске, поэтому мы можем соответственно расставить крестики в этих клетках. Они обведены синим цветом на изображении ниже.
Они обведены синим цветом на изображении ниже.
Как только вы это сделаете, вы увидите, сможем ли мы разгадать загадку этой подсказки и открыть верные ответы. Это говорит нам, что зеленый игрок — ЛИБО Мария, ЛИБО Северная Америка. Судя по подсказкам, которые у нас есть до сих пор, мы не знаем, какое из этих утверждений верно. Однако подсказка также говорит нам, что человек с наибольшим количеством армий также ЛИБО Мария, ЛИБО Северная Америка. Теперь, если мы посмотрим на сетку, мы увидим, что в Северной Америке на самом деле было 70 армий (обведено желтым), а НЕ самое большое, поэтому Северная Америка не может сравниться с наибольшим количеством армий. Если Северная Америка не может сравниться с наибольшим количеством армий, тогда она должна равняться зеленому, и мы можем заполнить Северную Америку и зеленый цвет как верный ответ (обведено желтым). Теперь мы знаем, что из этого также следует, что у Марии было больше всего армий, и мы также можем заполнить этот квадрат как верный ответ.
Подводя итог: подсказки «Или-Или» могут сразу же дать нам много информации, но иногда их секреты необходимо раскрыть, заполнив больше сетки, чтобы мы могли увидеть, какие из утверждений «Или-Или» верны или ложны.
Подробнее
Charlie11 февраля 2016 г. Советы по игре Комментариев нет
Распространенной ошибкой при решении логических головоломок является поиск единственного истинного или ложного ответа. Иногда группы неправильных ответов или пустые квадраты могут привести к выводу. В приведенном ниже примере мы показываем, как двойное отрицание может привести к ответу, но это также может относиться к тройному отрицанию.
В приведенном здесь примере с приговором к тюремному заключению мы видим, что человек в Сан-Квентине получил либо 15 лет, либо пожизненное заключение. Если мы посмотрим направо, то увидим, что человек, осужденный за кражу, НЕ получил 15 лет или пожизненное заключение, поэтому НЕ мог находиться в Сан-Квентине.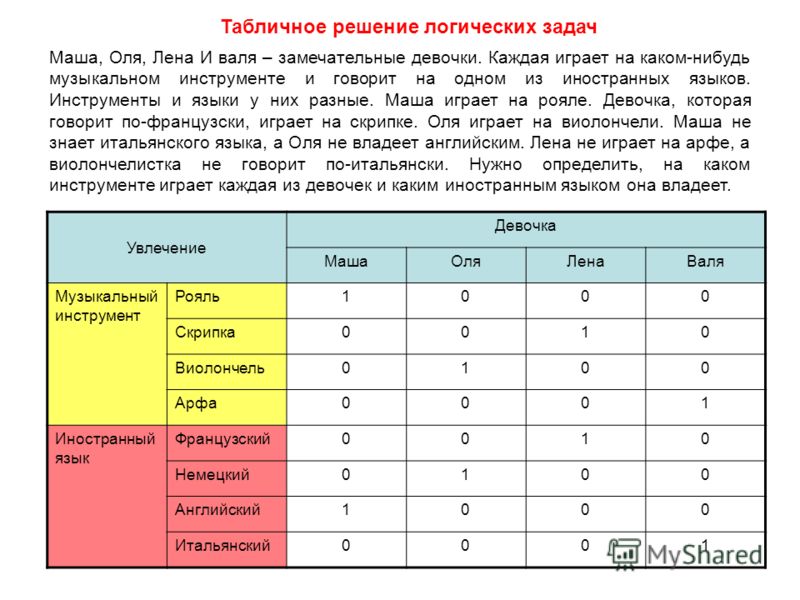 Поэтому мы можем пометить Сан-Квентина и Вора как X.
Поэтому мы можем пометить Сан-Квентина и Вора как X.
Иногда мы заморачиваемся в поисках единственного правильного или ложного ответа и можем сидеть и думать, что головоломка неразрешима. Это может быть что-то такое же простое, как двойное или тройное отрицание, которое может открыть следующую стадию. Удачи!
Подробнее
Charlie10 февраля 2016 г. Советы по игре Комментариев нет
В предыдущих постах мы много говорили о том, как можно сопоставлять фрагменты информации из одного раздела сетки с другим. Чтобы еще больше расширить это, мы можем использовать вещь, называемую перекрестным сопоставлением, когда дело доходит до истинных ответов. Чтобы объяснить это, взгляните на сетку ниже:
В верхней строке мы видим, что Гендель и Тенор верны. Если мы посмотрим на левую сторону сетки, мы также увидим, что Тенор и 1-й истинны. Затем это приводит нас к осознанию того, что Гендель и 1-е должны быть истинными, потому что горизонтальные и вертикальные линии истинных ответов должны пересекаться. Если теперь мы знаем, что вертикальный столбец для 1-го числа — это Гендель, Тенор, Дрю, то мы знаем, что горизонтальный ряд для Генделя должен иметь те же значения. . так 1-й, Дрю, тенор.
Если теперь мы знаем, что вертикальный столбец для 1-го числа — это Гендель, Тенор, Дрю, то мы знаем, что горизонтальный ряд для Генделя должен иметь те же значения. . так 1-й, Дрю, тенор.
Учитывая тот факт, что истинные ответы должны пересекаться, мы знаем, что можем также заполнить Тенора и Дрю как верный ответ . . множество истинных ответов, заполненных простым пересечением линий, созданных двумя правдами.
Подробнее
CharlieFev 08, 2016 Советы по игре Комментариев нет
Вы можете значительно ускорить решение логических головоломок, если сможете «видеть» узоры на сетке, когда они начинают формироваться. Все в логической сетке должно располагаться вместе, поэтому, если есть X для определенных событий по горизонтали, они также должны следовать по вертикали.
Например, на изображении ниже мы видим, что баритон и 2-я истинны. Если мы посмотрим на сетку как по горизонтали, так и по вертикали, вы увидите различные шаблоны, которые будут совпадать, когда есть верный ответ, связывающий их. В этом примере, когда мы смотрим вправо от Баритона и 2-го правильного ответа, мы видим, что есть крестики, показывающие, что Баритон НЕ был Дрю или Тейлором. Затем эти крестики нужно добавить в сетку внизу, потому что, конечно, если Баритон не может быть Дрю или Тейлором, то из этого следует, что 2-й также не может быть Дрю или Тейлором.
В этом примере, когда мы смотрим вправо от Баритона и 2-го правильного ответа, мы видим, что есть крестики, показывающие, что Баритон НЕ был Дрю или Тейлором. Затем эти крестики нужно добавить в сетку внизу, потому что, конечно, если Баритон не может быть Дрю или Тейлором, то из этого следует, что 2-й также не может быть Дрю или Тейлором.
Roblox Hack No Survey No Download
Глядя на тот же пример, есть несколько других ячеек, которые можно заполнить, просмотрев другие верные ответы и увидев, какую информацию мы знаем о них. Например, мы можем видеть, что Альт и 4 верны. Если мы посмотрим вниз, мы увидим, что Робин не был 4-м, поэтому естественно следует, что мы можем поставить X рядом с Альто и Робином.
Точно так же мы знаем, что Вивальди и Тейлор верны, и, глядя вдоль этой линии, мы видим, что Вивальди не сопрано и не тенор, поэтому отсюда следует, что Тейлор не может быть ни сопрано, ни тенором. После того, как вы некоторое время будете решать логические головоломки, вы сможете определить закономерности и то, как они связаны друг с другом, основываясь на верных ответах.
Подробнее
12 логических головоломок (с ответами), которые проверят вашу сообразительность
Поначалу может показаться, что для решения этих логических головоломок недостаточно информации, но это часть веселья!
Логика как академическая дисциплина изучает рассуждения. Таким образом, логические головоломки включают в себя ряд выводов и их оценку с помощью рассуждений. Более простые логические головоломки для детей, как правило, имеют более простые настройки и, следовательно, меньше возможностей для изучения и устранения. Однако более сложные логические головоломки для взрослых часто бывают обманчиво короткими. Поначалу они кажутся простыми, но решатель часто недоумевает, откуда на самом деле может быть достаточно информации, чтобы их вычислить.
Как и некоторые из самых сложных математических головоломок и математических загадок, эти головоломки могут быть очень сложными. Если вы поищите их в Интернете, вы найдете множество примеров логических головоломок с сетками, которые помогут вам следить за своим мышлением, пробираясь через различные подсказки.
СВЯЗАННЫЕ : Судоку для печати
Что такое логическая головоломка?
Эти головоломки бывают разных форм и могут иметь почти безграничное количество различных тем. Но по своей сути логические головоломки представляют собой ряд подсказок и ограничений. Затем решатели должны обрабатывать каждую по очереди, чтобы выявить противоречия и исключить возможности, пока не придут к решению.
СВЯЗАННЫЕ : Печатные кроссворды
Как решить логическую головоломку
Независимо от формата, ключом к решению любой из этих головоломок является использование процесса дедукции. В сложных логических головоломках для взрослых поначалу может показаться, что информации недостаточно. Но, прочитав подсказки несколько раз, у вас будет все меньше и меньше возможностей для анализа с каждым проходом.
Теперь, когда вы знаете, как их решать, давайте попробуем несколько. Мы начнем с более простых (которые также являются отличными логическими головоломками для детей), прежде чем мы дадим вам более сложные.
СВЯЗАННЫЕ : Головоломки с поиском слов для печати
Простые головоломки
Эти логические головоломки идеально подходят для начинающих или тех, кто хочет подготовиться к чему-то более сложному. Ищете хорошие логические головоломки для детей? Тогда те, что ниже, — ваш лучший выбор.
1. Летний лагерь
Мария Амадор для Ридерз Дайджест (4)
Эбигейл, Оливер, Роза и Блейк посещают один и тот же летний лагерь, где они могут готовить, кататься на байдарках, заниматься скалолазанием и кататься на зиплайне. У каждого ребенка есть любимое занятие.
- Любимое занятие Эбигейл не скалолазание.
- Оливер боится высоты.
- Роза не может заниматься любимым делом без шлейки.
- Блейку нравится постоянно стоять на ногах.
Можете ли вы выяснить, кто что любит?
Ответ: Эбигейл любит кататься на зиплайне, Оливер любит кататься на байдарках, Роза любит скалолазание, а Блейк любит готовить.
2. Хорошая жизнь
Сью Дорин, The Noun Project
Каждая из пяти соседских собак (Сабля, Джинджер, Мускатный орех, Перец и Медведь) наслаждается одним из следующих занятий: чешет уши, играет в мяч, вздремнет, закапывает жевательную игрушку и идет на прогулку.
- Пеппер либо играет в мяч, либо закапывает игрушку для жевания.
- Ни Джинджер, ни Сэйбер, ни Медведь не на прогулке.
- У одной из собак, названных в честь специи, чешутся уши.
- Собака, названная не в честь специи, играет в мяч.
- Медведь делает зарядку.
Можете ли вы понять, что делает каждый дворняжка?
Ответ: Сэйбер дремлет, Джинджер чешет уши, Мускатный орех собирается на прогулку, Перец закапывает игрушку для жевания, а Медведь играет в мяч. Попробуйте эти игры для мозга, которые действительно обострят ваш ум.
3. День президента
Марсель Данези
У Джорджа, Уильяма, Джона, Эйба и Милларда дни рождения в последовательные дни, все с понедельника по пятницу.
- День рождения Джорджа наступает за столько же дней до дня рождения Милларда, а день рождения Уильяма — после дня рождения Эйба.
- Джон на два дня старше Эйба.
- День рождения Милларда в четверг.
Можете ли вы определить, чей день рождения каждый день?
Ответ: У Джона в понедельник, у Джорджа во вторник, у Эйба в среду, у Милларда в четверг и у Уильяма в пятницу. Кстати, вы можете найти спрятанные предметы на этих картинках?
4. Долго и коротко
Марсель Данези, iStock
Вот отличная логическая задачка для детей: Вчера были измерены шестеро соседских детей (Лейша, Бенито, Делия, Шарлотта, Уэлдон и Зина).
- Уэлдон выше Делии, но ниже Зины.
- Лейша выше Бенито, но ниже Делии и Уэлдона.
- Бенито не самый низкий.
Можете ли вы расположить их в порядке высоты от самого высокого до самого низкого?
Ответ: Зина, Уэлдон, Делия, Лейша, Бенито, Шарлотта. Если вы действительно хотите взорвать свой мозг, попробуйте решить эти хитрые головоломки латерального мышления.
Если вы действительно хотите взорвать свой мозг, попробуйте решить эти хитрые головоломки латерального мышления.
Средние головоломки
Это немного сложнее, поэтому мы рекомендуем эти логические головоломки для взрослых. Это по-прежнему хорошие логические головоломки для детей, но младшие решатели могут быть не в состоянии решить их самостоятельно.
5. Папы и выпускники
rd.com, Getty Images
Для Майкла, Кена, Джеймса, Альберто, Элиаса и Стефани устраивается совместная вечеринка в честь Дня отца и выпускного вечера. Трое из них — новоиспеченные выпускники средней школы. Остальные трое — их папы.
- Стефани пошла на выпускной бал с сыном Майкла.
- Элиас и Джеймс играли в школьной бейсбольной команде. Один из них — сын Альберто.
- Майкл и Элиас не родственники.
Сможете ли вы сопоставить выпускников средней школы с их отцами на этом совместном празднике?
Ответ: Альберто — отец Элиаса, Кен — отец Стефани, а Майкл — отец Джеймса.
6. Сезон аллергии
rd.com, Getty Images (2)
Пятеро друзей (Аллегра, Бен, Клара, Флора и Зак) страдают аллергией на что-то свое: пыльцу, моллюски, пчелиные укусы, кошек или орехи.
- У Аллегры пищевая аллергия
- Бен может часами играть со своим котенком без проблем (или лекарств).
- Аллергия Клары не связана с животными.
- У Флоры сезонная аллергия.
Можете ли вы выяснить, у кого на что аллергия?
Ответ: У Аллегры аллергия на моллюсков, у Бена — на пчелиные укусы, у Клары — на орехи, у Флоры — на пыльцу, а у Зака — на кошек.
7. Вот в чем дело
Фрейзер Симпсон
Эта головоломка может стать хорошей логической головоломкой для детей, так как в ней также есть элементы математики. Четыре игральные карты, по одной каждой масти, лежат лицом вниз на столе. Это тройка, четверка, пятерка и шестерка.
- Карты по обе стороны от четверки черные.
- Дубинка находится справа от тройки, но не рядом с ней.
- Пика слева от червы.
- Две средние карты в сумме дают четное число. Ни один из них не является клубом.
Можете ли вы определить масти карт и их порядок?
Ответ: Слева направо: тройка бубен, шестерка пик, четверка червей, пятерка треф. Сколько из этих визуальных головоломок вы можете решить?
8. Вечеринка у Чарли
rd.com, Родерик Кимбалл
А это хорошая логическая задачка для взрослых. Вас пригласили на вечеринку в дом Чарли, но вы там никогда не были. У него есть семь друзей, которые живут поблизости. Они дали вам карту со всеми их домами и домом Чарли, а также следующую информацию:
- Даниэль: Я не вижу дом Бениты, потому что дом Греты мешает.
- Адам: Я живу прямо (не по диагонали) через дорогу от Даниэля.
- Бенита: Елена живет к западу от меня.

- Елена: Мне нужно пересечь три улицы, чтобы дойти до дома Франко.
- Хэл: Я живу к востоку от Бениты.
Сможете ли вы определить, какой дом принадлежит Чарли?
Ответ: Дом E.
Сложные головоломки
Эти более сложные задачи определенно являются логическими головоломками для взрослых. Но хотя они и сложны, не расстраивайтесь, если вы потратите столько времени, сколько вам нужно, чтобы проработать свою логику.
9. Передайте соль, пожалуйста
Эмили Гудман, The Noun Project
Идеальная логическая головоломка для взрослых, у которых есть дети: попробуй перехитрить своего озорного подростка!
В День дурака ваш сын-подросток заменяет соль в трех из четырех ваших солонок сахаром. Но он также оставляет сообщения на каждом.
Если только одна из этих надписей верна, в каком шейкере все еще есть соль?
Ответ: Shaker C.
10. True Blue
Фрейзер Симпсон, The Noun Project
Эта логическая головоломка для взрослых поставит в тупик даже самых сообразительных! Даниэль, Эмили, Марчиано и Кристина одеты в однотонные рубашки. Их рубашки красные, желтые, зеленые и синие. Только человек в синем говорит правду, а остальные трое лгут. Они делают следующие заявления:
Их рубашки красные, желтые, зеленые и синие. Только человек в синем говорит правду, а остальные трое лгут. Они делают следующие заявления:
- Даниэль: «Марчиано одет в красное».
- Эмили: «Дэниел не носит желтое».
- Марчиано: «Эмили носит синее».
- Кристина: «Завтра я буду в синем».
Можете ли вы определить цвет рубашки каждого человека и можем ли мы ожидать завтра увидеть Кристину в синем?
Ответ: Даниэль в желтом, Эмили в красном, Марчиано в зеленом, а Кристина в синем. Завтра Кристина снова наденет синюю рубашку.
11. Три ура новоиспеченным родителям
The Noun Project
В этой распечатанной логической головоломке вы узнаете, как будущие родители назовут своих тройняшек.
Руби и Льюис ждут… тройню! Они уже знают, как назовут своих троих детей, но не сообщают имен, пока малыши не родятся. Пока что это все, что они скажут:
- Все трое — мальчики.

- Их имена состоят из шести букв и являются анаграммами друг друга.
- Их имена включают инициалы обоих родителей, но ни одну из других букв в именах родителей.
Как Руби и Льюис назовут своих тройняшек?
Ответ: Арнольд, Роланд и Рональд. Теперь нам нужно получить ваш ответ: сколько уток вы видите на этой картинке?
12. Выиграй или проиграй
Даррен Ригби
И последняя логическая задачка для взрослых: угадаете, кто выиграл игру?
Красные, Серые, Синие и Черные проводят круговой турнир. Каждая команда играет друг с другом один раз, всего шесть игр.
- Черные выиграли больше игр, чем синие.
- Серые проиграли больше игр, чем синие.
- Красные сыграли вничью с черными. (Это была единственная ничья на турнире.)
Кто выиграл игру между красными и синими?
Ответ: Красные.
Теперь взгляните на эти оптические иллюзии, которые поразят вас.
Популярные видео
ⓘ
Как решить самую сложную логическую головоломку
Будучи докторантом Принстонского университета в 1957 году, обучаясь у основателя теоретической информатики, Рэймонд Смаллян время от времени посещал Нью-Йорк. В один из таких визитов он познакомился с «очень очаровательной женщиной-музыкантом», а на их первом свидании Смаллиан, неисправимый кокетливый человек, поступил очень логично — и скрытно.
«Не могли бы вы сделать мне одолжение?» — спросил он ее. «Я должен сделать заявление. Если утверждение верно, не могли бы вы дать мне свой автограф?»
Довольная подыгрывать, она ответила: «Не понимаю, почему бы и нет».
«Если утверждение ложно, — продолжал он, — вы не даете мне свой автограф».
«Хорошо…»
Его заявление было: «Ты не дашь мне ни автографа, ни поцелуя».
На это требуется мгновение, но со временем хитрость уловки Смалльяна становится очевидной.
За правдивое заявление он получает ее автограф, как они и договаривались. Но утверждение Смалльяна, если предположить, что оно верно, приводит к противоречию: оно исключает автограф. Это делает заявление Смалльяна ложным. А если заявление Смалльяна ложно, то очаровательная дама-музыкант подарит ему или автограф, или поцелует. Теперь вы видите ловушку: она уже согласилась не вознаграждать ложное заявление автографом.
Но утверждение Смалльяна, если предположить, что оно верно, приводит к противоречию: оно исключает автограф. Это делает заявление Смалльяна ложным. А если заявление Смалльяна ложно, то очаровательная дама-музыкант подарит ему или автограф, или поцелует. Теперь вы видите ловушку: она уже согласилась не вознаграждать ложное заявление автографом.
С логикой Смаллиан превратил ложное утверждение в поцелуй. (И в прекрасный роман: они в конце концов поженятся.)
Именно такую логическую игривость любит Смаллиан, и за нее, кажется, его любят все. Его книги на темы развлекательной математики и логики с такими названиями, как Как называется эта книга? и «Издеваться над пересмешником» не только поощряли людей делать карьеру в этих темах, но и изменяли методы преподавания математики и логики. За свой почти век жизни 96-летний Смаллян стал опытным пианистом и фокусником, внес фундаментальный вклад в современную логику и писал о даосской философии и шахматах. «Он бесспорный мастер логических головоломок, — говорит Брюс Горовиц, один из его бывших докторов наук. студенты, сказал.
«Он бесспорный мастер логических головоломок, — говорит Брюс Горовиц, один из его бывших докторов наук. студенты, сказал.
Одним из признаков наследия Смалльяна является интерес философов и логиков к его самой сложной головоломке, известной как «Самая сложная логическая головоломка всех времен». Это звание дал философ логики из Массачусетского технологического института, коллега Смалльяна по имени Джордж Булос, который — сам не сутулясь — обожал логические задачи любого рода. Однажды он проверил себя, прочитав лекцию о второй теореме Гёделя о неполноте, «одном из самых важных результатов современной логики», используя только односложные слова.
Самая сложная логическая головоломка звучит так:
Три бога A, B и C называются в определенном порядке Истинным, Ложным и Случайным. Правда всегда говорит правду, Ложь всегда говорит неправду, но говорит ли Рэндом правду или ложь — совершенно случайное дело. Ваша задача состоит в том, чтобы определить личности A, B и C, задав три вопроса «да-нет»; каждый вопрос должен быть задан ровно одному богу. Боги понимают английский, но ответят на все вопросы на своем родном языке, в котором слова «да» и «нет» — это «да» и «джа» в некотором порядке. Вы не знаете, какое слово что означает.
Боги понимают английский, но ответят на все вопросы на своем родном языке, в котором слова «да» и «нет» — это «да» и «джа» в некотором порядке. Вы не знаете, какое слово что означает.
Всегда готовый принять вызов, я сел на диван с ручкой и бумагой в руке, уверенный, что смогу решить головоломку максимум за два часа. Мне казалось, что все, что мне нужно сделать, это начать с того, что придумать сразу три вопроса, а затем проработать их последствия. Например, я спросил А, истинно ли В; спросил Б, правда ли А; и спросил C, правда ли он. Спустя несколько часов, задав богам все возможные вопросы, которые я только мог придумать, я понял, как головоломка получила свое название. Очевидно, мои вопросы не заставляли богов отвечать так, как я хотел.
Разочарованный, я отправился на поиски просветления. Мастером на вершине горы оказался Булос, решивший головоломку в 1996 году. То, как он это сделал, оказалось одним из лучших уроков логики и истины, которые я когда-либо получал. Если вы хотите попробовать решить головоломку самостоятельно, вы можете прекратить чтение здесь. Удачи! Если у вас получится, примите мои поздравления. Но если вы этого не сделаете, вернитесь, и вы можете обсудить со мной решение Boolos ниже.
Если вы хотите попробовать решить головоломку самостоятельно, вы можете прекратить чтение здесь. Удачи! Если у вас получится, примите мои поздравления. Но если вы этого не сделаете, вернитесь, и вы можете обсудить со мной решение Boolos ниже.
Первое, что говорит нам Булос, это то, что вы не должны совершать ошибку, составляя все свои вопросы сразу, как это сделал я, надеясь, что стратегия «предполагать и делать выводы» окупится. Вместо этого первое, что вы должны сделать, — это придумать вопрос, который определит, кто из не может быть случайным или кто может только быть либо истинным, либо ложным. Это поможет вам в процессе исключения раскрыть личность Рэндома. И как только вы идентифицировали Рэндома, легко разоблачить два других.
Чтобы лучше понять этот подход, говорит Булос, нам нужно увидеть, как он работает в трех более простых головоломках.
Первая простая головоломка на самом деле представляет собой итерацию классических загадок Смаллиана о рыцарях и лжецах, представленных в его книге Как называется эта книга? В головоломках рыцари всегда говорят правду, лжецы всегда лгут, и ваша задача выяснить, исходя из того, что они говорят, кто есть кто.
Итак, для нашей первой головоломки предположим, что вы не можете вспомнить, является ли Плутон карликовой планетой, и вам нужно выяснить это, спросив кого-нибудь поблизости, но вы не знаете, рыцарь ли этот человек или лжец. Какой вопрос можно задать, чтобы выяснить, является ли Плутон карликовой планетой?
Как объясняет Булос, вы хотите заманить рыцаря или лжеца в ловушку, чтобы они дали вам то, что вы хотите. И вы устанавливаете эту ловушку фразой тогда и только тогда, когда — логическая конструкция, называемая «бикондиционал». Так что в этом случае ваш вопрос будет звучать так: «Являетесь ли вы рыцарем тогда и только тогда, когда Плутон — карликовая планета?»
Когда вы вставляете тогда и только тогда, когда «между двумя утверждениями, которые либо оба истинны, либо оба ложны, вы получаете истинное утверждение; но если вы вставите его между одним истинным и одним ложным утверждением, вы получите ложное утверждение», — пишет Булос. Это похоже на знак умножения: так же, как вставка знака умножения между двумя положительными или двумя отрицательными числами дает вам число, которое всегда положительное, вставка тогда и только тогда, когда между двумя истинными или двумя ложными утверждениями дает вам утверждение, которое всегда истинно.
Это похоже на знак умножения: так же, как вставка знака умножения между двумя положительными или двумя отрицательными числами дает вам число, которое всегда положительное, вставка тогда и только тогда, когда между двумя истинными или двумя ложными утверждениями дает вам утверждение, которое всегда истинно.
Учитывая, что вы можете адресовать свой вопрос либо рыцарю, либо лжецу, есть четыре возможных ответа (при условии, что мы не знаем, что Плутон на самом деле карликовая планета):
1. Если человек рыцарь а Плутон — карликовая планета, то вы получаете ответ «да», так как оба утверждения с каждой стороны от тогда и только тогда, когда верны, а рыцари всегда говорят правду.
2. Если человек рыцарь, а Плутон не карликовая планета, вы получаете «нет», так как вопрос содержит ложное утверждение.
3. Если человек — лжец, а Плутон — карликовая планета, вы получаете «да», так как лжецы всегда говорят неправду, и правильный ответ — «нет».
4. Если человек лжец, а Плутон не карликовая планета, вы получаете «нет», так как правильный ответ «да».
Если человек лжец, а Плутон не карликовая планета, вы получаете «нет», так как правильный ответ «да».
Посмотрите, что только что произошло: сформулировав вопрос с помощью биусловия, вы получите нужную информацию: если Плутон — карликовая планета, вы получите в ответ «да», а если нет, вы получите «нет» — независимо от того, являетесь ли вы говоря с кем-то честным или нет. Однако помните, что в самой сложной логической головоломке рыцарь и лжец — в отличие от этого примера — не говорят по-английски.
Чтобы заставить их выдать, означают ли «да» и «джа» «да» и «нет» или наоборот, рассмотрите вторую простую головоломку Булоса.
В этой головоломке вы знаете, что спрашиваете рыцаря, который всегда говорит правду, но он отвечает только «да» и «джа». Какой один да-нет вопрос вы можете задать, чтобы выяснить, является ли Плутон карликовой планетой? Взяв за основу последнюю загадку, вы получили следующее: спросите рыцаря: «Означает ли «да» «да» тогда и только тогда, когда Плутон — карликовая планета?» Бинго: вы получаете ответ «да», если Плутон — карликовая планета, и «джа», если нет, хотя мы не знаем, что означают эти слова. Результат такой же полезный, как и приведенный выше: незнание того, был ли человек рыцарем или лжецом, не было препятствием, так же как и незнание значения «да» и «джа».
Результат такой же полезный, как и приведенный выше: незнание того, был ли человек рыцарем или лжецом, не было препятствием, так же как и незнание значения «да» и «джа».
Булос говорит нам, что самая сложная логическая головоломка — это две первые простые головоломки плюс третья. Прежде чем мы решим это, взгляните, как сочетаются первые две головоломки: вам нужно выяснить, является ли Плутон карликовой планетой, и вы должны спросить кого-то, кто может быть рыцарем или лжецом и , он отвечайте только «да» или «джа». Какой вопрос вы бы задали? Если вы думаете, что, поскольку это составная головоломка, правильно задавать составной вопрос, вы будете правы! Спросите: «Означает ли «да» «да» тогда и только тогда, когда вы рыцарь, и тогда и только тогда, когда Плутон — карликовая планета?» Задав этот вопрос, вы получите ответ «да», если Плутон — карликовая планета, и «джа», если нет, независимо от того, обращаетесь ли вы к рыцарю или лжецу. Этот хорошо продуманный вопрос подобен ключу от замка.
Каждое утверждение либо истинно, либо ложно — золотой середины нет.
А вот и третья простая головоломка. Его правила таковы. Предположим, я кладу перед вами в ряд три карты — два туза и валета — лицевой стороной вниз. Вы не знаете, как они упорядочены, но я знаю. Задав мне один вопрос «да-нет», указывая на одну из карт, вы сможете с уверенностью определить, что одна из карт является тузом. Если вы укажете на одного из двух тузов, я отвечу на вопрос правдиво, как рыцарь; если вместо этого вы укажете на валета, я отвечу «да» или «нет» наугад, как случайный бог. Куда ты укажешь и что спросишь?
Это может показаться немного сложнее, но на самом деле это не так. Укажите на любую карту и спросите, является ли одна из других карт тузом. Допустим, вы указываете на среднюю карту и спрашиваете, является ли левая карта тузом. « Независимо от того, является ли средняя карта тузом или нет, , — говорит Булос, — вы обязательно найдете туза, если выберете левую карту, если услышите, что я говорю «да», и выберете правильную карту, если услышите «нет». » Почему? Что ж, если средняя карта — туз, то, когда я говорю «да», левая карта — тоже туз; если я скажу «нет», правильная карта будет. Если средняя карта валет, это не имеет значения независимо от того, говорю ли я «да» или «нет» случайным образом: и левая, и правая карты должны быть тузами, так как средняя — валет. Таким образом, независимо от того, указали вы на туза или нет, мой ответ на ваш вопрос, «да» или «нет», всегда будет определять местонахождение другого туза, если карта, о которой вы задаетесь вопросом, является тузом, а не той. вы указываете на.
» Почему? Что ж, если средняя карта — туз, то, когда я говорю «да», левая карта — тоже туз; если я скажу «нет», правильная карта будет. Если средняя карта валет, это не имеет значения независимо от того, говорю ли я «да» или «нет» случайным образом: и левая, и правая карты должны быть тузами, так как средняя — валет. Таким образом, независимо от того, указали вы на туза или нет, мой ответ на ваш вопрос, «да» или «нет», всегда будет определять местонахождение другого туза, если карта, о которой вы задаетесь вопросом, является тузом, а не той. вы указываете на.
Указывая на любую карту и спрашивая о личности другой, вы должны адаптировать стратегию ловушки, чтобы выяснить, кто должен может быть либо истинным, либо ложным в самой сложной логической головоломке. То, как вы переводите указание на любую карту в слова, как часть вашего вопроса, состоит в том, чтобы заменить фактическое утверждение «Плутон — карликовая планета» в составной головоломке выше утверждением , кто такой Рэндом — что, вы заметьте, является столь же произвольным решением, как и то, на какую карту указывать. Кого мы называем Random в вопросе, будет зависеть от того, кому мы решим задать вопрос. Это не имеет значения; это мог быть любой из трех богов.
Кого мы называем Random в вопросе, будет зависеть от того, кому мы решим задать вопрос. Это не имеет значения; это мог быть любой из трех богов.
Давайте зададим вопрос богу А и утверждаем, что Б Случайно: «Означает ли «да» «да» тогда и только тогда, когда вы Истины тогда и только тогда, когда Б Случайно?» Это эквивалентно указанию на B при вопросе о личности A. В карточной головоломке независимо от того, ответил я правдиво или случайно , вы могли бы зависеть от моего ответа «да» или «нет», чтобы найти туза с уверенность. То же самое относится и здесь. « Независимо от того, является ли А истинным, ложным или случайным, , — говорит Булос, — если вы получаете ответ «да», С либо Истина, либо Ложь, а если вы получаете ответ «джа», В либо Истина, либо Ложь. или Ложь!»
Предположим, мы получили «ja» (мы должны предположить одно или другое). Это делает Б либо Истинным, либо Ложным, чего мы и хотели — мы уже знаем, как разоблачить кого-то подобным образом: спросите Б: «Означает ли «да» «да» тогда и только тогда, когда Плутон — карликовая планета?» Поскольку мы знаем, что Плутон на самом деле является карликовой планетой, есть два возможных ответа:
1. Если B верно, то вы получите ответ «да».
Если B верно, то вы получите ответ «да».
2. Если B неверно, то вы получаете «ja», так как правильный ответ — «da», а False всегда говорит неправду.
Давайте предположим, что мы получили «da», что делает B True. Теперь задайте True свой третий и последний вопрос: «Означает ли «da» «да» тогда и только тогда, когда A является Random? Учитывая, что Random должен быть A или C, возможен только один ответ:
1. Поскольку B — True, вы получаете «da», что означает A — Random, а значит, C — False.
Резюмируя: используя всю логику Булоса, наши три вопроса, чтобы определить, какой бог является Истинным, Ложным и Случайным, звучат так:
1. Богу А: «Означает ли «да» «да», если и только если вы Истинны и тогда и только тогда, когда Б Случайно?» (Мы предполагали, что A сказал «ja», что делает B истинным или ложным).
2. Богу Б: «Означает ли «да» «да» тогда и только тогда, когда Плутон — карликовая планета?» (Мы предположили, что Б сказал «да», сделав Б Истинным.

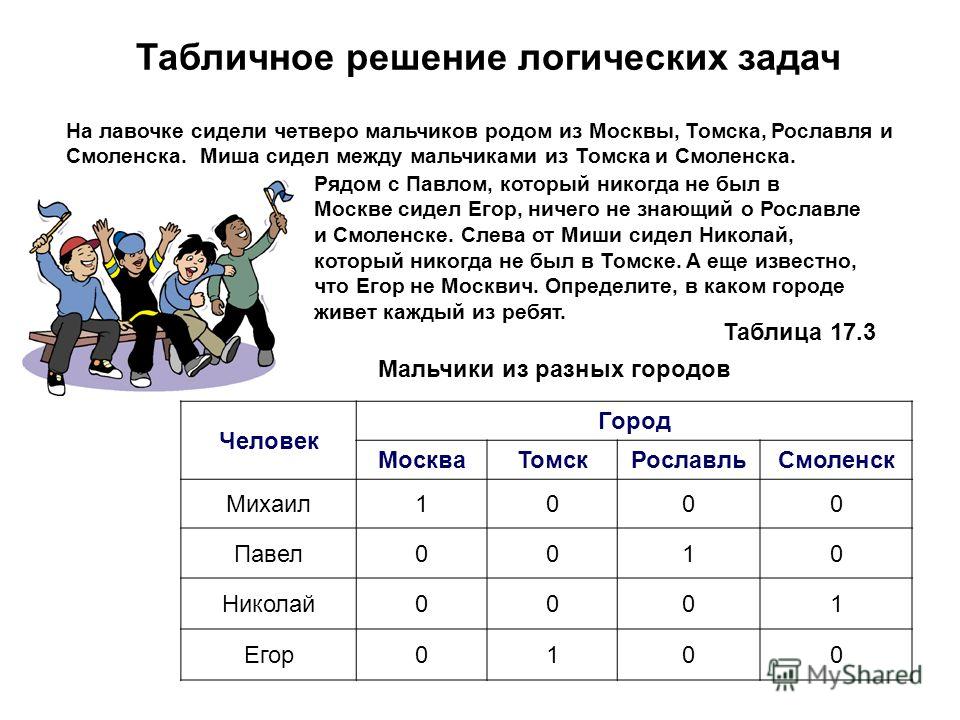
 Какой язык
изучает каждый из молодых людей?
Какой язык
изучает каждый из молодых людей? [5]
[5]


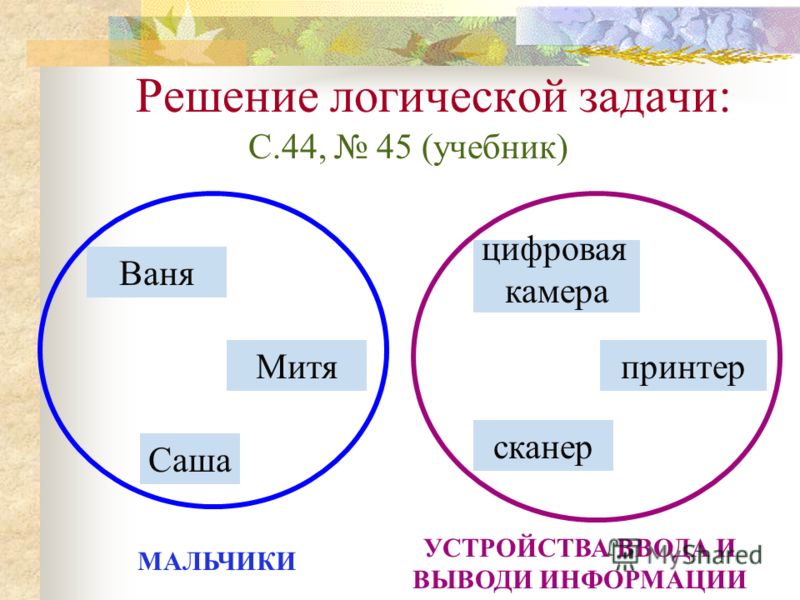 Чтобы
отмерить еще и 8 литров, надо наполнить оба сосуда.
Чтобы
отмерить еще и 8 литров, надо наполнить оба сосуда.
 Имеем четыре логические возможности, но
условию задачи удовлетворяет лишь путь АсВкКб, а остальные три пути — не
удовлетворяют. Значит, Аня была в синем платье, Варя — в красном, а Клава—в
белом.
Имеем четыре логические возможности, но
условию задачи удовлетворяет лишь путь АсВкКб, а остальные три пути — не
удовлетворяют. Значит, Аня была в синем платье, Варя — в красном, а Клава—в
белом.
 Являются читателями обеих
библиотек;
Являются читателями обеих
библиотек;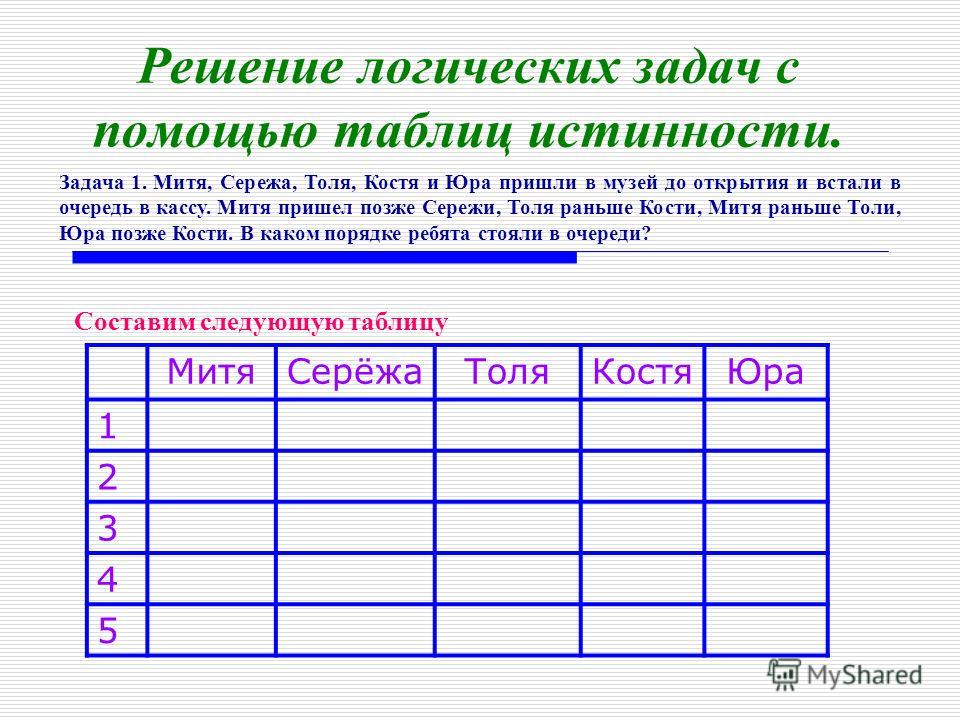 (На схеме правая часть правого круга)
(На схеме правая часть правого круга)