Масштаб математика 6 класс. Что показывает масштаб. Задачи на масштаб смотреть онлайн видео от Математика от Баканчиковой в хорошем качестве.
12+
3 месяца назад
Математика от Баканчиковой201 подписчик
Математика 6 класс. Что такое масштаб? Что означает масштаб? Как решать задачи на масштаб? Сегодня мы ответим на эти вопросы. Мы объясним Вам, что такое масштаб, зачем он нужен, и что означает масштаб. На примере двух задач, мы научим Вас решать задачи на масштаб, который увеличивает и уменьшает действительный размер или длину. Обратим Ваше внимание на то, что единицы длины в масштабе всегда должны иметь одинаковую размерность. Подробный план урока и ссылки на предыдущие уроки Вы можете найти в описании под видео.
00:00 Начало видео.
00:41 Что такое масштаб?
01:55 Что означает масштаб?
07:07 Задача 1.
12:31 Задача 2.
16:15 Подводим итоги.
Нам очень Важно Ваше мнение о наших уроках. Пишите, пожалуйста, в комментариях, что именно Вам понравилось, а что нет.
Если же у Вас появились какие-то вопросы, то мы с удовольствием ответим на них. Если урок Вам понравился, был понятен и полезен, пожалуйста, помогите нам в развитии канала, поставьте лайк и поделитесь ссылкой в соцсетях.
🙏Поддержка канала, карта Сбербанка 4274 3201 0521 8302 Маргарита Андреевна С.
Если Вы впервые на нашем канале или не смотрели предыдущие уроки, то рекомендуем Вам посмотреть следующие видео:
Обратно пропорциональные величины. Обратная пропорциональность величин в решении задач. Математика 6 класс. https://rutube.ru/video/ff33952d1503292c9c971b901399967d/
Прямо пропорциональные величины. Прямая пропорциональность величин в решении задач. Математика 6 класс. https://rutube.ru/video/f2f0c02b67f07078f68c552471b5dc41/
Решение уравнений с пропорциями в 6 классе с использованием основного свойства пропорции. Математика 6 класс. https://rutube.ru/video/dc5e4a42ea8ab624e8c29ca13f418fd8/
Пропорция по Виленкину и Мордковичу. Примеры на пропорции. Математика 6 класс. https://rutube.
Урок географии на тему «Масштаб».
6-й класс- Хабибуллина Алсу Фаритовна, педагог начальных классов
Разделы: Математика
Класс: 6
Цели:
- ввести понятие масштаба;
- учить читать масштаб;
- решать задачи, связанные с понятием масштаб
І. Организационный момент
ІІ. Устный счет:
- Выразите в километрах:
А) 32000000 см
Б) 600000 см
В) 32000 см
Г) 5000000 см
2. Выразите в метрах:
А) 32000000 см
Б) 600000 см
В) 32000 см
Г) 5000000 см
ІІІ.
Сообщение темы урока:
— Сегодня мы познакомимся с новой темой, прочитайте ее название в учебнике на странице 134 (Читаем тему и определение). Скажите, пожалуйста, где вы уже встречались с понятием масштаба? (Слушаю ответы)
ІV. Изучение нового материала:
Задача 1.Длина отрезка на карте 15 см. Найдем длину соответствующего отрезка на местности, если масштаб карты 1: 10000
Пусть x (м) – расстояние на местности.
Решение:
Расстояние |
Масштаб |
|
На карте |
15 см |
1 |
На местности |
x |
10000 |
15: x = 1:10000
x = 15·10000
150000 (см) = 1500 (м) = 1,5 (км)
Ответ: длина отрезка на местности 1,5
(км).
Задача 2.
Определите по карте расстояние от опушки леса (точка А) до точки пересечения дороги с рекой. Масштаб карты 1: 100000
— Можем сразу найти расстояние? Что нужно знать сначала? (Длину отрезка на карте)
— Как узнать длину отрезка на карте? (Измерить по карте с помощью линейки)
— Измерьте расстояние на карте (Расстояние равно 3 см)
Решение:
Пусть x (м) – расстояние на местности
| Расстояние | Масштаб |
|
На карте |
3 см |
1 |
На местности |
x |
100000 |
3: x = 1:100000
x = 3·100000
x = 300000
300000 (см) = 3000 (м) = 3 (км).
Ответ: длина отрезка на местности 3 (км).
Задача 3.
Расстояние между городами А и В на карте равно 8,5 см. Найдите расстояние между городами на местности, если масштаб карты 1:1000000
Решите эту задачу самостоятельно, а затем мы ее проверим.
Решение:
Пусть x (м) – расстояние на местности
Расстояние |
Масштаб |
|
На карте |
8,5 см |
1 |
На местности |
x |
1000000 |
8,5: x = 1:1000000
x = 8,5·1000000
x = 8500000
8500000 (см) = 85000 (м) = 85 (км).
Ответ: длина отрезка на местности 85 (км).
V. Повторение изученного материала.
Задача.
Чтобы приготовить 4 порции картофельной запеканки, нужно взять 0,44 кг картофеля. Сколько картофеля потребуется, чтобы приготовить 12 порции запеканки?
— Прочитайте задачу. Составьте пропорцию.
Решение:
Пусть x (кг) – картофеля для 12 порций
Количество порций |
Масса картофеля |
|
І |
0,44 кг |
|
ІІ. |
12 п. |
x кг |
4:12 = 0,44: x
x = 12·0,44/4
x = 1,32
1,32 кг – картофеля для 12 порций
Ответ: 1,32 картофеля потребуется, чтобы приготовить 12 порции запеканки.
VІ. Подведение итогов урока.
— Что называют масштабом карты?
— Где в практической деятельности человек пользуется этим понятием?
Упрощение выбора шкалы | Идеи
Учащиеся не могут понять, почему их нечеткие точки данных, сгруппированные в углу графика, нуждаются в улучшении. Фрейзер Скотт предлагает простые шаги, чтобы превратить ваш класс в экспертов по выбору масштаба
Студенты часто представляют вам график, показывающий весь набор данных, нанесенный в одном углу миллиметровки, с несколькими точками данных, сливающимися в неточное пятно.
Студенты не только борются с выбором подходящей шкалы, они часто не могут оценить выбранную ими шкалу, что затрудняет самокоррекцию. Это неудивительно, поскольку они видят только хорошо подобранные шкалы в ресурсах, используемых для их обучения.
Рисование графиков отнимает так много учебного времени, что его избегают ни для чего, кроме анализа данных школьного эксперимента. Однако отсутствие практики у студентов может усугубить их трудности. Я помогаю учащимся выбрать подходящие масштабы, сначала упрощая и структурируя задачу.
Уменьшите масштаб проблемы
Я начну с удаления лишних деталей: контекста, единиц измерения и меток осей. Более того, я использую набор данных 1D, поэтому масштаб всего один. Вместо того, чтобы учащиеся выбирали шкалу и выставляли баллы, я сначала сосредотачиваю их на оценке существующих шкал.
Например, покажите учащимся одномерный график с подходящим масштабом и один с теми же данными, но с неподходящим масштабом, и спросите их: «Почему масштаб на первом графике более подходит, чем масштаб на втором графике?»
Две числовые шкалы, но какая лучше и почему?
После этого смоделируйте процесс выбора подходящего масштаба, используя несколько примеров.
Это дает возможность продемонстрировать, что не обязательно есть один правильный ответ. Кроме того, важно показать трудности с построением графика в неудачно выбранном масштабе и проиллюстрировать момент, когда вы можете подумать о выборе альтернативного масштаба.
Я хотел бы дать учащимся следующие советы при демонстрации выбора подходящего масштаба:
- Постарайтесь, чтобы график заполнил большую часть пространства, используя разрывы шкалы оси, если это уместно. (Для наборов 2D-данных, по возможности, изучите миллиметровую бумагу как в альбомной, так и в портретной ориентации.)
- Чтобы упростить нанесение делений на оси, лучше всего использовать два или пять коэффициентов.
- Может быть трудно понять, подходит ли выбранный вами масштаб, пока вы не начнете рисовать график. Если сложно нанести точки, не нужно упорствовать — можно начать заново.
Перед тем, как позволить учащимся самостоятельно выбирать весы, проведите задание с опорой.
Представьте несколько примеров наборов данных с уже построенными графиками, и пусть учащиеся решат, подходят они или нет. Для тех, которые не подходят, попросите их повторно нанести данные, используя более подходящий масштаб. Я считаю, что для этих последних примеров уже визуализированные данные помогают учащимся выбрать более подходящие масштабы для набора данных.
Оценить весы
Загрузите этот рабочий лист (MS Word или pdf), чтобы учащиеся могли попрактиковаться в оценке масштабов и перерисовке неподходящих. Создайте больше одномерных графиков с различными наборами данных и масштабами, используя этот плоттер (MS Excel).
Загрузите рабочий лист с веб-сайта Education in Chemistry , чтобы учащиеся могли попрактиковаться в оценке масштабов и перерисовке неподходящих, а также создать больше одномерных графиков с различными наборами данных и масштабами с помощью графического плоттера Excel: rsc.li/2BfaozY
После этого учащимся будет разрешено самостоятельно строить наборы одномерных данных.
Наконец, весь процесс можно повторить для наборов 2D-данных. Тщательно попрактиковавшись с одномерными данными, учащиеся легко адаптируются к построению двумерных данных без дополнительных инструкций.
Только после того, как учащиеся смогут работать с точками построения безразмерных, контекстно-свободных наборов данных, я введу необходимость в названиях графиков и осей, а также в соответствующем представлении единиц измерения.
Фрейзер Скотт
Фрейзер Скотт Фрейзер Скотт — старший преподаватель химии в Университете Стратклайда.
- Математические навыки
Выбор масштаба для графика
Масштаб, выбранный для оси графика, оказывает существенное влияние на то, как аудитория интерпретирует сообщение, и является важной частью оптимизации визуализации данных. Здесь мы рассмотрим общие проблемы, с которыми сталкиваются специалисты по финансовому планированию и анализу при выборе осей диаграммы, и изложим рекомендации по передовому опыту.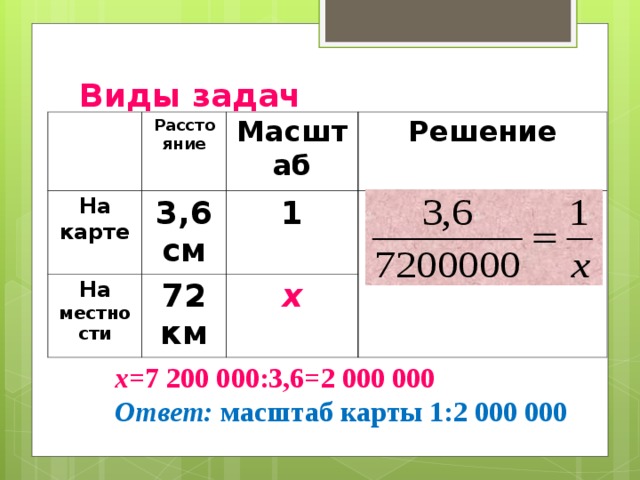
- Диапазон делений на каждом масштабе, включающий диапазон всех данных, которые должны быть нанесены на график
- Желание, чтобы масштабы были одинаковыми на всех графиках в пределах составная панель для простоты интерпретации аудиторией
- Необходимость включения определенного значения (например, нуля) в шкалу
- Необходимость в диаграмме надлежащим образом отображать ключевые тенденции в данных (часто искаженные аномалиями)
- Желание, чтобы точки данных не отображались на осях
Различные типы графиков впоследствии имеют разные принципы выбора масштабов. Подробнее о выборе правильного типа графика см. Выбор диаграммы для трендов Концепция визуализации 2 передовой практики – всегда включать ноль, если возможно данные. На рис. 1.0 зигзаги у основания столбцов предназначены для предупреждения читателя о том, что шкала не включает ноль. Однако длина столбцов в этом представлении графика не имеет смысла, поскольку они кодируют данные за вычетом произвольного значения 34.Рисунок 1.0 – шкала не начинается с нуля[/caption]Если предпочтительнее гистограмма, она всегда должна включать ноль, как показано на рисунке 2.0:
Рисунок 2.0 – шкала гистограммы всегда должна начинаться с нуля[/caption]Для на линейных и точечных диаграммах, где это уместно, ноль также должен быть включен в шкалу. Это необходимо для обеспечения согласованности с любыми другими типами графиков, представленными на той же панели.
Это также гарантирует, что тенденции в данных не усугубляются вводящим в заблуждение увеличением масштабов. Тем не менее, важные исключения см. в концепции передовой практики 3.
Для линейных диаграмм в рамках указанных выше ограничений стремитесь «использовать как можно большую часть области данных*». Что это значит? На рисунке 3.0 ниже пространство от 0 до 30 % не используется, данные занимают только 15 % вертикальной шкалы. Это тратит место и ставит под угрозу разрешение.
Рисунок 3.0 — область данных на графике не максимизируется[/caption] На рисунке 4.0 масштаб был скорректирован, чтобы использовать больше вертикального пространства, при этом гарантируя, что диапазон делений на вертикальной шкале включает все данные, которые были был построен. Это также лучше выявляет тенденцию, колебания и снижение показателя легче интерпретировать, чем на рисунке 3.
0.
Рисунок 4.0 — масштаб скорректирован для использования большего количества вертикального пространства[/caption]*William S Cleveland, The Elements of Graphich Data, 1985 интегрированы в нашу ведущую платформу финансовой аналитики Metapraxis Empower.
Связанные темы:- Выбор диаграмм для трендов
- Контрольный список для эффективной информационной панели
- Решения Metapraxis
Элемент форматированного текста позволяет создавать и форматировать заголовки, абзацы, цитаты, изображения и видео в одном месте вместо того, чтобы добавлять и форматировать их по отдельности. Просто дважды щелкните и легко создайте контент .
Редактирование статического и динамического содержимого
Элемент форматированного текста можно использовать со статическим или динамическим содержимым. Для статического контента просто перетащите его на любую страницу и начните редактирование.