Простая физика — EASY-PHYSIC
Сегодня порешаем немного заданий с модулями, вспомним, как они раскрываются, будут и уравнения, и неравенства. Поехали…
Задание 1. Решить уравнение:
Совсем простое уравнение. Раскрываем модуль со знаком «плюс» слева от точки 2 и со знаком «минус» – справа, так как в этой точке подмодульное выражение меняет знак с плюса на минус: , .
Получаем систему:
Решение найдено на промежутке , и, соответственно, этому промежутку не принадлежит, поэтому этот корень уравнения посторонний. Ответ:
Задание 2. Решить уравнение:
Приравняем к нулю оба подмодульных выражения, чтобы определить точки перемены их знаков:
Расставляем полученные точки на координатной оси, они нам ее разобьют на три промежутка. Расставляем знаки подмодульных выражений на каждом получившемся промежутке. Это просто сделать, подставив любое число из данного промежутка в модуль и определив, получается положительное число или отрицательное.
Раскрываем модуль
Теперь видно, с каким знаком надо раскрыть модуль на каждом интервале. Придется решить три уравнения, раскрыв модули с нужными знаками на каждом из них.
Интервал а) – оба модуля раскрываем со знаком «минус»:
Интервал б) – первый модуль раскрываем со знаком «минус», второй – со знаком «плюс»:
Интервал в) – оба модуля раскрываем со знаком «плюс»: – эта точка не принадлежит своему интервалу, поэтому этот корень – посторонний. Ответ: ,
Задание 3. Решить уравнение:
Решать можно либо графическим способом, либо постепенно раскрывая модули снаружи, как будто снимая листья с кочана капусты. Мы сделаем и тем способом, и другим. Сначала – аналитически (то есть раздевая капусту), снимаем первый модуль:
Раскрываем второй модуль:
Раскрываем третий модуль:
Теперь решим графически. Построим сначала прямую :
Построение прямой
Теперь «наденем» на нее модуль, то есть отразим всю ее часть, что оказалась ниже оси х, вверх:
Отражаем вверх все, что ниже оси х
Теперь построим — минус перевернет наш график вверх тормашками:
Снова отражаем
Поднимаем все вверх на три единицы:
Поднимаем вверх
«Надеваем» второй модуль, то есть снова отражаем всю отрицательную часть вверх:
Второй модуль
Снова ставим «минус»:
Снова отражаем
Снова поднимаем вверх на три единицы:
Поднимаем
Наконец, последний модуль:
Последний модуль
И проводим прямую , пересечения с которой и есть искомые корни:
Прямая пересекает график
Ответ:
Задание 4.
Решить неравенство:
Это неравенство также можно решить графически. Справа имеем прямую , слева под знаком модуля – парабола. Модуль переворачивает ту часть параболы, которая находится под осью х, вверх. Требуется найти те интервалы (отрезки), где прямая располагается выше параболы.
Графическое решение
Нас интересует, очевидно, интервал ВА, точки В и А не войдут в решение, так как неравенство строгое:
Можно также решить аналитически: раскрываем модуль с положительным и отрицательным знаками.
На рисунке показаны решения первого неравенства и второго, и область пересечения этих решений закрашена.
Пересечение решений
Ответ:
Задание 5. Решить уравнение:
Определяем точку перемены знака модуля:
Справа от этой точки модуль раскроем со знаком «минус», слева – со знаком «плюс»
Первое решение сделано на промежутке , точка этому промежутку не принадлежит, поэтому этот корень – посторонний.
Ответ:
Задание 6. Решить уравнение:
Приравниваем показатели степеней:
Определяем точки перемены знаков подмодульных выражений:
Раскрываем модуль
Раскрываем модули с соответствующими знаками на каждом из промежутков:
Интервал а) – оба модуля раскрываем со знаком «минус»:
Интервал б) – первый модуль раскрываем со знаком «минус», второй – со знаком «плюс»:
Интервал в) – оба модуля раскрываем со знаком «плюс»: -нет решений. Получается, что уравнению будет удовлетворять любое число из промежутка (]
Задание 7. Решить уравнение:
Воспользуемся формулой разности логарифмов и заменим ее частным:
По определению логарифма:
Раскрываем модуль
Интервал а) – оба модуля раскрываем со знаком «минус»: ,
Интервал б) – первый модуль раскрываем со знаком «минус», второй – со знаком «плюс»: , ,
Интервал в) – оба модуля раскрываем со знаком «плюс»: , – этот корень своему промежутку не принадлежит, он посторонний.
Ответ:
Задание 8. Решить неравенство:
В основании логарифма – модуль, и в зависимости от того, какое значение он принимает, неравенство может решаться по-разному, так как его знак меняется.
Рассмотрим два случая: когда основание логарифма от 0 до 1, и когда оно больше 1: а)
То есть область, где решение будет существовать, такая:
На этой области при решении основного неравенства мы поменяем знак:
б) Вторая область:
Знак неравенства не меняем, так как основание логарифма больше 1:
Осталось внимательно и аккуратно наложить области решения неравенства на те промежутки, где они существуют:
Наложение решений на промежутки
Ответ: ( ] [)
Задание 9. Решить неравенство:
В основании логарифма – модуль х, и в зависимости от того, какое значение он принимает, неравенство может решаться по-разному, так как его знак меняется.
Рассмотрим два случая: когда основание логарифма от 0 до 1, и когда оно больше 1: а)
Этот промежуток изображен на рисунке: Тогда знак неравенства меняем, так как основание логарифма меньше 1:
б) Знак неравенства не меняем, так как основание логарифма больше 1:
Наложим решения на области их существовавния
Наложим решения на области, к которым эти решения относятся:
Ответ: (]
Видео с вопросами: Алгебраическое решение неравенств с абсолютными значениями
Стенограмма видео
Алгебраически найдите множество решений неравенства, где единица на абсолютную величину четыре 𝑥 минус девять больше 17.
Во-первых, давайте внимательно рассмотрим неравенство. Здесь мы замечаем, что у нас есть 𝑥 в знаменателе. А это значит, что есть одно место, где 𝑥 не будет. У нас не может быть нуля в знаменателе. А это значит, что четыре 𝑥 минус девять не могут равняться нулю.
Сначала мы хотим выяснить, каким будет 𝑥, чтобы сделать это утверждение равным нулю.
Итак, мы решаем для 𝑥. Мы добавляем девять к обеим частям уравнения. Слева оно сокращается, и у нас остается четыре 𝑥, которые не могут равняться девяти. Нам все еще нужно изолировать 𝑥, и мы делаем это, разделив на четыре с обеих сторон. Четыре разделить на четыре равно единице, поэтому 𝑥 не может равняться девяти четвертям. В 𝑥 нет решения, равного девяти четвертям.
Но теперь нам нужно найти решение. А для этого нам нужно подумать о том, что мы знаем об абсолютной ценности. Когда мы решаем неравенство с абсолютным значением, мы имеем дело с двумя случаями. Положительный случай: один на четыре 𝑥 минус девять больше 17. И отрицательный случай: один на четыре отрицательных 𝑥 минус девять больше 17.
Начнем с нашего положительного случая. Наша цель — изолировать 𝑥. А для этого нам нужно вывести его из знаменателя. Умножаем обе части нашего неравенства на четыре 𝑥 минус девять на единицу. В левой части нашего уравнения эти две вещи сокращаются, в результате чего единица больше, чем 17, умноженная на четыре 𝑥 минус девять.
Чтобы избавиться от скобок, мы распределим наши 17. 17 умножить на четыре 𝑥 равно 68𝑥. 17 раз минус девять равно минус 153. Опустим наш символ неравенства. Теперь у нас есть единица больше, чем 68𝑥 минус 153.
Продолжая изолировать 𝑥, мы добавляем 153 к правой и левой сторонам. Отрицательное 153 плюс положительное 153 компенсируют друг друга. Они равны нулю. Один плюс 153 равно 154. 154 больше, чем 68𝑥. Мы можем изолировать 𝑥, разделив правую часть на 68. Чтобы все было равным, мы также должны разделить левую часть на 68. 68 разделить на 68 равно единице. 154 на 68 больше, чем 𝑥.
Я заметил, что и числитель, и знаменатель здесь четные, значит, мы можем упростить это, разделив числитель и знаменатель на два. 154 разделить на два равно 77. 68 разделить на два равно 34. 77 на 34 больше 𝑥. Или, в более распространенном формате, 𝑥 меньше 77 на 34. И это половина набора решений.
Теперь нам нужно рассмотреть отрицательный случай. Первое, что мы хотим сделать, это распределить этот негатив как на четыре 𝑥, так и на отрицательную девятку.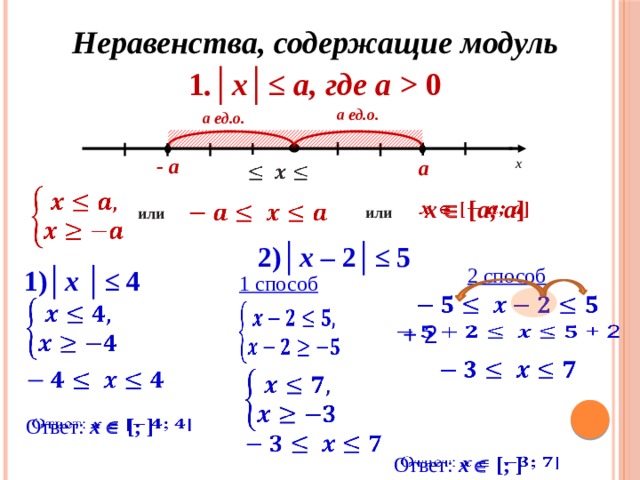
Если я это сделаю, я получу отрицательные четыре 𝑥 плюс девять больше 17.
Опять же, у нас есть 𝑥 в знаменателе, и мы хотим получить его из знаменателя. Мы можем сделать это, умножив его обратную величину слева и справа. В левой части отрицательные четыре 𝑥 плюс девять на единицу отменяют единицу на отрицательные четыре 𝑥 плюс девять. У нас остался только один. Один больше, чем 17 раз минус четыре 𝑥 плюс девять. Распределяем наши 17. 17 раз минус четыре 𝑥 равно минус 68𝑥. 17 умножить на девять равно положительному числу 153,9.0005
Теперь наше неравенство говорит о том, что единица больше, чем минус 68𝑥 плюс 153. Мы вычитаем 153 из обеих частей. Положительное 153 минус 153 равно нулю. Один минус 153 равняется минус 152, что больше, чем минус 68𝑥.
В нашем последнем шаге, чтобы изолировать 𝑥, мы делим правую часть на минус 68 и мы делим левую часть на минус 68. И вот наш ключевой момент. Когда мы делим на минусы и получаем неравенства, мы должны поменять знак. Мы разделили обе части на отрицательное число.
Следовательно, мы должны перевернуть символ неравенства.
Слева у нас есть отрицательное 152 над отрицательным 68. Отрицательное над отрицательным даст нам положительное число. Отрицательное 68 по сравнению с отрицательным 68 отменяется, оставляя нам 𝑥. 152 и 68 оба делятся на четыре. Если мы разделим 152 на четыре, мы получим 38. Если мы разделим 68 на четыре, мы получим 17. 38 на 17 меньше, чем 𝑥. Опять же, мы могли бы захотеть написать это в более общем формате. 𝑥 больше 38 на 17.
Теперь, как нам взять эти три фрагмента информации и соединить их вместе? Глядя на символ неравенства, мы видим, что имеем дело с меньше и больше чем, но не с равным. А это значит, что скобки, которые мы будем использовать, будут обращены наружу. 𝑥 должно быть больше 38 на 17 и меньше 77 на 34.
То, что мы сказали до сих пор, если вы представите числовую прямую, мы говорим, что 𝑥 не может быть равно 38 больше 17, но все между 38 больше 17 и 77 больше 34. Однако нам нужно исключить девять более четырех.
В этом домене есть дыра на девять четвертей. Чтобы исключить девять четвертей, мы можем сказать минус девять четвертей. 𝑥 попадает между тридцатью восемью семнадцатыми и семьюдесятью семью тридцатью четвертыми, за исключением девяти четвертых.
Как решить и построить график абсолютного неравенства $\\left| 2x+4 \\право|8$?
Подсказка: Чтобы решить неравенство, данное в приведенной выше задаче, выполните следующие действия: $\left| 2x+4 \справа|>8$. Мы знаем, что если нам нужно решить модульное неравенство этой формы $\left| x+a \right|>b$, то мы преобразуем эту форму модуля следующим образом: $\left( x+a \right)<-b$ и объединение с $\left( x+a \right)>b$ . Этот результат объединения дает нам решение вышеуказанного неравенства. И, используя это решение, мы также можем нарисовать график.
Полное пошаговое решение:
Неравенство формы модуля, данное в приведенной выше задаче, выглядит следующим образом:
$\left| 2x+4 \right|>8$
Теперь мы собираемся решить приведенное выше неравенство, открыв эту форму модуля, и мы получим,
$\begin{align}
& \Rightarrow \left( 2x+4 \right)< -8, \\
& \Rightarrow \left( 2x+4 \right)>8 \\
\end{align}$
Решение двух приведенных выше неравенств одно за другим, а затем объединение этих двух решений неравенства.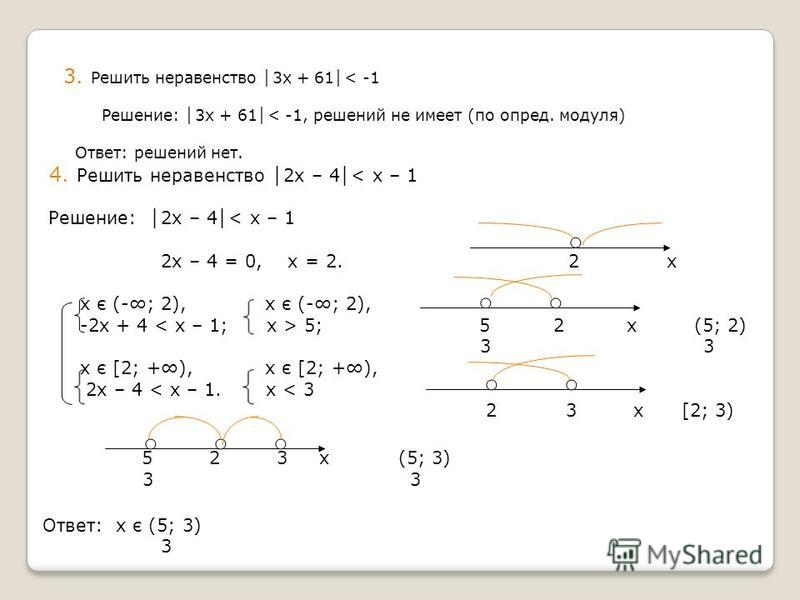
Решая первое из приведенных выше неравенств, получаем,
$\Rightarrow 2x+4<-8$
Вычитая 4 с обеих сторон в приведенном выше выражении, получаем
$\begin{align}
& \Rightarrow 2x+4-4<-8-4 \\
& \Rightarrow 2x<-12 \\
\end{align}$
Разделив 2 с обеих сторон, получим
$\begin{align}
& \Rightarrow \dfrac{2x}{2}<-\dfrac{12 }{2} \\
& \Rightarrow x<-6 \\
\end{align}$
Решая второе неравенство, получаем
$\Rightarrow 2x+4>8$
Вычитая по 4 с обеих сторон, получаем ,
$\begin{align}
& \Rightarrow 2x+4-4>8-4 \\
& \Rightarrow 2x>4 \\
\end{align}$
Деля 2 с обеих сторон получаем,
$ \begin{align}
& \Rightarrow \dfrac{2x}{2}>\dfrac{4}{2} \\
& \Rightarrow x>2 \\
\end{align}$
Теперь, объединив решение двух приведенных выше неравенств мы получаем,
$\left( x<-6 \right)\bigcup \left( x>2 \right)$
Теперь, преобразуя приведенные выше неравенства в интервальную запись, мы получаем,
Переводим $\left( x<-6 \right)$ в интервальную запись, получаем,
$\Rightarrow x\in \left( -\infty ,-6 \right)$
Преобразуем $\left( x>2 \ right)$ в интервальную запись мы получаем,
$\Rightarrow x\in \left( 2,\infty \right)$
Теперь объединение двух вышеуказанных интервалов выглядит следующим образом:
$x\in \left( -\ infty ,-6 \right)\bigcup \left( 2,\infty \right)$
Следовательно, решение приведенного выше неравенства будет следующим:
$x\in \left( -\infty ,-6 \right )\bigcup \left( 2,\infty \right)$
Теперь мы нарисуем график приведенного выше неравенства.
Для этого, прежде всего, нарисуем график модульной функции. Функция, записанная в модуль, выглядит следующим образом:
График этой функции выглядит следующим образом:
Теперь в приведенной выше задаче нам нужны значения, когда у принимает значение больше 8, поэтому мы удалим область на приведенном выше графике, где значение у меньше или равно 8.
На приведенном выше графике, как вы можете видеть, когда значение функции равно 8, приходят два значения x, т.е. (2 и -6), поэтому мы удаляем часть BFA из приведенного выше график, чтобы получить требуемый график.
Открытые отверстия в точках A и B предполагают, что при x равно -6 и 2 y не принимает значения. Таким образом, мы нарисовали график $\left| 2x+4 \справа|>8$.
Примечание: Как видите, график, который мы нарисовали выше, лежит в том же интервале, в котором мы вычислили решение неравенства.