Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Закономерность или совпадение?
Решено
Самостоятельная работа по теме: «Корни, степени, логарифмы»
Решено
Решите уравнения:
Решено
Необходимо сократить выражение
Решено
Помогите решить два примера, зарание огромное спасибо. Скриншот внутри
Скриншот внутри
Пользуйтесь нашим приложением
Использование законов экспонент для решения задач
Давайте начнем. Повторение законов экспонентыРешение для определенной переменной в формулеИспользование законов экспоненты для решения задачСловарный запас Занятие в журнале
Вы будете использовать законы экспоненты для нахождения переменных и решения задач.
Стандарты TEKS и ожидания учащихся
A(11) Численные и алгебраические методы. Студент применяет стандарты математического процесса и алгебраические методы, чтобы преобразовать алгебраические выражения в эквивалентные формы. Студент должен:
A(11)(B) упростить числовые и алгебраические выражения, используя законы показателей, включая целые и рациональные показатели
A(12) Числовые и алгебраические методы. Студент применяет стандарты математического процесса и алгебраические методы для написания, решения, анализа и оценки уравнений, отношений и функций. Ожидается, что учащийся будет:
Студент применяет стандарты математического процесса и алгебраические методы для написания, решения, анализа и оценки уравнений, отношений и функций. Ожидается, что учащийся будет:
A(12)(E) решать математические и научные формулы и другие буквенные уравнения для заданной переменной
Ресурс Цель(и)
Учитывая проблемные ситуации, связанные с показателями, учащийся будет использовать законы показателей для решения задач.
Основные вопросы
Как найти конкретную переменную в заданной формуле?
Что происходит с показателями степени, когда вы умножаете/делите степени с одинаковым основанием?
Словарь
- Экспоненты
- Законы показателей
- Замена
- Переменная
Видео
Посмотрите видео ниже, чтобы просмотреть законы экспонент и то, как их можно использовать для решения задач.
Мы собираемся изучить различные формулы на справочной таблице по математике, чтобы узнать, как найти определенную переменную в формуле. Давайте рассмотрим пример некоторых распространенных формул, используемых в стандартизированных тестах.
Найдите формулу
Используйте эту справочную таблицу по математике, чтобы найти следующие формулы. Затем сопоставьте формулы с правильной формой.
Видео
Прежде чем использовать законы экспонент для решения задач с формулами, вам, возможно, придется решить формулу для определенной переменной. Посмотрите видео ниже, чтобы узнать больше о решении формул для конкретной переменной. После просмотра видео выполните следующие задачи. Нажмите на проблему, чтобы увидеть решение.
Источник
Как решить формулу уравнения, tableclass, YouTube
Теперь вы будете использовать формулы и законы экспонент для решения задач.
Указания: Прочтите каждую задачу и определите ответ на каждую из них, используя математическую таблицу из предыдущего раздела и закон экспонент. Нажмите на плюсик, чтобы проверить решение.
1. Площадь прямоугольника равна 36x5y7. Длина прямоугольника 4x2y3. Какова ширина прямоугольника?
2. Высота трапеции 4ab3. Основания трапеции равны 2 ab и 5 ab соответственно. Чему равна площадь трапеции?
- Печать
- Поделиться
решенных примеров на экспонентах | Exponents and Powers Questions
Используйте примеры на Exponents во время подготовки и поймите несколько вопросов. Приведенные примеры вопросов используют законы показателей. Мы предоставили ответы на вопросы, чтобы вы могли проверить их и проанализировать, где вы ошиблись.
1. Оценить экспоненту?
(i) (1/2) -3
= 1/(1/2) 3
= (2/1) 3
= 8
(ii) 9002/ 5) -2
= (5/2) 2
= 25/4
(iii)(-3) -5
= 1/(-3) 4
= 1/-81
(iv) (-4) -3
= 1/(-4) 3
=1/-64
2,00 Оценить (-3/7) -4 × (-2/3) 2 ?
Решение:
Дано (-3/7) -4 × (-2/3) 2
= (7/-3) 4 × (-2/13) 900
= (-7/3) 4 × (-2/3) 2
= -7 4 /3 4 *-2 2 /3 2
9000 = = (-7 4 *-2 2 )/3 4 *3 2 =7 4 *2 2 /3 4 9 0003 = 9604/729 3. Решение: Дано (-1/2) -3 × (-1/2) -2 Поскольку основания одинаковые, показатели степени будут складываться = (-1/2) ) -3-2 = (2/-1) 5 4. Вычислить {[(-4)/2] 3 } -4 ? Решение: Данное выражение имеет вид (a m ) n = a mn Следовательно, нужно просто умножить степени. {[(-4)/2] 3 } -4 =(-4/2) -12 = (2/-4) 12 3.0 Упростить -1  Упростите и найдите значение (-1/2) -3 × (-1/2) -2 ?
Упростите и найдите значение (-1/2) -3 × (-1/2) -2 ?
=(-1/2) -5
= -32
Решение:
= (1/3 × 1/4) -1 ÷ 2 -1
= (3*4)÷1/2
= 12/(1/2)
= 12*2/1
= 24
6. Упростить: (1/ 4) -2 + (1/2) -2 + (1/5) -2 ?
Упростить: (1/ 4) -2 + (1/2) -2 + (1/5) -2 ?
Решение:
Данные (1/4) -2 + (1/2) -2 + (1/5) -2
= 4 2 +2. 2 + 5 2
= 16+4+25
= 45
7. По какому числу должно (1/3) -1 умножить так, чтобы произведение было (-3/4) -1 ?
Решение:
(1/3) -1 *x = (-3/4) -1
x= (-3/4) -1 /(1/3) -1
= (4/-3)/(3/1)
= 4*3/-3*1
= 12/-3
= -4
8. Если a = (3 /5) 2 ÷ (4/5) 0 найти значение числа -2 ?
Решение:
а = (3/5) 2 ÷ (4/5) 0
Мы знаем, что любое ненулевое число, возведенное в степень 0, равно 1.
a = (3/5) 2 ÷1
= 9/25÷1
= 9/25
a -2 = 1/a 2
= 1/(9/25) 2
= (25/9) 2
= 620/4031 90 Найти значение n.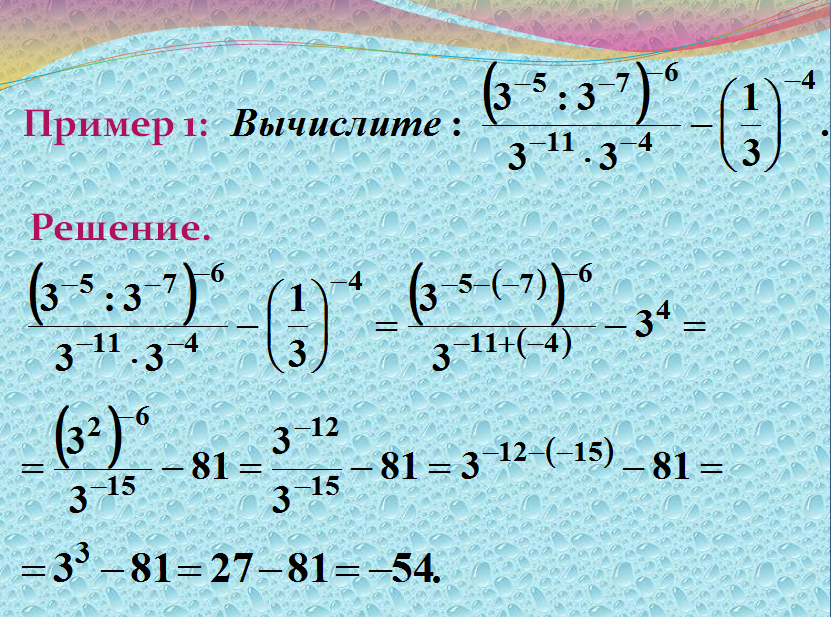

 01.18
01.18 01.18
01.18