Как решать ряды на сходимость: Как исследовать ряд на сходимость: примеры решений

9. Ряды. Высшая математика

9.1. Числовые ряды

9.2. Степенные ряды

9.1. Числовые ряды

Сходимость ряда. Сумма ряда

Пусть даны , тогда – ряд, где – член ряда.

Примеры различных рядов:

• 1+2+4+…+ – ряд сходится.
• 1–1+1–1+…+– расходится.

• – расходится (гармонический ряд).

• — сходится.

, при .

– частичная сумма

Если , то – сумма ряда. Ряд сходится, если этот предел существует, и расходится, если не существует.

Пример:

Теорема. О сходимости ряда

Сходимость ряда не измениться, если отбросить конечное число его членов.

Признаки сходимости ряда

1. Необходимый признак сходимости:
2. Достаточный признак расходимости:

Доказательство:

Если , то ряд сходится.

3. 3. Достаточный признак сходимости (для знакопостоянных рядов):
   4. Признак сравнения:

Имеем и , то

и – сходится, тогда – сходится.

или .

Если

Пример:

, а значит – сходится.

3. 3. Признак Даламбера:

Пусть , тогда при

– ряд сходится, – ряд расходится, – требуются дальнейшие исследования.

Доказательство:

Пусть , тогда , начиная с некоторого .

или

Получаем

Пример:

Ряд –

и

– ряд расходится.

• Радикальный признак Коши:

, при , .

Тогда если , то ряд сходится, если – ряд расходится.

Доказательство:

1. 1. Пусть и

Тогда, начиная с некоторого , , выполняется неравенство или .

– сходится (бесконечно убывающая геометрическая прогрессия), а значит –сходится по принципу сравнения.

• Пусть и

Тогда, начиная с некоторого , , выполняется неравенство или .

Получаем, что –расходится.

Пример:

Ряд – .

Получаем – ряд сходится.

7. Интегральный признак Коши:

, при .

Доказательство:

и

Значит, если – сходится – сходится.

Знакочередующиеся ряды

Ряды вида: , где .

Теорема Лейбница

Если и , то ряд – сходится.

Доказательство:

Пусть , тогда

. При

. ограниченна сверху .

Так как – возрастает и ограниченна сверху

Пример: – сходится.

Пусть дан ряд , тогда

1. 1. – сходится, тогда ряд – абсолютно сходится.

• – расходится и – сходится, тогда ряд сходится условно.

Теорема. Если ряд абсолютно сходится, то любая перестановка членов не меняет сумму.

Если ряд сходится условно, то подходящей перестановкой можно сделать его сумму равной любому числу и даже сделать его расходящимся.

Действия над рядами

, – абсолютно сходящиеся.

Тогда – абсолютно сходится.

Функциональные ряды

, где – функция.

Область сходимости

Пусть фиксировано.

Тогда сходится, если –точка сходимости, и расходится, если – точка расходимости.

– область сходимости.

Пример:

, то ряд сходится.

, где – остаток ряда.

Если ряд сходится, то

Мажорируемые ряды

, где – мажорируемы.

Тогда – мажоранжа (если ряд сходится), при .

Теорема. О непрерывности суммы ряда

Пусть .

– сходится и , – непрерывна на .

Тогда – непрерывна на .

Доказательство:

(из определения непрерывности)

,

где .

При и .

Отсюда

Пример:

на

, разрыв при

Теорема.

О почленном интегрировании ряда

Пусть на – мажорируемый, – интегрируемы на ( – существует). Тогда

Теорема. О почленном дифференцировании ряда

Пусть на – мажорируемый, – дифференцируемы на (– существует). Тогда

9.2. Степенные ряды

, где – коэффициент, – произвольная точка, .

Частный случай:

Теорема Абеля: У каждого степенного ряда существует радиус сходимости.

, при

– сходится

– расходится.

– точка сходимости.

Если , то , т.е. – мажорируемый.

Область сходимости:

– сходится при

Пример:

– сходится при .

Теорема. Радиус сходимости определяется как .

Доказательство:

Возьмем , тогда

По признаку Даламбера:

Отсюда или

Внутри радиуса сходимости степенной ряд мажорируем, его сумма непрерывна, его можно почленно интегрировать и дифференцировать.

Пример:

или при ряд сходится.

, значит ряд сходится при любых

, значит при ряд сходится.

Разложение функций в степенной ряд

– ряд Тейлора.

, тогда

При

– ряд Маклорена.

Разложение некоторых функций в степенной ряд

или – любое.

или – любое.

или – любое.

1. 1. или при ряд сходится

или при ряд сходится

Сумма знакочередующегося ряда имеет погрешность не превосходящую первого отброшенного члена.

Пример:

Имеем

Получаем

Считая, что

Пример:

Контрольные примеры:

1. 1. Разложим в ряд и посчитаем

1. Разложим в ряд и посчитаем

Пример разложения функции в ряд Маклорена:

Получаем

Необходимый признак сходимости числового ряда. Вторая часть.

Высшая математика » Числовые ряды » Необходимый признак сходимости числового ряда » Вторая часть.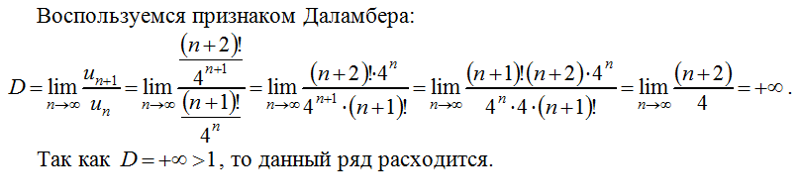 {\infty}\sin n$.

Решение

Общий член ряда имеет вид: $u_n=\sin n$. Поговорим о нём несколько неформально. Итак, что мы знаем о синусе? Мы знаем, что эта функция ограничена, и что она периодическая. Т.е. значения синуса повторяются и повторяются – до бесконечности. Это кстати, легко увидеть по графику функции $y=\sin x$. Обратите внимание, что если мы «пойдём в бесконечность» по синим точкам, то получим в пределе единицу; а если по красным точкам – то в пределе будет ноль:

Иными словами, совершенно логичным будет предположение, что $\lim_{n\to\infty}\sin n$ не существует, и ряд будет расходиться. Однако мы можем упростить себе задачу: нам ведь достаточно показать, что $\lim_{n\to\infty}\sin n\neq 0$. Итак, цель решения определена: показать, что предел общего члена ряда не равен нулю.

Пойдём методом от противного. Предположим, что $\lim_{n\to\infty}\sin n=0$. Если предел некоей последовательности равен числу $a$, то и предел любой её подпоследовательности также равен числу $a$. 2}}=\frac{1}{2}. $$

Так как предел общего члена ряда не равен нулю, т.е. $\lim_{n\to\infty}u_n\neq 0$, то необходимый признак сходимости не выполнен. Следовательно, ряд расходится.

Ответ: ряд расходится.

Первая часть

Вторая часть

Вернуться к списку тем

Задать вопрос на форуме

Записаться на занятия

Онлайн-занятия по высшей математике

Исчисление II — сходимость/расхождение рядов

Онлайн-заметки Пола
Главная / Исчисление II / Серии и последовательности / Сходимость/Расхождение рядов

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 10.4: Сходимость/расхождение серии

В предыдущем разделе мы потратили некоторое время на знакомство с рядами и кратко определили сходимость и расхождение. Прежде чем беспокоиться о сходимости и расхождении рядов, мы хотели убедиться, что начали чувствовать себя комфортно с обозначениями, связанными с рядами, и с некоторыми из различных манипуляций с рядами, которые нам иногда нужно будет делать.

Как отмечалось в предыдущем разделе, большая часть того, что мы там делали, в этой главе будет делаться немного. Итак, настало время поговорить о сходимости и расхождении рядов, так как это будет темой, которую мы в той или иной степени будем касаться почти во всех оставшихся разделах этой главы. \infty n \] 9\infty\]

сходится или расходится. В данном случае это не так уж сложно. Предел членов последовательности:

\[\ mathop {\lim }\limits_{n \to \infty} \frac{{n\left({n + 1} \right)}}{2} = \infty \]

Следовательно, последовательность частичных сумм расходится к \(\infty \), а значит, расходится и ряд.

Итак, как мы видели в этом примере, нам нужно было знать довольно непонятную формулу, чтобы определить сходимость этого ряда. Вообще найти формулу для общего члена в последовательности частичных сумм — очень трудный процесс. На самом деле после следующего раздела мы не будем много делать с частичными суммами рядов из-за чрезвычайной трудности, с которой столкнулись при нахождении общей формулы. Это также означает, что мы не будем много работать со значением ряда, поскольку для получения значения нам также нужно знать общую формулу для частичных сумм. 2} — 1}}} = \ frac {3} {4} — \ frac {1} {{2n}} — \frac{1}{{2\left( {n + 1} \right)}}\] 9п}} \]

Показать решение

В этом случае нам действительно не нужна общая формула для частичных сумм, чтобы определить сходимость этого ряда. Давайте просто запишем первые несколько частичных сумм.

\[\begin{align*}&{s_0} = 1\\ & {s_1} = 1 — 1 = 0\\ & {s_2} = 1 — 1 + 1 = 1\\ & {s_3} = 1 — 1 + 1 — 1 = 0\\ & etc.\end{align*}\]

9{n — 1}}}}} = \frac{3}{2}\]

Как мы уже отмечали, не стоит увлекаться определением общей формулы последовательности частичных сумм. Будет только один тип серии, где вам нужно будет определить эту формулу, и в этом случае процесс не так уж и плох. Фактически, вы уже знаете, как выполнять большую часть работы в процессе, как вы увидите в следующем разделе.

Итак, мы определили сходимость четырех рядов. Два ряда сошлись, а два разошлись. Давайте вернемся назад и рассмотрим термины ряда для каждого из них. Для каждого из рядов возьмем предел, когда \(n\) стремится к бесконечности членов ряда (не частичных сумм!!). 9{n — 1}}}} = 0 & \hspace{0,75 дюйма} & {\mbox{эта серия сходится}}\end{выравнивание*}\]

Обратите внимание, что для двух сходящихся рядов сам член ряда в пределе был равен нулю. Это всегда будет верно для сходящихся рядов и приводит к следующей теореме.

Теорема

Если \(\sum {{a_n}} \) сходится, то \(\mathop {\lim }\limits_{n \to \infty} {a_n} = 0\).

Доказательство

Сначала предположим, что ряд начинается с \(n = 1\). Если это не так, мы можем изменить вещи соответствующим образом ниже. Тогда частичные суммы равны 9\infty \) также сходится и что \(\mathop {\lim }\limits_{n \to \infty} {s_n} = s\) для некоторого конечного значения \(s\). Однако, поскольку \(n — 1 \to \infty \) как \(n \to \infty \), мы также имеем \(\mathop {\lim }\limits_{n \to \infty} {s_{n — 1 }} = с\).

Теперь у нас есть,

\[\ mathop {\lim }\limits_{n \to \infty} {a_n} = \mathop {\lim }\limits_{n \to \infty} \left({{s_n} — {s_{n — 1 }}} \right) = \mathop {\lim }\limits_{n \to \infty} {s_n} — \mathop {\lim }\limits_{n \to \infty} {s_{n — 1}} = с — с = 0\] 92}}}} \]

В обоих случаях члены ряда равны нулю в пределе, когда \(n\) стремится к бесконечности, но сходится только второй ряд. Первый ряд расходится. Прежде чем мы сможем это доказать, потребуется пара разделов, поэтому на данный момент, пожалуйста, поверьте в это и знайте, что вы сможете доказать сходимость этих двух рядов за пару разделов.

Опять же, как отмечалось выше, все, что делает эта теорема, — это требование сходимости ряда. Чтобы ряд сошелся, его члены в пределе должны стремиться к нулю. Если члены ряда не стремятся к нулю в пределе, то ряд не может сходиться, поскольку это нарушит теорему.

Это приводит нас к первому из многих тестов на сходимость/расхождение ряда, которые мы увидим в этой главе.

Проверка расходимости

Если \(\mathop {\lim }\limits_{n \to \infty } {a_n} \ne 0\), то \(\sum {{a_n}} \) будет расходиться.

Опять же, НЕ используйте этот тест неправильно. Этот тест говорит только о том, что ряд гарантированно расходится, если члены ряда не стремятся к нулю в пределе. Если члены ряда действительно стремятся к нулю, ряд может сойтись, а может и не сойтись! Снова вспомним следующие две серии, 92}}}} & \hspace{0,5 дюйма} & {\mbox{сходится}}\end{выравнивание*}\]

Одна из наиболее распространенных ошибок, которую делают учащиеся, когда они впервые попадают в серию, состоит в том, чтобы предположить, что если \(\mathop {\lim }\limits_{n \to \infty} {a_n} = 0\), то \(\ сумма {{a_n}} \) будет сходиться. Это просто невозможно гарантировать, поэтому будьте осторожны!

Давайте кратко рассмотрим пример использования этого теста.

Пример 5 Определите, является ли следующий ряд сходящимся или расходящимся. \infty {\left({{a_n} \pm {b_n}} \right)} \). Кроме того, эти ряды будут иметь следующие суммы или значения. 9\infty {{b_n}} \]

Мы увидим пример этого в следующем разделе после того, как получим еще несколько примеров. В этот момент просто помните, что сумма сходящихся рядов сходится, и умножение сходящегося ряда на число не изменит его сходимости.

Нам нужно быть немного осторожными с этими фактами, когда речь идет о расходящихся рядах. В первом случае, если \(\sum {{a_n}} \) расходится, то \(\sum {c{a_n}} \) также будет расходиться (при условии, что \(c\) не равно нулю), поскольку умножение ряда, который имеет бесконечное значение или не имеет значения, на конечное значение ( 9\infty {\left( {{a_n} \pm {b_n}} \right)} \) сходящийся ряд.

Теперь, поскольку основной темой этого раздела является сходимость ряда, следует упомянуть о более сильном типе сходимости. Говорят, что ряд \(\sum {{a_n}} \) сходится абсолютно , если \(\sum {\left| {{a_n}} \right|} \) также сходится. Абсолютная сходимость сильнее сходимости в том смысле, что абсолютно сходящийся ряд также будет сходящимся, но сходящийся ряд может быть абсолютно сходящимся, а может и не быть.

На самом деле, если \(\sum {{a_n}} \)сходится и \(\sum {\left| {{a_n}} \right|} \) расходится, то ряд \(\sum {{a_n}} \ ) называется условно сходящимся .

На данный момент у нас нет под рукой инструментов, чтобы должным образом подробно исследовать эту тему, и у нас нет под рукой инструментов, чтобы определить, является ли ряд абсолютно сходящимся или нет. Поэтому пока не будем больше ничего говорить на эту тему. Когда у нас, наконец, будут инструменты для более подробного обсуждения этой темы, мы вернемся к ней. А пока не беспокойтесь об этом. Эта идея упоминается здесь только потому, что мы уже обсуждали конвергенцию в этом разделе, и она связана с последней темой, которую мы хотим обсудить в этом разделе.

В предыдущем разделе после того, как мы представили идею бесконечного ряда, мы отметили тот факт, что мы не должны думать о бесконечном ряду как о бесконечной сумме, несмотря на то, что обозначение, которое мы используем для бесконечного ряда, кажется, подразумевает что это бесконечная сумма. Пришло время кратко обсудить это.

Во-первых, нам нужно представить идею перестановки . Перестановка ряда — это именно то, на что это могло бы звучать, это тот же ряд с членами, переставленными в другом порядке. 9{n + 1}}}}{n}} = 1 — \frac{1}{2} + \frac{1}{3} — \frac{1}{4} + \frac{1}{5} — \frac{1}{6} + \frac{1}{7} — \frac{1}{8} + \cdots = \ln 2\label{eq:eq1}\end{equation}\]

Поскольку этот ряд сходится, мы знаем, что если мы умножим его на константу \(c\), его значение также будет умножено на \(c\). Итак, давайте умножим это на \(\frac{1}{2}\), чтобы получить

. \[\begin{equation}\frac{1}{2} — \frac{1}{4} + \frac{1}{6} — \frac{1}{8} + \frac{1}{{ 10}} — \frac{1}{{12}} + \frac{1}{{14}} — \frac{1}{{16}} + \cdots = \frac{1}{2}\ln 2 \метка{уравнение:уравнение2}\конец{уравнение}\]

Теперь давайте добавим ноль между каждым членом следующим образом.

\[\begin{equation}0 + \frac{1}{2} + 0 — \frac{1}{4} + 0 + \frac{1}{6} + 0 — \frac{1}{8} + 0 + \frac{1}{{10}} + 0 — \frac{1}{{12}} + 0 + \cdots = \frac{1}{2}\ln 2\label{eq:eq3} \конец{уравнение}\]

Обратите внимание, что это не изменит значение ряда, поскольку частичные суммы для этого ряда будут частичными суммами для \(\eqref{eq:eq2}\), за исключением того, что каждый член будет повторяться. Однако повторение членов в ряду не повлияет на его предел, поэтому и \(\eqref{eq:eq2}\), и \(\eqref{eq:eq3}\) будут одинаковыми.

Мы знаем, что если два ряда сходятся, мы можем сложить их, складывая член за членом, и таким образом добавить \(\eqref{eq:eq1}\) и \(\eqref{eq:eq3}\), чтобы получить,

\[\begin{equation}1 + \frac{1}{3} — \frac{1}{2} + \frac{1}{5} + \frac{1}{7} — \frac{1} {4} + \cdots = \frac{3}{2}\ln 2 \label{eq:eq4}\end{equation}\]

Теперь обратите внимание, что члены \(\eqref{eq:eq4}\) — это просто члены \(\eqref{eq:eq1}\), переставленные так, что каждый отрицательный член идет после двух положительных членов. Однако значения определенно отличаются, несмотря на то, что термины одинаковы.

Также обратите внимание, что это не один из тех «трюков», которые вы иногда видите, когда вы получаете противоречивый результат из-за трудно обнаруживаемой математической/логической ошибки. Это вполне реальный результат, и мы не допустили никаких логических ошибок/ошибок.

Вот хороший набор фактов, которые определяют эту идею о том, когда перестановка приведет к другому значению ряда.

Факты

Учитывая ряд \(\sum {{a_n}} \),

1. Если \(\displaystyle \sum {{a_n}} \) абсолютно сходится и его значение равно \(s\), то любая перестановка \(\displaystyle \sum {{a_n}} \) также будет иметь значение \(s\).
2. Если \(\displaystyle \sum {{a_n}} \) условно сходится и \(r\) является любым действительным числом, то существует перестановка \(\displaystyle \sum {{a_n}} \), значение которой будет быть \(г\).

Опять же, у нас пока нет под рукой инструментов, позволяющих определить, является ли ряд абсолютно сходящимся, поэтому пока не беспокойтесь об этом. Это здесь просто для того, чтобы убедиться, что вы понимаете, что мы должны быть очень осторожны, думая о бесконечном ряду как о бесконечной сумме. Бывают моменты, когда мы можем ( 9{п + 1}}}}{п}} \]

должны быть условно сходящимися, так как две перестановки дали два отдельных значения этого ряда.