9 класс. Геометрия. Соотношения между сторонами и углами треугольника. Синус, косинус и тангенс угла. — Решение задач.
Комментарии преподавателяРешение задач по теме «Синус, косинус, тангенс угла»
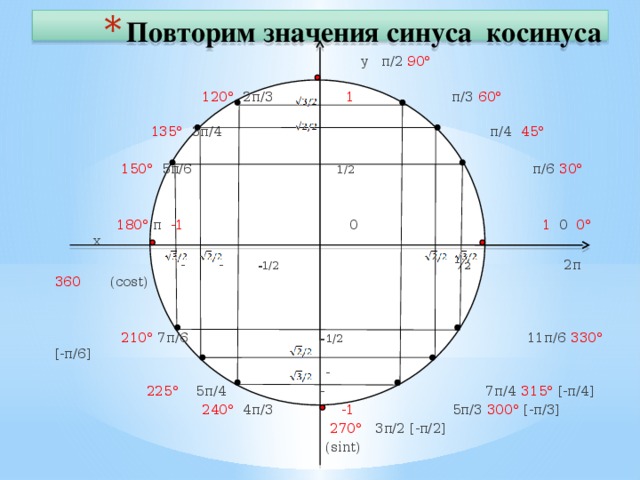
Напомним, угол определяет единственную точку М (хα; уα) на единичной полуокружности. На Рис. 1 представлена единичная полуокружность, она описывается следующим образом:
Рис. 1
, первое из этих выражений – это вся окружность, а второе ограничивает нас только верхней полуплоскостью.
Так вот, первую координату точки М (абсциссу) назвали косинусом угла. Вторую координату – ординату – назвали синусом угла.
Вот основные определения:
М = M (,).
tg α = ; ctg α =
Далее вспомним основное тригонометрическое тождество и основные формулы. Они здесь выписаны, проанализируем их и вспомним, откуда они получились.
, tg α · ctg α = 1 или
Во-первых, они получились из определений.
И во-вторых, из уравнения окружности.
Если есть Ð α, то ему соответствует единственная точка на окружности, и координаты этой точки назвали синусом угла и косинусом угла. Но это точка на единичной окружности, а любая точка единичной окружности подчиняется уравнению окружности ,
х – это косинус, а у – это синус, значит, для любого Ð α. Напомним, мы рассматриваем углы из отрезка [0°; 180°].
Рис. 2
Далее вспомним (Рис. 2) важные формулы для координат точки А (хА; уА)
α Î [0°; 180°].
Рис. 3
Итак, мы имеем синус, косинус, тангенс, котангенс для тупых углов в том числе, т. е. мы рассматриваем углы [0°; 180°]. Но при этом следует уметь вычислять и синус, и косинус таких углов. Этому помогают формулы приведения (Рис. 3). Напомним их:
при 0º£α £90º;
Полезно вспомнить значение тригонометрических функций основных острых углов.
Только что мы видели, что по формулам приведения к ним сводятся значения тригонометрических функций тупых углов.
|
|
30° |
45° |
60° |
|
sin |
½ |
|
|
|
cos |
|
|
½ |
|
tg |
|
1 |
|
|
ctg |
|
1 |
|
Итак, мы вспомнили важную таблицу для тригонометрических функций острых углов.
Рассмотренная таблица и формулы приведения позволяют решать многие типовые задачи.
Найти: sin 120°, cos 120°, tg 120°, ctg 120°.
Решение: сначала формальное решение.
sin 120° = sin (180° – 60°) = sin 60° по формулам приведения, а по таблице sin 60° = .
Часть задачи решена:
cos 120° = cos (180° – 60°) = – cos 60° = – ½ .
Таким образом, мы нашли синус и косинус тупого угла 120°.
Теперь посмотрим и проиллюстрируем этот факт на графике.
Рис. 4
Строим единичную полуокружность, на ней угол 120°. Напомним, что этот угол отсчитан против часовой стрелки от положительного направления оси Ох.
Он высекает единственную точку М2 на единичной полуокружности.
Выясняется, что оставшийся угол между отрицательной полуосью Ох и лучом ОМ2 равен 60° и еще один угол 60° (между положительной полуосью Ох и лучом ОМ1). Для угла 60° синус совпадает с синусом 120°, а косинус 60° и косинус 120° – это противоположные числа. Таким образом, для данной типовой задачи мы нашли синус и косинус 120° и проиллюстрировали факт нахождения на чертеже.
Таким образом, для данной типовой задачи мы нашли синус и косинус 120° и проиллюстрировали факт нахождения на чертеже.
Осталось найти тангенс и котангенс 120°.
Формулы известны, находим:
tg 120° = ;
ctg 120° =
Ответ:
sin 120° = , cos 120° = — ½ , tg 120° = , ctg 120° =
Задача решена.
Использованы и таблица, и формулы приведения.
Следующая типовая задача. Задана одна функция, найти другие функции или другую функцию.
Задача. Найдите , если = ¼ , α Î [0; 180°]. Сначала формальное решение. Мы имеем основное тригонометрическое тождество, которое связывает между собой и синус, и косинус: , откуда (Ответ).
Два ответа. Откуда они появились? Проиллюстрируем этот факт на чертеже (Рис. 5).
Единичная полуокружность, синус какого-то угла, неизвестно пока, какого, равна ¼. Перпендикуляр к линии синусов (оси ординат), проведенный в точке у = ¼, высвечивает две точки на единичной окружности.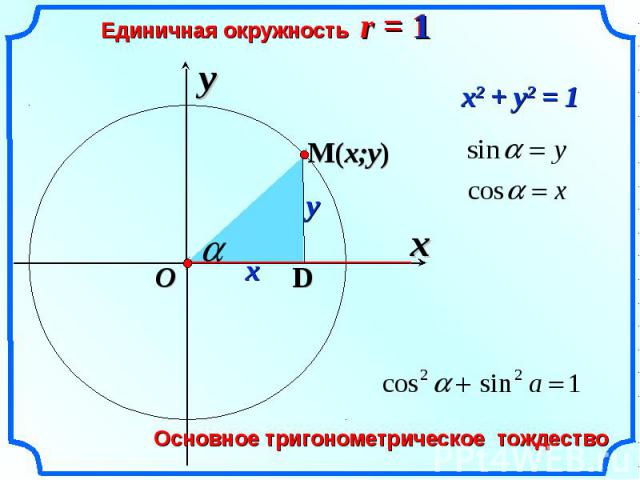 Двум точкам соответствуют два угла. Один угол α1, второй угол – α2.
Двум точкам соответствуют два угла. Один угол α1, второй угол – α2.
Угол α1 имеет , Угол α2 имеет .
Сделаем такое примечание: значение = ¼ определяет два угла – α1 и α2 = 180° – α1 , причем
(синусы равны одному и тому же числу), а косинусы – разные: ,
Рис. 5
В следующей задаче, наоборот, задано значение , требуется найти значение . И понять, в чем разница между этой задачей и предыдущей.
Задача. Найдите , если = , α Î [0; 180°].
Рис. 6
Как всегда, сначала формальное решение без чертежа:
по основному тригонометрическому тождеству , откуда , два ответа, но вспоминаем, что синус меняется в пределах [0; 1], поэтому выбираем и получаем единственный ответ.
Теперь проиллюстрируем все это на чертеже (Рис. 6).
Как обычно, на рисунке – единичная полуокружность, линия косинусов (ось абсцисс), на ней точки – 1, 0, 1, а у нас абсцисса (косинус) равна .
Перпендикуляр высвечивает единственную точку на единичной окружности и единственный Ðα. Он здесь тупой. Синус тоже имеет единственное значение. Сформулируем такое примечание: значение определяет единственный ÐαÎ[0°; 180°]. Задача решена.
Формулировка следующей задачи.
Задача. Найдите угол между лучом ОА и положительной полуосью Ох, если точка А имеет координаты ( ; 1 ).
Чертеж (Рис. 7).
Рис. 7
На рисунке – точка А (; 1), и надо найти угол, который обозначим α.
Известны координаты точки А.
Используем специфику исходных данных при решении (Рис. 8). Рассмотрим треугольник АОА1.
Рис. 8
Он прямоугольный, и катеты его известны. Первый катет равен 1, второй катет длиной .
Следовательно, tg ÐАОА1 = угол ÐАОА1 = 30°, искомый угол α = 180° – 30° = 150°
Ответ получен, но мы продемонстрируем другой способ его получения.
Сначала найти длину отрезка АО, ведь координаты точки А известны и координаты точки О известны.
Далее по формулам для координат точки найти косинус угла, синус угла. В любом случае специфика конкретных исходных данных нам позволила мгновенно найти угол. Задача решена.
Итак, мы повторили теорию по теме «Синус, косинус, тангенс угла» и решили типовые задачи.
ИСТОЧНИК
http://interneturok.ru/ru/school/geometry/9-klass/sinus-kosinus-i-tangens-ugla/reshenie-zadach-4
http://5klass.net/datas/algebra/Trigonometricheskie-funktsii/0007-007-Svojstva-sinusa-kosinusa-tangensa-i-kotangensa.jpg
http://lmenripacha.science/pic-reshak.ru/reshebniki/geometriya/10/wbatanasyan9/images/30.gif
http://fastform.ru/wp-content/uploads/media/%D0%9A%D0%BE%D0%BD%D1%81%D0%BF%D0%B5%D0%BA%D1%82-%D1%83%D1%80%D0%BE%D0%BA%D0%B0-%D0%BF%D0%BE-%D0%B3%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%B8-%D0%BD%D0%B0-%D1%82%D0%B5%D0%BC%D1%83-%D0%A1%D0%B8%D0%BD%D1%83%D1%81%D0%BA%D0%BE%D1%81%D0%B8%D0%BD%D1%83%D1%81-%D1%82%D0%B0%D0%BD%D0%B3%D0%B5%D0%BD%D1%81-%D1%83%D0%B3%D0%BB%D0%B0/image3. gif
gif
тригонометрия — Почему так много ошибок в законах синусов и косинусов?
спросил
Изменено 4 года назад
Просмотрено 7к раз
$\begingroup$
Я вычислял углы треугольника со сторонами a = 17, b = 6 и c = 15, используя закон косинусов, чтобы найти первый угол, а затем закон синусов, чтобы найти два других угла. Я следую принято называть углы, противолежащие этим сторонам, А, В и С соответственно. Вот мои результаты: 92}{2(6)(17)}) = 60,647$ градусов до 3 д.п.
$ B = \arcsin( \frac {6 \sin C}{15}) = 20,405$ градусов до 3 д.п.
$ A = \arcsin( \frac {17 \sin B}{6}) = 81,051$ градусов до 3 д.п.
Ясно, что их добавление должно дать $180$ градусов, но это дает 162 градуса на 3 н.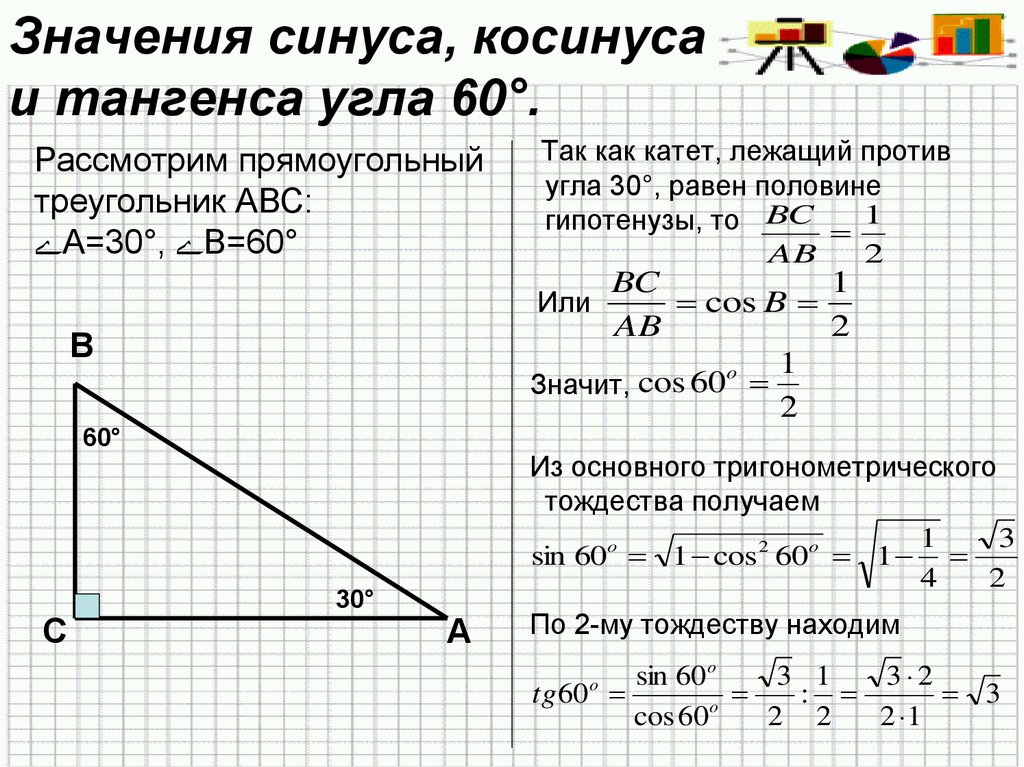 ф. Предполагая, что я не сделал никаких ошибок, ошибка кажется довольно высокой, и мне просто интересно, знает ли кто-нибудь, почему это так? Это кажется достаточно высоким, чтобы оспорить действительность законов.
ф. Предполагая, что я не сделал никаких ошибок, ошибка кажется довольно высокой, и мне просто интересно, знает ли кто-нибудь, почему это так? Это кажется достаточно высоким, чтобы оспорить действительность законов.
- тригонометрия
$\endgroup$
8
$\begingroup$
Хорошо, я вычислил закон косинусов 3 раза и получил 60,647, 20,404 и 98,949 соответственно для углов A, B и C. Помните, что закон косинусов не имеет неоднозначного случая, в отличие от закона синусов. Я подозреваю (без дальнейшего расследования), что он может быть виновником. Мой совет: всегда используйте закон косинусов, когда можете. В этом случае, когда известны все стороны, явно имеет место закон косинусов 9.0005
$\endgroup$
$\begingroup$
Переход от закона косинусов к закону синусов может привести к двусмысленному случаю и созданию посторонних решений, поэтому лучше придерживаться закона косинусов, насколько это возможно.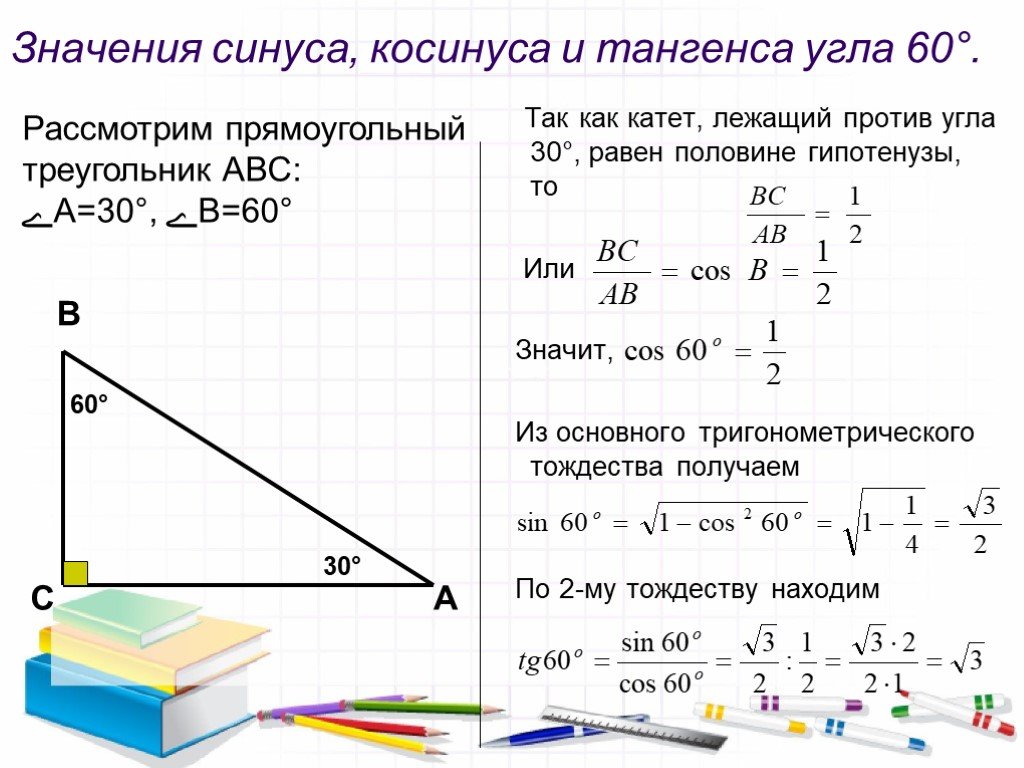 Если вы измените закон синусов, вы можете проверить свои результаты, подставив ВСЕ свои стороны и углы в пропорцию. Если вы не получите эквивалентных результатов, у вас есть лишнее решение, и вам нужно будет переработать задачу, используя дополнение угла, которое вы изначально получили.
Ссылка ведет на Google Slides, которую я подготовил для своих учеников. Тестирование решений с использованием закона синусов
Если вы измените закон синусов, вы можете проверить свои результаты, подставив ВСЕ свои стороны и углы в пропорцию. Если вы не получите эквивалентных результатов, у вас есть лишнее решение, и вам нужно будет переработать задачу, используя дополнение угла, которое вы изначально получили.
Ссылка ведет на Google Slides, которую я подготовил для своих учеников. Тестирование решений с использованием закона синусов
$\endgroup$
1
$\begingroup$
Помните, что $$sin(180-θ)=sinθ$$
$sin(180-81.051)=sin(98.949)=0.987$
$60.647+20.405+81.051=162.103$
$60.647+20.405+98.949=180.001$
Правильный угол должен быть 98,949
С точки зрения графика положительный косинус означает острый угол (Q1), а отрицательный косинус означает тупой угол (Q2).
Но с синусом мы должны проверить, находится ли угол в Q1 или Q2, поскольку он имеет те же значения синуса 0,9.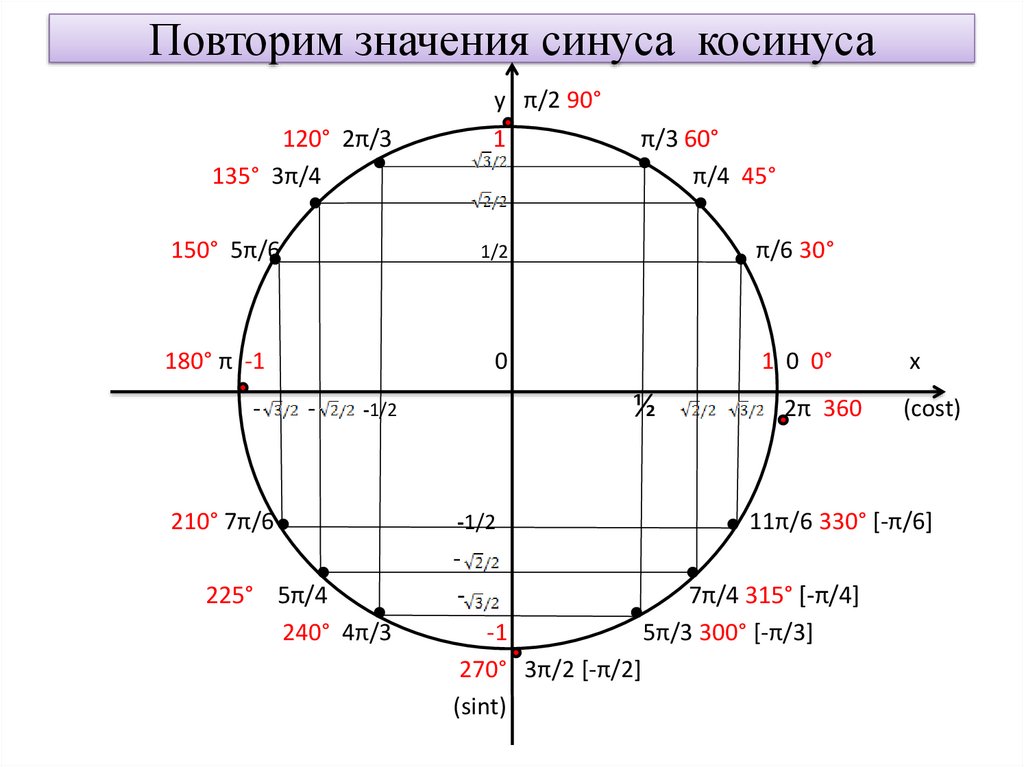 87. Следовательно, мы вычисляем, какая степень двух в сумме дает 180. Поэтому, как упоминалось другими, целесообразно использовать закон косинусов.
87. Следовательно, мы вычисляем, какая степень двух в сумме дает 180. Поэтому, как упоминалось другими, целесообразно использовать закон косинусов.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Решение задач 2-D и 3-D тригонометрии с использованием правил синуса и косинуса – Национальная учебная программа (профессиональная) по математике, уровень 4
Пространство, форма и измерение: решение задач путем построения и интерпретации тригонометрических моделей
Дилан Буса
К концу этого раздела вы сможете:
- Правильно применять правило синусов для решения 2-х и 3-х мерных задач.

- Правильно применяйте теорему косинусов для решения двухмерных и трехмерных задач.
Что вы должны знать
Перед запуском этого устройства убедитесь, что вы можете:
- Определите стороны и углы прямоугольного треугольника, используя три основных тригонометрических соотношения. Обратитесь к предметному результату 3.6 уровня 2, модулям 1 и 2, если вам нужна помощь в этом.
- Используйте формулы приведения для упрощения тригонометрических соотношений. Обратитесь к предметному результату 3.3, разделы 1 и 2 уровня 3, если вам нужна помощь.
- Определите и используйте правило синусов для решения двумерных задач. Обратитесь к предметному результату 3.3 блоков 6 и 8 уровня 3, если вам нужна помощь.
- Сформулируйте и используйте правило косинусов для решения двумерных задач. Обратитесь к предметному результату 3.3, блокам 7 и 8 уровня 3, если вам нужна помощь.
- Назовите и используйте формулы составного угла и двойного угла.
 Обратитесь к блоку 1 этого предметного результата, если вам нужна помощь в этом.
Обратитесь к блоку 1 этого предметного результата, если вам нужна помощь в этом.
Введение
Мы узнали о правиле синусов и правиле косинусов на уровне 3, предметный результат 3.3, блоки 6 и 7. Помните, что эти правила дают нам способ найти длины неизвестных сторон и размеры неизвестных углов в непрямоугольных треугольниках. .
Прежде чем продолжить, вы должны пересмотреть результаты 3.3 предмета 3.3, блоки 6, 7 и 8.
Проверка правил синусов и косинусов
Прежде чем мы узнаем что-то новое, давайте повторим то, что мы уже знаем.
Правило синусов:
В любом треугольнике [latex]\scriptsize \Delta ABC[/latex]:
Правило косинуса:
В любом [latex]\scriptsize \Delta ABC[/latex]:
- Правило косинуса работает, когда мы знаем длины любых двух сторон и размер в комплекте угол .
- Левая сторона формулы всегда равна стороне , противоположной углу, косинус которого мы берем.

Используйте правило синусов, если:
- прямой угол не указан
- даны две стороны и угол (не прилежащий угол)
- даны два угла и сторона.
Используйте теорему косинусов, если:
- прямой угол не указан
- даны две стороны и прилежащий угол 9{2}}(1+\sin\theta)[/латекс].
- На приведенной ниже диаграмме [латекс]\scriptsize O[/латекс] является центром полукруга [латекс]\scriptsize BAE [/латекс]:
- Найдите [латекс]\размер сценария A\шляпа{O}C[/латекс] в терминах [латекс]\размер сценария \тета[/латекс].
- В [latex]\scriptsize \Delta ABE[/latex] определите выражение для [latex]\scriptsize \cos \theta[/latex].
- В [latex]\scriptsize \Delta ACE[/latex] определите выражение для [latex]\scriptsize \sin \theta[/latex].
- В [latex]\scriptsize \Delta ACO[/latex] определите выражение для [latex]\scriptsize \sin 2\theta[/latex].
 \circ}[/latex]. Для соединения [латекс]\scriptsize C[/латекс] и [латекс]\scriptsize D[/латекс] необходим кабель.
\circ}[/latex]. Для соединения [латекс]\scriptsize C[/латекс] и [латекс]\scriptsize D[/латекс] необходим кабель. - Определите минимальную длину кабеля, необходимого для соединения [латекс]\scriptsize C[/латекс] и [латекс]\scriptsize D[/латекс] (с точностью до метра).
- На каком расстоянии друг от друга основания двух башен (с точностью до метра)?
Полные решения находятся в конце модуля.
Задачи в трех измерениях
Как мы видели, мы можем использовать правила синусов и косинусов, чтобы найти длины сторон и размеры углов в непрямоугольных треугольниках в двух измерениях. Мы можем применить эти же методы для работы в трех измерениях. Это означает, что мы можем начать решать больше реальных проблем.
Но работа в трех измерениях (особенно трехмерная визуализация на двухмерном экране или листе бумаги) для большинства из нас требует времени и практики. Если поначалу вам будет трудно, не сдавайтесь. Работать в трех измерениях можно научиться.
 Просто нужна практика.
Просто нужна практика.[latex]\scriptsize AD[/latex] представляет собой вертикальный флагшток, и его основание, [latex]\scriptsize A[/latex], находится в той же горизонтальной плоскости, что и точки [latex]\scriptsize B[/latex] и [латекс]\размер сценария C[/латекс]. Угол подъема от точки [латекс]\scriptsize C[/латекс] до вершины флагштока равен [латекс]\scriptsize {{29\circ}[/латекс]. Определить высоту флагштока.
Решение
В этом примере была дана схема ситуации. Иногда вам нужно будет создать свой собственный эскиз. Обратите внимание на затенение [latex]\scriptsize \Delta ABC[/latex]. Это помогает нам увидеть, что этот треугольник лежит на земле и находится под прямым углом к треугольнику, образованному точками [latex]\scriptsize A[/latex], [latex]\scriptsize C[/latex] и [latex]\scriptsize D. [/латекс]. Помните, что флагшток вертикальный (это означает, что он находится под прямым углом к земле). Заданные длины и углы заполнены.
Нам нужно вычислить длину [latex]\scriptsize AD[/latex].
 У нас есть один угол внутри этого треугольника, и это прямоугольный треугольник. Следовательно, если мы можем найти длину [латекс]\размер сценария AC[/латекс], мы можем использовать отношение тангенса, чтобы найти [латекс]\размер сценария AD[/латекс]. Мы выбираем [латекс]\scriptsize AC[/латекс], потому что это сторона, общая для обоих треугольников.
У нас есть один угол внутри этого треугольника, и это прямоугольный треугольник. Следовательно, если мы можем найти длину [латекс]\размер сценария AC[/латекс], мы можем использовать отношение тангенса, чтобы найти [латекс]\размер сценария AD[/латекс]. Мы выбираем [латекс]\scriptsize AC[/латекс], потому что это сторона, общая для обоих треугольников.Мы можем использовать правило синусов для вычисления [latex]\scriptsize AC[/latex], но для этого нам сначала нужно вычислить размер [latex]\scriptsize B\hat{A}C[/latex] . 9\circ}\\&=87.48\text{ m}\end{align*}[/latex]
Если вам все еще трудно представить себе описанную выше ситуацию, посетите эту «интерактивную версию схемы». Вы можете щелкнуть и перетащить, чтобы просмотреть ситуацию с разных сторон.
Пример адаптирован из Everything Maths 12 класс Рабочий пример 16
[латекс]\scriptsize D[/латекс] — верх здания высотой [латекс]\scriptsize h[/латекс]. Основание здания находится в точке [latex]\scriptsize A[/latex], а [latex]\scriptsize \Delta ABC[/latex] лежит на земле (горизонтальная плоскость). [латекс]\scriptsize BC=b[/латекс],[латекс]\scriptsize D\шляпа{B}A=\альфа[/латекс], [латекс]\scriptsize D\шляпа{B}C=\бета[/ латекс] и [латекс]\scriptsize D\шляпа{C}B=\тета[/латекс].
[латекс]\scriptsize BC=b[/латекс],[латекс]\scriptsize D\шляпа{B}A=\альфа[/латекс], [латекс]\scriptsize D\шляпа{B}C=\бета[/ латекс] и [латекс]\scriptsize D\шляпа{C}B=\тета[/латекс].Покажите, что [латекс]\scriptsize h=\displaystyle \frac{{b\sin \alpha \sin \theta}}{{\sin (\beta +\theta )}}[/latex].
Решение
Нас просят найти выражение для [latex]\scriptsize h[/latex]. Поскольку нам дан угол в [latex]\scriptsize \Delta ABD[/latex], это треугольник, на котором мы сосредоточимся. Чтобы найти [latex]\scriptsize h[/latex], нам нужно найти либо [latex]\scriptsize AB[/latex], либо [latex]\scriptsize BD[/latex]. [latex]\scriptsize DB[/latex] является общей стороной между [latex]\scriptsize \Delta ABD[/latex] и [latex]\scriptsize \Delta BCD[/latex] и [latex]\scriptsize \Delta BCD [/latex] — это хороший треугольник для работы, потому что мы получили информацию о нем. Начнем с написания выражения для [latex]\scriptsize h[/latex] в [latex]\scriptsize \Delta ABD[/latex].

[латекс]\scriptsize \begin{align*}\sin \alpha &=\displaystyle \frac{h}{{BD}}\\\следовательно h&=BD\times \sin \alpha \end{align*} [/latex]
Теперь давайте найдем выражение для [latex]\scriptsize BD[/latex] в [latex]\scriptsize \Delta BCD[/latex].
[латекс] \ scriptsize \ begin {align *} \ displaystyle \ frac {{BD}} {{\ sin \ theta}} & = \ displaystyle \ frac {b} {{\ sin B \ hat {D} C} }\\\поэтому BD & =\displaystyle \frac{{b\times \sin \theta}}{{\sin B\hat{D}C}}\end{align*}[/latex] 9\circ}-(\beta +\theta )} \right)\\&=\sin (\beta +\theta )\end{align*}[/latex]Следовательно:
[latex]\scriptsize BD = \displaystyle \frac{{b\times \sin \theta }}{{\sin (\beta +\theta )}}[/latex]Теперь мы можем заменить [latex]\scriptsize BD[/latex] в нашем исходное выражение с этим новым выражением для [латекс]\scriptsize BD[/латекс].
[латекс] \ scriptsize \ begin {align *} h & = BD \ times \ sin \ alpha \\ & = \ displaystyle \ frac {{b \ times \ sin \ theta}} {\ sin (\ beta + \ theta )}}\times \sin\alpha \\&=\displaystyle\frac{{b\sin\alpha\sin\theta}}{{\sin (\beta +\alpha)}}\end{align*}[ /латекс]- Вышка сотовой связи, [latex]\scriptsize AD[/latex], имеет базу в [latex]\scriptsize A[/latex].
 [latex]\scriptsize \Delta ABC[/latex] — горизонтальная плоскость на земле. Угол подъема к вершине башни от [латекс]\scriptsize B[/латекс] равен [латекс]\скриптсайз \бета[/латекс]. Геодезист стоит в точке [латекс]\scriptsize C[/латекс], так что он находится на одном и том же расстоянии, [латекс]\scriptsize y[/латекс], от [латекс]\скриптсайз А[/латекс] и [латекс]\ размер сценария B[/латекс]. [латекс]\scriptsize A\шляпа{B}C=\альфа[/латекс]. 9\circ}[/latex], посчитайте высоту здания с точностью до одного десятичного знака.
[latex]\scriptsize \Delta ABC[/latex] — горизонтальная плоскость на земле. Угол подъема к вершине башни от [латекс]\scriptsize B[/латекс] равен [латекс]\скриптсайз \бета[/латекс]. Геодезист стоит в точке [латекс]\scriptsize C[/латекс], так что он находится на одном и том же расстоянии, [латекс]\scriptsize y[/латекс], от [латекс]\скриптсайз А[/латекс] и [латекс]\ размер сценария B[/латекс]. [латекс]\scriptsize A\шляпа{B}C=\альфа[/латекс]. 9\circ}[/latex], посчитайте высоту здания с точностью до одного десятичного знака.
- Два корабля в море видят маяк на берегу. Расстояние от вершины маяка ([латекс]\scriptsize H[/латекс]) до корабля [латекс]\scriptsize S[/латекс] и до корабля [латекс]\scriptsize B[/латекс] равно [латекс]\ размер сценария 200\текст{м}[/латекс]. Угол возвышения от [латекс]\scriptsize S[/латекс] до [латекс]\scriptsize H[/латекс] равен [латекс]\scriptsize \alpha[/латекс], [латекс]\scriptsize H\шляпа{B} S=\beta[/latex] и [latex]\scriptsize S\hat{L}B=\theta[/latex].

Покажите, что расстояние между двумя кораблями определяется как [латекс]\scriptsize SB=400\cos \бета[/латекс]. - Как использовать тригонометрические соотношения, формулы приведения, формулы составного и двойного угла, правило синусов и правило косинусов для решения трехмерных задач.
- Ниже представлен вид сбоку вертикальной скалы. Точки [latex]\scriptsize B[/latex], [latex]\scriptsize C[/latex] и [latex]\scriptsize D[/latex] лежат в одной горизонтальной плоскости. [latex]\scriptsize A[/latex] — точка на вершине утеса, такая, что [latex]\scriptsize AB\bot BC[/latex]. [латекс]\scriptsize BD=30\text{ м}[/латекс], [латекс]\scriptsize DC=20\текст{ м}[/латекс], [латекс]\scriptsize A\шляпа{B}C={ {9\circ}[/латекс].
 \circ}[/latex]. 9{2}}(1+\sin\theta)\end{align*}[/latex]
\circ}[/latex]. 9{2}}(1+\sin\theta)\end{align*}[/latex] - .
- .
[латекс]\scriptsize \begin{align*}AO & =EO\quad \text{(радиусы)}\\\поэтому O\hat{A}E & =\theta \quad \text{(isos }\Delta \text{)}\\\поэтому A\hat{O}C & =2\theta \quad \text{(ext }\angle \text{ of }\Delta \text{ = opp int }\angle \text{ s)}\end{align*}[/latex] - В [латекс]\scriptsize \Delta ABE[/латекс]:
[латекс]\scriptsize \cos \theta =\displaystyle \frac{{AE}}{{BE}}[/latex] - В [latex]\scriptsize \Delta ACE[/latex]:
[latex]\scriptsize \sin \theta =\displaystyle \frac{{AC}}{{AE}}[/latex] - В [latex]\scriptsize \Delta ACO[/latex]:
[latex]\scriptsize \sin 2\theta =\displaystyle \frac{{AC}}{{AO}}[/latex] - [латекс]\scriptsize \sin 2\theta =\displaystyle \frac{{AC}}{{AO}}[/latex]
Но [латекс]\scriptsize \sin \theta =\displaystyle \frac{{AC} {{AE}}[/латекс]. Следовательно, [латекс]\scriptsize AC=AE\sin\theta[/латекс]. Следовательно, [латекс]\scriptsize \sin 2\theta =\displaystyle \frac{{AE\sin \theta }}{{AO}}[/latex]. \circ}-2\alpha \quad \text{(}\angle \text{s in }\Delta \text{ suppl) }\end{выравнивание*}[/латекс] 9\ circ}}}} \ right) \\ & = p \ tan \ beta \ left ( {\ displaystyle \ frac {{\ displaystyle \ frac {{\ sqrt {3}}} {2} \ cos \ theta — \ displaystyle \ frac {1} {2} \ sin \ theta}} {{\ displaystyle \ frac {{\ sqrt {3}}} {2}}}} \ right) \\ & = p \ tan \ beta \ left ( {\ displaystyle \ frac {{\ displaystyle \ frac {{\ sqrt {3} \ cos \ theta — \ sin \ theta}} {2}}} {\ displaystyle \ frac {{\ sqrt {3}}} {2}}}} \ right) \\ & = p \ tan \ beta \ left ( {\ displaystyle \ frac {{\ sqrt {3} \ cos \ theta — \ sin \ theta}} {2} \ times \ displaystyle \ frac {2} {{\ sqrt {3}}}} \ right) \\ & = p \ tan \ beta \ left ( {\ displaystyle \ frac {{\ sqrt {3} \ cos \ theta — \ sin \theta}}{{\sqrt{3}}}} \right)\quad \quad \text{Умножить на}\displaystyle \frac{{\sqrt{3}}}{{\sqrt{3}}}\ \&=p\tan\beta\left( {\cos\theta-\displaystyle\frac{{\sqrt{3}\sin\theta}}{3}}\right)\end{align*}[/latex ] 9\circ}\\\поэтому CD & =17.
\circ}-2\alpha \quad \text{(}\angle \text{s in }\Delta \text{ suppl) }\end{выравнивание*}[/латекс] 9\ circ}}}} \ right) \\ & = p \ tan \ beta \ left ( {\ displaystyle \ frac {{\ displaystyle \ frac {{\ sqrt {3}}} {2} \ cos \ theta — \ displaystyle \ frac {1} {2} \ sin \ theta}} {{\ displaystyle \ frac {{\ sqrt {3}}} {2}}}} \ right) \\ & = p \ tan \ beta \ left ( {\ displaystyle \ frac {{\ displaystyle \ frac {{\ sqrt {3} \ cos \ theta — \ sin \ theta}} {2}}} {\ displaystyle \ frac {{\ sqrt {3}}} {2}}}} \ right) \\ & = p \ tan \ beta \ left ( {\ displaystyle \ frac {{\ sqrt {3} \ cos \ theta — \ sin \ theta}} {2} \ times \ displaystyle \ frac {2} {{\ sqrt {3}}}} \ right) \\ & = p \ tan \ beta \ left ( {\ displaystyle \ frac {{\ sqrt {3} \ cos \ theta — \ sin \theta}}{{\sqrt{3}}}} \right)\quad \quad \text{Умножить на}\displaystyle \frac{{\sqrt{3}}}{{\sqrt{3}}}\ \&=p\tan\beta\left( {\cos\theta-\displaystyle\frac{{\sqrt{3}\sin\theta}}{3}}\right)\end{align*}[/latex ] 9\circ}\\\поэтому CD & =17. 43\text{ m}\end{align*}[/latex]
43\text{ m}\end{align*}[/latex]
- .
- sinerule © Geogebra находится под лицензией CC BY-SA (Attribution ShareAlike) a Лицензия CC BY-SA (Attribution ShareAlike)
- упражнение 3.1 Q2 © Geogebra находится под лицензией CC BY-SA (Attribution ShareAlike)
- упражнение 3.1 Q3 © Geogebra находится под лицензией CC BY-SA (Attribution ShareAlike)
- упражнение 3.1 Q4 © Geogebra находится под лицензией CC BY-SA (Attribution ShareAlike) a Лицензия CC BY-SA (Attribution ShareAlike)
- example3.2 © Geogebra находится под лицензией CC BY-SA (Attribution ShareAlike)
Вопрос 3 адаптировано из Everything Maths 12 класс Упражнение 4-5 вопрос 1
Вопрос 3 адаптировано из Everything Maths 12 класс Упражнение 4-6 вопрос 4
Полные решения находятся в конце модуля.
Резюме
В этом разделе вы узнали следующее:
Рекомендуемое время выполнения: 35 минут
Вопрос 1 адаптирован из документа NC(V) уровня 4 2, ноябрь 2016 г., вопрос 2.6
Вернуться к Разделу 3: Оценка


 Обратитесь к блоку 1 этого предметного результата, если вам нужна помощь в этом.
Обратитесь к блоку 1 этого предметного результата, если вам нужна помощь в этом.
 \circ}[/latex]. Для соединения [латекс]\scriptsize C[/латекс] и [латекс]\scriptsize D[/латекс] необходим кабель.
\circ}[/latex]. Для соединения [латекс]\scriptsize C[/латекс] и [латекс]\scriptsize D[/латекс] необходим кабель.  Просто нужна практика.
Просто нужна практика. У нас есть один угол внутри этого треугольника, и это прямоугольный треугольник. Следовательно, если мы можем найти длину [латекс]\размер сценария AC[/латекс], мы можем использовать отношение тангенса, чтобы найти [латекс]\размер сценария AD[/латекс]. Мы выбираем [латекс]\scriptsize AC[/латекс], потому что это сторона, общая для обоих треугольников.
У нас есть один угол внутри этого треугольника, и это прямоугольный треугольник. Следовательно, если мы можем найти длину [латекс]\размер сценария AC[/латекс], мы можем использовать отношение тангенса, чтобы найти [латекс]\размер сценария AD[/латекс]. Мы выбираем [латекс]\scriptsize AC[/латекс], потому что это сторона, общая для обоих треугольников. [латекс]\scriptsize BC=b[/латекс],[латекс]\scriptsize D\шляпа{B}A=\альфа[/латекс], [латекс]\scriptsize D\шляпа{B}C=\бета[/ латекс] и [латекс]\scriptsize D\шляпа{C}B=\тета[/латекс].
[латекс]\scriptsize BC=b[/латекс],[латекс]\scriptsize D\шляпа{B}A=\альфа[/латекс], [латекс]\scriptsize D\шляпа{B}C=\бета[/ латекс] и [латекс]\scriptsize D\шляпа{C}B=\тета[/латекс].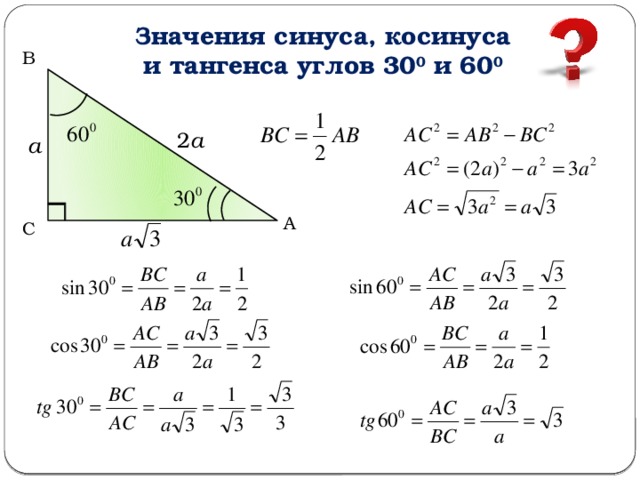
 [latex]\scriptsize \Delta ABC[/latex] — горизонтальная плоскость на земле. Угол подъема к вершине башни от [латекс]\scriptsize B[/латекс] равен [латекс]\скриптсайз \бета[/латекс]. Геодезист стоит в точке [латекс]\scriptsize C[/латекс], так что он находится на одном и том же расстоянии, [латекс]\scriptsize y[/латекс], от [латекс]\скриптсайз А[/латекс] и [латекс]\ размер сценария B[/латекс]. [латекс]\scriptsize A\шляпа{B}C=\альфа[/латекс]. 9\circ}[/latex], посчитайте высоту здания с точностью до одного десятичного знака.
[latex]\scriptsize \Delta ABC[/latex] — горизонтальная плоскость на земле. Угол подъема к вершине башни от [латекс]\scriptsize B[/латекс] равен [латекс]\скриптсайз \бета[/латекс]. Геодезист стоит в точке [латекс]\scriptsize C[/латекс], так что он находится на одном и том же расстоянии, [латекс]\scriptsize y[/латекс], от [латекс]\скриптсайз А[/латекс] и [латекс]\ размер сценария B[/латекс]. [латекс]\scriptsize A\шляпа{B}C=\альфа[/латекс]. 9\circ}[/latex], посчитайте высоту здания с точностью до одного десятичного знака.
 \circ}[/latex]. 9{2}}(1+\sin\theta)\end{align*}[/latex]
\circ}[/latex]. 9{2}}(1+\sin\theta)\end{align*}[/latex] \circ}-2\alpha \quad \text{(}\angle \text{s in }\Delta \text{ suppl) }\end{выравнивание*}[/латекс] 9\ circ}}}} \ right) \\ & = p \ tan \ beta \ left ( {\ displaystyle \ frac {{\ displaystyle \ frac {{\ sqrt {3}}} {2} \ cos \ theta — \ displaystyle \ frac {1} {2} \ sin \ theta}} {{\ displaystyle \ frac {{\ sqrt {3}}} {2}}}} \ right) \\ & = p \ tan \ beta \ left ( {\ displaystyle \ frac {{\ displaystyle \ frac {{\ sqrt {3} \ cos \ theta — \ sin \ theta}} {2}}} {\ displaystyle \ frac {{\ sqrt {3}}} {2}}}} \ right) \\ & = p \ tan \ beta \ left ( {\ displaystyle \ frac {{\ sqrt {3} \ cos \ theta — \ sin \ theta}} {2} \ times \ displaystyle \ frac {2} {{\ sqrt {3}}}} \ right) \\ & = p \ tan \ beta \ left ( {\ displaystyle \ frac {{\ sqrt {3} \ cos \ theta — \ sin \theta}}{{\sqrt{3}}}} \right)\quad \quad \text{Умножить на}\displaystyle \frac{{\sqrt{3}}}{{\sqrt{3}}}\ \&=p\tan\beta\left( {\cos\theta-\displaystyle\frac{{\sqrt{3}\sin\theta}}{3}}\right)\end{align*}[/latex ] 9\circ}\\\поэтому CD & =17.
\circ}-2\alpha \quad \text{(}\angle \text{s in }\Delta \text{ suppl) }\end{выравнивание*}[/латекс] 9\ circ}}}} \ right) \\ & = p \ tan \ beta \ left ( {\ displaystyle \ frac {{\ displaystyle \ frac {{\ sqrt {3}}} {2} \ cos \ theta — \ displaystyle \ frac {1} {2} \ sin \ theta}} {{\ displaystyle \ frac {{\ sqrt {3}}} {2}}}} \ right) \\ & = p \ tan \ beta \ left ( {\ displaystyle \ frac {{\ displaystyle \ frac {{\ sqrt {3} \ cos \ theta — \ sin \ theta}} {2}}} {\ displaystyle \ frac {{\ sqrt {3}}} {2}}}} \ right) \\ & = p \ tan \ beta \ left ( {\ displaystyle \ frac {{\ sqrt {3} \ cos \ theta — \ sin \ theta}} {2} \ times \ displaystyle \ frac {2} {{\ sqrt {3}}}} \ right) \\ & = p \ tan \ beta \ left ( {\ displaystyle \ frac {{\ sqrt {3} \ cos \ theta — \ sin \theta}}{{\sqrt{3}}}} \right)\quad \quad \text{Умножить на}\displaystyle \frac{{\sqrt{3}}}{{\sqrt{3}}}\ \&=p\tan\beta\left( {\cos\theta-\displaystyle\frac{{\sqrt{3}\sin\theta}}{3}}\right)\end{align*}[/latex ] 9\circ}\\\поэтому CD & =17. 43\text{ m}\end{align*}[/latex]
43\text{ m}\end{align*}[/latex]