Как решать систему уравнений способом подстановки: Метод подстановки — урок. Алгебра, 9 класс.

Методическая разработка урока математики по теме «Системы линейных уравнений и методы их решения» — Информио

План урока

Тема урока: Системы линейных уравнений и методы их решения.

Дисциплина: Математика

Специальность: 23.02.03 «Техническое обслуживание и ремонт автомобильного транспорта»

Учебная группа: ТМ-11

Тип урока: комбинированный.

Продолжительность: 90 мин.

Цели:

1. Повторение пройденного материала по теме «Квадратные неравенства».
2. Сформировать понятие системы линейных уравнений.
3. Научить решать системы линейных уравнений способом подстановки, способом сложения, графическим способом.
4. Развитие у студентов рациональных приемов и способов мышления.

Задачи:

1. Формирование умений решать системы линейных уравнений способом подстановки, способом сложения, графическим способом.
2. Развитие познавательной активности, внимания, логики, наблюдательности, самоконтроля.
3. Воспитание самостоятельности интереса к предмету.

Межпредметные связи: информатика.

Комплексно-методическое обеспечение:

• Интерактивная доска
• Учебно-методическое пособие по математике
• Компьютеры

ТЕХНОЛОГИЧЕСКАЯ КАРТА

Этапы урока	Деятельность преподавателя	Деятельность студента
1. Организационный момент, 5 мин.	Приветствие. Отметка в журнале отсутствующих студентов. Объяснение целей и задач урока, озвучивание плана урока.	Приветствие преподавателя. Доклад старосты. Слушание.
2. Проверка домашнего задания, 20 мин	Выполнение тестов и заданий на сайте http://learningaps.org и на доске (приложение 1)	Выполняют задания.
3. Изучение нового материала, 30 мин	Проводит изложение нового материала по теме урока с использованием интерактивной доски (приложение 2) Предлагает задать вопросы по новому материалу в случае, если что-то было непонятно	Записывают в тетрадь формулы, примеры, внимательно слушают Задают вопросы по неясным аспектам
4. Закрепление нового материала у доски, 25 мин	Вызывает к доске (приложение3)	Выходят к доске, выполняют задания
5. Рефлексия, 5 мин	Предлагает сделать выводы по уроку, высказать свои впечатления, что нового узнали.	Делают выводы, высказывают впечатления, что нового узнали
6. Выдача домашнего задания, 2мин	Объясняет домашнее задание (приложение 4)	Записывают домашнее задание
7. Подведение итогов урока, 3 мин	Обобщает урок, выставляет оценки.

 

Приложение 1

1. Решить квадратные неравенства графическим методом:

1. 2х² + 3х -2 > 0
2. 2х² – х – 3 ≤0
3. -2х² +11х – 14 > 0

2. Решить квадратные неравенства методом интервалов:

1. –х² +6х – 9 > 0
2. х² + 8х + 16 < 0
3. –х² + 10х -25 < 0

 

Приложение 2

Системы линейных уравнений и методы их решения.

1. Понятие системы линейных уравнений.
2. Решение систем линейных уравнений способом подстановки.
3. Способ сложения.
4. Графический способ.

1. Даны два уравнения

     х + у = 12     х – у = 2

Чтобы найти общие решения этих уравнений, требуется решить систему уравнений. Систему уравнений принято записывать с помощью фигурной скобки.

Пара значений переменных х = 7, у = 5 служит решением каждого уравнения системы, так как оба равенства 7+5=12 и 7-5=2 являются верными.

Такую пару чисел называют решением системы.

Решением системы называется пара значений переменных, обращающих каждое уравнение системы в верное равенство.

Решить систему неравенств – научит найти все е решения или доказать, что решений нет.

2. При решении систем линейных уравнений способом подстановки в каком – либо из уравнений системы одно из неизвестных выражается через другое. Полученное выражение подставляется в оставшееся уравнение, после решения которого находится одно неизвестное. Второе неизвестное может быть найдено из любого уравнения системы.   

Пример 1. Решить систему уравнений:

Пример 2. Решить систему уравнений:

3. При решении систем способом сложения переходим от данной системы к другой, равносильной ей системе, в которой оно из уравнений содержит только одну переменную

Пример 3. Решить систему уравнений:

Пример 4. Решить систему уравнений:

4. Для того, чтобы решить систему линейных уравнений с двумя переменными, можно использовать графики уравнений.

 

Приложение 3

Задание:

 

Приложение 4

Задания для самостоятельной работы

Вопросы для самоконтроля

1. Что называют системой линейных уравнений?
2. Как решить систему линейных уравнений способом подстановки?
3. Как решить систему линейных уравнений способом сложения?
4. Как решить систему линейных уравнений графическим способом?

Практические задания:

Задание на «3».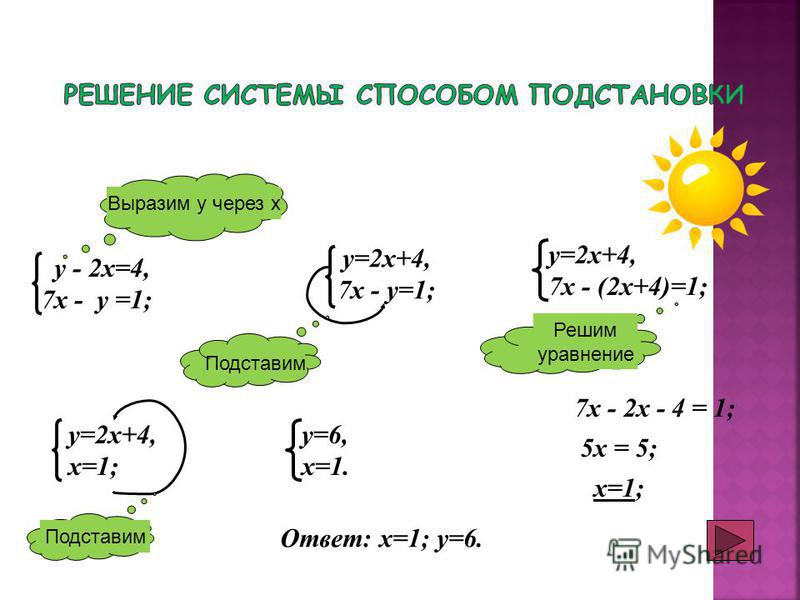 Решить системы линейных уравнений:

Задание на «4».

1. Решить систему линейных уравнений способом подстановки:
2. Решить систему линейных уравнений способом сложения:

Задание на «5»:

1. Решить систему линейных уравнений способом подстановки:
2. Решить систему линейных уравнений способом сложения:
3. Решить систему линейных уравнений графическим способом:

Решение систем уравнений с помощью подстановки — задача 3

В системе уравнений, если ни одно из уравнений не имеет изолированной переменной (например, они оба в стандартной форме), вы должны начать с выделения одной из переменных в одном из уравнения, чтобы иметь возможность использовать подстановку для решения системы. Выберите переменную, для которой было бы легче всего найти решение, имеющую коэффициент 1. Таким образом, вам не нужно будет делать слишком много шагов, чтобы изолировать переменную. После выделения переменной с помощью обратных операций подставьте это значение в другое уравнение и решите. Помните, что решением является точка, поэтому обязательно найдите значения x и y координатной точки. Проверьте свой ответ, подставив значения x и y в оба уравнения. Если уравнения верны, то решение верно.

система уравнений решение замена коэффициент

Меня попросили использовать подстановку для решения системы уравнений, и я немного растерялся, потому что подстановка не так уж плоха, если у вас изолирована одна из переменных. В обоих этих уравнениях ни одна переменная не является изолированной. Изолированное среднее, например, y равно бла, бла, бла или x равно бла, бла, бла. Но когда я ищу, какое уравнение мне нужно выделить, или какую переменную я собираюсь выделить и получить саму по себе, я буду смотреть на коэффициент. Коэффициенты — это числа, зависящие от переменных. Я хочу найти коэффициент, равный 1, который сделает мой процесс решения максимально простым и, возможно, уменьшит количество дробей, если бы у меня были дроби.

Итак, посмотрев сюда, я вижу, что коэффициент y равен 1. Это означает, что я собираюсь изменить эту формулу, чтобы изолировать y, и тогда я смогу выполнить свою замену. Добавляя 2x к обеим частям, я не меняю это уравнение, я просто переписываю его в форме, где y сам по себе.

Теперь я подставлю 2x плюс 8 прямо здесь. Все выражение 2x плюс 8 будет подставлено во второе уравнение. Я пытаюсь использовать цвет таким образом, чтобы показать вам, ребята, о чем я говорю. Эта штука малинового или пурпурного, красноватого цвета будет там какое-то время. 2 раза 2х плюс 8. Это замещающая фигура.

После того, как все сделано, остается решить. У меня есть 1 уравнение и 1 переменная, так что просто будьте очень осторожны, чтобы правильно распределять значения, что означает, что 2 умножается на 2x, а также на эти 8, комбинируйте подобные термины, и тогда вы просто счастливо решаете.

Вычтите 16 с обеих сторон, так что 7x равно -7, а x равно -1. Опять же, это только половина моего ответа. Мой ответ должен иметь значение x и значение y, поэтому я еще не закончил решение. Мне все еще нужно решить еще одну задачу, прежде чем я начну проверять.

Чтобы проверить или, извините, найти значение y, я возьму x равным -1 и подставлю его в любое исходное уравнение, чтобы найти значение y. У некоторых людей возникает искушение подставить свое значение x в это, что должно быть эквивалентным утверждением, эквивалентным уравнением этого первого парня, но если я сделаю какую-либо ошибку, мой ответ для y будет неверным.

Итак, вместо того, чтобы вставлять сюда, я собираюсь вставить его в одно из исходных уравнений, просто чтобы убедиться, что я все делаю правильно. Таким образом, умноженное на -2 мое число x, которое было -1 плюс y, будет равно 8. Идите вперед и решите, что +2 плюс y равно 8, поэтому y равно 6. Думаю, это мой ответ. Прежде чем я двинусь дальше, эта задача попросила меня проверить, и это всегда хорошая идея, когда вы делаете много подобных алгебр, чтобы проверить свое решение и убедиться, что вы не сделали никаких ошибок.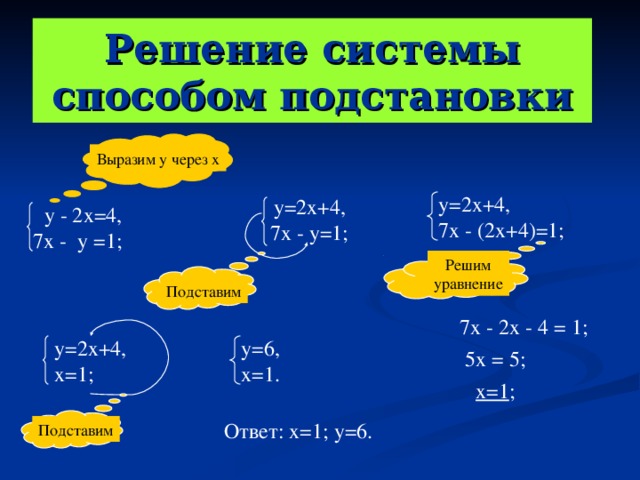

Способ проверки вашего решения системы уравнений состоит в том, чтобы подставить эту пару x, y в каждое уравнение отдельно и убедиться, что я получаю равенства. Как и в первом уравнении, -2 умножить на -1 плюс 6, надеюсь, будет равно 8, и я получил это из этого первого уравнения. +2 плюс 6 равно 8, хорошо, что сработало.

Давайте попробуем второе уравнение. 3 раза мое число x плюс 2 раза мое число y должны быть равны 9. Давайте сделаем это, упростив -3 + 12 = 9 хорошо. Это значит, что я получил правильный ответ. Моя пара координат x минус y. Это было решением обоих исходных уравнений, а это означает, что здесь пересекаются линии. Мне не пришлось рисовать их в виде графиков, и это здорово, потому что я не люблю графики. Мне не нужно было изображать их на графике, но я все же мог сказать, где линии пересекаются.

Итак, последнее, что вам нужно сделать, когда вы видите проблему, которая просит вас использовать подстановку, но ни одна переменная не существует сама по себе, посмотрите на коэффициенты. Найдите переменную с коэффициентом 1, а затем решите для этого парня, как мы сделали здесь.

Как решать системы уравнений с заменой?

Одним из методов решения системы линейных уравнений с двумя переменными является метод подстановки. В этом посте блога вы узнаете, как решать системы уравнений с заменой.

мы находим значение любой из переменных, изолируя ее с одной стороны и беря все остальные члены с другой стороны уравнения. Затем мы заменяем это значение во втором уравнении.

Связанные темы

• Как решать системы уравнений
• Как решать системы уравнений Словесные задачи

Пошаговое руководство по решению систем уравнений с подстановкой

Метод подстановки является простым для решения линейные уравнения и найти решения переменных. Как следует из названия, он включает в себя нахождение значения \(x\)-переменной через \(y\)-переменную, а затем подстановку значения \(x\)-переменной во второе уравнение. Таким образом, мы можем решить и найти значение \(y\)-переменной. Наконец, мы можем подставить значение \(y\) в каждое из заданных уравнений, чтобы найти \(x\).

Шаги для использования метода подстановки

Шаги для использования метода подстановки следующие:

Предположим, два линейных уравнения: \(2x+3(y+5)=0\) и \(x+4y +2=0\).

Шаг 1: Упростите данное уравнение, расширив скобки по мере необходимости. Итак, здесь мы можем упростить первое уравнение, чтобы получить \(2x+3y+15=0\).

Теперь у нас есть два уравнения:

\(2x + 3y + 15 = 0\) , уравнение \(1\)

\(x+4y+2=0\), уравнение \(2\)

Шаг 2: Решите любое уравнение для любой из переменных. Вы можете использовать любую переменную, исходя из простоты расчета. Предположим, мы решаем уравнение \(2\) относительно \(x\). Итак, мы получаем \(x=-4y-2\).

Шаг 3: Подставьте значение, полученное из \(x\), в другое уравнение. Итак, мы подставляем \(x=-4y-2\) в уравнение \(2x+3y+15=0\), получаем \(2(-4y-2)+3y+15=0\).

Шаг 4: Теперь упростим новое уравнение, полученное с помощью арифметических операций. Получаем \(-8y-4+3y+15=0\)

\(-5y+11=0\)

\(-5y=-11\)

\(y=\frac{11}{5}\)

Шаг 5: Теперь замените значение из \(у\) в каждом из данных уравнений. Подставим значение \(y\) в уравнение \((2)\).

\(x+4y+2=0\)

\(x+4×(\frac{11}{5})+2=0\)

\(x+ \frac{44}{5} +2=0\)

\(x+ \frac{54}{5}=0\)

\(x=-\frac{54}{5}\)

Следовательно, после решения данных линейных уравнений методом подстановки получаем \(x= -\frac{54}{5}\) и \(y=\frac{11}{5}\).

Разница между методом исключения и подстановки

Оба метода исключения и подстановки — это способы алгебраического решения линейных уравнений. Когда метод подстановки становится немного трудным для применения в уравнениях, содержащих большие числа или дроби, мы можем использовать метод исключения, чтобы облегчить наши вычисления.