Как решать системы уравнений квадратные: Решение систем квадратных уравнений

9 класс. Алгебра. Системы уравнений. — Решение систем уравнений методом замены переменных.

Комментарии преподавателя

На этом уроке мы рассмотрим последний метод решения систем уравнений – метод введения новых переменных. Сформулируем суть метода и будем рассматривать его применение на конкретных задачах.

 

Тема: Си­сте­мы урав­не­ний

Урок: Метод вве­де­ния новых пе­ре­мен­ных

На преды­ду­щих уро­ках для ре­ше­ния си­стем урав­не­ний при­ме­ня­лись гра­фи­че­ский метод, метод под­ста­нов­ки и метод ал­геб­ра­и­че­ско­го сло­же­ния. Сей­час будет рас­смот­рен метод вве­де­ния новых пе­ре­мен­ных.

Вве­де­ние новых пе­ре­мен­ных поз­во­ля­ет упро­стить ис­ход­ную си­сте­му. Рас­смот­рим в ка­че­стве при­ме­ра си­сте­му, ко­то­рая пред­ла­га­лась на всту­пи­тель­ном эк­за­мене в 1979 г. в МГУ на ме­ха­ни­ко-ма­те­ма­ти­че­ский фа­куль­тет.

При­мер 1. Ре­шить си­сте­му 

Ре­ше­ние.

По­лез­но вве­сти новые пе­ре­мен­ные  

 

До­воль­но слож­ная ис­ход­ная си­сте­ма све­лась к более про­стой. Это си­сте­ма двух ли­ней­ных урав­не­ний от­но­си­тель­но a и b. Решим ее ме­то­дом ал­геб­ра­и­че­ско­го сло­же­ния, вы­чтем из пер­во­го урав­не­ния вто­рое.

   

Мы ввели новые пе­ре­мен­ные и ре­ши­ли си­сте­му от­но­си­тель­но этих пе­ре­мен­ных. Воз­вра­ща­ем­ся к ста­рым пе­ре­мен­ным.

 

Мы по­лу­чи­ли вто­рую си­сте­му двух ли­ней­ных урав­не­ний от­но­си­тель­но x и y.

Решим си­сте­му ме­то­дом под­ста­нов­ки.

 

Ответ: 

Часто при за­мене пе­ре­мен­ных мы по­лу­ча­ем квад­рат­ное урав­не­ние. На­пом­ним ос­нов­ные све­де­ния о них:

Квад­рат­ное урав­не­ние в общем виде: 

Фор­му­ла кор­ней квад­рат­но­го урав­не­ния через дис­кри­ми­нант:

Если b – чет­ное число, имеем фор­му­лу: 

На­пом­ним тео­ре­му Виета: Если  корни квад­рат­но­го урав­не­ния , то 

Верно и об­рат­ное: Если числа  удо­вле­тво­ря­ют си­сте­ме  , то они яв­ля­ют­ся кор­ня­ми квад­рат­но­го урав­не­ния.

На­пом­ним прием, ко­то­рый поз­во­ля­ет упро­стить на­хож­де­ние кор­ней квад­рат­но­го урав­не­ния. Умно­жим квад­рат­ное урав­не­ние на  По­лу­чим  

По­лу­чи­ли новое урав­не­ние от­но­си­тель­но новой пе­ре­мен­ной  

 

Мы по­лу­чи­ли при­ве­ден­ное квад­рат­ное урав­не­ние с це­лы­ми ко­эф­фи­ци­ен­та­ми (если они были це­лы­ми в ис­ход­ном урав­не­нии).

При­мер 2. Ре­шить урав­не­ние 

Ре­ше­ние:

 

 

;

 

Это при­ве­ден­ное урав­не­ние, ко­эф­фи­ци­ен­ты – целые числа.

По тео­ре­ме Виета  

 

Ответ: 

При­мер 3. Ре­шить урав­не­ние 

Ре­ше­ние:

 

  

 

 

По­лу­чи­ли при­ве­ден­ное квад­рат­ное урав­не­ние от­но­си­тель­но z.

По тео­ре­ме Виета 

 

Ответ: 

Мы рас­смот­ре­ли еще один прием, ко­то­рый поз­во­ля­ет упро­стить на­хож­де­ние кор­ней квад­рат­но­го урав­не­ния.

После сде­лан­ных на­по­ми­на­ний для квад­рат­ных урав­не­ний решим си­сте­му:

При­мер 4. Ре­шить си­сте­му 

Ре­ше­ние: Про­из­ве­дем за­ме­ну: 

 

 

 

 

 

 

Вер­нем­ся к ис­ход­ной си­сте­ме:

   

Ответ:

При­мер 5. Ре­шить си­сте­му: 

Ре­ше­ние:

Вве­дем новую пе­ре­мен­ную:  По­лу­ча­ем квад­рат­ное урав­не­ние от­но­си­тель­но новой пе­ре­мен­ной.

 

 

 

Ис­ход­ная си­сте­ма све­лась к со­во­куп­но­сти двух си­стем:

Каж­дую си­сте­му ре­ша­ем ме­то­дом под­ста­нов­ки.

1. 

 

 

 

 

2. 

 

 

 

 

На­хо­дим y при из­вест­ных x.

  

Ответ: 

Сле­ду­ю­щая си­сте­ма – сим­мет­ри­че­ская. Сим­мет­ри­че­ской на­зы­ва­ет­ся такая си­сте­ма, ко­то­рая не из­ме­нит­ся, если пе­ре­мен­ные по­ме­нять ме­ста­ми.

 

Ре­ше­ние: Про­из­ве­дем за­ме­ну 

По­лу­ча­ем си­сте­му:

 

Мы ввели новые пе­ре­мен­ные, и нашли их.

Вер­нем­ся к ста­рым пе­ре­мен­ным. По­лу­ча­ем две си­сте­мы:

 

1.  

 

 

 

2.  

 

нет ре­ше­ний.

Ответ:  

За­ме­тим, что ре­ше­ни­ем сим­мет­ри­че­ской си­сте­мы яв­ля­ют­ся сим­мет­рич­ные пары чисел.

 

http://interneturok.ru/ru/school/algebra/9-klass/sistemy-uravneniy/metod-vvedeniya-novyh-peremennyh?konspekt&chapter_id=26

 

Источник видео: http://www.youtube.com/watch?v=hMUW7O1rPZE

Алгебра. Учебник для 6-8 классов

Алгебра. Учебник для 6-8 классов

Барсуков А.Н. Алгебра. Учебник для 6-8 классов. 11-е изд., стер. — М.: Просвещение, 1966. — 296 с. Учебник для средних общеобразовательных школ СССР в 50-60-е годы. Шестое издание „Алгебры» А.Н. Барсукова переработано и приведено в соответствие с новой программой. Переработка учебника и изложение вопросов, вновь включенных в программу восьмилетней школы, выполнены С. И. Новоселовым. Главу „Счётная (логарифмическая) линейка* и о возвышении в квадрат и куб, извлечении квадратного и кубического корней при помощи счётной линейки написал учитель математики школы № 315 Москвы И. Б. Вейцман. Одиннадцатое издание печатается с десятого без изменений. Оглавление ГЛАВА ПЕРВАЯ АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ. § 2. Алгебраические выражения. § 3. Допустимые значения букв. § 4. Порядок действий. § 5. Основные законы сложения и умножения. § 6. Краткие исторические сведения. ГЛАВА ВТОРАЯ. РАЦИОНАЛЬНЫЕ ЧИСЛА. § 7. Положительные и отрицательные числа. § 8. Числовая ось. § 9. Противоположные числа. § 10. Абсолютная величина числа. § 11. Сравнение рациональных чисел. § 12. Сложение рациональных чисел. § 13. Сложение нескольких чисел. § 14. Законы сложения. § 15. Вычитание рациональных чисел. § 16. Алгебраическая сумма. § 17. Умножение. § 18. Умножение нескольких чисел. § 19. Законы умножения. § 20. Деление. § 21. Свойства деления. § 22. Возведение в степень. § 23. Порядок выполнения действий. § 24. Уравнения. § 25. Решение задач с помощью уравнений. § 26. Графики. § 27. Краткие исторические сведения. (Из истории отрицательных чисел.) ГЛАВА ТРЕТЬЯ. ДЕЙСТВИЯ НАД ЦЕЛЫМИ АЛГЕБРАИЧЕСКИМИ ВЫРАЖЕНИЯМИ. § 28. Одночлен и многочлен. § 29. Тождества и тождественные преобразования. § 30. Коэффициент. § 31. Расположенные многочлены. § 32. Приведение подобных членов. § 33. Сложение одночленов и многочленов. § 34. Противоположные многочлены. § 35. Вычитание одночленов и многочленов § 36. Умножение одночленов. § 37. Умножение многочлена на одночлен. § 38. Умножение многочленов. § 39. Умножение расположенных многочленов. § 40. Возведение одночленов в степень. § 41. Формулы сокращённого умножения. § 42. Общие замечания о делении целых алгебраических выражений. 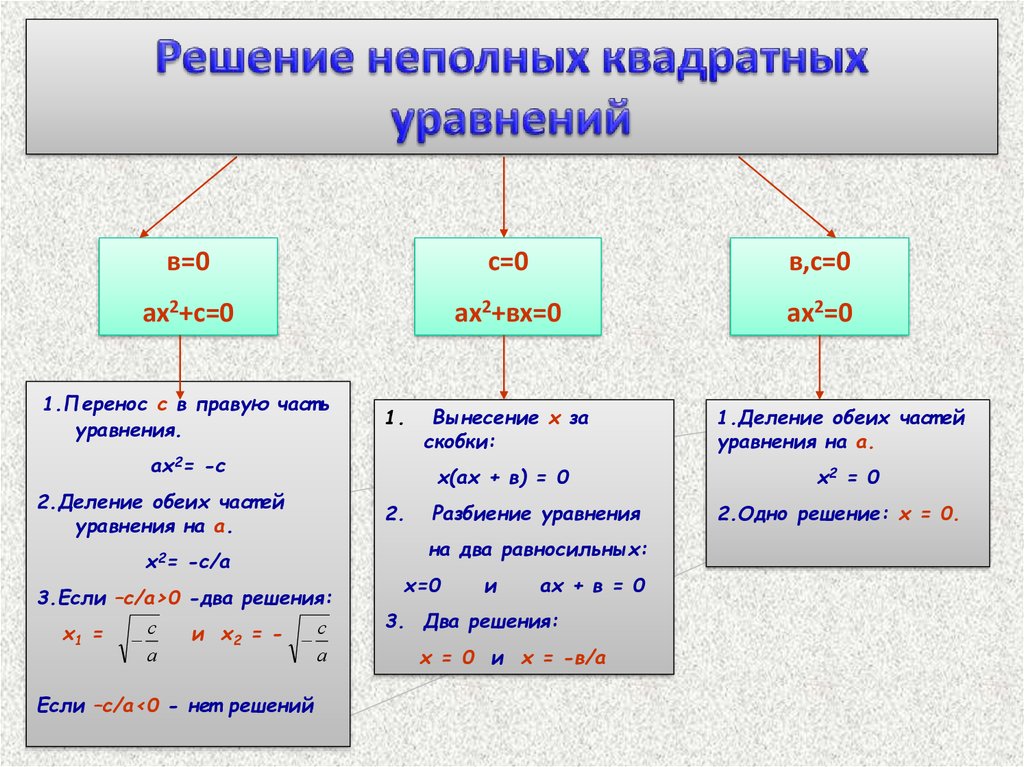§ 43. Деление одночленов. § 44. Деление многочлена на одночлен § 45. Примеры решения уравнений. ГЛАВА ЧЕТВЁРТАЯ. УРАВНЕНИЯ ПЕРВОЙ СТЕПЕНИ С ОДНИМ НЕИЗВЕСТНЫМ. § 47. Равносильные уравнения. § 48. Два основных свойства уравнений. § 49. Уравнения, содержащие неизвестное в обеих частях. § 50. Уравнение первой степени с одним неизвестным. § 51. Общие указания к решению уравнений. § 52. Решение задач с помощью уравнений. § 53. Краткие исторические сведения. (Из истории уравнений.) ГЛАВА ПЯТАЯ. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ. § 54. Понятие о разложении на множители. § 55. Вынесение за скобки общего множителя. § 56. Способ группировки. § 57. Применение формул сокращённого умножения. § 58. Применение нескольких способов. § 59. Деление многочленов при помощи разложения на множители. ГЛАВА ШЕСТАЯ. АЛГЕБРАИЧЕСКИЕ ДРОБИ. § 60. Понятие об алгебраической дроби. § 61. Основное свойство дроби и сокращение дробей. § 62. Перемена знака у членов дроби. § 63. Целая отрицательная и нулевая степени числа. § 64. Приведение дробей к общему знаменателю. § 65. Сложение дробей. § 66. Вычитание дробей. § 67. Умножение дробей. § 68. Деление дробей. § 69. Возведение дроби в натуральную степень. § 70. Дробные уравнения. § 71. Примеры решения уравнений с буквенными коэффициентами. ГЛАВА СЕДЬМАЯ. КООРДИНАТЫ И ПРОСТЕЙШИЕ ГРАФИКИ. § 72. Координаты точки на плоскости. § 73. Прямо пропорциональная зависимость. § 74. График прямо пропорциональной зависимости. § 75. Линейная зависимость. § 76. Обратно пропорциональная зависимость. ГЛАВА ВОСЬМАЯ. СИСТЕМА УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ С ДВУМЯ НЕИЗВЕСТНЫМИ. § 77. Уравнение первой степени с двумя неизвестными. § 78. Система двух уравнений первой степени с двумя неизвестными. § 79. Равносильные системы. § 80. Решение систем уравнений. § 81. Графическое решение системы двух уравнений. § 82. Решение задач. (1/3) § 130. Примеры графического решения уравнений и систем уравнений.

Решение линейных и квадратных уравнений: деление, исключение

Ключевые понятия

• Линейно-квадратичная система уравнений.
• Ликвидация.
• Подстановка

Введение 

На предыдущем уроке мы узнали о решении квадратного уравнения, а на предыдущем уроке мы узнали о решении линейных уравнений.

Теперь мы научимся совместно решать системы линейных и квадратных уравнений.

Линейно-квадратичная система уравнений

Мы узнали о линейном уравнении, имеющем вид y =mx + c, и

мы также знаем о квадратном уравнении, имеющем вид y = ax ² +bx +с.

Теперь мы узнаем о системе уравнений, которая включает

y = mx +c и y = ax ² +bx+c.

И мы увидим, как решения квадратных уравнений связаны с решениями линейно-квадратичной системы уравнений.

На следующем рисунке показано уравнение прямой и парабола,  

• если прямая пересекает параболу в двух точках, то система уравнений имеет два решения.
• если прямая пересекает параболу в одной точке, то система уравнений имеет одно решение.
• если прямая не пересекает параболу ни в одной точке, то система уравнений не имеет решения.

Решения, полученные для квадратных уравнений, подобны решениям, полученным в системе линейно-квадратичных уравнений.

В квадратном уравнении рассматривается пересечение параболы с осью x.

Здесь в системе линейно-квадратичного уравнения рассматривается пересечение уравнения прямой и параболы.

На следующем рисунке показаны решения квадратных уравнений.

Давайте рассмотрим несколько примеров.

Пример 1:  

Сколько решений имеет уравнение y = 2x и y = 4x ² ?

Решение:

Даны уравнения y = 2x и y = 4x ² .

Нарисуем график для двух приведенных выше уравнений.

Теперь из графика парабола и прямая пересекаются в двух точках (0,0) и (1, 1) 

Итак, у данных уравнений есть два решения.

То есть x=0, y=0 и x=1, y=1.

Решение линейно-квадратичного уравнения путем деления0023 2

+6 = 4x+2.

Решение: 

Данное уравнение x ² +6 = 4x+2.

Запишите уравнение путем деления, приравняйте каждую часть уравнения к y 

y = x ² +6

y = 4x+2

Теперь нарисуйте график для двух уравнений, 

Линия и парабола пересекаются в одной точке (2, 10)  

Такое, что решение x = 2, y =10 

Проверка решения: 

Прямая и парабола пересекаются в одной точке (2, 10)  

Такое, что решение равно x = 2. 

Теперь проверим, подставив в уравнение x ² +6 = 4x+2.

Для x=2,

x ² +6 = 4x+2.

(2)2+6 = 4(2)+2.

4+6 = 8+2.

10 = 10. 

Мы проверили, что решение линейно-квадратичного уравнения при x = 2 и y =10.

Решение системы уравнений методом исключения

Мы можем решить систему линейных и квадратных уравнений методом исключения.

В методе исключения мы вычитаем линейное уравнение и квадратное уравнение, чтобы исключить переменную «y», и мы запишем одинаковые члены с одной стороны.

Пример 1:  

Найдите решения системы уравнений

y = x ² −4x+4, y = x+4.

Решение: 

Дана система уравнений: y = x²-4x+4… (1)

y = x +4… (2)

Теперь исключим переменную y из системы уравнений

(1)-(2) =

x ² −4x−x=0

x ² −5x = 0

Получим x = 0, x = 5

, подставив значение x в по системе уравнений получаем

Для x = 0, y = x+4

=0+4=4.

Для x=5, y=x+4

= 5+4= 9.

Решениями системы уравнений являются (0, 4) и (5, 9).

Пример 2:  

Найдите решения системы уравнений

y = x ² +6x+9, y = x+3.

Дана система уравнений: y = 2+6x+9 … (1)

y = x+3…(2)

Теперь исключим переменную y из системы уравнений

(1) -(2) =

x ² +6x+9−x−3 = 0

x ² +5x+6 = 0

z +52 +6 = 0

Получаем x=-2 , x = -3

подставив значение x в систему уравнений, получим

Для x = -2, y = x+3

= -2+3=1.

Для х =-3, у = х+3

= -3+3 = 0.

Решениями системы уравнений являются (-2, 1) и (-3, 0).

Решение системы уравнений с помощью подстановки 

Мы можем решить систему линейных и квадратных уравнений также с помощью метода подстановки.

В методе подстановки подставим линейное уравнение в квадратное уравнение на место переменной ‘y’ и запишем с одной стороны одинаковые члены, а процесс квадратного уравнения продолжим разложением на множители.

Пример 1:  

Текстильная компания выпустила два товара в одном месяце. Продажи двух продуктов одинаковы в конкретном месяце. Продажи первого продукта равны y = −x ² −10x+25y, а продажи второго продукта равны y = 14x−119y. В каком месяце продажи одинаковы?

Решение:

Дано

y= x² – 10x + 25…(1)

y= 14x – 120… (2)

Подставить (2) в (1),

14 – 14= x ² – 10x +25

-x²-10x+25-14x + 120 = 0

x²+24x-145 = 0

Разложением на множители получаем x=5, x=-29

X не может будет отрицательным, поэтому мы считаем, что x = 5 

Итак, в 5 ^-м -м месяце от начала продажи одинаковы.

Пример 2:  

Решите систему уравнений подстановкой.

y = x ² +8x+81, y = −10x

Решение:

Дано

y = x² + 8x + 81…(1)

y = -10x … (2)

Замена (2) в (1),

-10x= x² + 8x + 81

x²+8x+10x+81 = 0

x²+18x+81 = 0

Факторами мы получаем x = -9

Для x = -9, y = -10x = -10 (-9) = 90

Следовательно, решение (-9, 90). Пример из реальной жизни Как далеко арбуз запущен?

Solution:  

Given y = -2x² +120 + 2000, =

y = 150x

We solve this by substitution,

150x = -2x² + 120x + 2000

2x²+150x120x – 2000 = 0

2x²+30×2000 = 0

Факторизуя приведенное выше квадратное уравнение, мы получаем x = 25, -40

Мы игнорируем отрицательное значение x,

Итак, x=25

Мы получаем y 150 x 25 = 3750

Итак, решение (25, 3750), это точка запуска арбуза.

Упражнение

1. Найдите решения системы уравнений y = 2x² + 4x – 5, y = 2x.
2. Найдите решения системы уравнений x² + 8x+16=x+3.
3. Найдите решения системы уравнений x²-10x+12=4x+ 6.
4. Найдите решения системы уравнений y = x²+6x-9, y= 4x методом исключения.
5. Найдите решения системы уравнений y = x² + 4x-6,y=2x+5 методом исключения.
6. Найдите решения системы уравнений y = x²+16x+25, y = x.
7. Найдите решения системы уравнений y = 6x²+20x+2,y=-4x подстановкой.
8. В матче по крикету уравнение брошенного мяча записывается как y = 5x²+10x+5, уравнение летучей мыши с земли y = 3x. Сколько времени мяч находится в воздухе после удара?
9. Найдите количество решений уравнения y = x²+4x-2,y=x-2 подстановкой. 10. Найдите решения уравнения y = x²+10x + 24, y = 2x.

Концептуальная карта

Чему мы научились

• Решение системы линейно-квадратичных уравнений графическим методом.
• Решение системы уравнений методом исключения.
• Решение системы уравнений с помощью замены.

Решение систем, для которых требуется квадратичная формула

Введение Понятия Графические концепцииРешение простых системРешение промежуточных системРешение сложных систем

Purplemath

Как квадратичная формула может помочь решить систему нелинейных уравнений?

Когда в нелинейном уравнении есть член, в котором x и y перемножаются, применение квадратичной формулы может позволить вам найти одну из переменных в терминах другой.

Содержание продолжается ниже. В приведенном ниже примере показано, как квадратичная формула иногда полезна при решении систем; это также показывает, насколько сложными могут быть ваши вычисления. (Подсказка: очень.)

• Решите следующую систему уравнений:
  
  x ² − xy + y ² = 21
  x ² + 2 xy − 8 y ² = 0

Эта система представляет собой эллипс и набор прямых линий. (Да, действительно; второе уравнение на самом деле представляет собой две прямые линии.) Если я решу каждое приведенное выше уравнение для y =, тогда я могу ввести уравнения «плюс-минус» в свой графический калькулятор, чтобы проверить свою работу.

Подставив первое квадратное уравнение выше в квадратичную формулу и решив y через x , я получаю:

Чтобы применить квадратную формулу к первому уравнению, я должен был учесть все, что не было t a y (или y ² ) как коэффициент при этом члене.

Это означало, что некоторые значения b и c в формуле содержали переменные. Это совершенно нормально; это совершенно законный способ применения Формулы.

Теперь я тоже решу второе квадратное число с помощью формулы:

(Откуда взялись эти столбцы абсолютного значения? Напомним, что технически квадратный корень из x ² является абсолютным значением x . Вот как я сделал это упрощение в предпоследней строке выше. И это абсолютное значение вскоре будет иметь значение.)

Абсолютное значение x во втором уравнении выше дает два случая для значений у :

Если x < 0, то | х | = − x , so:

y = ^{( x ± 3 x )} / ₈ = ^x / ₂ , − ^x

/ ₄

Если x > 0, то | х | = x , поэтому:

y = ^{( x ± 3 x )} / ₈ = − ^{x 0024} / ₄ , ^x / ₂

In either case, I get the same two solution expressions for the corresponding values ​​of y :

y = − ^x / ₄

y = ^x / ₂

фактические числовые значения:

Если

y = − ^x / ₄ , то я получаю:

Я получил эти два числовых значения, предположив, что

y  = − x /4.

Подставив эти значения x в это уравнение, я получаю:

Если, с другой стороны,

y  =  ^x / ₂ , то я получаю:

Я получил эти два числовых значения, предположив, что

y  =  ^x / ₂ . Подставив эти значения x в это уравнение, я получаю:

Тогда моими четырьмя решениями для этой системы являются следующие точки:

---

Предупреждение: Не пытайтесь писать точки решения как «

» или «», потому что это неверно. Не все комбинации этих значений x и y являются точками решения. Не будьте небрежными; правильно запишите решение.

Кстати, мой график системы выглядит так:

(Чтобы построить эллипс традиционными методами, вам придется сделать «вращение осей», процесс, который вы, вероятно, не увидите до исчисления, если вообще.

)

---

Кстати, есть еще один метод выполнения алгебры для вышеприведенного упражнения, потому что квадратное число во втором уравнении оказывается факторизуемым. (Эта факторизуемость обычно НЕ верна, но вы должны попытаться не забыть проверить на всякий случай.) Если вы факторизуете второе уравнение и решаете для x через y , вы получите:

x ² + 2 xy − 8 y ² = 0
( х + 4 у )( х — 2 у ) = 0
x + 4 y = 0 или x — 2 y = 0
x = −4 y

  или   x = 2 y

Вы можете подставить эти выражения для x = в первое уравнение вместо x и решите полученное уравнение для соответствующих значений y .

Этот последний пример (первый способ, которым я его обработал) настолько сложен, насколько это возможно.