Как решать уравнения графическим способом: Графическое решение уравнений — урок. Алгебра, 7 класс.

Содержание

Графический способ решения уравнения — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

МУНИЦИПАЛЬНОЕ КАЗЕННОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ХАРБАТОВСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА
ИНДИВИДУАЛЬНЫЙ ИТОГОВЫЙ ПРОЕКТ
«Графический способ решения уравнения»
предметная область – математика
Автор проекта:
Макарова Екатерина
Класс: 9А
Руководитель:
Зеленовская Мария Яковлевна
Учитель математики

2.

Цель: Изложить графический метод решения уравнений и неравенств, который дает возможность определить корни или доказать ,что Цель: Изложить графический метод решения уравнений и
неравенств, который дает возможность определить корни или
доказать ,что уравнение корней не имеет.
Задачи:
-Анализ материала, посвящённого графическому решению
уравнений в учебных пособиях «Алгебра и начала
математического анализа» разных авторов , учёт целей изучения
данной темы.
— Ознакомиться в каких случаях графический способ имеет
преимущества.
— Рассмотреть решение уравнений.
— Сравнить аналитический и графический способ
решения уравнений.
-Подобрать информацию для буклета в кабинет математики
Графический метод, опирающийся на знания
элементарных функций, удобно применять
при решении задач на нахождение числа
корней и на нахождение корней уравнений
Графическое изображение зависимостей и
исследование общих зависимостей началось в 14 веке
Французский ученый Николай Оресм
стал изображать интенсивность длинами
отрезков.

Когда он располагал эти отрезки
перпендикулярно некоторой прямой, их
концы образовывали линию, названную им
«линией интенсивностей» или «линией верхнего края.
Какие бывают функции?
График функции – это множество всех точек координатной плоскости,
абсциссы которых равны значениям аргументов, а ординаты – соответствующим
значениям функции.
Линейная функция задаётся уравнением у = kx + b, гдеk и b – некоторые числа.
Графиком этой функции является прямая.
Функция обратной пропорциональности у = k/x, где k¹ 0. График этой
функции называется гиперболой.
Функция (x – a)2 + (у – b)2 = r2, где а, b и r – некоторые числа. Графиком этой
функции является окружность радиуса r с центром в т. А (а, b).
Квадратичная функция y = ax2 + bx + c где а, b, с – некоторые числа и а ¹ 0.
Графиком этой функции является парабола
Уравнение у 2(a – x) = x2(a+ x). Графиком этого
уравнения будет кривая, называемая строфоидой
Уравнение (x2 + y2)2 = a (x2 – y2).

График этого
уравнения называется лемнискатой Бернулли
Уравнение График этого уравнения
называется астроидой
Кривая(x2 y2 – 2 a x)2 =4 a2 (x2 + y2).
Эта кривая называется кардиоидой
Алгоритм решения уравнений
графическим способом
1.Преобразуем уравнение на две части в которых
содержится функция .
2.В системе координат ХОУ строим графики функций.
3. Найдём абсциссы точек пересечения графиков.
4. Записываем ответ.
Задание. Решить уравнение : х 2+2x−8=0
Задание. Решить уравнение: √x – 0.5x = 0
Вывод
Построение графиков основывается на знании
основных элементарных функций, и на основные методы
построения графиков функций. В работе представлено
достаточное
количество
примеров,
раскрывающих
графический метод решения линейных и квадратных

уравнений и неравенств, который доступен для
понимания.
Теорию можно использовать так же при подготовки к
экзаменам , к олимпиадам . В старших классах я буду ещё
знакомиться с другими функциями , с другими
уравнениями и неравенствами и мне интересно
будет продолжить свой проект.

Спасибо за внимание

English Русский Правила

Графический метод решения задач с параметрами.

Содержание.

Введение2

Глава 1. Уравнения с параметром

История возникновения уравнений с параметром3

Теорема Виета4

Основные понятия5

Глава 2. Виды уравнений с параметрами.

Линейные уравнения6

Квадратные уравнения…………………………………………………………..7

Глава 3. Методы решения уравнений с параметром

Аналитический метод….…………………………………………………….8

Графический метод. История возникновения….…………………………9

Алгоритм решения графическим методом..………………..…………….10

Решение уравнения с модулем…………………………………………….11

Практическая часть………………………………………………………………12

Заключение……………………………………………………………………….19

Список литературы………………………………………………………………20

Введение.

Я выбрала эту тему, так как она является неотъемлемой частью изучения школьного курса алгебры. Готовя данную работу, я ставила цель более глубокого изучения этой темы, выявления наиболее рационального решения, быстро приводящего к ответу. Мой реферат поможет понять другим ученикам применение графического метода решения уравнений с параметрами, узнать о происхождении, развитии этого метода.

В современной жизни изучение многих физических процессов и геометрических закономерностей часто приводит к решению задач с параметрами.

Для решения таких уравнений графический метод является весьма эффективным, когда нужно установить, сколько корней имеет уравнение в зависимости от параметра α.

Задачи с параметрами представляют чисто математический интерес, способствуют интеллектуальному развитию учащихся, служат хорошим материалом для отработки навыков. Они обладают диагностической ценностью, так как с помощью них можно проверить знание основных разделов математики, уровень математического и логического мышления, первоначальные навыки исследовательской деятельности и перспективные возможности успешного овладения курса математики в высших учебных заведениях.

В моём реферате рассмотрены часто встречающиеся типы уравнений, и, я надеюсь, что знания, полученные мной в процессе работы, помогут мне при сдаче школьных экзаменов, ведь уравнения с параметрами по праву считаются одними из самых сложных задач в курсе школьной математики. Именно такие задачи и попадают в список заданий на едином государственном экзамене ЕГЭ.

История возникновения уравнений с параметром

Задачи на уравнения с параметром встречались уже в астрономическом трактате «Ариабхаттиам», составленном в 499 г. Индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:

αх2 + bx = c, α>0

В уравнении коэффициенты, кроме параметра , могут быть и отрицательными.

Квадратные уравнения у ал-Хорезми.

В алгебраическом трактате ал-Хорезми дается классификация линейных и квадратных уравнений с параметром а.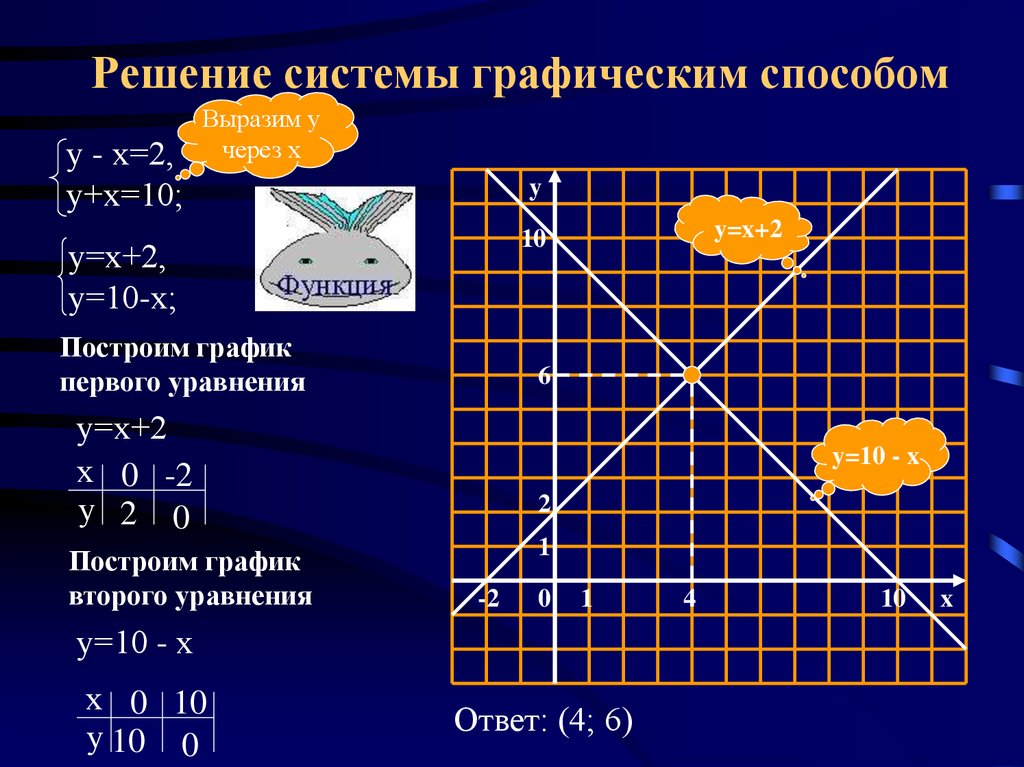 Автор насчитывает 6 видов уравнений, выражая их следующим образом:

1) «Квадраты равны корням», т. е. αx2 = bx.

2) «Квадраты равны числу», т. е. αx2 = c.

3) «Корни равны числу», т. е. αx = c.

4) «Квадраты и числа равны корням», т. е. αx2 + c = bx.

5) «Квадраты и корни равны числу», т. е. αx2 + bx = c.

6) «Корни и числа равны квадратам», т. е. bx + c = αx2.

Формулы решения квадратных уравнений по ал-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202 г. Итальянским математиком Леонардо Фибоначчи.

Вывод формулы решения квадратного уравнения с параметром в общем виде имеется у Виета, однако Виета признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в ХII в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принял современный вид.

Теорема Виета

Теорема, выражающая связь между параметрами, коэффициентами квадратного уравнения и его корнями, носящая имя Виета, была им сформулирована впервые в 1591 г. Следующим образом: «Если b + d, умноженное на α минус α2, равно bc, то α равно b и равно d».

Чтобы понять Виета, следует вспомнить, что α, как и всякая гласная буква, означала у него неизвестное (наше х), гласные же b, d – коэффициенты при неизвестном. На языке современной алгебры вышеприведенная формулировка Виета означает:

Если имеет место

(α + b)x – x2 = αb,

Т. е. x2 — (α –b)x + αb =0,

то x1 = α, x2 = b.

Выражая зависимость между корнями и коэффициентами уравнений общими формулами, записанными с помощью символов, Виета установил единообразие в приемах решения уравнений. Однако символика Виета еще далека от современного вида. Он не признавал отрицательных чисел и поэтому при решении уравнений рассматривал лишь случаи, когда все корни положительны.

Основные понятия

Параметр — независимая переменная, значение которой считается фиксированным или произвольным числом, или числом, принадлежащим заданному условием задачи промежутку.

Уравнение с параметром — математическое уравнение, внешний вид и решение которого зависит от значений одного или нескольких параметров.

Решить уравнение с параметром означает для каждого значения найти значения х, удовлетворяющие этому уравнению, а также:

1. Исследовать, при каких значениях параметров уравнение имеет корни и сколько их при разных значениях параметров.
2. Найти все выражения для корней и указать для каждого из них те значения параметров, при которых это выражение действительно определяет корень уравнения.

Рассмотрим уравнение α(х+k)= α +c, где α, c, k, x -переменные величины.

Системой допустимых значений переменных α, c, k, x называется любая система значений переменных, при которой и левая и правая части этого уравнения принимают действительные значения.

Пусть А – множество всех допустимых значений α, K– множество всех допустимых значений k, Х – множество всех допустимых значений х, C- множество всех допустимых значений c. Если у каждого из множеств A, K, C, X выбрать и зафиксировать соответственно по одному значению α, k, c, и подставить их в уравнение, то получим уравнение относительно x, т.е. уравнение с одним неизвестным.

Переменные α, k, c, которые при решении уравнения считаются постоянными, называются параметрами, а само уравнение называется уравнением, содержащим параметры.

Параметры обозначаются первыми буквами латинского алфавита: α, b, c, d, …, k , l, m, n, а неизвестные – буквами x, y,z.

Два уравнения, содержащие одни и те же параметры, называются равносильными, если:

а) они имеют смысл при одних и тех же значениях параметров;

б) каждое решение первого уравнения является решением второго и наоборот.

Виды уравнений с параметрами

Уравнения с параметрами бывают: линейные и квадратные.

1)Линейное уравнение. Общий вид:

αх = b, где х – неизвестное; α, b – параметры.

Для этого уравнения особым или контрольным значением параметра является то, при котором обращается в нуль коэффициент при неизвестном.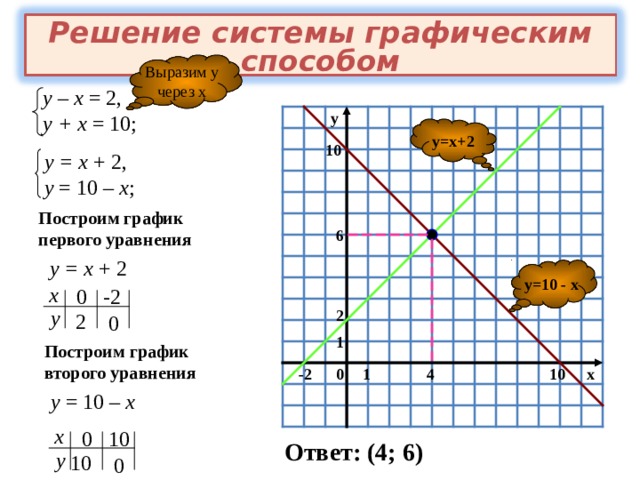

При решении линейного уравнения с параметром рассматриваются случаи, когда параметр равен своему особому значению и отличен от него.

Особым значением параметра α является значение α = 0.

1.Если, а ≠0 , то при любой паре параметров α и b оно имеет единственное решение х = .

2.Если, а =0,то уравнение принимает вид:0х = b. В этом случае значение b = 0 является особым значением параметра b.

2.1. При b ≠ 0 уравнение решений не имеет.

2.2. При b =0 уравнение примет вид:0х =0.

Решением данного уравнения является любое действительное число.

Квадратное уравнение с параметром.

Общий вид:

αx2 + bx + c = 0

где параметр α ≠0, b и с — произвольные числа

Если α =1, то уравнение называется приведённым квадратным уравнением.

Корни квадратного уравнения находятся по формулам

Выражение D = b2 – 4 αc называют дискриминантом.

1. Если D> 0 — уравнение имеет два различных корня.

2. Если D < 0 — уравнение не имеет корней.

3. Если D = 0 — уравнение имеет два равных корня.

Методы решения уравнений с параметром:

Аналитический — способ прямого решения, повторяющего стандартные процедуры нахождения ответа в уравнении без параметров.
Графический — в зависимости от условия задачи рассматривается положение графика соответствующей квадратичной функции в системе координат.

Аналитический метод

Алгоритм решения:

Прежде, чем приступить к решению задачи с параметрами аналитическим методом, нужно разобраться в ситуации для конкретного числового значения параметра. Например, возьмите значение параметра α =1 и ответьте на вопрос: является ли значение параметра α =1 искомым для данной задачи.

Далее уже на конкретном примере попробуем разобраться в аналитическом методе решения уравнений с параметром

Пример 1. Решить относительно Х линейное уравнение с параметром m:

По смыслу задачи (m-1)(x+3) = 0, то есть m=1, x= –3.

Умножив обе части уравнения на (m-1)(x+3), получим уравнение

, получаем

Отсюда при m= 2,25 .

Теперь необходимо проверить, нет ли таких значений m, при которых

найденное значение x равно –3.

решая это уравнение, получаем, что х равен –3 при m = –0,4.

Ответ: при m=1, m =2,25.

Графический метод. История возникновения

Исследование общих зависимостей началось в 14 веке. Средневековая наука была схоластической. При таком характере не оставалось места изучению количественных зависимостей, речь шла лишь о качествах предметов и их связях друг с другом. Но среди схоластов возникла школа, утверждавшая, что качества могут быть более или менее интенсивными (платье человека, свалившегося в реку, мокрее, чем у того, кто лишь попал под дождь)

Французский ученый Николай Оресм стал изображать интенсивность длинами отрезков. Когда он располагал эти отрезки перпендикулярно некоторой прямой, их концы образовывали линию, названную им «линией интенсивностей» или «линией верхнего края» (график соответствующей функциональной зависимости). Оресм изучал даже «плоскостные» и «телесные» качества, т.е. функции, зависящие от двух или трех переменных.

Важным достижением Оресма была попытка классифицировать получившиеся графики. Он выделил три типа качеств: Равномерные (с постоянной интенсивностью), равномерно-неравномерные (с постоянной скоростью изменения интенсивности) и неравномерно-неравномерные (все остальные), а также характерные свойства графиков таких качеств.

Чтобы создать математический аппарат для изучения графиков функций, понадобилось понятие переменной величины. Это понятие было введено в науку французским философом и математиком Рене Декартом (1596-1650). Именно Декарт пришел к идеям о единстве алгебры и геометрии и о роли переменных величин, Декарт ввел фиксированный единичный отрезок и стал рассматривать отношения других отрезков к нему.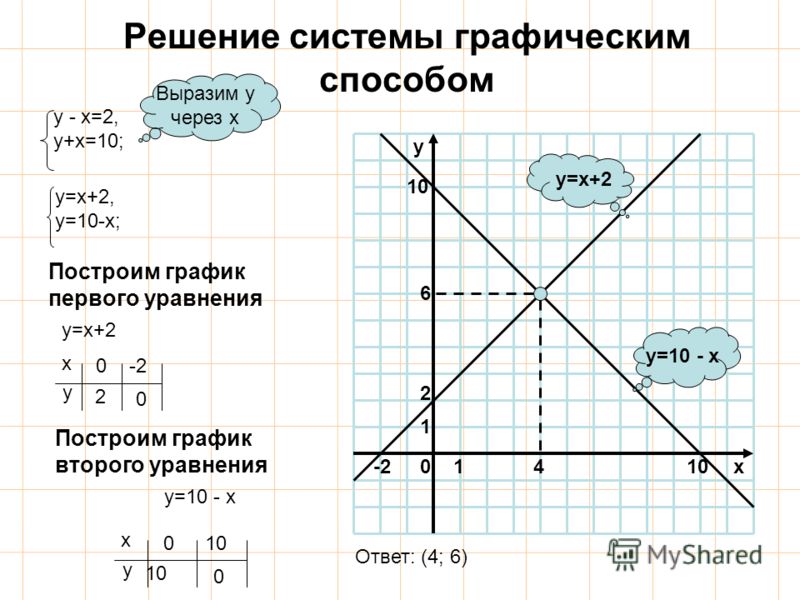

Таким образом, графики функций за все время своего существования прошли через ряд фундаментальных преобразований, приведших их к тому виду, к которому мы привыкли. Каждый этап или ступень развития графиков функций — неотъемлемая часть истории современной алгебры и геометрии.

Графический способ определения числа корней уравнения в зависимости от входящего в него параметра является более удобным, чем аналитический.

Алгоритм решения графическим методом

График функции — множество точек, у которых абсциссы являются допустимыми значениями аргумента , а ординаты — соответствующими значениями функции .

Алгоритм графического решения уравнений с параметром:

Находим область определения уравнения.
Выражаем α как функцию от х.
В системе координат строим график функции α (х) для тех значений х, которые входят в область определения данного уравнения.
Находим точки пересечения прямой α =с, с графиком функции

α (х). Если прямая α =с пересекает график α(х), то определяем абсциссы точек пересечения. Для этого достаточно решить уравнение c = α(х) относительно х.

Записываем ответ

Решение уравнений с модулем

При решении уравнений с модулем, содержащих параметр, графическим способом, необходимо построить графики функций и при различных значениях параметра рассмотреть все возможные случаи.

Например, │х│= а,

Ответ: если а < 0, то нет корней, а > 0, то х = а , х = -а, если а = 0, то х =0.

Решение задач.

Задача 1. Сколько корней имеет уравнение | | x | – 2 | = a в зависимости от параметра a?

Решение. В системе координат (x; y) построим графики функций y = | | x | – 2 | и y = a. График функции y = | | x | – 2 | изображен на рисунке.

Графиком функции y = α является прямая, параллельная оси Ox или с ней совпадающая (при a = 0).

Из графика видно, что:

Если a = 0, то прямая y = a совпадает с осью Ox и имеет с графиком функции y = | | x | – 2 | две общие точки; значит, исходное уравнение имеет два корня (в данном случае корни можно найти: x1,2 = + 2).
Если 0 < a < 2, то прямая y = α имеет с графиком функции y = | | x | – 2 | четыре общие точки и, следовательно, исходное уравнение имеет четыре корня.
Если a = 2, то прямая y = 2 имеет с графиком функции три общие точки. Тогда исходное уравнение имеет три корня.
Если a > 2, то прямая y = a будет иметь с графиком исходной функции две точки, то есть данное уравнение будет иметь два корня.

Ответ: если a < 0, то корней нет;
если a = 0, a > 2, то два корня;
если a = 2, то три корня;
если 0 < a < 2, то четыре корня.

Задача 2. Сколько корней имеет уравнение | x2 – 2| x | – 3 | = a в зависимости от параметра a?

Решение. В системе координат (x; y) построим графики функций y = | x2 – 2| x | – 3 | и y = a.

График функции y = | x2 – 2| x | – 3 | изображен на рисунке. Графиком функции y = α является прямая, параллельная Ox или с ней совпадающая (когда a = 0).

Из графика видно:

Если a = 0, то прямая y = a совпадает с осью Ox и имеет с графиком функции y = | x2 – 2| x | – 3 | две общие точки, а также прямая y = a будет иметь с графиком функции y = | x2 – 2| x | – 3 | две общие точки при a > 4. Значит, при a = 0 и a > 4 исходное уравнение имеет два корня.
Если 0 < a < 3, то прямая y = a имеет с графиком функции y = | x2 – 2| x | – 3 | четыре общие точки, а также прямая y=a будет иметь с графиком построенной функции четыре общие точки при a = 4. Значит, при 0 < a < 3, a = 4 исходное уравнение имеет четыре корня.
Если a = 3, то прямая y = a пересекает график функции в пяти точках; следовательно, уравнение имеет пять корней.
Если 3 < a < 4, прямая y = α пересекает график построенной функции в шести точках; значит, при этих значениях параметра исходное уравнение имеет шесть корней.
Если a < 0, уравнение корней не имеет, так как прямая y = α не пересекает график функции y = | x2 – 2| x | – 3 |.

Ответ: если a < 0, то корней нет;
если a = 0, a > 4, то два корня;
если 0 < a < 3, a = 4, то четыре корня;

если a = 3, то пять корней;
если 3 < a < 4, то шесть корней.

Задача 3. Сколько корней имеет уравнение

в зависимости от параметра a?

Решение.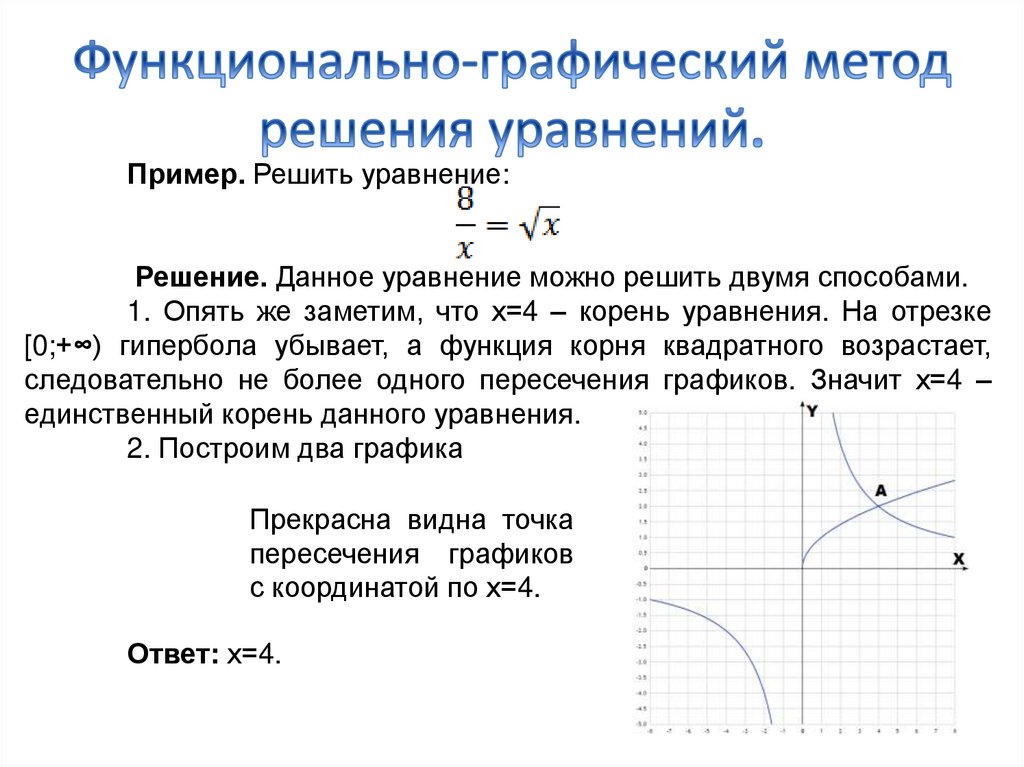 Построим в системе координат (x; y) график функции

но сначала представим ее в виде:

Прямые x = 1, y = 1 являются асимптотами графика функции. График функции y = | x | + a получается из графика функции y = | x | смещением на a единиц по оси Oy.

Графики функций пересекаются в одной точке при a > – 1; значит, уравнение (1) при этих значениях параметра имеет одно решение.

При a = – 1, a = – 2 графики пересекаются в двух точках; значит, при этих значениях параметра уравнение (1) имеет два корня.
При – 2 < a < – 1, a < – 2 графики пересекаются в трех точках; значит, уравнение (1) при этих значениях параметра имеет три решения.

Ответ: если a > – 1, то одно решение;
если a = – 1, a = – 2, то два решения;
если – 2 < a < – 1, a < – 1, то три решения.

Замечание. При решении уравнения задачи особо следует обратить внимание на случай, когда a = – 2, так как точка (– 1; – 1) не принадлежит графику функции но принадлежит графику функции y = | x | + a.

Задача 4. Сколько корней имеет уравнение

x + 2 = a | x – 1 |

в зависимости от параметра a?

Решение. Заметим, что x = 1 не является корнем данного уравнения, так как равенство 3 = a0 не может быть верным ни при каком значении параметра a. Разделим обе части уравнения на | x – 1 |(| x – 1 | 0), тогда уравнение примет вид В системе координат xOy построим график функции

График этой функции изображен на рисунке. Графиком функции y = a является прямая, параллельная оси Ox или с ней совпадающая (при a = 0).

Далее рассуждая так же, как и в предыдущей задаче, получаем ответ.

Ответ: если a – 1, то корней нет;
если – 1 < a 1, то один корень;
если a > 1, то два корня.

Рассмотрим наиболее сложное уравнение.

Задача 5. При каких значениях параметра a уравнение

ax2 + | x – 1 | = 0

имеет три решения?

Решение. 1. Контрольным значением параметра для данного уравнения будет число a = 0, при котором уравнение примет вид 0 + | x – 1 | = 0, откуда x = 1.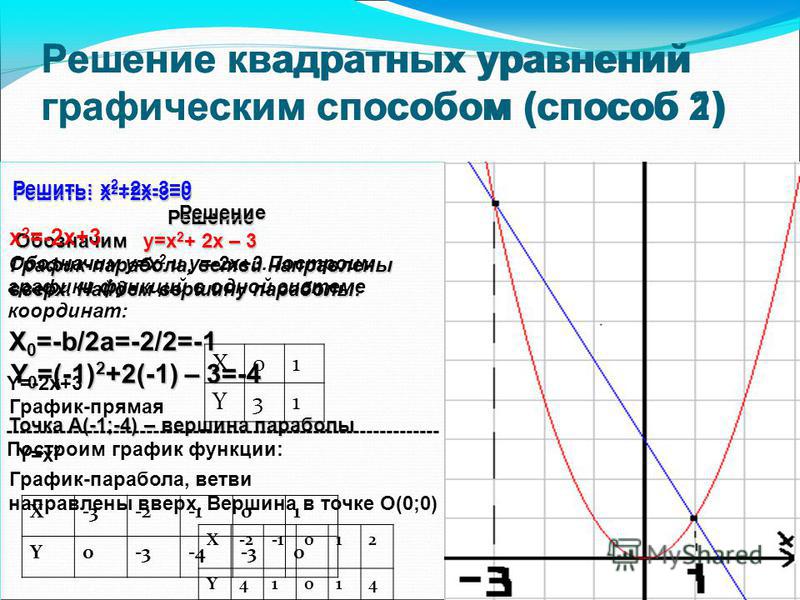 Следовательно, при a = 0 уравнение имеет один корень, что не удовлетворяет условию задачи.

2. Рассмотрим случай, когда a 0.

Перепишем уравнение в следующем виде: ax2 = – | x – 1 |. Заметим, что уравнение будет иметь решения только при a < 0.

В системе координат xOy построим графики функций y = | x – 1 | и y = ax2. График функции y = | x – 1 | изображен на рисунке. Графиком функции y = ax2 является парабола, ветви которой направлены вниз, так как a < 0. Вершина параболы — точка (0; 0).

Уравнение будет иметь три решения только тогда, когда прямая y = – x + 1 будет касательной к графику функции y=ax2.

Пусть x0 — абсцисса точки касания прямой y = – x + 1 с параболой y = ax2. Уравнение касательной имеет вид

y = y(x0) + y ‘(x0)(x – x0).

Запишем условия касания:

Данное уравнение можно решить без использования понятия производной.

Рассмотрим другой способ. Воспользуемся тем, что если прямая y = kx + b имеет единственную общую точку с параболой y = ax2 + px + q, то уравнение ax2 + px + q = kx + b должно иметь единственное решение, то есть его дискриминант равен нулю. В нашем случае имеем уравнение ax2 = – x + 1 (a 0). Дискриминант уравнения

Ответ:

Заключение.

Итак, мы узнали о происхождении, развитии и применении в современной жизни такого неотъемлемого раздела алгебры, как уравнения с параметрами. Рассмотрели различные виды таких уравнений и их решение.

Также мы узнали о различных методах решения данных уравнений, и выяснили, что графический метод решения является более удобным, чем аналитический. Затем мы рассмотрели алгоритмы решения разными методами и смогли применить их на практике.

Ещё в своей работе я рассказала о графике функций, его возникновении и мы узнали, что построение графика функций является очень удобным методом решения многих видов уравнений.

Также на практике мы разобрались с различными способами и методами построения графиков.

В современной жизни решение уравнений с параметрами является неотъемлемой частью выпускных и вступительных экзаменов в различные учебные заведения, поэтому очень важно понять и разобраться с этой темой ещё в школе.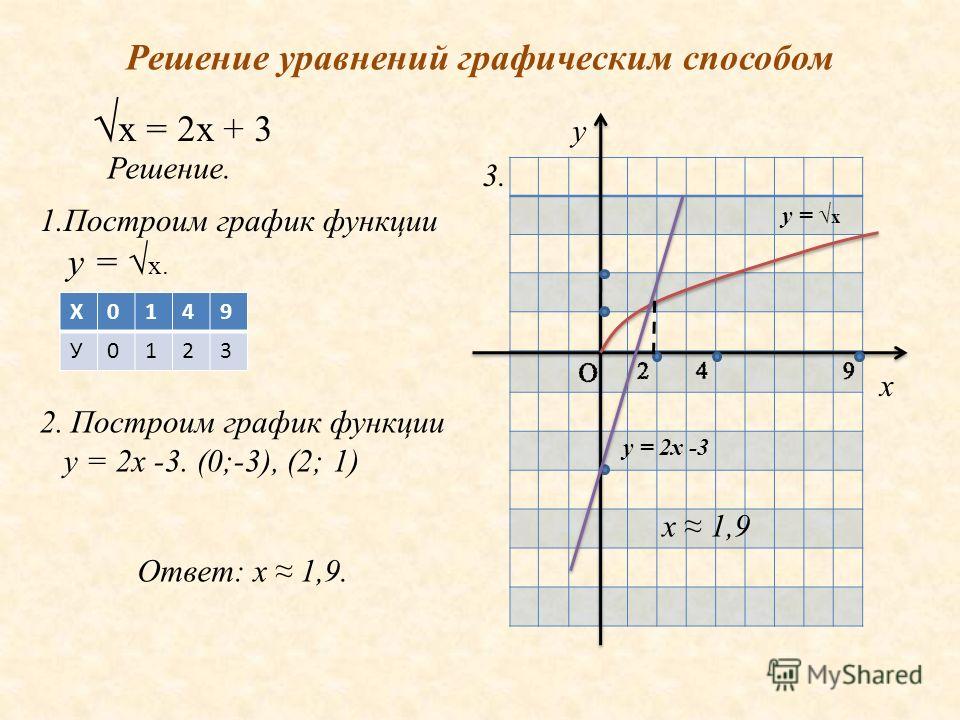

Список использованной литературы:

Справочник школьника по математике. Автор Гусев В. А.
Окунев А. А. “Графическое решение уравнений с параметрами”
Письменский Д. Т. “Математика для старшеклассников”.
Ястрибинецкий Г. А. “Уравнений и неравенства, содержащие параметры”.
Г. Корн и Т.Корн “Справочник по математике”
http://studentbank.ru/view.php?id=54456&p=2
http://works.tarefer.ru
http://festival.1september.ru
http://matem.biz
http://studentbank.ru
http://qp1qp.narod.ru
http://www.tutoronline.ru
http://mat.1september.ru
http://www.bestreferat.ru

αМ

Системы линейных уравнений: построение графиков

ОпределенияОсобые случаиЗаменаИсключение/добавлениеИсключение по ГауссуБольше примеров

Purplemath

Когда вы решаете системы уравнений (линейные или другие), вы, с точки зрения графических линий, связанных с уравнениями, находите любые точки пересечения из тех строк.

Если система уравнений состоит только из пары линейных уравнений с двумя переменными, то уравнение этой системы можно изобразить графически; график будет содержать две прямые линии, а решением системы будет точка (точки) пересечения этих линий. Поскольку две прямые линии на плоскости могут быть построены только тремя способами, то для данной системы уравнений существует только три соответствующих формы решения.

Содержание продолжается ниже

MathHelp.com

Решение систем с помощью графиков

Две прямые линии (1) имеют разные наклоны и точки пересечения, поэтому они пересекаются ровно в одной точке, (2) параллельны с разными точками пересечения, поэтому они никогда не пересекаются в любых точках, или (3) они имеют одинаковый наклон и точки пересечения, так что они на самом деле являются одной и той же линией, поэтому они «пересекаются» везде (где «везде» означает «везде идет одна линия, туда идет и другая линия). ; у них есть все свои точки — бесконечно много точек — общих»).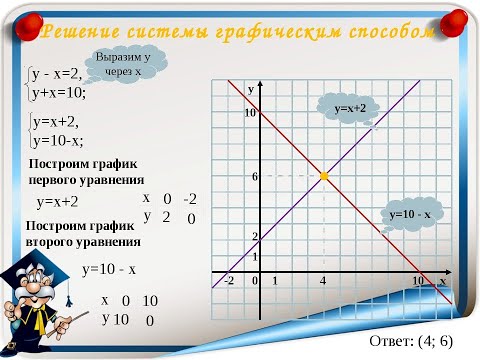 Эти три случая для пар прямых показаны ниже:

На первом графике выше, обозначенном как «Случай 1» в левой колонке, показаны две отдельные непараллельные линии, которые пересекаются ровно в одной точке. Соответствующая система уравнений называется «независимой» системой, а решением является одна ( x , y ) точка.

На втором графике выше, обозначенном как «Случай 2» в средней колонке, показаны две отдельные параллельные линии. Поскольку параллельные прямые никогда не пересекаются, то и пересечения этих прямых быть не может; то есть для системы двух линейных уравнений, которая изображается в виде двух параллельных линий, не может быть решения. Это называется «несогласованной» системой уравнений.

На третьем графике выше, обозначенном как «Случай 3» в правой колонке, показана только одна линия. На самом деле, это одна и та же линия, проведенная дважды. Эти «две» линии, на самом деле являющиеся одной и той же линией, «пересекаются» (в техническом смысле) в каждой точке своей длины. Это означает, что каждая точка на прямой(ых) является решением системы. Это называется «зависимой» системой, а «решением» является вся линия.

Это показывает, что система уравнений может иметь одно решение (конкретное x , y -точка), либо вообще нет решения, либо бесконечное решение (являющееся всеми решениями уравнения). У вас никогда не будет системы с двумя линейными уравнениями и двумя переменными с двумя или более решениями; он всегда будет один, ни один или бесконечно много.

Если это зависимая система, то почему «бесконечно» или «все точки» не является правильным ответом?

В то время как решение зависимой системы линейных уравнений представляет собой бесконечный набор точек, «бесконечность» не является числом, «бесконечность» недостаточно ясна, а точек off линия(и) системы не являются решениями. Только те точки, которые действительно лежат на прямой, являются решениями системы. Таким образом, ваш ответ для типа системы будет «зависимым», но решением на самом деле будет уравнение линии, поскольку это уравнение неявно перечисляет все точки, которые решают систему.

Например, если два уравнения в зависимой системе сведены к y = − x + 3, то вы должны представить решение как линейное уравнение, или вы можете использовать парное обозначение координат; а именно, ( x , − x + 3).

Решение с помощью графика

Вероятно, первым методом решения систем уравнений, который вы увидите, будет «решение с помощью графика». Предупреждение: вы должны относиться к этим проблемам с недоверием. Единственный способ найти решение на графике: , ЕСЛИ , вы рисуете очень аккуратную систему координат, , ЕСЛИ , вы рисуете очень аккуратные линии, , ЕСЛИ , решение оказывается точкой с хорошими аккуратными целочисленными координатами, и IF линии не близки к параллельным.

Например, если линии пересекаются под небольшим углом, практически невозможно сказать, где они пересекаются.

И если точка пересечения не является аккуратной парой целых чисел, все ставки сняты. Я имею в виду, можете ли вы сказать, просто взглянув на…

…что показанный выше перекресток имеет координаты (-4,3, -0,95)? Нет? Тогда вы понимаете мою точку зрения.

С положительной стороны, поскольку они будут вынуждены давать вам красивые и аккуратные решения для «решения с помощью графика», вы сможете получить правильные ответы , если вы рисуете очень аккуратно . Например:

2 x − 3 y = −2
4 x + y = 24

Я знаю, что мне нужен аккуратный график, поэтому я возьму линейку и начну. Сначала я решу каждое уравнение относительно « y =», чтобы легко построить график: 2/3) х + (2/3) = у

4 х + y = 24
y = −4 x + 24

Вторую линию будет легко построить, используя только наклон и точку пересечения, но мне понадобится T-диаграмма для первой линии.

Иногда вы заметите пересечение прямо на Т-диаграмме. Вы видите точку, которая находится в обоих уравнениях выше? Проверьте заштрихованную серым строку выше.

Теперь, когда у меня есть несколько точек, я аккуратно возьму линейку и график и поищу пересечение:

Даже если бы я не заметил точку пересечения на Т-диаграмме, картина.

решение: ( x , y ) = (5, 4)

Если вы застряли в решении с помощью графика, пожалуйста, ради бога, нарисуйте линии так, чтобы они действительно пересекались в точке решения . Не будь неряшливым!

Вы можете использовать приведенный ниже виджет Mathway, чтобы попрактиковаться в решении с помощью графика (или пропустить виджет и перейти к следующей странице). Попробуйте введенное упражнение (щелкнув стрелку и выбрав «Решить с помощью графика» во всплывающем окне) или введите свое собственное упражнение. Затем сравните свой ответ с ответом Мэтуэя. (Или пропустите виджет и продолжите урок.)

Пожалуйста, примите куки-файлы настроек, чтобы включить этот виджет.

(Нажмите здесь, чтобы перейти непосредственно на сайт Mathway, если вы хотите проверить их программное обеспечение или получить дополнительную информацию.)

URL: https://www.purplemath.com/modules/ systlin2.htm

Стр. 1 Стр. 3 Стр. 4 Стр. 5 Стр. 6 Стр.

Когда мы изображаем линейное уравнение на координатной плоскости, мы получаем прямую линию. Вы можете задаться вопросом, как это поможет решить систему линейных уравнений. А теперь посмотрите на эту систему.

y = −x − 2

y = 4x + 3

Если представить уравнения на сетке, мы получим: соответствующее уравнение. Но нам нужно искать решение, удовлетворяющее обоим уравнениям одновременно.

Как вы думаете, каким будет решение системы?

Ты прав! Точка пересечения двух прямых является решением системы. Здесь система имеет единственное решение, и это будет (−1, −1).

Что делать, если линии не пересекаются?

Есть две ситуации, которые мы должны рассмотреть.

✯ Когда прямые параллельны, система не имеет решения.
✯ Когда оба уравнения представляют одну и ту же прямую, система имеет бесконечно много решений.

В этом уроке мы займемся построением графиков и решением систем уравнений, имеющих единственное решение.

Решение системы уравнений с помощью графика

Давайте рассмотрим пошаговый процесс решения линейной системы с помощью графика.

Шаг 1: Проанализируйте форму каждого уравнения системы.

Шаг 2: Нарисуйте уравнения, используя наклон и точку пересечения по оси y или используя точки пересечения по оси x и y.

Случай 1: Если уравнения представлены в форме наклона и точки пересечения, определите наклон и точку пересечения по оси y и нанесите их на график.

Случай 2: Если одно из уравнений представлено в форме пересечения наклона, перепишите и другое уравнение в той же форме и изобразите его графически.

Случай 3: Если оба уравнения в других формах, найдите точки пересечения x и y и начертите их.

Шаг 3: Упорядоченная пара точек пересечения двух прямых является требуемым решением.

Рассмотрим решение систем уравнений в каждом из случаев.

Графические уравнения с использованием наклона и Y-пересечения и решение: Случай 1

Вот линейная система:

y = −x + 2

y = x + 6

Данные уравнения уже имеют форму y = mx + b, где m — наклон, а b — точка пересечения с осью y. Итак, давайте перейдем к их графическому изображению.

Чтобы построить график первого уравнения, нам нужно использовать наклон и точку пересечения по оси Y.

Точка пересечения с осью y в этом случае равна 2. Итак, давайте нанесем точку (0, 2) на координатную плоскость.

Теперь наклон равен −1. Итак, давайте переместимся на 1 единицу вниз и на 1 единицу вправо и построим еще одну точку.

Соединив эти две точки линией, мы получим график первого уравнения.

Аналогичным образом построим второе уравнение.

Пересечение по оси y равно 6. Итак, нам нужно нанести (0, 6) на сетку.

Наклон равен 1. Итак, мы должны переместиться на 1 единицу вверх и на 1 единицу вправо и нанести другую точку.

Проведя линию, соединяющую точки, имеем:

Как видите, обе линии пересекаются в одной точке. Обозначим его на нашем графике.

Теперь упорядоченная пара, соответствующая точке пересечения уравнений, является искомым решением.

Таким образом, решением системы уравнений является (−2, 4).

Пример

Решите y = −x + 7 и y = 2x 3 − 3 графически.

Оба уравнения представлены в форме пересечения наклона.

Уравнение 1: m = −1; b = 7

Уравнение 2: m = 2 3 ; b = −3

Графически представив уравнения, мы имеем:

Точка пересечения двух прямых (6, 1).

Решение: (x, y) = (6, 1).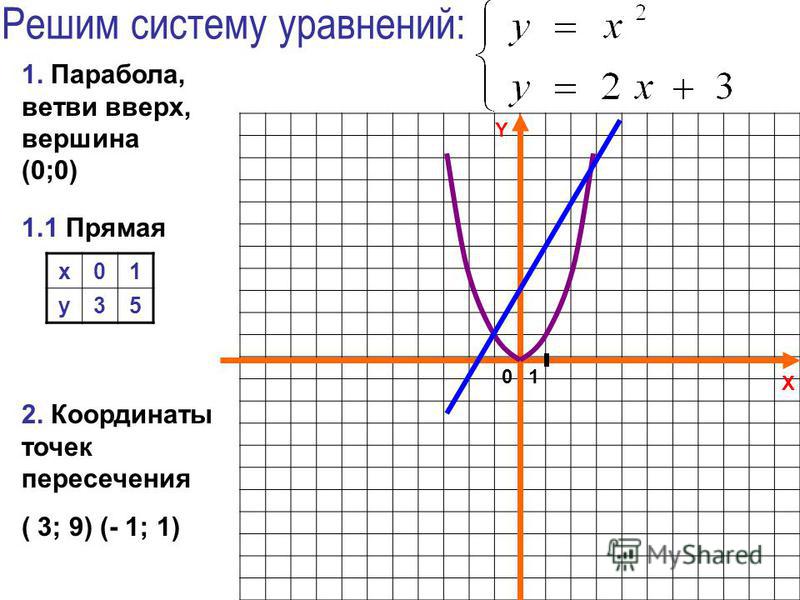

Проверьте свое решение!
Вы можете перепроверить правильность своего решения, подставив значения x и y в уравнения.
Подставив (6, 1) в уравнение 1, вы получите:
1 = −6 + 7
1 = 1 ✔
Подставив (6, 1) в уравнение 2, вы получите:
1 = 2 (6) 3 − 3
1 = 12 3 − 3
1 = 4 − 3
1 = 1 ✔

Графические уравнения наклона и пересечения Y с использованием этой системы х + 3у = 0

y = −x 2 + 5 2

Первое имеет стандартную форму, а второе — форму пересечения наклона. Переформируем и перепишем уравнение 1 в виде y = mx + c.

Вычитание x с обеих сторон:

3y = −x

Разделение обеих сторон на 3:

y = -x 3

SO, уравнение 1 имеет наклон −1 3

26262626262626262626262626262626262626262626262626262626262626262626262626262626262626262626262626262626262626262626262626262626262626262626262626262626262626262626262661 и точка пересечения 0.

Уравнение 2 имеет наклон −1 2 и Y-пересечение 5 2 .

Графически представив систему, мы имеем:

Как видите, линии пересекают друг друга в точке (15, −5).

Таким образом, решением этой системы является (x, y) = (15, −5).

Примечание. Вы также можете построить график второго уравнения, используя точки пересечения по осям x и y, а не переписывать их в форме точки пересечения с наклоном.

Графические уравнения с использованием осей X и Y и решение

Если оба уравнения представить в стандартной форме в виде этой системы:

−8x + y = −4

x − y = −3

Мы найдем точки пересечения x и y и решим эту систему. Когда мы подставим y = 0 в уравнения, мы получим x-пересечения; аналогично, когда мы установим x = 0, мы получим y-перехваты.

Подставив y = 0 в уравнение 1, получим:

−8x + 0 = −4

−8x −8 = −4 −8 −8 на [делим обе стороны0003

⇨ x = 1 2

Пересечение по оси x равно ( 1 2 , 0).

Подставив x = 0 в уравнение 1, мы получим:

−8(0) + y = −4

⇨ y = −4

Точка пересечения с точкой y равна (0, −4).

Подставляя y = 0 в уравнение 2, мы получаем:

x – 0 = −3

⇨ x = −3

Пересечение по оси x равно (−3, 0).

Подставив x = 0 в уравнение 2, получим:

0 – y = −3

−y −1 = −3 −1 [Деление обеих сторон на −1]

⇨ y = 3

Точка пересечения с осью y равна (0, 3).

Давайте построим точки пересечения по осям x и y и начертим оба уравнения.

Нарисовав уравнение 1, получим:

Нарисовав уравнение 2, получим:

Как видите, обе линии пересекаются в точках (1, 4).

Следовательно, решение (x, y) = (1, 4).

Примечание. Вы также можете построить график системы, переписав уравнения в форме пересечения наклона.

Таким образом, независимо от того, в какой форме находятся уравнения, все, что вам нужно сделать, это нарисовать их и определить точку пересечения.

Теперь твоя очередь!

Вопрос 1

Вопрос 2

Используйте интерактивный график ниже, чтобы найти решение этой системы.

y = 2x – 3

y = 3x – 2

Перетащите точку на линии в то место, куда вы хотите ее нанести.

(-5,5)(5,5)(-5,-5)(5,-5)xy
(x, y) =
,

Суть того, что мы узнали!
Решением системы уравнений является точка пересечения линий, полученных при графическом отображении уравнений.
Если прямые не пересекаются и параллельны, система не имеет решения.
Когда оба уравнения дают одну и ту же прямую, система имеет бесконечно много решений.
Независимо от того, какой метод вы используете для построения графика, решение системы уникально.
Графический инструмент
Используйте этот графический инструмент для решения линейных систем в разделе викторины. Это связано с возможностью изменения масштаба.
No related posts.