Как решать задачи на геометрическую вероятность: Геометрическая вероятность события. Теория вероятностей

alexxlab / / Разное

Геометрическая вероятность события. Теория вероятностей

  • Краткая теория
  • Примеры решения задач
  • Задачи контрольных и самостоятельных работ

Краткая теория

Одним из недостатков классического определения вероятности, ограничивающим его применение, является то, что оно предполагает конечное число возможных исходов испытания.

Этот недостаток можно преодолеть, используя геометрическое определение вероятности, т.е. находя вероятность попадания точки в некоторую область (отрезок, часть плоскости и т.п.).

Пусть, например, плоская фигура  составляет часть плоской фигуры . На фигуру  наудачу бросается точка. Это означает, что все точки области  равноправны в отношении попадания туда брошенной случайной точки. Полагая, что вероятность события  — попадания брошенной точки на фигуру  — пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно , ни от формы , найдем:

где  и  – соответственно площади областей  и .

Фигуру  называют благоприятствующей событию .

Область, на которую распространяется понятие геометрической вероятности, может быть одномерной (прямая, отрезок) или трехмерной (некоторое тело в пространстве). Получаем следующее определение геометрической вероятности:

Определение геометрической вероятности

Геометрической вероятностью события  называется отношение меры области, благоприятствующей появлению события , к мере всей области.

Смежные темы решебника:

  • Классическое определение вероятности
  • Статистическое определение вероятности

Примеры решения задач

Пример 1


Задача о встрече

Двое договорились встретиться в течение часа. Первый пришедший ждет второго 10 минут. Найти вероятность, что встреча произойдет.

Решение

Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:

ВКонтакте
WhatsApp
Telegram

Я буду работать с вами, над вашей проблемой, пока она не решится.

Обозначим время появления каждого из событий соответственно через х и у. В силу условия задачи должны выполняться неравенства: ;     (события происходят в интервале 1 час).

Введем в рассмотрение прямоугольную системы координат . В этой системе двойным неравенствам удовлетворяют координаты любой точки, принадлежащей квадрату . Таким образом,  эту фигуру можно рассматривать как фигуру G, координаты точек которой представляют все возможные значения моментов появления событий. 

События перекроются во времени, если разность появления их:

Этим неравенствам удовлетворяют точки, принадлежащие области . Эту область можно рассматривать как фигуру , координаты точек которой являются благоприятствующими перекрыванию событий по времени.

Вероятность того, что события перекрываются по времени (два человека встретятся):

Ответ: .

Пример 2

Внутри круга радиусом  наудачу брошена точка. Найти вероятность того, что точка окажется внутри вписанного в круг правильного шестиугольника.

Решение

Вероятность того, что точка окажется внутри вписанного в круг правильного шестиугольника:

Площадь правильного многоугольника с числом сторон , вписанного в окружность радиуса  составляет:

Площадь круга:

Искомая вероятность:

Ответ:

Задачи контрольных и самостоятельных работ

Задача 1

На некоторое обслуживающие устройство поступают две заявки. Каждая может поступить в любой момент времени в течение времени T=150 минут. Время обслуживания первой заявки τ1=20 минут, второй τ2=40 минут. При поступлении заявки на свободное устройство даже в последний момент времени T, она обслуживается. Найти вероятность того, что 1) обе заявки будут обслужены; 2) будет обслужена ровно одна заявка.

Задача 2

Какова вероятность того, что сумма двух наугад взятых положительных чисел, каждое из которых не больше X=5, не превзойдет X, а их произведение будет не больше Y=0,4?

Задача 3

Случайные величины X, Y независимы и равномерно распределены на отрезках: X — на [0,3], Y — на [0,4]. Найти вероятность P(X<Y).

Задача 4

В круг радиусом 4 см брошена точка. Найти вероятность того, что она удалена от центра круга не более чем на 1 см.

Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:

ВКонтакте
WhatsApp
Telegram

Я буду работать с вами, над вашей проблемой, пока она не решится.

Задача 5

В круг радиуса R вписан квадрат. Внутрь круга наудачу брошены 3 точки.

Найти вероятность того, что все точки попали внутрь одного из малых сегментов.

Задача 6

На 200-км газопроводе между компрессорными станциями А и В происходит утечка газа. Утечка равновозможная в любой точке газопровода. Найти вероятность того, что она расположена: 

а) не  далее 20 км от какой-нибудь из компрессорных станций А, В.

б) ближе к А, чем к В.

Задача 7

В квадрате стороной 10 наудачу появляется точка. Найти вероятность того, что она попадет вне вписанного в квадрат круга.

Задача 8

Решить задачу, используя геометрическое определение вероятности.

В куб вписан шар. Точка наудачу зафиксирована в кубе. Найти вероятность того, что точка попадет в шар.

Задача 9

Решить задачу, используя геометрическое определение вероятности.

В прямоугольник с вершинами N(1;0),K(-2;0),L(-2;5),M(1;5) наудачу брошена точка

Q(x;y). Найти вероятность того, что координаты этой точки удовлетворяют неравенствам x2+1≤y≤3-x

  • Краткая теория
  • Примеры решения задач
  • Задачи контрольных и самостоятельных работ

Геометрическая вероятность на прямой, на плоскости, в пространстве, примеры

Понятие геометрической вероятности было сформулировано в §37 данного справочника. В этом параграфе мы рассмотрим различные задачи, при решении которых используется геометрическая вероятность.

п.1. Геометрическая вероятность на прямой

В одномерном случае пространству всех событий соответствует длина отрезка Ω ↔ L. Событие A ↔ lA – попадание в отрезок lA ≤ L.
Тогда вероятность события A $$ \mathrm{ P(A)=\frac{l_A}{L} } $$ Говорят, что мерой множеств событий в одномерном случае является длина.

Например:
Оптический кабель длиной 1 м случайно разрезают ножницами. Какова вероятность того, что длина обрезка составляет не меньше 80 см?

Чтобы получить обрезок не менее 80 см, нужно попасть ножницами в отрезок 20 см справа или слева куска кабеля. Вероятности попадания \(\mathrm{P_{\text{справа}}=\frac{l_A}{L},\ P_{\text{слева}}=\frac{l_A}{L}}\). По правилу суммы, искомая вероятность при L=100 см, lA=20 см $$ \mathrm{ P_{\text{справа}}+P_{\text{слева}}=\frac{2l_A}{L},\ \ P=\frac{2\cdot 20}{100}=0,4 } $$ Ответ: 0,4.

п.2. Геометрическая вероятность на плоскости

В двумерном случае пространству всех событий соответствует площадь некоторой замкнутой области Ω ↔ SΩ.
Событие A ↔ sA – попадание в замкнутую подобласть с площадью sA ≤ SΩ.
Тогда вероятность события A $$ \mathrm{ P(A)=\frac{s_A}{S_{\Omega}} } $$ Говорят, что мерой множеств событий в двумерном случае является площадь.

Например:
Два друга договорились встретиться между 14 и 15 часами. Каждый может прийти в любой момент в течение назначенного часа. Тот, кто пришёл первым, ждёт другого в течение 15 минут, а затем уходит. Чему равна вероятность встречи?

Пусть 0≤x≤60 (мин) и 0≤y≤60 (мин) – моменты прихода первого и второго друга соответственно. 2=1575 }\\ \mathrm{ P(A)=\frac{s_A}{S_{\Omega}}=\frac{1575}{3600}=\frac{7}{16}=0,4375 } \end{gather*} Ответ: 0,4375.

п.3. Геометрическая вероятность в пространстве

В трёхмерном случае пространству всех событий соответствует объём некоторой замкнутой области Ω ↔ VΩ.
Событие A ↔ vA – попадание в замкнутую подобласть с объёмом vA ≤ VΩ.
Тогда вероятность события A $$ \mathrm{ P(A)=\frac{v_A}{V_{\Omega}} } $$ Говорят, что мерой множеств событий в трёхмерном случае является объём.

Например:
Телескоп находится на космической станции. В каждый момент времени он случайно направлен в одну из сторон и наблюдает часть неба. Пусть телескоп способен регистрировать все объекты в радиусе 10000 км. Какова вероятность, что он заметит астероид радиусом 100 км, залетевший в область регистрации?


Пространству всех событий соответствует сфера объемом: $$ \mathrm{ V_{\Omega}=\frac{4}{3}\pi R^3,\ R=10000\ \text{км} } $$ Событие A – астероид замечен – соответствует объему астероида: $$ \mathrm{ v_{A}=\frac{4}{3}\pi R^3,\ R=100\ \text{км} } $$ Вероятность того, что астероид будет замечен: $$ \mathrm{ P(A)=\frac{v_{A}}{V_{\Omega}}=\frac{\frac{4}{3}\pi R^3}{\frac{4}{3}\pi R^3}=\left(\frac{r}{R}\right)^3,\ \ P(A)=\left(\frac{100}{10000}\right)^3=10^{-6}=0,000001 } $$ Ответ: 0,000001. 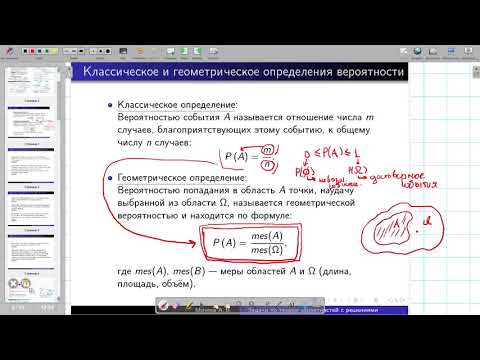2-0,004\geq 0} & \end{array}\right. \Rightarrow \left\{ \begin{array}{ l} \mathrm{(x-0,3)(x+0,3)\leq 0} &\\ \mathrm{(x-0,2)(x+0,2)\geq 0} & \end{array}\right. \Rightarrow \\ \Rightarrow \left\{ \begin{array}{ l} \mathrm{-0,3\leq x\leq 0,3} &\\ \left[ \begin{array}{ l} \mathrm{x\leq -0,2} &\\ \mathrm{x\geq 0,2} & \end{array}\right.& \end{array}\right. \Rightarrow \left[ \begin{array}{ l} \mathrm{-0,3\leq x\leq -0,2} &\\ \mathrm{0,2\leq x\leq 0,3} & \end{array}\right. \end{gather*} Учитывая x ∈ [0; 1], получаем: $$ \left\{ \begin{array}{ l} \mathrm{0\leq x\leq 1} &\\ \left[ \begin{array}{ l} \mathrm{-0,3\leq x\leq -0,2} &\\ \mathrm{0,2\leq x\leq 0,3} & \end{array}\right.& \end{array}\right. \Rightarrow 0,2 \leq x \leq 0,3 $$ Мерой в данной задаче является длина: LΩ = 1, lA = 0,3 — 0,2 = 0,1
Вероятность выбора точки при данных условиях: \(\mathrm{P(A)=\frac{0,1}{1}=0,1}\)
Ответ: 1) 0,2; 2) 0,1.

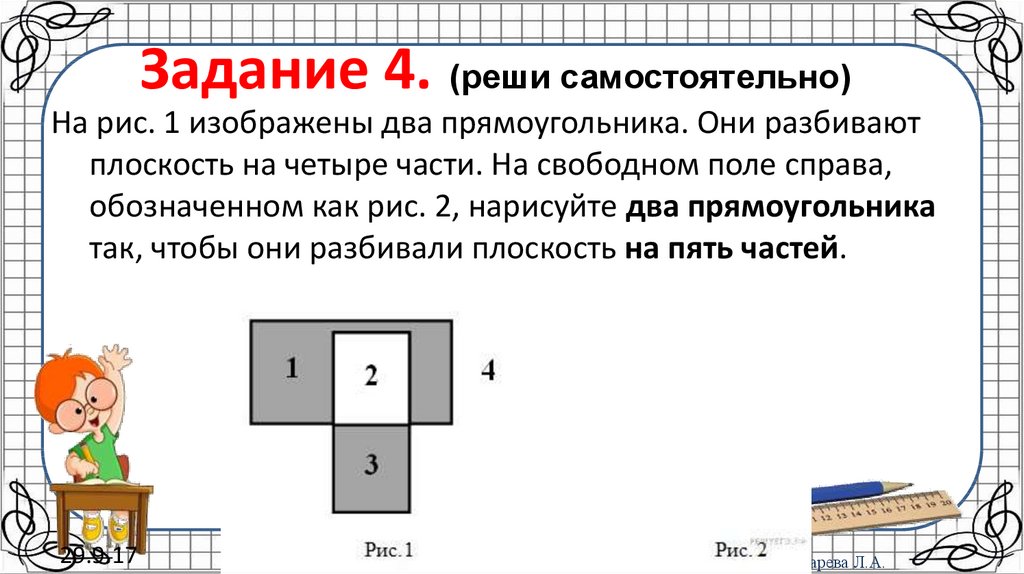
Пример 4. В сито, наполненное до краёв зерном, уронили жемчужину. Сито представляет собой цилиндр радиусом 20 см и высотой 12 см.
1) Какова вероятность случайно зачерпнуть горсть зерна вместе с жемчужиной, если объём горсти 0,1 л?
2) Если после неудачной попытки, высыпать зерно из горсти обратно в сито, перемешать, и снова зачерпнуть горсть, изменится ли вероятность?
3) Если после неудачной попытки, высыпать зерно из горсти в сторону и зачерпнуть следующую горсть, изменится ли вероятность?
4) Сколько «неудачных» горстей нужно отсыпать в сторону, чтобы вероятность удачи для следующей попытки превысила 1/3?
1) Мерой для этой задачи является объём.
Пространство всех событий – все возможные точки, где может оказаться жемчужина – это цилиндрическое сито, объемом

VΩ = πR2h,   R = 20 см = 2 дм,  h = 12 см = 1,2 дм
VΩ = π · 22 · 1,2 = 4,8 π дм3 = 4,8 π л

Событие A – зачерпнуть жемчужину в горсти объемом vA = 0,1 л
Вероятность: $$ \mathrm{ P(A)=\frac{v_{A}}{V_{\Omega}},\ \ P(A)=\frac{0,1}{4,8\pi} \approx 0,0066 } $$ 2) Если высыпать зерно обратно из горсти и перемешать, то пространство всех событий останется тем же, VΩ = 4,8π л. 2=7 } $$ Вероятность для разности: $$ \mathrm{ P(|x-y|\lt 1)=\frac{s_{A}}{S_{\Omega}}=\frac{7}{16} } $$

Ответ: \(\mathrm{ 1) \frac{23}{32};\ \ 2) \frac{7}{16}. }\)

Самая сложная и легкая задача по геометрии — воскресная головоломка — обдумывайте свои решения

Если вы покупаете по ссылке в этом посте, я могу заработать комиссию. Это не влияет на цену, которую вы платите. Как партнер Amazon я зарабатываю на соответствующих покупках. Узнать больше.

Опубликовано 4 сентября 2016 г. Прешем Талвалкаром. Прочитайте обо мне или напишите мне .

Задача известна как случайные углы Лэнгли и была поставлена ​​в 1922. Она также известна как самая сложная простая задача геометрии, потому что ее можно решить элементарными методами, но она сложна и трудоемка.

Вы можете это понять? Посмотрите видео для решения.

Можете ли вы решить самую сложную простую геометрическую задачу?

Или продолжайте читать для объяснения.
.
.

«Все будет хорошо, если вы будете использовать свой разум для принятия решений и думать только о своих решениях.» С 2007 года я посвятил свою жизнь разделению радости теории игр и математики. MindYourDecisions теперь содержит более 1000 бесплатных статей без рекламы благодаря поддержке сообщества! Помогите и получите ранний доступ к публикациям с залогом на Patreon.

.
.

.
.
.
.
М
И
Н
Д
.
Д
О
У
Р
.
D
E
C
I
S
I
O
N
S
.
P
U
Z
Z
L
E
.
.
.
.
Ответ на самую сложную простую задачу по геометрии

Есть два основных принципа решения задачи. Во-первых, сумма всех углов треугольника равна 180 градусам. Во-вторых, в равнобедренном треугольнике против двух равных сторон лежат два равных угла. Если известно, что у треугольника два равных угла, то противоположные стороны равны, а знание двух равных сторон означает, что противоположные углы равны.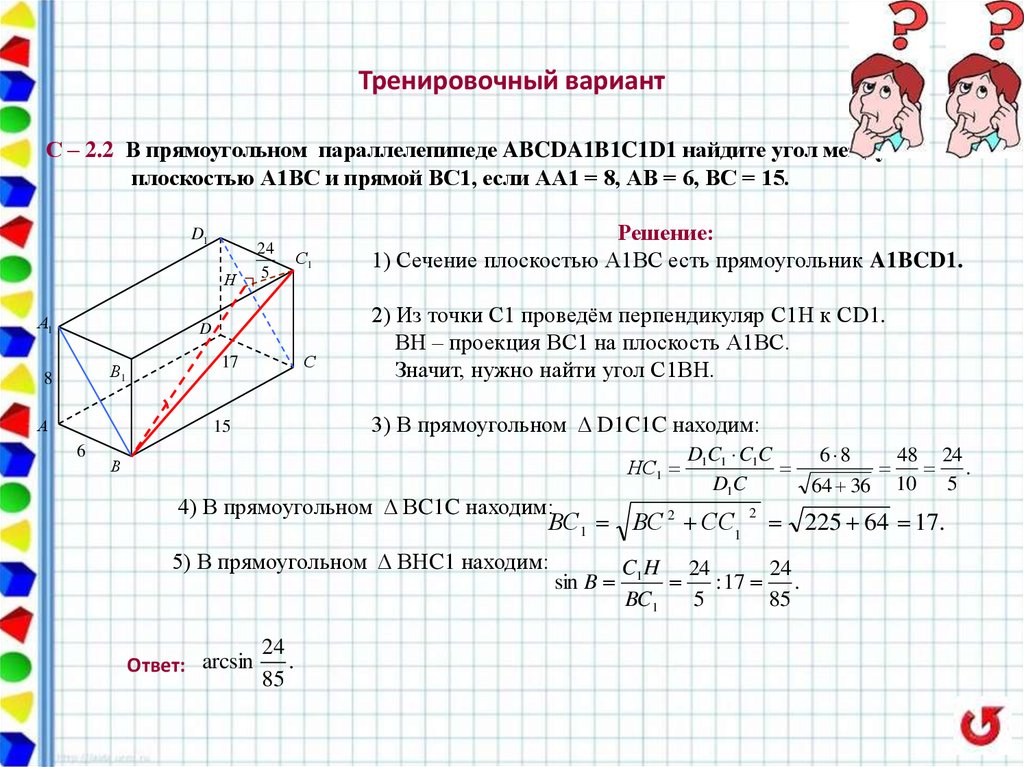

Доказательство включает в себя работу с рядом равнобедренных треугольников. Для начала начертите отрезок BG так, чтобы угол CBG был равен 20 градусам.

В треугольнике CBG мы знаем, что один угол равен 20 градусам, а другой равен 80 градусам, всего 100 градусов. Таким образом, сумма углов треугольника равна 180, мы можем решить, что ∠CGB = 80 градусов. Это означает, что треугольник CBG равнобедренный и BC = BG.

Углы CBG и BGE образуют прямую линию, поэтому их сумма должна составлять 180 градусов. Это означает, что угол BGE равен 100 градусам.

Затем, ориентируясь на треугольник BGE, мы можем решить, что ∠BEG = 40 градусов, потому что это должно быть 180 минус известные углы 40 и 100. В треугольнике BGE два угла равны 40 градусам, так что это еще один равнобедренный треугольник. , поэтому BG = GE.

Затем, ориентируясь на треугольник BFC, мы можем решить, что ∠BFC = 50 градусов, что означает, что треугольник BFC является еще одним равнобедренным треугольником. Это означает, что BF = BC.

Мы доказали BC = BG = GE = BF.

Теперь создаем еще треугольник BFG. Поскольку BG = BF, мы знаем, что противоположные углы должны быть равны. (Если вы следите за видео, я опечатался в этом шаге в видео на 5:04. Я хотел сказать, что стороны BG и BF равны.)

Третий угол в треугольнике, ∠GBF, равен 60 градусам, таким образом, остальные углы должны составлять половину от 180 – 60. Это (180 – 60)/2 = 60 градусов. Другими словами, все 3 угла равны, поэтому треугольник BFG равносторонний. Все его стороны должны быть равны, поэтому GF = BF.

Мы выяснили много информации. Есть еще один треугольник, который необходимо рассмотреть, поэтому ниже приведена диаграмма, посвященная треугольнику GFE, в которой опущена второстепенная информация.

Мы знаем, что GF = GE, поэтому у нас снова есть равнобедренный треугольник, и мы знаем, что угол при вершине равен 40 градусам. Это означает, что оставшиеся углы составляют половину от 180 – 40, что составляет 70 градусов.

Наконец, мы знаем, что 40 + x должно быть равно 70, значит, х = 30 градусов.

Вот и ответ! Значение  x  – 30 градусов.

Викпеда Лэнгли. Самая сложная простая задача по геометрии в мире
http://thinkzone.wlonk.com/MathFun/Triangle.htm
https://www.duckware.com/tech/worldshardesteasygeometryproblem.html

Спасибо покровителям!

Кайл
Брайан М. Муни

Вы можете поддержать меня и этот сайт на Patreon.

МОИ КНИГИ

Если вы совершаете покупку по этим ссылкам, я могу получить компенсацию за покупки, сделанные на Amazon. Как партнер Amazon я зарабатываю на соответствующих покупках. Это не влияет на цену, которую вы платите.

Рейтинги книг указаны с января 2022 года.

(ссылки для США и всего мира)
0007

Обдумывайте свои решения представляет собой сборник из 5 книг:

(1) Радость теории игр: введение в стратегическое мышление
(2) 40 парадоксов в логике, теории вероятностей и теории игр
(3) Иллюзия иррациональности: как принимать обдуманные решения и преодолевать предубеждения
(4) Лучшие приемы ментальной математики
(5) Умножение чисел путем рисования линий

Радость теории игр показывает, как вы можете использовать математику, чтобы превзойти подумайте о своем соревновании. (рейтинг 4,2/5 звезд по 224 отзывам)


40 парадоксов в логике, теории вероятностей и теории игр содержит наводящие на размышления и противоречивые результаты. (рейтинг 4,1/5 звезд в 38 обзорах)


Иллюзия иррациональности: как принимать разумные решения и преодолевать предубеждения — это руководство, в котором объясняется множество причин, по которым мы предвзято относимся к принятию решений, и предлагаются методы принятия разумных решений. (оценка 4/5 звезд в 24 обзорах)


Лучшие приемы ментальной математики учит, как можно выглядеть математическим гением, решая задачи в уме (оценка 4,2/5 звезд в 76 обзорах)


Умножение чисел путем рисования линий Эта книга является справочным пособием для моего видео, которое набрало более 1 миллиона просмотров по геометрическому методу умножения чисел. (оценка 4,3/5 звезд в 30 обзорах)


Размышляйте над головоломками представляет собой сборник из трех книг «Математические головоломки», тома 1, 2 и 3. Темы головоломок включают математические предметы, включая геометрию, вероятность, логика и теория игр.

Math Puzzles Volume 1 содержит классические головоломки и загадки с полными решениями задач по счету, геометрии, вероятности и теории игр. Том 1 получил оценку 4,4/5 звезд по 87 отзывам.

Математические головоломки, том 2 — продолжение книги с большим количеством больших задач. (оценка 4,1/5 звезд по 24 отзывам)

Math Puzzles Volume 3 — третья книга в серии. (рейтинг 4,2/5 звезд по 22 отзывам)

KINDLE UNLIMITED

Преподаватели и студенты со всего мира часто пишут мне о книгах по электронной почте. Поскольку образование может иметь такое огромное влияние, я стараюсь сделать электронные книги доступными как можно большему числу людей по минимально возможной цене.

В настоящее время вы можете читать большинство моих электронных книг через программу Amazon Kindle Unlimited. Включенный в подписку, вы получите доступ к миллионам электронных книг. Вам не нужно устройство Kindle: вы можете установить приложение Kindle на любой смартфон/планшет/компьютер и т. д. Ниже я собрал ссылки на программы в некоторых странах. Пожалуйста, проверьте доступность и условия программы на местном веб-сайте Amazon.

США, список моих книг (США)
Великобритания, список моих книг (Великобритания)
Канада, список моих книг (CA)
Германия, список моих книг (Германия)
Франция, список моих книг (Франция)
Индия, список моих книг (IN)
Австралия, список моих книг (AU)
Италия, список моих книг (IT)
Испания, список моих книг (ES)
Япония, список моих книг (JP)
Бразилия, результаты книги (BR)
Мексика, результаты книги (MX)

ТОВАРЫ

Возьмите кружку, футболку и многое другое на официальном сайте товаров: Следите за своими решениями в Teespring .

Практические вопросы по геометрии

1. В треугольнике 30-60-90 длина гипотенузы равна 6. Какова длина самой короткой стороны?

  1. 2
  2. 3

2. Какова площадь круга диаметром 16?

  1. 8
  2. 16
  3. 64
  4. 128
  5. 256

3. На рисунке ниже показаны только горизонтальные и вертикальные линии. Вычислить его периметр.

  1. 27
  2. 33
  3. 36
  4. 42
  5. 48

  1. 35°
  2. 40°
  3. 45°
  4. 50°
  5. 55°
5,0 9012 Площадь окружности равна 3?

  1. 15
  2. 225
  3. 400
  4. 900
  5. 3000

6. Чему равна сумма внутренних углов шестиугольника?

  1. 540°
  2. 720°
  3. 810°
  4. 1080°
  5. 1440°

7. Найдите площадь под треугольником.

  1. 20
  2. 30
  3. 35
  4. 40
  5. 80

8. На рисунке приведен параллель платель с двумя англами, приведенным в терминах

9999. Определить значение х .

  1. 9
  2. 10
  3. 20
  4. 22
  5. 24

9. Стороны треугольников какой длины могут быть прямыми?

  1. 3, 13, and 14
  2. 4, 5, and 6
  3. 4, 9, and 10
  4. 5, 10, and 15
  5. 5, 12, and 13

10. The figure внизу изображен равносторонний треугольник со сторонами длины 6. Чему равна площадь треугольника?

  1. 12
  2. 18
  3. 36

1. B. в 30-60-90-riangle, at baniio, рентайо. Другими словами, длина более длинного катета в  раз больше длины более короткого катета, а гипотенуза в два раза больше длины более короткого катета. Следовательно, наименьшая сторона равна половине длины гипотенузы, поэтому ее длина равна .

2. С. Площадь круга находится по формуле A = 2 , где r — радиус окружности. Задача дает диаметр окружности, который в два раза больше радиуса. Итак,

Теперь подставляем это значение в формулу площади и вычисляем площадь.

3. D. Периметр фигуры – это длина вокруг нее. Чтобы найти периметр многоугольника, сложите длины его сторон. Начните с заполнения недостающих длин сторон. Например, длина более короткой отсутствующей стороны равна 6, потому что, если вы прибавите ее к 3 слева, в результате должно получиться 9.справа.

Наконец, сложите длины сторон, чтобы найти периметр.

12 + 3 + 9 + 9 + 6 + 3 = 42

4. D. Сумма углов треугольника равна 180°. Следовательно, если мы вычтем два заданных угла из 180°, результатом будет недостающий угол.

180 – 95 – 35 = 50

Следовательно, недостающий угол равен 50°.

5. Б. Длина окружности находится по формуле С = 2, где r — это радиус окружности. Подставьте данную длину окружности в эту формулу и найдите r .
30 = 2
r = 15
Следовательно, радиус круга равен 15. Используйте это, чтобы найти площадь круга. Площадь круга находится по формуле A = 2 . Подставляем в эту формулу длину радиуса и вычисляем площадь.
A =(15) 2 = 225
6. B. Сумма мер внутренних углов многоугольника с н сторон 180 . ( n – 2) У шестиугольника шесть сторон. Поэтому подставьте 6 вместо n в формулу и посчитайте.

Следовательно, сумма мер равна 720°.

7. A. Площадь треугольника находится по формуле , где b длина основания и h высота треугольника. На рисунке основание равно 8, а высота равна 5. Подставляем эти значения в формулу и вычисляем площадь.

8. D. В параллелограмме смежные углы дополняют друг друга; то есть они складываются до 180°.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *