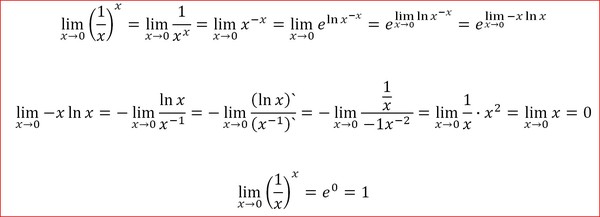Lim ln cosx x 2: Mathway | Популярные задачи

2

Вспомните, чему эквивалентны при функции , , , и все у Вас получится.

   

                  

незваный гость	16.04.2006, 19:28
Заслуженный участник 17/10/05 3709	Или дважды воспользуйтесь правилом Лопиталя, вынося не стремящиеся к нулю члены из предела.

kazak131	18.04.2006, 12:18
16/04/06 13	Всем спасибо за помощь. Предел нашел. Тема закрыта

Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию

Страница 1 из 1

[ Сообщений: 4 ]

Модераторы: Модераторы Математики, Супермодераторы

Содержание Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения

Найти:

2x}=-\frac{1}{2}$$

$\endgroup$

1

$\begingroup$

Решение без разложений Де-Л’Опиталя, Тейлора или асимптотических равенств, но при условии существования предела:

Сначала докажите, что $$\lim_{x\rightarrow0}\frac{\ln(\cos x)}{x}=0$$ Это следует из того, что $$\lim_{x\rightarrow0}\frac{\ln(\cos x)}{x}=\lim_{x\rightarrow0}\frac{\ln(\cos x)-\ln(\cos 0)} {х} = (\ пер (\ соз х)) ^ {\ простое число} (0) $ $ Теперь определите $$f(x)=\begin{case}\frac{\ln(\cos x)}{x}& x\neq 0\\ 0& х=0\конец{случаи}$$ $f$ всюду непрерывна и дифференцируема по крайней мере в $\mathbb{R}^*$ Обратите внимание, что $$\lim_{x\rightarrow0}\frac{\ln(\cos x)}{x^2}=\lim_{x\to 0}\frac{f(x)-f(0)}{x} $$ поэтому нам нужно вычислить $f^{\prime}(0)$ (после доказательства его существования). {\prime}(x)$ существует). 92}$ и готово

Конечно, если существование не предполагается, то придется использовать другие хитрости.

$\endgroup$

3

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie 92}{4}}\rightarrow1.