Примеры решения задач с векторами
Примеры решения задач с векторами
Вектора применяются во многих науках, таких как: математика, физика, геометрия и многих других прикладных науках. На практике, они позволяют не делать лишних операций и сократить время выполнения задач. Поэтому, будущим специалистам очень важно понять теорию векторов и научиться решать задачи с ними.
Перед изучением примеров решения задач советуем изучить теоретический материал по векторам, прочитать все определения и свойства. Список тем находится в правом меню.
Координаты вектора
Теоретический материал по теме — координаты вектора.
Пример
Запись означает, что вектор имеет следующие координаты: абсцисса равна 5, ордината равна -2.
Пример
Задание. Заданы векторы и . Найти координаты вектора
Решение.
Пример
Вектор
.
Найти координаты вектораРешение.
Пример
Задание. Найти координаты вектора , если
Решение.
Длина (модуль) вектора
Теоретический материал по теме — длина вектора.
Пример
Задание. Найти длину вектора
Решение. Используя формулу, получаем:
Пример
Задание. Найти длину вектора
Решение. Используя формулу, получаем:
Угол между векторами
Теоретический материал по теме — угол между векторами.
Пример
Задание. Известно, что скалярное произведение двух векторов , а их длины . Найти угол между векторами и .
Решение. Косинус искомого угла:Пример
Задание.
Найти угол между векторами
и
Решение. Косинус искомого угла
Пример
Задание. Найти угол между векторами и
Решение. Косинус искомого угла:
Разложение вектора по ортам координатных осей
Теоретический материал по теме — разложение вектора по ортам.
Пример
Задание. Зная разложения вектора по базисной системе векторов: , записать координаты этого вектора в пространстве.
Решение. Коэффициенты при ортах и есть координатами вектора, поэтому из того, что , получаем, что
Пример
Задание. Вектор задан своими координатами: . Записать разложение данного вектора по ортам осей координат.
Решение. Координаты вектора — это коэффициенты при ортах координатных осей в разложении вектора по базисной системе векторов, поэтому искомое разложение:
Скалярное произведение векторов
Теоретический
материал по теме — скалярное
произведение векторов.
Пример
Задание. Вычислить скалярное произведение векторов и , если их длины соответственно равны 2 и 3, а угол между ними 60°.
Решение. Так как из условия , , а , то
Пример
Задание. Найти скалярное произведение векторов и
Решение. Скалярное произведениеВекторное произведение векторов
Теоретический материал по теме — векторное произведение векторов.
Пример
Задание. Найти векторное произведение векторов и
Решение. Составляем определитель и вычисляем его:
Смешанное произведение векторов
Теоретический материал по теме — смешанное произведение векторов.
Пример
Задание.
Вычислить объем пирамиды, построенной
на векторах
,
,
Решение. Найдем смешанное произведение заданных векторов, для это составим определитель, по строкам которого запишем координаты векторов , и :
Практика. Решение задач 9 класс онлайн-подготовка на Ростелеком Лицей
Построение прямой
Мы знаем общий вид уравнения прямой:
Что это нам дает? Если мы видим уравнение: , то понимаем, что это уравнение задает именно прямую, а не какую-то другую линию.
Более того, нам совсем не сложно построить эту прямую. Для этого необходимо найти координаты двух любых точек, которые принадлежат этой прямой, а принадлежат этой прямой те точки, чьи координаты являются решением данного уравнения.
Пример. Построить прямую
Решение.
Например, возьмем , тогда:
Откуда получаем:
Т. е. точка принадлежит прямой (см.
рис. 1).
Рис. 1. Иллюстрация к примеру
Найдем вторую точку. Возьмем , тогда:
Откуда получаем:
Т. е. точка принадлежит прямой (см. рис. 2).
Рис. 2. Иллюстрация к примеру
Отмечаем две эти точки на координатной плоскости и проводим прямую (см. рис. 3).
Рис. 3. Иллюстрация к примеру
Нахождение уравнения прямой
Но существует и обратная задача. Нужно выписать уравнение прямой по имеющейся о ней информации. Самый простой вариант – известны координаты двух точек, через которые она проходит.
Задача 1. Найти уравнение прямой, проходящей через две точки и .
Решение
Мы можем эту прямую начертить (см. рис. 4), но нам нужно решить другую задачу – найти ее уравнение.
Рис. 4. Иллюстрация к задаче 1
Самый простой способ найти уравнение прямой – подставить координаты точек в уравнение прямой и найти неизвестные коэффициенты.
Получим систему уравнений:
Получается два уравнения с тремя неизвестными. Выразим две переменные через третью:
Получаем уравнение прямой:
Мы можем сократить обе части этого уравнения на и умножить на :
Несложно убедиться, что координаты точек и удовлетворяют этому уравнению.
Ответ: .
Нахождение уравнения прямой при помощи векторов
Но получить таким образом уравнение прямой, проходящей через две заданные точки, в общем виде довольно сложно. Попробуем сделать это другим способом.
Отметим на прямой точку с неизвестными нам координатами (см. рис. 5).
Рис. 5. Отмеченная на прямой произвольная точка с координатами
Если мы придумаем какое-то свойство, которое однозначно отделит все точки (лежащие на нашей прямой) от остальных точек (не лежащих на прямой), то сможем получить уравнение прямой.
Очевидно, что если лежит на прямой, то векторы и коллинеарны.
Наоборот, если точка не лежит на прямой, то эти векторы неколлинеарны. Вот мы и нашли необходимый и достаточный признак того, что точка лежит на прямой, – коллинеарность векторов и .
Вспомним, что векторы коллинеарны, если их координаты пропорциональны:
Получаем:
Условие коллинеарности приобретает следующий вид:
Это уравнение и задает нашу прямую. На первый взгляд, не очень похоже на то, что мы получили ранее:
Умножим обе части полученного уравнения на , перенесем все в одну сторону, получим:
Уравнение прямой, проходящей через две заданные точки
Обобщим полученный результат: запишем уравнение прямой , проходящей через две точки и (см. рис. 6).
Рис. 6. Прямая , проходящая через точки и
Выбираем произвольную точку прямой . Находим координаты векторов и (см. рис. 7):
Рис. 7. Векторы и
Тот факт, что точка принадлежит прямой, эквивалентен тому, что эти два вектора коллинеарны, что означает, в свою очередь, пропорциональность их координат:
Это и есть уравнение прямой, проходящей через две заданные точки.
Его можно преобразовать в стандартный вид. Но выглядеть оно станет сложнее, поэтому обычно общий вид оставляют таким. А если у нас есть конкретные координаты точек и , то от этого вида имеет смысл переходить к стандартному виду уравнения.
Уравнение прямой, проходящей через заданную точку параллельно заданному вектору
Попутно мы получили еще одно уравнение прямой. Действительно, пусть мы не знаем координаты второй точки, которая лежит на прямой. Но знаем, что прямая параллельна вектору (см. рис. 8).
Рис. 8. Прямая , проходящая через точку , параллельна вектору
Можно использовать ту же схему – возьмем произвольную точку , принадлежащую прямой (см. рис. 9).
Рис. 9. Отмеченная на прямой произвольная точка
Точка принадлежит прямой тогда и только тогда, когда векторы и коллинеарны. Получаем:
Это и есть уравнение прямой, проходящей через заданную точку параллельно заданному вектору.
Ноль в знаменателе в уравнении прямой, проходящей через две заданные точки
Бывают ситуации, когда мы не можем воспользоваться полученной формулой.
Задача 2. Составить уравнение прямой, проходящей через точки и .
Решение.
Если мы попытаемся подставить в нашу формулу координаты точек и , то получим в одном из знаменателей ноль:
Мы получили в знаменателе ноль. Что же делать?
Можно просто не использовать формулу, а заметить, что прямая проходит через две точки с ординатами . Т. е. прямая параллельна оси , и ее уравнение будет иметь вид (см. рис. 10):
Рис. 10. Иллюстрация к задаче 2
А можно переписать уравнение в другом виде по принципу пропорции:
Откуда получается то же самое уравнение:
Ответ: .
Составим уравнение прямой, проходящей через точки и .
Теперь у этих точек одинаковая координата х, точки расположены одна над другой. И прямая, которая через них проходит, вертикальная. У всех точек будет одинаковая абсцисса: . Уравнение прямой (см. рис. 11):
Рис. 11. График прямой
Перпендикулярные векторы
Мы использовали эквивалентное определение коллинеарности векторов – пропорциональность их координат:
Т.
е. по координатам векторов можно легко определить, коллинеарны они или нет.
А можно ли так же легко по координатам векторов понять, перпендикулярны ли они?
Да, если использовать тот факт, что скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда векторы перпендикулярны друг другу (см. рис. 12):
Рис. 12. Перпендикулярные векторы
Задача 3. Доказать, что четырехугольник , вершины которого имеют координаты
является квадратом.
Доказательство
Изобразим точки на координатной плоскости (см. рис. 13). В самом деле, похоже, что это квадрат.
Рис. 13. Иллюстрация к задаче 3
Чтобы доказать, что четырехугольник – квадрат, есть разные способы. Можно воспользоваться определением и показать, что все стороны равны и все углы прямые.
Можно воспользоваться свойствами диагоналей. Т. к. квадрат – это ромб и прямоугольник, то его диагонали точкой пересечения делятся пополам, равны друг другу и перпендикулярны.
Пойдем по первому пути. Покажем равенство длин и перпендикулярность соседних векторов, заданных сторонами четырехугольника.
Для начала посчитаем координаты этих четырех векторов:
Векторы и имеют одинаковые координаты. Значит, они равны. А это означает, что они параллельны и их длины равны друг другу. Это уже означает, что наш четырехугольник – параллелограмм.
Мы видим, что и у второй пары векторов и совпадают координаты, векторы равны.
Чтобы показать, что параллелограмм является квадратом, нужно доказать равенство одной пары соседних сторон (получится ромб) и показать, что один угол прямой, тогда все остальные тоже будут прямыми.
Посчитаем длину вектора :
Посчитаем длину вектора :
Итак, соседние стороны равны: , значит, все стороны равны и четырехугольник – ромб.
Осталось доказать перпендикулярность пары векторов. Возьмем те же векторы и . Найдем их скалярное произведение – для этого умножаем попарно их координаты и результаты складываем:
Т.
к. оба вектора ненулевые, то равенство нулю их скалярного произведения означает только одно: они перпендикулярны:
Ромб с прямым углом – это квадрат.
Доказано.
Нахождение угла между векторами
Итак, мы умеем определять, параллельны ли векторы, перпендикулярны ли они. А как найти угол между векторами? Вспомним, что в формуле для скалярного произведения фигурирует косинус угла между векторами. Попробуем этим воспользоваться:
Откуда:
Теперь алгоритм нахождения косинуса угла между векторами ясен: нужно вычислить скалярное произведение векторов и их длины. При этом обратите внимание, что знак скалярного произведения определяет вид угла: если скалярное произведение положительно, то угол острый; если отрицательно, то угол – тупой (см. рис. 14).
Рис. 14. Если скалярное произведение положительно, то угол острый; если отрицательно, то угол тупой
Можно, конечно, получить формулу для косинуса в координатах, но помнить ее не обязательно:
При необходимости, если вы помните, как вычислять скалярное произведение и длину вектора, вы всегда сможете ее вывести.
Задача 4. Найти угол между векторами .
Решение.
Найдем скалярное произведение векторов:
Найдем длины векторов:
Тогда косинус угла:
А сам угол:
Ответ: .
Нормальный вектор
Рассмотрим еще одну задачу, связанную с уравнением прямой и углами между векторами.
Задача 5. Составить уравнение прямой, проходящей через точку перпендикулярно вектору (см. рис. 15).
Рис. 15. Иллюстрация к задаче 5
Решение.
Используем уже известный нам алгоритм. Выберем произвольную точку на прямой. Условие ее принадлежности прямой:
Или, как мы знаем, эквивалентное условие:
Запишем это условие в координатах:
Раскроем скобки и получим:
Ответ: .
Заметили, что координаты перпендикулярного вектора (он еще называется нормальным вектором или вектором нормали) стали коэффициентами в уравнении прямой при и ? Это неслучайное совпадение.
В общем виде ситуация такова: уравнение прямой, проходящей через точку перпендикулярно вектору имеет вид:
Если раскрыть скобки, то координаты нормального вектора становятся коэффициентами при и в общем уравнении прямой.
Это можно использовать и в обратную сторону: для прямой, заданной своим общим уравнением, легко найти нормальный вектор. Например, прямая имеет нормальный вектор с координатами:
Связь координат нормального вектора с уравнением прямой
Понятие нормального вектора и связь его координат с уравнением прямой приводит к очень простому, но важному следствию.
Задача 6. Доказать параллельность прямых (см. рис. 16):
Рис. 16. Иллюстрация к задаче 6
Доказательство.
Коэффициенты при и в уравнениях задают нормальные векторы к этим прямым и (см. рис. 17).
Рис. 17. Иллюстрация к задаче 6
Но координаты этих векторов пропорциональны:
Следовательно, нормальные векторы параллельны.
Но тогда перпендикулярные им прямые тоже параллельны друг другу:
Итак, параллельность прямых однозначно определяется пропорциональностью коэффициентов при и . Свободный коэффициент на это никак не влияет.
Доказано.
Скалярное произведение векторов
Рассмотрим еще несколько задач, связанных со скалярным произведением векторов.
Задача 7. Вычислить и , если , , .
Решение.
Если нарисовать рисунок (см. рис. 18) то становится понятно, что нас просят найти длины диагоналей параллелограмма, стороны которого равны и , а острый угол равен . Это можно сделать с помощью, например, теоремы косинусов (можете проверить самостоятельно, что получится тот же самый результат).
Рис. 18. Иллюстрация к задаче 7
Но мы рассмотрим стандартный и универсальный алгебраический метод решения задач такого типа. А именно с использованием того факта, что:
Получим:
Но правую часть мы можем вычислить, т.
к. она равна:
Получаем, что:
Значит:
Несложно получить, что:
Откуда:
Ответ: .
Задача 8. При каком значении векторы и перпендикулярны, если , , ?
Решение.
Опять же ничего нового здесь нет. Мы знаем эквивалентное условие перпендикулярности векторов:
Или:
Откуда получаем, что:
Ответ: .
Решение геометрической задачи с использованием векторов и скалярного произведения
Рассмотрим обычную, на первый взгляд, геометрическую задачу, которую можно решить с использованием векторов и скалярного произведения.
Задача 9. Найти угол, лежащий против основания равнобедренного треугольника, если медианы, проведенные к боковым сторонам, взаимно перпендикулярны.
Решение
Рассмотрим равнобедренный треугольник , у которого , и – медианы к боковым сторонам (см. рис. 19).
Рис.
19. Иллюстрация к задаче 9
Введем обозначения:
Тогда:
Мы выразили через базисные векторы те векторы, о которых знаем важный факт: они перпендикулярны, т. е. их скалярное произведение равно :
Раскрываем скобки:
Тогда:
Ответ: .
Заключение
Такие инструменты, как векторы, координаты, действия с векторами, позволяют решать как новые задачи, так и прежние геометрические, но новыми методами – методами алгебры.
Список литературы
- Александров А.Д., Вернер А.Л., Рыжик В.И. Геометрия, 9 класс. Учебник. – М.: «Просвещение», 2017.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В./Под ред. Садовничего В.А. Геометрия, 9 класс. Учебник. – М.: «Просвещение», 2018.
- Мерзляк А.Г., Полонский В.Б., Якир М.С., Геометрия, 9 класс. Учебник. – М.: издательский центр «ВЕНТАНА-ГРАФ», 2018.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал cleverstudents.
ru (Источник) - Интернет-портал yaklass.ru (Источник)
- Интернет-портал mathprofi.ru (Источник)
ru (Источник)
Домашнее задание
1. Доказать, что четырехугольник является параллелограммом, если .
2. Найти угол между векторами и .
3. С помощью скалярного произведения доказать, что диагонали ромба взаимно перпендикулярны.
Решение задач с помощью векторов
Возраст от 16 до 18 лет
Статья Элисон Киддл
Опубликовано в 2014 г.
Многие студенты часто не хотят решать вопросы, используя векторы. Я думаю, это отчасти потому, что часто векторы не преподаются до тех пор, пока не пройдет школьный курс математики, поэтому они незнакомы. Эта короткая статья направлена на то, чтобы осветить некоторые из мощных методов, которые можно использовать для решения задач, связанных с векторами, и побудить вас попробовать такие задачи, чтобы лучше ознакомиться с ними.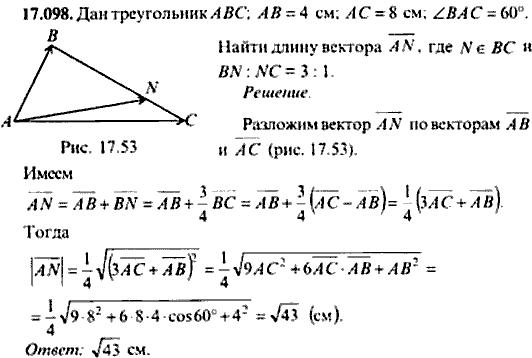
с векторными свойствами и приложениями.
Так что же такое векторы? Когда мы впервые сталкиваемся с ними, это часто происходит в контексте преобразований — перевод может быть выражен как вектор, сообщающий нам, насколько далеко что-то перемещается вправо (или влево) и вверх (или вниз). Путаница может возникнуть, когда мы сталкиваемся с векторами, используемыми для указания абсолютного положения относительно начала координат, а также для указания направления. Тогда нам могут сообщить, что вектор — это «просто» величина, которая имеет как величину, так и направление (в отличие от скаляра, который имеет только величину).
Диаграммы
Полезно выделить некоторые из этих идей о векторах, чтобы понять смысл вещей. Для меня диаграммы значительно упрощают понимание того, что происходит — я могу представить вектор положения как точку на диаграмме с отрезком линии, идущим из начала координат. Векторы направления просто становятся отрезками, соединенными с другими векторами, с полезной стрелкой, напоминающей мне, что $\mathbf{a}$
и $\mathbf{-a}$ направлены в противоположные стороны! Иногда полезно рисовать линии, параллельные и перпендикулярные моим координатным осям, чтобы я мог понять компоненты x и y вектора.
При наличии векторной задачи быстрый набросок может помочь вам увидеть, что происходит, а процесс переноса проблемы из письменного текста в диаграмму часто может дать вам некоторые идеи, которые помогут вам найти решение. Начните с решения векторных задач в двух измерениях — так легче рисовать диаграммы, — а затем переходите к трехмерным. (Для четырех и более измерений становится более трудно представить!)
Что делать, если вы застряли
Вот краткий контрольный список идей, о которых стоит подумать, если вы застряли на векторном вопросе, и рисование диаграммы не помогло.
Параллельные векторы
Знаете ли вы о каких-либо параллельных прямых? Векторные вопросы часто могут касаться геометрических фигур, таких как трапеции, ромбы или параллелограммы. Если два вектора параллельны, очень полезно выразить один через другой. Если $\mathbf{a}$ и $\mathbf{b}$ параллельны, попробуйте написать $\mathbf{b}=k\ mathbf{a}$ для некоторой константы $k$.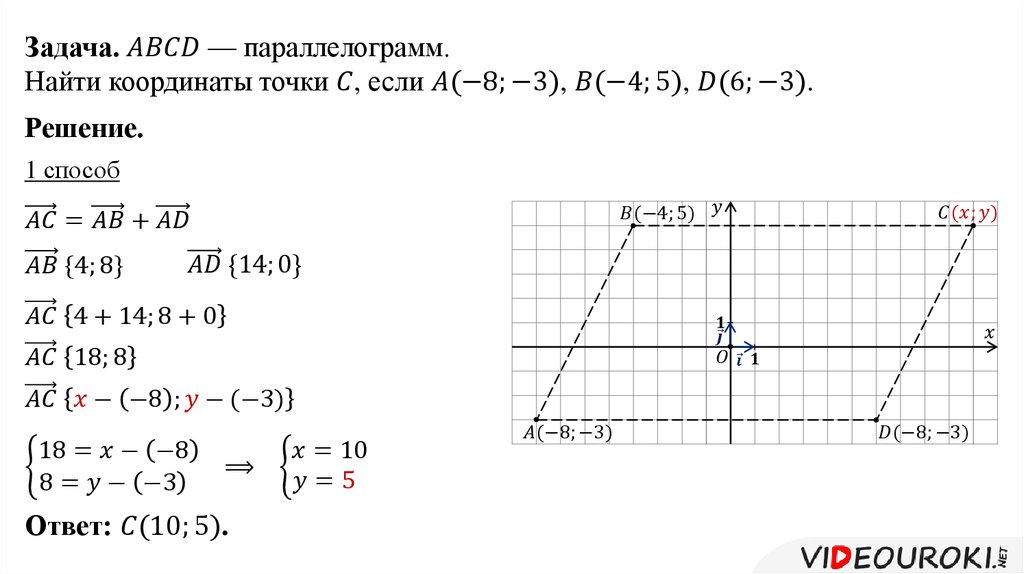
Величина и направление
Некоторые векторные задачи включают векторную функцию, которая, например, сообщает вам, как положение объекта изменяется во времени. Выяснение того, как величина и направление изменяются с течением времени, может помочь вам представить ситуацию.
Векторное уравнение прямой
Некоторые студенты пугаются векторного уравнения прямой, когда впервые сталкиваются с ним. Мы очень привыкли выражать линии с помощью декартовой геометрии в форме $y=mx+c$ и других вариантах. Векторное уравнение линии на самом деле не сложнее, это просто случай, когда к нему нужно привыкнуть. Проще говоря, линии представляются с помощью векторов путем указания точки на линии с позицией.
вектор, а затем с помощью вектора направления указать направление линии. Точно так же, как $y=mx+c$ задает прямую, проходящую через $(0,c)$ и имеющую градиент $m$, векторное уравнение $\mathbf{r}=\mathbf{a}+\lambda \mathbf{b}$ задает прямую, проходящую через точку с вектором положения $\mathbf{a}$ в направлении $\mathbf{b}$.
Последнее слово в обозначениях; в типе векторы обозначены полужирным шрифтом . В почерке принято подчеркивать векторы и оставлять скаляры (такие как константы $k$ и $\lambda$ выше) без подчеркивания. Греческие буквы $\lambda$ и $\mu$ часто используются в качестве констант в векторных уравнениях. , так почему бы не взять за привычку использовать их для себя?
Точки, векторы и функции Как решить математическую задачу
За три простых шага мы можем решить любую математическую задачу.И за три простых платежа..
Мы не пытаемся продать вам набор ножей, которые никогда не затупятся, или настольную духовку, в которой можно одновременно приготовить яйца, бекон и тосты. По крайней мере, мы можем продать основные шаги решения любой математической задачи.
Решение математической задачи состоит из трех шагов.
- Выясните, в чем проблема.
- Решите проблему.
- Проверьте ответ.
Пример задачи
Определить все точки, в которых график параметрической функции x ( T ) = -5 + 5 T , Y ( T ) = 4 T и график параметрической функции x ( T ) = 2 T + 1, y ( t )= t 2 пересекаются.
Округлите до 5 цифр и воспользуйтесь калькулятором.
- Выясните, в чем проблема.
Проблема заключается в запросе координат всех точек ( x , y ), которые встречаются на обоих графиках.
Важно: Если ( x , y ) встречается на обоих графиках, это, вероятно, является результатом разных значений параметра для каждого графика.
Мы могли бы приравнять уравнения x и решить
-5 + 5 t = 2 t + 1
для t , но это будет работать только при том же значении t906. генерирует точку для обоих графиков. Вероятно, это не так.
Вместо этого точка пересечения возникает, когда мы ставим какое-то значение t в первый набор уравнений и некоторое значение s во второй набор уравнений и найдите ту же точку ( x , y ).
Написание этого в символах, мы хотим
x = -5 + 5 T = 2 S + 1 и Y = 4 T = S 2 .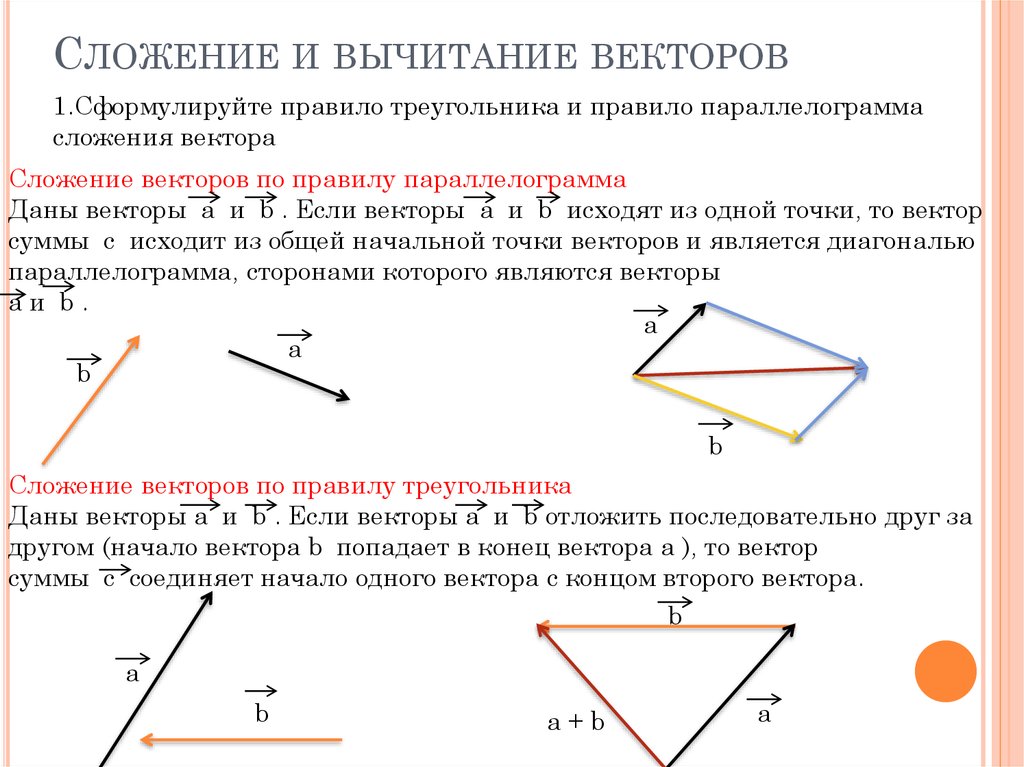
Отбрасывая x и y , мы хотим -5 + 5 t = 2 s + 1 и 4 t = с 2 .
Это система двух уравнений с двумя неизвестными, которую мы умеем решать.
После нахождения s и t нам нужно найти координаты точки или точек ( x , y ), которые встречаются на обоих графиках.
- Решить проблему.
Нужно решить систему
-5 + 5 t = 2 с + 1
4 t = с 2 .
Решите второе уравнение для t :
Затем подставьте t в первое уравнение:
Это квадратное уравнение. Приведите его в порядок, чтобы мы могли использовать квадратичную формулу для его решения.
Нам не нужно было делать последний шаг, где мы умножали на 4, но проще использовать квадратную формулу, когда коэффициенты представляют собой целые числа, а не дроби.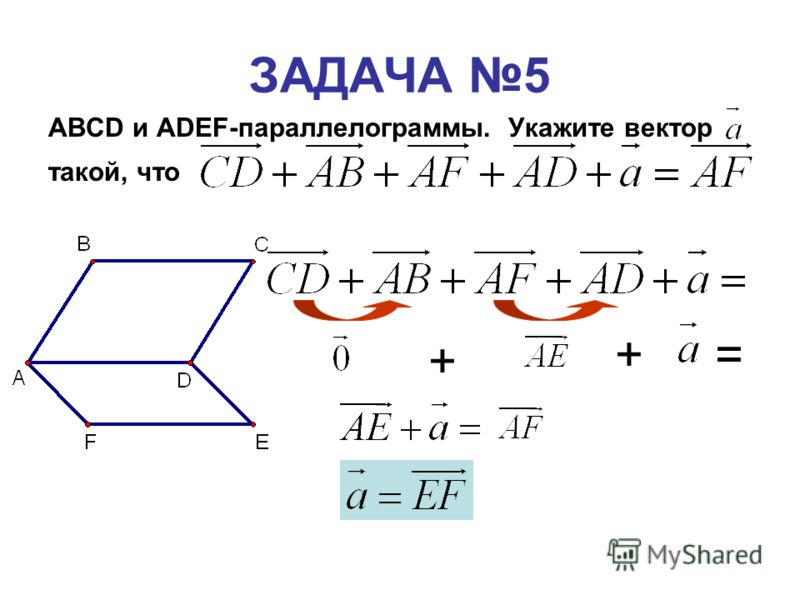
Квадратичная формула говорит
Здесь есть два значения s , которые нам нужно использовать. Чтобы найти соответствующие значения x и y , мы используем второй набор уравнений.
Когда
мы имеем
и
Одна точка пересечения приблизительно равна
(7,26476, 9,81181).
Когда
у нас есть
и
Другая точка пересечения примерно
(-2,06476, 2,34819).
- Проверьте ответ.
Для начала нарисуйте два набора уравнений.
Похоже, они дважды сталкиваются друг с другом, один раз где-то в районе (-2, 2) и один раз где-то в районе (7, 10).
Это говорит нам о том, что мы нашли правильное количество точек, и найденные нами числа кажутся правильными. На практике это, вероятно, все проверки, которые мы могли бы сделать.
Теперь мы покажем, как проверить ответы на самом деле.
Мы найдем значение t , которое соответствует каждому значению s , и убедимся, что мы нашли правильную точку, когда поместим это значение t в первый набор параметрических уравнений.