В выражении a,b,c – простые числа, y не равно нулю, вместо знака ˂ может стоять любой знак, выражающий неравенство.
Во многих источниках по математике можно встретить квадратные неравенства под наименованием «неравенства второй степени». Это легко пояснить. Левая часть приведенного выражения присутствует многочлен второй степени в виде квадратного трехчлена:
a×y2+b×y+c
Многие называют такие неравенства квадратичными, но это неправильно, так как квадратичными в математике принято называть функции. Они имеют вид:
\[x=a \times y 2+b \times y+c\]
Чтобы можно было легко понять разницу, лучше на примере рассмотреть, что такое квадратные неравенства системы уравнений.
Пример:
3×y2+1×y+14>0
В приведенном примере в качества a цифра 3, в качестве b число 1, в качестве c число 14.
В качестве простых чисел могут быть и положительные, и отрицательные числа, дроби, и т.
Как решать квадратные неравенства
Есть несколько методов решения неравенств квадратных уравнений:
- Графический.
- Методом интервалов.
- Посредством выделения квадратного двучлена из левой части выражения.
Рассмотрим подробнее особенности применения каждого метода.
Графический метод решения квадратных неравенств
Метод заключается в выполнении анализа и изучения графика квадратичной функции.
x=a×y2+b×y+c для квадратных неравенств типа a×y2+b×y+c<0.
В качестве решения квадратного неравенства выступают интервалы, на которых эта функция принимает или положительное, или отрицательное значение.
Метод интервалов
Еще один метод, как решить квадратное неравенство – метод интервалов, при условии, что в выражении только одна переменная. Этот способ актуален и используется для решения практически всех видов неравенств, а не только квадратных. Способ состоит в том, чтобы определить знаки интервалов, на которые делится координатная ось нулями трехчлена:
a×y2+b×y+c,
если таковые имеют место быть.
Для квадратного неравенства, имеющего вид a×y2+b×y+c<0, ответом будут интервалы со знаком минуса.
Для квадратного неравенства, имеющего вид a×y2+b×y+c>0, ответом будут интервалы со знаком плюс.
Если решение квадратных неравенств предполагает поиск ответа нестрогого неравенства, то решением будет интервал, на котором расположены точки, идентичные нулям трехчлена.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Выделение квадрата двучлена
Чтобы выделить квадрат двучлена из левой части выражения, потребуется выполнить равнозначное преобразование, после чего можно будет решать равносильное неравенство, имеющее вид:
\[(x-y) 2<z\]
Вместо знака ˂ может встречаться любой другой, кроме знака равенства (>,≥, ≤).
В неравенствах такого плана y и z – любые числовые значения.
Неравенства, которые сводятся к квадратным
К квадратному можно привести любое другое неравенство с помощью равносильного преобразования.
{<} 3\].
Этот метод решения назван методом интервалом из-за того, что при решении мы рассматривали интервалы между полученными значениями.
Квадратные неравенства по алгебре в 9 классе, урок и презентация, способы, методы и примеры решения
Дата публикации: .
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Скачать:Квадратные неравенства (PPTX)
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 9 класса
Электронное учебное пособие «Понятная геометрия» для 7-9 классов
Квадратные неравенства
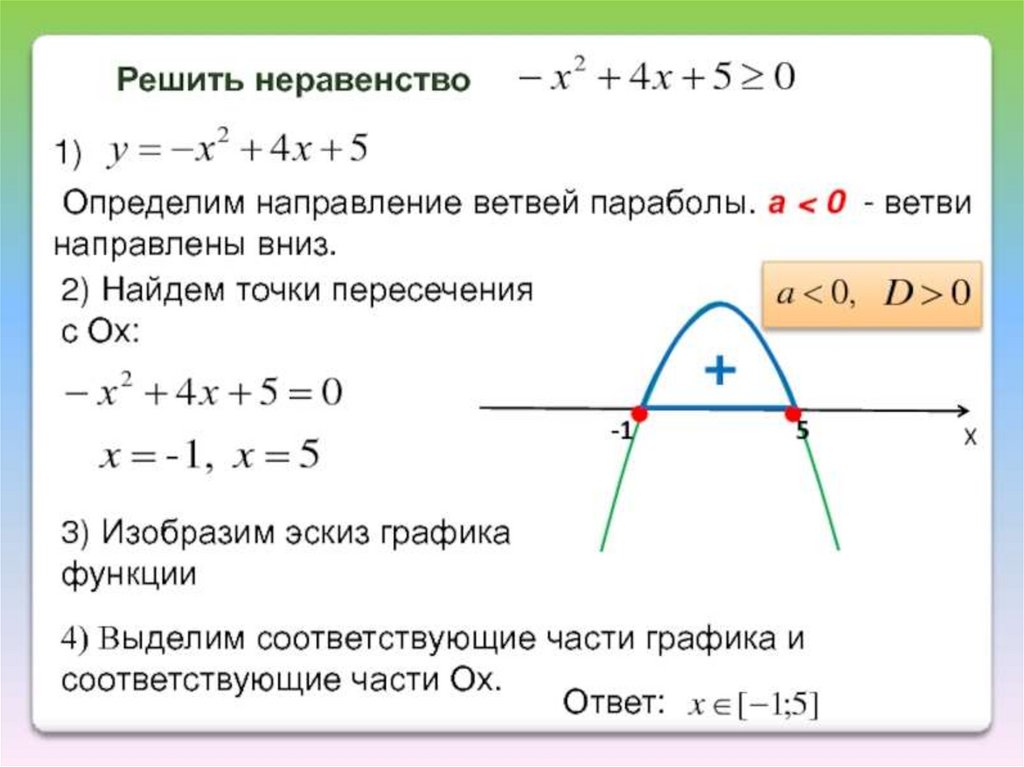
Ребята, мы уже умеем решать квадратные уравнения. Теперь давайте научимся решать и квадратные неравенства.
Квадратным неравенством называется неравенство вот такого вида:
$ax^2+bx+c>0$.
2-5x+2>0$.
OpenAlgebra.com: квадратные неравенства
Квадратные неравенства можно решить несколькими способами. Мы сосредоточимся на их решении, сначала построив график, а затем используя таблицы знаков. Важно понять, как выглядят решения этих неравенств, прежде чем изучать быстрый и простой метод их решения.
Плейлист «Решение квадратных неравенств» на YouTube
Метод 1: решение с помощью графика
Шаг 1 : Поместите неравенство в стандартную форму с нулем на одной стороне.
Шаг 2 : Нарисуйте квадратное уравнение.
Шаг 3 : Закрасьте значения x, которые дают желаемые результаты.
Шаг 4 : Преобразуйте штриховку в интервальную нотацию.
Решите и выразите набор решений в интервальной нотации .
В приведенном выше примере мы заштриховали значения x , для которых график находился выше оси x .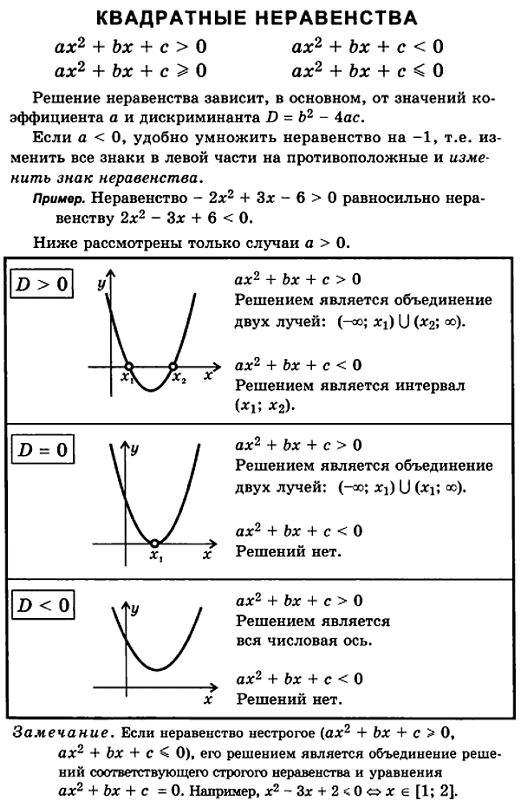
Если проблема попросила нас решить
или для того, что x -значений квадратично меньше или равно 0, тогда решением были бы все x -значения в интервале [1, 3] — x -значения, где график ниже ось х. Обратите внимание, что числа на оси x x = 1 и x = 3 разделяют положительные и отрицательные y -значения на графике, они являются точками пересечения x . Точки пересечения x или нули полинома называются критическими числами.
Решить графически .
Не забудьте использовать открытые точки для строгих неравенств < или > и закрытые точки для включающих неравенств.
Часто довольно утомительно и сложно отображать каждое неравенство в виде графика при попытке их решения. Есть более короткий метод, и он включает в себя таблицы знаков. Идея состоит в том, чтобы найти критические числа, значения x , где значения y могут измениться с положительного на отрицательное, и создать диаграмму знаков, чтобы определить, какие интервалы заштриховать на x — ось.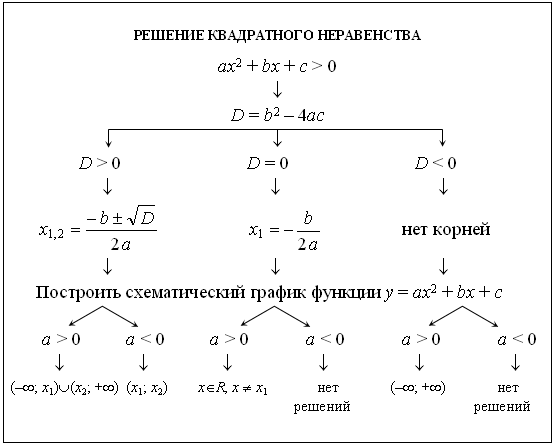
Способ 2: Решите с помощью таблиц знаков.
Шаг 1 : Приведите неравенство к стандартной форме с нулем на одной стороне.
Шаг 2: Найдите критические числа (для квадратичных вычислений — точки пересечения x ).
Шаг 4 : Используйте таблицу знаков, чтобы ответить на вопрос.
Решите и нарисуйте набор решений .
Найдите критические числа, приравняв квадратное выражение к нулю, и решите.
Определите результаты + или — в каждом интервале, ограниченном критическими числами, путем проверки значений в каждом интервале.
Используйте таблицу знаков, чтобы ответить на вопрос. В этом случае мы ищем значения x , которые дают отрицательные результаты, на что указывает неравенство <0 «меньше нуля» в исходном вопросе.
При проверке значений в интервалах, созданных критическими числами, фактическое значение не обязательно, нас интересует только его знак.
Знак + или — будет одинаковым для любого значения в интервале, поэтому при тестировании вы можете выбрать любое число в пределах интервала.
Решить и построить график набора решений
.
Совет : Сэкономьте время и просто определите, является ли соответствующее значение y положительным или отрицательным. Если полиномиальные факторы, то используйте факторы, чтобы определить, будет ли интервал давать положительные или отрицательные и -значения. Нет необходимости искать реальные значения.
Видео YouTube :
Графические функции — Решение квадратного неравенства
спросил
Изменено 8 лет, 10 месяцев назад
Просмотрено 1к раз 92>0$$
Мой ответ: $2 < x < 7$
Хотя я знаю, что мой ответ правильный, я хочу знать, как я могу его решить и как его можно представить графически.